The Effect of End Constraints on Protein Loop Kinematics

Abstract

Despite the prevalent involvement of loops in function little is known about how the constraining of end groups influences their kinematics. Using a linear inverse-kinematics approach and assuming fixed bond lengths, bond angles, and peptide bond torsions, as well as ignoring molecular interactions to assess the effect of the end-constraint only, it is shown that the constraint creates a closed surface in torsion angle space. For pentapeptides, the constraint gives rise to inaccessible regions in a Ramachandran plot. This complex and tightly curved surface produces interesting effects that may play a functional role. For example, a small change in one torsion angle can radically change the behavior of the whole loop. The constraint also produces long-range correlations, and structures exist where the correlation coefficient is 1.0 or −1.0 between rotations about bonds separated by >30 Å. Another application allows some torsion angles to be targeted to specified values while others are constrained. When this application was used on key torsions in lactate dehydrogenase, it was found that the functional loop first folds forward and then moves sideways. For horse liver alcohol dehydrogenase, it was confirmed that the functional loop's Pro-Pro motif creates a rigid arm in an NAD-activated switch for domain closure.

Introduction

The prevalent role of loops in protein function is due to their flexibility and location on the surface. Loops bind partner proteins in protein-protein interactions (1,2), bind DNA in DNA-binding proteins (3), bind antigens in immunoglobulins (4), and bind ligands in enzymes such as in horse liver alcohol dehydrogenase (5), lactate dehydrogenase (6), and serine proteases (7). A loop on the surface of a protein is characterized by being fixed at both ends where the polypeptide emerges from the protein core. This constraint will greatly influence the dynamical behavior of the loop as changes in torsion angles at one location will be compensated for by changes in torsion angles at other locations such that the two end groups remain fixed relative to each other. It is reasonable to expect, therefore, that the constraint will cause correlations in torsion angle changes along the chain. Despite the important role surface loops play in protein function, the nature of loop dynamics has remained largely unexplored. However, loops receive considerable attention from the homology modeling community (8,9), because for the very same reasons that they typically have a role in protein function—namely, their flexibility and location on the surface—they are found to be variable in composition and length among homologous proteins. Methods developed to model loops of specified length that bridge two disconnected residues have quite a long history and are related to the method presented in this article. The problem, referred to as the local deformation problem, was solved originally using an ab initio method for the case of rigid bond lengths and bond angles by Gō and Scheraga (10). Determination of structures with N torsions that span two end groups involves the variation of N − 6 torsion angles, leaving six torsion angles to be found by solving a set of equations numerically (10). In this way, various structures with more than six free torsions can be generated. The method was extended by Bruccoleri and Karplus to allow for bond angle variation (11). The problem of placing the end of a loop at a desired location and orientation by rotation about torsion axes has an analogy in robotics where rotatable joints move an end effector. The determination of the angles at the rotatable joints to position the end effector at a desired location and orientation is referred to as inverse kinematics, and techniques used in robotics to solve this problem have also been applied to the protein loop modeling problem (12–14). In robotics, the most effective way found to solve this problem for six rotatable joints results in determination of the real roots of a polynomial of degree 16 (15), which means that the maximum number of different solutions is 16. In practice, the number of solutions is case-dependent, but for proteins the number of solutions seems to be limited to 10 (13), although for a slightly idealized case, where C_α-C and N- C_α on the same peptide unit are parallel, it has been proven that for some orientations and positions of the end group, there are indeed 16 different solutions (16).

Iterative methods have also been applied to this problem, most notably the random tweak method (17) and, more recently, cyclic coordinate descent (18). In the former method, random conformations are generated that are iteratively changed to satisfy the distance constraints imposed by the requirement that the loop span the start and end group. In the latter, each torsion angle is changed sequentially along the chain such that the distances between end-group atoms in their current positions and their target positions are reduced. Cyclic coordinate descent has been applied to model not only fluctuations within loops but also fluctuations in whole proteins (19).

The method presented here is also iterative, as it is based on a linear approximation where the rotation and displacement of the end group of a loop relative to those of the beginning group are expressed as a linear combination of small torsion angle changes along the loop. In contrast to the methods described above, which are normally applied to model possible loop structures in what has been termed the minifolding problem, our method lends itself more naturally to understanding the effect of fixing end groups on the dynamics of a loop of known structure. In our formulation, given a loop structure, nearby structures can be determined by simply finding solutions to a homogeneous system of six linear equations in N unknown torsional displacements. It is applied iteratively to find structures far from the starting structure. The method is equivalent to a method from robotics (20) that has been applied to model loops into electron density maps from x-ray crystallography (21) and to determine local deformations after an initial loop structure has been modeled (22). The method is used to understand the nature of the constraint surface in torsion angle space, to investigate the structural dependence of correlations along the chain, and to generate possible intervening structures on a functional path between two known structures.

Methods

Here, we show how to write down a linear approximation for the displacement and rotation of a coordinate system at the end of a loop or segment in the coordinate system at the beginning of the segment due to torsion angle variation with fixed bond lengths and angles. Although related methods have been used in robotics (20), the method presented here is different in that it is based on a pair of vector equations. The segment considered extends from the C_α of residue 1 to the C_α of residue N_res, covering $N_{\text{res}}-1$ peptide units. The number of bonds, $N_{\text{b}}=3N_{\text{res}}-3$, and the number of ϕ,ψ angles, $N_{\varphi \psi }=2\left(N_{\text{res}}-1\right)$. The case of $N_{\text{res}}=4$ for which $N_{\varphi \psi }=6$ is shown in Fig. 1. Note that the atoms are numbered from 0 and the bonds (and thus the bond length index and torsion angle index) are given the number of the backbone atom on the C-terminal side of the bond (see Fig. 1). Some previous studies have considered the segment to extend from the N atom of residue 1 to the C atom of residue $N_{\text{res}}$ which means that for $N_{\text{res}}=3$, there are six ϕ and ψ angles.

Figure 1.

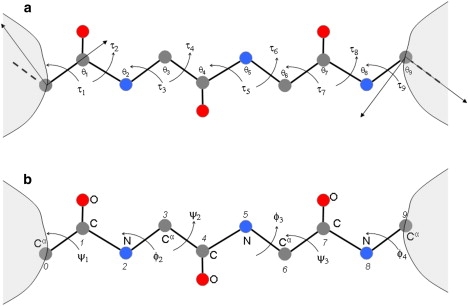
The segment with six ϕ,ψ angles extends from the C_α of residue 1 to the C^α of residue 4 ($N_{\text{res}}=4$), covering three peptide units. (a) Definition of torsion and bond angle numbering showing the coordinate system on atom 0 and atom 9 (atom numbering as defined in b). Bonds, and consequently bond lengths and torsion angles, are indexed with the number of the atom on the C-terminal side of the bond. The torsions shown determine the relative position and orientation of the coordinate systems and consequently everything flanking atoms 0 and 9. The x and y axes of the coordinate systems on the first and last atoms are shown. (b) Atom numbering and ϕ,ψ angle numbering.

Assuming fixed bond lengths and bond angles, in the linear approximation, the rotation vector, $\mathbf{\delta }\mathbf{\varphi }$ (magnitude is the angle of rotation and direction is along the axis of rotation given by the righthand rule) for the rotation of the polypeptide on the C-terminal flank of the segment relative to the polypeptide on the N-terminal flank, due to torsion angle changes along the $N_{\text{b}}$ bonds of the segment is

$$\mathbf{\delta }\mathbf{\varphi }=\sum _{i=1}^{N_{\text{b}}}\delta {\tau }_i{\mathbf{n}}_i,$$ (1)

where $\delta {\tau }_i$ is the change in the ith torsion and ${\mathbf{n}}_i$ is the unit vector along the ith bond from atom i − 1 to i, the torsion axis direction. The linear approximation for the displacement vector, $\mathbf{\delta }\mathbf{d}$, of the end atom relative to the first is given as

$$\mathbf{\delta }\mathbf{d}=\sum _{i=1}^{N_{\text{b}}-1}\delta {\tau }_i{\mathbf{n}}_i\times \left(\sum _{j=i+1}^{N_{\text{b}}}{\text{r}}_j{\mathbf{n}}_j\right)=\sum _{i=1}^{N_{\text{b}}-1}\delta {\tau }_i{\mathbf{D}}_i,$$ (2)

where ${\mathbf{D}}_i={\mathbf{n}}_i\times \left(\sum _{j=i+1}^{N_{\text{b}}}{\text{r}}_j{\mathbf{n}}_j\right)$, $r_j$ is the length of the jth bond, $\sum _{j=i+1}^{N_{\text{b}}}{\text{r}}_j{\mathbf{n}}_j$ the displacement vector between atom i and the end atom of the segment, and × denotes the vector product. Thus, each term in Eq. 2 gives the displacement of the end atom due to rotation about each bond, i. On each atom there is a coordinate system as defined by Eyring (23) (see Fig. 1), and in column vector form in the coordinate system on atom 0, the ${\mathbf{n}}_i$ can be written down in terms of bond angles and torsion angles along the segment using (23,24)

$${\mathbf{n}}_i=\prod _{j=1}^{i-1}{\mathbf{A}}_j\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),$$ (3)

where

$${\mathbf{A}}_j=\left(\begin{array}{ccc}-\cos {\theta }_j& -\sin {\theta }_j& 0\\ \sin {\theta }_j\cos {\tau }_j& -\cos {\theta }_j\cos {\tau }_j& -\sin {\tau }_j\\ \sin {\theta }_j\sin {\tau }_j& -\cos {\theta }_j\sin {\tau }_j& \cos {\tau }_j\end{array}\right),$$ (4)

and ${\theta }_j$ and ${\tau }_j$ are the bond angles and torsion angles, respectively. In Eq. 3, the unit vector (1 0 0)^t, where superscript t denotes the transpose, is the unit vector along bond i (the torsion axis of bond i) in the coordinate system on atom i − 1, i.e., it lies directly along the x axis. In Eq. 3, this is transformed to the coordinate system on atom 0 by use of the matrices ${\mathbf{A}}_j$, j = 1, i − 1.

Equation 3 is used to calculate the ${\mathbf{n}}_i$ in column vector form in terms of the coordinate system situated on atom 0. Substitution into Eqs. 1 and 2 leads to a set of linear equations in $\delta {\tau }_i$ for the rotation and displacement at the end of the segment, which can be written as

$$\left(\begin{array}{c}\mathbf{\delta }\mathbf{\varphi }\\ \mathbf{\delta }\mathbf{d}\end{array}\right)=\sum _{i=1}^{N_{\text{b}}}\left(\begin{array}{c}{\mathbf{n}}_i\\ {\mathbf{D}}_i\end{array}\right)\delta {\tau }_i=\left(\begin{array}{cccc}{\mathbf{n}}_1& \mathrm{..}& {\mathbf{n}}_{N_{\text{b}}-1}& {\mathbf{n}}_{N_b}\\ {\mathbf{D}}_1& \mathrm{..}& {\mathbf{D}}_{N_{\text{b}}-1}& \mathbf{0}\end{array}\right)\mathbf{\delta }\mathbf{\tau }=\mathbf{Y}\left(\mathbf{\tau }\right)\mathbf{\delta }\mathbf{\tau },$$ (5)

where ${\mathbf{D}}_{N_{\text{b}}}=\mathbf{0}$ (rotation about the final bond does not displace the end atom), $\mathbf{\delta }\mathbf{\tau }$ is a column vector of $N_{\text{b}}$ torsion angle changes, $\delta {\tau }_i$, τ represents the set of torsion angles,${\tau }_i$, and $\mathbf{Y}\left(\mathbf{\tau }\right)$ is a $6\times N_{\text{b}}$ matrix. $\mathbf{Y}\left(\mathbf{\tau }\right)$ is a function of τ and is dependent on the structure of the segment. $\mathbf{Y}\left(\mathbf{\tau }\right)$ is a Jacobian and is well known in the field of robotics (20), where $\mathbf{\delta }\mathbf{\varphi }$ and $\mathbf{\delta }\mathbf{d}$ correspond to the rotation and displacement of an end effector, and $\mathbf{\delta }\mathbf{\tau }$ corresponds to the angle changes at rotatable joints along the arm of the robot. The method used to derive the Jacobian in the robotics literature is different from the method used here, which we believe is more accessible to the structural biology community. It also has the advantage of giving directly the axis of rotation of the end group. If one wants to constrain the kth torsion angle, then, as one can see from the structure of Eq. 5, the kth column of $\mathbf{Y}\left(\mathbf{\tau }\right)$ and the kth row of $\mathbf{\delta }\mathbf{\tau }$ should be deleted. If, as in many previous studies, peptide torsion angles are fixed, i.e., $\delta \omega$ = 0, then the corresponding columns in $\mathbf{Y}\left(\mathbf{\tau }\right)$ and rows in $\mathbf{\delta }\mathbf{\tau }$ should be deleted. In such a case, $\mathbf{Y}\left(\mathbf{\tau }\right)$ is a $6\times {\text{N}}_{\varphi \psi }$ matrix with $\mathbf{\delta }\mathbf{\tau }={\left(\delta {\psi }_1\delta {\varphi }_2\delta {\psi }_2\delta {\varphi }_3\delta {\psi }_3\dots \delta {\varphi }_{{\text{N}}_{\text{res}}-1}\delta {\psi }_{{\text{N}}_{\text{res}}-1}\delta {\varphi }_{{\text{N}}_{\text{res}}}\right)}^{\text{t}}$.

In this article, we are interested in the situation where the end groups are fixed and its effect on the dynamical behavior of the segment. In this case, $\mathbf{\delta }\mathbf{\varphi }=\mathbf{0}$ and $\mathbf{\delta }\mathbf{d}=\mathbf{0}$. This gives rise to a set of $\mathbf{\delta }{\mathbf{\tau }}_j^0$, j = 1, $N_{\varphi \psi }-r$, that satisfies the condition

$$\mathbf{Y}\left(\mathbf{\tau }\right)\mathbf{\delta }{\mathbf{\tau }}_j^0=\mathbf{0}$$ (6a)

or

$$\mathbf{Y}\left(\mathbf{\tau }\right)\mathbf{\delta }{\mathbf{\tau }}^0=\mathbf{0},$$ (6b)

where $\mathbf{\delta }{\mathbf{\tau }}^0=\left(\begin{array}{ccccc}\mathbf{\delta }{\mathbf{\tau }}_1^0& \mathbf{\delta }{\mathbf{\tau }}_2^0& \mathrm{..}& \mathbf{\delta }{\mathbf{\tau }}_j^0& \begin{array}{cc}\mathrm{..}& \mathbf{\delta }{\mathbf{\tau }}_{{\text{N}}_{\varphi \psi }-r}^0\end{array}\end{array}\right)$ and $r=\text{rank}\left(\mathbf{Y}\left(\mathbf{\tau }\right)\right)$, which for $N_{\varphi \psi }\ge 6$ has a maximum value of 6. The $\mathbf{\delta }{\mathbf{\tau }}_j^0$ can be found from the set of right singular vectors of $\mathbf{Y}\left(\mathbf{\tau }\right)$ determined by performing singular-value decomposition of $\mathbf{Y}\left(\mathbf{\tau }\right)$ for which the MATLAB function Null was used. To find solutions to Eq. 6 when a set of ϕ,ψ angles are constrained then, one need only delete the corresponding columns of $\mathbf{Y}\left(\mathbf{\tau }\right)$. Null-space vectors of the Jacobian have been used in the refinement of protein structures from x-ray crystallography (21) and in determining local deformations once an initial seed structure has been modeled (22).

Correlation along the chain

Orthogonal unit vectors spanning the null space of $\mathbf{Y}\left(\mathbf{\tau }\right)$ can be used to estimate the correlation of torsion angles changes along the chain. If $\delta {\tau }_{lj}^0$ represents the lth component of $\mathbf{\delta }{\mathbf{\tau }}_j^0$ and ${\sigma }_{ij}$ are the elements of a covariance matrix in the null space, i.e., the covariance of the ith and jth null-space modes, then the correlation coefficient between the kth and lth torsions is given by

$$\text{corr}\left(\delta {\tau }_k\delta {\tau }_l\right)=\frac{\sum _{ij}\delta {\tau }_{ki}^0{\sigma }_{ij}\delta {\tau }_{lj}^0}{\sqrt{\sum _{ij}\delta {\tau }_{ki}^0{\sigma }_{ij}\delta {\tau }_{kj}^0\sum _{ij}\delta {\tau }_{li}^0{\sigma }_{ij}\delta {\tau }_{lj}^0}}\text{.}$$ (7)

Since we are interested in long-range correlation, corr($\delta {\tau }_1\delta {\tau }_{N_{\varphi \psi }}$), the correlation coefficient between the first and last torsion of the segment is of interest. As our torsions are $\varphi ,\psi$ torsion angles, the first torsion will be $\delta {\psi }_1$ and the last torsion will be $\delta {\varphi }_{N_{\text{res}}}$, and so, corr($\delta \tau /\delta {\tau }_{N_{\varphi \psi }}$) will be written as corr($\delta {\psi }_1\delta {\varphi }_{N_{\text{res}}}$). corr($\delta {\psi }_1\delta {\varphi }_{N_{\text{res}}}$) is a function of the $\varphi ,\psi$ angles and will depend on the structure of the segment.

In this work, three main algorithms were used: constraint surface exploration; steepest descent and gradient ascent on the constraint surface (performed to minimize or maximize any function of the torsions, $\Phi \left(\mathbf{\tau }\right)$); and torsion angle targeting. These algorithms are given in the Supporting Material.

Unless otherwise stated, bond lengths, bond angles, and ω torsions used are those given in Table S1 in the Supporting Material.

All calculations were performed using MATLAB version 7.4.0.287 (R2007a).

Results

Exploring conformations on the constraint surface for short polypeptides

Segments shorter than a pentapeptide

If $\text{rank}\left(\mathbf{Y}\left(\mathbf{\tau }\right)\right)=r$, then the dimension of the null space of $\mathbf{Y}\left(\mathbf{\tau }\right)$ is $N_{\varphi \psi }-r$. Only when $N_{\varphi \psi }-r>0$ can Eq. 6 be satisfied beyond the trivial solution, $\mathbf{\delta }{\mathbf{\tau }}^0=\mathbf{0}$. If r achieves its maximum value, which for $N_{\varphi \psi }>6$ is 6, and for $N_{\varphi \psi }\le 6$ is $N_{\varphi \psi }$, then the dimension of the null space for the former is $N_{\varphi \psi }-6$ and for the latter 0. Using the fact that $N_{\varphi \psi }=2\left(N_{\text{res}}-1\right)$, means that when $N_{\text{res}}\le 4$ and r is maximum, i.e., $N_{\varphi \psi }$, then the dimension of the null space is 0. This means that Eq. 6 is only satisfied when $\mathbf{\delta }{\mathbf{\tau }}^0=\mathbf{0}$. For most structures tested, r did achieve the maximum and therefore for loops comprising four or fewer residues, each conformation is dynamically trapped, as was pointed out originally by Gō and Scheraga (10). In the Supporting Material, structures are found where for $N_{\text{res}}=4$ and even $N_{\text{res}}=3$, full rank is not achieved and small movements are allowed.

Pentapeptides

Pentapeptides, with three loop residues flanked by two brace residues, are very common among loop structures (25). In the case of a pentapeptide with one constrained ϕ or ψ angle, there are seven free torsions, and solving Eq. 6 gives a single null-space vector. Exploration of this one-dimensional surface was performed using Algorithm A1 (see Supporting Material) for the case where ${\varphi }_2$ is constrained, e.g., the second residue mimics a proline. These results can be found in the Supporting Material (see Fig. S1), where it is shown for various loop structures that the ϕ,ψ angles of individual residues cycle around closed loops in the Ramachandran plot.

For a pentapeptide, there are 2 degrees of freedom under the fixed-end-group constraint. Thus, in the 8D ϕ,ψ angle space the constraint produces a two-dimensional surface. Exploration of this surface using Algorithm A1 was performed using two systematic methods, as described in the Supporting Material. Starting from both α-helix and extended structures (as in a β-strand), the combined ϕ,ψ traces from these two methods for residue 3 (the central residue) are shown in Ramachandran plots in Fig. 2 a (for residues 2 and 4, see Fig. S2 and Fig. S3, respectively). It is noticeable that the end-group constraint allows a much greater degree of flexibility in the extended conformation than in an α-helix irrespective of any nonbonded interactions. In fact, an interesting finding is that for an α-helix, the end constraints on residues i and i + 4 alone constrain the intervening residues in the α-helix conformation.

Figure 2.

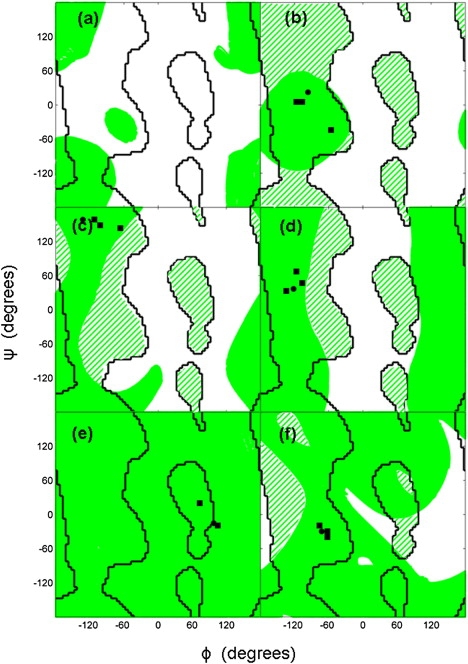
Starting from pentapeptide structures, the two-dimensional null space was explored as explained in the Supporting Material. The green areas in this Ramachandran plot show the regions visited by ϕ,ψ angles of residue 3 (for residues 2 and 4, see Fig. S2 and Fig. S3, respectively), the black lines are the boundaries between favorable and disfavorable regions, and the patterned regions show favorable regions that are inaccessible due to the constraint. Also shown are points indicating the ϕ,ψ angle of the residue in the starting structure (solid black circle) and from other structures in the same class (solid black squares), as given at the loop database website (http://www.bmm.icnet.uk/loop/index.html). (a) Starting from an extended conformation with ϕ,ψ angles (−123,136) at all residues, and a pentapeptide α-helix segment with ϕ,ψ angles (−57,−47). (b) Starting from loop α-α 1.1.5 (using the Oliva et al. classification code, PDB code 1ECA, segment 49–53A) (c) α-β 1.2.5 (PDB code 5P21, segment 137–141A) (d) β-α 3.1.1 (PDB code 2TMD, segment 395–399A). (e) β-β link 2.1.1 (PDB code 1EFT, segment 248–252A). (f) β-β hairpin 2.3.2 (PDB code 1HOE, segment 16–20A).

Oliva et al. (25) have classified loop structures that occur between five types of motifs: α-α loops between two α-helices, α-β loops between an α-helix and a β-strand, β-α loops between a β-strand and an α-helix, β-β links between two β-strands, and β-hairpins between neighboring strands in antiparallel β-sheets. We have randomly selected a single pentapeptide loop (three loop residues flanked on either side by a brace residue) from each motif in the database. The selected loop structures have the following Oliva et al. classification codes: α-α 1.1.5, α-β 1.2.5, β-α 3.1.1, β-β link 2.1.1 and β-β hairpin 2.3.2. Exploration of the constraint surface was performed for each loop as described above for the α-helix and extended structure. The accessible ϕ,ψ region for residue 3 (the central residue of the loop) is shown in a Ramachandran plot in Fig. 2 for each of the five loop structures (for residues 2 and 4, see Fig. S2 and Fig. S3, respectively). Fig. 2 also shows the boundaries between favorable and unfavorable regions. As can be seen, in most cases the constraint creates forbidden zones within the Ramachandran plot that have nothing to do with local or nonlocal interactions. The patterned regions in the plots show regions that are favorable due to local interactions but are in fact inaccessible due to the constraint. Also shown are ϕ,ψ of the residue concerned in the starting structure and in related structures as given at the database website (http://www.bmm.icnet.uk/loop/index.html). In all cases except for residue 4 of α-α, the ϕ,ψ angles are located within or near the boundaries. For α-α, this is probably explained by the considerable difference in the locations of the brace residues in this case. It is noticeable from Fig. 2, Fig. S2, and Fig. S3 that the motifs involving an α-helix as a bracing structure have considerably less torsional flexibility (based on space covered in a Ramachandran plot) than those solely with β-strand bracing structures (see Discussion).

These results indicate that the constraint surface is bounded and can be built from one-dimensional closed loops such as those in Fig. S1. This suggests, in the language of topology, that the surface of constraint is a closed manifold.

Cusps on the surface

For pentapeptides, it was noticed that when a single ϕ or ψ angle is constrained, the resulting cycling trajectories (see Fig. S1) could sometimes be radically different even for very small differences in the value of the constrained angle. Algorithm A1 was used to demonstrate this effect. First, ${\psi }_2$ was constrained and conformations were selected from the trajectory based on the ${\varphi }_2$ angle. From these conformations, cycling trajectories, now with ${\varphi }_2$ constrained, were generated. Fig. 3 shows the result when the ${\varphi }_2$ angle was constrained at 104.6° and 106.3° in a pentapeptide β-α loop (β-α 3.1.1, PDB code 2TMD, segment 395–399A). The ${\varphi }_3,{\psi }_3$, and ${\varphi }_4,{\psi }_4$ trajectories for the ${\varphi }_2$ = 106.3° case follow the trajectories for the ${\varphi }_2$ = 104.6° case, but loop out where the 104.6° trajectory makes an abrupt turn. Similar looping out was found at other starting conformations, although over large regions the change in trajectory is commensurate with the change in starting conformation. This effect was also found with other structures. Thus, a single torsion angle can act as a sensitive switch for the dynamical behavior of the whole loop, an effect that may be exploited in protein function. In terms of the constraint surface, these findings show that there are cusps separating regions that exhibit radically different behavior.

Figure 3.

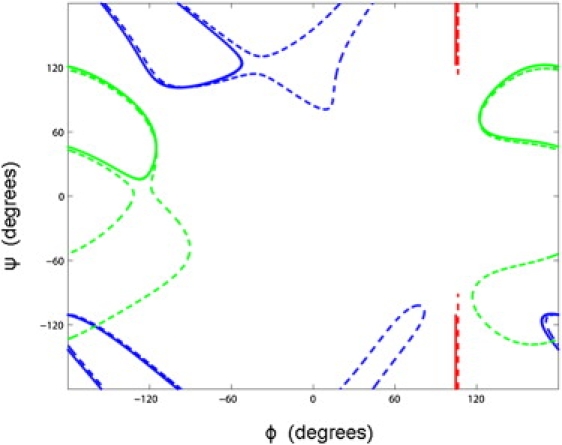
Cycling trajectories for a pentapeptide β-α loop (β-α 3.1.1, PDB code 2TMD, segment 395–399A). ${\varphi }_2$ is constrained at two slightly different values, 104.6° (solid lines) and 106.3° (dashed lines), but this small difference causes radically different trajectories for ${\varphi }_3$,${\psi }_3$ and ${\varphi }_4$,${\psi }_4$(in green and blue, respectively; the ${\varphi }_2$,${\psi }_2$ trajectory is red). The 106.3° trajectory follows the 104.6° trajectory but loops out where the 104.6° trajectory makes a sharp turn.

Correlation along the chain

Decapeptides

As we are interested in long-range correlation caused by fixing end groups, we carried out this analysis on a 10-residue segment. Using Eq. 7, and assuming ${\sigma }_{ij}={\delta }_{ij}$, the Kronecker δ (i.e., assuming homogenous and uncorrelated fluctuations in the null space), the correlation coefficient between $\delta {\psi }_1$ and $\delta {\varphi }_{10}$, corr($\delta {\psi }_1\delta {\varphi }_{10}$), was calculated for α-helix and extended structures. For a decapeptide, there are 18 ϕ or ψ angles and the null space spans 12 dimensions. Fig. 4 a shows the correlation coefficient, as defined in Eq. 7, with ${\sigma }_{ij}={\delta }_{ij}$ between ${\psi }_1$ and every ϕ and ψ angle up to ${\varphi }_{10}$ in an α-helix and extended structure. As one can see, for both structures, there is an appreciable anticorrelation between ${\psi }_1$ and the ${\varphi }_2$ angle. This is the well-known peptide-plane rotation, also known as the crank-shaft motion (26–29). Although generally the absolute value of the correlation coefficient decreases the further along the chain the torsion is located, there are long-range correlations, as exemplified by the correlation between the first and last torsion for the extended structure, which has a correlation coefficient of 0.29. Using Algorithm A2 (see Supporting Material) for the function corr($\delta {\psi }_1\delta {\varphi }_{10}$) (i.e., $\Phi \left(\mathbf{\tau }\right)$ is equal to corr($\delta {\psi }_1\delta {\varphi }_{10}$)), it was possible to find α-helix-like structures with |corr($\delta {\psi }_1\delta {\varphi }_{10}$)| > 0.9 starting from an α-helix. However, for the extended structure, |corr($\delta {\psi }_1\delta {\varphi }_{10}$)| < 0.6, even after 100,000 iterations of gradient ascent or steepest descent.

Figure 4.

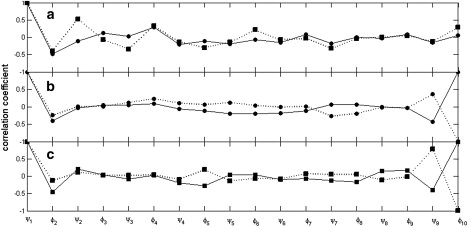
(a) Correlation coefficient between $\delta {\psi }_1$ and each subsequent $\delta \varphi$ or $\delta \psi$ angle in a 10-residue α-helix (solid line with solid circles) and 10-residue extended structure (dashed line with solid squares). (b and c) Correlation coefficient between $\delta {\psi }_1$ angle and each subsequent $\delta \varphi$ or $\delta \psi$ angle in a 10-residue segment in structures that have a correlation coefficient of 1.0 (solid lines) between $\delta {\psi }_1$ and $\delta {\varphi }_{10}$ and in structures that have a correlation coefficient of -1.0 (dashed lines) between $\delta {\psi }_1$ and $\delta {\varphi }_{10}$. Results are shown for structures where the search started from the α-helix conformation (b) and those where the search started from the extended conformation (c). The ϕ,ψ angles for these structures are given in Table S2.

Our search need not be restricted to those structures where the end groups are fixed at the starting positions. We can simply search for any structure that has a large value for |corr($\delta {\psi }_1\delta {\varphi }_{10}$)|, allowing the end groups to change position. This was achieved using a simplex search method implemented in the MATLAB function fminsearch to find a maximum or a minimum value of corr($\delta {\psi }_1\delta {\varphi }_{10}$). As before, we started from the α-helix and extended structures, and assumed ${\sigma }_{ij}={\delta }_{ij}$. It is indeed possible to find structures for which corr($\delta {\psi }_1\delta {\varphi }_{10}$) = ±1; their $\varphi ,\psi$ angles are given in Table S2 and the correlation along the segment is shown for all four structures in Fig. 4, b and c. For the structures that originated from extended structures, the distance between these torsion angles is ∼30 Å, suggesting that very long-range correlation is possible. Indeed, appreciable correlation over much longer distances was found in segments of >10 residues. There is a geometrical interpretation of this result that is instructive. The null space is an $N_{\varphi \psi }-6$ dimensional subspace in a space of $N_{\varphi \psi }$ dimensions. Perfect correlation or anticorrelation means that the first row of the matrix $\mathbf{\delta }{\mathbf{\tau }}^0$ (corresponding to ${\psi }_1$) and the last row of $\mathbf{\delta }{\mathbf{\tau }}^0$ (corresponding to ${\varphi }_{10}$) are collinear, or that the submatrix comprising these two rows only has rank 1. This can be imagined as the null space being perpendicular to the two-dimensional space defined by $\delta {\psi }_1$ and $\delta {\varphi }_{10}$. This means that the correlation between $\delta {\psi }_1$ and $\delta {\varphi }_{10}$ is independent of the form of the fluctuations in the null space, and therefore, ${\sigma }_{ij}$ in Eq. 7 can have any permissible form (i.e., the fluctuations in the null space need not be homogenous and uncorrelated). Thus, for the structures in Table S2, the first and last torsion angles will always be perfectly correlated or anticorrelated. The ratio of $\delta {\tau }_{18i}^0$ to $\delta {\tau }_{1i}^0$ for i = 1,12 has the same value, which gives the ratio of $\delta {\varphi }_{10}$ to $\delta {\psi }_1$. These ratios are given in Table S2. Thus, for the structure originating from an extended structure with corr($\delta {\psi }_1\delta {\varphi }_{10}$) = −1, when $\delta {\psi }_1$ rotates 1°, $\delta {\varphi }_{10}$ rotates −3.1°. In fact, using a random search, we have discovered structures that give considerable amplification of the rotation of ${\psi }_1$ at ${\varphi }_{10}$. We have shown, therefore, that for an appropriate structure, and within the model of fixed end groups, ω torsions, and bond angles, small torsion angle changes can be transmitted and amplified over large distances.

To demonstrate the fact that fixing end groups can give rise to long-range correlations, we have considered only the first and last torsion angles. It is clear that under this constraint, correlations can exist between any pair of torsion angles, given the appropriate structure.

Loop modeling using torsion angle targeting

The aim of the modeling procedure is to change selected ϕ or ψ torsion angles from initial values to specified target values under the fixed-end-group constraint. The algorithm used is Algorithm A3 in the Supporting Material. The basic requirement is to specify the start and end residue of the segment from a protein of known structure, the ψ angles for targeting and their target values, and the ϕ,ψ angles that are to be constrained. If $N_{\text{constr}}$ is the number of constrained ϕ,ψ angles, then for targeting to be possible, $N_{\varphi \psi }-N_{\text{constr}}-6>0$ (as r = 6 in most realistic cases). We have applied this to the enzymes horse liver alcohol dehydrogenase (LADH) and lactate dehydrogenase (LDHase), both of which have functional loop movements. It was found that $\Delta s=0.1$ worked well in both cases, with the end groups remaining fixed at their starting positions. The bond lengths, bond angles, and ω torsions were fixed at their values in the starting structure.

Loop movement in LADH

A loop movement accompanies the domain movement in LADH, which is induced by NAD⁺ binding to the coenzyme-binding domain (5). It has been shown that the loop, residues 290–300, acts as a blocker to domain closure in the absence of NAD⁺ (30) caused by contacts between Pro²⁹⁶ on the loop, and residues His⁵¹, Thr⁵⁶, and Leu⁵⁷ in the catalytic domain. It was proposed that as the side chain of Val²⁹⁴ rotates (facilitated by a large change in the ϕ angle of Gly²⁹³) to contact NAD⁺, it moves the blocking residue Pro²⁹⁶ out of the way through the region defining the torsions ${\psi }_{294}$, ${\varphi }_{295}$, ${\psi }_{295}$, and ${\varphi }_{296}$, acting as a rigid arm (30). The region 293–296 has the sequence Gly-Val-Pro-Pro and it is known that a proline will inhibit not only rotation about its own ϕ torsion axis but also rotation about the ψ torsion axis of the preceding residue (31–33). Thus, the suggestion is that the Pro-Pro motif constrains the torsions ${\psi }_{294}$, ${\varphi }_{295}$, ${\psi }_{295}$, and ${\varphi }_{296}$ to create the rigid arm. However, our knowledge is not sufficient to confidently assert that the block cannot be removed unless these torsions are constrained. Therefore, if we are able to show that only with constraints on torsions ${\psi }_{294}$, ${\varphi }_{295}$, ${\psi }_{295}$, and ${\varphi }_{296}$ is the block removed, then we have provided further evidence that the Pro-Pro motif is there to create the rigid arm for the distinct purpose of linking the binding of NAD⁺ to the removal of the block to domain closure.

Initially, the segment 290–300 was selected from the open structure (PDB code 1ADG), the torsions ${\psi }_{294}$, ${\varphi }_{295}$, ${\psi }_{295}$, and ${\varphi }_{296}$ were constrained, and the torsions ${\varphi }_{291}$, ${\psi }_{291}$, ${\varphi }_{292}$, ${\psi }_{292}$, ${\varphi }_{293}$, ${\psi }_{293}$, and ${\varphi }_{294}$ were targeted to their values in the closed structure (PDB code 2OHX). However, target values could not be achieved exactly with $\Vert \mathbf{\Delta }\mathbf{T}\left(n\right)\Vert =3.91°$ when $\Vert \mathbf{\delta }{\mathbf{\tau }}^0{\left(n\right)}^t\mathbf{\Delta }\mathbf{T}\left(n\right)\Vert$ (see Supporting Material) fell below its 0.001 threshold after 66,890 iterations. Therefore, the segment was extended to include residue 301. In this case, target values were achieved after only 2214 iterations. The final result is shown in Fig. 5 a. It can be seen that residue Pro²⁹⁶ has moved away from residues 51, 56, and 57 on the catalytic domain, as in the closed structure. Fig. 5 b shows the result when torsions ${\psi }_{294}$, ${\varphi }_{295}$, ${\psi }_{295}$, and ${\varphi }_{296}$ are not constrained, mimicking a Pro²⁹⁵nonPro, Pro²⁹⁶nonPro double mutant. It shows that Pro²⁹⁶ (or whatever residue substitutes for it) has not moved away from residues 51, 56, and 57, and the loop's structure is close to that of the open domain case, with Pro²⁹⁶ still in contact with His⁵¹. In this case, the loop remains a block to closure.

Figure 5.

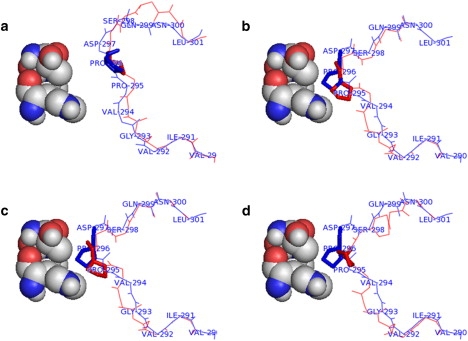
Starting from the open structure (PDB code 1ADG), torsions ${\varphi }_{291}$, ${\psi }_{291}$, ${\varphi }_{292}$, ${\psi }_{292}$, ${\varphi }_{293}$, ${\psi }_{293}$, and ${\varphi }_{294}$ were targeted to their values in the closed x-ray structure (PDB code 2OHX), keeping residues 290 and 301 fixed. Pro²⁹⁶ is indicated in thick-stick model, and His⁵¹, Thr⁵⁶, and Leu⁵⁷ are shown in the spacefilling model. Target values were achieved in all cases. Movies of the movements in a–d are available in the Supporting Material. (a) Torsions ${\psi }_{294}$, ${\varphi }_{295}$, ${\psi }_{295}$, and ${\varphi }_{296}$ constrained to their values in the starting structure mimicking the Pro-Pro motif. The final structure of targeting is shown in red contrasted against the closed x-ray structure in blue. As can be clearly seen, Pro²⁹⁶ has moved away from His⁵¹, Thr⁵⁶, and Leu⁵⁷, which would allow the domains to close. (b) No torsions were constrained mimicking a Pro²⁹⁵nonPro, Pro²⁹⁶nonPro double mutant. The final structure of targeting is shown in red in contrast to the open x-ray structure in blue. As in the open structure, Pro²⁹⁶ remains in contact with His⁵¹, thus inhibiting domain closure. (c) Torsions ${\psi }_{294}$ and ${\varphi }_{295}$ only were constrained mimicking a Pro²⁹⁶nonPro mutant. The final structure of targeting is shown in red in contrast to the open x-ray structure in blue. As in the open structure Pro²⁹⁶ (or more correctly its nonPro substitution) remains in contact with His⁵¹, thus inhibiting domain closure. (d) Torsions ${\psi }_{295}$ and ${\varphi }_{296}$ only were constrained to mimic a Pro²⁹⁵nonPro mutant. The final structure of targeting is shown in red and contrasted with the open x-ray structure in blue. Pro²⁹⁶ has moved away from His⁵¹, Thr⁵⁶, and Leu⁵⁷, slightly, but the conformation of the loop is more like that of the open than the closed. It suggests that in the presence of NAD, the domains of a Pro²⁹⁵nonPro mutant would be slightly more closed than a Pro²⁹⁶nonPro mutant or a Pro²⁹⁵nonPro, Pro²⁹⁶nonPro double mutant but not a fully closed structure like the wild-type.

Would a single proline at 295 or 296 be sufficient to move Pro²⁹⁶ away from residues 51, 56, and 57? Constraining torsions ${\psi }_{294}$ and ${\varphi }_{295}$ only (so effectively mimicking a Pro²⁹⁶nonPro mutant) resulted in Pro²⁹⁶ (or whatever the nonPro residue is) still remaining in contact with residues 51, 56, and 57, as shown in Fig. 5 c. Constraining torsions ${\psi }_{295}$ and ${\varphi }_{296}$ only (so effectively mimicking a Pro²⁹⁵nonPro mutant) results in a structure where Pro²⁹⁶ has moved slightly away from residues 51, 56, and 57, but still not as far away as the wild-type case (see Fig. 5 d). This mutant would be expected to have a predominantly open structure in the presence of NAD⁺, but perhaps one slightly more closed than the Pro²⁹⁶nonPro mutant or the Pro²⁹⁵nonPro, Pro²⁹⁶nonPro double-mutant structures.

Movies of the movement of the loop during targeting for all four cases are available in the Supporting Material.

Thus, for the loop to move to an unblocking position, torsions ${\psi }_{294}$, ${\varphi }_{295}$, ${\psi }_{295}$, and ${\varphi }_{296}$ need to be constrained, because without constraints they act to cancel out the effect of rotations at preceding torsions. Without these constraints, the block to domain closure cannot be removed. Therefore, this study provides further supporting evidence that the Pro-Pro motif is essential for function and is part of the NAD⁺ activated switch for domain closure.

In the Supporting Material, we show that ±1 residue change in the definition of the loop segment does not alter our main conclusion.

Loop movement in LDHase

LDHase catalyzes the interconversion of lactate and pyruvate and, like LADH, it uses NAD as a coenzyme. LDHase has a large loop movement that is induced by the binding of NAD (6). In dogfish M₄ LDHase, the loop movement was analyzed using the DynDom program (34,35) between the open apoenzyme structure (PDB code 6LDH) and the closed ternary complex structure with NAD and oxamic acid (PDB code 1LDM). This analysis shows that the loop is defined by residues 98–110, with hinging residues at 97 and 98 on one side of the loop and 110 and 111 on the other side. We would like to know how many ϕ,ψ angles we would need to change in the open loop structure to get close to the closed-loop structure and to understand the nature of the loop movement.

The segment 95–115 (i.e., extended slightly beyond the DynDom definition (see the end of this section for further comments regarding the segment definition)) was selected, and starting with ${\psi }_{95}$, the apoenzyme structure's ϕ,ψ angles were targeted to those in the ternary structure, progressively working along the chain (so after ${\psi }_{95}$, ${\psi }_{95}$ and ${\varphi }_{96}$ were targeted; then ${\psi }_{95}$, ${\varphi }_{96}$, and ${\psi }_{96}$; and so on, working forward along the chain). This will be referred to as the N-terminal process. The equivalent process was carried out from the opposite end of the segment (targeting ${\varphi }_{115}$ only, then ${\varphi }_{115}$ and ${\psi }_{114}$, and so on, moving backward along the chain). This will be referred to as the C-terminal process. Both processes were continued until the targeted ϕ,ψ angles failed to reach their target values. The backbone root-mean-squared deviation (RMSD) between the loop in the final structure of each targeting procedure and the loop in the experimental ternary complex structure was calculated by least-squares best-fitting on backbone atoms of residues 1–94 and 116–327. The RMSD between the experimental open and closed loop structures when fitting was performed in this way was 5.6 Å. It was found that the C-terminal process failed to achieve an RMSD of <5.6 Å. However, the N-terminal process, targeting on all ϕ,ψ between ${\psi }_{95}$ and ${\varphi }_{101}$ inclusive, produced a final structure within an RMSD of 1.5 Å from the closed-loop structure. This was the optimal result. This is an interesting result, as less than one-quarter of the ϕ,ψ angles in the loop were targeted, and it is this region that interacts most directly with NAD.

Fig. 6 also shows intervening structures along the trajectory. The movement of the loop is complicated, folding initially in a direction perpendicular to the approximate plane of the loop, but finally making a sideways movement roughly parallel to this plane. These two difference phases of movement can be seen clearly in Fig. 6 b and in the movie available in the Supporting Material.

Figure 6.

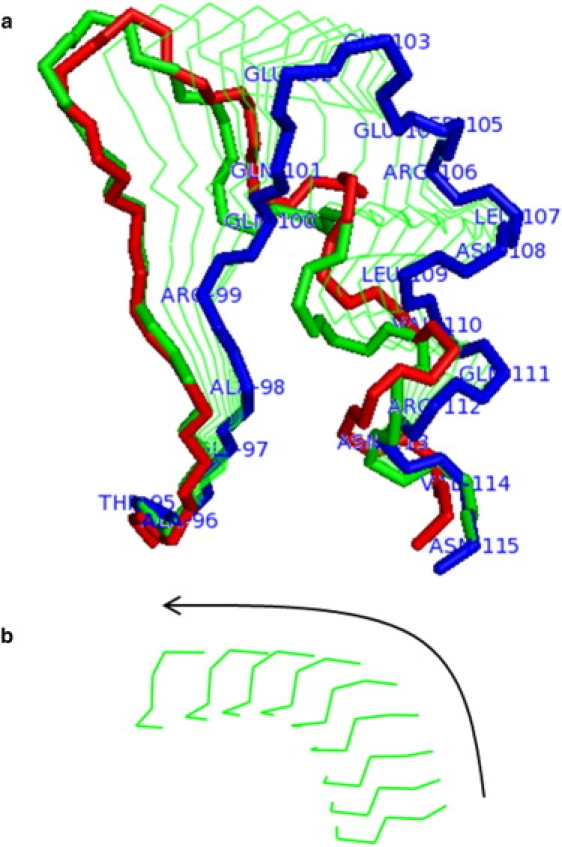
Targeting trajectory for the loop movement in dogfish M₄ lactate dehydrogenase. The open loop 95–115 from the apo structure (PDB code 6LDH) has been targeted to its closed ternary complex structure (PDB code 1LDM), keeping residues 95 and 115 fixed. Targeting was performed on all ϕ,ψ angles between ${\psi }_{95}$ and ${\varphi }_{101}$ inclusive, and targets were achieved. (a) The starting open loop structure is in blue, the target closed loop structure in red, and the resulting final structure from the targeting process in green with a thick stick depiction. The structures depicted in green with thin sticks are intervening structures generated during the targeting process. (b) View of the tip of the loop (residues 102 and 103).

How is our result influenced by the loop segment definition? We have reduced the loop length from each end and established that the minimal loop segment is 95–110. That is, our results are qualitatively the same (the backbone RMSD was reduced by ∼4 Å to within 2 Å of the closed-loop structure via the same perpendicular, then sideways movement) for loops segments 95–110, 95–111, 95–112, 95–113, 95–114, and 95–115. This minimal segment definition makes sense, as there are significant torsion angle differences at residues 96 and 109 between the x-ray structures.

Discussion

A linear inverse-kinematics technique has been applied to understand how the fixed-end-group constraint influences loop kinematics. The method lends itself very naturally for this purpose. A new result is that the fixed-end-group constraint creates a closed $N_{\varphi \psi }-6$ surface in a $N_{\varphi \psi }$ torsion angle space on which the state point moves. For example, for $N_{\varphi \psi }=7$, the surface is one-dimensional and the state point moves on a one-dimensional closed loop. The concept of the state point moving on a closed surface in torsion angle space provides us with a new way of thinking about loop kinematics.

The kinematics of the loop is highly dependent on the shape of the constraint surface and due to its highly curved nature (see Fig. S1 and Fig. 3), a steady movement over the surface can result in rapid switches in the rate of change of particular torsion angles as the state point moves over tightly curving regions. We have shown that for a pentapeptide, there are regions on the surface where a very small change in starting conformation can result in a highly divergent trajectory. This result can surely be generalized to longer polypeptides. One could imagine that these cusp regions are involved in function, whereby a change in one or more torsion angles, perhaps as a result of ligand binding, acts as a switch that allows the loop to access conformations that it would otherwise be unable to reach.

The simulations on the five loop structures show that the relationship between loop flexibility and the relative positions of the end constraints is not a simple one, e.g., the distance between the α-α loop and the β-β link brace residues is ∼7 Å in both cases, but as can be seen by comparing Fig. 2, b and e, Fig. S2 b and e, and Fig. S3 b and e, there is a considerable difference in torsion angle flexibility imposed by the constraint. Our simulations show that an α-helical conformation has dramatically less torsional flexibility than an extended conformation, as found in β-strands. This may explain why loops with α-helix brace structures have considerably less torsional flexibility than those with solely β-strand brace structures, as they have conformations closer to the α-helix conformation. An interesting finding that may have implications for protein folding is that for an α-helix, the constraining of residues i and i + 4 is enough to keep the intervening residues in the α-helix conformation.

We have shown that within the constraints of the model, there exist structures that have very long-range correlative effects in rotations about their ϕ and ψ angles. It is to be expected that these correlative effects will be weakened but not eliminated completely by flexibility in other degrees of freedom. One can imagine these correlative effects being exploited for allosteric mechanism.

For LADH, our results have provided further evidence that the Pro-Pro motif in the loop is crucial for communicating the rotation of the Val²⁹⁴ side chain upon NAD⁺ binding to Pro²⁹⁶ to remove it as a block to domain closure (30). The structure of a Gly²⁹³Ala, Pro²⁹⁵Thr double mutant in complex with NAD⁺ and 2,2,2-trifluoroethanol has been reported (36) to have an open structure. The loop in this structure is different to those modeled here in that its Val²⁹⁴ side chain has not rotated. In all three of our mutants and our wild-type, this side chain has rotated after targeting. Therefore, it would appear that it is not the Pro²⁹⁵Thr mutation that has caused the loop to remain in its open conformation, but the Gly²⁹³Ala mutation, where the large change in ϕ in the wild-type is unable to occur in alanine. Our results suggest that even mutation of either or both of the proline residues at 295 and 296 alone would still result in a largely open structure when bound to NAD⁺.

The application of targeting to the loop movement in LDHase showed good agreement between the final structure and the true closed structure, even though less than one-quarter of ϕ,ψ angles were targeted from the open structure. The path taken by the loop is not direct, but one that involves two almost orthogonal movements of the tip of the loop: a forward movement followed by a sideways movement. This is obviously due to the shape of the constraint surface along the path. The process can be regarded as akin to morphing applied to a subset of the total number of degrees of freedom. However, our path is quite different from that calculated by the morph server (37), which shows a direct route between the open and closed-loop structures. This difference is not surprising, as in contrast to our procedure, targeting is done in Cartesian coordinates rather than torsion angles and involves atoms spanning the whole loop rather than a set of variables limited to one side of the loop. An interesting finding was that targeting applied to torsion angles on the other side of the loop failed to move it toward the closed structure at all.

One possible criticism of our approach is that the model is oversimplified. However, comparing results from Cartesian coordinate space and dihedral angle space, normal-mode analysis has shown that fixing bond lengths and bond angles only has an effect (10–20% increase) on the total root-mean-square fluctuation but does not affect the pattern of atomic displacements in the important low-frequency modes, suggesting that our results will not be qualitatively changed by this approximation (38,39). Nonbonded forces of interaction are also excluded, as their inclusion would have obscured the effect of the constraint on the kinematics. However, future work will include side chains and molecular interactions to investigate how the avoidance of high-energy states guides the state point over the constraint surface.

Supporting Material

Methods, results, three tables, seven movies, and three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00147-5.