Abstract
Gastrointestinal slow waves are generated within networks of interstitial cells of Cajal (ICCs). In the intact tissue, slow waves are entrained to neighboring ICCs with higher intrinsic frequencies, leading to active propagation of slow waves. Degradation of ICC networks in humans is associated with motility disorders; however, the pathophysiological mechanisms of this relationship are uncertain. A recently developed biophysically based mathematical model of ICC was adopted and updated to simulate entrainment of slow waves. Simulated slow wave propagation was successfully entrained in a one-dimensional model, which contained a gradient of intrinsic frequencies. Slow wave propagation was then simulated in tissue models which contained a realistic two-dimensional microstructure of the myenteric ICC networks translated from wild-type (WT) and 5-HT2B knockout (degraded) mouse jejunum. The results showed that the peak current density in the WT model was 0.49 μA mm−2 higher than the 5-HT2B knockout model, and the intracellular Ca2+ density after 400 ms was 0.26 mM mm−2 higher in the WT model. In conclusion, tissue-specific models of slow waves are presented, and simulations quantitatively demonstrated physiological differences between WT and 5-HT2B knockout models. This study provides a framework for evaluating how ICC network degradation may impair slow wave propagation and ultimately motility and transit.
Introduction
Phasic contractile activity in the gastrointestinal (GI) tract is regulated by propagating electrical activity termed slow waves. Slow waves are autonomously generated and propagated by specialized pacemaker cells called the interstitial cells of Cajal (ICCs), and conduct passively to the adjacent smooth muscle cells (1).
In isolated preparations, individual ICCs demonstrate self-excitatory behavior at specific intrinsic frequencies, with a decreasing gradient of intrinsic ICC frequencies occurring in the aboral direction of the stomach and small intestine (1,2). In the intact tissue, ICCs are organized in an electrical syncytium and become entrained to neighboring ICCs with higher intrinsic frequencies. The entrainment response is considered to be the key mechanism underlying the active propagation of slow waves through ICC networks. Although slow wave frequencies vary between different regions of the GI tract, the importance of entrainment for coordinated motility remains fundamental to the entire GI tract (1).
ICC loss and ICC network degradation have been associated with several disorders of GI motility and transit, most notably diabetic gastroparesis and slow transit constipation (3). However, the effect of structural degradation on physiology of the GI tract has not been clearly established and remains an active subject of investigation (3,4). Such research is experimentally challenging, because it is technically difficult to relate changes in ICC network structure with the functional consequences for entrainment and motility simultaneously in living GI tissues.
Mathematical models offer a virtual medium in which hypothetical physiological conditions can be tested in silico, thus presenting an attractive strategy for investigating complex biological phenomena such as GI slow waves (5). Recent decades of research in cardiovascular electrophysiology have resulted in sophisticated multiscale mathematical models, which have been applied to successfully address complex clinical problems such as the mechanisms underlying atrial fibrillation (6). In comparison, the mathematical modeling of GI electrophysiology is still relatively underdeveloped. To date, most multiscale mathematical models of GI slow waves have relied on relatively simplistic phenomenological cell models, which cannot be applied in studies evaluating important intracellular physiological dynamics (7,8). Furthermore, whereas cardiac models have incorporated detailed microstructural tissue information to relate tissue structure to function (6,9), all previous tissue models simulating GI slow waves have employed idealizations of ICC and smooth muscle layers that are relatively simplistic and lacking in realistic detail (5).
Recently, several new biophysically based GI cell models have been introduced, which accurately quantify changes in the cellular membrane potential by incorporating detailed mathematical descriptions of experimentally defined ion conductances (10–14). In addition, intracellular processes such as calcium ion (Ca2+) dynamics are also described in these new ICC models. Unlike phenomenological models, biophysically based ICC models allow physiological meaningful quantities such as ion concentrations to be evaluated in physically realistic quantities, allowing GI slow waves to be investigated without relying entirely on experimental observations (15,16).
This study aims to present and integrate two major advances in GI multiscale modeling, in order to introduce a new framework for mathematically quantifying the functional consequences of ICC network degradation. The first aim was to adapt a biophysically based ICC model so that it could be applied to simulate slow wave entrainment in multiscale tissue models. The second aim was to simulate slow wave entrainment in realistic normal and degraded ICC network structures. The tissue model we chose was the 5-HT2B knockout mouse, which has been shown to have a decreased volume of Kit-positive ICC of 30% in the myenteric plexus region and 40% in the deep muscular plexus in the small intestine (17). Finally, the resultant multiscale models were used to quantitatively define, using physiologically relevant parameters, the differences in functional outcomes after slow wave entrainment across the WT and 5-HT2B knockout models.
Materials and Methods
Cell model
The Corrias and Buist ICC model is a Hodgkin-Huxley-based biophysical cell model that simulates gastric slow wave activity at a nominal frequency of three cycles per min(cpm) (11). The Corrias and Buist ICC model simulates membrane potential (Vm) through quantitative descriptions of 10 types of ion conductances, and intracellular calcium ([Ca2+]i) dynamics through adopting an established [Ca2+]i model by Fall and Keizer (18). The symbols for the model parameters used to represent the different types of ion conductances in Eqs. 1 and 2, are consistent with the published version of the Corrias and Buist ICC model (11):
| (1) |
| (2) |
In this study, a number of simplifications were made to the Corrias and Buist ICC model to increase its computational efficiency for larger simulations in tissue models. The details of the updated model components are illustrated in Fig. 1.
Figure 1.
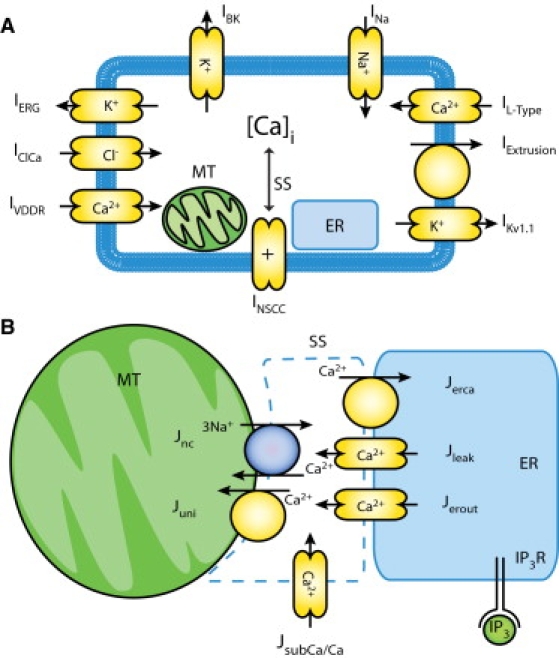
(A) Schematic of Corrias and Buist ICC model (11), which includes 10 types of ion conductances, and an intracellular Ca2+ dynamic quantified through the interactions of the mitochondria (MT), the endoplasmic reticulum (ER), and a subspace compartment (SS) within the cytoplasm. (B) The updated intracellular components between MT, ER, and SS. The IP3 component was adopted from the model by Imtiaz et al. (22), which includes a voltage-dependent, IP3-induced Ca2+ release and in turn activates slow waves.
Previous studies have shown that acute reduction in adenosine triphosphate (ATP) production did not affect the generation of slow waves (19). Therefore, the components and equations of the Corrias and Buist ICC model associated with ATP production in the subcomponent representing the mitochondria were simplified. Specifically, equations representing ATP hydrolysis were eliminated from the model, and the processes of mitochondrial respiration and H+ diffusion were approximated by flux constants. Although experimental evidence has shown that ICCs contain an ATP-sensitive K+ conductance, this type of conductance was not included in the original Corrias and Buist ICC model, so simplifying the ATP components has no effect on the generation of slow waves by the Corrias and Buist ICC model (11,20).
The original Corrias and Buist ICC model was unresponsive to injected current sources and therefore was unsuitable for simulations of entrainment in a voltage-dependent manner. A number of studies have demonstrated that an inositol 1,4,5-trisphosphate (IP3)-mediated intracellular calcium ([Ca2+]i) mechanism is likely to be responsible for slow wave entrainment (1,21). Therefore, the Corrias and Buist ICC model was further modified for this study by introducing a voltage-dependent, IP3-related mechanism based on the equations previously published by Imtiaz et al. (22). The effect of this modification was to invoke an active slow wave in the Corrias and Buist ICC model in response to an appropriate current source, such as from another depolarizing ICC. The IP3 component in the model by Imtiaz et al. assumes a positive feedback of IP3 kinetics in slow wave generation using
| (3) |
| (4) |
where parameter β is a constant that represents a chemical stimulus agent (such as ACh) that can modulate the sensitivity of [IP3] to the changes in Vm (22). A higher β leads to a higher intrinsic frequency in a relationship quantified in Fig. 2. The temporary surge of IP3 due to an increase in Vm allows the ICC model to respond to a current source by producing a phase shift relative to its intrinsic slow wave activity. The full descriptions and values of the parameters in Eqs. 3 and 4 are listed in Table S1 (Supporting Material). The parameter values were redimensionalized to be consistent with the units of Corrias and Buist ICC model.
Figure 2.
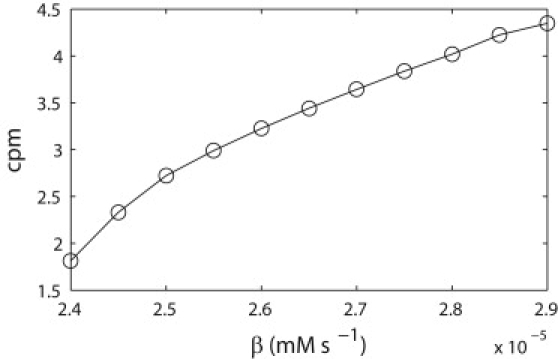
Relationship between slow wave frequency in cycles per min and β. The parameter β was varied over a range of values and the slow wave frequency was calculated from the resulting traces of membrane potential over 60 s simulated time.
Tissue model
ICC network geometries
Slow wave entrainment was modeled over two ICC network geometries obtained from mouse jejunum. The first geometry was derived from a WT mouse intestine with an intact ICC network, and the second geometry was obtained from a mouse with a germline deletion of the 5-HT2B serotonin receptor. The 5-HT2B receptors are expressed on ICCs. Stimulation by serotonin induces proliferation of ICC populations, and therefore is an important regulator of ICC network density (17,23).
There are two principal ICC layers in the murine small intestine: the ICC-MY, which lies in the plane of the myenteric plexus, and ICC-DMP, which lies in close association with the nerves of the deep muscular plexus (1). ICC-MY is the primary ICC structure responsible for the generation and propagation of slow waves and for this reason ICC-DMP was not included in this study (24).
Two-dimensional bitmap images of the Kit-positive ICC structures were obtained as previously described (17). Briefly, whole-mount preparations of the muscularis propria from the jejunum of four-week-old mice were used. ICCs were labeled by incubation with a primary monoclonal antibody against Kit (ACK2; Ebiosciences, San Diego, CA) and a secondary polyclonal antibody was conjugated to Cy3 and raised against rat IgG (Jackson Immunoresearch, West Grove, PA). Images of the labeled structures were collected using a model No. FV1000 laser-scanning confocal microscope using 40× water, 1.2 NA, and 40× oil 1.3 NA objectives (Olympus America, Center Valley, PA). Images were collected using a z-axis step size (0.46–0.54 μm) that matched an Airy number of 1 for the objective and the excitation wavelength for the fluorophore. Voxel dimensions were corrected for aberrations in the z-axis depth using calibration beads to determine the actual pixel dimensions. Stacks of confocal image slices were volume-rendered in three dimensions and bitmaps of the positively labeled structures obtained by using Analyze software (AnalyzeDirect, Overland Park, KS) running on a PC operating MS Windows, as previously described (25). The volume quantification was done using unbiased thresholding algorithms to segment the images and determine the volume of Kit positive structures, thereby minimizing any human influence in assessing the differences.
Continuum-based modeling
A continuum modeling approach was used to simulate the entrainment of slow waves in tissue models. The bidomain equations are the standard equations used in simulation of cardiac electrical events (6,9,26). The principal reason for choosing the bidomain equations over monodomain or cable equations was to maintain a high degree of flexibility in the descriptions of material properties of GI tissue, which remains an ongoing area of research. The bidomain equations represent Vm and extracellular potentials in electrically active tissues in the GI tract. Equations 5 and 6 summarize the system of equations used in this study to simulate propagation of slow waves,
| (5) |
| (6) |
where Φe represent the extracellular potentials, and Am is the surface/volume ratio of the membrane. The σ terms represent tissue conductivity tensors, where subscript i represents the intracellular domain and subscript e represents the extracellular domain. The intracellular conductivities σi were chosen to be 500 nS mm−1, whereas the extracellular conductivities σe were chosen to be 300 nS mm−1, based on the values reported by Edwards and Hirst (27). The Iion term in Eq. 6 is the sum of ion conductances in Eq. 1, thereby relating the continuum model to the updated Corrias and Buist ICC model. The system of bidomain equations was chosen to be a voltage-dependent system, in line with the standard of previous simulation studies of both cardiac and GI electrical activity (5,6). However, one difference between the bidomain equations adopted in this study and general cardiac studies is the absence of a stimulus current, generally termed Istim, due to the self-excitatory behaviors of ICCs.
Equations 5 and 6 were solved numerically using the finite element technique. A Jacobi preconditioned conjugate gradient method with an adaptive integrator solver was used to solve the discrete forms of Eq. 5 and 6, with the term Iion described through Eq. 1. Applications of these computational methods have been described in the literature (6,26).
One-dimensional model setup
To demonstrate that entrainment was stable over a significant temporal scale, simulation was first carried out in a one-dimensional model to represent entrainment of slow waves over a simulated period of 120 s. Simulations were conducted over a linear one-dimensional model in a single geometric element of length 2 mm, at 0.2-mm spatial discretization. A linear gradient of intrinsic frequencies was assigned to the one-dimensional model by varying the parameter β linearly over the geometric element to obtain an intrinsic frequency gradient between 3.0 and 2.8 cycles per min.
Tissue model setup
The segments of images of the WT and 5-HT2B knockout mouse tissues containing only the ICC-MY networks were rendered into three-dimensional stacks of images sequentially taken at many transmural depths (Fig. 3 A). There were 43 slices in the myenteric plexus region of the WT tissue image stack and 41 slices in the 5-HT2B knockout tissue image stack. The physical dimensions were 316 × 316 × 7 μm for the WT image stack and 316 × 316 × 8 μm for the 5-HT2B knockout image stack. Each in-plane (x-y) image was sampled at 512 × 512 pixels for both tissue blocks. The in-plane resolution was 0.62 μm in both tissue blocks, and the transmural resolution was 0.17 μm in the WT image stack and 0.20 μm in the 5-HT2B knockout image stack.
Figure 3.
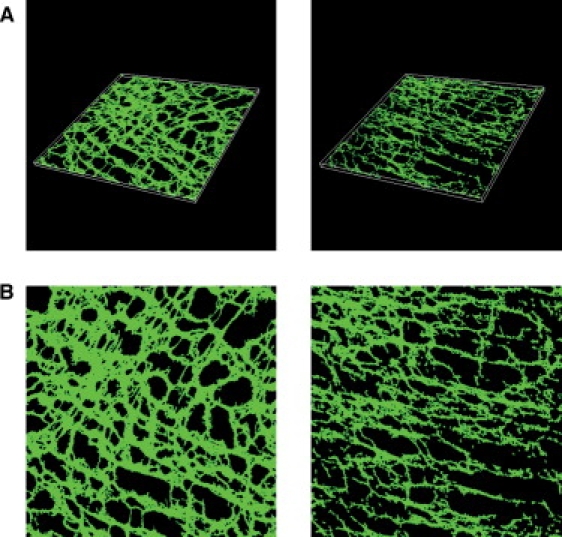
(A) Three-dimensional anatomical image blocks of wild-type mouse specimen (left) and 5-HT2B knockout (right) mouse intestinal samples. The physical size of the WT tissue block is 316 × 316 × 7 μm, and the physical size of the 5-HT2B knockout tissue block is 316 × 316 × 8 μm. (B) Two-dimensional representation of the depth-averaged WT model (left) and 5-HT2B knockout model (right).
Due to the relative thinness of the transmural direction of the myenteric plexus ICC networks, and because the majority of the network geometry lay in the in-plane directions, the image stacks were depth-averaged into two-dimensional images as shown in Fig. 3 B. Reducing the dimensionality of the images stacks allowed a significant reduction in the computational time of the simulations. A similar two-dimensional tissue modeling strategy was also recently employed in a tissue-specific model of atrial function, where a comparison study between thin three-dimensional and thin two-dimensional modeling showed no significant quantitative differences in the functional outcome (6).
The ICC network geometries were obtained from the two-dimensional images of the WT and 5-HT2B knockout mouse samples at the original in-plane resolutions. Each pixel in the image was represented by a node point in the tissue models, such that each resultant tissue model consisted of a regular two-dimensional finite element mesh with a total of 262,144 nodes. More importantly, this allows the tissue models to be investigated at the same spatial discretizations as the original tissue images. These tissue models therefore represented a substantially higher spatial resolution (0.62 μm) than previous comparable cardiac simulations (300 μm) that used a similar modeling technique (6), highlighting the need for the steps taken above to reduce computational usage.
The nodes in the tissue models were grouped into either a continuum ICC node (green/gray in Fig. 3 B) or a non-ICC tissue (black in Fig. 3 B). Equations 5 and 6 were solved to simulate propagation of slow waves. The non-ICC tissue nodes were represented using an invariant Vm term with Iion = 0 pA. The purpose of the invariant Vm term is to eliminate any active responses of the background tissue to the slow waves in the simulations.
The ICC network in each tissue model was assigned a gradient of intrinsic frequencies by linearly varying β between 2.55 × 10−5 mM s−1 and 2.54 × 10−5 mM s−1, which correlated to a frequency gradient from 3.0 to 2.9 cpm. The gradient of the intrinsic frequency was very small due to the limited physical dimensions of the tissue models.
Frequencies close to the intrinsic frequency of gastric slow waves were applied to the intestinal tissue geometries for two practical reasons. Firstly, the Corrias and Buist ICC model was originally designed to reproduce gastric slow waves and it is most stable between 1 and 5 cpm. Secondly, the simulations in this study focused only on the activation phase of the first 400 ms of slow wave activity, whereas the duration of the slow wave is in the order of seconds. Therefore, the absolute value of the intrinsic slow wave frequencies was not an important factor for the simulation outcomes. In both the WT and 5-HT2B knockout tissue models, the highest intrinsic frequencies were assigned to ICCs in the top-left corner of the tissue domain, where the density of ICCs was qualitatively the highest (see Figs. 6 and 7).
Figure 6.
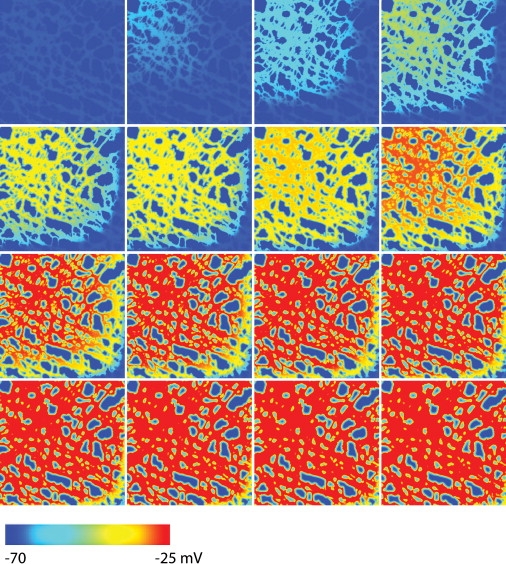
Simulated slow propagation in the WT model containing a normal ICC network structure. The blue color (left end of the color bar) represents the resting membrane potential and the red color (right end of the color bar) represents depolarized activity. The first image on the left in the top row shows the Vm at time t = 0 ms and each subsequent image, from left to right, then down to the next row, is 20-ms apart. The propagation velocity is ∼1.6 mm s−1, and the main direction of depolarization occurred from the top-left corner toward to the bottom-right corner of the tissue domain.
Figure 7.
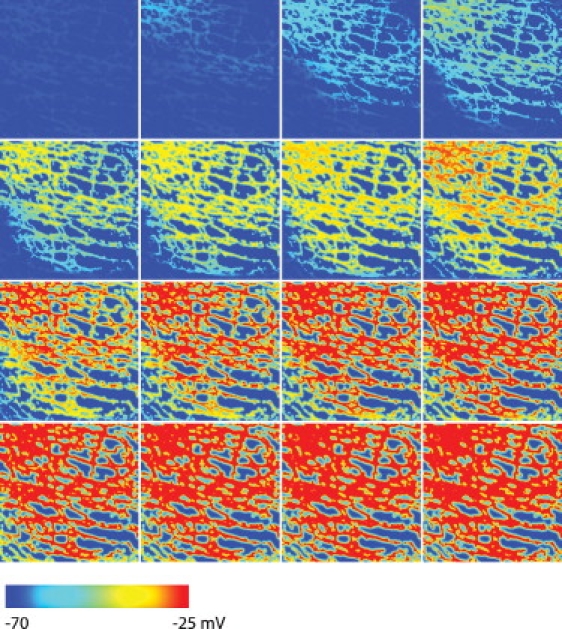
Simulated slow propagation in the 5-HT2B knockout model containing a degraded ICC network structure. The blue color (left end of the color bar) represents the resting membrane potential and the red color (right end of the color bar) represents depolarized activity. The first image on the left in the top row shows the Vm at time t = 0 ms and each subsequent image, from left to right, and then down to the next row, is 20-ms apart. The main direction of depolarization occurred from the left to right of the tissue domain.
Slow waves were simulated in the anatomically realistic two-dimensional ICC networks over a much shorter temporal scale (400 ms) compared to the one-dimensional model (120 s). The activation period of 400 ms was deemed sufficient time to capture a complete depolarization phase of the tissue model assuming a propagation velocity of ∼2 mm s−1 (28).
Quantification
To relate the simulation results of the tissue models to physiologically meaningful quantities, the functional outcomes of the simulated slow wave activity across each tissue model were quantified by calculating [Ca2+]i density and current density (J) during activation across the tissue model. The [Ca2+]i density was calculated by averaging the [Ca2+]i from the Corrias and Buist ICC model at each node in the intracellular domain in the tissue model at each solution time step. The J of the simulated slow waves was calculated using Eq. 7 (as reported by Austin et al. (29)),
| (7) |
where σ is the conductivity tensor.
Results
Single cell
Slow wave entrainment at the single cell level was evaluated by comparing the response of the original and updated Corrias and Buist ICC models to the same injected current source of amplitude 25 pA and duration 800 ms (Fig. 4 A). This injected current source is analogous to the current arising as the result of the potential difference between the Vm of the resting ICC and a neighboring ICC undergoing depolarization. The intrinsic frequency of both versions of the Corrias and Buist ICC model was identical at three cycles per min after a pulse applied after 15 s of simulated time. The stimulus resulted in a depolarization in the original Corrias and Buist ICC model, as shown in Fig. 4 B, reaching a peak Vm of −25 mV, which is similar to the Vm peak of a normal slow wave of −24 mV. However, the plateau of the stimulus-invoked activity was not maintained in the original Corrias and Buist ICC model, with the Vm repolarized to −51 mV at 5 s after the onset of the stimulus. The subsequent onsets of slow waves at 20 s and 40 s in the original Corrias and Buist ICC model thereafter occurred at times and rates as dictated by the intrinsic frequency.
Figure 4.
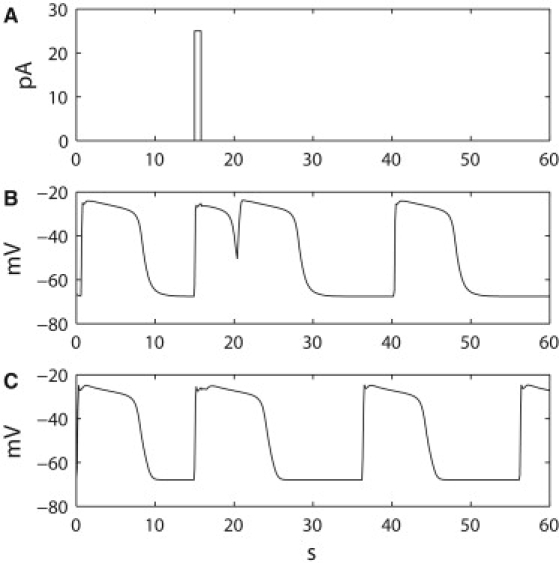
Comparison of response of the original and updated Corrias and Buist ICC models to a stimulus. (A) A single pulse stimulation current of amplitude 25 pA and duration 0.8 s was applied to (B) the original version of the Corrias and Buist ICC cell model, in which a partial slow wave was invoked but plateau was not maintained. The timings of slow waves did not change after the stimulus. (C) The updated version of the Corrias and Buist ICC cell model, in which a phase shift in slow waves was invoked and the subsequent activity was pulled to an earlier onset time without changing the underlying intrinsic frequency.
In the updated Corrias and Buist ICC model, the same stimulus successfully invoked and maintained a slow wave event, with the plateau of the invoked slow wave maintained for the nominal duration of ∼9 s as per a normal slow wave cycle, after the onset of stimulus (Fig. 4 C). The peak Vm of the invoked slow wave in the updated Corrias and Buist ICC model was also −25 mV, identical to the peak of Vm simulated by the original Corrias and Buist ICC model. The onset times of subsequent slow waves generated by the updated Corrias and Buist ICC model were at 36 s and 56 s, which were 4 s in advance of the timings by the intrinsic frequency without the stimulus. This implies that the updated Corrias and Buist ICC model responded to the stimulus by phase-advancing its intrinsic activity by 4 s while maintaining the same intrinsic frequency, and therefore demonstrates that the updated Corrias and Buist ICC model was capable of producing an active response of slow wave generation to an extracellular current source.
The updated Corrias and Buist ICC model contains 18 state variables and 65 cell parameters. Overall, the simplifications resulted in a 1.15 s (6.26–5.11 s) saving in solution time per cell model per 60 s simulated time (calculated using the ODE15s solver in MATLAB 2007b; The MathWorks, Natick, MA) on a PC.
One-dimensional model
In the one-dimensional model (Fig. 5 A), slow waves in a simplified network of coupled ICCs were simulated to investigate entrainment for 120 s. Slow wave entrainment in a decoupled one-dimensional network was investigated first. When the electrical connections between the nodes were reduced by setting σ to 0 mS mm−1, the simulated slow waves demonstrated out-of-phase activity, with each ICC responding according to the intrinsic frequency assigned to its node (Fig. 5 B). As the simulated Vm of the nodes in the decoupled one-dimensional model gradually became out-of-phase over time, the apparent velocity of propagation also decreased over time, from ∼0.9 mm s−1 during the first cycle of slow wave activity to 0.3 mm s−1 during the last cycle of slow wave activity. However, the velocities in the decoupled one-dimensional model reflected the timings of the intrinsic events of the ICC cell models in the network, rather than a constant entrained wave front. In the functionally coupled network, simulated Vm using the updated Corrias and Buist ICC model at the boundary nodes of the one-dimensional network displayed a constant phase-locking of ∼3.1 s (Fig. 5 C), demonstrating that the ICC with the highest intrinsic frequency effectively pulled, i.e., entrained, all of the ICCs with lower intrinsic frequencies into phase. The constant phase-lock also allowed the active propagation of slow wave events to occur at a stable velocity over time, in this case, ∼0.6 mm s−1, through the functionally coupled one-dimensional model.
Figure 5.
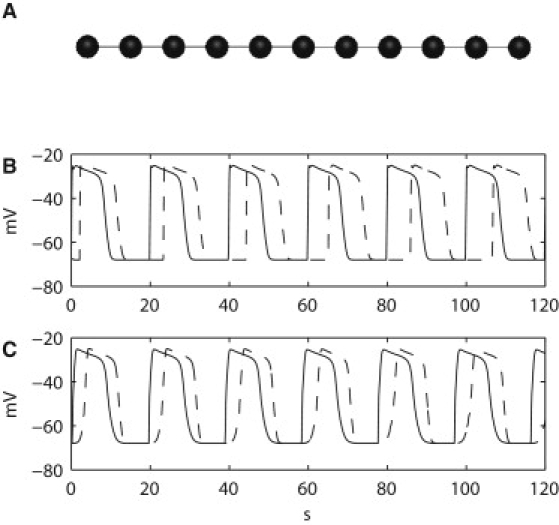
(A) The one-dimensional setup consisted of 11 coupled nodes (cell models), with an intrinsic frequency gradient that was assigned to the one-dimensional network. (B) The electrical connection between the nodes interrupted in the decoupled one-dimensional network. Simulated membrane potentials at the two boundary nodes demonstrate slow waves' different intrinsic frequencies. Slow waves at the ICC with the highest intrinsic frequency (solid line) occurred at 3.0 cycles per min, whereas slow waves at the ICC with the lowest intrinsic frequency (solid line) occurred at 2.8 cycles per min. (C) Entrained activity of the two boundary nodes. The ICC with the lowest intrinsic frequency was entrained to the ICC with the highest intrinsic frequency, with a constant phase-lock of 3.1 s.
Tissue models
Slow wave propagation was simulated in the tissue models containing realistic ICC network geometries in WT and 5-HT2B knockout models. Both tissue models contained an identical gradient of intrinsic frequencies. In the WT model, slow waves were activated from near the top-left corner of simulation domain as shown in Fig. 6, in accordance with the assignment of the highest-frequency ICCs to this region. The activation timings in this region reached a peak voltage of −25 mV ∼140 ms after time t = 0 ms. The direction of propagation followed the orientation of the ICC network in the WT model. The subsequent activation of ICCs after the initial 140 ms in the WT model was noticeably slower, taking ∼280 ms to activate the whole of the WT model.
The simulated slow wave activity in the 5-HT2B knockout model (Fig. 7) demonstrated a different propagation behavior compared to the WT model. The slow wave activity still originated from a pacemaker region near the top-left corner in the 5-HT2B knockout model, but the subsequent propagation predominately progressed horizontally through the ICC network. It required an additional 40 ms approximately for the entrained slow wave activity to reach the bottom-left corner of the 5-HT2B knockout model (260 ms) when compared to the normal model (220 ms).
The simulation time for each tissue models was 2 h for an activation time of 400 ms using a single processor of an IBM p595 HPC.
The peak J in the WT model was 0.49 μA mm−2 higher than in the 5-HT2B knockout model, and furthermore, the peak J was reached 15 ms faster in the WT model compared to the 5-HT2B knockout model (Fig. 8 A). The average simulated current density in the normal model was 0.98 mA mm−2, which was 0.04 mA mm−2 higher than the level achieved in the 5-HT2B knockout model. However, the 5-HT2B knockout sample displayed a more gradual reduction in J. The 2/3-density return time (i.e., the time taken for the J to return to 2/3 of its peak value) was 331 ms in the 5-HT2B knockout model and 257 ms in the WT model.
Figure 8.
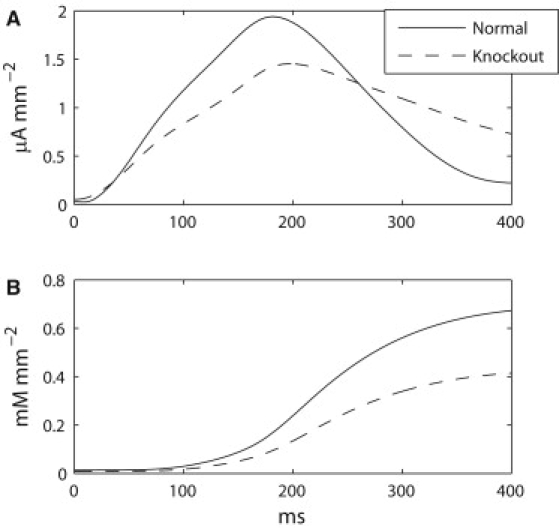
Comparison of current density and calcium concentration in WT and 5-HT2B knockout models. (A) Current density of normal model (solid line) and 5-HT2B knockout model (dashed line). The normal model produced a higher peak current density than the 5-HT2B knockout sample. (B) [Ca2+]i density of normal and 5-HT2B knockout models (same notations as in A). The normal model achieved consistently higher [Ca2+]i density compared to the 5-HT2B knockout model.
The resting levels of simulated [Ca2+]i density in both tissue models were similar at ∼0.01 mM mm−2 (Fig. 8 B). On average, the simulated [Ca2+]i density was greater in the WT model compared to the 5-HT2B knockout model (0.67 mM mm−2 vs. 0.41 mM mm−2). The level of [Ca2+]i density over time displayed a regular sigmoidal increase for both models, with the WT model achieving a consistently higher [Ca2+]i density than the 5-HT2B knockout model.
Discussion
An established body of evidence now associates degradation of ICC network with motility disorders in all parts of the GI tract (3). However, the electrophysiological and clinical consequences of the variable degradations seen in ICC networks are uncertain, and there is a need for new methods to relate the structural defects observed in GI motility problems with their functional consequences (4). This study presents biophysically based GI models that employ detailed ICC structural information as a new strategy for quantifying the physiological consequences of ICC network degradation. The new tissue models have been successfully applied to demonstrate differences in the current density (J) and density of [Ca2+]i achieved during slow wave entrainment in realistic ICC network geometries derived from wild-type (WT) and 5-HT2B knockout mouse jejunum.
Two significant advances in GI mathematical modeling have been achieved in establishing this modeling framework.
Firstly, an adapted biophysically based ICC model was successfully applied to simulate entrainment within a multiscale framework. The two principal reasons for choosing the Corrias and Buist ICC model were its biophysical representation of the ICC ion conductances and its computational efficiency (9). To allow a voltage-dependent response of slow wave activation in the Corrias and Buist ICC model, a proposed IP3 component of the model by Imtiaz et al. was adopted and successfully integrated into the updated Corrias and Buist ICC model, while maintaining computational efficiency (18). The updated IP3 component is necessary for the application of the ICC model at the tissue level because it allows an ICC with higher intrinsic frequency to entrain ICCs with lower intrinsic frequencies, as shown in Fig. 5 B. Using these modifications to the Corrias and Buist ICC model, stable entrainment was first successfully demonstrated over several cycles in a one-dimensional linear model, before being achieved over tissue models that contained much larger number of nodes at a fine spatial resolution.
The second significant modeling advance achieved in this study was to simulate slow wave entrainment over realistic ICC network geometries. Multiscale simulations over detailed tissue models have been extensively applied in investigations examining the physiological significance of complex cardiac tissue architectures (6). In contrast, until this study, simulations of GI electrical events have been based solely on idealized ICC and smooth muscle layers which bear little relation to the true tissue microstructure (5). This study therefore advances GI biophysical modeling closer to the sophistication achieved in the cardiac field (6,9).
The potential for detailed tissue models to relate tissue structure to function have been addressed by Trew et al. (9), who pointed out that electrophysiological recordings at the cell or large-scale levels is routinely practicable, whereas experimentally evaluating activity at the mesoscales is technically challenging. The tissue-specific modeling framework developed here now enables the direct correlation of anatomical structure with physiological function in GI tissues, and this was utilized to quantify some of the physiological differences in entrainment outcomes between the WT and 5-HT2B knockout models. The simulation demonstrated quantifiable differences with regard to the J and [Ca2+]i density, which could not have been demonstrated under previous modeling frameworks that employed simplistic phenomenological or cellular automata representations for ICC networks (5,16). The faster and greater total accrual of [Ca2+]i density in the WT model than in the 5-HT2B knockout model was as to be expected, given the greater density of ICCs in the WT tissue. Interestingly, the decline in J was slower in the knockout model than the WT model (Fig. 8 A). The slower decline in J across the degraded ICC network is likely related to the relatively longer time window where the gradient of Vm was maintained in the knockout model compared to the WT model. However, the peak J achieved was substantially lower for the 5-HT2B knockout model than the WT model, and accordingly less depolarizing current will have been delivered by this ICC network to the smooth muscle layers of the knockout mouse in vivo.
Upon closer inspection of the activation wave fronts, it can be seen that the WT model demonstrates a more even propagating slow wave front, due to the relatively uniform distribution of the intact ICC network (Fig. 6). In the 5-HT2B knockout model, the propagation of slow waves was impeded by the degraded ICC network structure as demonstrated by the longer time taken for the wave front to arrive at the bottom-left corner of tissue domain in the 5-HT2B knockout model. The physiological significance of the longer activation time in the 5-HT2B knockout model could be a slower transit time of the intestinal contents. Recent experimental evidence revealed a small trend to prolong transit time of liquid contents in 5-HT2B knockout mice; however, this was not a statistically significant increase (17). It is predicted that there is a degree of surplus capacity in ICC networks, such that ICC loss up to a threshold level may be inconsequential to transit, with impairments only manifesting below a certain threshold (17). Future modeling studies within the framework established here could focus on predicting the level of ICC loss that will lead to functional consequences for motility and transit in the gut.
The findings of the relationship between structural loss and slow waves are of relevance to clinical conditions such as diabetic gastroparesis, in which ICC network depletion and degradation is a central pathogenic feature (3,4). ICC loss in diabetic gastroparesis is a consequence of factors that promote ICC death, such as via inhibition of the protective enzyme heme oxygenase-1, as well as factors that reduce ICC survival or regeneration, such as via inhibiting the ICC-promoting hormones insulin and IGF-1 (4). To investigate how the physiological consequences of ICC network degradation quantified in this study translate to functional outcomes in GI smooth muscle behavior, it would be useful in future to couple anatomically and biophysically based representations of the smooth muscle cells into the ICC tissue models. At present, the background tissue was assumed to possess no active voltage response to the simulated slow waves, whereas in reality this space will be partly occupied by smooth muscle cells. A biophysically based smooth muscle cell model has recently been presented (10), which could be applied within this tissue modeling framework in future. Furthermore, the same simulation technique is also applicable to tissue models that represent larger physical dimensions.
Although both diabetic gastroparesis and the 5-HT2B knockout phenotypes are characterized by a widespread general depletion of ICC populations, the ICC loss in diabetes has been recognized as having a more patchy distribution (30). Slow wave dysrhythmias have been commonly recognized to occur in gastroparesis patients (31), and a recent study has demonstrated that gastric dysrhythmia can feature complex focal events and re-entrant behaviors that are similar to the mechanisms underlying atrial fibrillation (32). Detailed tissue models have been effectively applied in cardiology to define the role of complex tissue architectures in the generation and maintenance of fibrillation-type behaviors (6), and this study now paves the way for similar studies to investigate the structural basis of GI dysrhythmia. For example, future work could investigate whether uncoordinated propagation circuits arise within the heterogeneously-depleted ICC networks of patients with diabetic gastroparesis, and whether re-entrant slow wave propagation behaviors could arise as a result.
Two assumptions employed in this study warrant further comment.
Firstly, the simulations were conducted on ICC network geometries that were compressed into two-dimensional images. The thinness of the ICC-MY layer was principally used to justify the two-dimensional modeling approach. However, human ICC layers may be substantially thicker than murine layers and therefore future modeling studies employing human-derived geometries will need to reconsider the validity of this assumption.
Secondly, the Corrias and Buist ICC model is currently formulated to reproduce the characteristics of gastric slow waves, whereas the tissue geometries in this study were sourced from murine jejunum. The choice of adopting a gastric ICC model is justified because the entrainment mechanism is conserved between the stomach and small bowel, and because only the activation phase of one slow wave cycle was simulated in the tissue blocks, meaning that differences in gastric and intestinal plateau durations and frequencies were inconsequential.
Furthermore, alternative biophysically based cell models to the Corrias and Buist ICC model have been put forth, notably the ICC model recently proposed by Faville et al. (13). The ICC model by Faville et al. is the first to incorporate a mathematical description of the unitary potentials, which in summation and coupled with whole-cell ionic conductances result in the whole cell slow wave (12,13). Although the ICC model by Faville et al. has the potential to be applied to multiscale framework, in its current state the Faville model does not support cell-to-cell entrainment. A proposed mechanism of entrainment based on unitary potentials is that the elevated voltage-dependent activation of unitary potentials induces a small but highly localized Ca2+ influx, which in turn activates a Ca2+-induced- Ca2+-release involving IP3 receptors (1). Although there is a consensus that Ca2+ release is mediated via IP3 receptors, there remains a controversy over whether the IP3-mediated release is Vm-dependent or Ca2+-dependent (13). Our study favors the hypothesis of a Vm-dependent IP3 model, because the IP3 component of the model by Imtiaz is mediated through Vm, therefore providing a direct way of coupling ICC cell models at a continuum level in a tissue model. In future studies, a Ca2+-dependent mechanism could be included in the ICC model by Faville et al. to simulate entrainment; nevertheless, the Vm-dependent entrainment mechanism adopted for the Corrias and Buist ICC model in this study also remains a valid strategy.
In conclusion, this study has presented an integrated biophysically based and multiscale modeling framework for simulating GI slow wave entrainment within realistic tissue structures. The framework was successfully applied to quantify differences in the peak current density and density of [Ca2+]i between a normal and a degraded ICC network geometry, which could help to explain functional impairments that arise when ICC populations are depleted. This study advances the sophistication of GI modeling toward that of cardiac modeling, and the framework developed here can now be applied to better understand the pathological consequences of ICC network defects in GI motility disorders such as diabetic gastroparesis.
Supporting Material
One table is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00136-0.
Supporting Material
Acknowledgments
The authors thank Pulasthi Mithraratne for his technical assistance with the design of the CellML diagrams and Dr. Vivek Tharayil for assistance with tissue labeling.
Peng Du is supported by a University of Auckland Doctoral Scholarship. This work is partially funded by grants from the New Zealand Health Research Council, the New Zealand Society of Gastroenterology/Ferring Pharmaceuticals Research Fellowship, and National Institutes of Health grants No. DK57061, No. DK68055, and No. R01 DK64775.
References
- 1.Sanders K.M., Koh S.D., Ward S.M. Interstitial cells of Cajal as pacemakers in the gastrointestinal tract. Annu. Rev. Physiol. 2006;68:307–343. doi: 10.1146/annurev.physiol.68.040504.094718. [DOI] [PubMed] [Google Scholar]
- 2.Code C.F., Szurszewski J.H. The effect of duodenal and mid small bowel transection on the frequency gradient of the pacesetter potential in the canine small intestine. J. Physiol. 1970;207:281–289. doi: 10.1113/jphysiol.1970.sp009061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Farrugia G. Interstitial cells of Cajal in health and disease. Neurogastroenterol. Motil. 2008;20(Suppl 1):54–63. doi: 10.1111/j.1365-2982.2008.01109.x. [DOI] [PubMed] [Google Scholar]
- 4.Ordög T. Interstitial cells of Cajal in diabetic gastroenteropathy. Neurogastroenterol. Motil. 2008;20:8–18. doi: 10.1111/j.1365-2982.2007.01056.x. [DOI] [PubMed] [Google Scholar]
- 5.Cheng L.K., O'Grady G., Pullan A.J. Gastrointestinal system. WIREs Sys. Biol. Med. Wiley Interdiscip.Rev. 2009 DOI:10.002/wsbm.019. [Google Scholar]
- 6.Zhao J., Trew M.L., Pullan A.J. A tissue-specific model of reentry in the right atrial appendage. J. Cardiovasc. Electrophysiol. 2009;20:675–684. doi: 10.1111/j.1540-8167.2008.01420.x. [DOI] [PubMed] [Google Scholar]
- 7.Cheng L.K., Komuro R., Pullan A.J. Anatomically realistic multiscale models of normal and abnormal gastrointestinal electrical activity. World J. Gastroenterol. 2007;13:1378–1383. doi: 10.3748/wjg.v13.i9.1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Aliev R.R., Richards W., Wikswo J.P. A simple nonlinear model of electrical activity in the intestine. J. Theor. Biol. 2000;204:21–28. doi: 10.1006/jtbi.2000.1069. [DOI] [PubMed] [Google Scholar]
- 9.Trew M.L., Caldwell B.J., Smaill B.H. Cardiac electrophysiology and tissue structure: bridging the scale gap with a joint measurement and modeling paradigm. Exp. Physiol. 2006;91:355–370. doi: 10.1113/expphysiol.2005.031054. [DOI] [PubMed] [Google Scholar]
- 10.Corrias A., Buist M.L. A quantitative model of gastric smooth muscle cellular activation. Ann. Biomed. Eng. 2007;35:1595–1607. doi: 10.1007/s10439-007-9324-8. [DOI] [PubMed] [Google Scholar]
- 11.Corrias A., Buist M.L. Quantitative cellular description of gastric slow wave activity. Am. J. Physiol. Gastrointest. Liver Physiol. 2008;294:G989–G995. doi: 10.1152/ajpgi.00528.2007. [DOI] [PubMed] [Google Scholar]
- 12.Faville R.A., Pullan A.J., Smith N.P. Biophysically based mathematical modeling of interstitial cells of Cajal slow wave activity generated from a discrete unitary potential basis. Biophys. J. 2009;96:4834–4852. doi: 10.1016/j.bpj.2009.03.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Faville R.A., Pullan A.J., Smith N.P. A biophysically based mathematical model of unitary potential activity in interstitial cells of Cajal. Biophys. J. 2008;95:88–104. doi: 10.1529/biophysj.107.122507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Youm J.B., Kim N., Earm Y.E. A mathematical model of pacemaker activity recorded from mouse small intestine. Philos. Transact. A Math. Phys. Eng. Sci. 2006;364:1135–1154. doi: 10.1098/rsta.2006.1759. [DOI] [PubMed] [Google Scholar]
- 15.Du P., Li S., Chen J.D. Effects of electrical stimulation on isolated rodent gastric smooth muscle cells evaluated via a joint computational simulation and experimental approach. Am. J. Physiol. Gastrointest. Liver Physiol. 2009;297:672–680. doi: 10.1152/ajpgi.00149.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Du P., O'Grady G., Pullan A.J. A tissue framework for simulating the effects of gastric electrical stimulation and in vivo validation. IEEE Trans. Biomed. Eng. 2009;56:2755–2761. doi: 10.1109/TBME.2009.2027690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tharayl V.S., Wouters M.M., Farrugia G. Lack of serotonin 5-HT2B receptor alters proliferation and network volume of interstitial cells of Cajal in vivo. Neurogastroenterol. Motil. 2009 doi: 10.1111/j.1365-2982.2009.01435.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fall C.P., Keizer J.E. Mitochondrial modulation of intracellular Ca2+ signaling. J. Theor. Biol. 2001;210:151–165. doi: 10.1006/jtbi.2000.2292. [DOI] [PubMed] [Google Scholar]
- 19.Ward S.M., Ordog T., Sanders K.M. Pacemaking in interstitial cells of Cajal depends upon calcium handling by endoplasmic reticulum and mitochondria. J. Physiol. 2000;525:355–361. doi: 10.1111/j.1469-7793.2000.t01-1-00355.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Park C.G., Kim Y.D., Jun J.Y. Inhibition of pacemaker currents by nitric oxide via activation of ATP-sensitive K+ channels in cultured interstitial cells of Cajal from the mouse small intestine. Naunyn Schmiedebergs Arch. Pharmacol. 2007;376:175–184. doi: 10.1007/s00210-007-0187-1. [DOI] [PubMed] [Google Scholar]
- 21.Koh S.D., Ward S.M., Horowitz B. Conductances responsible for slow wave generation and propagation in interstitial cells of Cajal. Curr. Opin. Pharmacol. 2003;3:579–582. doi: 10.1016/j.coph.2003.09.002. [DOI] [PubMed] [Google Scholar]
- 22.Imtiaz M.S., Smith D.W., van Helden D.F. A theoretical model of slow wave regulation using voltage-dependent synthesis of inositol 1,4,5-trisphosphate. Biophys. J. 2002;83:1877–1890. doi: 10.1016/S0006-3495(02)73952-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wouters M.M., Gibbons S.J., Farrugia G. Exogenous serotonin regulates proliferation of interstitial cells of Cajal in mouse jejunum through 5-HT2B receptors. Gastroenterology. 2007;133:897–906. doi: 10.1053/j.gastro.2007.06.017. [DOI] [PubMed] [Google Scholar]
- 24.Huizinga J.D., Thuneberg L., Bernstein A. W/kit gene required for interstitial cells of Cajal and for intestinal pacemaker activity. Nature. 1995;373:347–349. doi: 10.1038/373347a0. [DOI] [PubMed] [Google Scholar]
- 25.Miller S.M., Farrugia G., Szurszewski J.H. Heme oxygenase 2 is present in interstitial cell networks of the mouse small intestine. Gastroenterology. 1998;114:239–244. doi: 10.1016/s0016-5085(98)70473-1. [DOI] [PubMed] [Google Scholar]
- 26.Austin T.M., Trew M.L., Pullan A.J. Solving the cardiac bidomain equations for discontinuous conductivities. IEEE Trans. Biomed. Eng. 2006;53:1265–1272. doi: 10.1109/TBME.2006.873750. [DOI] [PubMed] [Google Scholar]
- 27.Edwards F.R., Hirst G.D. An electrical analysis of slow wave propagation in the guinea-pig gastric antrum. J. Physiol. 2006;571:179–189. doi: 10.1113/jphysiol.2005.100743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Park K.J., Hennig G.W., Sanders K.M. Spatial and temporal mapping of pacemaker activity in interstitial cells of Cajal in mouse ileum in situ. Am. J. Physiol. Cell Physiol. 2006;290:C1411–C1427. doi: 10.1152/ajpcell.00447.2005. [DOI] [PubMed] [Google Scholar]
- 29.Austin T.M., Li L., Cheng L.K. Effects of gastrointestinal tissue structure on computed dipole vectors. Biomed. Eng. Online. 2007;6:39. doi: 10.1186/1475-925X-6-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ordög T., Takayama I., Sanders K.M. Remodeling of networks of interstitial cells of Cajal in a murine model of diabetic gastroparesis. Diabetes. 2000;49:1731–1739. doi: 10.2337/diabetes.49.10.1731. [DOI] [PubMed] [Google Scholar]
- 31.Chen J.D., Lin Z., McCallum R.W. Abnormal gastric myoelectrical activity and delayed gastric emptying in patients with symptoms suggestive of gastroparesis. Dig. Dis. Sci. 1996;41:1538–1545. doi: 10.1007/BF02087897. [DOI] [PubMed] [Google Scholar]
- 32.Lammers W.J., Ver Donck L., Schuurkes J.A. Focal activities and re-entrant propagations as mechanisms of gastric tachyarrhythmias. Gastroenterology. 2008;135:1601–1611. doi: 10.1053/j.gastro.2008.07.020. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


