A Mathematical Model of Human Semicircular Canal Geometry: A New Basis for Interpreting Vestibular Physiology

Abstract

We report a precise, simple, and accessible method of mathematically measuring and modeling the three-dimensional (3D) geometry of semicircular canals (SCCs) in living humans. Knowledge of this geometry helps understand the development and physiology of SCC stimulation. We developed a framework of robust techniques that automatically and accurately reconstruct SCC geometry from computed tomography (CT) images and are directly validated using micro-CT as ground truth. This framework measures the 3D centroid paths of the bony SCCs allowing direct comparison and analysis between ears within and between subjects. An average set of SCC morphology is calculated from 34 human ears, within which other geometrical attributes such as nonplanarity, radius of curvature, and inter-SCC angle are examined, with a focus on physiological implications. These measurements have also been used to critically evaluate plane fitting techniques that reconcile many of the discrepancies in current SCC plane studies. Finally, we mathematically model SCC geometry using Fourier series equations. This work has the potential to reinterpret physiology and pathophysiology in terms of real individual 3D morphology.

Electronic supplementary material

The online version of this article (doi:10.1007/s10162-009-0195-6) contains supplementary material, which is available to authorized users.

Introduction

For over 100 years, there has been interest in how the unique three-dimensional (3D) geometry of the semicircular canals (SCCs) determines their function (Dickman 1996). Until recently, it was possible to study SCC geometry only in cadaveric specimens, but now, with the development of high-resolution computed tomography (CT) and magnetic resonance imaging (MRI), it has become possible not only to admire living SCCs but also to mathematically model their geometry. Our aim here was to do so and in the process to study the variability in SCC geometry within and between individuals and to try to use these results to begin reinterpreting vestibular physiology and pathophysiology in terms of real individual 3D geometry.

Maximal endolymph displacement within a SCC occurs with head rotations in a fixed plane that is close to but not necessarily equal to the anatomical SCC plane (Ifediba et al. 2007; Curthoys and Oman 1987; Rabbitt et al. 2003; Rabbitt 1999) and it is dependent on the 3D geometry and cross-sectional area of the membranous SCC (Spoor and Zonneveld 1995, 1998). The geometry of the membranous SCC can be inferred from reconstructed bony SCCs because of the direct connection between the spatial paths of the bony and membranous labyrinth (Igarashi 1966; Curthoys et al. 1977b).

Our goal was to make precise measurements and a mathematical model of SCC geometry from CT imaging in living subjects to allow correlation with physiological data from the same subjects. There have been many CT or MRI studies of the bony labyrinth whose primary focus is illustrative (e.g., Harada et al. 1990; Kassemi et al. 2005; Klingebiel et al. 2002); in contrast, here, we derive a mathematical model from optimization formulations directly verified with micro-CT of cadaveric temporal bone (Uzun et al. 2007).

We apply these techniques to 34 ears and, from this dataset of SCC geometry, derive akin to the Talairach atlas of the brain an “average labyrinth” and describe individual variations from the average. Precise measurement of SCC geometry allows us to accurately describe the dimensions and geometry of the SCC planes, interplane angles, the radii of curvature, extent of planarity, length of the common crus, and other spatial attributes.

The SCC are not orthogonal and not planar (Fig. 1; Sato et al. 1993; Ifediba et al. 2007; Blanks et al. 1975; Della Santina et al. 2005). The effect of non-orthogonality of the SCCs has been explored (Ifediba et al. 2007; Curthoys and Oman 1987); however, little is known of the variability within and between subjects. Two accepted studies of SCC geometry have specified the location of average human SCC planes in the head (Blanks et al. 1975; Della Santina et al. 2005), but have a large discrepancy with each other. By using our current data, we have reconciled this discrepancy. We also quantify the entire SCC path, modeling it concisely using a Fourier series equation and providing a precise, simple, and accessible way of completely describing their 3D geometry.

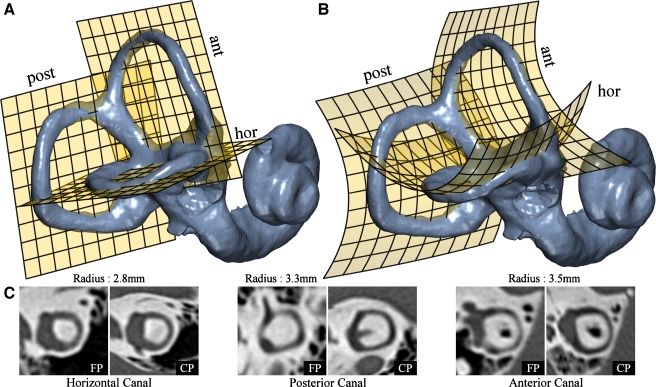
FIG. 1.

Nonplanarity of the SCCs. Least squares “flat” planes were fitted to the centroid paths of each of the SCCs as shown in A. To demonstrate canal nonplanarity, a second-order polynomial was used to also fit a “curved” plane shown in B. This comparison clearly demonstrates nonplanar components of each SSC. C Resliced CT images for each of the planar (FP) and nonplanar (CP) fits. The flat plane slices appear to be good; however, the “curved plane” images show a canal with a higher level of contrast for the entire path. This is because the curved plane passes closer to the centerline of the canal, while the former result can often be deceptive due to the thickness of the canal. The radius of each particular canal is provided to indicate scale in comparison to the original resolution of 0.5 mm. Note that the resliced curved plane images have a non-uniform scale due to the nature of the curved space mapping.

Ifediba et al. (2007) used fluid dynamic modeling to study the operation of actual SCC geometry, based upon detailed reconstruction of labyrinth anatomy taken from histological sections of two cadaveric temporal bones. They suggested that the physiological planes are best estimated by plane fitting using weights proportional to the inverse square of the cross-sectional area of the membranous duct; we have followed that suggestion. Their reconstructions were performed by hand-tracing histological sections, whereas we have used semi-automated reconstructions of high-resolution CT from 34 ears of live subjects.

Methods

Subjects

CT scans were acquired for each subject during routine diagnostic imaging of patients being investigated for vertigo, superior canal dehiscence, cholesteatoma, hearing loss for cochlear implant, and conductive deafness. The anatomy of each inner ear was assessed as normal by a radiologist. The subjects were between 17 and 84 years of age (mean of 58 ± 18 years). There were nine males and 11 females with six ears being discarded for technical reasons, leaving a total of 34 ears and 14 complete pairs. The data reported here were from clinical CT and involved no experimentation on human subjects but only reprocessing of existing anonymized scan data. As such, the study is in accord with the Department of Health and Human Services criteria 45 CFR 46.101 (b) (4) policy for the protection of human research subjects.

CT and micro-CT scans were also acquired from a human temporal bone specimen. The specimen was fixed by a standard 4% formaldehyde-based fixative. The use of the human temporal bone for the micro-CT studies was approved by the New South Wales Department of Health.

Data acquisition

High-resolution CT scans were acquired using either a General Electric (GE) Lightspeed VCT or Lightspeed 16 CT or a Siemens Somatom Emotion 16 CT scanner. These are 64, 16, and 16 slice scanners, respectively, and all have an effective resolution of approximately 0.5 mm with an axial slice thickness of 0.625, 0.625, and 0.5 mm, respectively. Our procedure followed standard temporal bone imaging practice and consisted of scanning the subject's head in the supine position with a capture volume that encompassed both temporal bones in a single acquisition, allowing for an additional 1 cm at both upper and lower boundaries. The scans were acquired helically. The tomographic reconstruction was performed using a 9.6-cm field of view with an effective voxel size of 0.18 × 0.18 × 0.3 mm and using a bone reconstruction kernel. The 3D datasets were exported as axial images in uncompressed Digital Imaging and Communications in Medicine format.

The datasets are imported into 3D image-processing software written in Labview 7.1 (National Instruments, Texas, USA) and C. Preprocessing involved importing the dataset to form a 3D image which was then interpolated to form an image with isotropic voxels of size 0.06 mm. A high-order interpolation kernel was used to ensure there was no distortion of frequency components within the Nyquist bandwidth (Blu and Unser 2000). Anatomical illustrations were rendered using Houdini 9.0 (Side-FX, Toronto, Canada).

Validation

We validate the accuracy of our methods and verify our assumptions by using micro-CT as a “ground truth” comparison. The same temporal bone specimen was scanned using both clinical high-resolution CT (GE VCT) and micro-CT (Skyscan 1172). Micro-CT provides a modality for imaging small objects with very high spatial resolution; our paradigm had an isotropic resolution of 17 µ for an object volume of 5 × 5 × 5 cm. The respective 3D images were rotated and translated with respect to each other using automated software, as to be optimally coregistered with respect to a least squares cost criterion. This provided a comparison that was very close to a “ground truth” and a reliable indication of the measurement errors resulting from our procedure.

The major factors that contribute to errors are from processes internal to the CT imaging system, primarily noise and partial voluming (Brooks and Chiro 1976). CT noise at object boundaries is amplified in the image gradient domain, which results in errors during edge detection. Image blurring from partial voluming (or volume averaging) causes morphological dependent distortion, which tends to be much greater for small objects.

Labyrinth surface reconstruction

Surface reconstructions of the labyrinth are shown here solely for illustrative purposes and are not used for anatomical measurements. Reconstructions were segmented semi-automatically using the watershed algorithm (Beucher and Lantuejoul 1979), designed for boundary determination in situations where objects appear to overlap or are blurred together. After segmentation, the object surfaces were reconstructed as a triangular mesh using the marching cubes algorithm (Lorensen and Cline 1987).

Active contour model

Many medical imaging settings require the extraction of image features such as edges, lines, and other regions. An automated analysis is highly desirable as it minimizes subjectivity and operator variability. Reconstruction of small structures that are at or near the resolution and noise limits of the scanning modality presents a challenge. An active contour is an automated method of extracting object boundaries from images while preserving desired characteristics such as smoothness and regularity (Jacob et al. 2004; Brigger et al. 2000; Kass et al. 1987). More specifically, it is an energy-minimizing contour guided by balancing internal and external energy functions. The internal energy is derived from elastic and tension properties given to the curve, designed to keep the curve smooth and regular. The external energy is constructed to direct the contour onto the desired image features such as object edges. So the active contour will find the best smooth solution that matches object morphology. Active contours have several advantages over widely used threshold methods. They do not critically depend upon subjective parameter selection (such as thresholds) as object boundaries are identified using image gradient information and they are less sensitive to artifacts such as noise and variations in background intensity.

B-splines have been used extensively to mathematically represent active contours as they require few parameters, are inherently smooth, and permit local control of the curve via adjustment of individual control points. Our procedure uses a two-dimensional (2D) B-spline active contour to accurately reconstruct cross-sectional slices of the SCCs taken from CT imaging. The mathematical formulation of the active contour modeling employed is discussed in the Appendices.

Our strategy for reconstructing a complete SCC is by combining the cross-sectional modeling with an automated tracking system that propagates the active contour along the canal and automatically detects canal endpoints. The steps of the system are as follows and are illustrated in Figure 2:

1. An operator selects a starting position anywhere on the canal.

2. A 2D multiplanar reformatted CT slice of the canal cross-section is extracted from the 3D image at the designated position.

3. Active contour modeling is performed on the slice, reconstructing the canal cross-sectional morphology.

4. The centroid is calculated as the contour's center of mass.

5. The position and orientation of the next slice is predicted from the previous centroids.

6. If a canal endpoint is not detected, go to step 2.

7. When the entire canal is traversed in both directions, the centroids are combined to form the 3D centroid path.

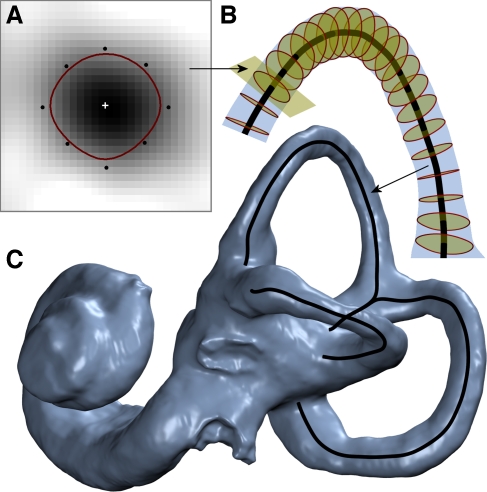
FIG. 2.

Modeling of SCCs. A A cross-sectional slice of the bony canal is modeled using a B-spline active contour, with the centroid determined by a center of mass calculation. B This modeling is performed along the entire length of the canal, with the contour centers tracing out the 3D geometrical centroid path. C Modeling of all three bony canals produces the complete canal centroid path shown overlaid on the labyrinth reconstruction.

The automatic detection of the canal endpoints uses the cross-sectional area to determine whether the contour has either passed into the vestibule or has reached the bifurcation of the common crus. The two boundary slices are adjusted via manually guided rotations to ensure a consistent alignment with the ends of the canal.

After the centroid path sections of the three canals and the common crus have been determined, the common crus section is attached to both the anterior and posterior canal sections. The joint is calculated using spline interpolation to maintain a smooth and continuous transition with the geometry at both ends. Each canal path is three-dimensionally resampled using spline interpolation to the predetermined number of samples and with a uniform sampling interval not exceeding 0.1 mm.

SCC coordinate systems

To understand labyrinth operation, knowledge of the 3D geometry in space is required. This represents two separate problems, one of labyrinth morphology and the other of labyrinth location and orientation within the head. The former requires a labyrinth-based system of coordinates and the latter head-based coordinates. This study is primarily concerned with labyrinth morphology and hence a labyrinth-based framework was used to facilitate direct computations of 3D morphological variability. This system mutually aligns the set of labyrinths using their canal plane vectors, effectively eliminating any net translational and rotational differences between them.

For congruence with previous studies, the “labyrinth-fixed” coordinate system is referenced back into “head space” using a technique developed by Ifediba et al. (2007) of aligning the current mean results as closely as possible to an accepted published set of average canal planes specified in Reid’s coordinate system (Della Santina et al. 2005).

Reid’s plane is defined as the plane that passes through the center of each external auditory canal and the inferior margin of the two orbits (Blanks et al. 1975). The coordinate system is defined from the orthogonal basis formed by the axes of this plane. Reid’s plane was not measured directly in this study because the landmarks could not be reliably detected; this is in part due to a limited acquisition volume, designed to meet a low radiation dose requirement. We will refer to our system as the Referential Reids System of Coordinates (RRSoC).

The left ear was mirrored onto the right side for cases when the labyrinths were to be analyzed individually.

Mathematical model of the SCCs

The SCCs are geometrically difficult to describe due to a complex morphology that has many degrees of freedom. We have applied a Fourier series equation to provide a complete and accessible mathematical model of the canals. This model implicitly encapsulates many SCC attributes that are currently specified only in isolation, such as the canal planes and radius of curvature. Most importantly, this equation describes the nonplanar curvature of the canals and permits direct application in fluid dynamic modeling.

The 3D Fourier series equation of the canal, given in Eq. 1, is a parameterization based upon the angle of the arc from the center of the canal. The Fourier series can represent any continuous 3D contour, given a sufficient number of terms. Generally, three terms are adequate to achieve a very close representation of the canals and their nonplanar curvature, as demonstrated in Figure 3.

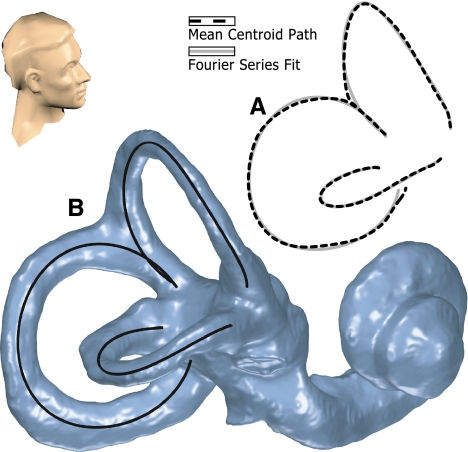
FIG. 3.

Fourier series model of the SCCs. A Plot of the average SCC geometry shown against the corresponding Fourier series model of that data, shown from a superior-right point of view. This illustrates the closeness of fit that is achieved with this model. B Also demonstrated for an individual ear where the SCC model is shown superimposed on the bony labyrinth reconstruction.

Measurement of the derived attributes

Planes

A plane is the simplest form of numerically describing a SCC. This basic measurement is important because it simply describes the direction that closely resembles the axis about which rotations elicit a maximal canal response. Since the canals are generally not planar, measurements attempt to find the plane that best fits the canal with respect to some criterion. This criterion will determine the relative influence or weighting that each part of the canal has on the result. Since we have access to the complete canal path, we sought to formalize this problem by explicitly specifying canal weighting. This permitted us to perform a critical analysis of different weighting paradigms that help to explain the results of previous studies. The generalized weighted least squares formulation for fitting a plane to a SCC is given in Eq. 2. A section with a weight of 1 will have a maximal influence, while a section with a weight of 0 will have no influence:

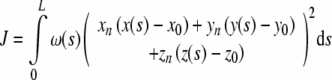where (x_n, y_n, z_n) is the unit length plane normal vector; (x₀, y₀, z₀) is the plane origin vector; (x(s), y(s), z(s)) is the centroid path which is a function of cumulative distance (s) along the path; w(s) is the weighting function; and L is the length of the centroid path.

The cross-sectional area-based weights Ifediba et al. (2007) suggested that the best weighting system to use, in a functional sense, is one proportional to the inverse square of the cross-sectional area of membranous labyrinth at that location. This is given in Eq. 3 where CSA(s) is the cross-sectional area along the path:

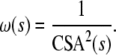Since there is no direct access to the cross-sectional area of the membranous duct in CT, an approximate measure was used. This was derived through the consideration of previous studies of membranous duct dimensions (Curthoys and Oman 1987; Ifediba et al. 2007). A good approximate model assumes that the duct cross-sectional area is constant along the majority of the canal, only deviating from this towards the ends of the duct where it does so linearly. Numerical values for the parameters of this model were taken from the literature.

The reduced span weights Original data from Blanks et al. (1975), consisting of bony canal centroid data points taken from dried skulls, were compared to the results from our current study. This revealed that the original measurements did not include the entire canal path: data points were not taken in the region of the common crus and the ampulla due to difficulties with the dissection. We found the average span of these measurements by calculating the average the start and end points, represented as percentage distance along the path relative to current results. This measurement process was simulated using “reduced span” weights constructed by setting the weight to 1 within the average span and to 0 elsewhere.

Angle between planes

The angle between two planes is calculated using the dot product of the two plane normal vectors a and b, as shown in Eq. 4. The sign of the normal vector to a SCC plane is selected to correspond to the activation direction of that canal according to the right hand rule:

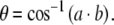Radius of curvature

The radius of curvature was measured for each SCC by projecting the canal centroid path onto its least squares plane and then using a least squares elliptical fit to this 2D data. The radius was calculated by taking the geometric mean of the major and minor radii of the ellipse, as given in Eq. 5; this solution corresponds to the radius of a circle with equal area. An elliptical fit is preferential to direct circle fitting because the latter will result in biased measurements when applied to noncircular data. The coordinates of the ellipse center are also used to define the center of the canal plane:

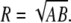Degree of nonplanarity

SCC nonplanarity appears as either a twisting or a bending of the canal depending upon the viewing direction, as illustrated in Figure 4. There are several different methods of quantifying nonplanarity that have been used in the past, such as maximum displacement from the plane, greatest angular displacement as measured from the plane center, or angular difference between a planes fitted to either end of the canal. However, we suggest that, from both mathematical and physiological point of views, the most useful measure is the angular span of the canal path. This is measured geometrically by the range of the angle made between the local canal tangent and the plane; this can be closely considered to be the angle formed between the canal paths in Figure 4B. In practice, this measurement is derived from the SCC model described in the “Mathematical model of the SCCs” section: this captures the characteristic first-order bend or twist while minimizing the influences of small perturbations.

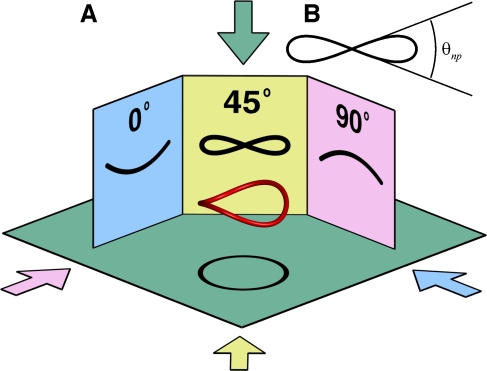
FIG. 4.

A. Projections made from a typical nonplanar canal show an alternating between a bending and a twisting as the viewing direction is rotated. The nonplanarity metric used in the study is the range of angles which the tangential path makes with the average canal plane. This range is approximately equal to the range of angles made by the 45° projection shown in B.

Relationship between the bony canal and membranous duct

Our results pertain to the centroid of the bony canal. However, the functional geometry that is of interest is that of the membranous duct. The membranous duct is located at the outermost margin of each bony canal (Curthoys et al. 1977b; Igarashi 1966), although in cross-sectional area, the duct only occupies a small proportion, about 5%, of the cross-sectional area of the bony canal (Curthoys et al. 1977a; Ifediba et al. 2007). Assumptions based upon this anatomical evidence can be incorporated in a straightforward manner into an estimation of the location of the ducts, which are not visible with clinical CT. A technique for doing this is presented in the Appendices.

In short, anatomical evidence has shown that there is a direct connection between the curvature of the bony canal and that of the membranous duct, so that geometrical attributes of the membranous duct are reflected in the bony canal (Curthoys and Oman 1987; Ifediba et al. 2007). So, discussions of variability, canal radius, and canal curvature are valid when considering either the bony canal or membranous duct.

Results

The labyrinths from each subject were reconstructed and each SCC centroid path was calculated using the spline modeling procedure. The dataset was mutually aligned using least squares optimization and was referenced to the RRSoC as described in the “Methods” section. The full results are plotted in Figure 5. The average set of SCCs was calculated from the entire dataset of 34 ears and our mathematical model was applied to this result (given in the Appendices). The model of the approximate location of the average membranous ducts was also calculated and is also presented in the Appendices.

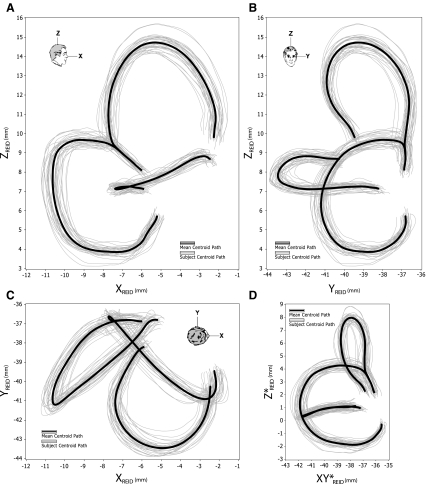
FIG. 5.

Individual and average SCC geometry. Plots of the mutually aligned data from 34 subject ears with the mean in bold, specified in the RRSoC. The pitch, roll, and yaw planes are given in A, B, and C, respectively. A perspective view in the plane of the horizontal canal is given in D that highlights the marked trend of horizontal canal nonplanarity. The datasets appear to have strong mutual resemblance: this is partly due to the gross alignment method employed; however, upon closer inspection, there is much variation in both canal orientation and morphology.

Comparison of plane fitting techniques

In order to determine the sensitivity of plane fitting approaches, we compared the results found by using four different weighting paradigms. As discussed in the “Planes” section, we tested uniform weighting (Uniform) of the entire canal, uniform weighting but excluding the common crus (NonCrus), uniform weighting in the “reduced” span (RedSpan), and the inverse square of the approximate cross-sectional area of the membranous duct (CrossSect).

Angular differences between each of these plane fitting techniques are shown in Table 1. The inclusion of the common crus region contributes an average of 2° to the result. Most importantly, the weights that attempt to replicate measurements made by Blanks et al. (1975) result in differences of up to 10°. The cross-sectional area-based weight, which attempts to account for the functional plane, influences the posterior and superior canals by 4° and the horizontal only marginally.

TABLE 1.

The mean angle (± standard deviation) between the SCC planes for each pair of weighting paradigms

	Comparison of plane weighting strategies
	Horizontal (°)	Posterior (°)	Anterior (°)
Uniform − NonCrus		1.8 ± 0.5	1.7 ± 0.8
Uniform − CrossSect	1.2 ± 0.9	3.9 ± 1.3	4.0 ± 1.0
Uniform − RedSpan	10.7 ± 4.4	8.0 ± 2.9	10.0 ± 3.0
NonCrus − CrossSect	1.2 ± 0.9	2.3 ± 1.2	5.1 ± 0.9
NonCrus − RedSpan	10.7 ± 4.4	6.6 ± 2.6	10.9 ± 3.2
CrossSect − RedSpan	10.1 ± 4.8	4.3 ± 1.5	6.0 ± 2.2

Angles between canal planes

The mean set of angles between each pair of canal planes in a single ear is given in Table 2 for each of the four weighting paradigms. The cross-sectional area-based weights result in the plane equations given in Table 3, which have measurements of 89.6 ± 5.2° for the horizontal–posterior angle, 85.6 ± 4.4° for the horizontal–anterior angle, and 91.6 ± 3.4° for the posterior–anterior angle; the complete set of angles between each pair of canals from both left and right ears is given in Table 4. Labyrinth reconstructions of the dataset’s extremes cases are illustrated in Figure 6A.

TABLE 2.

The mean angle (± standard deviation) between each pair of SCC planes resulting from each weighting paradigm

	Mean angle between plane pairs comparing different weighting strategies
	Horizontal–Posterior (°)	Horizontal–Anterior (°)	Posterior–Anterior (°)
Uniform	90.2 ± 4.9	89.8 ± 3.6	96.9 ± 2.9
NonCrus	90.7 ± 5.0	91.2 ± 3.7	94.1 ± 3.1
CrossSect	89.6 ± 5.2	85.6 ± 4.4	91.6 ± 3.4
RedSpan	91.2 ± 6.5	71.2 ± 6.2	85.0 ± 4.9
Study A	95.9 ± 4.7	67.8 ± 7.6	86.2 ± 4.7
Study B	90.3 ± 4.9	90.4 ± 6.2	94 ± 4.0

These results show angular differences of up to 18°. These differences explain the discrepancies found between study A (Blanks et al. 1975) and B (Della Santina et al. 2005)

TABLE 3.

The average plane equations for the six SCCs; calculated using the CrossSect weights and referenced to the RRSoC

Average canal plane equations
L hor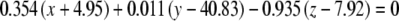
L pos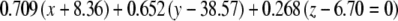
L ant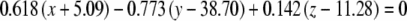
R hor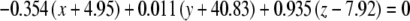
R pos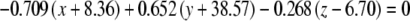
R ant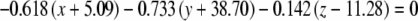

This representation incorporates both the normal to the plane and the center of the canal; given in millimeters.

L – left, R - right, hor - horizontal, pos - posterior, ant - anterior

TABLE 4.

The mean angle (± standard deviation) between each pair of canal planes from both left and right ears; calculated using the CrossSect weights

Canal pair	Mean angle between SSC plane pairs
	Angle (°)	Angle Pooled (°)
LH–LP	90.7 ± 5.6	89.6 ± 5.6
RH–RP	88.5 ± 5.7	89.6 ± 5.6
LH–LA	85.8 ± 5.6	85.2 ± 4.5
RH–RA	84.7 ± 3.2	85.2 ± 4.5
LP–LA	90.9 ± 2.9	91.3 ± 3.2
RP–RA	91.8 ± 3.5	91.3 ± 3.2
LH–RP	91.5 ± 8.9	92.1 ± 8.0
LP–RH	92.7 ± 7.3	92.1 ± 8.0
LH–RA	91.8 ± 9.5	92.6 ± 9.3
LA–RH	93.5 ± 9.3	92.6 ± 9.3
LP–RA	164.1 ± 6.5	164.5 ± 6.3
LA–RP	164.9 ± 6.3	164.5 ± 6.3
LH–RH	168.3 ± 6.3	168.3 ± 6.3
LP–RP	101.6 ± 8.0	101.6 ± 8.0
LA–RA	76.7 ± 9.1	76.7 ± 9.1

L left, R right, H horizontal, P posterior, A anterior

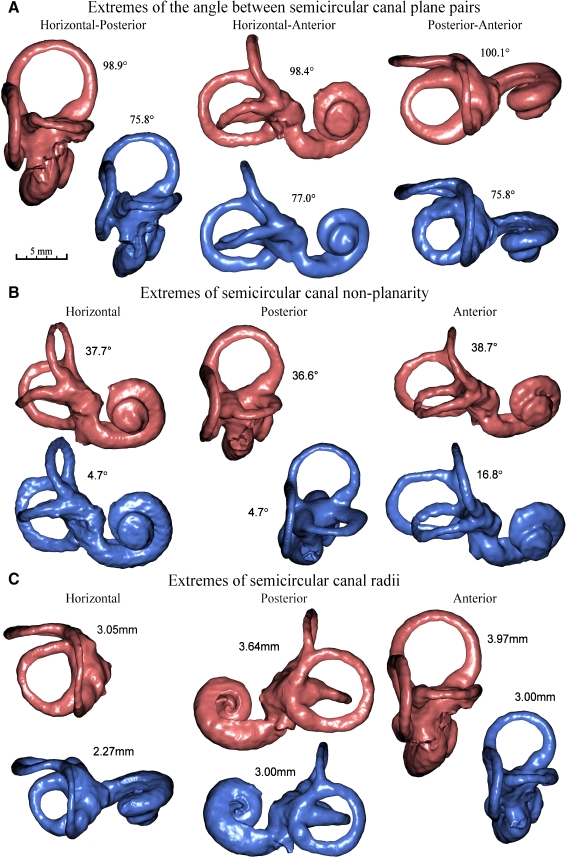
FIG. 6.

Comparison of geometrical attributes via labyrinth reconstruction. Labyrinth reconstructions showing the extreme cases of the A angle between SCC plane pairs, B SCC nonplanarity, and C SCC radius. In each case, the orientation was chosen to best highlight the attribute being inspected. All reconstructions shown on this page are presented at the same scale as shown in A. In one subject, CT noise from a cochlear implant prevented reconstruction of the cochlear portion of one labyrinth.

Nonplanarity of the semicircular canals

The mean nonplanarity coefficients for the three canals were 23.4 ± 7.1, 20.9 ± 7.3, and 27.6 ± 5.2 for the horizontal, posterior, and anterior canals, respectively. This confirms the notion that the anterior canal exhibits the greatest amount of nonplanarity of the three canals, with the posterior canal having the least. As can be seen in Figure 5, the canal curvature tends to be orientated in a consistent direction. The degree of nonplanarity does vary significantly between subjects as indicated by the large standard deviations and also by the extremes illustrated in Figure 6B.

Radius of curvature of the semicircular canals

The mean radii for the three canals were 2.69 ± 0.20 mm for the horizontal, 3.32 ± 0.19 mm for the posterior, and 3.43 ± 0.23 mm for the anterior. The extremes of canal radii present in the dataset are illustrated in Figure 6C for each of the canals.

Validation

The same temporal bone specimen was scanned with both CT and micro-CT, the 3D images coregistered, and the same modeling procedures were applied to each. Centroid modeling in the two modalities showed a root mean squared difference of 0.08 mm, which means that the centroid reconstruction system performs at subpixel resolution, as 0.08 mm is less than 20% of the clinical CT pixel size. The plane fitting of the three canals resulted in a mean error of 0.55°.

Discussion

Canal morphology and orientation

One goal of our measurements is to provide the necessary information to understand the functional operation of the SCCs. Canal attributes can specify much of this information, whereas the mathematical model we have presented gives a complete and accurate description of SCC morphological structure. It is important not only to identify the average canal morphology but also to understand normal variations about that average through both the standard deviation and extreme cases. Attributes can be helpful here but are best served when complemented with an understanding of how they manifest in actual morphological structure. The means of the individual attributes were within the ranges reported in the literature, although the actual values of nonplanarity differ due to various metrics used (Curthoys et al. 1977a; Sato et al. 1993; Della Santina et al. 2005). An analysis of attribute correlations reveals that a large degree of codependency exists in seemingly independent variables. Notably, the horizontal–posterior angle has correlation coefficients of 35% with the anterior radius and 45% with the anterior twist; the horizontal–anterior angle has a correlation coefficient of 39% with the posterior twist; and the posterior–anterior angle has a correlation coefficient of 46% with the posterior twist. There is a detailed coverage of this analysis presented in the supplementary material.

The SCCs do not lie within a plane but have a variable amount of curvature with respect to a flat plane. We have shown that the selection of the plane fitting method can have a direct bearing on the solution; note that the angular range that is possible here is directly quantified by the degree of nonplanarity attribute. Our intercanal angles using the cross-sectional area-based weight differ by up to 5° from the angles found by Della Santina et al. (2005). This disparity constitutes differences in the weighting approach used, the precision of the measurement techniques, and the actual population sample. The greatest divergence was found to involve the anterior canal, the canal that possesses the greatest degree of nonplanarity and the most difficult to fit visually by an operator.

We attempted to replicate the methods of Blanks et al. (1975) through the use of reduced span weights. We did not reproduce the methods used by Della Santina et al. (2005) as they cannot be represented mathematically and are difficult to reproduce due to the inherent subjectivity, but they do show close correspondence to the NonCrus weighting strategy. The reduced span weights showed a marked disparity with the other results, most prominently in the horizontal–anterior angle with a difference of 10°; this is due to characteristic bend in the horizontal canal as seen in Figure 5D. We suggest that this is the reason for the large discrepancies found between the studies of Blanks et al. (1975) and Della Santina et al. (2005).

Difference between anatomical and functional canal planes

Fluid dynamic modeling has suggested that maximal response planes are independent of any canal curvature out of that plane. We have shown that curvature itself plays an important role in plane fitting, through the application of weighting and due to the high correlation with other attributes such as nonplanarity.

To understand the normal range of SCC function, it is crucial to determine the variability of canal geometry and to what degree this will affect the maximal response planes. The maximal response plane is defined as the plane that exhibits the maximal response when the three-canal system is rotated about that plane. Current modeling shows that, for arbitrary SCC geometry, the maximal response plane can differ significantly from the anatomical plane (Ifediba et al. 2007). This difference is due to two factors.

Firstly, the amount of friction exerted on the endolymph from the sides of the membranous duct wall varies along the canal in a relationship with duct cross-section area Muller (1994). Models, such as the model used in Ifediba et al. (2007), have suggested that this property can be reasonably accounted for by fitting a plane to the membranous duct path using a weighting along the path that corresponds to this friction or to the inverse of the cross-sectional area squared. This means that the path of the thin membranous duct around the canal has the greatest influence upon these planes. The planar results found in this study have been calculated following this suggestion.

Secondly, this is not a system of three isolated canals: the canals are linked together and possess shared sections, such as the common crus and the vestibule. In such a system, the pressure gradient in one canal will influence fluid movement in adjacent canals; any rotation will cause a continuous pressure field across the three canals (Hullar and Williams 2006). The net pressure gradient around any canal path will determine fluid movement in that canal and hence mediate corresponding afferent signals to the brain. The brain combines these mismatched signals to form an anatomically consistent head movement.

While the use of weighting can account for cross-sectional area-dependent frictional variations, the differences due to the interconnectedness of the three canals need to be determined via other means, such as fluid dynamic modeling. Functional studies that refer the SCC planes to behavioral responses would be better served by comparison with maximal response planes rather than with the anatomical planes. In order to permit this comparison, a set of mean maximal response planes is needed to complement the mean planes given in Table 3. Such a set of mean maximal response planes can be determined through the application of fluid dynamic modeling on the mean SCC geometry presented here. The technique would also make it possible to determine the maximal response planes in individual subjects. For the first time, such a system could calculate the stimulus that each SCC end organ is receiving for any given head rotation in a living patient. In such a framework, it would also be possible to examine closely the influence of individual geometric characteristics such as canal nonplanarity and their precise effect upon the function of the mechanical system. Furthermore, one could study the relationship between the anatomical and functional results and begin to reinterpret vestibular physiology and pathophysiology in terms of the individual 3D geometry.

Bilateral labyrinth relationships

Our descriptions of SCC geometry confirm results of previous studies that examine single labyrinths (Curthoys et al. 1977a). However, in normal subjects, the responses generated by vestibular stimulation (such as the vestibulo-ocular reflex) depend on the synergistic action of SCCs in both labyrinths. The output from each labyrinth is combined centrally to generate behavioral responses. Neurophysiological studies show that bilaterally paired SCCs function as a “push–pull” pair (Wilson and Jones 1979). A head rotation will generate a pattern of endolymph flow in the SCCs on both sides, but any symmetry in the exact pattern of fluid flow (and thus stimulation) will depend upon the symmetry of SCC geometry.

During development, the whole labyrinth migrates from the base of the skull to its final position and orientation in the head (Bast and Anson 1949; Cox and Jeffery 2007; Curthoys et al. 1982). As that migration takes place, there are many opportunities for a departure from parallelism for the synergistic canals in the two labyrinths. It is likely that mechanisms of neural plasticity act to overcome the functional consequences of such departures from parallelism; however, the effects of the precise anatomical arrangement may be revealed in diseases where one labyrinth becomes dysfunctional, where the function of a single SCC is disturbed (e.g., benign paroxysmal positional vertigo [BPPV]), or in unusual vestibular environments analogous to the asymmetric otolith model of space motion sickness (von Baumgarten 1987). To understand these situations, it is important to consider the normal range of deviations from ideal symmetry.

Asymmetry can arise from misalignment of the labyrinth as a whole, from variations in the orientation of individual SCCs, or differing morphology such as radius of curvature and nonplanarity. The methods developed in this study provide a tool for measuring in living subjects all aspects of these asymmetries and not just those associated with planar descriptions. This analysis can be done by examining the maximal response plane symmetry using fluid dynamic simulations or by considering the symmetry of individual attributes. We found that, in the 14 pairs of labyrinths we studied, the canals had an average correlation coefficient of 91.9% for the radius of curvature, 69.4% for the nonplanarity angle, and 81.6% for the intercanal angles. While this dataset shows reasonable attribute correlation, there are several individual attributes that show marked asymmetry, with differences up to 0.21 mm in the radius of curvature, 12.3° in the nonplanarity angle, and 9.1° in the intercanal angles. These measurements are important as left–right labyrinthine functional asymmetry is the basis of much vertigo pathophysiology. Detailed coverage of these results is provided in the supplementary material.

Clinical significance

There are many methods available to the diagnostic radiologist for viewing CT imaging, including in-plane and perpendicular to the canal plane views, curved plane reformatting, cross-sectional views of the canal, and lengthwise curved slice views of the canal. As highlighted in Figure 1, an optimal orientation provides maximal contrast by minimizing the effects of partial voluming and is essential for correct diagnosis in cases such as SCC dehiscence (Belden et al. 2003). The automated methods described here provide the accurate anatomical information necessary for optimal slice positioning.

Imaging reports commonly include volume rendering of inner ear anatomy, an approach different to the methods presented here. Volume rendering produces a qualitative visual depiction rather than accurate quantitative 3D geometry, and as such, its interpretability is limited, especially when the exact location of the SCC is important such as in SCC occlusion for intractable positional vertigo or superior SCC dehiscence (Agrawal and Parnes 2008).

Knowledge of precise SCC geometry could be important to clinical diagnosis and treatment. For example, repositioning treatment of BPPV involves rotation in the plane of the affected canal in order to exert inertial forces upon the otoconia crystals within the SCC so as to move them from the SCC into the vestibule (Bhattacharyya et al. 2008). Otoconial movement is determined by the component of the force that is tangential to the SCC. Since the SCC is generally nonplanar, this implies that there is no fixed rotation plane that is optimal for all points along the canal. The angular range to which this tangential component varies within a single canal is directly specified in this study by the nonplanarity angle. When this range is considered together with the natural variability of nonplanarity and plane orientation within the population, the range of tangential components will span over 40°. While successful treatment can be made by rotation with small angular differences with the tangential path, the extremes in the population may account for the 10% of patients whose treatments remain unsuccessful: this may be especially important in cases of cupulolithiasis. Another issue is conversion, where the simplified repositioning maneuvers inadvertently move the otoconia into an adjacent canal. A more detailed model of the SCCs makes possible the development of new techniques that optimize clinical guidance and limit the number of conversions during treatment. We suggest in cases of unsuccessful repositioning treatment and where prior imaging is available that consulting patient 3D SCC geometry may provide insight into the interpretation of the pathophysiology and treatment.

Note that the discussions within this report are also applicable to other 3D imaging modalities such as MRI.

Appendices

Appendix A: availability of data

We have made the 3D raw data, the dataset of geometrical attributes, and a set of 3D labyrinth reconstructions available as supplementary files for this article. This material is in the form of an Adobe Acrobat 3D file that can be viewed using Adobe Acrobat Reader version 8 and higher. This allows the reader to rotate and examine the data in 3D.

Appendix B: 2D active contour model

The parametric description of the 2D B-spline contour used in this study is given by Eq. 6 and is illustrated in Figure 2A. It is formed piecewise by continuous polynomial segments, whereby control points (P_i) have a local influence on the contour as determined by the basis functions 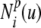. The basis functions are periodic in parameter u, thus resulting in a closed contour. The system used a cubic B-spline (p = 3) with eight control points:

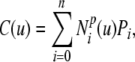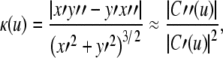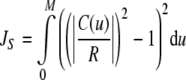where:

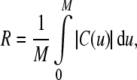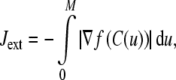Definition of terms:

C(u)

active contour

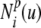
ith B-spline basis function

p

degree of polynomial

P_i

ith control point

u

B-spline parameter

x, y

spatial coordinates

M

parametric extent of u

Κ

contour curvature

f

CT Image

J

total energy

λ₁ , λ₂, λ₃

energy weights

The energy formulations used in this study are based upon methods discussed in Jacob et al. (2004). The total energy of the active contour (J) is defined as the weighted sum of three separate energy terms J_S, J_C, and J_ext. Uniform parametric sampling is achieved using J_S (Eq. 8); it serves to keep the sampling rate at a constant value. The smoothing term J_C (Eq. 10) minimizes the square of the contour curvature, where curvature is defined in Eq. 7; this approximation is valid when the magnitude of the first derivative remains roughly constant, which is ensured by J_S. The external energy in Eq. 11 is based upon the magnitude of the image gradient; this attracts the contour towards edges. Weights were chosen to provide the best balance of contributions from all energy terms.

The active contour is initialized to a circle centered on the slice, with the energy minimizing solution found by performing gradient descent with a line search upon the active contour parameters. This is efficient due to the small number of control points, the simple morphology, and the initial proximity of the final solution.

Appendix C: average semicircular canal equations

The parameters for the mathematical model of the average geometrical centroid path of each of the bony SCCs, defined in RRSoC, are presented in Table 5.

TABLE 5.

Parameters of the mathematical model of the average geometry of the bony SCCs; aligned to RRSoC

SCC model parameters	Horizontal	Posterior	Superior
az	7.77	6.73	11.31
ay	−40.81	−38.68	−38.42
ax	−4.93	−8.24	−4.99
bz	0.82	3.07	3.39
by	2.67	2.29	2.09
bx	2.42	2.58	2.79
ϕz	131.8	−68.1	−152.5
ϕy	24.3	9.1	−36.6
ϕx	112.7	36.9	111.4
cz	0.25	0.03	0.06
cy	0.04	0.23	0.39
cx	0.02	0.20	0.17
φz	−86.9	−119.7	151.7
φy	71.3	−137.4	125.0
φx	35.0	57.2	151.1
θs	258.8	317.9	272.3

a, b, c in millimeters, θ_s, ϕ, φ in degrees

Appendix D: approximation of the membranous ducts

The micro-CT images of the temporal bone specimen provided accurate measurements of the bony canal wall; these were used to determine the approximate location of the membranous duct. This was done by following the path along the outermost wall of the canal, with adjustments to account for the thickness of the membranous duct. The relative location of the membranous duct path to the bony canal path, in this one specimen, was used to infer the location of the membranous duct from the bony canal path for the remaining ears in the dataset.

We applied this procedure to the average SCC geometry to give an approximate model of average membranous semicircular duct. The parameters of its mathematical model equations are given in Table 6.

TABLE 6.

Parameters of the mathematical model of the approximate average geometry of the membranous semicircular ducts; aligned to RRSoC

SCC model parameters	Horizontal	Posterior	Superior
az	7.72	6.55	11.30
ay	−40.45	−38.59	−38.33
ax	−4.72	−8.26	−4.65
bz	1.15	3.77	3.88
by	3.74	2.92	2.66
bx	3.33	3.06	3.45
φz	144.8	−75.3	−150.8
φy	29.6	2.9	−33.3
φx	119.2	33.9	105.7
cz	0.40	0.08	0.10
cy	0.06	0.25	0.39
cx	0.05	0.25	0.28
ϕz	−75.7	177.1	104.0
ϕy	72.8	−128.0	111.8
ϕx	−61.6	78.2	107.8
θs	249.2	324.7	271.7

a, b, c in millimeters, θ_s, ϕ, φ in degrees

This measurement is taken from only one particular specimen and is not known to be representative of a global population; the bony canal cross-sectional diameter does have an amount of intersubject variability. We provide these details for completeness and to demonstrate how membranous duct information can be estimated from diagnostic CT imaging.