Abstract
A series of flow-cell experiments was conducted to investigate aqueous dissolution and mass-removal behavior for systems wherein immiscible liquid was non-uniformly distributed in physically heterogeneous source zones. The study focused specifically on characterizing the relationship between mass flux reduction and mass removal for systems for which immiscible liquid is poorly accessible to flowing water. Two idealized scenarios were examined, one wherein immiscible liquid at residual saturation exists within a lower-permeability unit that resides in a higher-permeability matrix, and one wherein immiscible liquid at higher saturation (a pool) exists within a higher-permeability unit adjacent to a lower-permeability unit. The results showed that significant reductions in mass flux occurred at relatively moderate mass-removal fractions for all systems. Conversely, minimal mass flux reduction occurred until a relatively large fraction of mass (>80%) was removed for the control experiment, which was designed to exhibit ideal mass removal. In general, mass flux reduction was observed to follow an approximately one-to-one relationship with mass removal. Two methods for estimating mass-flux-reduction/mass-removal behavior, one based on system-indicator parameters (ganglia-to-pool ratio) and the other a simple mass-removal function, were used to evaluate the measured data. The results of this study illustrate the impact of poorly accessible immiscible liquid on mass-removal and mass-flux processes, and the difficulties posed for estimating mass-flux-reduction/mass-removal behavior.
Keywords: transport, DNAPL, contamination, groundwater
Introduction
One of the most critical issues associated with hazardous waste sites is the potential presence of immiscible-liquid source zones in the subsurface. Immiscible liquids serve as long-term sources of subsurface contamination, and their presence can greatly impact the costs and time required for site remediation. In fact, the presence of dense nonaqueous-phase liquids (DNAPLs) is usually considered the single most important factor constraining the risk assessment, characterization, and cleanup of organic-contaminated sites (NRC 1994, 1997, 1999, 2000, 2005; ITRC, 2002; EPA, 2003). The contaminant mass flux or mass discharge emanating from a source zone, also referred to as the source strength or source function, is recognized as a primary determinant of the risk associated with a contaminated site. Concomitantly, the reduction in mass flux achieved with a specified level of source-zone mass removal (or mass depletion) is a key metric for evaluating the effectiveness of a source-zone remediation effort. Thus, there is great interest in characterizing, estimating, and predicting relationships between mass flux reduction and mass removal.
The fundamental concept of contaminant mass flux, its relationship to mass-removal processes and source-zone properties, and its impact on risk has long been established (e.g., Fried et al., 1979; Pfannkuch, 1984). The impact of subsurface heterogeneity and non-uniform immiscible-liquid distribution on mass-removal behavior and associated aqueous-phase concentrations (mass flux) has been examined for some time through laboratory, modeling, and field studies (e.g., Schwille, 1988; Dorgarten, 1989; Guiguer, 1991; Anderson et al., 1992; Brusseau, 1992; Guarnaccia and Pinder, 1992; Mayer and Miller, 1996; Berglund, 1997; Nelson and Brusseau, 1997; Blue et al., 1998; Powers et al., 1998; Unger et al. 1998; Broholm et al., 1999; Brusseau et al., 1999; Frind et al., 1999; Zhang and Brusseau, 1999; Brusseau et al., 2000; Nambi and Powers, 2000; Saba and Illangasekare, 2000; Zhu and Sykes, 2000; Rivett et al., 2001; Sale and McWhorter, 2001; Brusseau et al., 2002; Jayanti and Pope, 2004; Lemke et al., 2004; Parker and Park, 2004; Phelan et al., 2004; Soga et al., 2004; Falta et al., 2005; Jawitz et al., 2005; Rivett and Feenstra, 2005; Fure et al., 2006; Lemke and Abriola, 2006; Brusseau et al., 2007). An early effort to quantify the relationship between contaminant mass flux reduction and mass removal, and the resultant reduction in risk, was presented by Freeze and McWhorter (1997). The specific relationship between mass flux reduction and mass removal has since been examined and discussed in a number of studies (e.g., Enfield et al., 2002; Rao et al., 2002; Rao and Jawitz, 2003; Stroo et al., 2003; Brooks et al., 2004; Jayanti and Pope, 2004; Lemke et al., 2004; Parker and Park, 2004; Phelan et al., 2004; Soga et al., 2004; Falta et al., 2005; Jawitz et al., 2005; NRC, 2005; Fure et al., 2006; Lemke and Abriola, 2006; Brusseau et al., 2007).
Three simplified, prototypical relationships between mass flux reduction and mass removal useful for comparative discussion are illustrated in Figure 1A. Such relationships can be readily developed by employing a simple limiting-case analysis of the temporal contaminant-elution/mass-removal function for immiscible-liquid systems (as shown in Figure 1B), from which the mass-flux-reduction/mass-removal relationship can be obtained directly. The curve in the lower right of Figure 1A represents the relationship for a system governed by relatively ideal mass-transfer behavior, wherein mass removal is relatively efficient, as illustrated by the corresponding contaminant elution curve presented in Figure 1B. Because mass removal is relatively efficient, the aqueous-phase contaminant concentrations are maintained at maximal or near-maximal levels, and thus there is minimal reduction in mass flux until almost all of the mass has been removed. The curve in the upper left of Figure 1A represents the relationship for a system governed by non-ideal mass-transfer behavior (e.g., rate-limited dissolution, by-pass flow phenomena), wherein mass removal is relatively inefficient (Figure 1B), and there is a significant reduction in mass flux with minimal mass removed. The third curve represents the special case wherein there is a one-to-one relationship between mass flux reduction and mass removal (e.g., first-order mass removal).
Figure 1.
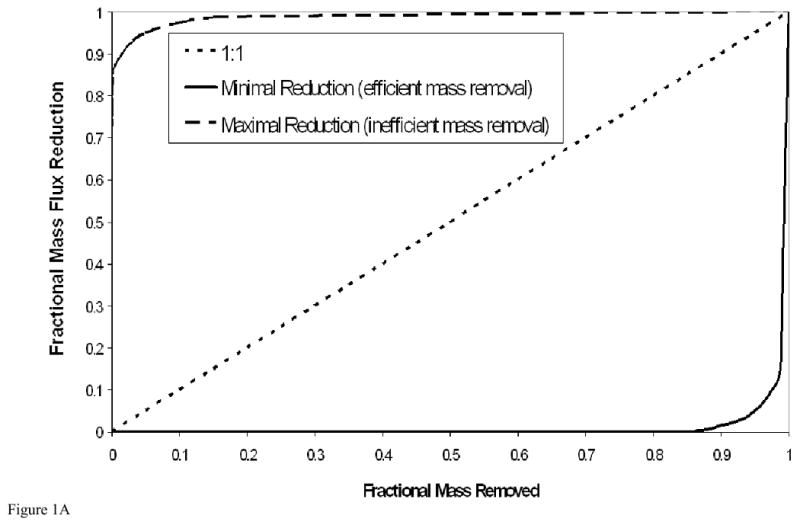
Figure 1A. Three simplified, prototypical relationships between mass flux reduction and mass removal. These curves are derived from the concentration-time functions presented in Figure 1B.
Figure 1B. Contaminant elution curves corresponding to the two limiting cases of mass removal (efficient and inefficient), and that of first-order mass removal.
There are two general approaches to characterizing the relationship between mass flux reduction and mass removal, end-point analysis and time-continuous analysis. End-point analysis is based on comparing mass fluxes measured before and after a source-zone remediation effort. For example, Suchomel and Pennell (2006) conducted flow-cell experiments to examine the impact of surfactant-enhanced solubilization on mass-flux-reduction/mass-removal behavior. Several examples of end-point analyses based on field studies have recently been reported (Brooks et al., 2004; Childs et al., 2006; McGuire et al., 2006; Brusseau et al., 2007). The end-point analysis approach provides critical information for evaluating the impact of a source-zone remediation effort on mass flux. However, the single-snapshot characterization of mass-flux-reduction/mass-removal behavior obtained with this approach is constrained in that the antecedent behavior remains indeterminate. Conversely, as the name implies, time-continuous analysis incorporates a “complete” characterization of the relationship between mass flux reduction and mass removal, from the initial stages of mass removal to a given end point. This approach provides a more robust characterization of mass-flux behavior as a function of mass removal. Direct, experiment-based investigations of time-continuous mass-flux-reduction/mass-removal behavior are just now beginning to be reported. For example, Fure et al. (2006) conducted flow-cell experiments under continuous water-flushing conditions to examine the impact of source-zone architecture on mass-flux-reduction/mass-removal behavior. Brusseau et al. (2007) report a time-continuous mass-flux-reduction/mass-removal relationship for a large chlorinated-solvent contaminated Superfund site in Tucson, AZ.
An expert-panel workshop was convened recently to discuss the research needs for characterization and remediation of DNAPL source zones (SERDP, 2006). The panel noted that significant uncertainty remains with respect to the impact of source-zone architecture and mass-transfer dynamics on mass-removal and mass-flux-reduction behavior. One issue that was particularly emphasized was the behavior of systems in which immiscible liquid is associated with regions of the subsurface that are poorly accessible to flowing groundwater (i.e., that are “flow limited”). For example, the majority of the chlorinated-solvent contaminated sites in the U.S. are several to many decades old. For such sites, it would generally be expected that a large fraction of the more hydraulically accessible immiscible-liquid mass has been removed in the intervening time (thus producing the associated aqueous contaminant plumes). For another example, source-zone remediation efforts are generally considered to be able to remove or deplete only a portion of the total contaminant mass, and it is likely that the majority of mass removed is primarily that which is more accessible. Thus, for both examples (i.e., both unremediated and remediated source zones), a “residual” mass of immiscible liquid will typically remain in the source zones, and this mass will most likely be associated with regions of the subsurface that are poorly accessible to flowing groundwater, such as within or adjacent to lower-permeability zones. This poorly accessible mass will have a significant impact on long-term mass flux, and thus on long-term site management efforts.
Improved understanding of the impact of immiscible liquid located within low-permeability matrices and other flow-limited domains was deemed a critical research need in the SERDP review (SERDP, 2006). The purpose of the study reported herein was to investigate mass-flux-reduction/mass-removal behavior for idealized systems in which immiscible liquid is hydraulically poorly accessible. This was accomplished with flow-cell experiments conducted under continuous water-flushing conditions, wherein immiscible liquid was emplaced within (residual saturation) or adjacent to (pool) lower-permeability matrices.
Materials and Methods
System Design
As noted above, the objective of the study was to investigate mass-flux-reduction/mass-removal behavior for systems wherein immiscible liquid is poorly accessible to flowing water. Thus, the flow-cell systems were designed to represent in an idealized manner source zones that have undergone an extensive degree of water flushing (“aged” systems) such that contaminant mass associated with hydraulically accessible domains (e.g., so-called residual or ganglia immiscible liquid within higher-permeability units) has been removed, and immiscible liquid associated with flow-limited regions remains. Two representative scenarios were examined, one wherein immiscible liquid at residual saturation exists within a lower-permeability unit that resides in a higher-permeability matrix, and one wherein immiscible liquid at higher saturation (a pool) exists within a higher-permeability unit adjacent to a lower-permeability unit. The flow-cell systems were prepared in such a manner to focus specifically on the issue of poorly accessible immiscible liquid. Thus, the immiscible liquid was emplaced only in the target zones, rather than being “spilled” into the system. In addition, an idealized permeability distribution was used to eliminate the impact of non-uniform flow associated with permeability variability in regions upgradient and downgradient of the source zone on mass removal and mass flux. It should be emphasized that the systems are designed to represent the specific idealized scenarios noted above, and that the immiscible-liquid distributions employed are not necessarily those that would occur if immiscible liquid were spilled into the top of a water-saturated flow cell with these particular permeability configurations.
Materials
The porous media used in the experiments are commercially-available natural sands obtained from Unimin Corporation (Le Sueur, MN). Three media with different median particle diameters were used, 724 μm (20-30 mesh), 360 μm (40-50 mesh), and 172 μm (70-100 mesh). Representative hydraulic conductivities for the three media are 460, 72, and 7 cm/h, respectively. Trichloroethene and carbon tetrachloride, ACS grade (Aldrich Chemical Col, Inc., Milwaukee, WI), were used as the immiscible liquids. They were dyed with certified Sudan IV (Aldrich Chemical Col, Inc., Milwaukee, WI) at a concentration of 100 mg/L, which has been shown to have minimal impact on fluid properties and behavior (e.g., Schwille, 1988; Kennedy and Lennox, 1997). Dichloromethane (DCM) used in extractions was ACS/HPLC certified solvent (Burdick and Jackson, Muskegon, MI).
Both rectangular and cylindrical flow cells were used in the study. The rectangular flow cells (used for experiments Lower-K-1, Lower-K-2, and Pool as referenced below) were constructed of stainless steel and tempered glass, with approximate dimensions of 50 cm long by 40 cm high by 5 cm wide. These flow cells were equipped with multiple, evenly spaced injection/extraction ports on the upgradient and downgradient edges, the latter of which could be used to collect vertically discrete aqueous samples and flow-rate measurements. The cylindrical flow cell (used for experiment Lower-K-3 as referenced below) was constructed of stainless steel and was 7.65 cm in diameter and 10 cm long.
Methods
A total of five sets of experiments were conducted for this study. Three sets of experiments were conducted to examine the case wherein immiscible liquid is located within a lower-permeability unit. The porous-medium configuration was changed for each of these experiments to examine the impact of source-zone architecture on mass-flux and mass-removal behavior. For the first experiment (Lower-K-1), two rectangular lower-permeability zones, composed of 360-μm diameter and 172-μm diameter sand, respectively, were emplaced within a higher-permeability (724-μm diameter sand) matrix (see Figure 2). For the second experiment (Lower-K-2), immiscible liquid was located within three lenticular lower-permeability zones (360-μm) packed within a higher-permeability matrix (724-μm) (see Figure 3A). A third experiment (Lower-K-3) was conducted to examine the impact of source-zone length scale on mass flux and mass removal behavior. For this system, a single cubic lower-permeability zone (2.5-cm each side) composed of 360-μm sand was placed within a uniform packing of higher-permeability (724-μm) sand. A fourth experiment (Pool) was conducted to examine the case wherein greater-than-residual saturations of immiscible liquid reside within higher-permeability units adjacent to a lower-permeability unit. Three lenticular higher-permeability zones, composed of 724-μm diameter sand, were emplaced within a lower-permeability (360-μm) matrix (see Figure 3A). For this system, the immiscible liquid was injected into the designated zones during packing. Finally, a control experiment was conducted to characterize mass removal and associated mass flux reduction under conditions wherein mass removal was as ideal as possible. This would represent a system comprised of a homogeneous porous medium, uniform flow field, and a residual saturation of immiscible liquid distributed throughout the system. Dye and non-reactive tracer tests were conducted for each of the source-zone configurations to characterize the associated flow fields.
Figure 2.
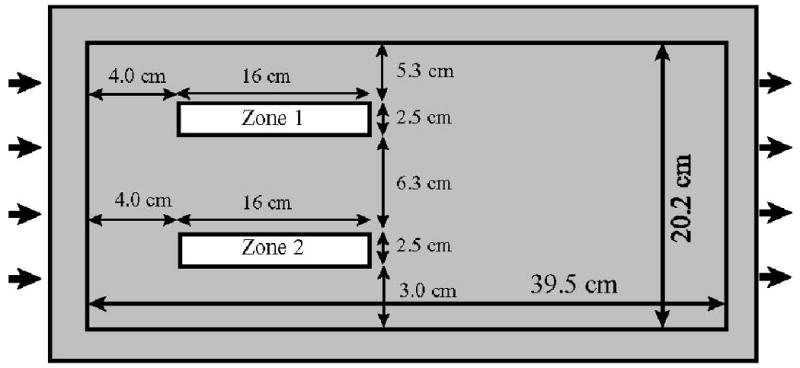
Schematic of source-zone configuration for experiment Lower-K-1.
Figure 3.
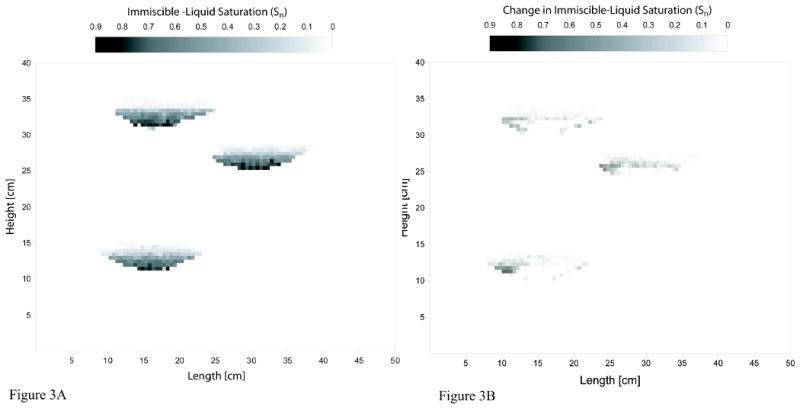
Figure 3A. Schematic of source-zone configuration for the Pool experiment. Also shown is the initial immiscible-liquid saturation distribution measured with the dual-energy gamma system.
Figure 3B. Immiscible-liquid saturation removed after approximately 63 pore volumes of water flushing (low values correspond to minimal removal and vice versa).
The flow cells were packed under saturated conditions (ponded water). The flow cell was packed to a height coincident with the top boundary of each of the planned inclusions. The matrix was then excavated to the lower boundary of the planned immiscible-liquid zone, and the selected source-zone material was added. For the Lower-K experiments, the media for each source zone was prepared by thoroughly mixing a pre-determined amount of damp sand (moisture content of ∼20%) with an amount of immiscible liquid that would yield a saturation close to residual. This material was then packed into each designated location. Subsamples of the contaminated media were collected during packing and subjected to solvent extraction to ensure that the saturations were close to the target value (approximately 14% for all experiments except the Pool experiment). The results of prior studies have shown that this method of emplacement produces relatively uniform distributions of immiscible liquid within the source zone (e.g., Brusseau et al., 2000, 2002). For the “pool” experiment, the water table was raised above the top boundary after excavation, and the zone was packed with 724-μm diameter sand. The water table was then lowered to 1 cm below the bottom of the zone, and immiscible liquid was injected into the top of the zone at a rate of 1.0 ml/min using a syringe pump. After emplacement of the zones, the water table was slowly raised and the matrix sand was packed above the zone. The source zones employed for the experiments (except for Lower-K-3) were approximately 15-cm long. Thus, a 2.5-cm diameter by 15-cm long column packed homogeneously with the 724-μm diameter sand was used for the control experiment. A residual saturation of trichloroethene was established throughout the column using standard procedures (e.g., Imhoff et al., 1994; Powers et al., 1994; Johnson et al., 2003).
Once a flow cell was prepared, water was inject at a constant rate, equivalent to an average pore-water velocity of approximately 20 cm/h, to initiate the dissolution study. For all experiments, effluent samples were collected with a glass syringe and either analyzed immediately with an ultraviolet-visible (λ = 210) spectrophotometer (Shimadzu 1601) or injected into glass autosampler vials. The latter samples were stored at 4 °C until analyzed using a gas chromatograph (Shimadzu 14A or 17A) equipped with a flame ionization detector (FID) and electron capture detector (ECD). Higher-concentration samples were analyzed by direct aqueous phase injection (1 μl) using GC-FID equipped with an autosampler. Lower-concentration samples were analyzed via GC-ECD equipped with a headspace autosampler. Methods were the same for both applications: Supelco SPB-624 capillary column, oven temperature was held at 40 °C for 2 minutes and then ramped at a rate of 10 °C/min to a final temperature of 170 °C, injector temperature at 180 °C, detector temperature at 200 °C. The quantifiable detection limits were approximately 1 mg L-1 (UV-VIS), 1 mg L-1 (GC-FID), and 0.0001 mg L-1 (GC-ECD). Upon completion of all experiments (except for which the dual-energy gamma system was used as discussed below), the flow cell was opened and sub-samples of the porous media were collected for solvent-extraction analysis. The sub-samples were added to vials containing DCM, which were then sealed and placed on a shker table for 24 h. Aliquots of the extractant were removed and analyzed via GC-FID. The results of these analyses indicated that all immiscible-liquid mass was removed to the limit of detection for all experiments. Integration of the effluent concentration data provided total mass, cumulative mass removed, and mass flux as a function of time.
The initial distribution of immiscible liquid within the source zones was relatively uniform for the residual-saturation experiments as noted above. Conversely, a nonuniform distribution was expected for the pool experiment. Thus, a dual-energy (280 mCi Americium and 100 mCi Cesium) gamma radiation system was used to measure immiscible-liquid saturations within the flow cell for this experiment, following procedures used in prior experiments (e.g., Oostrom et al., 1999; Brusseau et al., 2000; 2002). The spatial resolution was approximately 0.25 cm2, with a saturation measurement sensitivity of approximately 0.003. The scans required 60 seconds per location, for a total of approximately 12 hours for the entire flow cell. Scans were obtained prior to the start of water flushing, at the end of the experiment, and at two additional times during the experiment.
Results and Discussion
Contaminant Elution Behavior
The contaminant elution curves obtained from the flow-cell and control experiments are presented in Figure 4. The effluent concentrations for the flow-cell experiments are less than aqueous solubility values as expected due to dilution effects associated with the system configurations. The elution curves exhibit relatively extensive periods wherein the concentrations decrease gradually, reflecting the impacts of mass-removal constraints. Mass removal was constrained primarily by the limited contact between flowing water and the immiscible liquid, due to the specific source-zone configurations. This was true for the pool system as well as the lower-K-zone systems, as confirmed by the results of dye tracer tests (data not shown).
Figure 4.
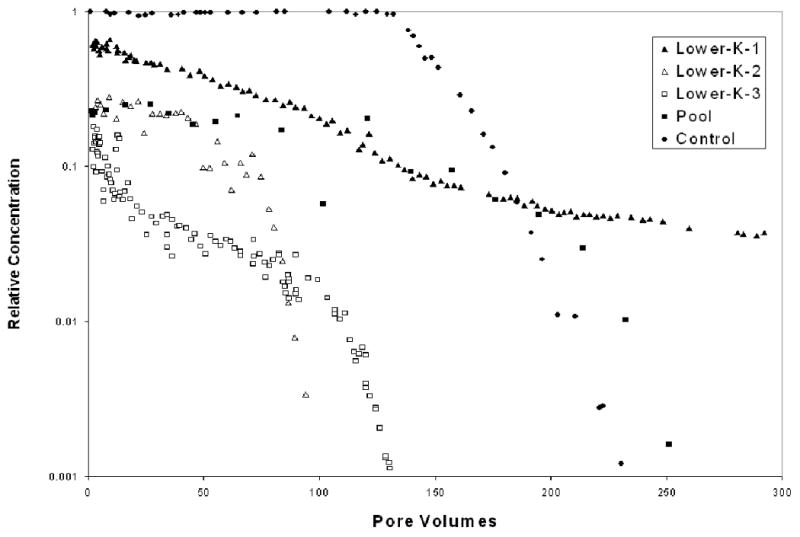
Contaminant elution curves for the experiments. Effluent concentrations are normalized by the aqueous solubility of the contaminant.
For the pool system, measurements obtained with the dual-energy gamma system prior to the start of water flushing showed that immiscible-liquid saturations were non-uniformly distributed within each of the three source zones (Figure 3A). Immiscible liquid at saturation values close to residual (∼16%) spanned the upper and middle sections of each zone, whereas saturations much greater than residual (i.e., pools) were present at the bottom of each zone. Approximately 90% of the immiscible liquid volume was associated with the pool regions. The proportion of immiscible liquid residing in the pools was greater for the second gamma scan, conducted after approximately 63 pore volumes of water flushing, reflecting the preferential removal of mass from the regions containing residual saturation (Figure 3B).
Mass-Flux-Reduction/Mass-Removal Behavior
The reductions in mass flux associated with mass removal for the flow-cell and control experiments are presented in Figure 5. For the control experiment, minimal mass flux reduction occurred until a relatively large fraction of mass (>80%) was removed. This behavior is what is expected for an ideal system wherein immiscible liquid is distributed throughout the entire system and is fully accessible (Figure 1). An approximate one-to-one relationship is observed between mass flux reduction and mass removal for the first flow-cell experiment (Lower-K-1), wherein immiscible liquid resided within two lower-permeability units surrounded by coarser sand. Comparison of these results to those obtained for the control experiment illustrates the impact of poorly accessible immiscible liquid on mass-removal efficiency, and associated mass-flux reductions. A slightly lesser magnitude of mass flux reduction is observed for the Lower-K-2 experiment. The difference in behavior observed between the Lower-K-1 and Lower-K-2 experiments reflects the lesser degree of hydraulic accessibility of the immiscible liquid (and resultant less efficient mass removal) for the former experiment, due to the source-zone architecture employed in that experiment. Recall that two source zones were emplaced for experiment Lower-K-1, one consisting of 360-μm diameter sand and one of 172-μm diameter sand. Conversely, the source zones consisted only of the coarser 360-μm diameter sand for experiment Lower-K-2.
Figure 5.
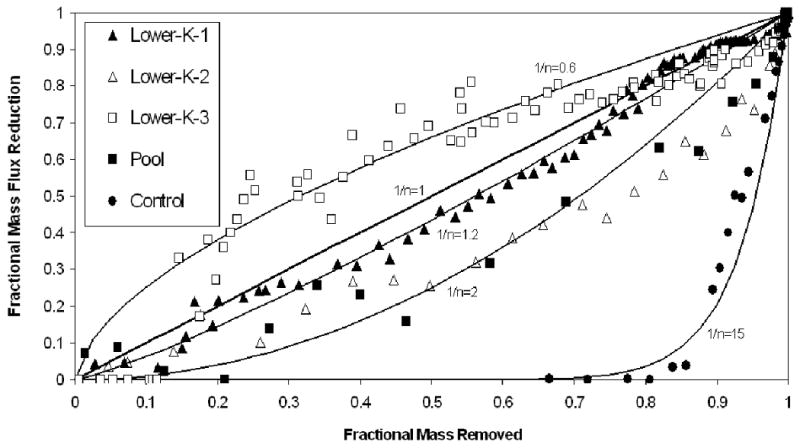
Mass flux reduction versus mass removal behavior for the experiments. Also shown are mass-flux-reduction/mass-removal curves produced with a simple mass-removal function (the 1/n values are labeled in the figure).
The mass-flux-reduction/mass-removal relationship for experiment Lower-K-3 exhibits non-singular behavior, comprising three discrete stages. Initially, no mass flux reduction is observed until after 10% mass removal, at which point mass flux decreases rapidly to approximately 50% reduction with minimal mass removal (additional 10% removed). Thereafter, mass flux reduction and mass removal both increase at a moderate rate for the remainder of the experiment. This behavior may be related in part to the specific configuration employed (three-dimensional), wherein water flow occurred along all sides of the source-zone unit for this experiment, in contrast to the other, two-dimensional, flow-cell experiments wherein flow occurred only along the upper and lower boundaries of the units. Such non-singular or multi-step mass-flux-reduction/mass-removal behavior was observed for selected individual realizations in recent mathematical-modeling studies (Phelan et al., 2004; Soga et al., 2004). It is also observed in the measured field data reported by Brusseau et al. (2007).
The results for the experiment conducted with a pool-dominated source zone, for which initially approximately 90% of the total immiscible-liquid volume resided in regions wherein saturations were greater than residual, are also presented in Figure 5. The degree of mass flux reduction is similar to that observed for the Lower-K-2 experiment. The results for the pool system are generally similar to those obtained from mathematical-modeling analyses of mass-flux/mass-removal behavior for systems wherein immiscible liquid is distributed as both residual saturation and pools in physically heterogeneous sources zones (Lemke et al., 2004; Parker and Park, 2004; Phelan et al., 2004). Analysis of the results of these modeling studies reveals that mass-flux-reduction/mass-removal behavior primarily ranged from slightly lesser to slightly greater than one-to-one, depending upon the specific source-zone architecture. Similarly, approximate one-to-one relationships were observed for the integrated mass-flux-reduction/mass-removal data obtained from flow-cell experiments conducted with immiscible liquid distributed as both residual and pools (Fure et al., 2006).
System-Indicator Parameters and Simple Mass-Removal Functions
There is interest in the use of system-indicator parameters for delineating the type of mass-flux-reduction/mass-removal behavior expected for a given set of conditions. One example is the ganglia-to-pool ratio (e.g., Lemke et al., 2004; SERDP, 2006). The ganglia-to-pool ratio provides some qualitative measure of immiscible-liquid accessibility with respect to the degree of contact between flowing water and the immiscible liquid, under the assumption that immiscible liquid in regions comprising primarily “ganglia” (residual saturation) would generally be more accessible than immiscible liquid associated with pools. In prior studies, lesser degrees of mass flux reduction have been observed for systems with higher ganglia-to-pool ratios, whereas one-to-one and greater than one-to-one reductions were observed for systems with moderate to low ratios (Lemke et al., 2004; Phelan et al., 2004; Lemke and Abriola, 2006; Suchomel et al., 2006). Mass-flux-reduction/mass-removal behavior may also be influenced by the time scale of contact between the flowing water and the source zone (flow rate, system dimensions), and the overall amount of immiscible liquid present, especially under conditions wherein one or more mass-transfer processes are rate limited. Thus, other potential system-indicator parameters include global immiscible-liquid saturation, source-zone residence time, source-length:system-length ratio, and source-area:system-area ratio (cross-sectional areas). The values of selected system-indicator parameters for the experiment systems are presented in Table 1.
Table 1.
System-indicator parameters for the experiments.
| Experiment | Ganglia:Pool1 | Global SN (%)2 | tsz3 (h) | Lsz/LT4 | Asz/AT5 |
|---|---|---|---|---|---|
| Lower-K-1 | all ganglia | 2 | 3 | 0.4 | 0.25 |
| Lower-K-2 | all ganglia | 1 | 1 | 0.3 | 0.3 |
| Lower-K-3 | all ganglia | 0.5 | 0.1 | 0.3 | 0.14 |
| Pool | 0.1 | 2 | 1 | 0.3 | 0.22 |
| Control | all ganglia | 14 | 1 | 1 | 1 |
Ganglia-to-pool ratio, defined as the volume of immiscible liquid occurring as “ganglia” (Sn≤residual saturation) divided by the volume of immiscible liquid residing in pools (Sn>residual saturation)
Global Sn is defined as the volume of immiscible liquid divided by the pore volume of the entire system (source zones plus matrix)
Residence time in source zone (source-zone length/mean pore-water velocity)
Length of source zone/Length of system
Cross-sectional area of source zone/Cross-sectional area of system
The ganglia-to-pool ratio provides a representative assessment of the respective mass-flux-reduction/mass-removal behaviors observed for the pool system (low ratio) versus the control experiment (all ganglia), consistent with the results noted above. The ganglia-to-pool ratio does not, however, provide a complete assessment of hydraulic accessibility effects, particularly with respect to the impact of immiscible liquid trapped within lower-permeability matrices. For example, the mass-flux-reduction/mass-removal behavior observed for experiment Lower-K-2 is similar to that observed for the Pool experiment, although the immiscible liquid was distributed entirely as ganglia (high ratio) for the Lower-K-2 experiment. The potential impact of other factors listed in Table 1 is illustrated by comparing the results obtained for experiment Lower-K-3 to those obtained for the first two Lower-K experiments (see Figure 5). A generally greater degree of mass flux reduction was observed for Lower-K-3. Note that the source-zone residence time and global immiscible-liquid saturation were lower for the Lower-K-3 experiment than for the other experiments (Table 1).
The ability to predict the mass-flux-reduction/mass-removal relationship for a given system would obviously be of great assistance in evaluating the potential benefits and cost-effectiveness of a proposed remediation effort. To that end, several approaches, based on simple “mass-removal” functions or “source-depletion” models, have been proposed recently for estimating mass-flux-reduction/mass-removal behavior (e.g., Enfield et al., 2002; Rao et al., 2002; Rao and Jawitz, 2003; Parker and Park, 2004; Zhu and Sykes, 2004; Falta et al., 2005; Jawitz et al., 2005; Christ et al., 2006). One simple approach is based on treating changes in mass flux as a direct function of the change in contaminant mass. This leads to a relationship of the form: (1-J(t)/J0) = (1-M(t)/M0)1/n, where J is mass flux, J0 is initial mass flux, M is contaminant mass, and M0 is initial mass. The parameter “n” defines the specific mass-flux-reduction/mass-removal relationship, and thus incorporates the impact of source-zone architecture, flow-field dynamics, and mass-transfer processes on mass-flux and mass-removal behavior. Applications of this approach are discussed in several recent publications (e.g., Rao et al., 2002; Zhu and Sykes, 2004; Falta et al., 2005).
The simple function was applied to the data sets reported herein (see Figure 5). The special case of 1/n=1 produces the one-to-one mass-flux-reduction/mass-removal curve. The measured data obtained for the Lower-K-1 experiment are observed to vary between the curves produced with 1/n=1 and 1.2 (Figure 5). The results of the Lower-K-2 and Pool experiments are roughly approximated by the curve produced with 1/n=2. The control-experiment data are well represented by the curve produced with1/n=15. In these cases, the simple function provides reasonable matches to the measured data. In contrast, the singular curves produced with the simple function can not reproduce the multi-step behavior exhibited by the data obtained for experiment Lower-K-3.
Conclusion
A series of flow-cell experiments was conducted to investigate mass-flux-reduction/mass-removal behavior for simplified systems wherein immiscible liquid was poorly accessible to flowing water. Two scenarios were examined, one wherein immiscible liquid at residual saturation existed within a lower-permeability unit residing in a higher-permeability matrix, and one wherein immiscible liquid at higher saturation (a pool) existed within a higher-permeability unit adjacent to a lower-permeability unit. The results showed that significant reductions in mass flux occurred at relatively moderate mass-removal fractions for all systems. Conversely, minimal mass flux reduction occurred until a relatively large fraction of mass (>80%) was removed for the control experiment, which was designed to undergo efficient mass removal (ideal mas-transfer conditions). In general, mass flux reduction was observed to follow an approximately one-to-one relationship with mass removal.
The ganglia-to-pool ratio was used to assess the relative behavior observed for the experiments. The ganglia-to-pool ratio provided a representative assessment of the respective mass-flux-reduction/mass-removal behaviors observed for the pool system versus the control experiment. The ratio was not effective, however, for characterizing the behavior observed for the experiments for which immiscible liquid was trapped within lower-permeability matrices. This illustrates the limitations of employing the ganglia-to-pool ratio to characterize the hydraulic accessibility of immiscible liquid, particularly with respect to the assumption that immiscible liquid present as ganglia is more accessible than that associated with pools. A more generally applicable system-indicator parameter would incorporate the specific disposition of the ganglia (e.g., account for the possible presence of immiscible liquid in lower-permeability matrices).
A simple mass-removal function was applied to the measured data and provided reasonable matches for all but one experiment. For this latter case, the singular curves produced with the simple function could not reproduce the multi-step behavior exhibited by the data obtained for experiment Lower-K-3. Use of these functions for predicting mass-flux-reduction/mass-removal behavior requires a priori determination of specific values for “n”. This may prove difficult in some cases, considering the complexities associated with the impacts of source-zone architecture, flow-field dynamics, and mass-transfer processes on mass flux and mass removal.
The results of this study illustrate the impact of poorly accessible immiscible liquid on mass-removal and mass-flux processes, and the relationship between mass flux reduction and mass removal. Additional research is needed to further develop methods for characterizing and predicting mass-flux and mass-removal behavior for systems wherein the hydraulic accessibility of immiscible liquid is limited. The efficacy of existing methods are likely to be especially constrained for these systems, and thus they should be used with caution.
Acknowledgments
This research was supported by The National Institute of Environmental Health Sciences Superfund Basic Research Program (ES04940), and the Dept. of Energy Research Fellowship Program in Interfacial and Condensed Phase Chemical Physics at the Pacific Northwest National Laboratory. Part of the experimental work was conducted at the Environmental Molecular Sciences Laboratory (EMSL), a national scientific user facility sponsored by the Department of Energy's Office of Biological and Environmental Research, located at Pacific Northwest National Laboratory. We wish to thank Asami Murao and Dr. Geoff Tick of the Contaminant Transport Laboratory, Larry Acedo of the University Research Instrumentation Center at the University of Arizona, and Tom Wietsma and Matt Covert from the Pacific Northwest National Laboratory.
References
- American Petroleum Institute (API) Groundwater Remediation Strategies Tool. Regulatory Analysis & Scientific Affairs Department; Wash, DC: Dec, 2003. Publication Number 4730. [Google Scholar]
- Anderson MA, Johnson RL, Pankow JF. Dissolution of dense chlorinated solvents into ground water: 1. Dissolution from a well-defined residual source. Ground Water. 1992;30(2):250–256. [Google Scholar]
- Berglund S. Aquifer remediation by pumping: A model for stochastic-advective transport with nonaqueous phase liquid dissolution. Water Resour Res. 1997;33(4):649–661. [Google Scholar]
- Blue JE, Brusseau ML, Srivastava R. Simulating tracer and resident contaminant transport to investigate the reduced efficiency of a pump-and-treat operation. In: Herbert M, Kovar K, editors. Groundwater Quality:Remediation and Protection. Vol. 250. IAHS Publ.; 1998. pp. 537–543. [Google Scholar]
- Broholm K, Feenstra S, Cherry JA. Solvent release into a sandy aquifer: 1. Overview of source distribution and dissolution behavior. Environ Sci Technol. 1999;33:681–690. [PubMed] [Google Scholar]
- Brooks MC, Annable MD, Rao PSC, Hatfield K, Jawitz JW, Wise WR, Wood AL, Enfield CG. Controlled release, blind test of DNAPL remediation by ethanol flushing. J Contam Hydrol. 2004;69:281–297. doi: 10.1016/S0169-7722(03)00158-X. [DOI] [PubMed] [Google Scholar]
- Brusseau ML, Rohrer JW, Decker TM, Nelson NT, Linderfelt WR. Contaminant transport and fate in a source zone of a chlorinated-solvent contaminated superfund site: overview and initial results of an advanced site characterization project. In: Brusseau ML, Sabatini DA, Gierke JS, Annable MD, editors. Chapter 19 in: Innovative Subsurface Remediation: Field Testing of Physical, Chemical, and Characterization Technologies. American Chemical Society; Washington DC: 1999. [Google Scholar]
- Brusseau ML, Nelson NT, Oostrom M, Zhang ZH, Johnson GR, Wietsma TW. Influence of heterogeneity and sampling method on aqueous concentrations associated with napl dissolution. Environ Sci Technol. 2000;34(17):3657–3664. [Google Scholar]
- Brusseau ML, Zhang Z, Nelson NT, Cain RB, Tick GR, Oostrom O. Dissolution of nonuniformly distributed immiscible liquid: intermediate-scale experiments and mathematical modeling. Environ Sci Technol. 2002;36(5):1033–1041. doi: 10.1021/es010609f. [DOI] [PubMed] [Google Scholar]
- Brusseau ML, Nelson NT, Zhang Z, Blue JE, Rohrer J, Allen T. Source-Zone Characterization of a Chlorinated-Solvent Contaminated Superfund Site in Tucson, AZ. Journal of Contaminant Hydrology. 2007;90:21–40. doi: 10.1016/j.jconhyd.2006.09.004. [DOI] [PubMed] [Google Scholar]
- Childs J, Acosta E, Annable MD, Brooks MC, Enfield CG, Harwell JH, Hasegawa M, Knox RC, Rao PSC, Sabatini DA, Shiau B, Szekers E, Wood AL. Field demonstration of surfactant-enhanced solubilization of DNAPL at Dover Air Force Base, Delaware. J Contam Hydrol. 2006;82:1–22. doi: 10.1016/j.jconhyd.2005.08.008. [DOI] [PubMed] [Google Scholar]
- Einarson MD, Mackay DM. Predicting impacts of groundwater contamination. Environ Sci Technol. 2001;35:67A–73A. doi: 10.1021/es0122647. [DOI] [PubMed] [Google Scholar]
- Environmental Protection Agency. The DNAPL Remediation Challenge: Is There a Case for Source Depletion? 2003 [Google Scholar]
- Fure AD, Jawitz JW, Annable MD. DNAPL source zone depletion: Linking architecture and response. J Contam Hydrol. 2006;85:118–140. doi: 10.1016/j.jconhyd.2006.01.002. [DOI] [PubMed] [Google Scholar]
- Imhoff PT, Jaffe PR, Pinder GF. An experimental-study of complete dissolution of a nonaqueous phase liquid in saturated porous-media. Water Resour Res. 1994;30(2):307–320. [Google Scholar]
- Interstate Technology and Regulatory Council (ITRC) Regulatory Overview: DNAPL Source Reduction: Facing the Challenge 2002 [Google Scholar]
- Jawitz
- Johnson GR, Zhang Z, Brusseau ML. Characterizing and quantifying the impact of immiscible-liquid dissolution and non-linear, rate-limited sorption/desorption on low-concentration elution tailing. Water Resour Res. 2003;39(5) art. no. 1120. [Google Scholar]
- Kennedy CA, Lennox WC. A pore-scale investigation of mass transport from dissolving DNAPL droplets. J Cont Hydrol. 1997;24:221–246. [Google Scholar]
- Lemke LD, Abriola LM, Lang JR. Influence of hydraulic property correlation on predicted dense nonaqueous phase liquid source zone architecture, mass recovery and contaminant flux. Water Resour Res. 2004;40:W12417. doi: 10.1029/2004WR003061. [DOI] [Google Scholar]
- Lemke LD, Abriola LM. Modeling dense nonaqueous phase liquid mass removal in nonuniform formations: Linking source zone architecture and system response. Geosphere. 2006;2(2):74–82. [Google Scholar]
- Mayer AS, Miller CT. The influence of mass transfer characteristics and porous media heterogeneity on nonaqueous phase liquid dissolution. Water Resour Res. 1996;32(6):1551–1567. [Google Scholar]
- McGuire TM, McDade JM, Newell CJ. Performance of DNAPL source depletion technologies at 59 chlorinated solvent-impacted sites. Ground Water Monit R. 2006 Winter;:73–84. [Google Scholar]
- Nambi IM, Powers SE. Immiscible-liquid dissolution in heterogeneous systems: an experimental investigation in a simple heterogeneous system. J Contamin Hydrol. 2000;44(2):161–184. [Google Scholar]
- National Research Council (NRC) Alternatives for Ground Water Cleanup. Natl. Acad. Press; Washington, D.C.: 1994. [Google Scholar]
- National Research Council (NRC) Barriers to Implementation of Innovative Groundwater Remediation Technologies. Natl. Acad. Press; Washington, D.C.: 1997. [Google Scholar]
- National Research Council (NRC) Groundwater and Soil Cleanup: Improving Management of Persistent Contaminants. National Acad. Sciences; Washington, D.C.: 1999. p. 304. [Google Scholar]
- National Research Council (NRC) Research Needs in Subsurface Science. National Academy of Sciences; Washington, D.C.: 2000. [Google Scholar]
- National Research Council (NRC) Contaminants in the Subsurface: Source Zone Assessment and Remediation. Natl. Acad. Press; Washington, D.C.: 2005. [Google Scholar]
- Oostrom M, Hofstee C, Walker RC, Dane JH. Movement and remediation of trichloroethylene in a saturated heterogeneous porous medium 1. Spill behavior and initial dissolution. J Cont Hydrol. 1999;37:159–178. [Google Scholar]
- Parker JC, Park E. Modeling field-scale dense nonaqueous phase liquid dissolution kinetics in heterogeneous aquifers. Water Resour Res. 2004;40:W05109. doi: 10.1029/2003WR002807. [DOI] [Google Scholar]
- Phelan TJ, Lemke LD, Bradford SA, O'Carroll DM, Abriola LM. Influence of textural and wettability variations on predictions of DNAPL persistence and plume development in saturated porous media. Adv Water Resour. 2004;27:411–427. [Google Scholar]
- Powers SE, Abriola LM, Weber WJ. An experimental investigation of nonaqueous phase liquid dissolution in saturated subsurface systems - transient mass-transfer rates. Water Resour Res. 1994;30(2):321–332. [Google Scholar]
- Powers SE, Nambi IM, Curry GW. Non-aqueous phase liquid dissolution in heterogeneous systems: mechanisms and a local equilibrium modeling approach. Water Resour Res. 1998;34(12):3293–3302. [Google Scholar]
- Rao PSC, Jawitz JW, Enfield CG, Falta RW, Annable MD, Wood AL. Groundwater Quality- Natural and Enhanced Restoration of Groundwater Pollution. IAHS; 2002. Technology integration for contaminated site remediation: clean-up goals and performance criteria; pp. 571–578. Publ. 275. [Google Scholar]
- Saba T, Illangasekare TH. Effect of groundwater flow dimensionality on mass transfer from entrapped nonaqueous phase liquid contaminants. Water Resour Res. 2000;36(4):971–979. [Google Scholar]
- Sale TC, McWhorter DB. Steady state mass transfer from single-component dense nonaqueous phase liquids in uniform flow fields. Water Resour Res. 2001;37(2):393–404. [Google Scholar]
- Schwarz R, Ptak T, Holder T, Teutsch G. Groundwater risk assessment at contaminated sites: a new investigation approach. In: Herbert M, Kovar K, editors. GQ'98 Groundwater Quality: Remediation and Protection. Vol. 250. IAHS Publication; 1998. pp. 68–71. [Google Scholar]
- Schwille F. In: Dense chlorinated solvents in porous and fractured media. Pankow JF, translator. Lewis Publications; Chelsea, MI: 1988. p. 144. [Google Scholar]
- Soga K, Page JWE, Illangasekare TH. A review of NAPL source zone remediation efficiency and the mass flux approach. J Hazard Mater. 2004;110:13–27. doi: 10.1016/j.jhazmat.2004.02.034. [DOI] [PubMed] [Google Scholar]
- Strategic Environmental Research and Development Program (SERDP) Final Report: SERDP/ESTCP Expert Panel Workshop on Reducing the Uncertainty of DNAPL Source Zone Remediation 2006 [Google Scholar]
- Suchomel EJ, Pennell KD. Reductions in contaminant mass discharge following partial mass removal from dnapl source zones. Environ Sci Technol. 2006;40:6110–6116. doi: 10.1021/es060298e. [DOI] [PubMed] [Google Scholar]
- Unger AJA, Forsyth PA, Sudicky EA. Influence of alternative dissolution models and subsurface heterogeneity on DNAPL disappearance times. J Contam Hydrol. 1998;30:217–242. [Google Scholar]
- Zhang ZH, Brusseau ML. Nonideal transport of reactive solutes in heterogeneous porous media 5. Simulating regional-scale behavior of a trichloroethene plume during pump-and-treat remediation. Water Resour Res. 1999;35(10):2921–2935. [Google Scholar]


