Tradeoffs for Assuming Rigid Target Motion in Mlc-Based Real Time Target Tracking Radiotherapy: A Dosimetric and Radiobiological Analysis

Abstract

We report on our assessment of two types of real time target tracking modalities for lung cancer radiotherapy namely (1) single phase propagation (SPP) where motion compensation assumes a rigid target and (2) multi-phase propagation (MPP) where motion compensation considers a deformable target. In a retrospective study involving 4DCT volumes from six (n=6) previously treated lung cancer patients, four-dimensional treatment plans representative of the delivery scenarios were generated per modality and the corresponding dose distributions were derived. The modalities were then evaluated (a) Dosimetrically for target coverage adequacy and normal tissue sparing by computing the mean GTV dose, relative conformity gradient index (CGI), mean lung dose (MLD) and lung V₂₀; (b) Radiobiologically by calculating the biological effective uniform dose (D̿) for the target and organs at risk (OAR) and the complication free tumor control probability (P₊). As a reference for the comparative study, we included a 4D Static modality, which was a conventional approach to account for organ motion and involved the use of individualized motion margins. With reference to the 4D Static modality, the average percent decrease in lung V₂₀ and MLD were respectively (13.1±6.9) % and (11.4±5.6) % for the MPP modality, whereas for the SPP modality they were (9.4±6.2) % and (7.2±4.7) %. On the other hand, the CGI was observed to improve by 15.3±13.2 and 9.6±10.0 points for the MPP and SPP modalities, respectively while the mean GTV dose agreed to better than 3% difference across all the modalities. A similar trend was observed in the radiobiological analysis where the P₊ improved on average by (6.7±4.9) % and (4.1±3.6) % for the MPP and SPP modalities, respectively while the D̿ computed for the OAR decreased on average by (6.2±3.6) % and (3.8±3.5) % for the MPP and SPP tracking modalities, respectively. The D̿ calculated for the GTV for all the modalities was in agreement to better than 2% difference. In general, respiratory motion induces target displacement and deformation and therefore the complex MPP real time target tracking modality is the preferred. On the other hand, the SPP approach affords simplicity in implementation at the expense of failing to account for target deformation. Radiobiological and dosimetric analyses enabled us to investigate the consequences of failing to compensate for deformation and assess the impact if any on the clinical outcome. While it is not possible to draw any general conclusions on a small patient cohort, our study suggests that the two tracking modalities can lead to comparable clinical outcomes and as expected are advantageous when compared with the static conventional modality.

Introduction

Intra-fraction errors caused by respiratory induced organ motion are of major concern in the accurate delivery of radiation to tumors of the abdomen and thorax. This is significant for lung cancers and can lead to discrepancies between planned and delivered dose distributions (1–3). The need to properly account for these errors become even more important when newly emerging technologies such as stereotactic body radiation therapy (SBRT) requiring the delivery of high levels of radiation dose to the target in fewer fractions compared to conventional radiotherapy are utilized.

Respiration-induced tumor motion can be accounted for by employing approaches that focus on achieving adequate tumor coverage and better normal tissue sparing (4). Most of the existing methodologies perform fairly well with tumor coverage and may significantly differ in sparing normal tissues. Thus, the rationale for investing in sophisticated motion correction strategies is to achieve better normal tissue sparing. Respiratory gating, abdominal compression, tumor tracking, and active breath control are among several validated forms of respiratory control to account for intra-fraction motion errors (5, 6). Four-dimensional (3D spatial plus time) tracking radiotherapy (4DTRT) in real time is a promising but challenging technique and will be the focus of this work.

The concept of 4DTRT in real time is relatively new and its clinical implementation is still in the developing stage. Much of the work that has been done can be regarded as proof-of-concept (7). In a recent feasibility study, phantom investigations were reported for a prototype MLC-based 4DTRT delivery system, TrackBeam (Initia Ltd, Israel) (8). The TrackBeam real time target tracking system and other practically realizable MLC-based real time tracking systems track a single implanted fiducial marker and synchronize the MLC motion with respect to this single reference trajectory. This tracking type is simple to implement albeit two major limitations, namely unavoidable system latency effects and the fact that target deformation is not accounted for.

System latency arises because the system response to a detected change in the implanted marker trajectory is not instantaneous. Rather a finite time delay exists, which will lead to a certain geometric error in the dose delivery. The effect is inherent in the delivery of any real time target tracking radiotherapy system and can be reduced but not avoided. Advanced corrective mechanisms to reduce system latency rely on predicting the tumor location. Linear prediction, neural networks, Kalman filtering and recently, local regression are among the most commonly investigated predictive methods (9). In this work, we shall assume system latency effects are negligible and focus on the latter factor.

The other limitation is the fact that most simple real time target tracking systems, including TrackBeam, compensate for target motion as if the target moved from one respiratory phase to another as a rigid body. In general, the target can undergo deformation as well as translation. An ideal real time tracking system should also account for target deformation. In principle, this can be realized by tracking multiple implanted markers such that each leaf trajectory is synchronized with the detected trajectory of a unique implanted marker. Such a system is complex and not realizable at this stage. For reasons that will be explained in the next section, we shall refer to the simple and complex real time target tracking modalities as single phase propagation (SPP) and multi-phase propagation (MPP) respectively.

Given the complexity of an MPP real time tracking technique, it is of interest to investigate the benefit if any, for investing in this target tracking modality. In other words, what are the tradeoffs for assuming a rigid target as opposed to a deformable target? Clearly, on the upside, this can be attributed to simplicity of design and implementation. On the downside, we lose important details associated with organ deformation effects which will lead to geometric errors in the treatment delivery. Our focus was to evaluate the scale of the downside and its effect on the treatment outcome.

In addition to the tracking techniques, we included for the comparison a conventional method to account for respiratory induced organ motion, which involved the use of individualized motion margins derived from each patient’s 4DCT study. We shall refer to this modality as 4D static radiotherapy. This category was used as a reference for the comparative study and also for assessing the potential of 4D real time tracking radiotherapy against 4D static delivery methods.

Materials and Methods

This study involved six lung cancer patients (n=6) previously treated at our center. The tumor characteristics of these patients are summarized in Table I. In order to closely simulate each of the delivery scenarios, we used 4DCT image based treatment planning. This is because 4D planning takes into account organ deformation effects as it uses a temporally dynamic anatomy, representative of the relative anatomic changes that occur in normal respiration such as change in organ shape, volume, position and density (10–13), and therefore it will more accurately represent the dose distribution deliverable in either of the SPP or MPP techniques.

Table I.

Summary of patient characteristics; RUR = right lung and upper right lobe; RLL = right lung and lower left lobe; RMR = right lung and mid right lobe. SI (superior inferior), AP (anterior posterior) and LR (left right) motions are peak to peak. The 3D motion (mm) is the resultant scalar motion considering all directions.

Patients	Gender	Tumor	Volume (cc)		Motion (mm)
		Location	Lung	Tumor	3D	SI	AP	LR
P1	male	RUR	5448	59.6	10.2	8.7	4.4	2.9
P2	male	RLL	2780	199.7	9.1	7.0	4.8	3.3
P3	male	RMR	3695	59.4	8.6	4.4	4.4	5.9
P4	female	RMR	2210	152.8	7.3	5.3	2.3	4.5
P5	male	RUL	2753	408.7	4.0	3.9	0.3	0.7
P6	female	RMR	3901	247.9	2.0	0.7	1.5	1.1

The 4D plans were developed on 4DCT volumes generated per patient as follows: 3DCT images were continuously acquired for each patient under quiet breathing at a slice width of 2.5 mm using a LightSpeed 16-slice CT (General Electric, WI). Simultaneously, the respiratory signal was acquired via the Varian real time respiratory position management (RPM) system (Varian Corporation, Palo Alto, CA). 4DCT images were then generated in retrospect from the 3DCT images providing the three spatial dimensions and the respiratory signal providing the 4^th temporal dimension. The 4DCT images were further sorted into 10 distinct images corresponding to the various phases of the respiratory cycle and a single clinician segmented the target (GTV) and organs at risk (OAR) on all image sets using pulmonary window/level.

The process of binning the image data into ten consecutive image sets corresponding to the various phases of the respiratory cycle is automated after the 3DCT images and the RPM file containing the patient respiratory signal have been uploaded into the Advantage GE work station (General Electric, WI). The image sets representing one patient 4DCT study will be referred to as the 0%, 10% … 90% phase image sets where the sorted image sets are labeled by the percentage of the respiratory cycle such that 0% and 50% corresponds to the end-of-inhale and end-of-exhale phases respectively. These images were then exported to the Pinnacle treatment planning system (TPS).

4DCT image-based planning

Margin definition in the course of planning played a key role in distinguishing the three modalities considered. First, a clinician segmented the GTV on a given phase CT image set. The standard clinical practice is to expand the GTV to account for potential microscopic spread of the disease and thus produce a clinical target volume (CTV). In this work, we did not account for any microscopic spread of the disease and therefore the GTV and CTV coincided in all the three modalities.

Internal margin (IM) accounts for organ motion and further expands the CTV to the internal target volume (ITV). The internal margin for the tracking modalities, SPP and MPP was set to zero. This is due to the fact that organ motion in this case is accounted for by synchronizing the treatment beam with the target trajectory and therefore in the coordinate system of the treatment beam, the target is stationery. The difference between the two tracking techniques arise from the synchronization characteristics; while MPP synchronization accounts for both translation and deformation, SPP only accounts for translation. For the 4D static modality, IM was defined by the composite GTV which constituted an envelope of the GTVs from all the phases.

Finally, set up margin (SM) accounts for set up or patient positioning errors and expands the ITV to the planning target volume (PTV). We used the same set up margins across all the plans and modalities. Although the size of the set up margins can depend on a variety of factors including tumor site, treatment technique, patient fixation, departmental policy, etc., the fact that we applied the same set up margins across all the modalities reduced the impact of this factor on the outcome of this comparative study.

Planning for 4D static radiotherapy

It follows from the margin definition that the 4D static plan was characterized by larger margins. To generate the plans and obtain the 4D dose distribution, we proceeded as follows. First, a reference image set was chosen, which was the end of exhale for most of the patients. One advantage of using the end-of-exhale phase as a reference is the fact that it exhibits smaller variability in breathing pattern (14, 15). In this comparative study a different reference phase such as the end-of-inhale (16) could be used but we emphasize that the reference phase chosen be consistent. In other words, if the 50% phase were chosen as the reference phase for the 4D Static study, then the same reference phase should be used for the other modalities compared, i.e., the MPP and SPP in this case.

The delineated targets from the other image sets (phases) were then imported to the reference phase and a composite target, namely the union of all the targets was formed. It should be noted that the composite target (volume) is also referred to as the internal target volume (ITV) according to the definition and nomenclature of the International Commission on Radiation Units and Measurements report 62, ICRU 1999 (17). A planning target volume (PTV) was generated to allow for set up errors by expanding the composite target by 10mm in the cranio-caudal direction and 5mm in the anterior/posterior (A/P) and left/right (L/R) directions. A treatment plan was developed on the reference phase based on the PTV and its center of mass as the beam isocenter. It should be noted that the dose distribution calculated on the reference plan represents the absorbed distribution at the end of exhalation phase of the respiratory cycle. If the patient geometry remained constant throughout the respiratory cycle, then the same dose distribution could be assumed throughout. To account for respiratory induced geometry changes and hence obtain the composite or 4D dose distribution, the reference plan parameters were exported to the remaining image sets and 9 other treatment plans were developed resulting in ten treatment plans per patient. A 4D dose distribution was derived from the multiple plans by applying a validated, non-rigid deformable image registration (DIR) algorithm.

The implemented DIR method used is primarily based on Thirion’s diffusion model also known as the ‘demons’ algorithm (18, 19). The demons DIR algorithm was implemented using the National Library of Medicine Insight Toolkit (ITK), an open source cross-platform C++ software toolkit (20). The result of the DIR application was a deformation vector field between each image set and the reference image set which was then used to deform the dose distributions from each of the phases back to the reference phase where a weighted sum of the dose distribution was computed to constitute the 4D dose distribution.

$$D_{R,4D}(\overrightarrow{r})={\displaystyle \sum _{i=1}^{10}{W}_i}*{\tau }_i^R[D_{i,3D}(\overrightarrow{r})]$$ [1]

Here, D_R,4D(r⃗) is the 4D dose distribution accumulated on the reference phase image, W_i is the weight associated with the i^th phase, and set to 0.1 as the image sets were equally separated in time; ${\tau }_i^R$ is the transformation, which results from the DIR application and it takes as its argument a dose distribution from the i^th phase and deforms it to the reference phase (R).

The accuracy of the 4D dose calculation results depends to a large extent on the validity of the DIR program. A rigorous validation of the DIR algorithm can be performed via various techniques, including use of landmark features, mathematically simulated deformation, and/or use of 4D deformable phantoms. An extensive discussion on the DIR validation is out of the focus of this work and the reader can refer to elaborate work performed elsewhere (21, 22). It is important to note however that based on an approach involving mathematically simulated deformation (21), we quantified the registration error for the ‘demons’ DIR algorithm implemented in this work to be approximately 2mm. This is comparable to the (1.96 ± 1.26) mm quantified registration errors reported for the ‘demons’ DIR algorithm based on 34 manually identified landmarks inside the lung (22).

Treatment planning was performed on the ADAC Pinnacle3® treatment planning system (TPS), version 8.0m (Philips, Fitchburg, WI) with a dose grid setting of 3mm by 3mm by 3mm. We prescribed 60.0Gy to the 70% isodose shell and renormalized the plans such that 95% of the planning target volume (PTV) received at least the prescribed dose. It should be noted that the Pinnacle TPS used in the present study, as well as most currently available commercial TPS do not calculate dose distributions using 4DCT image data sets. Therefore, the TPS was used to calculate the 3D dose distributions for each of the phases and the results were exported to a windows desktop where the dose distributions were deformed according to equation [1] and a 4D dose distribution was accumulated using a MATLAB programming software (The Mathworks Inc., Natick, MA).

Planning for the MPP real time tracking delivery

A treatment plan that simulates this delivery consisted of independent treatment plans per image set based on each phase delineated target (GTV) shape and location. For each phase plan, a PTV was generated directly from the GTV by further expansion to allow for patient set up errors with the same margins as those applied in the 4D static plans. The tracking 4D dose distribution was derived from the multiple plans in the same manner as the 4D dose distribution for the 4D static modality described above.

It should be noted that due to organ deformation, the target shape changed from one phase to another. The complex tracking modality was designed to account for the deformation. Therefore, the MLC patterns were synchronized with the target translation as well as deformation. Because of the fact that all the ten phase plans were independently considered in the treatment design, we refer to this tracking type as multi phase propagation (MPP).

Planning for the SPP real time tracking delivery

The SPP modality was designed to account for target translation only. First, a reference phase was chosen, and for most of the patients, it was the end-of-exhale phase. A PTV was generated from the reference GTV using the same set up margins implemented in the 4D static and MPP modalities. A reference treatment plan was then generated based on the reference PTV. The reference plan parameters were exported to the other image sets and nine other treatment plans were developed. It must be underscored that the beam isocenter used per phase plan was unique and it was based on the target location as this was determined per phase. The other plan parameters, for example beam aperture were the same irrespective of organ deformation that could change the GTV shape from one phase to the other.

Therefore, the SPP plan accounted for target translation as it is reflected by the use of phase dependent beam isocenters and did not account for deformation as all the other parameters were kept constant. Because of the fact that the parameters of a single phase were propagated across the other phases to generate the rest of the plans, we refer to this modality as single phase propagation (SPP). The tracking 4D dose distribution was derived from the ten plans in the same manner as the 4D dose distribution for the 4D static modality described above.

To summarize, three modalities were considered for this comparative study, namely 4D Static, MPP and SPP. Treatment plans were then developed to replicate the delivery scenarios for each of the modalities as closely as possible. A common reference phase (end-of-exhale phase) was chosen across the modalities for each patient study and was the phase where the 4D dose was accumulated. Furthermore, each treatment plan involved at least seven non-opposing coplanar conformal beams where the beam arrangements for a given study were kept consistent across the modalities. The 4D Static plan was characterized by motion margins to account for target motion. First a treatment plan was generated on the reference phase plan. Then to account for respiratory induced geometric changes, the reference phase plan parameters were exported to the other phases and nine other treatment plans generated. A 4D dose was then derived from the planned dose distributions from all ten phases. No motion margins were used for either the MPP or SPP modality. For the MPP modality, ten independent treatment plans were developed with the MLC shape unique and conformal to the target geometry per phase therefore accounting for both translation and deformation. For the SPP planning, a reference plan was generated based on the target geometry at the reference phase. The same MLC shape was then moved to different phases based on the target location per phase therefore accounting for target translation but not accounting for deformation. The MPP and SPP 4D dose was derived in a similar fashion as in the 4D Static modality.

Physical dosimetric analysis

The modalities were evaluated for normal tissue sparing and/or tumor coverage adequacy. For normal tissue sparing, we focused on quantifiers that predict the likelihood of the patient developing radiation pneumonitis after radiotherapy. Radiation pneumonitis (RP) is one of the most common dose-limiting toxic effects in patients receiving thoracic radiotherapy for lung cancer and severe RP can be life-threatening (23, 24). The risk of developing RP following radiotherapy of the lung can be related to a wide range of factors including total dose, fractionation schedule and irradiated lung volume although the precise nature of the relationship remains unclear (25).

Several parameters derived from the dose volume histogram (DVH) such as mean lung dose (MLD), V₂₀, V₃₀ and normal tissue complication probability (NTCP) have been reported as useful predictors of the risk for RP. Lung V₂₀ (V₃₀) is the fraction of the lung volume irradiated by 20Gy (30Gy) or more. However, as to which, if any, of these predictors has a stronger association to severe RP is a question that has not been resolved. In this work, we computed and compared lung V₂₀ and MLD. The lung as defined here is the total lung volume excluding the gross tumor volume (GTV).

We also computed and compared the mean GTV dose and the conformity gradient index (CGI) for the treatment modalities. The CGI index (26, 27) was developed for application in the field of intracranial radiosurgery. It was designed to quantify how well a radiosurgery plan maximizes both the conformity of the prescription isodose surface and the dose fall-off with respect to distance away from the external layer of the target volume. This scoring tool is very effective in ranking competing stereotactic radiosurgery plans and correlates extremely well with clinical judgment and radiobiological model predictions. Differences in plan ranking by normal tissue complication probability (NTCP) correlate to differences of approximately 5 or more CGI points (27).

The CGI is the average of two terms: the conformity score (CGI_c) and the gradient score (CGI_g), which are defined as follows:

$${\mathit{\text{CGI}}}_C=\left(\frac{\text{Target Volume}}{\text{Prescription Isodose Volume}}\right)*100$$ [2]

$${\mathit{\text{CGI}}}_g=100[1-(R_{\mathit{\text{Eff}},50\%\mathit{\text{Rx}}}-R_{\mathit{\text{Eff}},\mathit{\text{Rx}}}-0.3\text{cm})]$$ [3]

Here, R_Eff,Rx and R_Eff,50%Rx are respectively the effective radius of the prescription isodose volume and the effective radius of the volume encompassed by the isodose surface equal to one half of the prescription isodose surface. The effective radius of a volume is the radius of a sphere of equal volume.

$$R_{\mathit{\text{Eff}}}=\sqrt[3]{\frac{3V}{4\pi }}$$ [4]

The CGIg is scaled such that a CGIg ≥ 100 corresponds to an optimum 3 mm or less gradient. This ideal 3 mm gradient was obtained empirically from radiosurgery planning cases, and corresponds to the gradient that is possible with linac radiosurgery when using multiple non-coplanar arcs and small (<20 mm) circular collimators (28). This value was modified to suit our purposes. A relative CGIg was defined with the gradient value chosen so that one of the plans had a perfect CGIg score of 100. The CGIg scores of the other plans were then calculated relative to the plan with the perfect CGIg score. The modified formula used is given by:

$$\begin{array}{c}{\mathit{\text{CGI}}}_g=100\hfill \\ [1-(R_{\mathit{\text{Eff}},50\%\mathit{\text{Rx}}}-R_{\mathit{\text{Eff}},\mathit{\text{Rx}}}-\mathit{\text{Min}}(R_{\mathit{\text{Eff}},50\%\mathit{\text{Rx}}}-R_{\mathit{\text{Eff}},\mathit{\text{Rx}}})\left)\right]\hfill \end{array}$$ [5]

Here, Min(R_{Eff, 50%Rx} − R_{Eff, Rx}) is the smaller of the gradient values for the plans compared. The average of the conformity and gradient indices yield the CGI as given by the equation:

$$\mathit{\text{CGI}}=\frac{1}{2}({\mathit{\text{CGI}}}_c+{\mathit{\text{CGI}}}_g)$$ [6]

It should be noted that the CGI increases with plan desirability or quality. As either the conformity or gradient worsens, the CGI_c or CGI_g decreases leading to a subsequent decrease of the CGI score (28). To calculate the CGI of any plan, we need to know the target volume, the volume of the prescription isodose shell and the volume encompassed by the 50% prescription isodose surface, which can be extracted from the 4D dose volume histogram.

Radiobiological analysis

In addition to the physical/dosimetric evaluation described above, we assessed the treatment modalities based on a complete radiobiological analysis. The radiobiological modeling considered both the physical/dosimetric characteristics and individual organ radiosensitivities and therefore provided a more sensitive assessment of the clinical merits of a treatment plan.

The model used in describing tumor control or normal tissue complication probability P(D) is based on the linear-quadratic-Poisson and relative seriality models and have been thoroughly described elsewhere (29). A short summary and application of these models is presented here.

$$P(D)=\text{exp}\{-{\mathrm{N}}_0{\mathrm{e}}^{-(D/D_{50})(e\gamma -\text{ln}\text{ln}2)}\}=\text{exp}\{-e^{e\gamma -\mathit{\text{and}}-\beta {\mathit{\text{nd}}}^2}\}$$ [7]

Here D is the uniform dose, d=D/n is the dose per fraction and n is the number of fractions applied. D₅₀ is the dose that causes response to 50% of the patients, and γ is the steepness of the dose-response curve; α and β are the fractionation parameters of the model and account for the early and late effects expected. Both D₅₀ and γ depend on N₀, the initial number of the clonogenic cells for tumors or functional subunits for healthy tissues. These parameters are specific for each organ and injury type and are derived from clinical data.

Given a heterogeneous dose distribution (D⃗) and the required dose-response parameters as presented above, two useful quantities can be derived from this model; the control response of tumors, also known as the probability of benefit, P_B(D⃗) and the normal tissue response also referred to as the injury probability, P_I(D⃗).

$$P_{\mathrm{B}}(\overrightarrow{D})={\displaystyle \prod _{j=1}^M{[P_{\mathrm{B}}(D_j)]}^{\mathbf{\Delta }{v}_j}}$$ [8]

$$P_{\mathrm{I}}(\overrightarrow{D})={\left\{1-{\displaystyle \prod _{j=1}^M{[1-{[P_{\mathrm{I}}(D_j)]}^s]}^{\mathbf{\Delta }{v}_j}}\right\}}^{1/s}$$ [9]

Here, Δν_j is the j^th subvolume of the tumor or normal tissue (OAR) receiving dose D_j and M is the number of such subvolumes. The parameter s is the relative seriality that characterizes the internal organization of the organ. This is not applicable to tumors as they are assumed to have parallel structural organization since the eradication of all their clonogenic cells is required. Note that P_B(D_j) and P_I(D_j) are derivable from equation [7] as (D_j) is a single dose value (uniform dose). It should also be noted that equations [8] and [9] are valid for a single target and a single OAR, respectively. These formulae can be easily extended to cover multiple targets or OARs in the same fashion that multiple subvolumes were incorporated to describe the probability.

The biological effective uniform dose (BEUD) is defined as the uniform dose (D̿) that causes the same tumor control or normal tissue complication probability as the real dose distribution on a complex target or normal tissue (29–31). BEUD can be derived directly from the expressions of P_B(D_j) and P_I(D_j) by a straightforward application of its definition. For example, to calculate the D̿ _B, we set up the equation P_B (D̿) = P_B (D), and then solve forD̿.

To assess the radiobiological effectiveness and clinical merits of a treatment plan, the plan’s advantages in terms of tumor control with its disadvantages in terms of normal tissue complications should be evaluated. Until now, the P₊ objective, known as the complication-free tumor control probability is the most popular concept that quantifies the radiobiological effectiveness of a dose plan (29). The general expression for P₊ (30, 32, 33) is given by

$$P_{+}=P_B-P_B\cap P_I$$ [10]

This expression can be approximated by

$$P_{+}=P_B-P_I+\delta P_I(1-P_B)$$ [11]

Where the parameter δ ≈ 20% describes the fraction of the patients with statistically independent responses in the tumor and normal tissues and can be determined from clinical data (34). By recognizing that δP_I (1−P_B) contributes negligibly to the P₊, we can simplify this expression further and write (35)

$$P_{+}=P_B-P_I$$ [12]

For each of the patients studied and for each of the modalities considered, we evaluated and compared the complication-free tumor control probabilities. In addition, we also calculated and compared the values of (D̿ _B) and(D̿ _I).

Results

4DCT image-based planning

A total of 180 pinnacle treatment plans including ten phase dependent treatment plans per modality and per patient were generated for this study. The 3D dose distribution from each phase was deformed using equation [1] to the reference phase where a weighted sum of all the deformed dose distributions was performed to constitute the 4D dose distribution.

Dosimetric analysis

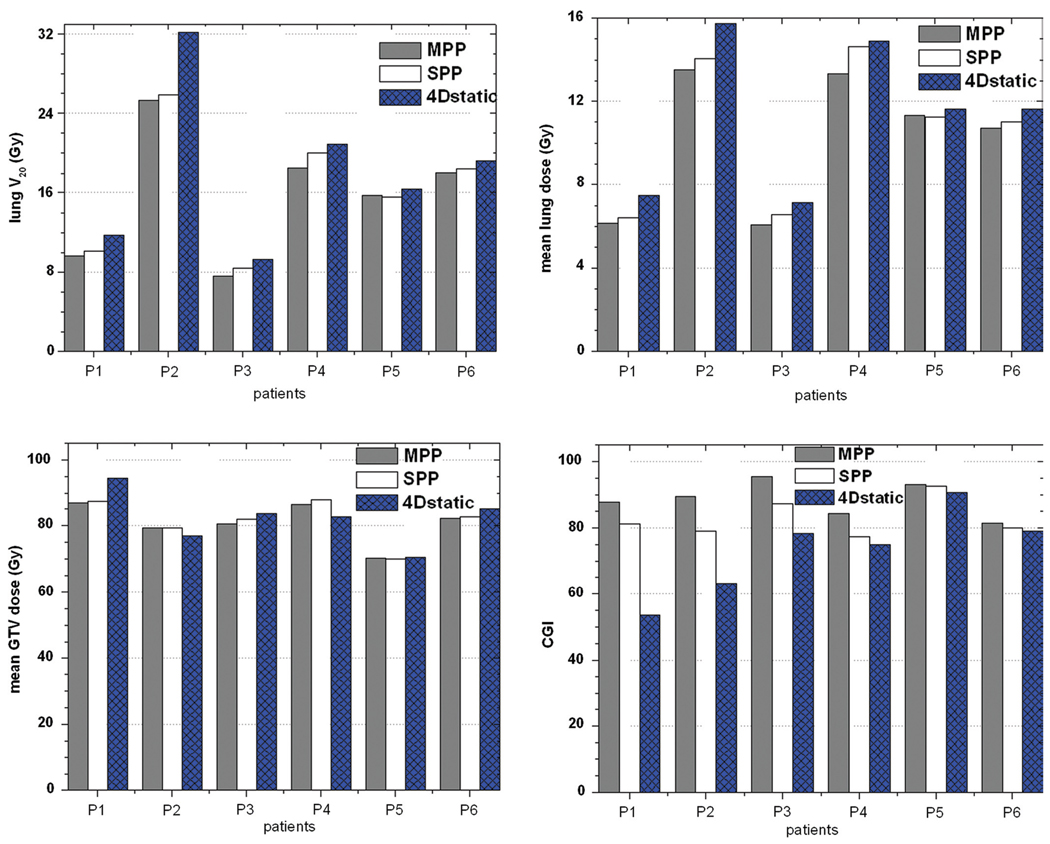
With reference to the 4D Static modality, the average percent decrease in lung V₂₀ was (13.1±6.9) % and (9.4±6.2) % for the MPP and SPP modalities, respectively. The observed percent decrease in MLD was (11.4±5.6) % and (7.2±4.7) % for the MPP and SPP modalities, respectively. On the other hand, the mean GTV dose across all the modalities were on average in agreement to better than 3% difference. The results of the dosimetric analysis are summarized in Figure 1.

Figure 1.

Histogram plots for lung V₂₀, mean lung dose (MLD), mean GTV dose and CGI index. Patients arranged in decreasing magnitude of motion extent.

CGI values give a quantitative ranking of the plans. For all the patients studied, Figure 1 shows that the relative CGI values ranked the modalities in the order MPP, SPP and 4D-Static for plan quality and desirability. With reference to the 4D static technique, the average increase in CGI was 15.3±13.2 and 9.6±10.0 for the MPP and SPP modalities, respectively. Note that the stated variation of the differences among the patient studies is 1 standard deviation. The high errors were due to the variability of the tumor characteristics across the patients. It is obvious that as the motion extent decreases, the differences between the three modalities also decrease. This seems to have a dramatic effect on the relative quality and desirability of the modalities.

Radiobiological analysis

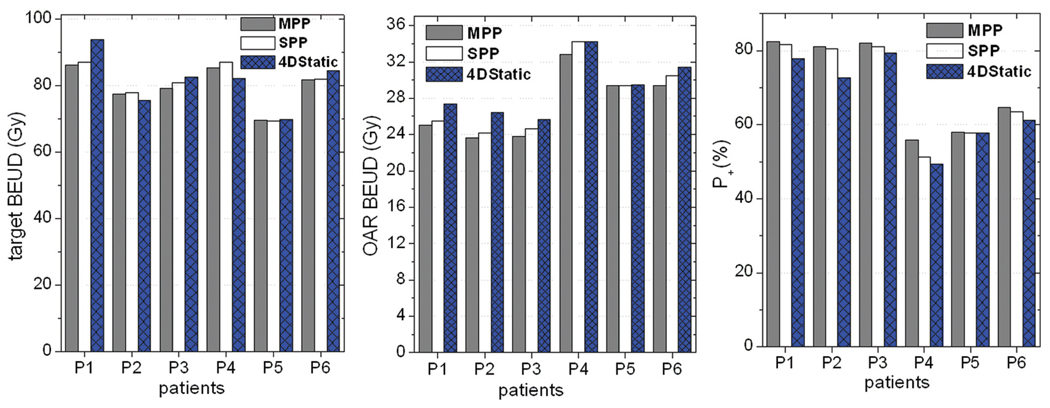
In general, the radiobiological analysis showed that the two real time tracking techniques were comparable and advantageous over the 4D static modality, a trend quite consistent with the physical dosimetric evaluations. With reference to the 4D Static modality, the average observed improvement in the complication-free tumor control probability (P₊) was (6.7±4.9) % and (4.1±3.6) % respectively for the MPP and SPP modalities. The BEUD computed for the OAR (D̿ _I) on average decreased by (6.2±3.6) % and (3.8±3.5) % for the MPP and SPP tracking modalities, respectively, compared with the 4D static technique. As it was expected, the BEUD calculated for the GTV (D̿ _B) for all the three modalities was on average in agreement to better than 2% difference. The radiobiological plots for all the patients are displayed in Figure 2.

Figure 2.

Radiobiological analysis based on the target and OAR BEUD as well as the complication free tumor control probability (P+) for the three modalities. Note that the patients are arranged in decreasing order of tumor motion.

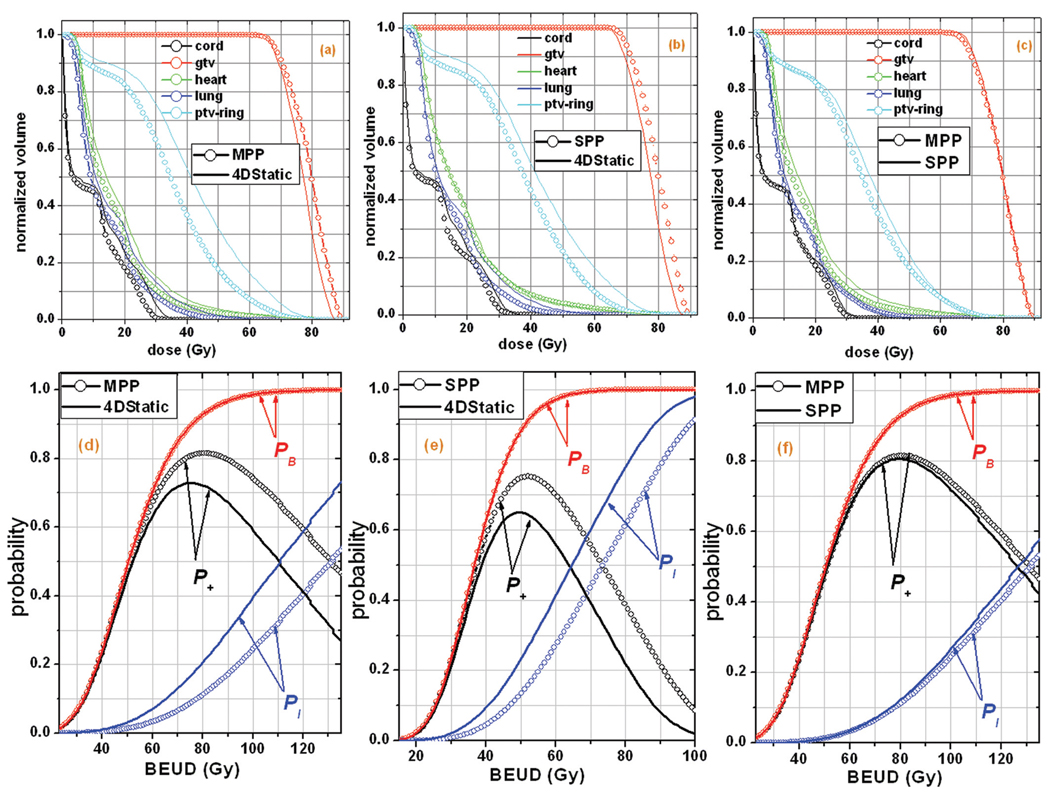
Finally, we note that graphical display of the 4D dose volume histogram (4D-DVH) is often useful as a qualitative dosimetric assessment of a treatment plan. An equivalent concept in radiobiological analysis is the probability (P₊, P_B and P_I) versus BEUD plot. In Figure 3, this type of analysis is illustrated for patient P2, showing the superiority of the tracking modalities compared with the conventional modality. More specifically, in Figures 3 (a), (b) and (c), the 4D-DVHs of the different targets and OARs involved in the study are illustrated for the three modalities. It can be observed that the curves of the targets are more separated from the curves of the OARs in the MPP and SPP modalities compared to the 4D Static modality. This means that the former modalities are characterized by a larger therapeutic window, which leads to better expected therapeutic results (lower risk for complications for the same tumor control rate or increased tumor control rate for the same risk for complications). This picture is also depicted in more detail in Figures 3 (d), (e) and (f), where the positions of the normal tissue response curves (P_I) are shown against the response curves of the targets (P_B). It is apparent that in the whole range of prescribed doses (as this is expressed by the BEUD), the complication-free tumor control probability (P₊) curves of the MPP and SPP are significantly higher than the corresponding curves of the 4D Static modality, whereas between the MPP and SPP modalities, the difference is very small. Visual inspection shows that the radiobiological analysis is more useful in assessing the differences between the treatment modalities and one of the reasons why it is an attractive tool in radiotherapy treatment planning and analysis.

Figure 3.

The dosimetric analysis (upper diagrams) using 4D DVH plots versus the radiobiological analysis (lower diagrams) using probability-BEUD plots, is illustrated for patient P2.

Discussion

The TrackBeam real time target tracking system (Initia Ltd, Israel) and other practically realizable MLC-based real time target tracking radiotherapy systems are designed to track a mobile target as if the target were a rigid body. In general, tumors can undergo translation as well as deformation. Consequently, an ideal target tracking system should also account for deformation. We referred to the former real time tracking modality as the single phase propagation (SPP) modality and the latter as the multi-phase propagation (MPP) modality. The goal of this work was to investigate if there are significant differences between the two modalities. We included as a reference to this comparative study a conventional approach in accounting for organ motion. This involved the use of individualized motion margins, and it was referred to as the 4D Static modality.

In the present retrospective study, which involved 4DCT volumes of six (n=6) lung cancer patients treated at our institution, we applied four-dimensional treatment planning techniques to derive 4D dose distributions representative of each delivery scenario. Dosimetric analysis, based on physical dose distributions and radiobiological analysis considering in addition the radiobiological dose-response characteristics of the different targets and OARs were performed to assess the differences, if any, between the modalities. Both assessments showed that while the MPP modality was superior to the SPP modality even for the patient with the least motion and target deformation, the advantage was small in comparison to the benefit that either real time target tracking modality had over the conventional 4D Static approach.

Dosimetric analysis showed that lung V₂₀ and MLD decreased on average by 13% and 11% respectively for the MPP modality and 9% and 7% respectively for the SPP modality with reference to the 4D Static modality. The conformity gradient index (CGI) was observed to increase on average by 15 and 10 points for the MPP and SPP modalities respectively compared to the 4D Static modality. It should be noted that the CGI scoring tool has been shown to correlate well with clinical judgment and radiobiological modeling where differences in plan ranking by normal tissue complication probability (NTCP) correlate to differences of approximately 5 or more CGI points (27).

Consistent with the dosimetric analysis trend were the observations from the radiobiological analysis, which showed that the BEUD of the organs at risk decreased on average by 6% and 4% respectively for the MPP and SPP modalities with reference to the 4D static modality. The complication-free tumor control probability (P₊) on the other hand increased on average by 7% and 4% respectively for the MPP and SPP modalities. The dosimetric and radiobiological analyses showed that target coverage adequacy was comparable across all the modalities. The mean GTV dose that was computed across the modalities agreed on average to within 3% difference while the BEUD that was computed for the GTV agreed on average to within 2% difference.

The extent of target deformation played a key role in the differences observed between the two real time target tracking modalities. It was therefore important to quantify this factor for the 4DCT volumes studied. We estimated the extent of deformation (ED) of any region of interest (ROI) between two phases as the standard deviation of the displacement vectors of the constituent voxels. We used deformation vector fields derived in the course of image registration for our calculations. The computed extent of deformation of the clinician delineated GTV contour surface ranged from 2.6mm to 6.8mm for the patients studied. For rigid target translation, each voxel will propagate with the same displacement and therefore the extent of deformation will be zero. We verified this assertion by estimating in a similar manner the ED of a rigid tumor using the 4DCT volume acquired of the CIRS dynamic lung tissue equivalent phantom (CIRS Inc., Norfolk VA). The estimated ED for the CIRS phantom was 0.5mm, 0.4mm, and 0.5mm in the left/right (L/R), anterior/posterior (A/P) and superior/inferior (S/I) directions, respectively. Note that registration errors associated with the DIR algorithm contributed to the non-zero but negligible values observed. It should be noted that tumor characteristics such as the extent of motion and the target size relative to the lung volume can be used to predict the extent of target deformation. Such a study will require a very large patient cohort for any useful correlation to be established and will be performed in the future.

Finally, we note that although the observable variation between the two real time tracking modalities can depend on various factors including tumor size relative to lung volume, extent of motion, extent of deformation, location of tumor within the lung, etc., in our patient selection we mainly focused on the extent of motion. Over 30 lung cancer patient 4DCT volumes from our department database were evaluated and six patients were selected. The goal was to have a patient cohort with tumor motion range representative of the extent of motion commonly encountered in clinical practice.

A compilation of lung tumor motion reported in the literature show that motion in the superior inferior (S/I) axis is usually predominant with the following range of average values of tumor motion extent; 1.5mm to 14.0mm, 0.7mm to 7.4mm, and 0.2mm to 8.1mm for tumors located in the lower, middle and upper part of the lung, respectively. This compilation was based on several independent studies with patient cohorts ranging from 3 to 43 patients per study (36). The AAPM TG-76 publication is another useful literature review of lung cancer patient tumor motion extent, which also points out that motion in the S/I direction is predominant with the average value of tumor motion ranging from 3.9mm to 7.5mm for upper and middle lobe tumors and average values of up to 18.5mm for tumors located in the lower lobe (6). The average values of tumor motion were based on several independent studies with 4 to 51 patients per study. Therefore, our patient selection is comparable, at most, with the typical mean tumor motion range encountered in clinical practice.

However, larger tumor motion ranges of up to 38.7mm, 25.9mm and 48.2mm, respectively for lower, middle and upper lung tumors (36) and up to 50mm (37) have been reported in the literature. The high tumor motion ranges will likely lead to a greater deformation. Hence, while the patient cohort selected for this study (Table I) is comparable with the average lung tumor motion extent commonly encountered in the clinic, it is not exhaustive to include patients with very high extent of motion. For those extreme motion ranges, further data is required to be analyzed in the framework developed in this study for assessing if there are significant differences between the two real time target tracking modalities employing both dosimetric and radiobiological analyses.

Conclusion

Although accounting for both respiratory induced target deformation and displacement in lung cancer radiotherapy using the complex type MPP delivery is the ideal approach, for the range of lung tumor motion studied, dosimetric and radiobiological analysis suggest that the simple type and practically realizable SPP delivery which account for target displacement only, is comparable with the ideal approach and advantageous over the conventional 4D static modality in sparing normal tissues. For lung cancer patients with a very high tumor motion extent, a higher tumor deformation is more likely to occur. However, more data are required to investigate if the MPP and SPP real time target tracking modalities remain comparable. Finally, this study provides suitable framework and methodology for further investigation of the presented and other upcoming methods that are employed to resolve the problem of organ motion in radiotherapy delivery.