The Computational Integrated Myocyte

Abstract

The presentation outlines an integrative approach for developing a computational model of cardiomyocytes. A modular approach is proposed, and strategies of linking the modules (intermediary metabolism, electrophysiology, and mechanics) of the model are presented. A strong recommendation is given toward an integrated system approach backed by experimental validation.

INTRODUCTION

As we enter the era of the renewal of integrative biology, we can reflect on the reflections of those who emphasized it long ago as being fundamental to life. Claude Bernard’s many experimental studies in the 1860s and the 1870s led to his formulation of the idea that there were overriding features of human physiology that dominated over local events and resulted in a relative stability, or “homeostasie du milieu interieure.”¹ What Bernard labeled “homeostasis” we might now call homeodynamics, as Bernard himself might have done, recognizing that the stability of plasma electrolyte and substrates composition was caused by the interactions of many ongoing processes. The turn of Bernard’s century saw the expansion of his ideas revealed in the kinetics and mechanisms of circulatory exchange processes^2–4 and in elements of their hormonal-humoral control.⁵ A century later, marking the passing through of a strenuously productive era of emphasis on molecular biology and the remarkable insights coming out of genomics, biologists generally have assumed that it is timely to look at the interactions among molecules. The genotype-to-phenotype relationship is recognized as not merely an associative one, but one that lends itself to determining mechanism.

Systems biology, outlined in Science magazine^6–10 at the gene-to-protein level, is now ready to envelop thinking at the organism level. Whereas the phrase systems biology is new, it is in the style of research that Bernard espoused. That style dominated physiology for over a century and then was largely displaced by molecular biology, although it never actually vanished from the scene.

Swayed by the belief that “discovery science” was at the gene and molecule level, which was an accurate portrayal of where major funding in science was to be found, physiologists, pharmacologists, biophysicist, bacteriologists, and pathologists—almost all became molecular biologists, then genetic interventionists. Although some may have lost their intellectual breadth in these reductionist efforts, most maintained the larger goal of understanding biology by developing an understanding of the underlying mechanisms. Not all reductionism is bad. Nevertheless, over these decades, certain scholarly aspects of integrative science have been all but lost. The teaching of systems analysis, control systems, physiological signal acquisition and analysis, and simulation analysis of data through mathematical modeling vanished from the curricula of our medical schools and basic biological science departments, with remarkably few exceptions. The reassignment of teaching responsibilities from basic science departments to the clinical practitioners may have given researchers more time to indulge in the latest nuances of cell and molecular biology but deprived them of the obligation to think and teach in terms of the whole organism.

This same period saw islets of integrated analysis in physiology and the growth of bioengineering approaches. In a few laboratories, the studies centered on whole-animals studies; Rushmer¹¹ developed instrumentation for recording physiological responses in running dogs and countered the trend to rely on isolated organ studies, particularly those of Sarnoff,¹² with whom he joined in vociferous debates. Guyton and his colleagues pioneered the development of large-scale integrated models;^13,14 these tended to be ignored by most academic physiologists: whereas the models demonstrated remarkable fidelity in simulating observed physiological responses to blood loss, salt loading, and other conditions, this success was compromised by the fact that the models were, at the component level, descriptive rather than mechanistic. The critics, rather than accepting these models as an invitation to work out the mechanisms of the components, decried them as useless, nonintuitive, or artificial. They should have recognized their predictive and integrative success and built upon them. A few cardiovascular investigators did continue integrative whole-animal studies,^15,16 but most of those not involved in molecular and cell biology worked with anesthetized preparations or isolated organs, arguably still pursuing the goal of understanding the intact system.

Sam Sideman and his group at Technion, Israel Institute of Technology in Haifa, initiated an engineering approach in 1982, focusing their efforts on the heart and vascular system. Their three-dimensional imaging techniques and analytical quantitative cardiology allowed them to relate structure and function to mechanical, electrical, and hemodynamical parameters in the macroscale, followed by relating ventricular function to microscale intracellular sarcomere characteristics. Sideman developed an international forum, in the form of a series of annual conferences—the Henry Goldberg conferences, named in honor of the New York stockbroker who funded these “think-tank” efforts to fathom how the system worked quantitatively.^17–26 The outcome of this effort brought about widespread alliances and collaborations in the cardiovascular sciences, and there were many exchanges of scientists among the participants. Much new science, and even new attitudes, evolved.

Formal recognition of the need to coalesce diverse sets of information emerged. My own version of this was the description of a framework for gathering and integrating physiological information as the “Physiome Project,”²⁷ and even applying its lessons as a potential vehicle for aiding the selection of targets for new drugs. This was not an isolated event. Boyd and Noble’s book, The Logic of Life,²⁸ was distributed at the 1993 Congress of the International Union of Physiological Sciences (IUPS), and the Union endorsed the formation of a Commission on Bioengineering in Physiology in the same year, which I chaired, with the goals of contributing engineering approaches to physiological research and teaching. The Physiome Project was more or less formally kicked off in 1997, at a satellite meeting of the next IUPS Congress at St. Petersburg, Russia; and a separate IUPS Physiome Commission was established in 2001, with Peter Hunter as chair.

Symposium volumes covering these efforts to integrate the cardiac systems were published in 1998,²⁹ 2000,³⁰ 2001,³¹ and 2003.⁷⁹

THE CELL AS A COMPONENT OF THE HEART

The need to develop models encompassing major portions of biochemical and genetic regulatory networks and their control is evident. Integrative models are the key to providing context for the individual reactions and for eliciting an understanding of the influences of the various components upon whole-system behavior. The methods for formulating a virtual cell model or for constructing models of more limited expanse such as cellular energetics are still more or less ad hoc, but we will later attempt to define these.

Small portions of a metabolic system can be described in detailed form. For a sys tem such as glycolysis, it is useful to develop several representations, providing different levels of complexity or accuracy or computational speed. Having the highest level of precise detail is not compatible with computing solutions rapidly, yet speed is required to allow widespread exploration to gain insight, develop predictions, or optimize the fits of model solutions to data. Making compromises for specific purposes therefore is essential.

Larger, more all-encompassing models are best composed of smaller modules, each of which has been validated previously by comparisons with data and verified for computational accuracy. The individual modules must adhere to a prechosen standard and provide a scientifically accurate representation of the system, using semantics compatible with those of the larger system. Individual modules are best developed and maintained by individual investigators or groups who are expert in the particular science. Models are merely working hypotheses that must be kept at the forefront of the field if they are to be useful as tools for experiment design and for data analysis. Leaving them in model repositories tended by technical staff relegates them to obsolescence in a short time.

Certain principles and practices should be upheld so that modules be maintainable. Here is our strategy for constructing the “eternal” or “sustainable cell” model.³² The list begins with the science and extends to matters of style, convenience, and dissemination to the scientific community.

1. Write model code to conserve mass, charge, volume, energy, and redox state.

2. Define variables and parameters, with symbol, name, description, and units.

3. Identify all inputs and outputs, for linking purposes.

4. Identify all assumptions and approximations.

5. Identify all information sources.

6. Write the code for maximal computational speed.

7. Provide operations manuals and tutorials for developed models.

8. Publish models on the web, so they can be run or downloaded.

9. Establish open-forum discussion of models and modules.

Speed, though only number 6 on our list, is vital: to use the computer as a mind expander, one needs to compute at the speed of thought to facilitate exploration and to gain insight into the behavior of complex biological processes. Moreover, speed is critical to the use of models as tools to analyze experimental data through automated optimization procedures. Of the list above, the first four are essential to using a module as a component in a more comprehensive system. The fifth and the last three are essential for documentation and dissemination.

LINKING MODULES TO FORM COMPOSITE MODELS

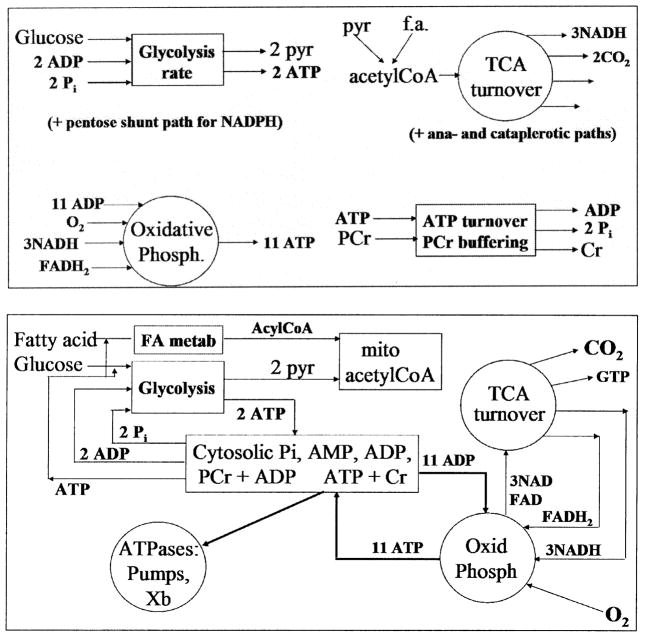
The process of linking modules is suggested by the composite model in FIGURE 1. The top panel shows a set of modules for intermediary metabolism that are linked with known stoichiometry. Consider each to be a separate model, each the evolutionary result of years of research. Linking them through the stoichiometric relationships of input substrates and output products appears straightforward and results in the integrated model shown in the bottom panel. It appears as if the integrity of the individual modules remains intact, and in fact it is almost this simple. Problems arise, not so much in accounting for NADH and other slowly changing variables, but in accounting for the influences of rapidly changing calcium and hydrogen ion concentrations in some circumstances.

FIGURE 1.

Building composite modules from prebuilt modules in intermediary metabolism. Top: Individual models for glycolysis, Krebs (TCA) cycle, oxidative phosphorylation, and nucleotide energetics showing their main inputs and outputs. Bottom: Combining the modules from the top panel and adding fatty acid metabolism gives a composite model of intermediary metabolism. Stoichiometric balance is maintained, and the modules remain distinct from each other.

The argument that models are best developed and maintained by a group working in the particular field leads to complications when models become modules of larger system models. The expertise required to develop and maintain a given model may not be available in the group that chooses it as the best version of the desired component of a higher level integrative model. From the technical point of view, putting together two models from different sources is not too difficult when both submodels or modules can be described by ordinary differential equations (ODEs). Using a simulation system such as JSim <http://nsr.bioeng.washington.edu>, Madonna <http://www.berkeleymadonna.com>, SAAM II <http://www.saam.com>, Gepasi <http://www.gepasi.org>, or XPPAUT <http://www.compcell.appstate.edu>, one simply combines the two modules into a common piece of source code, combining all those equations that have common variables. If all the variables common to both modules have been defined with the same names, their identity will be easily recognized.

Another issue is how to build a composite model out of modules while maintaining the identity of the code of the module so that it can be replaced automatically when the originating group advances the module’s code to a new level. Ideally the composite model should be reconfigured whenever it is judged that improvements have been achieved in any particular module. Automating this is possible when common variables are named identically; it is also possible, but requires human intervention, to define equivalences, when the variable names in each module are not identical. There is a trade-off here: when the variable names are identical, combining the modules can be automated because the equations for the common variable can be automatically combined, as has been achieved by Gary Raymond in our laboratory; but the cost is that the two source codes are now intermixed. For computational reasons, this is good because it minimizes the numbers of different variables and facilitates solving the whole system simultaneously. But its cost is that a composite model composed of a large set of modules must be entirely formed anew when a module is to be replaced.

A biological component language has been developed at our resource for simulating biochemical reaction networks with transporters and flows as a part of the JSim simulation system. This system enables one to add modules using the appropriate biological component representation. The ODEs describing the system under consideration are automatically constructed by JSim. Modules can be added or removed without having to rewrite the ODEs.

Separating Modules from One Another for Computational Speed

Solving a large set of simultaneous equations as a whole gives high accuracy when the system is linear but is computationally costly when it is composed of nonlinear equations with drastically different rate constants in different parts of the model: the set of equations is “stiff.” Then one would like to solve separately those submodels that have rate or time constants that are relatively slow and to solve at higher frequencies those submodels that have time constants orders of magnitude faster. Allowing differences in time steps from one module to another greatly reduces the “stiffness” of the overall system and increases computation speed. This argument favors keeping modules separated even while linked in the composite model and enhances the incentive to use automated methods for composite model building.

A situation in which modular separation can be maintained occurs whenever the common variables change slowly relative to the internal rates of the modules to which they are relevant. An example is ATP, which is at such a high concentration normally that its concentration changes only very slowly, even with drastic changes in circumstances. By treating ATP as an external variable from the point of view of the individual modules, its concentration can be considered constant during a time step; by preserving the fluxes of ATP into or out of the relevant modules, ATP concentration can still be represented to a high degree of accuracy without solving for it at the high rates required for the fast modules. Another way of achieving the same objective is to give the local ATP a local name, as if local concentrations differed slightly from one another, but exchanged with one another with moderately fast exchanges. Thus, using a differential equation to describe ATP1 ↔ ATP2 allows independence of the modules from one another while maintaining exchange and mass balance, bringing their solutions together through the exchange. This same approach lends itself to parallel computation of the different modules on different CPUs. Because computation time is a major factor for metabolic and electrophysiologic cell models and a huge issue for integrated organ models, such approaches need much further development to achieve maximal efficiency of computation and improve the efficiency of investigation.

COMPOSITION OF THE “ETERNAL CELL”

The reason for defining an “eternal cell” is to have a clearly defined and finite first objective as a component of the ultimate “complete” model of a functioning cell. By “eternal,” we mean that there is no proteolysis or protein synthesis, so that the cell’s functional proteins are held at constant concentrations. For the simplest “eternal” cell, we ignore structural proteins and pretend that the only proteins we need are those that serve as enzymes, transporters, channels, pumps and leaks, buffer proteins, and contractile elements. In addition to proteins there must be substrates, ions, metabolites, the solutes participating as energy pools, and those governing redox state.

The essential components to be modeled are (1) systems for uptake and metabolism of substrates for energy production: glucose, fatty acids including acetate, and oxygen; (2) the cell’s central system for energy supply, including mitochondrial oxidative phosphorylation; (3) ionic currents, leaks and pumps, and their role in governing the membrane potential; (4) energy usage for contraction, biochemical reactions, and ion pumping; (5) excitation-contraction coupling, calcium balance, and the contractile process; and (6) balances of reducing equivalents and pH.

Figure 1 is a simplified diagram of the first of these. The initial steps in glucose and fatty acid metabolism require the use of ATP to form phosphorylated intermediates, so that ATP breakdown occurs before there is any ATP production from these substrates. The glycosome of the trypanosome isolates the glycolytic enzymes from the rest of the cytosol and so prevents the total depletion of cell ATP when substrate is first delivered to a starved cell.³³ The mammalian cell has no such protection, so one may expect transient cytosolic ATP depletion at the onset of reperfusion following a period of ATP-depleting ischemia. The modeling of Garfinkel and colleagues pioneered this area in the late 1960s through the 1980s.^34–47 The red blood cell (RBC) models of Palsson and colleagues^48–50 and of Mulquiney and Kuchel^51,52 are valuable descriptions of glycolysis. The flux expression for hexokinase in the Joshi and Palsson⁵³ article differs from the original source cited in the positioning of a parenthesis. Development of databases of physiological information on-line will enable investigators to conveniently access the relevant information for error-free model development. The Mulquiney and Kuchel articles are to be admired as excellent examples of providing the detailed enzyme kinetic mechanisms that serve as the basis for the reversible flux expressions in their articles. (As a side comment, our experience is that many models published or made available on a web site in the past 10 years have had errors. We have, however, had the pleasure of rapid responses from authors whose models we have found wanting, so it has for the most part been not too painful to obtain and implement corrections, just as one would like to see in modern science.) However, even a pathway as long known as glycolysis needs improvement when new experimental data become available. The glycogenolysis model of Lambeth and Kushmerick⁵⁴ accounted for the reversibility of all the reactions known to be reversible; the RBC glycolyis model of Bali and Thomas⁵⁵ provides for feed forward activation of pyruvate kinase, an adaptation that allows for rapid responses when ATP production needs to be increased.

Fatty acid uptake and metabolism is remarkably parallel to that of glucose: the first step requires ATP. There is storage as di- and triglyceride, which is analogous to glucose storage as glycogen. And there is uptake into the TCA cycle for generating NADH, the reducing equivalents that help to form the proton gradient that drives mitochondrial ATP production. The model for this that we prefer is that of Kohn and Garfinkel,^45–47 simply because most of the reactions are described in reversible equations and fulfill Haldane conditions as required by the thermodynamics. (Haldane conditions means that every reaction is reversible and that the forward and backward rate constants lead to zero net flux at equilibrium.) The ratios of reactant concentrations at thermodynamic equilibrium are independent of whether or not a catalyst or enzyme is present. Other models will work under physiological steady state conditions, but any with irreversible equations cannot match the thermodynamically determined equilibrium state and therefore are more subject to failure in stress states deviating from the normal physiological state. Models by Cortassa et al.⁵⁶ and Salem et al.⁵⁷ fall into this category and are not applicable over a wide range of conditions.

The second component, the cell’s central system for energy production, is mitochondrial oxidative phosphorylation. Several models have been devised for this. A peculiar problem is how oxygen is linked to the production of ATP, and the variation in opinion on what is the appropriate value for the affinity of binding of oxygen by cytochrome oxidase. Mitchell’s chemiosmotic hypothesis serves as the basis of the models. Currently accepted models⁵⁸ fail when oxygen falls to low levels.

The third set of components, ion currents during the action potential, the spread of excitation, and the pumping of ions to maintain ionic balance are relatively well worked out. Action potential models such as those of Noble et al.,⁵⁹ Winslow et al.,⁶⁰ and Luo and Rudy,⁶¹ are being updated and improved each year. For example, Michailova and McCulloch⁶² augmented the Winslow model by adding the Ca buffering systems, thus modifying the shape of the calcium transient. Winslow’s group have inserted or substituted genetic variants of particular channels to illustrate the peculiarities of their currents (e.g., Greenstein et al.⁶³). All the currents flowing during the action potential, and the passive exchangers (NaCa exchanger and NaH exchanger), dissipate the ionic electrochemical gradients. Energy-dependent pumps, the NaK ATPase and the CaATPase, are key to maintaining the gradients. For a composite cell model, the pump fluxes determine both the ionic gradients and the energy utilization. Lauger’s text⁶⁴ gives an excellent resume of their kinetics and specific models. Because perhaps one-third of the energy of a cardiomyocyte goes into ionic pumps, they must be accounted for in the expenditures.

The fourth process, balancing the energy usage for contraction, biochemical reactions, and ion pumping, is the production of energy through anaerobic metabolism (glycolysis) and aerobic metabolism (Krebs cycle fluxes and oxidative phosphorylation). We consider this a separable topic because it requires linking all of these various modules and yet achieves an energy balance over a wide range of steady states. A particular example that tests any model system severely would be an analysis of studies where energy sources are limited and the functional state impaired, but yet where steady state can be reached. An example is the observation of Chen and Gueron^65,66 on acetate Ringer-perfused rabbit heart: when 2 mM 2-deoxy-D-glucose was added to the perfusate, all the NMR-visible phosphate was converted to DG-6P, so that one has to ask how energy was being provided for cellular metabolism. Yet contractions continued at approximately 60% of peak control tension, still with acetate as the only substrate. The rate of diminution of the DG-6P peak in the NMR spectrum after stopping the 2-DG perfusion gives clear evidence of the hydrolysis of DG-6P by a phosphatase, without which the cell could have no free phosphate. Considering the persistence of contraction as a bioassay for cellular phosphorylation potential, one has to think that it was still at approximately 60% of control levels despite the absence of NMR visible ATP or P_i. Other data sets at low P_O2s will similarly challenge current models.

The fifth set of models are those of excitation-contraction coupling, calcium balance, and the contractile process. Bers’s book⁶⁷ provides a masterful compendium of the information on the heart, part of which is incorporated into LabHeart, a model developed and distributed by Puglisi and Bers⁶⁸ and run under LabView. It is an excellent teaching tool, and, although we have not tested it this way, it should be a good test vehicle for designing critical experiments to test the model. The several action potential models all contain elements of excitation-contraction coupling—that is, Ca release and reuptake—as these are essential to define the gradient for calcium currents during the action potential, but none are very detailed for the contractile process itself. The relationships between the Ca binding to troponin C, the actin-myosin interactions, the tension on the sarcomere, and the rates of shortening and the rate of utilization of ATP are complex. The models of Hill,⁶⁹ Taylor et al.,^70,71 Landesberg and Sideman,^72–74 and others reviewed by Gordon et al.⁷⁵ attest to the critical thinking going into understanding this process. One source of difficulty is the contribution of stretch activation of Ca channels versus the influences of stretch and tension on actin-myosin interactions.⁷⁶ Increasingly refined cross-bridge models continue to be developed.

The sixth set of considerations are balances of reducing equivalents and pH. Although these involve many transporters, exchangers, and shuttles (e.g., aspartate-malate shuttle), the emphasis is on assuring balances among the various processes of intermediary metabolism. For example, because NAD and NADH scarcely cross the mitochondrial inner membrane, the totals of NADH and NAD should remain constant in cytosol and inside mitochondria. This makes for a more useful check on mass balance than simply keeping track of the cellular total. However, to balance reducing equivalents and to express a cellular redox potential means also accounting for –SH groups, which we have not done in our “eternal cell” to this point. Balancing H⁺ is much more complex because of the host of reactions in which H⁺ is either used or produced, and because it is rapidly exchanged across cell membranes. At the whole-tissue level, pH balance is further complicated by such events as the release of approximately 0.7 moles H⁺ for each mole of oxygen bound to Hb. The many buffering systems for H⁺ include ones with clear stoichiometry (bicarbonate, etc.) and others (such as proteins in interstitial fluid and cells) in which no fixed stoichiometries can be assigned.

MODELING STRATEGY AND TACTICS

Given the complexity of the task, it is no wonder that complete cell models are not yet available; but now that there are demonstrated needs and increasing computer power, there will be soon. Therefore, we might try to define a set of questions that might be asked of each new model as it comes off the press. Second, we might determine how to define a model so that it can be understood and reproduced. Third, we might devise a set of tests or test cases that every “cell model” should be able to pass; there might be a set of levels of these. Fourth, we must expand on a “correct” “eternal cell” model that will be useful to the scientific community.

The questions to ask of a newly published model start with: (1) Is it reproducible? (2) Is the code verifiable? Over what range of parameters and variable values does it run correctly? (3) Is the model scientifically valid, and for what situation or species or cell?

Reproducibility (question 1) demands that the equations and parameter sets be completely correct, and that the numerical methods are such that behavior can be reproduced to so many decimal places. Of the many models we have tried to reproduce from publications in our laboratory, the only substantial one that survived this first test is that of Hodgkin and Huxley,⁷⁷ for which all the parameters were given for every figure. (Another one might have been the Luo-Rudy action potential,⁶¹ but we converted to different solvers and got slightly different solutions.) Other models have required corrections of misprints in the publication or in the material first received from authors; but, in general, authors have been most responsive, immediately, for requests for corrections or further information. This is, indeed, the time of international collaboration.

The verification question (2) is mainly answered by reproducibility of the operational code, but there is an additional nuance at a deeper level: do the solutions obtained through a particular numerical method give the correct solutions to the original equations? Because implementation methods can be expected to be peculiar to each laboratory, an error in the methods of solution in the originator’s computations will not be recognized through a failure to reproduce if the originator’s computational code is used. A better test is to run it with different solvers on different platforms after retranslating from the equations into computational code. Nowadays, for example with JSim or XPPAUT, the original mathematics-like source code is parsed and solution methods are automatically chosen. Because these two platforms provide different solvers, if a model is run under both systems and the results are the same, then one is virtually assured that the solutions are correctly obtained for the equation set.

The validity question (3) is open ended. All models are wrong, in the sense of being inexact or incomplete, or not sufficiently refined. All models are a statement defining a working hypothesis in a quantitative fashion. Models are made to be disproved and are the best vehicle for the advancement of science. A giant stride is taken whenever “a beautiful hypothesis is destroyed by an ugly fact,”⁷⁸ and one moves on to try to find the improved version of “truth.” The generality is that the more data, and the better the data, that one has, the better they serve as a test of the model. Biological models are based on anatomic structure, the nature of physical and chemical processes, and their thermodynamic constraints. The models used to analyze a particular data set should use all of these information types, not simply those data which came from a few variables measured in a single set of experiments. The idea of using a minimal model to characterize a data set is to abandon the idea of testing a hypothesis about a system and settling for a mere descriptor of that data set; this may be acceptable for diagnostic purposes, but it is not systems modeling.

THE FUTURE OF MODELING IN THE BIOLOGICAL SCIENCES

There is a new wind blowing in the halls of academia, driven in part by the pharmaceutical industry’s needs for quantitative, predictive modeling to assist in target selection for new agents. This fresh breeze is opening minds to the utility and beauty of models as aids to thinking and to advancing science at accelerated rates. Even though the American Journal of Physiology abandoned its Modeling Forum a few years ago, there are now more modeling articles published there than ever. Although Circulation Research appears at first glance to have a heavy emphasis on molecular and genetic studies, it still manages to publish key articles on the modeling of electrophysiology and of mechanics. The receptivity to models is really higher now than it has been in more than 20 years, in my view. However, there is a commandment: the model shall be coupled with experimental data. Pure mathematical modeling for its own sake does not appear in the leading biological journals, and even journals such as the Annals of Biomedical Engineering and the Journal of Mathematical Biology are weighted toward models applied to well-defined data, where the model fits to the data create new insight into processes and are not mere exercises in descriptive parameterization.

What is becoming recognized is that the modeling, in parallel with experiments, is essential for scientific development; and that the modeling analysis is powerful, although often still difficult. Training programs in the areas of computational and integrative physiology are still too small to satisfy the demands of industry and academia, and students are still reluctant to enter a demanding career requiring deep knowledge of both biology and engineering analysis. The advances in genomics, proteomics, and now metabolomics as fields of endeavor now make it more than obvious that the next big field in computational biology is integrative.