The folding trajectory of RNase H is dominated by its topology and not local stability: a protein engineering study of variants that fold via two-state and three-state mechanism

Abstract

Proteins can sample a variety of partially folded conformations during the transition between the unfolded and native states. Some proteins never significantly populate these high-energy states and fold by an apparently two-state process. Many proteins, however, populate detectable, partially folded forms during the folding process. The role of such intermediates is a matter of considerable debate. A single amino acid change can convert E. coli ribonuclease H from a three-state folder that populates a kinetic intermediate to one that folds in an apparent two-state fashion. We have compared the folding trajectories of the three-state and two-state RNases H, proteins with the same native state topology but altered regional stability, using a protein engineering approach. Our data suggest that that both versions of RNase H fold through a similar trajectory with similar high-energy conformations. Mutations in the core and the periphery of the protein affect similar aspects of folding for both variants, suggesting a common trajectory with folding of the core region followed by the folding of the periphery. Our results suggest that formation of specific partially folded conformations may be a general feature of protein folding that can promote, rather than hinder, efficient folding.

INTRODUCTION

Elucidating the high-energy conformations a protein samples as it traverses its folding landscape is the key to understanding which factors determine its folding trajectory. Many proteins are known to populate intermediates, and the role of these partially formed species has been the subject of much debate.¹ Intermediates may aid the protein in its search for the native state by greatly reducing the number of accessible conformations.² Alternatively, intermediates containing non-native interactions can result in a kinetic trap, inhibiting the folding progress and in some cases leading to the formation of disease-associated amyloid fibrils.³ What characteristics of these intermediates contribute to their helpful or harmful nature? Furthermore, understanding the nature of the rate-limiting transition state can lend insight into what restrictions are placed on an efficient folding process.⁴ How strictly encoded are these species? Can perturbations in these regions of the landscape uncover alternative folding routes to the same native structure?

Several factors are known to guide a protein’s folding trajectory. The native state structure, or topology, is clearly important. Contact order, the average sequence separation of native contacts, was the first topological parameter observed to correlate with the free-energy barrier for simple two-state folding proteins.⁵ Contact order itself, however, does not appear to be the defining factor,⁶ and other structural parameters such as long-range order,⁷ secondary structure content,⁸ and the total number of long-range contacts⁹ have also been observed to correlate with folding rates. Circular permutants of the ribosomal protein S6¹⁰ and α-spectrin SH3¹¹ fold through different transition states, demonstrating the malleability of the pathway in response to changes in topology.

Conversely, comparing the folding trajectories within families of proteins shows that, in many cases, the general properties of the folding pathway are conserved while the details vary widely, highlighting the importance of sequence-dependent effects^{12; 13; 14; 15; 16; 17}. While topology clearly plays a role in determining folding pathways, the detailed physical basis of its role is unclear.

Local or regional stability has also been implicated in guiding the folding process and intermediate formation. For the proteins cytochrome c¹⁸ and RNase H,¹⁹ the stability of partially folded forms identified by native-state hydrogen exchange has been shown to correspond with the order of structure formation along the kinetic pathway; the most stable regions appear to fold first. Folding pathways have also been re-routed based on thermodynamic considerations. Tripp and Barrick successfully moved the transition state of an ankyrin repeat protein by introducing stabilized consensus repeats at various locations in the Notch ankyrin domain.²⁰ These designed repeats were observed to fold first, showing that local energetics guide the folding mechanism of this protein. A similar plasticity was demonstrated with the structurally similar proteins G and L. In the transition state of protein L, the first β hairpin is structured while the second is not, and the opposite is true for the transition state of protein G.²¹ The first β hairpin of protein G was redesigned to increase its stability, and the folding of the resulting protein proceeded through the stabilized first turn so that it resembled the folding pathway of protein L.²²

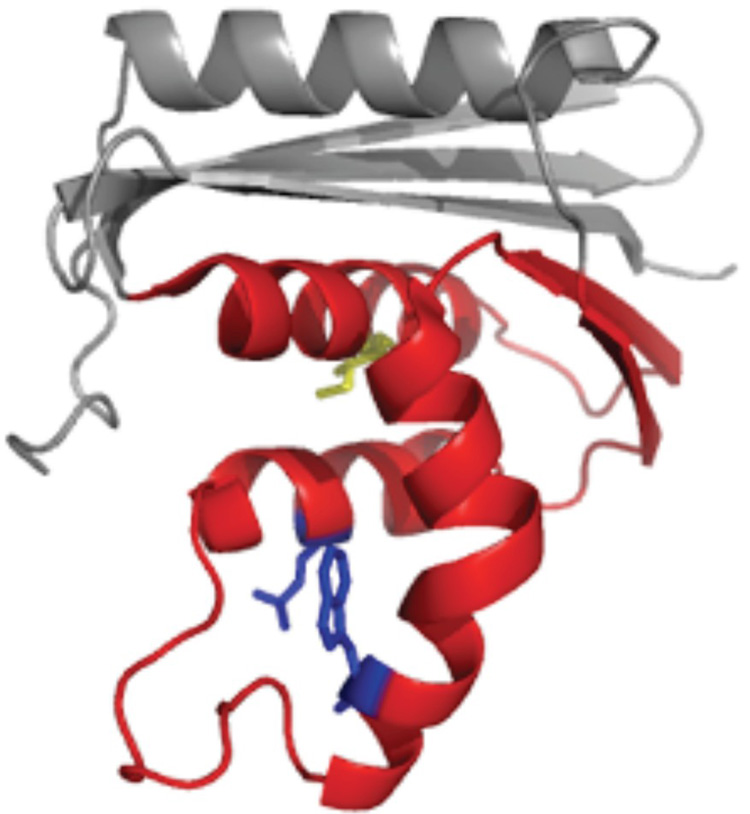
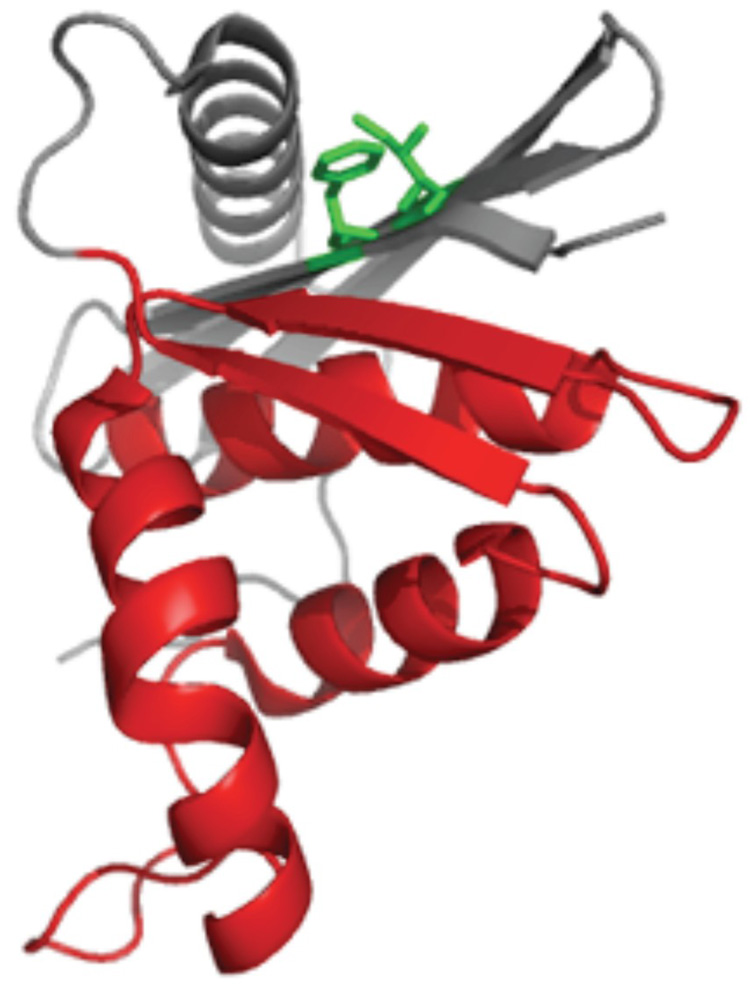
Here, we set out to explore the relative contributions of topology and regional stability by comparing variants of the same protein that fold via distinctly different kinetics. The energy landscape of E. coli RNase H has been well-characterized using native-state hydrogen exchange,^{23; 24; 25} stopped-flow kinetics, quenched-flow hydrogen exchange,¹⁹ and protein engineering.²⁶ The protein populates a kinetic refolding intermediate whose structure is mirrored by a partially folded form detected by the equilibrium native-state hydrogen exchange experiment. Recently, single-molecule experiments confirmed that the intermediate is on-pathway and obligatory.²⁷ This partially folded form is characterized by a high degree of secondary structure formation in the protein core and a relatively unfolded periphery (Figure 1).

Figure 1.

Structure of E. coli RNase H with the “core” colored red and “periphery” in grey. (a) The core mutations are shown as sticks, with Ile 53 in yellow and Asp 105 and Trp 85 in blue. (b) The periphery mutations, Phe 8 and Ile 25, are shown in green.

In a point mutant that introduces a potentially-charged residue into this core, I53D, the intermediate is no longer detected, and the protein folds with an apparently two-state mechanism.²⁸ Using this mutant, we compare the folding mechanisms of a three-state and a two-state version of the protein that differ by only one amino acid. The I53D mutation destabilizes the protein, and the addition of subsequent mutations was expected to result in further destabilization. To counter this effect and ensure sufficient stability of all constructs, we used a stabilized mutant, D10A, as our reference protein. ^{24; 26} This mutation relieves charge repulsion in the periphery of the protein and stabilizes the protein by more than 3 kcal/mol. Introducing this mutation also allowed us to ask if destabilizing the core and stabilizing the periphery simultaneously (D10A/I53D) results in an altered kinetic trajectory in which folding proceeds through a more diffuse transition state with looser interactions over a greater portion of the protein. A phi-value (ϕ-value) analysis on these variant proteins that share the same RNase H fold, but differ dramatically in their distribution of regional stability, allow us to evaluate the nature of the transition state for both two-state and three-state folders.

RESULTS

Our reference protein for three-state folding is the variant D10A RNase H, referred to herein as RNH3. ^{24; 26} The variant D10A/I53D, abbreviated as RNH2, serves as our two-state reference protein. These two proteins differ only by a single mutation: the insertion of a potentially charged residue in the core of the protein (Figure 1).

Design of Mutants

Significant changes in stability without notable alterations in structure are required to measure ϕ-values.²⁹ Since we sought to examine the effect of core mutations on both the three-state and two-state variants, we did not want to destabilize the core of the protein so much that the intermediate would no longer be apparent, as is the case with I53D. This requirement places an upper limit on ΔΔG_UN of approximately 3.5 kcal/mol (the stability of the intermediate) for the effect of mutations in this region. A variant containing a mutation in helix D of the core, Q105G (Figure 1a), was previously characterized in the wild type background and is known to destabilize the molecule by just over 2 kcal/mol, making this a good target.²⁶ The Trp at position 85 in helix C (Figure 1a) was also targeted as a likely residue to destabilize the core. Ile 25 and Phe 8 were chosen as the structural probes for the periphery. Both residues are part of a hydrophobic cluster in this region (Figure 1b).

Equilibrium Characterization of the Mutants

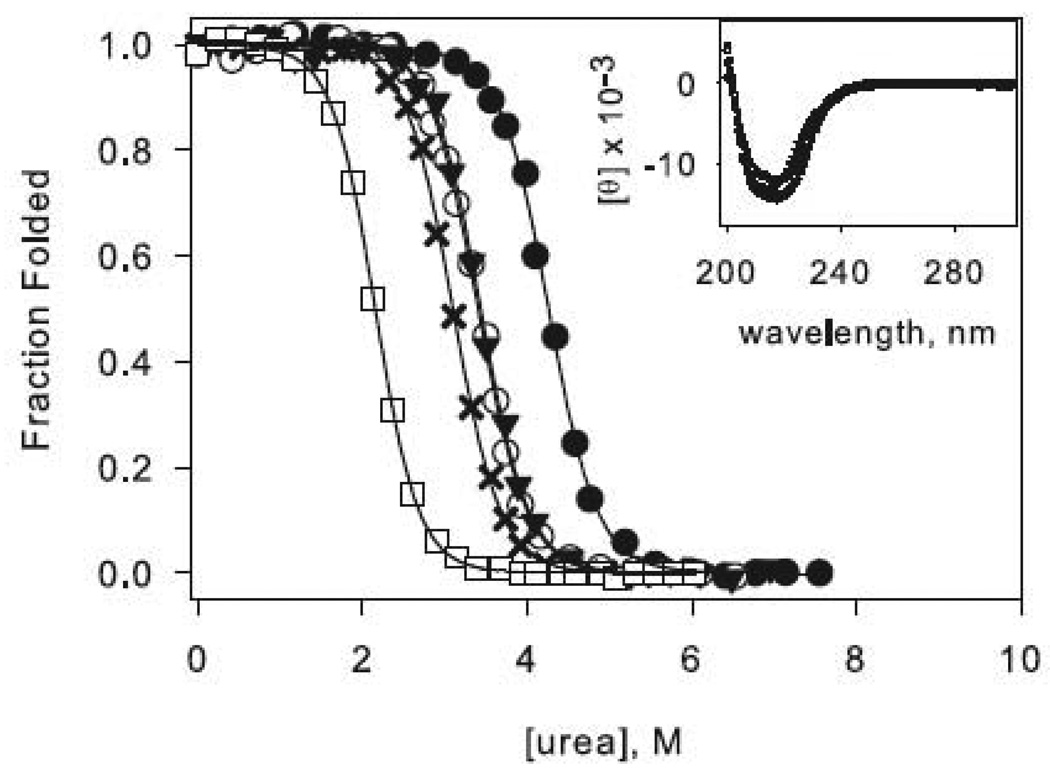
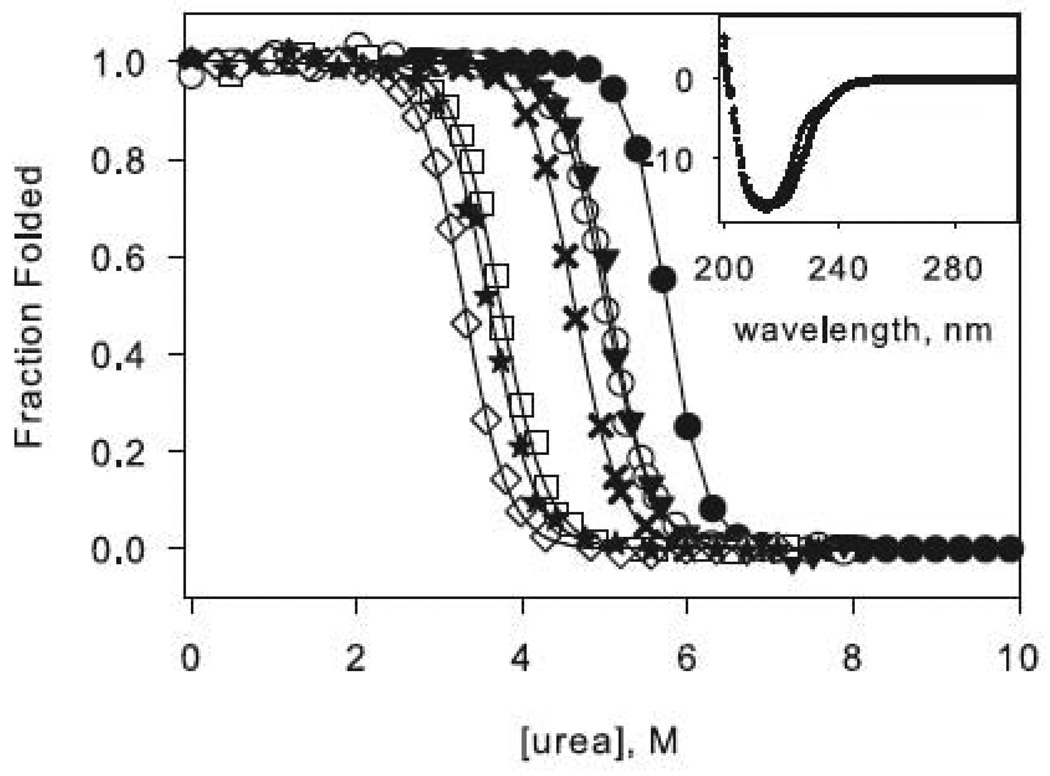
The circular dichroism (CD) spectra of all of the proteins used in this study are shown in Figure 2 (insets). All variants exhibit similar profiles characteristic of the RNase H α/β fold, indicating that the mutations do not significantly disturb the native structure. The stabilities of the variants, as measured by the free energy of unfolding, were determined by urea-induced denaturation profiles assuming a two-state transition and linear extrapolation.³⁰ A representative normalized denaturation melt of each protein is shown in Figure 2.

Figure 2.

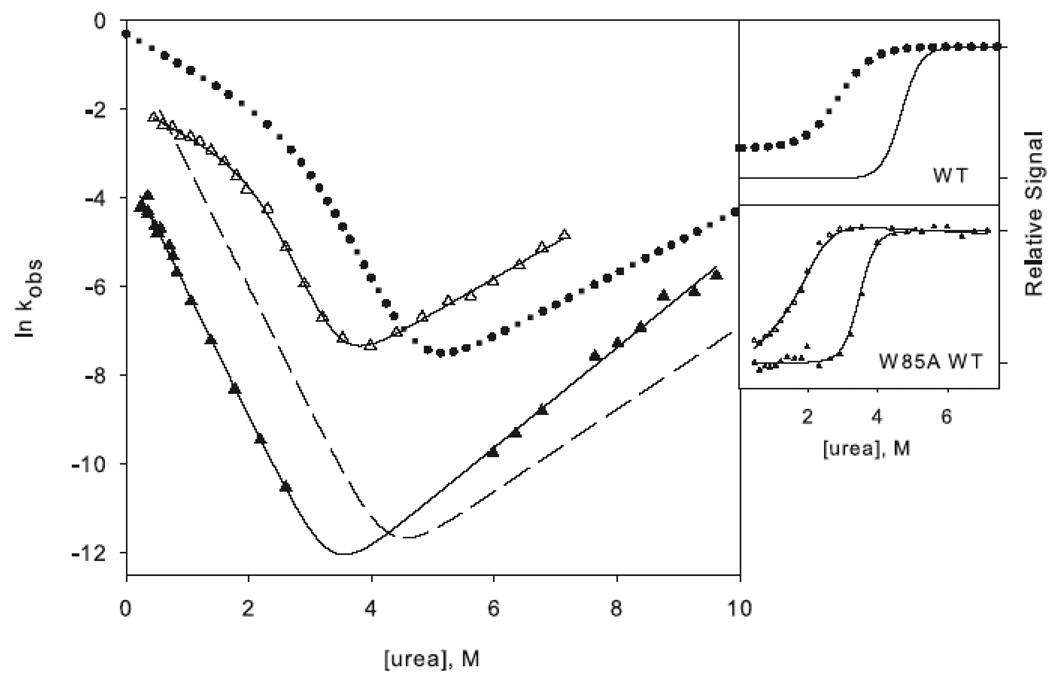
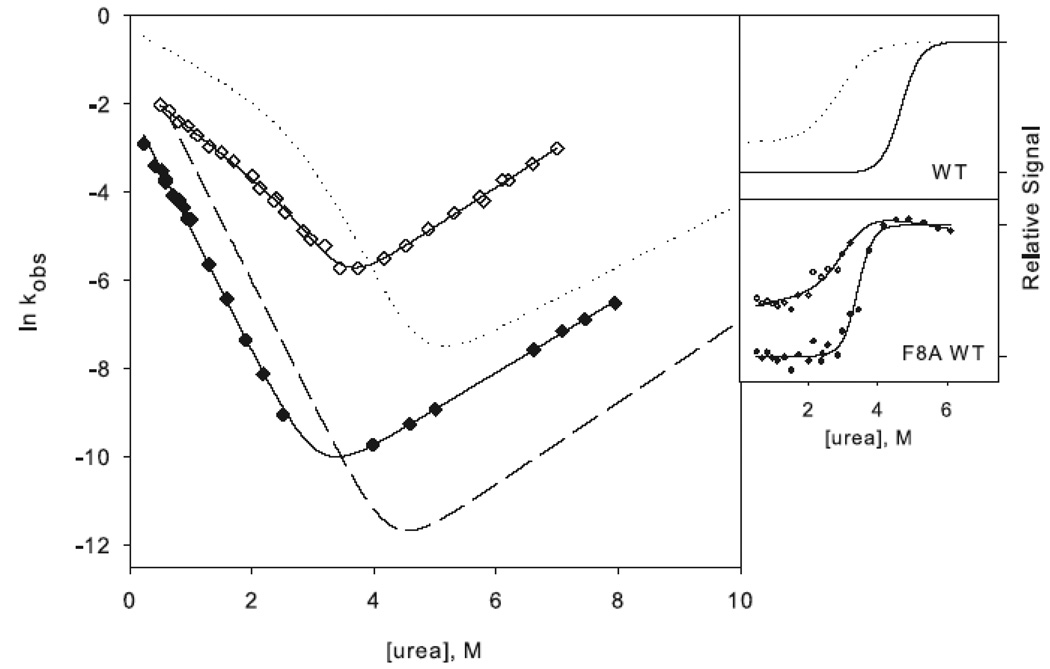
Representative urea denaturation curves of variants of RNase H normalized to fraction folded. The two-state (a) and three-state (b) proteins are separated for clarity. Black lines represent the linear extrapolation fit assuming a two-state model. The data for the reference proteins RNH2 in panel (a) and RNH3 in panel (b) are shown as filled circles, and the mutations in each of these backgrounds are as follows: Q105G (open circles), W85A (closed triangles), F8A (filled crosses), I25A (open squares). In panel (b) F8A in the wild type background is shown as open diamonds, and W85A in the wild type background is shown as stars. CD spectra of the mutants are shown as insets in the same symbols.

Treatment of the equilibrium data

When each denaturation profile was fit independently, variation in the m-value (the denaturant-dependence of the free energy) never exceeded 10 %. Fixing the m-value for all the proteins to that obtained for both the wild type and RNH3 variant (m = 2.1 kcal mol⁻¹ M⁻¹)²⁶ fit the data equally well. Since the magnitude of the stability change between the reference proteins and the variants is especially crucial for the calculation of ϕ-values and is highly dependent on the m-value, we calculated the ϕ-values three different ways: 1) using ΔΔG_UN’s obtained from urea melts with no constraint on the m-value, 2) using ΔΔG_UN’s from the fits with fixed m-values, and 3) using ΔΔG_UN’s calculated from fits to the kinetic data (see Tables 1 and 2 for a complete summary). Although absolute values vary somewhat, the general trends and conclusions remain the same. For this reason, we describe the effect of the mutations in terms of the data obtained by fixing the m-values.

Table 1.

Summary of equilibrium and kinetic data for the three-state RNases H. The values in parentheses indicate the standard deviation calculated from at least three separate denaturant melts.

			Periphery		Core		Periphery	Core
		RNH3*	I25A RNH3	F8A RNH3	Q105G RNH3	W85A RNH3	F8A	W85A
Δ G urea melt (kcal mol −1 )		13	8.2 (0.4)	10.0 (0.2)	10.6 (0.5)	11.3 (0.5)	6.5 (0.5)	6.8 (0.5)
meq urea melt (kcal mol −1 M−1 )		2.1	2.2 (0.1)	2.14 (0.03)	2.11 (0.05)	2.24 (0.1)	1.9 (0.2)	1.9 (0.1)
Δ G fixed m (kcal mol −1 )			7.86 (0.07)	9.78 (0.07)	10.5 (0.2)	10.56 (0.06)	7.05 (0.08)	7.5 (0.1)
Δ G kinetic (kcal mol −1 )		13.4	8.1	11.02	11.9	11.67	9.22	8.6
m kinetic (kcal mol −1 M−1 )		2.25	2.13	2.35	2.43	2.37	2.7	2.48
kin (H 2O) (s −1 )		1.89	0.37	0.55	0.59	0.48	0.227	0.1514
min (kcal mol −1 M−1 )		0.28	0.49	0.50	0.15	0.19	0.647	0.415
kni (H 2O) (s −1 )		1.5E-07	4.4E-05	2.6E-06	5.5E-08	1.6E-07	9.50E-05	2.50E-05
mni (kcal mol −1 M−1 )		−0.48	−0.49	−0.48	−0.60	−0.51	−0.529	−0.472
Kui		585	110	611	54	133	2580	350
mui (kcal mol −1 M−1 )		1.50	1.15	1.37	1.68	1.66	1.505	1.596
Δ Gui (kcal mol −1 )		3.76	2.77	3.79	2.35	2.89	4.64	3.46
ϕ I	1		0.19	−0.01	0.56	0.36	−0.42	0.04
	2		0.2	0.0	0.6	0.5	−0.1	0.0
	3		0.19	−0.01	0.94	0.51	−1.64	0.07
ϕ t.s.	1		0.35	0.47	1.23	0.97	0.51	0.78
	2		0.3	0.4	1.2	1.0	0.4	0.5
	3		0.37	0.29	1.39	0.96	−0.93	0.62
β T	1	0.77	0.77	0.77	0.71	0.76	0.75	0.78
	2	0.8	0.8	0.8	0.7	0.8	0.7	0.8
	3	0.79	0.77	0.80	0.75	0.78	0.80	0.81

^*These values were previously determined by Raschke, Kho, and Marqusee.²⁶

1. calculated using a fixed m-value of 2.1

2. calculated using the m-value from urea melts

3. calculated using the m-value from the kinetic data; m_kinetic = m_ui + m_in − m_ni

Table 2.

Summary of equilibrium and kinetic data for the two-state RNases H. The values in parentheses indicate the standard deviation calculated from at least three separate denaturant melts.

			Periphery		Core
		RNH2	I25A RNH2	F8A RNH2	Q105G RNH2	W85A RNH2
Δ G urea melt (kcal mol −1 )		8.5 (0.4)	4.8 (0.1)	6.32 (0.4)	7.1 (0.5)	7.2 (0.3)
meq urea melt (kcal mol −1 M−1 )		2.0 (0.1)	2.24 (0.01)	2.0 (0.1)	2.1 (0.1)	2.08
Δ G fixed m (kcal mol −1 )		8.9 (0.1)	4.5 (0.1)	6.62 (0.08)	7.05 (0.08)	7.219 (0.006)
Δ G kinetic (kcal mol −1 )		9.09	4.60	6.56	7.24	7.76
m kinetic (kcal mol −1 M−1 )		2.07	2.05	2.13	2.31	2.34
kun (H 2O) (s −1 )		0.40	0.058	0.126	0.020	0.037
mun (kcal mol −1 M−1 )		1.51	1.58	1.64	1.62	1.67
knu (H 2O) (s −1 )		8.10E-08	2.40E-05	2.10E-06	9.54E-08	7.61E-08
mnu (kcal mol−1 M−1)		−0.56	−0.47	−0.49	−0.69	−0.67
ϕt.s.	1		0.26	0.30	0.95	0.84
	2		0.31	0.31	1.26	1.05
	3		0.25	0.27	0.95	1.06
βT	1	0.72	0.75	0.78	0.77	0.80
	2	0.76	0.71	0.80	0.77	0.80
	3	0.73	0.77	0.77	0.70	0.71

1. calculated using a fixed m-value of 2.1

2. calculated using the m-value from urea melts

3. calculated using the m-value from the kinetic data

Core mutations

The core mutation Q105G was previously shown to destabilize the wild type protein by 2.2 kcal/mol.²⁶ In the background of RNH3, this mutation has a similar effect, bringing the global stability to 10.5 kcal/mol (compare to 13 kcal/mol for RNH3²⁶). In RNH2, this mutation appears to be slightly less destabilizing (ΔΔG_UN ~1.9 kcal/mol). The core mutation W85A destabilizes the wild type protein and RNH3 to a similar extent, 2.2 and 2.4 kcal/mol respectively, and the magnitude of this effect also decreases in the background of RNH2, with a change in stability of 1.7 kcal/mol.

Periphery mutations

I25A has an unexpectedly dramatic effect on the stability of RNase H; this variant destabilizes the periphery enough to populate the intermediate under native conditions in the wild type background, prohibiting a full kinetic analysis. In the stabilized background of RNH3, this mutation destabilizes the protein by approximately 5.1 kcal/mol. In the two-state background, RNH2, I25A destabilizes the protein by 4.4 kcal/mol. The F8A mutation destabilizes the protein by 2.6 kcal/mol in the context of the wild type protein and 3.2 kcal/mol in the background of RNH3. The effect of this mutation decreases to 2.3 kcal/mol in the two-state background of RNH2.

Kinetic phi-value analysis in the two-state and three-state RNases H

Core mutations

The mutations introduced into the core, while destabilizing, were selected to avoid being so disruptive that they abrogate detection of the burst-phase kinetic intermediate. Indeed, a large percentage of the CD signal was acquired in the dead time of the stopped-flow instrument for both Q105G RNH3 and W85A RNH3; these burst-phase signals melted out cooperatively with urea (Figure 3a), as expected for the formation of an early intermediate. Furthermore, the chevron plots display the significant rollover in the folding limbs characteristic of the formation of an intermediate. These data were therefore fit using a three-state mechanism with an on-pathway intermediate in pre-equilibrium with the unfolded state:³¹

$$\mathrm{U}\rightleftarrows \mathrm{I}\to \mathrm{N}$$ Scheme 1

The stability of the intermediate was inferred from an analysis of the burst phase amplitudes as a function of urea (Figure 3a)²⁸. Both Q105G and W85A shift the C_m of the intermediate to lower urea concentrations. The ratio of the change in stability to the intermediate and the native state, ϕ^I, for Q105G is 0.9 (Table 1), indicating that native-like interactions are formed at this position in the intermediate. W85A, in helix C, has a ϕ^I-value of 0.5, suggesting that there may be some native-like interactions in the intermediate, but that they are only partially formed or are fully formed in only some portion of the molecules in the ensemble.

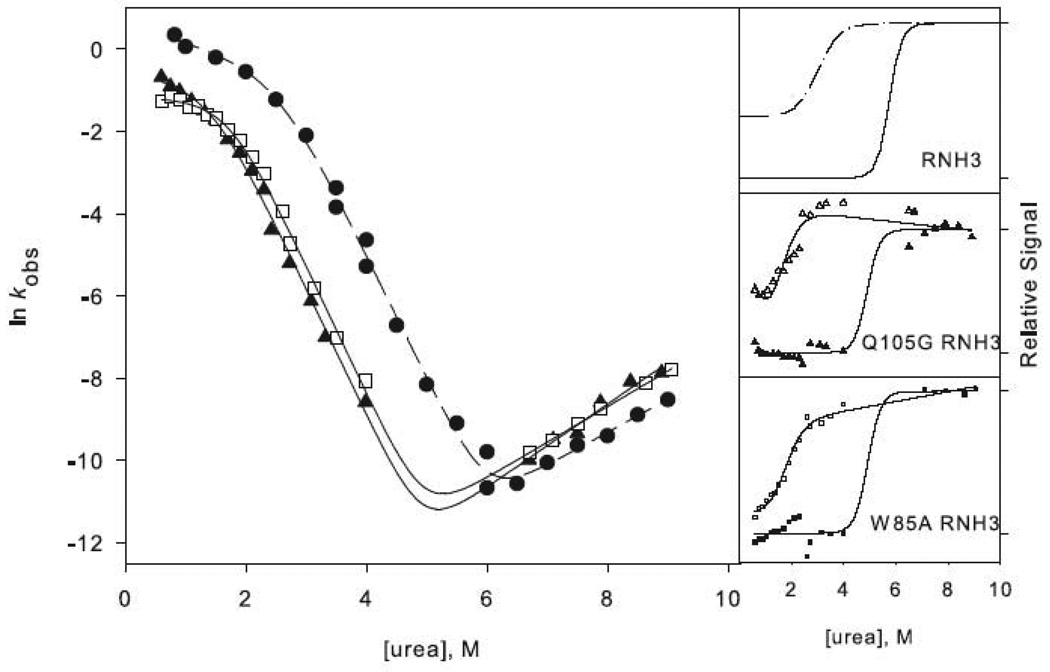
Figure 3.

Chevron plots for the three-state ((a) and (c)) and two-state ((b) and (d)) RNases H. The data for the reference proteins, RNH3 and RNH2, are filled circles. Panels (a) and (b) show the core mutation Q105G (filled triangles) and W85A (open squares). Panels (c) and (d) show the data for the periphery mutations F8A (open diamonds) and I25A (filled squares). The solid lines in (a) and (c) represent the fit to Scheme 1 and in (b) and (d) the fit to Scheme 2. The amplitudes are shown to the right of each chevron plot, with the initial signal shown as open symbols and final shown in closed symbols. The data are plotted as the fraction of relative overall signal. The black lines represent a linear extrapolation fit obtained by fixing the value for ΔG and m calculated from the chevron fit to show that they are consistent.

If these two residues are also structured in the transition state, as is expected, the change in stability should manifest itself in a shift in the folding limb of the chevron while the unfolding limb remains unchanged. This is indeed observed for both Q105G RNH3 and W85A RNH3 (Figure 3a). The quantitative effects of these core mutations corroborate the qualitative observations. The ϕ^t.s.-values, the ratio of the change in stability of the transition state to that of the native state (Equation 1 in Materials and Methods), for both of these mutants are high, 1.3 for Q105G and 0.96 for W85A (Table 1). The ϕ^t.s.-value over 1 for Q105G arises from an unfolding rate that is actually slower than that of the reference protein. Given the errors inherent in the calculation of ϕ-values, we feel it is best to interpret them qualitatively as low, medium, and high rather than quantitatively.^{32; 33} ϕ^t.s.˜-values for these core residues are classified as high, confirming that, as expected, the core region is very important for the energetics of the transition state.

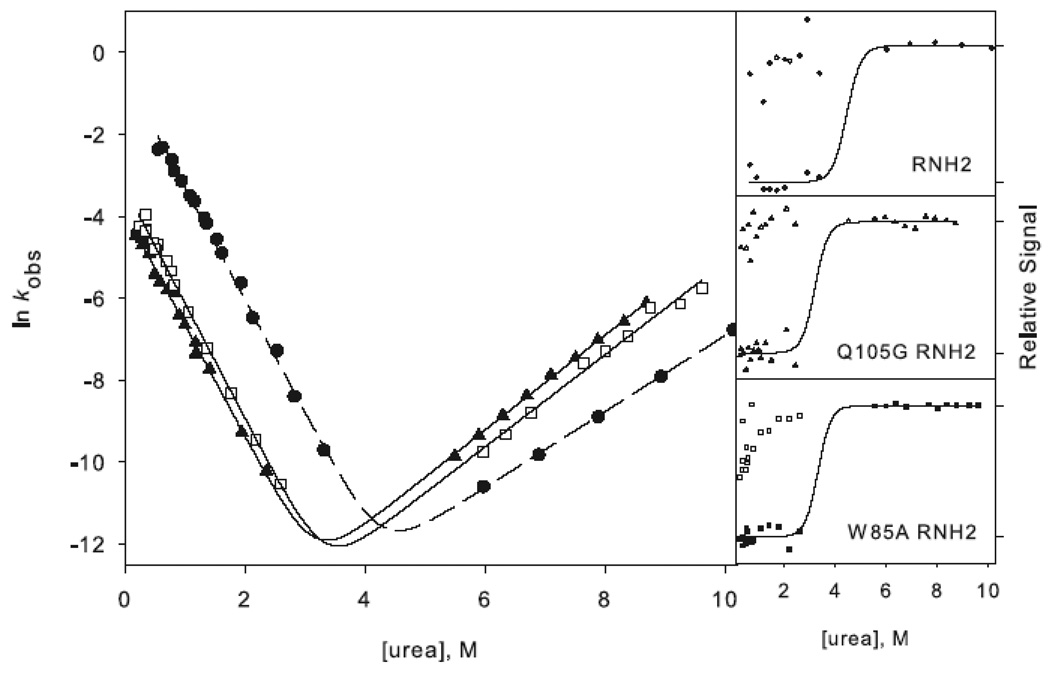
In the background of RNH2, no burst phase intermediate was observed, and there was no apparent rollover in the folding limb of any of the variants (Figure 3b). The chevrons for these proteins were fit to a simple two-state mechanism:

$$\mathrm{U}\rightleftarrows \mathrm{N}$$ Scheme 2

These mutations show qualitatively similar shifts in the folding limb of the RNH2 variant as they do in RNH3. Q105G RNH2 and W85A RNH2 have very similar unfolding rates in water as RNH2 but have a steeper unfolding limb, the implications of which are discussed below. The ϕ^t.s.-values (Equation 2 in Materials and Methods) are high (0.95 for Q105G and 1.06 for W85A (Table 2)), similar to those calculated for these mutations in the background of RNH3. Therefore, in both the three-state and two-state proteins, it appears that the core residues are in a native-like conformation in the rate-limiting transition state.

Periphery Mutations

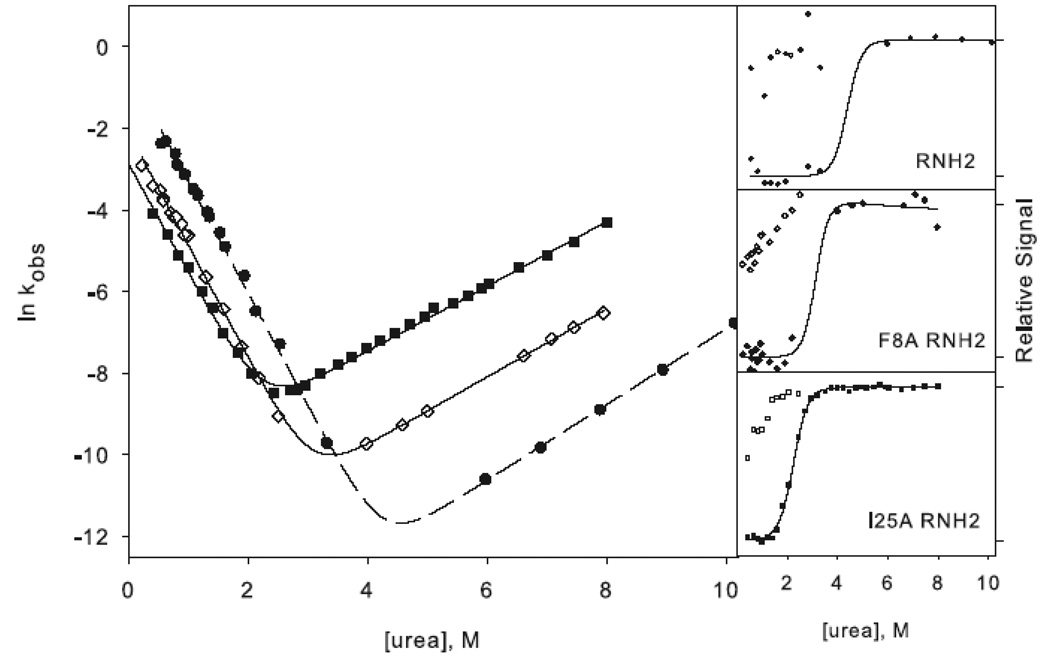
I25A RNH3 and F8A RNH3 both show a notable burst phase amplitude and rollover in the folding limb of the chevron plots (Figure 3c), and the data were therefore fit to the three-state mechanism shown in Scheme 1. Mutations in the periphery of RNH3 are not expected to affect the energetics of the intermediate or the transition state of the protein, and indeed, in contrast to the core mutations, the C_m for the burst-phase amplitudes in these periphery mutants is similar to that of RNH3 (Figure 3c). The ϕ^I-value for I25A is 0.2 and 0 for F8A (Table 1), confirming that these residues are relatively unstructured in the intermediate. The unfolding limbs of I25A RNH3 and F8A RNH3 are clearly shifted from that of RNH3; these variants unfold more rapidly than the reference protein. The folding limbs also exhibit some shift, however, suggesting that these mutations do not leave the stability of the transition state totally unaffected. The ϕ^t.s.-value (Equation 1) is 0.35 for I25A RNH3 and 0.47 for F8A RNH3 (Table 1). These are intermediate ϕ-values, indicating that there may be some limited native-like structure in this region of the transition state.

In the two-state background, there is no evidence of rollover and no apparent burst phase intermediate (Figure 3d); hence these data were fit to Scheme 2. The trends observed for these mutations in the background of RNH2 are similar to those in RNH3. Dramatic shifts are evident in the unfolding limbs of I25A RNH2 and F8A RNH2 while the folding limbs are slightly shifted. The ϕ^t.s.-values (Equation 2) are also similar to those in the background of RNH3, at 0.25 and 0.27 for I25A RNH2 and F8A RNH2, respectively (Table 2).

Destabilized core/stabilized periphery

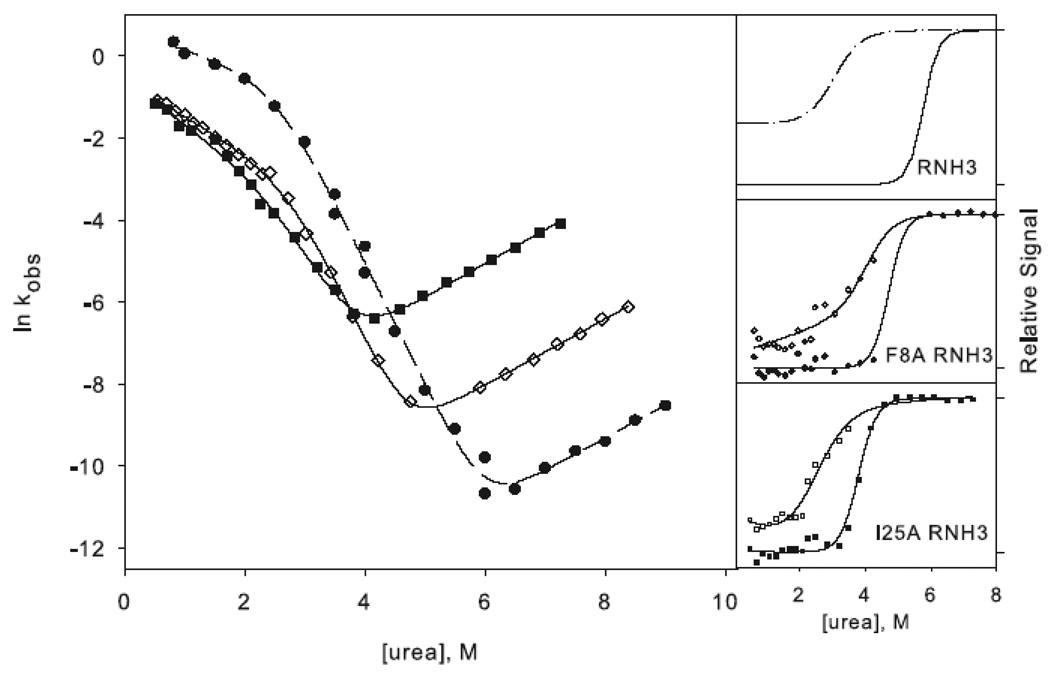
We also examined the kinetic trajectory of W85A and F8A in the wild type background (the kinetics of Q105G were reported previously²⁶, and I25A cannot be examined in the wild type background). This allows a direct comparison between the wild type mechanism and that of RNH2, in which the unfolded part of the intermediate and transition state is stabilized (D10A) and the folded part is destabilized (I53D), a more drastic alteration of the relative stability of the core and periphery.

W85A WT (W85A in the wild type background) shows a rollover in the folding limb along with cooperative melting of burst phase amplitudes (Figure 4a). Although the rollover is less apparent for F8A WT (F8A in the wild type background), this variant also has a large burst-phase amplitude (Figure 4b). Scheme 1 was therefore used to fit the chevron plots of both variants. Qualitatively it is clear from the burst phase signals that the core mutation compromises the stability of the intermediate while the periphery mutation leaves it unaffected, although the ϕ^I-values are not well defined (Table 1). Because the intermediate is only present in very limited range of urea concentrations, the value for m_UI, defined by the curvature in the chevron, is ill defined for F8A, and the intermediate appears stabilized, resulting in negative ϕ^I-values. Similarly, the m_UI value for W85A is larger than that of wild type, resulting in a calculated value for ΔΔG_UI very close to that of wild type. However, it is clear from the burst phase amplitudes that the intermediate is indeed destabilized.

Figure 4.

Chevron plots for the core mutation W85A (a) and the periphery mutation F8A (b) in the wild type background. W85A RNH3 is shown as open triangles and W85A RNH2 as closed triangles. The dotted lines represent the wild type chevron while the dashed line represents a fit to the RNH2 chevron. F8A RNH3 is shown as open diamonds and F8A RNH2 as closed diamonds. The data for the two-state proteins are shown as in Figure 3 for comparison. The amplitudes are shown as in Figure 3.

The ϕ^t.s.-values, calculated from the unfolding limb data (Equation 1), appear more reliable. W85A, with a value of 0.8, clearly affects the energetics of the transition state. F8A shows a moderate ϕ^t.s.-value of 0.5. These are very similar to those calculated in the background of RNH3, although slightly less polarized. It is clear that the transition state of RNH2 is no more diffuse than that of the wild type protein; if anything, structure is more localized to the core.

Burial of solvent accessible surface area in the transition state

The ratio of solvent accessible surface area buried in the transition state compared to the native state, m_t.s./m_eq, where m_t.s. is the change in solvent accessible surface area upon folding and m_eq is the equilibrium m-value, is quantified as the Tanford β-value (β_T). β_T was calculated as 1 – (m_ni/m_eq) for the three-state proteins, where m_ni represents the denaturant dependence of the unfolding rate constant. m_t.s. was taken directly as m_un for the two-state proteins, where m_un is the denaturant dependence of the folding rate constant. For all variants studies, β_T is 0.7 – 0.8, indicating that 70 to 80 % of the total surface area buried upon folding is buried in the transition state (Tables 1 and 2). This speci24es is similar in compactness across all variants.

DISCUSSION

Both native state topology and regional stability have been shown to play a role in determining protein-folding pathways. To further investigate the relative contributions of these factors, we manipulated the distribution of regional stability in E. coli RNase H through mutation while maintaining native state topology. One of these mutations, in the core of the molecule, transforms the three-state folder into one that folds without the accumulation of an intermediate. We used phi-value analysis to compare the folding trajectories of the three-state and two-state reference proteins and found that RNase H folds through a structured core and comparatively unstructured periphery regardless.

Coupling of distal regions of RNH2

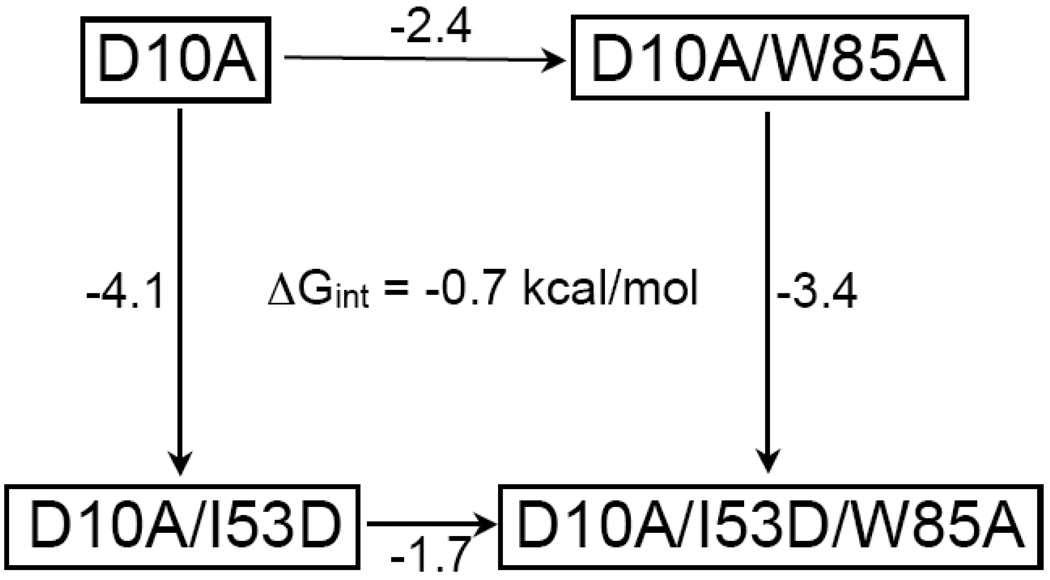
Each of the four mutations chosen for this investigation destabilized the two-state protein less than the three-state protein. Given that the only difference between these proteins is a single mutation at position 53, this non-additivity suggests that the charge introduced at residue 53 couples to other regions of the protein. Applying a thermodynamic cycle suggests that the magnitude of this coupling effect ranges from 0.6 kcal/mol (residue 105) to 0.9 kcal/mol (residue 8); the value is 0.7 kcal/mol for positions 85 and 25 (Figure 5). Since coupling between the core and the periphery has not been detected in previous experiments,²⁵ this suggests that the coupling is due to the insertion of a charge at position 53 in the background of D10A.

Figure 5.

A thermodynamic cycle addressing the interaction between Ile 53 and the mutated sites, represented here by Trp 85. The ΔΔG (kcal/mol) of unfolding upon making the indicated mutation is reported along the arrows. This cycle shows an interaction energy of 0.7 kcal/mol for residues 53 and 85.

The folding mechanism of RNase H is robust; two-state and three-state RNases H fold through similar pathways

With the introduction of a single mutation into the folding core of RNase H (I53D), the protein is converted from a three-state folder with an observable intermediate to one that folds in an apparently two-state mechanism. A comparison of the ϕ^t.s.–values for each site in each of these backgrounds is presented in Table 3. RNH3 shows high values for the core mutations and intermediate values for the periphery mutations. These intermediate values suggest that although it is less involved, some regions of the periphery may be more important for the structure of the transition state than originally proposed during the initial discovery of this trajectory.^{19; 26} It is clear, however, that the transition state of RNH3 is highly polarized with a native-like core and a comparatively unstructured periphery. The periphery of the two-state protein appears to be no more structured in the transition state than in the three-state protein, with very similar ϕ-values for each mutation. Furthermore, all variants bury a similar proportion of solvent accessible surface area upon folding.

Table 3.

Direct comparison of ϕ^t.s.-values for the four mutations in each of the three backgrounds.

	ϕt.s.
	Periphery		Core
	I25A	F8A	Q105G	W85A
Three-State	0.35	0.47	1.23	0.97
Two-State	0.31	0.30	0.95	0.84
wt		0.51	1.19	0.78

The wild type trajectory can also be compared to that of RNH2, which has two residue changes resulting in a stabilized periphery as well as a destabilized core. Even these drastic changes in the distribution of stability do not appear to re-route folding. This is somewhat surprising considering that folding of the wild type enzyme appears to follow a hierarchical mechanism in which the most stable regions fold first. When the core is destabilized by more than 6 kcal/mol, in both the I53D/W85A and I53D /Q105G mutations, this region is still capable of initiating folding without apparently incorporating additional elements from the periphery. The stability of the core of the molecule only determines whether the protein folds through an observable intermediate in a three-state fashion or through an apparent two-state mechanism. When this region is destabilized to such an extent that this intermediate is no longer detectable, this region still dominates the folding trajectory and presumably the intermediate species still exists, albeit at a higher energy on the folding trajectory.²⁸ Apparently, the topology of RNase H places strict constraints on the order of folding events and gives rise to the apparent robustness of this mechanism.

What makes RNase H different from proteins such as protein G and the Notch ankyrin domain, whose pathways were successfully re-routed based on thermodynamic considerations? One possible explanation is the simplified architecture of these two proteins. The notch protein is made up of repeats of the ankyrin domain, consisting entirely of sequence-local interactions. The modular arrangement of structurally identical units may account for its plasticity in response to changes in the distribution of stability. Proteins G and L are small (~60 residues) and symmetric in structure.³⁴ Though globular, these proteins can be thought of as modular as well, with two structurally identical halves, in which folding proceeds through the half with the more stable β-hairpin.

Changes in m_nu for RNH2 mutants

It is interesting to note that in the background of RNH2, the values for m_nu of the core mutants increases quite drastically while they decrease very slightly for the periphery mutants. The slight decrease for I25A and F8A RNH2 results in kinetic m-values that agree nicely with the equilibrium m-values. This is not the case for the core mutants Q105G and W85A RNH2, whose kinetic m-values are greater than those calculated from the fit to the equilibrium denaturant melts. The increase in slope of the unfolding limb for the core mutants can also be detected in the background of RNH3, though to a much lesser extent.

Increased values for m_nu upon mutation can arise from a movement of the transition state, a complete change in the barrier traversed upon folding, or ground state effects in the native state.³⁵ The equilibrium m-values for all proteins studied are the same within error, and ground state effects are much less common for the native state than the unfolded state. Whether this increase in m_nu reflects a complete change in mechanism under high urea or movement³⁶ of the transition state is unclear and in a sense describes two extremes of the same phenomenon. This debate is beyond the scope of this paper. Nonetheless, ϕ-values calculated from the unfolding rates in 8M urea are ~0.5 as opposed to ~1, suggesting that in high urea, the protein may indeed not incorporate as much of the core into the transition state. Under conditions in which the native state is destabilized, movement of the structure of the transition state away from that of the native is indicative of anti-Hammond behavior. Similar increases in the m-value for unfolding upon mutation have been observed and interpreted as anti-Hammond behavior for TI I27.³⁷ One explanation for the observed shift in m_nu in our two state proteins is that in high levels of denaturant and with the folding core severely compromised, folding can proceed through a more loosely structured core.

Ruggedness in the energy landscape can be productive for folding

The results presented here support the argument that formation of specific ensembles of partially-folded species are a universal feature of folding that play an important role even for proteins that appear to proceed in a two-state manner. The development of new tools to study the progression of folding may uncover these important high-energy ensembles. For instance, novel NMR studies have recently uncovered a high energy intermediate for the FynSH3 domain, which was until recently considered to be a two-state system.³⁶ Trapping partially folded intermediates at equilibrium to gain experimental access is another novel approach. This can be accomplished by introducing destabilizing mutations in the unfolded regions of the intermediate^{38; 39; 40} (also see Connell, Horner, and Marqusee, accompanying manuscript) or by constructing a fragment representing the folded region.⁴¹

Folding studies between different members of a protein family also suggest that two-state behavior masks some of the inherent complexities of folding. Both two-state and multi-state folding has been observed in the immunity proteins,¹³ immunoglobulin-like proteins,³⁷ and members of the homeodomain family.^{42; 43} Im7 was observed to populate a kinetic intermediate while Im9, sharing 60% sequence identity, appeared two-state;¹³ however, under different conditions both proteins folded through an intermediate, albeit with different structural properties.¹⁷ Changing just a few key residues of Im9 led to the population of an intermediate closely resembling that of Im7 under the original conditions in which Im9 appeared two-state.¹⁴ Changes in sequence or in folding conditions have actually led to the switching from one kinetic mechanism to another for members of all of the above families, suggesting that high-energy structures are only detectable with increases in the ruggedness of the landscape large enough to bring the stability of the species below that of other states.

It is important to note that this increased ruggedness does not necessarily slow folding. In the case of RNase H, populating the intermediate actually promotes efficient folding; the folding rate of RNH3 is an order of magnitude higher than that of RNH2. Wagner and Kiefhaber⁴⁴ explored the effect of intermediates on the rate of protein folding applying Kramer’s theory of diffusive barrier and found that introducing additional local barriers and valleys (roughness) can actually enhance the folding rate without altering the rate-limiting barrier. In light of the possibility that such partially folded ensembles are ubiquitous and that transient population of such species can promote rather than hinder folding, their characterization remains a crucial step in enhancing our understanding of folding.

Materials and Methods

Construction and purification of RNase H variants

The RNase H variants described in this manuscript were generated using the Quikchange mutagenesis protocol. A plasmid containing the gene encoding D10A RNase H²⁶ was used as a template to create the double mutants. These variants were expressed and purified as described.¹⁹ The triple mutants were created using a plasmid containing D10A/I53D RNase H, pGH101, as a template. These variants expressed insolubly as inclusion bodies and were purified accordingly.²⁸

CD Spectra

CD spectra were obtained on an Aviv 410 circular dichroism spectropolarimeter. Protein concentrations were determined based on the extinction coefficient, calculated according to the number of Trp and Tyr residues.⁴⁵ The buffer conditions for all experiments were 20 mM sodium acetate pH 5.5 and 50 mM potassium chloride. Spectra were collected with a 1 mm pathlength cuvette at a protein concentration of 500 µg/mL.

Equilibrium urea denaturation

For each variant described, samples containing varying amounts of urea and 50 µg/mL protein were equilibrated for the required time and the CD signal was measured at 222 nm at 25°C in a 1 cm cuvette. The signal over 60 seconds was averaged for each sample. The slow folding and unfolding of many of the variants used in this study necessitates long equilibration times, over a week for the slowest folding proteins. All equilibrium denaturation melts were repeated at least three times. The data were fit to a two-state model with a linear free energy extrapolation.³⁰ Even though the kinetics of the three-state proteins reveal a transient intermediate, at equilibrium this species never populates to more than a few percent due to its substantially lower stability compared to the native state. The equilibrium curves of the three-state proteins can be well-represented by a two-state model, as the unfolded and native forms are the dominant species.

Kinetics of folding and unfolding

Refolding of the mutants was initiated in one of two ways. For the double mutant in low denaturant conditions, refolding was initiated by a 1:11 dilution from a urea concentration in the unfolded baseline and monitored using an Aviv 202-SF stopped-flow device (1 mm pathlength). Final protein concentration in the stopped-flow device was at least 500 µg/mL. For the double mutants in higher urea conditions and for all triple mutants, refolding was induced by a 1:30 dilution via manual mixing and monitored using an Aviv 410 spectrometer. Unfolding for all variants was initiated by manual mixing and a 1:30 dilution from a urea concentration in the folded baseline. The final protein concentration for all manual mixing experiments was 50 µg/mL. Progression of folding and unfolding was monitored at 222 nm, and the resulting curves were fit to a single exponential. Kinetic data were fit as previously described.²⁸

Calculation of ϕ-values

ϕ-values in the folding direction for the three-state variants were calculated as

$${\mathrm{\varphi }}^{\mathrm{t}.\mathrm{s}.}=1{-}_{\mathrm{\Delta }|{\mathrm{G}}_{\text{mut}}-\mathrm{\Delta }{\mathrm{G}}_{\text{wt}}}^{\text{RTln}({{𝓀}_{\text{ni}}}^{\text{mut}}/{{𝓀}_{\text{ni}}}^{\text{wt}})}$$ Equation 1

For the two-state proteins, ϕ-values were calculated directly from the folding rates:

$${\mathrm{\varphi }}^{\mathrm{t}.\mathrm{s}.}{=}_{\mathrm{\Delta }{\mathrm{G}}_{\text{wt}}-\mathrm{\Delta }{\mathrm{G}}_{\text{mut}}}^{\text{RTln}({{𝓀}_{\text{f}}}^{\text{mut}}/{{𝓀}_{\text{f}}}^{\text{wt}})}$$ Equation 2