Data-driven automated acoustic analysis of human infant vocalizations using neural network tools

Abstract

Acoustic analysis of infant vocalizations has typically employed traditional acoustic measures drawn from adult speech acoustics, such as f₀, duration, formant frequencies, amplitude, and pitch perturbation. Here an alternative and complementary method is proposed in which data-derived spectrographic features are central. 1-s-long spectrograms of vocalizations produced by six infants recorded longitudinally between ages 3 and 11 months are analyzed using a neural network consisting of a self-organizing map and a single-layer perceptron. The self-organizing map acquires a set of holistic, data-derived spectrographic receptive fields. The single-layer perceptron receives self-organizing map activations as input and is trained to classify utterances into prelinguistic phonatory categories (squeal, vocant, or growl), identify the ages at which they were produced, and identify the individuals who produced them. Classification performance was significantly better than chance for all three classification tasks. Performance is compared to another popular architecture, the fully supervised multilayer perceptron. In addition, the network’s weights and patterns of activation are explored from several angles, for example, through traditional acoustic measurements of the network’s receptive fields. Results support the use of this and related tools for deriving holistic acoustic features directly from infant vocalization data and for the automatic classification of infant vocalizations.

INTRODUCTION

Over the course of their first year of life, human infants’ vocalizations become progressively more speech-like in their phonation, articulation, timing, and in other respects (Stark, 1980; Oller, 1980, 2000; van der Stelt, 1993). The exploration of the sound-making capability by infants, the formation of new contrastive categories of sound, and the systematic use of these categories in vocal play and in flexible expression of emotional states appear to form a critical foundation for speech (Koopmans-van Beinum and van der Stelt, 1986; Vihman et al., 1985). In fact, failure to reach milestones of vocal development is associated with hearing impairment and other medical conditions as well as with slower vocabulary development (Roe, 1975; Stoel-Gammon, 1989; Eilers and Oller, 1994; Oller et al., 1999). However, in the first months of life, infant sounds bear little resemblance to speech and thus their description presents unique methodological challenges.

Acoustic analysis is central to the study of prelinguistic vocalization development. Since recordings of infant vocalizations constitute high-dimensional time series data, their acoustic analysis presents a challenge of data reduction. It is necessary to represent the signal in terms of the most significant features, the ones around which development is fundamentally organized. Some of the acoustic measures that have been applied to infant vocalizations include duration, f₀ means, peaks, standard deviations, contours, formant frequencies, spectral concentration∕standard deviation, and degree of tremor (as measured by within-syllable f₀ and amplitude modulation) (Kent and Murray, 1982; Robb and Saxman, 1988; Papaeliou et al., 2002). Such measures are inspired by a priori assumptions rooted in acoustic phonetic theory. They are usually treated as independent, with relatively limited attention paid to possible interactions. This is likely an oversimplification, since vocal categories are based on interactive, multivariate acoustic features in mature speech (Repp, 1982), and it seems likely that early infant sounds are also composed of acoustic features in interactive ways. Further, the traditional approach assumes that the selected a priori acoustic measures represent the fundamental dimensions of vocal development, exploration, and manipulation. There is a need for methods that address the multivariate and high-dimensional acoustic properties of infant vocalizations directly.

In addition, the need for automated analysis of infant vocal development is rapidly growing. Samples involving millions of utterances from thousands of hours of all-day audio recordings are being collected and analyzed (Zimmerman et al., 2009). It is important to develop a set of automated acoustic analysis tools appropriate for such infant vocalization data, which would be impractical to analyze manually.

Here a method is presented for reducing high-dimensional samples of infant vocalizations to a smaller set of holistic acoustic features derived directly and automatically based on the patterns exhibited by a set of infant vocalizations. The approach makes relatively few a priori assumptions and is intended to complement research using more traditional acoustic measures derived from speech science principles. It utilizes a computational algorithm that would be suitable as an automated analysis method for application to large sets of infant utterances from naturalistic recordings.

Infant vocalizations are first analyzed using a type of unsupervised artificial neural network, the self-organizing map (SOM). The SOM derives a set of 16 holistic spectrographic features based on clusters detected in an input corpus consisting of spectrograms of infant utterances. Then a type of supervised neural network, the single-layer perceptron, is used to classify utterances on the basis of the SOM’s derived acoustic features. The classification types are (1) prelinguistic vocal categories (squeals, vocants, and growls), (2) when in the first year of life the utterances were produced, and (3) the identity of the individual who produced a given utterance.

The relationship between the SOM’s features and vocal categorizations, age, and individual differences is explored by looking at the patterns of activations across the SOM features and through some simple acoustic measurements (spectral mean, spectral standard deviation, and duration) made on the SOM features and the perceptron’s weightings of those features. The perceptron’s performance is also evaluated quantitatively and is compared to performance by a prominent neural network classifier, the multilayer perceptron (MLP). Note that the SOM and perceptron neural networks can be used either (1) purely for statistical analysis purposes or (2) as models of human perception and classification. The present study falls into the first category of usage, with the second being a potential future direction.

Section 1A below provides background on prelinguistic vocal categories, developmental changes, and individual differences. This is followed in Sec. 1B by a brief review of previous work that has used SOMs or perceptrons to analyze vocalization data.

Three areas of investigation in infant prespeech vocalization research

Prelinguistic phonological categories

The fact that vocalizations produced during the first year exhibit some of the characteristics of adult speech yet are still in many respects immature poses a challenge to phonological description. It is clear that phonetic transcription at the phonological segment level is not appropriate for early infant vocalizations (Lynip, 1951). As an alternative, some researchers have identified prelinguistic vocal categories, termed “protophones” (Oller, 2000), that seem to appear relatively universally during development across the first months of life (Stark, 1980; Nathani and Oller, 2001).

Some protophone categories relate to the purposeful variation of phonatory characteristics, especially pitch and voice quality. One such category is squeal, which includes utterances that are high in pitch and often accompanied by pitch variation, loft (falsetto) quality, and∕or harshness (Nathani et al., 2006). Another category is growl, which includes utterances with low pitch, harshness, creaky voice, and∕or pulse register (Buder et al., 2008). Perhaps the most frequently occurring protophone is the vocant, which refers to vowel-like utterances (Martin, 1981; Kent and Bauer, 1985). Vocants have intermediate pitch and relatively normal phonation. Purposeful variation of pitch and vocal quality usually appears by at least 4 months of age and continues to be explored throughout the first year and beyond (Stark, 1980). Although other protophone categories address maturation in the timing of syllable production (marginal and canonical syllables; Oller, 1980) and the capacity to produce multisyllabic utterances of various sorts (reduplicated and variegated babbles; Smith et al., 1989), the present study focuses only on the early emerging phonatory protophones—squeal, growl, and vocant—as an illustration of how our method can be applied to the acoustic analysis of protophone categories.

Protophone categories have an inherent element of subjectivity, since they are seen as protophonological constructs that form the basis for interpretation of emotional states and intentions by caregivers (Papaeliou et al., 2002; Scheiner et al., 2002). Their validity is supported by the fact that squeals, growls, and vocants are often spontaneously reported by parents when asked to identify sounds their babies produce (vocants being called “vowels;” Oller et al., 2001). Laboratory research involving these categories primarily uses trained adult listeners’ perceptual judgments (Nathani and Oller, 2001).

Little relevant acoustic data on the key categories have been published for the squeal, vocant, and growl protophones. However, a primary acoustic correlate has been proposed to be fundamental frequency (f₀) (Nathani et al., 2006; Oller, 1980; Stark, 1980). A goal of the present study is to explore the acoustic correlates of human listeners’ protophone judgments via inspection and visualization of neural network weights and activations. The present study also lays a foundation for the development of automatic protophone classification. This is important because protophone classification is otherwise a costly and time-consuming procedure, involving prior training of analysts and repeated careful listening to individual utterances.

Developmental changes across the first year

Because during most or all of the first year of life infants do not produce recognizable words, their prelinguistic vocalizations are the main means of assessing the development of speech- and language-related production capabilities. While ethologically oriented auditory studies of changes in vocalizations across the first year have been informative in determining stages of vocal development and the protophones that emerge with each stage (Holmgren et al., 1986; Koopmans-van Beinum and van der Stelt, 1986), developmental patterns have also been studied using acoustic phonetic methods. For example, Kent and Murray (1982) tracked a number of acoustic measurements, including duration, mean f₀, f₀ intonation contours, first and second formant frequencies, and a variety of glottal and supraglottal quality characteristics such as fry, tremor, and the spectral concentration of noise, in a cross-sectional study of 3-, 6-, and 9-month-old infants’ vocalizations. Across age, they found changes in formant frequency values (see also Lieberman, 1980 and Kuhl and Meltzoff, 1996) as well as in amount of tremor.

Despite the important contributions of such research, it does not address the possibility that the changes in such acoustic measures across development are not independent of each other. For example, increases in duration and decreases in phonatory variability may emerge in coordination with each other, driven by common physiological and cognitive maturation that lead to increased control over the larynx. Unsupervised statistical analysis may help to address this concern, either (1) by reducing the large number of acoustic measures to a smaller number of component dimensions that are weighted on each of those acoustic parameters or (2) by deriving a limited number of new, holistic acoustic measures directly from relatively unprocessed recordings of infant vocalizations. The present study takes the second approach.

An aim of this work is to develop potential methods for automatic measurement of the acoustic maturity of infant utterances. This goal is motivated by fact that “language age” or “age-equivalence” is commonly used as an index of language development status in both research and clinical assessment of children older than 1 year (e.g., Stevenson and Richman, 1976; Thal et al., 2007). Automatic classification of vocalization maturity is already being pursued with some success using statistical algorithms incorporating automatic calculation of more traditional acoustic measures, such as duration, and automatic detection of phonetic features, such as bursts, glottal articulations, sonorant quality, and syllabicity (Fell et al., 2002). The method presented here lays groundwork for the automatic measurement of the maturity of an utterance on the basis of holistic, data-driven features, which could prove a worthwhile addition to current methods for automatic detection of utterance maturity.

Individual differences

The ordering of phonological stages of vocal development appears to be robust across infants, even those from different language environments, with differing socioeconomic status, and in large measure with differences in hearing function (Oller and Eilers, 1988). However, reports of notable individual differences are also common in literature on infant vocal development (Stark, 1980; Vihman et al., 1986; Nathani Iyer and Oller, 2008). These individual differences appear to be associated with differences in later language styles and abilities. For example, Vihman and Greenlee (1987) found that the degree of use of true consonants (consonants other than glottals and glides) in babble and words at 1 year of age predicted phonological skill at 3 years. It is important to be able to quantify individual differences in preverbal vocalizations within normally developing infants as this might be used to predict later differences in speech and language ability and usage. The study of individual differences in typical infants also sets the stage for the study of infant vocalizations across groups, e.g., across various language or dialect environments, genders, and populations with hearing, language learning, or cognitive impairments.

As with the study of age differences, the study of individual differences is likely to benefit from the introduction of data-driven acoustic measures that convert high-dimensional acoustic input to a smaller number of essential holistic features. In this study, the problem of characterizing and quantifying individual differences among infants is addressed through exploration of differences across infants in the presence of such holistic features. Automatic detection of infant identity provides groundwork for future detection of differences in the vocalization patterns across different infant populations of clinical significance.

Previous applications of neural networks to related problems

Neural networks are often used as tools for statistical pattern analysis and are particularly appropriate for high-dimensional data that are suspected of having nonlinear cluster or class boundaries (Bishop, 1995). The networks are typically trained through exposure to data exemplars. They can be used both in cases where the classes in a data set are known and used to provide explicit feedback to the network (supervised networks), or when they are unknown and discovered without explicit supervision (unsupervised networks).

The perceptron is perhaps the most commonly used supervised neural network. It consists of an input layer, an output layer, and zero or more hidden layers. Each layer except the output has a set of weights that describes the strength of the connections between its nodes and the nodes of the following layer. Activation from the input is propagated to the hidden layers (if there are any) and then to the output. The network’s output activations are then compared to the known classifications for that input, and the network’s error is determined. Based on that error, the network’s weights are adjusted, typically using the delta rule, or with backpropagation if there are any hidden layers (Bishop, 1995).

A common unsupervised network is the SOM (also known as Kohonen network). SOMs are typically used for unsupervised cluster analysis and visualization of multidimensional data (Kohonen, 2001; Ritter, 2003; Xu and Wunsch, 2005). A SOM consists of an input layer and an output layer and a set of connection weights between them. The nodes of the output layer are arranged spatially, typically on a two-dimensional (2D) grid. When an input is presented, each of the output nodes is activated to varying extents depending on the input and its connection weights from the input layer. The output node with the highest activation is the winner. It and, to a lesser extent, its neighboring nodes have their connection weights strengthened so that their receptive fields (i.e., their preferred inputs) more closely resemble the current input stimulus. The result after training is that the output nodes’ receptive fields reflect the patterns found in the input and that the receptive fields are topographically organized; i.e., nearby nodes have similar patterns of weights from the input layer.

There appear to be few, if any, previous applications of neural networks to recordings of infant prespeech non-cry vocalizations. However, neural networks have been used to analyze recordings of vocalizations produced by songbirds, disordered and normal adult human voice, and infant crying. Many of these applications were developed in response to a need to represent high-dimensional, complex acoustic signals in a data-driven way. For example, Janata (2001) used a SOM to cluster spectrographic representations of segments of juvenile zebra finch song into 200 topographically arranged holistic spectrogram prototypes. The visualizations of the loadings of features across 30 consecutive days represented a map of the developmental pathways by which adult songs emerged. In addition to permitting data-driven detection of song features, Janata (2001) pointed out that the SOM provides automated acoustic analysis and classification of a very large set of vocalization data, permitting the study of a data set that would have been unrealistic to attempt to score manually.

In another application of neural networks to avian vocalizations, Nickerson et al. (2007) used a single-layer perceptron, a type of supervised neural network, to discover the acoustic features most relevant to the distinction between three different note types in black-capped chickadee (Poecile atricapillus) “chick-a-dee” calls (notes being the primary units of these calls). The network received seven frequency- and duration-related acoustic features as input and learned to predict the note type for these inputs. Testing the network with systematically modified inputs enabled them to determine which acoustic features were most important in discriminating note types.

SOMs or SOM-inspired networks have also been used in a number of studies to model the perception and classification of speech sounds of one’s native language. For example, Guenther and Gjaja (1996) trained an unsupervised network on formant frequency inputs. They then showed that the distribution of learned receptive fields exhibited the perceptual magnet effect humans exhibit in the perception of the vowels of their native language. Another example is a study by Gauthier et al. (2007) that used a SOM to successfully classify Mandarin tones based on the first derivative of f₀ contours. This classification was robust in the face of the surface variability present in the multiple speakers’ connected speech from which the inputs were taken.

SOMs have also been applied to the study of disordered adult human voices. In one study, Leinonen et al. (1992) trained a SOM on short-time spectra from 200 Finnish words. They then provided the network input from both normal and dysphonic speakers and tracked the trajectory of winning SOM nodes for the vowel [a:]. Normal and dysphonic voices differed in the amount of area on the SOM that was visited by these vowel trajectories. The work illustrates that a SOM tool can discriminate between normal and dysphonic voices, and that acoustic differences for these two populations can be portrayed topographically. Callan et al. (1999) also used a SOM to study normal and dysphonic voices. However, instead of raw spectra, their inputs were scores on six acoustic measures that had previously been used in studies of dysphonia (e.g., amplitude perturbation quotient, first cepstral harmonic amplitude, and standard deviation of f₀). After training, they marked each SOM node according to which clinical group activated it the most. The SOM was able to reliably classify voices according to group. Output node activations and weights from the input (the six acoustic measures) were also visualized.

Finally, in an application of a neural network to the study of infant vocalizations, Schönweiler et al. (1996) used a SOM to cluster recordings of cries by normal and deaf infants. The input consisted of 20-step Bark spectra. It was noted that different individuals’ cries mapped onto different areas of the SOM, which is in agreement with the idea that different infants produce identifiably different cries.

The results of the studies reviewed in this section suggest that neural networks, including the unsupervised SOM and the supervised perceptron networks, are appropriate and useful tools for visualization, feature-extraction, and classification purposes in the study of acoustic vocalization data. Thus, it seems fitting to explore the application of neural networks to study infant vocal development.

METHOD

Participants

Data from six typically developing human infant participants, four female and two male, are used in this study. Participants were recruited for a study of both interactive and spontaneously produced vocalizations and were recorded longitudinally from early in the first year until age 30 months (see Buder et al., 2008 for additional details on participants and recording setup and procedures). The present study focuses on a subset of those recordings spanning three age intervals across the first year of life: 3;0–5;4, 6;0–8;4, and 9;0–11;4.

Recording

Infants were recorded for two to three 20-min sessions on each day of recording. For each infant, two of the 20-min sessions were selected from each age interval for use in the present study. The selections were made from among available recordings based on there being a relatively high vocal activity level of the infant and a relative lack of crying.

Recordings took place in a minimally sound-treated room furnished with soft mats and toys while the parent was present. Siblings were sometimes present during recordings as well. Infants and their mothers interacted relatively naturalistically although some periods of time were dedicated to an oral interview between laboratory staff and the parent while the infant played nearby. Both mother and infant wore wireless microphones [Samson Airline ultra high frequency (UHF) transmitter, equipped with a Countryman Associates low-profile low-friction flat frequency response MEMWF0WNC capsule, sending to Samson UHF AM1 receivers]. The infant’s was sewn into a custom-built vest adapted from models designed by Buder and Stoel-Gammon (2002). The microphone capsule was housed within a velcro patch to locate the grill at a distance of approximately 5–10 cm from the infant’s mouth. Using TF32 (Milenkovic, 2001) operating a DT322 acquisition card (Data Translation, Inc., Marlboro, MA), signals were digitized at 44.1–48.1 kHz after low-pass filtering at 20 kHz via an AAF-3 anti-aliasing board. Microphone signals were concurrently sent to digital video recorders via separate UHF receivers to eliminate contamination to the signals that would otherwise have been transmitted from the video monitors via direct cables. The recordings for infant 1 are an exception to this procedure. This infant’s recordings were made according to an earlier laboratory protocol in which audio from the infant’s and mother’s microphones were compressed in mp3 format as part of an mpeg recording file that combined audio with video. These recordings were subsequently extracted from mp3 format to wav format. Based on detailed inspection of these wav files, the only noticeable compression-based difference between the mp3-based wav file and those for infants 2–6 was that mp3 compression eliminated frequency components above about 12 kHz. To ensure signal comparability across all the recordings, only frequencies 12 kHz or lower are included in the signals processed by the neural networks in this study.

Utterance location and coding by human analysts

Prior to analysis by the neural networks, recordings underwent two types of processing by trained adult human analysts: (1) location of infant utterances within recording session files and (2) labeling these utterances according to protophone categories. Infants’ utterances were located within each recording using the spectrographic display feature of action analysis coding and training (AACT) software (Delgado, 2008), marking the beginning and end of each utterance. In addition to listening to the recordings, analysts were permitted to consult spectrograms, waveform views, rms contours, and videos for both the infant and the caregiver as they performed this localization task. An utterance was defined as a vocalization or series of vocalizations perceived as belonging to the same breath group (Oller and Lynch, 1992). Crying and other distress vocalizations as well as vegetative sounds were excluded. The first 49 utterances from each 20-min session are used in this study. Since 49 was the minimum total number of utterances produced in a session, this ensures equal representation of recording sessions, infants, and ages (see Table 1).

Table 1.

Number of vocalizations of each vocal type for each infant at each age.

Infant	Age 3;0–5;4			Age 6;0–8;4			Age 9;0–11;4			Total
	Vocant	Squeal	Growl	Vocant	Squeal	Growl	Vocant	Squeal	Growl
1	73	2	23	53	5	40	77	6	15	294
2	72	21	5	67	15	16	70	22	6	294
3	79	14	5	72	19	7	74	23	1	294
4	68	20	10	78	7	13	80	3	15	294
5	71	0	27	66	0	32	84	1	13	294
6	71	2	25	91	1	6	75	11	12	294
Total	434	59	95	427	47	114	460	66	62	1764

After locating infants’ utterances, analysts then coded each utterance as one of the following protophones: vocant, squeal, or growl. Analysts were encouraged during training to use intuitive auditory judgments rather than strict criteria. They were told that generally squeals are perceived as high pitched (beyond the range of habitual pitch for the individual) and can be dysphonated as well. Growls were portrayed as often having low pitch (again out of the range of habitual pitch) and as often being harsh or dysphonated, but it was noted that they are sometimes within the habitual pitch range with harsh or rough voice quality. Vocants were portrayed as the kinds of sounds that fit within the normal pitch of the infant, with relatively little deviation from normal phonation. Analysts were encouraged to attend to the most salient aspects of utterances in making squeal and growl judgments. For example, an utterance was not required to be high pitched throughout to be categorized as squeal; a brief but salient high pitched event could form the basis for the categorization. These instructions were designed to encourage coders to mimic the discriminatory behavior presumed to underlie the categorizations reflected in reports of caregivers regarding these kinds of sounds in their infants (Stark, 1980; Oller et al., 2001). The coding procedures are similar to those used by Nathani et al.’s (2006) V (vocant) and SQ (squeal) categories. The difference was that in this study there is an additional growl category (see Buder et al., 2008) and classifications regarding vocal type category were made independently of any syllabicity judgment. Table 1 provides a summary of the number of utterances in each protophone category for each infant at each age.

Preprocessing of utterances

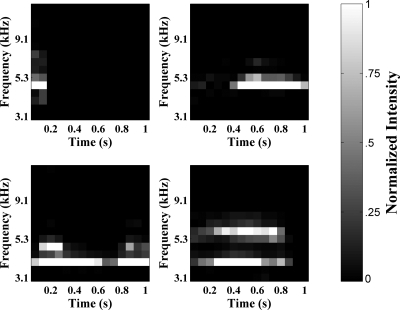
Processing of utterances from this point on was done in MATLAB using the signal processing and neural networks toolboxes (MathWorks, 2008). Each utterance was extracted from the digital recording for the session during which it was recorded. As all inputs to a standard SOM (see following description) must be the same length, only the first second of each utterance was used (utterances were therefore aligned at the beginning). Longer utterances were truncated and shorter utterances were zero-padded. A spectrogram was obtained for each utterance using the fast Fourier transform (FFT)-based spectrogram function. Fifteen time bins were used, each with 50% overlap and a maximum frequency of 22 kHz. The frequency scale of this spectrogram was converted to a 15-bin sine-wave approximation of the Bark scale (Zwicker, 1961), and the maximum frequency was capped at 12 kHz using Ellis’s (2007) inverse hyperbolic sine approximation algorithm from the RASTAMAT toolbox. For each utterance, the power spectral density values represented by this spectrogram were normalized to the maximum power spectral density magnitude within that utterance. Each utterance was thus represented as 225 spectrogram pixels corresponding to the normalized power spectral density at each frequency bin for each time bin. Figure 1 illustrates some examples of the spectrographic representations of infant utterances in our data set.

Figure 1.

Four examples of inputs provided to the SOM. Inputs are 225-pixel Bark-scaled spectrograms of utterances produced by infants recorded naturalistically. All inputs are 1 s long, with longer utterances truncated and shorter utterances zero-padded. White indicates high intensity and black indicates zero intensity. All spectrograms are normalized to the value of the highest intensity pixel. Clockwise, from top-left: a vocant produced by infant 1 at 3;2, a squeal produced by infant 2 at 4;1, a growl produced by infant 4 at 6;2, and a vocant produced by infant 3 at 10;2.

Neural network architecture

In this section, the architecture of the neural networks and the functions of each component are described. Section 2F will describe neural network training. This will be followed by a description of how the infant utterance data were divided into a set for training and a set for testing each network in Sec. 2G.

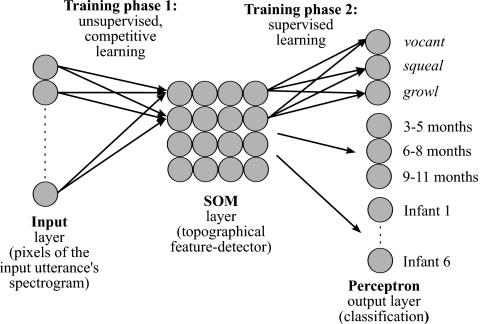
The main type of neural network used in this study is a hybrid architecture with two components (Fig. 2). The first component is a SOM consisting of 16 nodes arranged on a 4×4 grid. The choice of number of nodes and their arrangement was made on the basis of pilot analyses using various configurations, considering ease of visualization and balance between specificity and over-fitting of data. The SOM receives utterance spectrograms as input, transformed into a vector with the time-slice columns of the spectrogram laid end-to-end. Note that this is a common procedure for formatting neural network input data (e.g., see Janata, 2001), and that the transformation has no effect on the function of the SOM since the SOM algorithm does not take the location of input nodes into account. The SOM categorizes these utterances according to learned holistic features extracted based on a set of training utterances, as described in Sec. 2F. Learning in the SOM is unsupervised and involves changing the weights from the input layer to each of the SOM nodes over the course of training. Eventually, these weights come to represent the nodes’ ideal inputs (or receptive fields), and neighboring nodes end up having similar ideal inputs (topographic organization). This SOM component of the hybrid architecture thus serves as a data-driven holistic feature detector, reducing the 225-pixel spectrographic input to 16 learned features. It also serves as a means for visualizing utterance features topographically (Kohonen, 2001; Ritter, 2003; Xu and Wunsch, 2005). The SOM component was implemented using functions custom written for this study in MATLAB.

Figure 2.

Schematic of the neural network used in the present study. The network is a hybrid of a SOM and a single-layer perceptron. Pixels of an utterance are presented first to the SOM. Activations of the SOM nodes are then sent to the perceptron output nodes for classification according to protophone, age, and infant identity. The weights from the input layer to the SOM layer are trained first. After this first phase of training, weights to the SOM are frozen and the perceptron’s weights are trained.

The second component is a set of three single-layer perceptrons, which are used to read the output from the SOM in order to obtain a quantitative measure of the learned SOM features’ relevance to various classification tasks, to actually perform those classifications, and to determine which SOM nodes best distinguish different classes of utterances from each other. The perceptron is a type of supervised classifier and in single-layer form it essentially performs a logistic linear regression (Bishop, 1995). Each perceptron receives activations of the SOM layer nodes (produced in response to a single utterance input to the SOM) as input (see Kuang and Kuh, 1992, for another example of a perceptron trained on SOM activations). Based on the product of these SOM activations and the perceptron’s weights (which can be either positive or negative) from the SOM layer to its output nodes, the perceptron classifies a given utterance according to its perceived protophone type as judged by trained human analysts, the age at which an utterance was produced, and the identity of the infant who produced it. Thus, the supervised perceptrons relate the features learned by the unsupervised SOM to known protophone, age, and identity classifications. The output layer of each of these perceptrons was constructed to have one node for each class of utterances. The vocal type protophone perceptron thus has three output nodes: one for squeals, a second for vocants, and a third for growls. The age-predicting perceptron has three output nodes: one for utterances produced at age 3;0–5;4, a second for utterances produced at age 6;0–8;4, and a third for utterances produced at age 9;0–11;4. Finally, the identity-predicting perceptron has six output nodes, one for each infant in our data set. The perceptron component was implemented using the feed-forward network functions in MATLAB’s neural network toolbox (Demuth et al., 2006). Logistic activation functions were used for the output nodes of the perceptron classifiers, and default values were used for all other parameters in initializing the network (further details can be found in Demuth et al., 2006).

To compare the hybrid SOM-perceptron classifier to the MLP, which is probably the most popular neural network used in supervised classification (Bishop, 1995), we also trained a set of MLPs to perform the age and vocal type classifications using the leave-one-infant-out training data. These MLPs were run using the same procedures and parameter settings as for the single-layer perceptrons described above. The number of hidden layer nodes was set to 16, which is the same as the number of nodes in the SOM layer of our SOM-perceptron hybrid. Thus, the numbers of weights (i.e., free parameters that the networks adjust during training) are roughly similar. We then compared the MLP’s classification performance to that of our SOM-perceptron hybrid. In addition, we trained a single-layer perceptron to predict age on the basis of protophone-trained MLP’s hidden layer activations. Likewise, we trained a single-layer perceptron to predict protophones on the basis of age-trained MLP’s hidden layer activations. Comparing classifications of these perceptrons to classifications from the SOM-perceptron hybrid assesses whether using the SOM layer is truly critical to obtaining a task-general hidden layer.

Neural network training

For the SOM-perceptron hybrid, training was conducted in two phases. During the first phase, only the SOM component was involved. Prior to training, its weights were set to random values with a different randomization for each of the 15 SOM runs. The SOM training algorithm was adapted from Berglund and Sitte’s (2006) parameterless SOM algorithm. This algorithm takes three parameters (β, Θ, and ε), which determine the behavior of the SOM during training. The following parameter values were used: β=1, method 2 for calculating Θ, and ε multiplied by a factor of 0.5. The exact roles of β, Θ, and ε are described in Berglund and Sitte (2006). In essence, training involved presenting an utterance as input (randomly chosen from the set of training utterances, discussed in Sec. 2G) to the SOM, finding the SOM’s node whose weights to the input layer are the most similar to that input (as measured by the Euclidean distance between the input vector and the vector representing weights from the input to a given output node), and then updating that node’s weights and (to a lesser extent) its neighbors’ weights to make them even more similar to the input. This procedure was repeated 1407 times. This was the number of utterances per session times the number of sessions times the reciprocal of the scaling factor for ε in the SOM training algorithm. This amount of training was more than sufficient for the network’s performance to stabilize as judged by the mean squared distances between testing set inputs and their winning node’s weights and by visual inspection of changes in network weights across training.

After completion of this first phase of training, the weights from the input layer to the SOM nodes remained fixed during the next training phase. This second phase of training the SOM-perceptron hybrid involved only the perceptron component. Perceptrons were trained using the delta rule with regularization using MATLAB’s trainbr function. This is a variation on the traditional delta rule algorithm that balances reduction in classification error against parsimony of network weight. This method (sometimes also referred to as “learning with forgetting”) has been shown to produce good generalization of performance to previously unseen data and increases the interpretability of network weights (Foresee and Hagan, 1997; Kasabov et al., 1998; Demuth et al., 2006). In essence, this training algorithm involves presenting training set examples, which are the SOM node activations produced in response to an infant utterance, one at a time. After presentation of each example, the network’s classification predictions are calculated, and then, based on the difference between these classification predictions and the correct classifications, the weights from the SOM layer to each of the perceptrons’ output nodes are updated so as to reduce this error (as measured by the squared error) in classifying subsequent inputs while also maintaining parsimony of network weights. All parameters other than the training method (trainbr) and the activation transfer function (log-sigmoid) were set to default values. Further details can be found in the MATLAB documentation and in Demuth et al. (2006).

The MLPs were trained in mostly the same way as the perceptron described above but with the following exceptions: The MLP was trained directly on the spectrographic input and was done in a single phase. Training was performed using the same MATLAB training method (trainbr), but since there were two layers instead of just one, backpropagation was involved in addition to the delta rule (Bishop, 1995).

Partitioning of data into training and testing sets

In order to train the SOM, perceptron, and MLP while also allowing for testing the networks’ generalization abilities, the infant utterance data were divided into two subsets: one for training the network and the other for evaluating the network’s classification performance. From each recording session (of which there were two for each child at each age), 37 of the 49 utterances (approximately 75%) were randomly chosen to be used in training; the remaining 12 utterances (approximately 25%) were reserved for testing the network (discussed in Sec. 2I). This random partitioning was done 15 times and the SOM-perceptron hybrid was run 15 times, each corresponding to a different random partitioning. The means and standard deviations presented in Sec. 3 were computed over these 15 runs.

In a variation on this training procedure, an alternative leave-one-infant-out method of partitioning the data into training and testing sets was applied to a second set of 36 networks, wherein all the utterances produced by five infants were used in training and the utterances from the sixth remaining infant were reserved for use in testing only. Across these 36 networks, each infant was used as the test infant six times. As with the perceptron, means and standard deviations were computed over these 36 runs. The MLP simulations were trained and tested using the leave-one-infant-out method, although only 6 simulations (rather than 36) were run due to the long time it took for MLP runs to complete. Each infant was used exactly once in testing.

In addition, a SOM-perceptron hybrid was trained on all utterances from all recordings for the purpose of visualizing the trained network weights and activations. This network was used for generating Figs. 345 but was not included in any of the quantifications of network performance.

Figure 3.

Weights from the input layer to each SOM node for a network trained on the full set of utterances. Each spectrogram represents the input preference for that node. Note that input preferences are holistic spectrographic features and represent complex acoustic patterns. Also note the topographic organization of these inputs. White represents high weight (high intensity preference for that pixel on the input layer), and black represents zero weight.

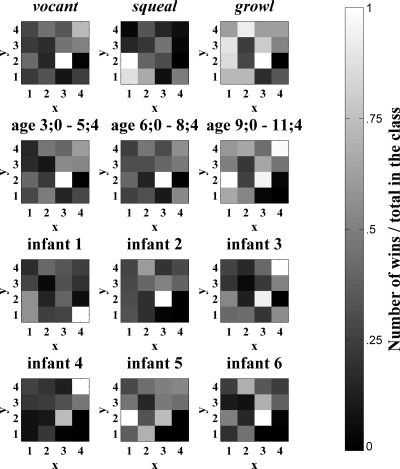
Figure 4.

Activations of the SOM layer by utterances with different protophone labels, produced at different ages, and produced by different infants. Bright indicates that a SOM node was often the winner and black indicates that a node was never the winner. Each 4×4 map corresponds to nodes of the SOM shown in Fig. 3. Note that the number of utterances belonging to each protophone category was not uniform; there were more vocants than squeals and more squeals than growls.

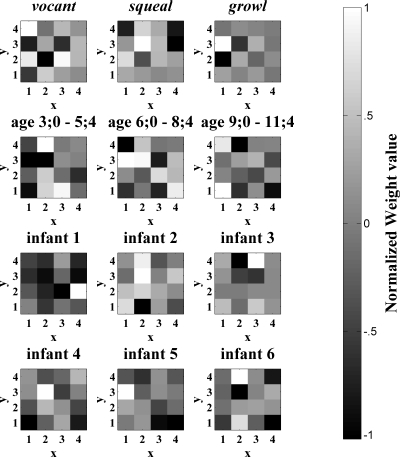
Figure 5.

Weights from the SOM layer to each perceptron output node. Bright indicates a large positive weight from the SOM node to that perceptron output node, black indicates a large negative weight, and gray indicates a near-zero weight. Each 4×4 map corresponds to the SOM nodes shown in Fig. 3. Note that for protophones, the weights are based on training the perceptron on a set of utterances that was adjusted to be balanced across vocant, squeal, and growl protophones by randomly repeating exemplars from the less frequent categories.

Adjusting for unequal representation of protophone categories

When training and testing the perceptrons and MLPs responsible for predicting protophone judgments, it is a concern that vocants occur much more frequently than squeals and growls (see Table 1). This inequality inflates the percent correct that would be expected by chance, since with unequal numbers, the baseline strategy would be to give all utterances the classification corresponding to the most frequent category. With such a strategy, if 70% of the utterances were vocants, the baseline percent correct would be 70%. This would be very difficult for even a “smart” classifier making use of acoustic information to outperform. We thus ran the perceptron component two ways: once without any adjustment for unequal numbers of vocal types and once with an adjustment. To adjust for the frequency bias, exemplars from the squeal and growl categories were repeated as many times as was necessary for their numbers to equal the number of vocants.

Evaluating the network’s performance

After training the hybrid network, the network’s performance was assessed (1) through visualization and descriptive acoustic measurement of network weights and activations and (2) through quantitative evaluation of classification performance. The visualizations are of the weights from the spectrographic input layer to the SOM output grid and from the SOM’s grid to the perceptron classifier nodes. We also visualized the winning SOM nodes (an illustration of SOM activations) for utterances with different protophone judgments, from different ages, and from different individuals.

To supplement the visualizations, we made 3 theoretically derived acoustic measurements for each of the 16 SOM receptive fields. The first measure was the mean of the time-averaged spectrum and the second was the standard deviation of this spectrum, both measured in absolute frequency. These correspond to the first and second spectral moments computed by Forrest et al. (1988). The third measure was the median point in time of the frequency-averaged intensity contour. This should give a rough measure of the preferred duration of the receptive field. After calculating these three values for each SOM node, we calculated each perceptron output node’s preferred value for each of the three acoustic measures by finding the average SOM receptive field values weighted by the perceptron output node’s weights from the SOM layer.

Quantitative evaluation involved feeding the networks’ utterances from the set that were reserved for testing. The networks’ classifications regarding the protophone, age group, and infant identity for each of these test utterances were then obtained, and an overall mean percentage correct for each type of classification for each type of network was computed. Cohen’s κ reliability statistics and their corresponding probabilities were computed using Cardillo's (2009)MATLAB function, in order to evaluate the magnitude and significance of the agreement between each network’s classifications and the correct classifications.

RESULTS

Visualization and descriptive acoustic measurement of network weights and activations

Each of the SOM’s output nodes can be thought of as a holistic spectrographic feature formed by the SOM based on the training inputs. This is illustrated in Fig. 3, where the weights from the input layer to each node of the SOM are visualized as spectrograms representing the preferred spectrographic input for that node (white indicates a high value for a given weight and black indicates a zero value). Each node’s spectrogram of weights can be thought of as a receptive field, specifying a particular preferred holistic feature derived from the input infant utterance data via the SOM’s training algorithm. Note that these preferred inputs are arranged topographically; that is, neighboring nodes have similar preferred inputs. This is one of the characteristic properties of SOMs. Also note that, because the SOM nodes adjust their preferred inputs (i.e., their weights from the input layer) on the basis of exemplars from the training set of utterances, the nodes of the SOM come to represent global features of a complex nature such as would occur in an actual infant utterance. Thus, it seems that these features have a complex relationship with more basic acoustic features, such as duration and spectral compactness versus diffuseness. For example, the receptive fields for the SOM nodes pictured in the leftmost column (x=1) of Fig. 3 appear to exhibit long duration. In addition, the bottom two nodes of that leftmost column (x=1, y=1–2) have relatively high spectral means and spectral standard deviations. These observations are supported by measurements of the frequency-averaged intensity contours’ median times, the time-averaged spectral means, and the time-averaged spectral standard deviations given in Table 2.

Table 2.

Acoustic properties of the SOM receptive field spectrograms.

Spectral meansa				Spectral standard deviationsa				Temporal mediansb
0.7	0.7	0.7	0.6	0.7	0.7	0.7	0.6	7	5	4	4
0.7	0.8	0.7	0.6	0.8	0.8	0.7	0.7	9	4	3	3
1.3	1.1	0.7	0.5	1.3	1.8	0.9	0.8	8	4	2	3
1.7	1.3	0.6	0.3	1.6	1.3	1.1	0.9	6	4	3	5

^aIn kilohertz.

^bIn number of time bins (each bin is 66 ms).

Figure 4 illustrates how often each node of the SOM was the winning node (defined as the node with the highest activation) for utterances of each perceived protophone type, age group, and individual. This method of visualization provides a way of mapping from global features learned by the SOM to different utterances classes.

For example, it appears in the figure that growls may span a broader set of global features in the acoustic space represented by the SOM, as evidenced by the large number of relatively bright squares (bright indicates high activation) for this protophone category. To quantify the diffuseness of activation across the SOM for a given utterance class, we first calculated for each node the number of inputs for which that node was the winner, divided by the total number of inputs belonging to that class. Then the median of these proportion values was computed. These medians were compared across the three protophone categories. Indeed, the median was higher for growls (0.24) than for vocants (0.18) or for squeals (0.15). This indicates that the winning nodes for this category are distributed more evenly across the map than for the other categories.

Another observation that is evident in Fig. 4 is the overlap between utterance classes. While there is some distinctness across protophones, as indicated, for example, by there being different most highly activated nodes for squeals (the node at x=1, y=2) than for vocants and growls (the node at x=3, y=2), there is also a high degree of overlap in the SOM node activations, as indicated by numerous nodes that show gray activation for all three protophone types.

Figure 5 illustrates the weights from the SOM to the perceptron output nodes for each age, infant, and protophone prediction. Recall that the goal of the perceptron is differentiation of categories (protophone type, age, and infant) via positive and negative weights. Thus for Fig. 5 the scaling is different from that of Fig. 4. In Fig. 5, white indicates high positive weight, black indicates high negative weight, and mid-gray indicates near-zero weight. The weights indicate which of the SOM’s holistic features are informative for classification purposes, highlighting the differences between utterance classes and ignoring features that are common to all classes.

The visualizations in Figs. 45 exhibit both similarities and differences. This is evident in the correlation coefficients between a given class’s SOM activations (Fig. 4) and the weights from the SOM to its perceptron node (Fig. 5). The mean, across all class types, of these correlation coefficients is r=.31 where r was always positive, ranging from 0.03 to 0.58. As an example of a specific similarity between activation and weight patterns, the SOM nodes located at (x=1, y=4), (x=4, y=4), and (x=4, y=3) are very dark for squeals in both figures. This indicates that these SOM nodes are both infrequent (Fig. 4) and negatively associated characteristics (Fig. 5) of squeals. An example of a difference between the two figures is that, while the SOM node located at (x=4, y=4) is the second highest activated for vocants as shown in Fig. 4, it does not have a very large positive weight to the perceptron vocant node, as indicated in Fig. 5. Differences between Figs. 45 are due to the fact that Fig. 4 indicates the frequency with which features were observed whereas Fig. 5 highlights the particular SOM nodes that, when activated at least partially by an utterance, distinguish utterances of one class (e.g., vocants) from utterances of other classes (e.g., squeals and growls).

Recall the discussion of duration, spectral mean, and spectral standard deviation from the discussion of the SOM receptive field spectrograms (Fig. 3). It was observed that the leftmost column was associated with long duration and that the bottom two nodes of that column also had high spectral means and standard deviations. Interestingly, this leftmost column appears both in Fig. 4 and in Fig. 5 to be associated more (as evidenced by light-colored pixels in this column) with the older two age groups than with the younger age group. This suggests that increase in duration is associated with increase in age. In addition, the bottom two nodes of that leftmost column are associated with the oldest age group. This suggests that the oldest age group is associated also with increase in spectral mean and standard deviation. Combining information about the acoustic properties of SOM weights and the values of the weights from the SOM layer to each of the perceptron output nodes, it is possible to explore whether these acoustic features are present in the nodes that distinguish between different ages. Table 3 shows the spectral mean, spectral standard deviation, and temporal duration properties for each age, protophone type, and infant. Indeed, the spectral duration of perceptron weights appears to increase across the three age groups, and the spectral mean and standard deviation are highest for the oldest age group.

Table 3.

Acoustic properties of the perceptron weights from the SOM layer, given the acoustic features of the SOM nodes (shown in Table 2).

		Spectral meana	Spectral SDa	Temporal medianb
Age	3;0–5;4	0.80	0.91	4.11
	6;0–8;4	0.75	0.89	4.67
	9;0–11;4	0.87	0.95	4.84
Protophone	Vocant	0.78	0.89	4.49
	Squeal	0.85	0.96	4.69
	Growl	0.80	0.91	4.68
Infant	Infant 1	0.81	0.94	4.55
	Infant 2	0.83	0.93	4.62
	Infant 3	0.82	0.94	4.69
	Infant 4	0.77	0.87	4.47
	Infant 5	0.89	0.95	5.12
	Infant 6	0.84	0.92	4.41

^aIn kilohertz.

^bIn number of time bins (each bin is 66 ms).

Table 3 also reveals interesting patterns with respect to the three protophones’ acoustic properties. Squeals have the highest spectral mean and spectral standard deviation. This is in accordance with previous descriptions of this category as high pitch often accompanied by harshness and∕or pitch variation. However, growls do not differ from vocants in either mean or spectral standard deviation. Perhaps the high harshness∕pulse∕creaky-voice combine with the low pitch of growls to yield moderate spectral mean values. Thus, although the differentiating acoustic properties of squeals fit with their previous perceptual descriptions, the differentiating acoustic properties of growls may be less straightforwardly defined in this neural network.

Classification performance

Protophone-classification performance

When predicting human-judged protophone categories after equated-frequency training, the 15 hybrid networks had a mean percent correct on the previously unseen test utterances (selected randomly at the recording session level) of 54.4% (see the first column of Table 4). Since there were three protophone types, each of which was equally represented in both the training and the testing utterance sets, the classification performance that would be expected for a classifier performing at chance is 33.3%. The vocal-type-predicting networks’ 54.4% correct performance was significantly better than chance, κ=0.316, p<0.001.

Table 4.

Classification task performance of the SOM-perceptron hybrid neural network.

Type of test set	Protophones		Ages		Identities
	25% per recording	100% of one infanta	25% per recording	100% of one infant	25% per recording
Mean % correct	54.4 (chance=33.3)	55.0 (chance=33.3)	42.8 (chance=33.3)	35.6 (chance=33.3)	32.4 (chance=16.7)
Standard deviation	3.2	6.5	1.4	4.7	1.9
Mean Cohen’s κ	0.316	0.325	0.142	0.034	0.189
Mean p	<0.001	<0.001	<0.001	0.146	<0.001

^aWith adjustment for unequal category sizes. When there is no adjustment and one infant is reserved for testing, the mean percent correct is 73.4 (chance=74.9) with a standard deviation of 5.4.

Recall that 36 additional hybrid networks were trained on utterances from five infants and tested on the sixth remaining infant’s utterances. Each infant was used for testing for exactly 6 of the 36 networks. The purpose of this variation on the method for partitioning utterances into training and testing sets was to see if classification of protophones would generalize across infants. Mean classification performance for these networks was 55.0% correct, where chance level performance would have been 33.3% (see the second column of Table 4). This was statistically better than chance, κ=0.325, p<0.001. This shows that for protophone prediction, performance did not differ from when the session-level train-test partition method was used to when the leave-one-infant-out method was used. Thus, it appears that the network’s protophone-classification capabilities are based on features of utterances that are generalizable even to infants the network has never previously encountered.

When no adjustment was made for the inequality in the number of exemplars in each protophone category, the percentage correct was 73.4% where the baseline percent correct for an algorithm that always guessed vocant would be 74.9%.

For the six MLPs that were trained using a leave-one-infant-out data partition to predict protophones (where the numbers of protophones were adjusted to give equal representation of all categories), the mean percent correct was 45.9% (see the first column of Table 5). This was not quite as high as performance of the SOM-perceptron hybrid, although across runs, this performance was within a standard deviation of the SOM-perceptron hybrids. When no adjustment was made for the inequality in the number of exemplars for each protophone category, the percentage correct was 65.3% where the baseline percent correct for an algorithm that always guessed vocant would be 74.9%. When six MLPs were trained using the same leave-one-infant-out method to predict age and then a single-layer perceptron layer was trained to take those MLPs’ hidden layer activations as input and produce protophone classifications as output, performance was 46.6% correct (see the second column of Table 5). This was lower than the SOM-perceptron hybrid by more than eight percentage points. These combined results of the MLP networks suggest that while a MLP trained to perform protophone prediction may perform similarly to the SOM-perceptron hybrid, the hidden layer of other MLP trained on a different classification task (age-prediction) is not as good as the general-purpose unsupervised SOM layer. Furthermore, the MLP did not fare any better than the SOM when there was no adjustment for the overrepresentation of vocants.

Table 5.

Classification task performance of the MLP neural network. All data are for leave-one-infant-out partitioning of utterances.

Type of hidden layer	Protophones		Ages
	Protophone-predictinga	Age-predicting	Age-predicting	Protophone-predicting
Mean % correct	45.9 (chance=33.3)	46.6 (chance=33.3)	35.1 (chance=33.3)	36.1 (chance=33.3)
Standard deviation	10.3	5.7	3.6	3.0
Mean Cohen’s κ	0.191	0.200	0.026	0.041
Mean p	<0.001	<0.001	0.118	0.018

^aWith adjustment for unequal category sizes. When there is no adjustment and one infant is reserved for testing, the mean percent correct is 65.3 (chance=74.9) with a standard deviation of 6.9.

Age classification performance

For the 15 hybrid networks trained to predict infant age with a session-level training-test data partition, the mean percent correct was 42.8% (see the third column of Table 4). This was significantly better than the 33.3% that would have been expected by chance, κ=0.142, p<0.001. Mean classification performance for the 36 additional hybrid networks that were trained on utterances from five infants and tested on the sixth was approximately 35.6% correct, where chance level performance would have again been 33.3% (see the fourth column of Table 4). This did not reach statistical significance, κ=0.034, p=0.146.

The six MLPs that were trained using a leave-one-infant-out data partition to predict age had a mean percent correct of 35.1% (see the third column of Table 5). This was very similar to the performance of the SOM-perceptron hybrid. When six MLPs were trained using the same leave-one-infant-out method to predict protophones (numbers adjusted for equal representation of protophone categories) and then a single-layer perceptron layer was trained to take those MLPs’ hidden layer activations as input and produce age classifications as output, performance was 36.1% correct (see the fourth column of Table 5). This was again very similar to the performance of the SOM-perceptron hybrid. These combined results of the two MLP variations suggest that both a MLP and the SOM-perceptron hybrid are approximately equally suited to the task of predicting age, though neither does very well when forced to generalize to an infant it has never previously encountered before.

Infant identity classification performance

For the 15 hybrid networks trained to predict the identity of the infant who produced an utterance (with session-level training-test data partition), the mean percent correct was approximately 32.4% correct (see the fifth column of Table 4). Compared to the 16.7% correct that would be expected had the networks been performing at chance, this performance was statistically significant, κ=0.189, p<0.001.

DISCUSSION

Visualization of network weights and activations

One of the main advantages of the SOM-perceptron hybrid is its usefulness for data visualization purposes. By plotting the weights from the input layer to the SOM (Fig. 3), it is possible to visualize the range of holistic spectrographic features exhibited by the vocalizations in the present data set. These holistic features are extremely complex, which can be seen as both an advantage, in that they retain the complexity of prototypical utterances, and as a disadvantage, in that they are difficult to interpret. By plotting the activations of each SOM node according to protophone, age, and identity, and by plotting the weights from each SOM node to each perceptron node, it is also possible to explore the relationship between the holistic spectrographic features learned by the SOM and different categories of utterances.

One method that was used to quantitatively interpret the trends observed in the figures was to get the median number of wins per SOM node for a specific utterance type (e.g., for each of the protophone types) to see which tended to occupy more of the SOM’s representational space. Using this method, it was found that growls had more diffuse activation of the SOM than squeals or growls, suggesting that growls have a larger range of acoustic variability.

In another approach to interpreting the trained network we showed that since the SOM’s receptive fields take the same form as their inputs, which in this case are coarse-grained spectrograms, more traditional acoustic descriptions, such as spectral mean, spectral standard deviation, and temporal median (related to duration) can be gotten. As observed in Sec. 3, the leftmost column of SOM nodes in Fig. 3 had long durations and the bottom two nodes of that column had high spectral mean and standard deviation. These nodes also had a tendency to be activated more by utterances from the older two age groups (6;0–11;4) than by utterances from the youngest age group (3;0–5;4), as evidenced by their lighter colorings in Figs. 45. Thus, a hypothesis for future investigation might be that utterances produced at older ages are not only longer in duration but also higher in spectral mean and variance.

Classification performance

The hybrid neural network, consisting of a perceptron classifier operating on the SOM’s holistic spectrographic features, is able to reliably classify 1-s-long utterance samples according to vocal type protophones, ages at which they were produced, and the identities of the individuals who produced them. Reliable performance on these classification tasks provides support for the validity of the SOM’s learned utterance features, suggesting that they reflect meaningful acoustic variation in infants’ vocal productions. One of the most important possible applications of the work represented here may be in contributing to the rapidly growing field of automated analysis of vocalization. MLPs trained on the same classification tasks also performed well, so when the goal is purely classification, and comparison of holistic features across different classifications is not important, MLPs may also be a good choice of tool.

It should be emphasized that the most critical issue for the future of automated vocal analysis is that reliability be significant, not necessarily that it be high. With very large data sets, relatively low kappa values do not necessarily present an important problem. If a signal is consistently (even though at low levels) detectable, it can become highly discernible at high Ns. This principle is widely recognized, for example, in the field of averaged evoked potentials (Burkard and Secor, 2002). It should also be noted that, although the methods used in the present study did involve some processing by human analysts, this was only in order to perform utterance extraction and protophone labeling. An automated infant utterance extraction method has already been developed for very large vocalization data sets taken from day-long recordings (see Zimmerman et al., 2009), and such a method could be substituted for the manual utterance extraction performed here. As for protophone labeling, for model training and evaluation, the use of human judgments in establishing gold-standard classifications is unavoidable. However, for automated analysis of large data sets, training and evaluation of a network using manually labeled utterances need not be done on the entire large data set, but only on a sample of data large enough to ensure satisfactory network performance and generalization.

The ability to reliably classify utterances according to protophone is of considerable interest. At present, protophone categories are widely used in studies of infant speech development in both typically and atypically developing children (e.g., Hardin-Jones et al., 2003; Salas-Provance et al., 2003; Iverson and Wozniak, 2007; Goldstein and Schwade, 2008) as well as in tools that use infants’ vocalizations in their assessment of infants’ communicative function (e.g., Bryson et al., 2008). The ability to predict trained analysts’ perceptual judgments suggests that neural networks and other data-driven statistical tools have the potential to be used for automatic classification of protophone categories (although a workaround for the issue of frequency imbalance across categories would have to be devised). This would be useful in many research and clinical settings where coding by trained analysts is costly or difficult. In the future, it would be interesting to apply either the SOM-perceptron-hybrid or a MLP to the classification of other protophones, such as marginal syllable and canonical syllable—categories related to the articulation timing of syllables that have been shown to be of particular importance as indicators of normal development (Oller, 2000).

The ability to identify age, combined with the network’s ability to identify the individual who produced a given utterance, suggests that neural networks and related approaches have the potential for future use in classifying utterances produced by delayed or disordered individuals. Prediction of infant identity also lays groundwork for future work that might attempt to classify utterances produced by infants from different cultural or linguistic backgrounds and by female versus male infants.

Future development

Manipulating the network’s input

The SOM-perceptron architecture is highly flexible with regard to the type of information it can be given as input. Although 225-pixel spectrograms of 1-s-long utterance samples were used in this study, such an input representation was chosen primarily for its computational efficiency and because it involved relatively little preprocessing of data. It is possible that other formats of input would yield better performance or additional insights. Future studies might compare features learned by SOMs trained on different types of input, be they relatively raw input (e.g., raw waveforms, spectrograms of various frequencies and time resolutions), more traditional acoustic measures (e.g., f₀ means, formant frequency means, amplitude means, durations), or measures that represent intermediate amounts of preprocessing (e.g., f₀ contours, formant frequency contours, and amplitude contours).

In discussing the visualizations afforded by the SOM-perceptron hybrid, reference was made to how these visualizations might be related to acoustic patterns described in more traditional terms. For example, it was noted that the SOM features’ duration preferences appear to increase with increasing age. Although beyond the scope of the present study, this hypothesis could be tested by comparing the present SOM-perceptron hybrid (trained on raw spectrographic input) with a SOM-perceptron hybrid network trained on duration alone. That is, rather than providing the network with pixels of spectrograms as input, one could provide the network with a single value representing an utterance’s duration. If such a network trained on utterance durations also performs significantly well, this would indicate that changes in utterance duration are indeed associated with increasing age. One could then train a SOM-perceptron network on input consisting of a spectrogram plus an additional feature representing the utterance’s duration. If this network performed better than the network trained only on spectrograms (e.g., as measured by a hierarchical regression), this would imply that duration changes systematically with development but was not adequately represented by the SOM trained only on spectrograms. On the other hand, if the two networks perform equally well, this might suggest that the SOM had already encoded the relevant duration information in its features. This type of approach could provide a means for parsing out the role of various acoustic measures in how well they predict the age (or identity, protophone category, etc.) of infant utterances.

Finally, it would be highly desirable to explore input representations that deal more flexibly with temporal aspects of vocalizations. Infant utterances vary in length and often have prosodic and syllabic components that vary in their timing. The current static spectrograms used as input do not adequately deal with this fact. A better solution might be one in which small time segments of spectrograms (or other acoustic features) of infant utterances are presented in sequence. The network would then make classifications at each time point or at the conclusion of the entire sequence. A change of this sort in the temporal nature of the input would, however, require changes in the network architecture. Some possibilities are proposed as part of Sec. 4C2.

Alternative architectures and algorithms

The choice of a SOM-perceptron hybrid architecture was motivated by the fact that its components had been previously applied to related problems involving the visualization and classification of acoustic vocalization data, including avian song, disordered adult voice, and infant crying. The choice of a SOM as the first element of this architecture was also motivated by studies suggesting that SOMs can produce results that are comparable to other statistical clustering and visualization methods (Flexer, 2001; de Bodt et al., 2002). Choosing a SOM for the first component of the two-component hybrid network also has the advantage that the same first component is used regardless of the classification task performed by the subsequent perceptron component. Thus, the middle layer activations and weights can be compared across different classification tasks (e.g., the SOM node activations and weights for younger utterances can be compared to the SOM node activations and weights for vocants, squeals, and growls). Finally, the biologically inspired features of the SOM, notably its topographical self-organization and incremental learning algorithm, are also seen as advantages (see Sec. 4C3 below on future modeling directions; Miikkulainen, 1991; Kohonen and Hari, 1999; Ritter, 2003).

Nevertheless, exploration of other architectures could yield better performance or additional information. For example, a two-layer perceptron may be worth using for situations where classification performance and differentiation between classes is the primary goal. Furthermore, non-neural-network statistical models, such as mixtures of Gaussians, k-nearest-neighbors analysis (Xu and Wunsch, 2005), and possibly even linear discriminant analysis and regression techniques could potentially yield as good or better clustering and classification performance, respectively. Future work could compare such methods on their performance on a specific visualization or classification task.

In addition, recurrent neural networks are often considered better for temporal sequence processing than networks that take static input (Elman, 1990). Thus, given that infant vocalizations are temporal patterns occurring in temporal sequences, it would be worthwhile to explore recurrent versions of the SOM (e.g., Euliano and Principe, 1996) when unsupervised analysis is desired, or the simple recurrent network (SRN) (Elman, 1990), when classification or prediction is the primary goal. Perhaps even a hybrid of the recurrent SOM and the SRN could be used, which would be analogous to the static SOM-perceptron hybrid explored in the present study. Moving to such temporal architectures would involve changing the nature of the network’s input representation as discussed in Sec. 4C1. A fixed moving window of spectral input would be appropriate.

Finally, variations on the SOM that allow for uncertainty in the number of features∕categories or that allow for hierarchical organization of features∕categories (Carpinteiro, 1999; Rauber et al., 2002) might also prove useful and informative. The SOM-perceptron hybrid presented in this early study is thus only one of a number of statistical and neural network options.

Modeling the perception and production of infant vocalizations

The SOM is a neural network inspired in large part by biological considerations, namely, the self-organizing topographic nature of its feature representations and unsupervised learning in response to stimulus exposure (Miikkulainen, 1991; Kohonen and Hari, 1999; Ritter, 2003). Although the present study focuses solely on acoustic analysis and classification applications, this work provides a potential foundation for future modeling of the perception of infant vocalizations by humans, including learning through exposure to such vocalizations.

Caregivers are commonly infants’ primary communication partners, responding and providing feedback to infants. Furthermore, much of the current research on infant vocal development relies critically on naturalistic judgments by laboratory personnel. It is therefore important to understand how adults perceive infant vocalizations and to understand what acoustic features are relevant to adult communication partners. There are several ways in which the ability of the SOM to model adult humans’ perceptions of infant utterances might be assessed. One way would be to have human participants perform tasks directly matched to those the SOM-perceptron hybrid performed. Another possibility would be to compare the topography of features on the SOM to listeners’ similarity judgments.