Aggregation of a multidomain protein: A coagulation mechanism governs aggregation of a model IgG1 antibody under weak thermal stress

Abstract

Using an IgG1 antibody as a model system, we have studied the mechanisms by which multidomain proteins aggregate at physiological pH when incubated at temperatures just below their lowest thermal transition. In this temperature interval, only minor changes to the protein conformation are observed. Light scattering consistently showed two coupled phases: an initial fast phase followed by several hours of exponential growth of the scattered intensity. This is the exact opposite of the lag-time behavior typically observed in protein fibrillation. Dynamic light scattering showed the rapid formation of an aggregate species with a hydrodynamic radius of about 25 nm, which then increased in size throughout the experiment. Theoretical analysis of our light scattering data showed that the aggregate number density goes through a maximum in time providing compelling evidence for a coagulation mechanism in which aggregates fuse together. Both the analysis as well as size-exclusion chromatography of incubated samples showed the actual increase in aggregate mass to be linear and reach saturation long before all molecules had been converted to aggregates. The CH2 domain is the only domain partly unfolded in the temperature interval studied, suggesting a pivotal role of this least stable domain in the aggregation process. Our results show that for multidomain proteins at temperatures below their thermal denaturation, transient unfolding of a single domain can prime the molecule for aggregation, and that the formation of large aggregates is driven by coagulation.

Introduction

Most proteins fold to a specific three-dimensional structure essential for their biological function. The net thermodynamic stability stemming from various stabilizing and destabilizing intramolecular forces is low and may be corrupted by relatively small changes in external variables (pH, temperature, salt, etc.).^1,2 When the protein structure is destabilized, parts of the interior is exposed and this may lead to irreversible formation of aggregates.^3–5 The mechanisms leading to aggregates are as diverse as the nature of the aggregates themselves—ranging from oligomers and micelles to amorphous aggregates and fibrils^6–9—and remain a major challenge in protein science.^10,11

Due to minute transient perturbations of the molecular structure, heating may induce aggregation even well below the melting temperature of the protein.^1,12 Furthermore, higher temperature accelerates aggregation because of its impact on the individual rate constants involved in the aggregation kinetics. This is the reason why high temperature is often used to probe the stability of a given protein. Model proteins for folding/misfolding and aggregation are often single-domain proteins (BSA, β-lactoglobulin, lysozyme, insulin, etc.), which exhibit two-state unfolding, with far fewer studies of more complex multidomain proteins despite their acknowledged importance in pharmaceutical sciences.¹³ Low aggregate content is especially crucial in pharmaceutical formulations as aggregates here may elicit an inflammatory immune response to neutralize the aggregate.¹⁴ This would not only diminish the effect of the drug itself but could also lead to more serious adverse effects related to cross-reactivity with autologous proteins.^15,16

In this study, we used the monoclonal IgG1 antibody Rituximab¹⁷ as a model system to better understand the mechanisms leading to the formation of large aggregates when incubating a multidomain protein under weak thermal stress. Aggregation of antibodies due to various kinds of stress have been addressed in a number of studies,^18–24 with a few key observations highlighted later. In this context, we distinguish between the formation of oligomers (dimers, trimers, etc.) and larger aggregates: by size-exclusion chromatography (SEC), oligomers can be separated and characterized individually, while aggregates comprise a broad range of sizes that elute in the void.²⁵ Jøssang and coworkers^18,19,23 used light scattering under conditions similar to those applied in this work to study aggregate formation of antibodies purified from blood. They found that the antibodies generate large fractal aggregates with no discernable amount of oligomers and that the aggregates were not stabilized by disulfide bonds. In contrast, in a more recent study by Remmele et al.,²² the IgG1 formulation Epratuzumab was found to contain dimers, 70% of which were covalently linked. The appearance of large aggregates, if any, was not reported. Finally, Van Buren et al.²⁴ incubated an IgG2 monoclonal antibody (mAb) for 15 weeks at 37°C in two different pH regimes, and found the aggregation pathways to be pH dependent: at high pH, dimers had ∼75% covalent character, while the formation of large aggregates was largely suppressed; at low pH, on the other hand, both dimers and large aggregates were formed. To generalize these findings, incubation at elevated temperatures may lead to the formation of large aggregates, dimers, or both. The dimers appear to be linked by disulfide bridges, while this appears not to be the case for the aggregates. For certain globular proteins, such as β-lactoglobulin, the oligomers have been shown to be on-pathway to larger aggregates,²⁶ but such a simple link between oligomers and aggregates has yet to be demonstrated for antibodies.

By light scattering, we show that Rituximab aggregation kinetics have a distinct two-phase appearance starting with a rapid doubling of the scattered intensity followed by hours of exponential increase. This observation is in stark contrast to the lag-time behavior, typically ascribed to heterogenous nucleation,^27,28 commonly observed in protein fibrillation. Light-scattering analysis demonstrates that the main mechanism for aggregate growth is the continuous coagulation of smaller aggregates into larger ones. The initial rapid generation of aggregates is less clearly resolved. The comparison of light-scattering data with calorimetry data shows that the activation energy of the aggregation process is linked to the stability of the thermally least stable antibody domain.

Results

Thermal denaturation

Figure 1 shows the heat capacity of the protein solution as a function of temperature. The thermal denaturation by differential scanning calorimetry (DSC) resulted in three partially overlapping transitions with T_m values of ∼71, 74, and 83°C, respectively. The results are in good agreement with previous results from an IgG1 mAb, in which case the three transitions were assigned to the unfolding of the CH2 domain, the antigen-binding fragment (Fab), and the CH3 domain, respectively.^29–31 CH2 and CH3 comprise the constant fragment (Fc) of the antibody. The denaturation of Rituximab was always irreversible, and the T_m values were also scan rate dependent (results not shown), which precluded full thermodynamic analysis.³² This is a common property of large, complex proteins such as mAbs and has been described earlier.^30,33 However, the use of the denaturation enthalpy is still permissible according to the first law of thermodynamics, even if the process is irreversible.³⁴ In addition, no distortion, which is sometimes observed when the samples aggregate irreversibly, was seen on the shape of the heat capacity profiles for the Rituximab samples. A calorimetric enthalpy of 320 kcal/mol and a Van't Hoff enthalpy of 144 kcal/mol were obtained for the first thermal transition. From the irreversible two-state model of Sánchez-Ruiz,^34,35 it is also possible to calculate the activation energy of unfolding given that only the native state (N) and the final irreversible state (F) are significantly populated:

1

where k_ap is the first-order rate constant for the irreversible denaturation process. Then the activation energy can be calculated using the following equation:

2

where e is the base of the natural logarithm, R is the gas constant, is the excess heat capacity measured at T_m, and is the total heat of the process. Using this equation, an activation energy of 98.4 kcal/mol was obtained for the first thermal transition corresponding to the denaturation of the CH2 domain.

Figure 1.

Rituximab unfolds in three steps reflecting the stability of individual domains. The heat-induced unfolding was monitored by Sypro orange fluorescence (dashed line) and DSC (solid line). The scan rate in both experiments was 1°C/min. Each peak in the DSC profile (dotted lines) has been assigned to a specific domain or fragment as devised previously.^29,30 The activation energy of the first thermal transition corresponding to the CH2 domain was found to be 98.4 kcal/mol (see main text for details).

Figure 1 also shows the intensity of the fluorescent probe Sypro orange as a function of temperature. The intensity is essentially unchanged up to 62°C at which point it starts to increase. Two characteristic melting temperatures are observed at 69 and 75°C in accordance with the melting temperatures obtained by DSC at the same temperature rate.

Finally, thermal stability was probed by far-and near-UV CD, which probes secondary and tertiary structure, respectively. Figure 2(a) shows far-UV spectra in the wavelength range from 205 to 260 nm recorded while ramping the sample temperature. The spectra are characterized by a single negative peak with a minimum at 218 nm, which is characteristic of proteins—such as antibodies—rich in β-structure. Below 61.4°C, no change in spectra characteristics was noticed, and they have been averaged for clarity. Above this temperature, the negative signal of the spectra increases and becomes broader. This behavior suggests an amplification on the level of secondary structure before unfolding and has been observed for antibodies previously.^33,36 Above 70°C, the spectra decreased in intensity as the secondary structure was gradually lost (spectra omitted for clarity). Figure 2(b) shows near-UV spectra in the wavelength range from 250 to 350 nm recorded while ramping the sample temperature. The spectra recorded below 66.5°C all have a maximum at 298 nm. Above that temperature, the characteristic features of the spectra disappear due to the loss of tertiary structure.³³ Figure 2(c) shows the CD signal at 218 and 298 nm as a function of sample temperature from two separate experiments similar to the ones detailed earlier. The figure confirms that the antibody is remarkably stable in the incubation temperature interval (52–65 °C) applied in this study.

Figure 2.

Under the weak thermal stress applied in this study, secondary and tertiary structure elements are essentially conserved. The thermal unfolding was monitored by far and near-UV CD. (a) Far-UV CD temperature scan. The spectra from 23.4 to 61.4°C were similar and have been averaged for clarity. At temperatures above 63°C, the negative signal with a minimum at 218 nm becomes more intense. (b) Near-UV CD spectra with a maximum at 298 nm showing the abrupt loss of tertiary structure. The solid line is a guide to the eye. (c) Thermal scans at 218 and 298 nm demonstrate that the antibody is stable up to ∼68°C, at which point the protein denatures.

Concentration and temperature dependence of the aggregation kinetics

Figure 3 shows the scattered intensity from 1 mg/mL Rituximab samples incubated at 52–65°C as a function of incubation time. We observe that the scattered intensity is dominated by two phases: an initial fast increase is followed by several hours of exponential growth. Phenomenologically, we define the initial phase as starting at time zero and lasting until exponential growth takes over, but we also note that the two processes are most likely overlapping. The temperature is seen to affect both the initial phase—which is shortened from about 8 h at 52°C to being practically instantaneous at 65°C—as well as the subsequent exponential phase. The two phases of each curve were fit separately with a simple model to extract the rate constants: I(t) = a(k_init/(1 + k_init))²exp(k_expt) + b, where a is an amplitude, b is a baseline, and k_ini and k_exp are rate constants of the initial and the exponential phase, respectively. In this phenomenological model, the first phase is fitted by a power law and the second phase by an exponential. Figure 4 shows the natural logarithm of each of these rate constants plotted against the reciprocal temperature in an Arrhenius plot. Both data sets fit a straight line with activation energies of 117 and 71 kcal/mol for the initial and exponential phase, respectively.

Figure 3.

Aggregation kinetics are characterized by two phases: an initial fast phase followed by an exponential phase, and both are temperature dependent. Static light scattering of 1 mg/mL Rituximab samples as a function of incubation time. The kinetics were studied at temperatures ranging from 52 to 65°C as indicated in the figure.

Figure 4.

The activation energy of the first phase of the kinetics is similar to the denaturation energy of the CH2 domain. The Arrhenius plot shows the natural logarithm of the rate constants calculated from the kinetics at various incubation temperatures (Fig. 3) plotted against the reciprocal temperatures. The initial phase (open circles) has an activation energy of E_a = 117 kcal/mol, whereas the exponential phase (solid squares) has an activation energy of E_a = 71 kcal/mol.

Figure 5 shows the scattered intensity of 0.2–10 mg/mL Rituximab samples as a function of incubation time at 60°C. The concentration dependence of the rate constants of the first phase is approximately linear, k_ini ∝ c, while the rate constants of the exponential phase have a weak concentration dependence: k_exp ∝ c^0.2 (inset of Fig. 5). The autocorrelation functions acquired during each experiment were analyzed using the two-species model in Eq. (9) (Materials and Methods), which assumes a monomer population with a fixed hydrodynamic radius of 5.6 nm and a polydisperse aggregate population. By visual inspection, the model fit every autocorrelation function very well without any constraints on the fitting parameters (not shown). The polydispersity parameter, which is subject to the largest uncertainty especially at low concentration, generally increased during the experiment and reached a maximum value of 0.3 after 16 h of growth. The Tween 80 present in the sample buffer forms micelles with a hydrodynamic radius similar to that of the protein monomers, but only contributes very little to the total scattered intensity.

Figure 5.

Protein concentration has a surprisingly weak effect on both phases of the aggregation kinetics. Static light scattering of 0.2–10 mg/mL Rituximab samples as a function of incubation time at 60°C. The kinetics are composed of an initial fast phase followed by an exponential phase. The reaction rates of the exponential phase (inset) have a weak concentration dependence, k_exp α c^0.2 (solid line).

Figure 6 shows the increase in the hydrodynamic radius of the aggregate species formed at concentrations of 0.5 to 10 mg/mL as a function of incubation time at 60°C. The hydrodynamic radius of the aggregate population is seen to increase continuously throughout the experiment. The initial hydrodynamic radius of the aggregates, as determined by extrapolation to time zero, increases from 22 to 26 nm with increasing concentration (inset of Fig. 6).

Figure 6.

Aggregate sizes increase continuously throughout the incubation period. Aggregate hydrodynamic radius for various concentrations of Rituximab plotted as a function of incubation time at 60°C. The initial hydrodynamic radius, as obtained by extrapolation to time zero, is plotted as a function of the concentration (inset).

From the light-scattering data, the accumulated aggregate mass and aggregate number density are calculated as follows. First, the intensity due to aggregates is given as a sum of the individual aggregate contributions:

3

where α(t) is the monomer fraction defined in Eq. (9), I₀/cM_m represents a normalization of the scattered intensity at time zero with respect to the sample concentration and the molecular weight, and the sum is taken over all aggregate species of concentration c_i(t), mass M_i(t), and form factor P_i(q,t). In the following calculations, we approximate the aggregate species by a single population of aggregates with an average aggregate mass, , and an average mass concentration, . The above equation is then rewritten as follows:

4

where P_ag(q,t) is the form factor of the aggregate population. Rearranging Eq. (4), we obtain the following expression for the average aggregate mass concentration:

5

We may also obtain an expression for the average aggregate number density, , from the expression above:

6

The average mass concentration and average aggregate number density [Eqs. (5) and (6), respectively] are central for understanding the aggregation mechanism. To that end, estimates of the form factor, P_ag(q,t), and the mean mass of an average-size aggregate, 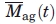, are required. The form factor was measured every hour during the kinetics, and a satisfactory fit was obtained using the Fisher-Burford approximation. The Fisher-Burford approximation is an extension of the Guinier law and is originally developed to include mass fractals³⁷:

7

where R_g(t) is the radius of gyration, and the fractal dimension, d, concerns the structure of the aggregate. Typical fractal dimensions for protein aggregates are in the range 2.0–2.7.^38,39 We chose d = 2.5, close to the value of 2.56 reported previously for antibodies,¹⁸ but choosing other values in the interval did not qualitatively change the results. The radius of gyration in Eq. (7) was similar to the hydrodynamic radius of the aggregates obtained from the dynamic light-scattering (DLS) analysis, R_g,ag(t) ∼ R_h,ag(t), and as the hydrodynamic radius is more accurately determined in the beginning of the experiments, we used this parameter in Eq. (7) when calculating the aggregate mass concentration [Eq. (5)] and the aggregate number density [Eq. (6)]. Some deviation between the hydrodynamic radius and the radius of gyration was observed in the last part of the kinetics in the 10 mg/mL data set. The mean mass of a typical aggregate, 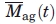, is estimated by assuming that the aggregates are fractal objects with an average density equal to the monomer density:

8

Figure 7(a) shows the aggregation number density as a function of incubation time calculated from Eq. (6). For clarity, only the 1 and 2.3 mg/mL data sets are shown, but the other data sets follow similar behavior. The number density increases for several hours, reaches a maximum, and then decreases in the last part of the kinetics. Figure 7(b) shows the percentage of monomers converted into aggregates as a function of incubation time of a 1 mg/mL solution as calculated from Eq. (5). The aggregate mass percentage increases from 0 to 20% for 16 h, at which point the growth slows down and the aggregate mass reaches a plateau. Figure 7(b) also contains SEC data as discussed later. The increase in aggregate mass is mirrored by a decrease in monomer mass; however, the latter quantity is subjected to larger error in the light-scattering analysis.

Figure 7.

Aggregate number density goes through a maximum in time, and aggregate mass reaches a plateau. These are hallmarks of a coagulation mechanism. (a) Aggregate number density, , as a function of incubation time. Samples of 1 mg/mL (red diamonds) and 2.3 mg/mL (blue dots) were incubated at 60°C. The dashed lines are guides to the eye. (b) A comparison of aggregate mass percentage, , of a 1 mg/mL Rituximab sample as a function of incubation time at 60°C as estimated by DLS analysis (black data points) and SEC (red dots). The two approaches measure aggregate mass in fundamentally different ways, but the end result is very much in accordance. The aggregate mass is seen to increase for hours and then reach a plateau. The SEC data point at 22 h was obtained immediately after the DLS experiment shown in the figure.

The effect of Tween 80 and salts on the Rituximab aggregation kinetics was examined by removing Tween 80 from the stock solution and then changing the sample buffer into a similar buffer without Tween 80 and also into pure milli-Q water. In Supporting Information Figure 1, the aggregation kinetics of these two samples are compared with the kinetics of a regular 1 mg/mL Rituximab sample and found to have the same distinct two-phase kinetics.

Quantification of aggregate mass by SEC

Aggregate mass may also be measured directly by SEC. In Figure 8, SEC of samples incubated at 60°C for 0, 0.25, 0.5, 1, 4, 8, 16, and 22 h is shown. With increasing incubation time an aggregate peak appears, but as with the light-scattering data, no significant formation of small oligomers is observed. The figure shows eluent absorption at 280 nm as a function of eluent volume. The inset in Figure 8 shows the aggregate mass percentage as a function of incubation time. After 15 min, 2.5% aggregate mass have formed, and in the following hours, the aggregate mass increases until a plateau is reached at ∼18% after 16 h. The sum of the monomer and aggregate areas was constant as expected for mass conservation. In Figure 7(b), the same SEC data have been superimposed on the aggregate mass percentage calculated from the light-scattering data, and the agreement is seen to be satisfactory. This supports the main assumption, that the aggregates can be approximated by an average-sized population in deriving Eqs. (5) and (6).

Figure 8.

Aggregate mass increases over time and then reaches a plateau. SEC of a fresh 1 mg/mL Rituximab sample is compared with samples incubated at 60°C for 0.25, 0.5, 4, 8, 16, and 22 h. The eluate absorption at 280 nm is plotted as a function of the eluate volume. The monomers elute at 13.2 mL, and the aggregates elute at ∼8.2 mL. Only minute amounts of dimers and trimers were present. During incubation, the height of the monomer peak decreases, and the height of the aggregate peak increases as indicated by arrows. The aggregate mass percentage (inset) increases continuously and then reaches a plateau around 18% after 16 h.

Aggregate visualization

Aggregated samples were visualized by AFM. Figure 9(a) shows a representative 1 mg/mL sample incubated for 16 h at 60°C with aggregates embedded on the monomer-covered mica. Figure 9(b) shows aggregates from another sample in more detail. The height scale is the same in both pictures. A buffer-only sample showed a clean mica surface and ensures that the buffer preparation does not give rise to any artifacts that could be mistaken for aggregates. A monomeric sample showed the mica surface covered with objects with an average radius of 6 nm. From an analysis of more than 400 aggregates, the average radius was found to be about 30 nm. These observations are in accordance with the DLS and SEC data in Figure 7(b), which show that under these conditions, ∼80% of the sample remain monomeric, and also in accordance with the hydrodynamic radius of the aggregates after 16 h of incubation (Fig. 6).

Figure 9.

The size of aggregates visualized by AFM is in accordance with aggregate sizes determined by light scattering. (a) A 1 mg/mL Rituximab sample was incubated for 16 h at 60°C. Aggregates with an average radius of 30 nm are embedded on a background of monomers with an average radius of 6 nm. (b) A closer look at aggregates from a similar sample. The scale bars indicate 100 nm.

Discussion

In this study, we investigate the aggregation kinetics of an IgG1 antibody when stressed by incubation at temperatures below the lowest thermal transition. In proteins such as antibodies, where several domains unfold separately, the influence of the stability of individual domains on the aggregation propensity is as of yet not clear. Moreover, the exact aggregation mechanisms involved remain largely unresolved when compared with the large number of studies done on single-domain model systems. Untangling the molecular mechanisms leading to aggregates typically involves interpreting a kinetics experiment, which probes the bulk of the aggregating solution. To that end, a large number of models have been proposed, each relying on a specific aggregation mechanism.^10,11,27 Very often more than one model will fit the data, and this is also the case for the antibody aggregation study at hand. However, we show how a stringent interpretation of light-scattering data help narrow down the number of plausible mechanisms. In addition, we demonstrate that light-scattering and calorimetry data in concert point to the importance of a specific domain in initiating the aggregation process.

Initial fast formation of aggregates

The principal observation in this study is the fact that the scattered light—under a wide range of concentrations and temperatures—exhibits a distinct two-phase behavior (Figs. 3 and 5). The first aggregation step does not involve the formation of long-lived oligomers, as shown by DLS and SEC data (Figs. 6 and 8, respectively). This phase is puzzling, because it apparently goes to completion and paves the way for the second, slower phase. If the process goes to completion due to a monomer-aggregate equilibrium, we would expect a strong concentration dependence, quite opposite to the actual observations. This kind of fast initial aggregate assembly has been previously observed by other groups. For example, the amyloid β-peptide has been observed to assemble into a micelle-like structure with a hydrodynamic radius of 7 nm at ambient temperature,^9,40 and β-lactoglobulin has been reported to initially form clusters with a hydrodynamic radius of 15 nm, which later on were incorporated into large fractal structures.⁴¹ In principle, the first process could also rely on a component in the buffer. However, Rituximab, when prepared in milli-Q water and incubated at 60°C, had a similar two-phase behavior (Supporting Information Fig. 1). We hence conclude that Tween 80 and salts have negligible impact on the kinetics presented in this article. The mechanistic details of the initial aggregate formation remain unresolved due to methodological limitations.

Coagulation governs aggregate growth

The second phase is characterized by a remarkable continuous exponential increase in scattered light (Fig. 5). Exponential increase in weight-averaged aggregate mass can be associated with either reaction-limited cluster–cluster aggregation^42,43 or secondary nucleation mechanisms.^28,44,45 Secondary nucleation mechanisms are often observed for fibril-forming proteins capable of generating new fibril ends by branching or breakage mechanisms, and reaction-limited cluster-cluster aggregation is a coagulation process where the rate of coalescence of two clusters is not dependent upon cluster size. The fundamental difference between these two mechanisms manifests itself through the conversion of monomers into aggregates: in secondary nucleation, the aggregate mass increases exponentially, while this is not explicit in coagulation. Furthermore, aggregate number density, although not always readily obtainable from light scattering experiments, conveys important information about the underlying mechanism. We rely on these facts to distinguish between the two mechanisms as detailed in the following.

As mentioned earlier, the exact growth of the aggregate mass provides a litmus test for a coagulation mechanism versus a secondary nucleation mechanism. We calculated this quantity from the DLS data and independently confirmed it by SEC [Fig. 7(b)]. The correlation between DLS and SEC data shows that although not explicit in the light-scattering analysis, mass is conserved. We found that rather than being exponential, the growth in aggregate mass is linear and approaches a plateau. This is clearly inconsistent with a secondary nucleation mechanism. Furthermore, the aggregate number density goes through a maximum in time [Fig. 7(a)], and this is compelling evidence of a coagulation process. The combination of an exponential increase in the scattered light (Figs. 3 and 5), the continuous increase in the aggregate size (Fig. 6), the maximum in aggregate number density [Fig. 7(a)], and the growth in aggregate mass [Fig. 7(b)] leads to the conclusion that a coagulation process, such as reaction-limited cluster-cluster aggregation, governs the growth of aggregates. In the light of the many events involved in the coagulation mechanism, the activation energy of the exponential phase (71 kcal/mol) is not readily associated with a single physical process.

Coagulation processes are essentially second order,⁴⁶ and hence do not readily offer an explanation for the weak concentration dependence observed, k_exp ∝ c^0.2 (inset of Fig. 5). A possible explanation may be that another process with a lower reaction order is effectively controlling the aggregate formation.⁴⁷ For example, concomitant micelle formation in fibrillating amyloid β-peptide solutions has been shown to effectively keep the monomer concentration constant and hence mask the true concentration dependence of the fibrillation process.⁹ In any case, a realistic description of the concentration dependence of the rate constants of the exponential phase should probably take into full account the process governing the initial fast phase.⁴⁸

Conceptually, it is difficult to understand why the majority of the monomers do not convert into aggregates. Although still being investigated in our group, it appears that the plateau in the aggregate mass percentage is not significantly affected by concentration, but rather strongly influenced by temperature (data not shown). Jøssang and Feder¹⁹ made a similar observation for polyclonal antibodies under conditions similar to ours. They showed that when reincubating the heat-stable monomers, they exhibited a much different aggregation kinetics; however, that phenomenon may be ascribed to the inherent heterogeneity of polyclonal antibodies purified from blood. In this study on mAbs, heterogeneity is unlikely to have a significant impact on the aggregation kinetics. Instead, the partial aggregation could point to the presence of the reverse process of coagulation, namely fragmentation. By fragmentation, aggregates repeatedly break apart into smaller aggregates, and monomers are detached from the aggregates as sketched in Figure 10.

Figure 10.

Sketch of the proposed mechanisms involved in Rituximab aggregation. During the first phase, a population of large aggregates is quickly formed by a mechanism not yet fully understood. Then, aggregates increase in size by coagulation, while fragmentation may play a role in preventing the aggregation from going to completion. Coagulation and fragmentation may involve both monomers and aggregates.

AFM pictures showed structures with an average size of 30 nm embedded on a background of monomers in accordance with our kinetics data. The structures themselves (Fig. 9) are somewhat different from the spherical aggregate structures observed previously by transmission electron microscopy for antibodies⁴⁹ and for a number of other proteins.^8,26

Transient unfolding correlates with aggregation

We now turn to the structural events priming molecules for conversion into aggregates. All incubation temperatures were below the denaturation temperature of the CH2 domain (T_m,1 = 71°C), and no structural changes were detected in the incubation temperature range studied here (Figs. 1 and 2). However, even at temperatures well below the melting temperature, thermal fluctuations are expected to transiently expose the hydrophobic interior to the solvent while keeping structural elements intact, and this may prime aggregation.¹² In fact, even subtle changes to the protein conformation may trigger the prevalence of attractive intermolecular forces.³ Aggregation is hence most likely initiated by minor structural changes to certain parts of the molecule and possibly to just a small fraction of the sample. In the study of IgG2 aggregation mentioned earlier, Van Buren et al.²⁴ showed that oligomerization and aggregation were mainly driven by unfolding of the CH2 domain, although no changes in far-and near-UV spectra were observed. The isolated oligomers and aggregates did, however, exhibit minor changes in far-UV CD spectra, demonstrating that in studies such as ours, where only a small fraction of the monomers aggregate, the signal will be dominated by the most numerous species. A similar conclusion was reached by Kalonia and coworkers⁵⁰ in a study of irreversible aggregation of a mAb under nonstressed conditions. In our study, the CH2 domain is the least stable domain and the overall irreversible aggregation process is most likely determined by the activation barrier for unfolding of this particular domain.⁵¹ We find it intriguing that the activation energy of the initial reaction (117 kcal/mol) is similar to the activation energy of the unfolding of the CH2 domain (98.4 kcal/mol). Thus, a structural change in the CH2 domain is likely to prime the molecule for aggregation.

Conclusions

Temperature-induced aggregation of the model multidomain protein exhibits two phases: the first phase represents the fast assembly of monomers into aggregates with a hydrodynamic radius of about 25 nm by a mechanism not yet fully understood. This phase is followed by a second phase characterized by several hours of exponential growth of the scattered intensity. During this phase, the aggregates continuously increase in size, the aggregate number density goes through a maximum in time, and the aggregate mass percentage approaches a plateau. All of these observations, including the exponential increase in the scattered light itself, are consistent with a coagulation mechanism, likely involving both reaction-limited cluster–cluster aggregation as well as fragmentation (Fig. 10). Therefore, this study gives a rare insight into the complex mechanism controlling the aggregation of multidomain proteins. Transient structural fluctuations are likely to prime the antibody molecules for aggregation, and our data show that the CH2 domain may play an important role to that effect.

Materials and Methods

Protein and reagents

Rituximab (marketed as MabThera by Roche, Basel, Switzerland, and Rituxan by Genentech, San Francisco, CA) 10 mg/mL was in a liquid formulation composed of 7.35 mg/mL NaCitrate·2H₂O pH 6.5 with 9 mg/mL NaCl and 0.7 mg/mL Tween 80.¹³ It was diluted in a similar buffer containing analytical grade tri-NaCitrate · 2H₂O (Merck, Darmstadt, Germany), NaCl (Honeywell Riedel-de Haën, Seelze, Germany), and Tween 80 (Polysorbate 80; Sigma-Aldrich, St. Louis, MO) diluted in milli-Q water (Millipore, Billerica, MA). The buffer was filtered through a Millex-LG sterilizing 0.2-μm filter (Millipore, Billerica, MA). In all light-scattering experiments, the protein samples were filtered through Anotop 10 filters (Whatman, Maidstone, England) with a pore size of 20 nm. The first three drops were discarded to saturate the filter with protein and Tween 80. Concentration was measured after filtration by absorbance measurement at 280 nm on a Shimadzu UV–2401 PC spectrophotometer (Kyoto, Japan) using the Rituximab extinction coefficient ɛ₂₈₀ = 1.7 mL/(mg cm) available from the U.S. Food and Drug Administration homepage.

Removing Tween 80 and salts from Rituximab

This procedure is described in Section 1.1 of the Supporting Information.

Size-exclusion chromatography

Aggregate mass percentage was measured using a Superdex 200 10/300 GL SEC column (GE Healthcare, Buckinghamshire, UK) connected to a Smimadzu HPLC (Kyoto, Japan). Samples of 1 mg/mL Rituximab were incubated at 60°C for various time intervals in the light-scattering setup described below and transferred directly to a 500 μL loop on the HPLC. The samples were eluted at a flow of 0.8 mL/min in Rituximab sample buffer, and the eluate was monitored by absorption at 280 nm. The percentage of monomers converted to aggregates was estimated from the area of the aggregate peak with respect to the total area of monomers and aggregates. The total integrated area of aggregates and monomers was constant.

Static and dynamic light scattering

The scattered light intensity at 90° and its time autocorrelation function, g₂(τ), were measured simultaneously, and the structure factor was obtained every hour by measurements at 12 different angles. The Brookhaven light-scattering setup (Brookhaven Instr. Corp., Holtsville, NY) was equipped with a BI-200SM goniometer, a BI-APD avalanche photodiode detector, a BI-9000AT autocorrelator, and a Melles Griot (Carlsbad, CA) Omnichrome Series 43 vertically polarized solid-state laser tuned at a wavelength of either λ₀=488 nm or λ₀=514 nm. The temperature was measured with a Fluke 2180A RTD digital thermometer (Everett, WA) in the oil surrounding the circular quartz cuvette and controlled by a Haake F8 circulator (Karlsruhe, Germany) with a tolerance of 0.05°C. Thermal equilibrium in the cuvette was achieved within 5 min.

Absolute values for the scattered intensity (Rayleigh ratio) were obtained by normalization with respect to a toluene measurement performed before each experiment assuming a toluene Rayleigh ratio at 488 and 514 nm of 39.6 × 10⁻⁶ and 32.0 × 10⁻⁶ cm⁻¹, respectively. Raw intensity data were normalized with respect to the instrument-dependent contrast constant 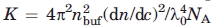, where n_buf is the refractive index of the buffer, dn/dc is the incremental refractive index, λ₀ is the wavelength, and N_A is the Avogadro constant. Volume and refraction effects were taken into account by multiplying the intensity measurements by sin θ and (n_buf/n_tol)², respectively, where θ is the scattering angle and n_tol is the refractive index of toluene. The excess Rayleigh ratio was further normalized with respect to the protein concentration, c. All relevant constants are listed in Supporting Information Table I. Autocorrelation functions g₂(τ) were analyzed by fitting to a double-exponential function assuming two independent populations: a monodisperse monomer population and a polydisperse aggregate population⁵²:

9

where β is the amplitude of the autocorrelation function, α is the relative amplitude of the two populations, D_m and D_ag are the diffusion times of the monomer and aggregate population, respectively, μ₂ is the variance about the mean, and q = 4πn_bufsin(θ/2)/λ₀ is the scattering vector. Assuming diffusion of spherical particles of radius R_h in a medium of viscosity η, the diffusion times were converted to hydrodynamic radii using the Stokes–Einstein relation D = k_BT/6πηR_h, where k_B is the Boltzmann constant and T is the temperature. The hydrodynamic radius of the Rituximab monomer was fixed at R_h,m = 5.6 nm, a value measured in a 1 mg/mL Rituximab solution at ambient temperatures. This hydrodynamic size is in accordance with the value predicted by using the Hydropro software⁵³ on the crystal structure of an intact IgG1 mAb (PDB ID 1hzh).⁵⁴

Refractive index, refractive index increment, and viscosity

For the light-scattering analysis, the refractive index, n, the refractive index increment, dn/dc, and the viscosity, η, must be measured. The refractive index of the Rituximab buffer was measured at 56.0, 60.1, and 66.2°C on an Abbe refractometer (Sun Instr. Corp., Torrance, CA) temperature controlled by a Haake F3 circulator (Karlsruhe, Germany). The refractive index increment was measured on a differential refractometer (BI-DNDC; Brookhaven Instr. Corp., Holtsville, NY). Viscosity of the Rituximab buffer was measured on an AR 1000 rheometer (TA Instr., New Castle, DE) using a 40-mm 4° Ti cone with a truncation length of 26 μm. Viscoelastic spectra were measured at 60°C with the shear stress ramped from 0.15 to 3 Pa in 3 min. The values measured are reported in Supporting Information Table I.

Atomic force microscopy

Aggregates were visualized by AFM. First, samples were diluted 1:1000 in milli-Q water, and then 10 μL sample solution was deposited on a mica surface. After 20 min at room temperature, excessive sample solution was washed off from the mica with 20 drops of milli-Q water. Without any washing, salt and Tween 80 structures easily mistaken for aggregates were observed even when visualizing the buffer alone. The samples were dried gently with a flow of nitrogen. Samples of pure buffer, 1 mg/mL Rituximab, and 1 mg/mL Rituximab aggregated for 16 h at 60°C were visualized on a MultiMode scanning probe microscope (Veeco Instr. Inc., Santa Barbara, CA), equipped with a NanoScope 3D controller and operated in tapping mode. Rigid cantilevers (RFESP; Veeco Instr. Inc.) with resonance frequencies of 81–92 kHz, a spring constant of 3 N/m, and single-crystal Si tips with a nominal radial curvature of 8 nm were used. The typical scan rate was 1.0 Hz. Using Gwyddion 2.10 data analysis software,⁵⁵ the average size of monomers and aggregates was determined by 2D autocorrelation function analysis.

Differential scanning calorimetry

The thermal stability of individual domains were measured by DSC. Measurements were performed on a 10 mg/mL Rituximab solution using a capillary VP-DSC (MicroCal LLC, Northampton, MA) with a cell volume of 0.135 mL. Temperature scans were performed from 25 to 90°C at a scan rate of 1°C/min and an excess pressure of 51 psi. A buffer–buffer reference scan was subtracted from each sample scan prior to concentration normalization. Baselines were created in Origin 7.0 (OriginLab, Northampton, MA) by cubic interpolation of the pretransition and posttransition baselines. Subsequent calculations of thermodynamic parameters were performed using the MicroCal Origin software. Values of calorimetric enthalpy, the Van't Hoff enthalpy, and the midpoint melting temperatures (T_m) were obtained using the non-two-state model in the software.

Circular dichroism

Thermal unfolding of Rituximab was studied by far and near-UV circular dichroism (CD) using a Chirascan CD spectropolarimeter (Applied Photophysics, Surrey, UK). The temperature was ramped linearly from ambient temperature to >75°C at a rate of 1°C/min and spectra acquired with a 1 nm step size, a 1-nm bandwidth, and a 1-nm/sec scan rate. Far-UV CD spectra were recorded from 205 to 260 nm on a 0.15-mg/mL Rituximab sample in a quartz cuvette with a 1-mm path length. The spectra were truncated at 211 nm, at which point the photomultiplier voltage exceeded 650 V. In a similar unfolding experiment, the unfolding was measured at 218 nm, the global minimum of the far-UV CD spectra. Near-UV CD spectra were measured from 250 to 350 nm on a 0.5-mg/mL Rituximab sample in a quartz cuvette with a path length of 10 mm. In a similar unfolding experiment, the unfolding was measured at 298 nm, the global maximum of the near-UV CD spectra. The signal from a buffer sample was subtracted from each run, and no additional filtering was applied. The CD signal is reported in residual molar ellipticity, and the temperature was recorded directly using a temperature probe placed inside the cuvette.

Sypro orange fluorescence

Sypro orange is a fluorescent probe sensitive to changes in protein hydrophobicity with excitation and emission maxima at 472 nm and 569 nm, respectively.⁵⁶ Thermal unfolding of Rituximab was explored using a high-throughput microarray method,⁵⁷ in which the fluorescence is detected by a MyiQ single-color real-time PCR detection system (Bio-Rad Labs., Hercules, CA). A 480-nm excitation filter with 40-nm bandwidth and a 540-nm emission filter with 50-nm bandwidth were used. Fifty Microliters of 0.2 mg/mL Rituximab with a 2000-fold dilution of Sypro orange (Life Tech., Carlsbad, CA) was transferred to a 96-well PCR plate and sealed with adhesive QPCR tape pads (Porvair Sciences, Leatherhead, UK). Sypro orange fluoresces in the presence of Tween 80, hence the sample was diluted in a buffer made without Tween 80. The Peltier-controlled plate holder was ramped from 25 to 90°C at 1°C/min, and the data were adjusted for the background signal.

Glossary

Abbreviations:

CD

circular dichroism

CH2

heavy chain domain 2

DLS

dynamic light scattering

DSC

differential scanning calorimetry

Fab

antigen-binding fragment

Fc

constant fragment

IgG

immunoglobulin gamma

mAb

monoclonal antibody

SEC

size-exclusion chromatography.