Amino acid interaction preferences in proteins

Abstract

Understanding the key factors that influence the interaction preferences of amino acids in the folding of proteins have remained a challenge. Here we present a knowledge-based approach for determining the effective interactions between amino acids based on amino acid type, their secondary structure, and the contact based environment that they find themselves in the native state structure as measured by their number of neighbors. We find that the optimal information is approximately encoded in a 60 × 60 matrix describing the 20 types of amino acids in three distinct secondary structures (helix, beta strand, and loop). We carry out a clustering scheme to understand the similarity between these interactions and to elucidate a nonredundant set. We demonstrate that the inferred energy parameters can be used for assessing the fit of a given sequence into a putative native state structure.

Introduction

The protein folding problem has remained unsolved because of the sheer complexity of the system. There are typically thousands of atoms in a protein molecule. In addition, the solvent molecules play a crucial role in the folding process. A simplifying approximation is to adopt a coarse-grained description of the protein within which one considers what one hopes are the essential degrees of freedom. The degrees of freedom not explicitly considered can be averaged over yielding effective interactions. The determination of these interactions is an important challenge.

In spite of the complexity of a protein, there are hints of great simplicity. Not only are protein native state structures built up of the same emergent building blocks, helices and strands assembled into almost planar sheets, but also the total number of distinct folds is only of the order of a few thousand.¹ It has been suggested that one can understand the common features of proteins based on protein structures occupying a marginally compact phase of matter.^2–4 The key idea is that a chain molecule is inherently anisotropic and that the interactions between the constituents of a chain cannot be fully characterized through pair-wise couplings alone but rather that the context of the chain constituents matter. In other words, it does not suffice to merely specify the distance between pairs of amino acids. Addition relevant information includes the sequence separation between the amino acids in contact and the relative orientations of the Frenet coordinate systems⁵ of the tangent-normal–binormal at each of the two amino acid locations.⁶

A simple and powerful method of inferring the relative strength of the pair wise interactions between amino acids is the quasi-chemical method.⁷ This method can be rationalized through information theory. The method entails taking a training set of proteins with known native state structures and counting the numbers of different types of pair wise contacts (e.g., alanine-leucine or valine-tryptophan) among all the native state structures. These numbers are then compared with a reference set, which is obtained through the assumptions of isotropy and independence in the probabilities of occurrence of individual amino acids constituting an interacting pair. If the actual number of contacts exceeds that in the reference set, the presumption is that the interaction is attractive and the strength of the interaction is measured by the degree of excess. Likewise, fewer contacts than in the reference set indicate a repulsive interaction. In the simplest scenario, the reference set is obtained by imagining that the amino acids constituting the proteins in the training set form a random admixture of amino acids, so that the reference probability of amino acid X and amino acid Y being in contact is taken to be simply proportional to the product of the fraction of amino acid X and the fraction of amino acid Y. Such a scheme is merely an approximation because neither the topology of the connectivity is taken into account nor can the treatment go beyond pair wise interactions because of poor statistics of many-body interactions. Yet, the quasi-chemical method provides a rough estimate of the interactions between pairs of amino acids in the native state structures. Recent work has considered cooperative models with four body contacts.^8,9

Here we extend the application of the quasi-chemical method to study the influence of two other key factors that influence the behavior of proteins: The propensity of specific amino acids to be in secondary structures (for simplicity, we consider just three: Helix, strand, and loop) as well as their tendency to avoid contact with water (We use as a simple surrogate the number of neighbors, defined by some convenient criterion, of an amino acid in its native state structure—Amino acids in the core of the native state structure have more neighbors in the native state than amino acids at the edge of the native state conformation; for simplicity, we consider five distinct classes of neighborhoods.). Given that there are 20 types of amino acids, we are able to derive several interaction matrices: 20 × 20 for just the amino acids, 60 × 60 for the amino acids along with secondary structure, 100 × 100 for the amino acids and their contact based propensities, and 300 × 300 for the amino acids with both their secondary structure as well as contact based propensities. We analyze these interaction matrices and we test their efficacy in sequence design by comparing the scores of randomly generated sequences with the same composition as the protein sequence within its native state structure. We also test the performance of our scoring functions on two different decoy sets. Our principal finding is that a parsimonious description of the interactions is provided by the 60 × 60 matrix, which encodes information about the secondary structure propensity of an amino acid. We carry out a hierarchical clustering of the interaction matrix and divide up the 60 entities (20 amino acids each in three secondary structures) into several groupings, which provide useful biological insights.

We briefly summarize previous work on the development of knowledge-based pair-potentials with protein native state structures as input. One of the very first attempts was made more than three decades ago¹⁰ with about 25 protein structures. Since then, numerous studies have been carried out (some of which are summarized in Table I). These studies differ principally in the way that contacts are defined between the interacting amino acids, the dataset used and the method of estimation of the scores. These different potentials have been compared with each other by Pokarowski et al.³⁰ Some of these studies have focused on the statistical distribution of the number of contacts made by different amino acids. However, protein structures are more complex and subtle differences from the averages carry more information about their structure. Specifically, it has been recognized that understanding the distribution of amino acids in different contact environments will provide valuable information.^8,9,19 A few other studies have also considered the environment, two of which are somewhat similar to the present study.^28,29 The methodology used here is different from these earlier studies as are our derived scoring matrices.

Table I.

Different Potential Energy Matrices

S. No.	Potential Matrices	Method	Comments
1	TS (Tanaka and Scheraga)10	Distance less than sum of van der waals radii	Oldest statistical potential, 25 proteins
2	RO (Robson and Osguthorpe)11	Included van der Waals, electrostatic, hydrogen bonding, and solvent-dependent interactions	25 proteins
3	MC (Maiorov and Crippen)12	Backbone–backbone contact if d(0, N) < 32 Å and d(C, N) > 3.9 Å; a backbone sidechain contact if d(N or O, CB) < 5.0 Å and no other atom between the interacting pair closer than 1.4 Å to the line segment joining them; and a sidechain–sidechain contact if d(Cβ, Cβ) < 9 Å	73 proteins
3	BL (Bryant and Lawrence)13	At various distances in 0–10 Å	161proteins
4	TD (Thomas and Dill)14	Contacts between backbone and Cβ atoms at 5–9 Å	73 proteins, based on MC
5	MS (Mirny and Shakhnovich)15	Heavy atoms in 4.5 Å	104 proteins
6	VD (Vendruscolo and Domany)16	Cα atoms in 8.5 Å, optimization based of perceptron criteria	Based on Ref.12
7	BFKV17	Heavy atoms in 4.5 Å	1169 proteins
8	MJ (Miyazawa and Jernigan)7	Cα atoms in 6.5 Å	42 proteins
9	MJ (Miyazawa and Jernigan)18	Modified with new dataset	1198 proteins
10	MJ (Miyazawa and Jernigan)19	Approximation of equilibrium mixtures of residues with Bethe approximation
11	DT (Krishnamoorthy and Tropsha)9	Four body statistical potential	Two datasets (1563 and 1167 chains)
12	Feng et al.8	Four body contact potential from reduced amino acids alphabet	Two datasets (774 and 513 chains)
13	BT (Betancourt and Thirumalai)20		Rescaled MJ matrix
14	HL (Hinds and Levitt)21	Atom–atom contact in 4.5 Å	246 proteins
15	GKS (Godzik et al.)22	Atom–atom contact in 4.5 Å	381 proteins
16	TE (Tobi et al.)23	Matrices for different distance cut-offs (2–9)	572 proteins
17	MSBM (Micheletti et al.)24	Cα atoms in 6.5 Å, Optimization based
18	OPUS-Ca (Wu et al.)25	Distance dependent pairwise energy with orientational preference
19	Baker and coworkers26,27	Used in Rosetta
20	Bolser et al.28	Distance between Cα and Cβ atoms at different cutoff	Matrix based on degree
21	Zhang and Kim29	Centroids of amino acids in 6.5 Å	Secondary structure based energy matrix

The propensity of amino acids in different environments in the protein is related to the concept of hydrophobicity, which was introduced by Kauzmann³¹ and Tanford.^32,33 At the basic level, it is a measure of the free energy of partition of amino acids in aqueous and nonpolar solvent.¹⁰ The scale has been modified by large number of people³⁴ and the details of their findings have been reviewed in several articles.^35,36 According to the recent literature, at least 56 hydrophobicity scales are available.³⁷ Most commonly, the amino acid hydrophobicity scales are derived based on the propensity of amino acids to be buried in the protein environment or exposed to the aqueous medium. The solvent accessible area and number of contacts made by amino acids in proteins are used to measure the protein environment.^38–42 Hydrophobicity scales are derived based on the average value obtained for a given amino acid. However, a key difficulty arises because proteins do not provide a uniform environment as in the case of liquids, and hence, an accurate estimation of the free energy of partitioning cannot be made. Here we revisit hydrophobicity in a simplified manner based on the amino acid propensity preferences in different environments. As stated before, we have also considered secondary structure propensity of the amino acids making contacts and find that the performance of the resulting 60 × 60 matrix is comparable with the 100 × 100 contact based scoring matrix in capturing the effective interactions.

Results

Analysis based on C_α—C_α based contacts

Contact based environment

The amino acids in the protein structure are divided into different groups depending on the number of connections (degree) they make. (The results are presented for C_α—C_α connections, unless otherwise specified.). Note that the coarse-grained representation used here is an approximation which yields an effective scoring matrix for the degrees of freedom considered here, that is, the C_α atoms of the amino acids. The degree varies from 1 to 11. However, the interactions between residues of very high and very low degree are rare. As discussed in the Methods section, we have five categories of environments based on the degree. The environments with lower degree are exposed and the environments with higher degrees are buried.

Distribution of amino acids in different contact based environments

The plots of the distribution of amino acid contacts in different environments (five figures for five different environments) are shown in Supporting Information Figure S1. The distribution of contacts in different environments is different. For example, amino acids in environment I have roughly the same propensity for making contacts with all amino acids from different environments, whereas buried amino acids tend to have contacts principally with other buried amino acids. Surprisingly, the pattern is independent from the size and type of amino acids. The total number of contacts is more for more buried amino acids.

Scoring matrix

The amino acids have been divided into five different environments, and hence, the size of the contact matrix is 100 × 100. It is a symmetric matrix so the total number of unique elements is 5050. Thus, each element of the matrix gives the number of contacts made by a specific amino acid in a particular environment, with another specific amino acid in one of the five environments. These numbers are converted into scores following the procedure outlined in the Methods section. The scores range from −2.737 to +2.333. The scoring matrix is given in the Supporting Information Table T1. The values are also presented in pictorial form in Figure 1. The matrix elements are ordered in such a way that first 5 entries are for L (leucine) (i.e., L1, L2, L3, L4, and L5), the next five entries are for F, and so on. For example, the matrix element M (12, 24) gives the score between amino acid I (ile) in environment 2 making contact with amino acid V (val) in environment 4. The color code ranges from blue to red, with the blue and red representing the most negative (attractive) and the most positive (repulsive) values, respectively. Surprisingly, an amino acid in one environment has approximately the same color (with some exceptions) for its score with all amino acids in different environment. For example, boxes in the row for L in environment 5 are mostly cyan in color. The boxes representing the scores for Cys–Cys from different environments are all in blue, that is, these pairs are energetically most favorable, irrespective of the environment. The least stable pairs are in dark red colors, for example, C (cys) in environment I with Y (tyr) in environment III. The main points to notice are: (1) The same amino acid, pairing with other amino acids, shows different environment dependent scores; (2) the hydrophobic amino acids show more positive values in environments with low degree and more negative values in environments with high degree, and the trend is reversed for polar and charged amino acids; (3) although the scores of amino acids in one environment are approximately the same for the interactions with all amino acids in different environments, there are variations in the values, justifying the need for a 100 × 100 scoring matrix.

Figure 1.

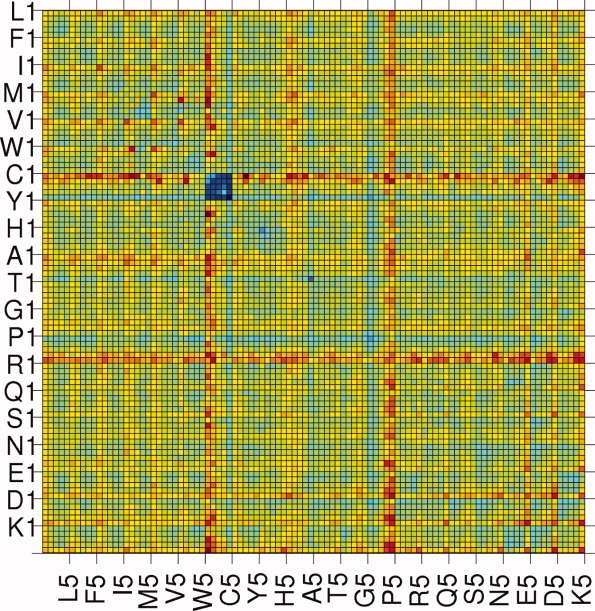
A pictorial representation of the environment based scoring matrix. The blue color is for the most negative score (the most attractive) and the red is for the highest positive value (the most repulsive). The range of scores (−2.737 to +2.333) has been divided into 10 equal intervals and are represented by different colors decreasing from blue to red. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Secondary structure based environment

The secondary structures of all the amino acids in the protein dataset have been identified (described in Methods) and divided into three different groups.

Distribution of amino acids in different secondary structural environments

The contacts between amino acids from different secondary structures are shown in Figure 2. Generically, the amino acids in one secondary structure prefer to make contacts with the same type of secondary structure in proteins. The probability of contact of amino acids from the same type of secondary structures is higher in the case of helix and sheet, whereas for residues in the loop structure, the interacting residues are distributed in all types of secondary structures. Amino acids L, A, E, V, I, R, and K make more contacts within helices and V, L, I, A, T, and F dominate in beta-sheets. G, P A, S, and D amino acids favor contacts within loop.

Figure 2.

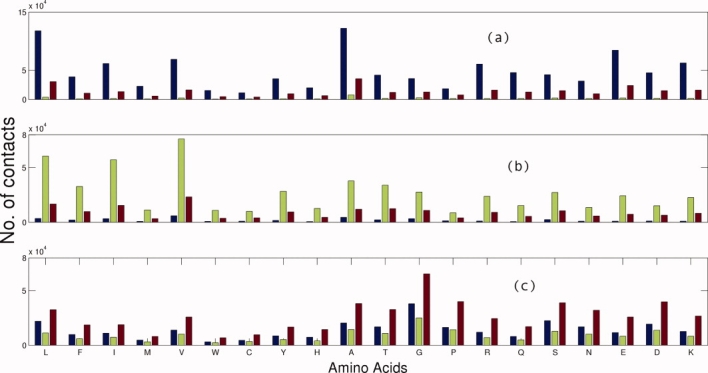
Distribution of the number of contacts between one amino acid and other amino acids in their respective secondary structural environment. Three bars are shown for each amino acid, representing the interaction of other amino acids in helix, beta sheet, and loop environments. (a), (b), and (c) are the plots corresponding to the selected residues in helix, beta-sheet, and loop environment, respectively. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Scoring matrix

The scoring matrix of size 60 × 60 is based on three secondary structure groups of 20 amino acids. The matrix has 1830 unique elements due to symmetry. The scoring matrix is given in Supporting Information Table T2 and the values are presented in a pictorial form in Supporting Information Figure S2. The scores are in the range of −2.978 to +2.538. The order of amino acids along the matrix in the table and in the figure is the same as in the case of the contact based environment. The matrix element M (22, 33), for example, is the score between the pair of Y (tyr) in helix with T (thr) in loop. Here also the blue and the red colors indicate the most negative (attractive) and the most positive (repulsive) scores. Again, the Cys–Cys pairs are the most favorable ones irrespective of the secondary structure. The least favorable pairs are prolines in helices, prolines in sheets, Glu (E) in sheet contacting with His (H), or Phe (F) in helix. The scores indicate a preference for the hydrophobic residues to be in a helix or sheet environment compared with their presence in the loop environment. The polar–polar interactions are by and large less favorable in most environments. The helix–helix and sheet–sheet contacts are more favorable than the other type of interactions. A similar result has also been observed by Zhang and Kim.²⁹

Contact based hydrophobicity

We have shown that the tendency for amino acids to make contact with other amino acids depends sensitively on their preferred environment. Some of the amino acids (L, F, I, M, V, W, C, Y, and A) make more contacts with degrees 5–8, whereas others make preferential contacts in a lower environment. This tendency has been observed in C_α—C_α based contacts as well as for all atom–atom based contacts. This is related to the hydrophobicity of amino acids. However, our results show that this tendency is dependent on the environment and it leads to variations in the hydrophobicity values as a function of contact based environment. Thus, a set of hydrophobicity values can be given for each environment rather than as an average value and we call this contact based environmental hydrophobicity. We calculate the modification factor (F_A−x) from the distribution of amino acid contacts in different environments as follows:

(1)

where n_A−x = number of amino acid A in environment x, n_A = total number of amino acid A, n_x = total number of amino acids in environment x, and N = total number of contacts.

A plot of F_A−x value for each of the 20 amino acid in five environments is presented in Figure 3. The base line (with value of zero) in the figure represents the average (from all the environments) distribution of contacts for a given amino acid. The negative and the positive values represent the decrease and the increase of the contact from the average value in a given contact based environment.

Figure 3.

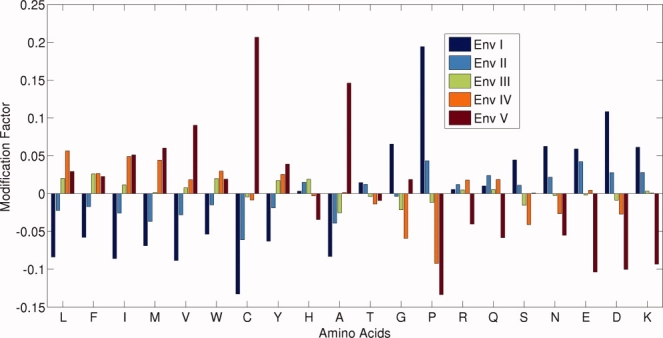
A plot of the modification factor F_A−x (on Y-axis) of 20 amino acids in five different environments. The values are relative to the average and so a more negative value indicates that it is less favored than the other environments and vice versa. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

As expected, the factor F_A−x is positive in environments of higher degrees and negative in lower degrees for hydrophobic amino acids, and the reverse trend is seen for polar and charged amino acids. However, it is worth noting that the variations are not uniform for different amino acids. For instance, the hydrophobic amino acid valine shows the highest positive value (+0.0902) and tryptophan shows a lower value (+0.0191) in environment V. Similarly, in the case of charged and polar amino acids, glutamic acid shows the highest (−0.1037) and arginine has the lowest (−0.0402) negative value. Also, the residues like threonine, glycine, and proline follow their own patterns. Thus, the modification factor F_A−x, (for amino acid A and environment x) reflects the contact propensity variations and it can be used to obtain the hydrophobicity value of amino acids in different environments, which can be defined as:

(2)

where H_A−x = modified hydophobicity for amino acid A in environment x, F_A−x = modification factor for amino acid A in environment x, and h_A = hydrophobicity value for amino acid A from any known hydrophobicity scale.

As an illustration, we have used the hydrophobicity scale given by Tanford and later modified by Jones⁴³ and the values are given in Table II.

Table II.

Environment Dependent Hydrophobicity for All Amino Acids

		Environment Dependent Hydrophobicity*
S. No.	AA	I	II	III	IV	V	Hydrophobicity (h)
1	L	2.080	2.220	2.316	2.398	2.337	2.27
2	F	2.799	2.919	3.048	3.049	3.037	2.97
3	I	2.971	3.166	3.287	3.409	3.416	3.25
4	M	1.468	1.705	1.773	1.848	1.876	1.77
5	V	1.796	1.915	1.985	2.006	2.148	1.97
6	W	3.662	3.812	3.946	3.985	3.943	3.87
7	C	1.405	1.521	1.613	1.606	1.955	1.62
8	Y	2.596	2.718	2.818	2.840	2.878	2.77
9	H	0.973	0.985	0.988	0.967	0.937	0.97
10	A	0.890	0.932	0.946	0.971	1.112	0.97
11	T	0.173	0.172	0.169	0.167	0.168	0.17
12	G	0.213	0.199	0.200	0.188	0.204	0.20
13	P	3.427	2.994	2.836	2.605	2.487	2.87
14	R	0.955	0.961	0.955	0.967	0.912	0.95
15	Q	0.101	0.102	0.101	0.102	0.094	0.10
16	S	0.178	0.172	0.167	0.163	0.170	0.17
17	N	0.202	0.194	0.190	0.185	0.180	0.19
18	E	1.715	1.688	1.617	1.627	1.452	1.62
19	D	0.842	0.781	0.753	0.739	0.684	0.76
20	K	1.847	1.788	1.746	1.741	1.578	1.74

^*Bold numbers are highest and italic bold numbers are lowest among different environments for an amino acid.

The hydrophobicity values presented in this table are centered on the input value and are different in different environments. Furthermore, the values for hydrophobic residues are least in the lower environment and maximum in the environments IV or V. A reverse trend is seen for the polar and charged amino acids. However, in the case of histidine and arginine, the highest value is not in the lowest environment. Because of this sensitivity to the environment, we have referred to this as contact based environmental hydrophobicity.

Environment based solvent accessible surface area

The degree of the amino acid is inversely correlated to the solvent accessible surface area (ASA), because the lower contact residues are exposed to the solvent and the higher contact residues are buried in the interior of the protein. Several hydrophobicity scales are derived on the basis of ASA and recently more than 50 scales³⁷ have been compared with the ASA derived hydrophobicity. Here again, we would like to point out that the hydrophobicity derived from average ASA is only approximate and perhaps this is the reason that there was no good correlation (highest correlation coefficient was 0.40) between the ASA derived and other hydrophobicity scales.³⁷ We suggest that as in the case of contact environments, the ASA of each amino acid be divided into different classes (as given in Table III) and that the propensity of amino acids in different ASA ranges be evaluated.

Table III.

Solvent Accessible Surface Area (ASA) Based Classification of Amino Acids in Proteins

Environment	ASA Range (Å2)	Type of Amino Acids	No. of Amino Acids
I	>50.0	Completely Exposed	144,979
II	>30.0 ≤ 50.0	Exposed	111,384
III	>14.0 ≤ 30.0	Intermediate	106,594
IV	>2.5 ≤ 14.0	Partially Buried	125,173
V	≤2.5	Totally Buried	143,763

The hydrophobicity modification factor, which was evaluated using Eq. (4), is used in this case also and the results are presented in Figure 4. Qualitatively, we see the same features as was observed in the contact based environment. Interestingly, the correlation coefficient between the modification factor from ASA and degree based analysis is 0.8. Thus, the contact based environment dependent hydrophobicity is a reasonable measure of the amino acid properties in proteins.

Figure 4.

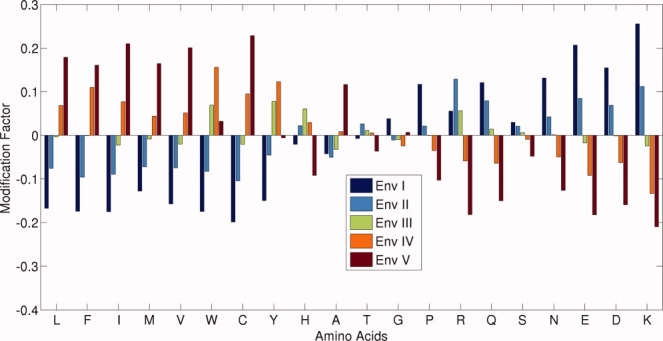
Modification factor (on Y-axis) for all 20 amino acids in five ASA based environments. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Evaluation of scoring matrices

Comparison with random sequences

We have considered 10 proteins [ribonuclease A (7RSA), hydrolase (1OD3), Bacillus subtilis LuxS (1J98), T4-lysozyme (1LYD), Bacillus stearothermophilus adenylate kinase (1ZIP), triosephosphate isomerase (5TIM), tryptophanyl-trna synthetase (1I6M), exchange factor (1R8M), mesophile reductase (1LVL), and theromophile reductase (1EBD)] with different native state structures and sizes from the Protein Data Bank⁴⁴ to test our four scoring matrices and to compare with the frequently used 20 × 20 scoring matrix (MJ).¹⁸ A set of 10,000 random sequences with the same amino acid composition as that of the native sequence was generated for all 10 proteins and the scores were calculated for all these sequences by using MJ and our scoring matrices. The summary of the scores of native and random sequences is presented in Table IV.

Table IV.

Scores of Native and Energetically Best Random Sequence for Ten Different Proteins Calculated From Five Different Scoring Matrices

S. No.	PDB (No. of Residues)	MJ Native (Best of Random)	20 × 20a Native (Best of Random)	60 × 60b Native (Best of Random)	100 × 100c Native (Best of Random)	300 × 300d Native (Best of Random)
1	7RSA (124)	−816.02 (−798.75)	−15.60 (−14.90)	−61.38 (−33.98)	−35.74 (−29.30)	−58.32 (−14.17)
2	1OD3 (131)	−1010.73 (−1027.94)	−9.37 (−10.14)	−67.11 (−65.71)	−26.32 (−30.88)	−58.97 (−54.19)
3	1J98 (153)	−1187.00 (−1227.20)	−2.91 (−5.30)	−25.05 (−43.52)	−26.66 (−26.08)	−65.98 (−11.30)
4	1LYD (164)	−1331.50 (−1376.75)	−6.56 (−10.95)	−49.73 (−35.85)	−32.13 (−40.48)	−56.04 (−35.85)
5	1R8M (195)	−1606.68 (−1661.40)	1.82 (0.26)	−24.80 (−20.19)	−56.84 (−42.28)	−72.58 (−25.98)
6	1ZIP (217)	−1824.61 (−1835.77)	−7.99 (−8.12)	−117.49 (−36.04)	−62.39 (−38.45)	−152.35 (−8.98)
7	5TIM (249)	−2017.69 (−1991.50)	−32.43 (−25.46)	−120.02 (−44.26)	−90.90 (−51.32)	−139.20 (+8.28)
8	1I6M (326)	−2752.46 (−2771.34)	−13.22 (−5.89)	−74.90 (−22.29)	−96.17 (−34.39)	−113.20 (+27.30)
9	1LVL (458)	−3838.06 (−3826.37)	−55.40 (−42.77)	−197.68 (−23.49)	−114.11 (−57.18)	−214.59 (+62.18)
10	1EBD (951)	−7945.87 (−7797.99)	−104.44 (−46.70)	−383.91 (+62.50)	−304.19 (−32.54)	−491.93 (+327.85)

^aScore calculated from 20 × 20 scoring matrix.

^bScore calculated by using secondary structure based scoring matrix.

^cScore obtained from environment based scoring matrix.

^dScore calculated by using scoring matrix which uses the information about the secondary structure and environment of the contacting amino acids.

The best score among the random sequences, which is better than the score of the native sequence, is indicated in italics. There are 6, 5, 2, and 1 cases (out of 10) with the MJ matrix, our 20 × 20 matrix, the environment dependent 100 × 100 matrix, and the secondary structure dependent 60 × 60 matrix, respectively, in which the best score among the random sequences is better than that of the native sequence. Interestingly, the score of the native sequences is better than the random sequences in all the 10 proteins with the 300 × 300 scoring matrix. Thus, the 60 × 60 scoring matrix turns out to be the most parsimonious and effective description of the scoring matrix.

The analysis of these scoring matrices in terms of z-score has been presented in Table V. The z-score has been defined as:

Table V.

Z-Score from 5 Different Scoring Matrices for Selected Proteins

S. No.	PDB	MJ	20 × 20	60 × 60	100 × 100	300 × 300
1	7RSA	2.17	1.84	2.54	1.92	2.34
2	1OD3	3.54	3.79	3.82	3.08	3.73
3	1J98	3.43	3.08	3.44	3.35	5.10
4	1LYD	0.88	1.16	2.10	1.53	2.06
5	1R8M	2.28	3.43	3.10	4.89	4.98
6	1ZIP	1.56	1.65	3.15	2.18	3.21
7	5TIM	2.10	2.47	3.09	2.50	3.46
8	1I6m	1.52	2.41	2.62	2.65	3.17
9	1LVL	3.97	5.99	8.05	5.18	8.39
10	1EBD	6.32	10.57	11.60	9.09	13.07

(3)

where E_n = score of native protein sequence, μ_rand = mean of the scores of random sequences, and σ_rand = standard deviation of the scores of random sequences.

The secondary structure based scoring matrix yields a higher z-score than the MJ, 20 × 20 and 100 × 100 and a roughly comparable performance with the 300 × 300 scoring matrix.

Comparison with decoy structures

In principle, one would like to choose a potential function, which unambiguously identifies the native state structure as the lowest energy state among all the decoys. Note that our analysis, like many other studies, is entirely based on just the sequences and the native state structures of the proteins in the learning set. Unlike other more complicated methods, several studies, including our own, do not consider an exploration of structure space as determining the scoring function. The performance of these scoring functions in structure space is thus a more stringent test, which folds in the quality and the realism of the decoy structures. In addition to exploring the rank of the native state structure within the decoy set, one can also use the so-called Z-score for an evaluation of the scoring function. The Z-score, as defined in Eq. (3), is a measure of how much lower in energy the sequence is in the native state structure compared with the mean energy in the decoy structures measured in units of the standard deviation of the energies in the decoy structures. This parameter can be related to the funnel-like characteristics of the free energy landscape⁴⁵—The higher the Z-score, the better the folding. Here we have performed preliminary testing of our scoring functions on two sets of decoys,^46,47 with 12 proteins taken from each set (see Table VI). Our scoring functions do moderately well in predicting the native state structure as being in the top 50% among the decoys in some cases, within the top 10% in others, and as the very best in a few cases. The Z-scores show a similar quality trend. Our analysis reiterates the point^48,49 that the performance in such tests is not only a function of the scoring function but also depends substantially on the decoy set, for instance the method of decoy generation, the quality and fidelity of the decoys, as well as the length of the protein.

Table VI.

Z-Score^a for the Decoy Sets

S. No.	PDB	Sequence length	60 × 60	100 × 100	300 × 300
(a) Decoy setsb from Andrej Sali
1	1onc	101	1.54	1.19	1.12
2	1cew	108	1.76	1.47	1.91
3	1cid	109	2.05	2.82	0.94
4	1c2r	115	2.38	1.80	1.96
5	1bbh	127	1.15	0.62	0.72
6	1mdc	130	1.25	1.39	1.01
7	1dxt	143	−0.30	2.12	1.74
8	1cau	178	1.92	1.27	1.90
9	1gky	186	2.40	2.71	2.44
10	1eaf	201	1.86	1.89	1.98
11	1lga	279	1.06	2.44	1.07
12	2afn	289	1.23	3.08	1.65
	Average		1.53	1.90	1.54
(b) Decoy setsc from Rosetta
1	1ksr	100	2.98	1.15	2.53
2	1kte	100	3.93	−0.33	2.05
3	1ag2	103	−0.26	1.80	1.42
4	1aa2	105	2.10	0.27	2.32
5	1erv	105	3.35	1.36	2.45
6	1lis	111	−0.19	2.01	2.36
7	1pd0	121	3.90	1.53	3.24
8	4fgf	121	0.14	3.09	1.07
9	1acf	123	1.24	3.39	1.49
10	1hlb	138	1.10	1.30	1.42
11	1mbd	147	0.10	2.95	3.01
12	2gdm	149	0.35	2.06	2.37
	Average		1.56	1.72	2.14

^aHere the values in bold indicate that the native state structure is the best, bold and italics means that the native state structure is among the top 10% of decoy structures, whereas italic refer to those which have a z-score less than 1.

^bEach set has 1000 model structures.

^cEach set has 300 model structures.

Clustering of 60 flavors

The 60 different flavors of 20 amino acids in three different secondary structural types have been grouped into 16 clusters, which exhibit biologically sensible characteristics (shown in Table VII). In general, the clusters typically comprise amino acids from the same secondary structural environment (with a few exceptions). For example, F, Y, R, K, I, and V in a helical environment form a cluster. It is interesting to note that the grouping of residues is clearly based on their secondary structural environment. It emphasizes the fact that the behavior of a given amino acid is dictated by its presence in a given secondary structural environment. It also indicates that the ‘‘distance’’ between amino acids from different secondary structures is greater than the ‘‘distance’’ between amino acids in same secondary structural environment.

Table VII.

Groups of Amino Acids in Different Secondary Structures

S. No.	Groups	Remarks
1	[Lh Qh Mh Eh Wh]	Bigger amino acids in helices
2	[Hh Th Nh Sh Dh]	Polar/charged and smaller residues in helices
3	[Fh Yh Rh Kh Ih Vh]	Aromatic, positively charge, and bigger residues in helices
4	[Gh Ph]	Helix breaker
5	[Rs Qs Ks]	Contains positively charged residues in sheets
6	[Es Ds]	Negatively charged residues in sheets
7	[Ls Ms Hs]
8	[As Gs]	Small residues in sheets
9	[Fs Ys Is Ws Pl]	Contains aromatic residues in sheets (with exception of proline in loops)
10	[Hl Tl Sl Nl Dl Ts]	Contains polar/charges residues in loops
11	[Fl Yl Al Wl Rl Ql Kl Ml Ss]	Contains aromatic and positively charges residues in loops
12	[Ll Il Vl El Ns]	Contains hydrophobic residues in loops
13	[Vs Gl Ah Cs]
14	[Cl]
15	[Ch]
16	[Ps]

Discussion

The interaction preferences of amino acids in folded proteins have been investigated for several decades using knowledge based approaches. As the number of accurately known structures has increased, so also has the quality of the measurement of the propensity of amino acids to make contacts with each other. There are distinct regions of the protein native state structure such as the type of secondary structure or whether the amino acid is in the hydrophobic core or in the periphery of the native state structure. One would expect that the environments of the amino acids making contact ought to matter. Our main result is the incorporation of such environmental factors into the scoring matrix for amino acid interactions using the simple, albeit approximate, quasi-chemical approach.

The basic input for our calculations is knowledge of the amino acid composition of all the proteins in the training set (in order to define a reference system based on invoking random contacts between amino acids taking into account their concentration) along with a count of the actual numbers of distinct types of contacts (in order to compare with the numbers in the reference system). The amino acid composition is determined straightforwardly and objectively. The actual numbers of contacts, however, depend on one's definition of when a contact is made. Here we consider two distinct definitions of a contact, one based on the distance between alpha-carbon atoms and the second based on checking whether there is at least a single pair of atoms, one from each amino acid, within a certain threshold distance. The results described in the main text rely on the first method and a detailed comparison of the results obtained using the two definitions of contacts is presented as Supporting Information. The number of amino acids with a high coordination number is larger in the atom–atom contact definition than for the C_α—C_α based contacts and the distribution of contacts are quite different in the two cases. Yet, there are qualitative similarities in the scoring matrix for the two cases.

Generically, we replace the 20 distinct amino acids by a larger number of flavors: 60 corresponding to the 20 amino acids in three distinct secondary structures, 100 corresponding to the 20 amino acids in five distinct contact based environments, and 300 corresponding to 20 amino acids in three secondary structures and five contact based environments. The issue is whether the cost of introducing more flavors (and more scores) is offset by a gain of a refinement in the determination of the propensities of the flavors to be in contact with each other. Another question is the relative importance of the secondary structures or the contact based environment in encoding a useful score. We find that a 20 × 20 scoring matrix may not be detailed enough to effectively capture the complete picture of amino acid placement within the native state structure. Using a test based on the scores of randomly shuffled sequences of ten proteins, the 60 flavor scheme of the amino acids in three distinct secondary structures is found to be the most effective and parsimonious description for modeling and structure prediction.

We have revisited the definition of hydrophobicity based on our analysis of the contact based environment (the 100 flavors case). Conventionally, the scale is defined based on an amino acid preference to be buried in the interior of the protein or exposed to the solvent. Here we find that this preference, for any given amino acid, is a sensitive function of the contact environment it is in. We argue that it is more meaningful to define an environment dependent hydrophobicity scale. It is well-known that the ASA of an amino acid can also be associated with the concept of hydrophobicity. However, there is a poor correlation between ASA and the hydrophobicity evaluation from different methods.³⁷ Interestingly, we find that the ASA evaluated as a function of the contact environment correlates well with the contact based hydrophobicity values. Thus, a contact based definition of hydrophobicity may prove to be useful in the design of better sequences for a given structure,⁵⁰ in the selection of ligands for docking, and for other modeling studies.

As more and more sequences of proteins are being determined, there is a drive to predict the structure of these sequences using homology modeling, threading, and ab initio structure prediction methods. All of these methods rely on accurate scoring functions. Although the scoring functions developed here may be directly useful in certain situations when the parameterization used here is used, more generally, the lessons learned from our studies ought to be useful for deducing increasingly accurate scoring functions. Progress along these lines would have applications in structure prediction and sequence design.

Methods

Dataset

We have curated the dataset of 1654 proteins from the PISCES server⁵¹ and obtained structural information from the PDB⁴⁴ with the following constraints:

1. Only globular proteins.

2. minimum sequence length is 80.

3. Sequence identity is less than 15%.

4. X-ray structures with resolution better than 1.8 Å.

5. R factor better than 0.3.

The data set has been further manually analyzed to remove membrane related proteins and proteins with several model structures and multiple occupancies.

Connectivity matrix

We have considered two different measures of connectivity:

Based on C_α—C_α distance

Adjacency matrices have been generated for each protein based on the distance cut-off of 6.5 Å between C_α—C_α atoms of amino acids with the exclusion of nearest neighbors along the sequence. The adjacency matrix is:

Atom–atom contact between two residues

Here residues i and j are considered to be in contact if any atom (hydrogen atoms have not been included) of the residue i is within a distance of 4.5 Å⁵² with any atom of the residue j. Nearest neighbors (i ± 2) along the sequence are not considered. The elements of this matrix are:

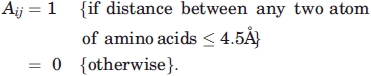Amino acid composition

The sequences of all the proteins in the dataset were extracted and the amino acid composition of the entire dataset is given in Table VIII.

Table VIII.

Amino Acid Composition

		Composition
S. No.	AA	In Number	(%)
1	L	58,290	(9.27)
2	F	25,214	(4.00)
3	I	36,132	(5.75)
4	M	11,260	(1.78)
5	V	45,703	(7.26)
6	W	9280	(1.47)
7	C	8224	(1.31)
8	Y	22,236	(3.53)
9	H	14,854	(2.34)
10	A	53,204	(8.43)
11	T	34,323	(5.43)
12	G	47,105	(7.45)
13	P	29,246	(4.57)
14	R	32,583	(5.16)
15	Q	23,739	(3.76)
16	S	36,842	(5.81)
17	N	27,019	(4.28)
18	E	43,366	(6.84)
19	D	37,157	(5.86)
20	K	36,119	(5.70)

Degree (number of connections)

We have calculated the number of contacts made by each amino acid in all the proteins and define it as the degree of the given amino acid. The maximum degree obtained in the whole dataset is 21 and 34 for (C_α—C_α) and all atom–atom contacts, respectively. Based on the degree, we have categorized the contact based environment into five classes:

• Environment I = Degree (1 + 2 + 3),

• Environment II = Degree 4,

• Environment III = Degree 5,

• Environment IV = Degree 6, and

• Environment V = Degree 7 and higher.

Such a classification is necessary because the number of contacts in certain degree-pairs (e.g., degree 1–degree 11 pair) is negligibly small. This categorization also helps reduce the size of the scoring matrix between amino acids from different environments to 100 × 100.

Secondary structure determination

The program DSSP⁵³ has been used to identify the secondary structure of each residue in the proteins of the dataset.

Seven classes of secondary structures given in DSSP have been merged into three basic types (helix, sheet, and loops) as:

1. Helix (H)–H, G, and I,

2. sheet (S)–E,

3. loop (L)–B, T, and S.

The amino acid distribution in these three different secondary structures is shown in Table IX.

Table Table IX.

Amino Acid Distribution in Different Secondary Structures

S. No.	AA	Helix	Sheet	Loop
1	L	27,034	14,710	16,546
2	F	8779	8077	8358
3	I	13,043	13,850	9239
4	M	4804	2643	3813
5	V	14,552	19,064	12,087
6	W	3651	2690	2939
7	C	2449	2346	3429
8	Y	7970	6976	7290
9	H	4924	3350	6580
10	A	27,054	9098	17,052
11	T	9718	9144	15,461
12	G	8099	7243	31,763
13	P	5801	2745	20,700
14	R	14,096	6544	11,943
15	Q	11,178	4154	8407
16	S	10,653	7335	18,854
17	N	7737	3791	15,491
18	E	22,080	6674	14,612
19	D	12,338	4318	20,501
20	K	15,259	6505	14,355

Solvent accessible surface area

The solvent ASA of each amino acid in the dataset was computed by using the program NACCESS,⁵⁴ which is an implementation of the Lee and Richards algorithm.⁵⁵ The absolute (ABS) value of ASA for all atoms has been chosen for the contact based environment based analysis in our study.

Contact based scoring matrices

A total of eight different scoring matrices have been generated, four are based on (C_α—C_α) contacts and the other four are the corresponding ones based on all atom–atom contacts. Operationally, we add the 1654 adjacency matrices from the dataset to get a single symmetric matrix giving information about the number of contacts between amino acids in a given category (secondary structure or contact based environment or both). We will denote an amino acid in a specific state generically as a flavor. Thus, we deal with 20 flavors or 60 flavors or 100 flavors or 300 flavors depending on whether we are dealing with the 20 amino acids, the amino acids in a specific secondary structure, the amino acid in a specific contact based environment or an amino acid in a specific secondary structure, and contact based environment.

Scoring matrix of size 20 × 20

The interaction score between amino acid pairs has been calculated as follows:

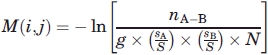(4)

where n_A−B = number of contacts between amino acid A and amino acid B, N = total number of contacts in dataset, 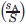= fraction of amino acid A in dataset, 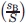= fraction of amino acid B in dataset, g = 1 when the amino acids in contact are the same, and g = 2 otherwise.

The combinatorial factor of g is introduced because when the amino acids in contact are the same, there is exactly one way of picking the pair, whereas when the amino acids are different, there are two distinct ways in which they could arise, for example, (alanine and leucine) and (leucine and alanine). Similar g factors are introduced in the calculations of the scoring matrices later.

Scoring matrix of size 60 × 60

A 60 × 60 scoring matrix has been generated for the 60 flavors case by using the secondary structural information (obtained from DSSP) of all the 20 amino acids. The matrix elements are a measure of the interaction between the 60 flavors. For example, the matrix element M (5, 10) yields the score for the contact between amino acid F (phe) in sheet and amino acid M (met) in helix. The score matrix element is:

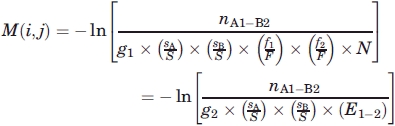(5)

where n_A1−B2 = number of contacts between amino acid A in secondary structure 1 and amino acid B in secondary structure 2, 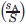= fraction of amino acid A in dataset, 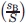= fraction of amino acid B in dataset, 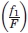= fraction of amino acids in secondary structure 1 in dataset, 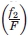= fraction of amino acids in secondary structure 2 in dataset, 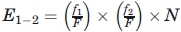= number of contacts between secondary structure 1 and secondary structure 2, S = F = total number of amino acid in dataset, and g₁ = 1 for all diagonal elements and g₁ = 2, otherwise g₂ = 2 when the contacting pair are comprised of different amino acids in the same environment and g₂ =1 otherwise.

Scoring matrix of size 100 × 100

A 100 × 100 connectivity matrix was created by considering each of the 20 amino acids in five different contact based environments leading to 100 flavors.

The matrix element:

m(i, j) = number of contacts between amino acid A in environment x and amino acid B in environment y.

The interactions score between amino acid A in environment x with amino acid B in environment y is:

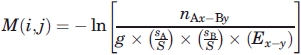(6)

where n_Ax−By = number of contacts between amino acid A in environment x and amino acid B in environment y, 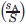= fraction of amino acid A in dataset, 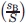= fraction of amino acid B in dataset, E_x−y = number of contacts between environments x and y, S = total number of amino acid in dataset, and g = 2 when the contacting pair are comprised of different amino acids in the same environment and g =1 otherwise.

Scoring matrix of size 300 × 300

This is the 300 flavors case corresponding to an amino acid in a specific secondary structure and in a specific contact based environment. The matrix element:

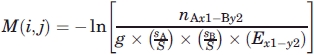(7)

where n_Ax1−By2 = number of contacts between amino acid A in secondary structure 1 in environment x and amino acid B in secondary structure 2 in environment y, 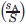= fraction of amino acid A in dataset, 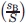= fraction of amino acid B in dataset, E_x1−y2 = number of contacts between secondary structure 1 in environment x and secondary structure 2 in environment y, S = total number of amino acid in dataset, and g = 2 when the contacting pair are comprised of different amino acids from same environments and g = 1 otherwise.

The calculations are done for two different ways of measuring contacts and so we have eight distinct scoring matrices based on noncovalent contacts between amino acids.

Grouping of amino acids in different secondary structures

The amino acids in different secondary structure were grouped by using PHYLIP software with the (C_α—C_α) contact based 60 × 60 scoring matrix as the starting input. The distance matrix of 60 flavors was constructed using the following formula:

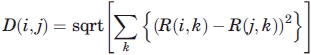(8)

where 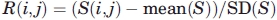, and mean (S) and SD(S) are the mean and the standard deviation of the upper triangular elements of the symmetric scoring matrix S.

The unweighted pair group method with arithmetic mean (UPGMA)⁵⁶ technique was applied to the distance matrix to study the clustering properties of 60 flavors.