Plasma Membrane Permeabilization by Trains of Ultrashort Electric Pulses

Abstract

Ultrashort electric pulses (USEP) cause long-lasting increase of cell membrane electrical conductance, and that a single USEP increased cell membrane electrical conductance proportionally to the absorbed dose (AD) with a threshold of about 10 mJ/g. The present study extends quantification of the membrane permeabilization effect to multiple USEP and employed a more accurate protocol that identified USEP effect as the difference between post- and pre-exposure conductance values (Δg) in individual cells. We showed that Δg can be increased by either increasing the number of pulses at a constant E-field, or by increasing the E-field at a constant number of pulses. For 60-ns pulses, an E-field threshold of 6 kV/cm for a single pulse was lowered to less than 1.7 kV/cm by applying 100-pulse or longer trains. However, the reduction of the E-field threshold was only achieved at the expense of a higher AD compared to a single pulse exposure. Furthermore, the effect of multiple pulses was not fully determined by AD, suggesting that cells permeabilized by the first pulse(s) in the train become less vulnerable to subsequent pulses. This explanation was corroborated by a model that treated multiple-pulse exposures as a series of single-pulse exposures and assumed an exponential decline of cell susceptibility to USEP as Δg increased after each pulse during the course of the train.

INTRODUCTION

Exposure to ultrashort electric pulses (USEP) has been shown to affect mammalian cells causing nuclear granulation, calcium release, permeabilization of vacuoles, nuclear DNA damage, and necrotic and apoptotic cell death [1–7]. These effects have been largely attributed to permeabilization of intracellular membranes without permeabilization of the plasma membrane, supported by the lack of uptake of propidium iodide (PI) or other membrane integrity marker dyes. However, recent studies have shown that USEP can significantly impact the permeability of the plasma membrane. Vernier et al. demonstrated that USEP facilitate influx of calcium ions through the plasma membrane and trigger fast externalization of phosphatidylserine (PS) residues [8–10]. The latter effect was thought to result from PS drift from the internal face of the membrane alongside the lipid-water interface in USEP-opened lipid pores. Using a different technique (whole-cell patch clamp), Pakhomov et al. have shown a profound increase in membrane electrical conductance that persisted for minutes after USEP exposure [11, 12]. These findings have supported model predictions [13–15] that USEP exposure can lead to formation of small pores or “nanopores” in the plasma membrane, which would allow passage of small ions but not necessarily larger propidium cations. A recent study that combined electrophysiological and fluorescent microscopy techniques demonstrated that nanopores are not just “plain holes” in the plasma membrane, but may exert complex conductive properties akin to classic ion channels [16].

In most USEP studies, the parameters describing USEP exposure are listed as pulse width, pulse amplitude, number of pulses, and repetition rate. However, the exact values of these parameters in each study vary based on custom pulser system configurations and appearance of desired effects rather than on a quantitative knowledge of how the effects actually depend on the exposure. Further research that links the appearance and magnitude of USEP bioeffects to exposure parameters is needed to establish true poration thresholds and reveal mechanistic connections between various cellular effects of this modality.

Isolated studies that attempted to explore how exactly USEP bioeffects depend on the exposure parameters have arrived at somewhat different and contradictory conclusions. Numerous studies reported that various effects of USEP are proportional to so called “electric impulse,” which is a product of the electric field, individual pulse duration, and pulse number [17–19]. On the contrary, studies of cell survival after exposure to trains of 10-ns pulses pointed to the absorbed dose (AD) as a metric that determined USEP-induced cell death [7, 18]. At present, it is unclear whether such diverse results are related to the diversity of specimens, biological endpoints, different exposure conditions (e.g., cells in suspension versus cells in tissue or affixed to a substrate), or different experimental protocols.

Recently, we explored how a single pulse of either 60- or 600-ns duration would change the electrical resistance of cell plasma membrane [20]. This endpoint was specifically chosen for being a likely primary bioeffect of USEP, since membrane permeabilization was readily and consistently observed at electric field (E-field) amplitudes several times lower than required for most other known nsEP effects [11, 12]. The membrane resistance was measured by whole-cell voltage clamp within 120–150 seconds after exposure in GH3 (rat pituitary) and CHO (Chinese hamster ovary) cells. We found that in both cell lines, the effect of a single USEP depends on both the applied E- field and pulse width in a dose-dependent manner. The E-field threshold for membrane permeabilization by 60-ns pulses was about 6 kV/cm, much higher than about 1 kV/cm threshold for 600-ns pulses. However, for both these pulse durations, the permeabilization threshold corresponded to the same AD of about 10 mJ/g. Overall, for a single-pulse exposure, the magnitude of membrane permeabilization was proportional to AD regardless of the specific duration or amplitude of the pulse.

The goal of the present study was to quantify the impact of multiple USEP on membrane permeabilization. Specifically, we explored: (1) whether increasing the number of pulses has a similar effect as changing the E- field amplitude of the individual pulses within a train, (2) whether applying multiple pulse lowers the E-field and AD thresholds as compared to a single-pulse exposure, and (3) whether the AD concept is applicable to multiple pulse exposure and the AD parameters can serve as a universal metric the same way as for single-pulse exposures [20].

MATERIALS AND METHODS

Electrophysiological experiments were performed at the Radio Frequency Radiation Branch, 711^th Human Performance Wing, Air Force Research Laboratory (AFRL) in Brooks City-Base, TX. Fluorescent confocal microscopy was performed at the Frank Reidy Research Center for Bioelectrics of Old Dominion University (ODU) in Norfolk, VA.

Cell propagation

GH3 cells (rat pituitary), growth media, and supplements were obtained from American Type Culture Collection (ATCC, Manassas, VA). Cells were grown at 37°C with 5% CO₂ in air, in Ham’s F12K medium supplemented with 2.5% fetal bovine serum and 15% horse serum, and containing 1% penicillin/streptomycin. For the cell passage immediately preceding the experiments, cells were grown on glass cover slips that were pre-treated with poly-L-lysine to improve cell adherence.

USEP Exposure

The USEP exposure devices utilized at AFRL and ODU are essentially similar and have been described previously[11, 12]. In brief, both systems delivered USEP to an individual cell attached to a cover slip by means of two tungsten rod electrodes, which are precisely positioned using a micromanipulator and under visual control with a microscope. At AFRL, a high speed switch controlled via LabView 8.0® software (National Instruments, Austin, TX) triggered USEP trains from a Blumlein line-based pulser [21]. At the ODU laboratory, USEP were generated in a transmission line-type circuit and triggered by external TTL pulses using pClamp software and the Digidata board (MDS, Foster City, CA). In both set-ups, the single pulse width was 60 ns and the trains were delivered at a repetition rate of 5Hz. The pulse shapes and amplitudes were captured using 5-GHz TDS 3052 oscilloscopes (Tektronix, Beaverton, OR).

Local E-field modeling

Accurate evaluation of the electric field delivered to the cells is critical for the goals of this study. The amplitude and 3-D spatial distribution of the E-field were obtained by numerical simulation using a Finite Difference Time Domain (FDTD) technique[22, 23].

The exposure set-up geometry used for the simulation included a homogenous saline solution (0.9%), a glass coverslip (180 μm thick), and a pair of tungsten electrodes (125 μm diameter, 375 μm separation) positioned 50 μm above the glass at a 30° angle. The voxel size of 4×4×4 μm was chosen to ensure that the smallest geometric feature of interest can be adequately resolved. The dielectric properties of the saline (permittivity 75.3, conductivity 1.55) and glass (permittivity 3.8, conductivity 0) were taken from [24, 25] and the tungsten electrodes were treated as perfect conductors. The electrodes were excited by a voltage-gap source with a long trapezoidal pulse waveform. The quasi-static excitations were considered appropriate for predicting the steady-state electrical fields in the solution during the direct current (DC) component of the nanosecond pulse. The impact of the rise time was therefore disregarded here, but may be investigated in the future by implementing a dispersive FDTD algorithm.

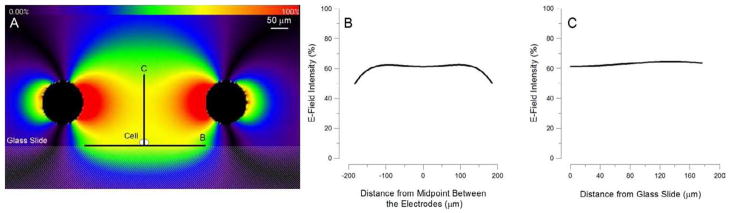
The local E-field distribution simulated by FDTD is shown in Figure 1A. The model predicted that, in our setup, 1 V applied between the electrodes results in a maximum of 30 V/cm local E-field in the vicinity of the electrodes. The E-field strength at the location of the exposed cell was approximately 17.5 V/cm per 1 volt applied. Importantly, the field at the cell location was practically uniform both in the horizontal and vertical directions (Fig. 1, B and C).

Fig. 1.

Finite difference time domain (FDTD) simulation of the E-field amplitude and distribution in the exposure cuvette.

USEP-delivering electrodes were lowered into the bath buffer and positioned 50 μm above the surface of the glass cover slip. The 3D model of the setup was generated using 4-μm voxels. See “Methods” for more detail. A: E-field distribution in a vertical plane through the tips of the USEP-delivering electrodes (seen as black circles). The USEP-exposed cell is situated in the middle of the gap between the electrodes. The E-field intensity is color coded from 0 to 100%, where 100% corresponds to the calculated maximum intensity of 30 V/cm per 1 V applied between the electrodes. B and C: numerical representation of the E-field variation within the same plane, along B and C lines shown in panel A. Zero distance corresponds to the location of the exposed cell. Note that the E-field at the cell location is essentially uniform, so small inaccuracies of the electrode positioning (e.g., by 20–50 μm) would have little impact on the E-field seen by the cell.

Patch clamp

Whole-cell currents were acquired in voltage-clamp mode using a Multiclamp 700B amplifier, Digidata 1440A A-D converter, and pCLAMP10 software (MDS, Foster City, CA). Recording pipettes were manufactured by pulling borosilicate glass (1B150F-4, World Precision Instruments, Sarasota, FL) to a tip resistance of 1.5–3 MOhm using a Flaming/Brown P-97 Micropipette puller (Sutter, Novato, CA). Exposures of individual cells to USEP and subsequent measurements were performed in a glass-bottomed chamber (Warner Instruments, Hamden, CT) mounted on a stage of a Leica DMI4000 microscope (Leica Microsystems, Germany). The bath buffer contained (mM): NaCl, 140; KCl, 5; CaCl₂, 2; MgCl₂, 2; HEPES, 10; glucose, 10; adjusted to a pH of 7.4. The pipette buffer contained (mM): NaCl, 5; KCl, 140; MgCl₂, 1; HEPES, 10; K-EGTA, 10; adjusted to a pH of 7.2. The solutions’ osmolality was checked with a model 3250 osmometer (Advanced Instruments, Inc., Norwood, MA) and measured about 300 mOsm. All chemicals were purchased from Sigma-Aldrich (St. Louis, MO).

In the previous study [20], we exposed an intact cell to USEP, and afterwards brought a recording pipette in contact with the cell membrane. This procedure was intended to prevent potential artifacts from the recording pipette presence when USEP was applied (such as destruction of the gigaohmic seal or saturation and “freezing” of the amplifier). However, this procedure resulted in a delay of 1–2 minutes between USEP exposure and the onset of measurements. Later on, we found that USEP effects on the membrane, at least at relatively low USEP voltages, were not caused by the artifact of pipette presence (16). Whether the pipette was present or not, the USEP effect was distinguished by a characteristic inward current rectification lasting minutes after exposure [16]; see also Fig. 2 as an example. Furthermore, the effect of membrane permeabilization was independently confirmed by optical methods in the absence of the recording pipette [16]. Therefore, in the present study we chose to employ a protocol where a whole cell configuration is established prior to USEP exposure (typically within 2–3 min). This approach allowed us to: (1) test the quality of the cellular preparation before exposure, (2) record baseline (pre-exposure) membrane characteristics for each individual cell, and (3) start measuring membrane currents as soon as 5 sec after USEP exposure.

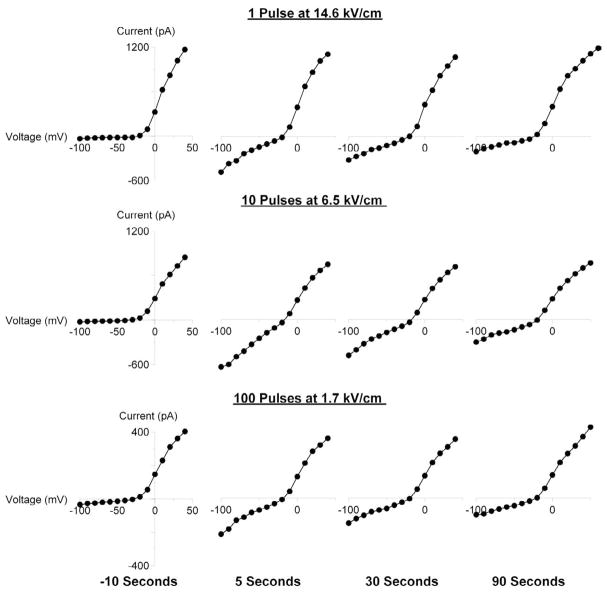
Fig. 2.

Characteristic changes in the current-voltage (I-V) function of cell plasma membrane following USEP exposure.

Shown are representative I-V curves for three cells, as recorded by a step-voltage protocol immediately prior to USEP exposure and at indicated intervals after it (See Methods for more detail). Before exposure, all cells display a subtle inward “leak” current at negative potentials and much stronger outward current at potentials between (−40) to (−30) mV due to activation of voltage-gated K⁺ channels. USEP exposure profoundly and reversibly enhanced the inward current component, but had little or no effect on the outward current. Note that a single pulse at a high E-field produced qualitatively the same effect as multiple pulses at lower voltages.

With this protocol, a cover slip with cells was placed into the chamber filled with bath buffer at room temperature, and a cell was selected for USEP exposure. Using a robotic manipulator (MP-225, Sutter, Novato, CA), USEP-delivering electrodes were lowered to the glass cover slip so that the selected cell would be in the middle of the gap between the electrodes’ tips. Next, the electrodes were brought up to exactly 50 μm above the cover slip using the digital readout of the manipulator. This location was saved in the manipulator’s memory as a “work position”, and the electrodes were removed from the bath, in order to minimize the electrical interference pick-up by the patch-clamp amplifier. Next, the cell was approached with a recording pipette driven by a second manipulator, and a whole cell recording configuration was established. The cell was held at −80 mV membrane potential, and membrane currents were probed by 120-ms voltage steps, from −100 to 50 mV with 10-mV intervals. This stimulation protocol took about 5 seconds and was repeated at least twice before exposure, to ensure the quality of the preparation and to establish the baseline current-voltage (I-V) function for the cell. Next, the USEP delivering electrodes were promptly returned into the saved “work position” and a fixed number of pulses at a chosen voltage were applied to the cell at a rate of 5 Hz. The electrodes were evacuated again, and currents were probed starting 5 sec after the completion of the USEP treatment. These procedures were performed identically for control cells, but no USEP were triggered (“sham exposure”).

The values of whole-cell current in response to the voltage steps were measured as a mean value when the current response reached a plateau, avoiding any transients at the onset of the step. Currents measured before and after exposure were used to plot the baseline and post-exposure I-V functions for each cell (Fig. 2). In order to identify the membrane conductance contributed by either USEP or sham exposure, the post-exposure current values were corrected by subtracting the respective baseline values for each individual cell. The exposure-induced change in the passive electrical conductance of the cell membrane (Δg was) measured as the mean slope of the corrected I-V curve for membrane potentials between −100 and −50 mV. This region was chosen (a) for the lack of any voltage-activated currents which could be affected by USEP in an unpredictable manner, thereby making data interpretation more complicated, and (b) because USEP exposure increased predominantly the inward current at negative membrane potentials, whereas the outward current at positive potentials was far less affected. Except for Figure 2, all results presented and discussed below are based on measurements of membrane current that were performed from 5 to 10 seconds after USEP or sham exposure.

Cell Imaging

Fluorescent and differential-interference contrast (DIC) images were obtained using an IX71 inverted microscope (Olympus America Inc., Center Valley, PA), configured with an Olympus FluoView TM 300 confocal laser scanning attachment. Real-time imaging of thallium (Tl⁺) uptake by cells was accomplished using a FluxOR^™ Thallium Detection Kit (Invitrogen, Eugene, OR). Cells were loaded with a Tl⁺-sensitive fluorophore for one hour at room temperature. To prevent potential Tl⁺ entry through voltage-gated K⁺ channels, the bath buffer contained high concentrations of several K⁺ channel antagonists. It was composed of (mM): Tl₂SO₄, 8; Cs-Acetate, 70; MgSO₄, 2; Ca-Acetate, 2; tetraethylammonium acetate, 50; 4-aminopyridine, 5; HEPES, 10; and glucose, 10 (pH 7.4). FluxOR dye was excited with a blue laser (488 nm), and emission was recorded at 530 nm. Images were repeatedly taken every 3 seconds before and after USEP exposure and quantified off-line with MetaMorph v. 7.5 (MDS).

RESULTS

Electrophysiology

The experiments established that USEP exposures, at least within a certain range of E-field intensities, produced characteristic changes in the shape of I-V curves. Specifically, the exposure profoundly enhanced the inward current at negative membrane potentials, but had little or no effect on the outward current at positive potentials (Fig. 2). These changes were qualitatively similar when induced by either a single high-amplitude pulse, or by multiple pulses at a lower E-field amplitude. USEP-exposed cells could slowly recover, typically within several minutes after the treatment. The variability seen between these cells prior to exposure, likely based upon difference in cell size or state within the cell mitotic cycle, provides a clear example of the advantage of obtaining a whole cell configuration prior to exposure as discussed in the methods section. The reversible increase of inward conductance at negative membrane potentials (inward rectification) is a “signature effect” of USEP exposure [16, 19], which supposedly results from nanoelectroporation of the cell membrane.

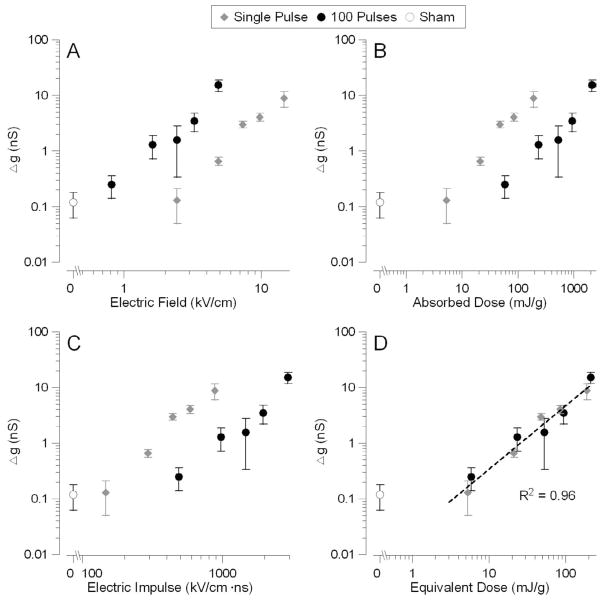
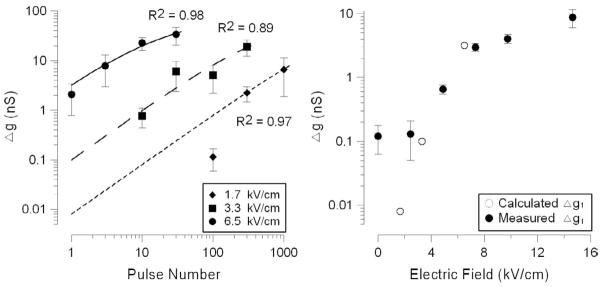
The efficiency of multiple pulses versus a single pulse was studied using 100-pulse trains at different E-field amplitudes. Figure 3A compares Δg as a function of the applied electric field amplitude for 1- and 100-pulse exposures. WE found that a train of 100 pulses requires 3–5 times less electric field to produce the same increase in membrane conductance as a single pulse. Notably, using multiple pulses also lowered the threshold E-field intensity from ~6 kV/cm for a single pulse to ~1.7 kV/cm for 100 pulses.

Fig. 3.

Comparative effectiveness of a single USEP and a train of 100 USEP as judged by the increase of the electrical conductance of the plasma membrane.

Panels A–C present the same data plotted against the electric field intensity (A), absorbed dose (B), and two different empirical characteristics of the applied field (C and D). Note that the E-field threshold for 100-pulse trains was lower than for a single pulse; however, the absorbed dose (AD) threshold was higher for the multiple pulse exposure. In C, the membrane conductance was plotted against the product of the E-field, pulse duration, and square root of the number of pulses applied. This parameter was proposed earlier as a universal metric to characterize USEP effects in cells in suspension [20]; however, this parameter does not appear appropriate for cells attached on a substrate. Lastly, in panel D, we corrected the AD by an empirical factor of n^−1/2 to account for gradually decreasing cell sensitivity to USEP when multiple pulses are applied. The resulting exposure parameter called the “Equivalent Dose” adequately predicted the effect of both single and multiple pulse exposures. The coefficient of determination (R²) for the best fit using a power function was 0.96 for all data pooled together. Shown are mean values +/− s.e. for 5 to 20 independent experiments per data point.

However, this decrease of the applied E-field occurred at the expense of higher energy. When the same data were plotted against the absorbed dose (Fig. 3 B), 100-pulse trains were ~10-fold less efficient in producing the effect of plasma membrane permeabilization. The dose threshold of ~10 mJ/g for a one-pulse exposure that was established previously [20] has been confirmed in this study, and this suggest that the “true” threshold cannot be further reduced by using multiple pulses. In other words, multiple pulses produced the same biological effect at a lower E-field, but at a higher absorbed dose as compared with a single USEP. Importantly, Figure 3B also shows that the dose can no longer serve as a universal exposure metric when multiple pulses are applied, as the effect of multiple pulses is weaker than of a single pulse at the same dose.

Using a different approach and considering the membrane charge as a factor that determines USEP bioeffects, Schoenbach and colleagues [26] have recently proposed a “scaling law” model to account for gradually decreasing efficiency of pulses as the USEP train proceeds. In brief, this model considers cells in suspension, which are able to move and rotate randomly during the USEP exposure. Individual pulses in the train are thought to electroporate plasma membrane locally, only at the cell pole(s) facing the USEP-delivering electrode(s). If the cell rotates between the successive pulses so that now an intact portion of the plasma membrane will be facing the electrodes, then the next pulse will produce additional membrane permeabilization. However, if the cell does not rotate, or rotates so that an already permeabilized membrane will be facing the electrodes, then the next pulse will have a reduced or no effect. Based on these assumptions, the model predicts that the efficiency of multiple pulses should be described by a simple metric, which is a product of the E-field intensity, pulse duration, and the square root of the number of pulses. However, in our experiments where cells were immobilized on the class cover slip throughout the exposure, it was not surprising that the “scaling law” gave vastly different predictions for 1- and 100-pulse exposures (Fig. 3 C).

Nonetheless, it makes sense that a cell permeabilized by the first pulse in the train becomes less vulnerable to the next pulse(s): Since the first pulse increases membrane conductance, the next pulse(s) will not charge the membrane as effectively as the first one. Although the absorbed dose metric was adequate to predict single-pulse effects, it obviously requires a correction factor when multiple pulses are used. An empirically found correction factor was the reduction of the absorbed dose by n^(−1/2), where n is the number of pulses. The corrected absorbed dose was named an “equivalent dose”, similar to the terminology accepted in classic radiation biology to account for different dose efficiency of different types of ionizing radiations. Figure 3D shows that both 1- and 100-pulse data can be fit with the same power function when the equivalent dose is used as the exposure metric.

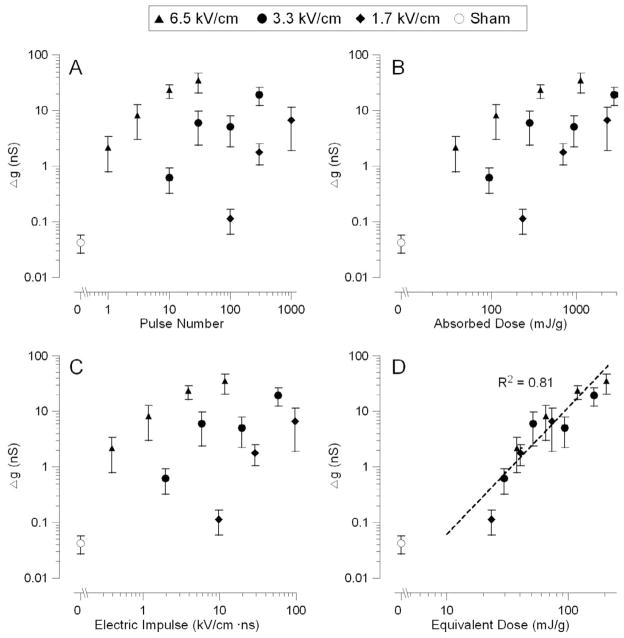
This concept was verified in a separate series of experiments, where different numbers of pulses were delivered at a chosen E-field intensity (1.7, 3.3, or 6.6 kV/cm). The data from over 70 independent experiments are summarized in Figure 4, A–D. Notably, a 2-fold decrease in the electric field required about a 20-fold increase in the pulse number to produce the same biological effect. Similarly to the previous series, neither the absorbed dose nor the “scaling law” were able to adequately predict the efficiency of the treatment (Fig. 4, B and C), whereas the equivalent dose was an adequate metric regardless of what were the exact values of the E-field and the number of pulses (Fig. 4 D).

Fig. 4.

Comparative effectiveness of USEP trains applied at different E-field intensities (1.7, 3.3, or 6.5 kV/cm).

All details are the same as in Fig. 3, except for using pulse number for horizontal axis in panel A (instead of E-field). Note that the equivalent dose (panel D) was the only exposure metric that predicted reasonably well the efficiency of exposure for different E-field intensities and pulse train durations.

Cell Imaging

Electrophysiological recording of whole-cell currents, while arguably the most sensitive technique to detect the impact of USEP on cells, requires direct coupling of the glass pipette to the cell, which may modify the effect of exposure. Therefore, it was important to demonstrate the phenomenon of USEP-induced plasma membrane permeabilization under experimental conditions that do not require the presence of the pipette. This goal was accomplished by fluorescent detection of Tl⁺ ion uptake by USEP-treated cells. Compared to more common Ca²⁺, Na⁺, and K⁺ detection techniques, Tl⁺ is not present in living cells in any considerable amount, hence any increase in Tl⁺-dependent fluorescence points to increased Tl⁺ entry from the outside and serves as a manifestation of membrane permeabilization.

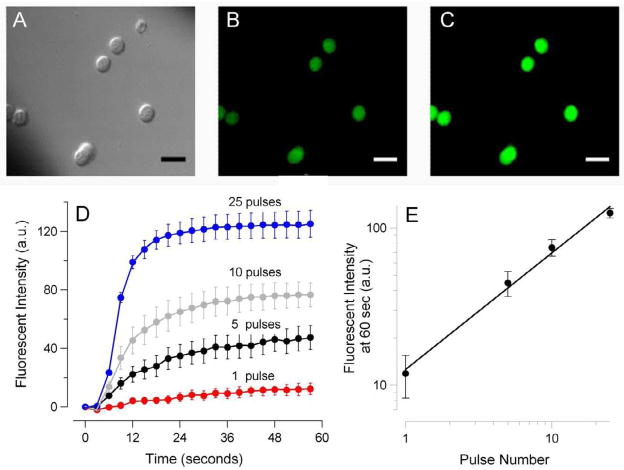
When cells loaded with a Tl⁺-sensitive fluorophore were bathed in a Tl⁺-containing solution, USEP exposure caused an immediate and profound surge in fluorescence due to Tl⁺ uptake by cells (Fig. 5, A–E). The emission intensity increased rapidly after the pulse, reaching a plateau level in 20–30 seconds. The extent of membrane permeabilization, as measured from the level of this plateau, increased proportionally to the number of pulses delivered to the sample. We did not explore this effect in the same detail as with patch clamp; the principal conclusion from the cell imaging experiments is that the dose-dependent membrane permeabilization by USEP can equally well be observed in undisturbed cells and by a method that does not rely on electrical measurements.

Fig. 5.

Nanosecond-duration electric pulses trigger Tl⁺ uptake by exposed cells.

GH3 cells were loaded with Tl⁺ sensitive fluorophore FluxOR^™ and bathed in a solution containing 16 mM Tl⁺. DIC and fluorescence images were taken repeatedly every 2 sec. Exposure to a train of 1, 5, 10, or 25 60-ns pulses at 14 kV/cm started at 5 sec. A–C: representative images of cells using DIC optics (A) and fluorescence detection at 530 nm, immediately before nsEP exposure (B) and 20 sec after a train of 25 pulses (C). Calibration bar: 20 μm. (D): The amplitude and time dynamics of nsEP-induced surge in Tl⁺-dependent fluorescence in cells exposed to a different number of pulses (mean +/− s.e., n=3 to 5). The mean intensity of fluorescence before exposure (baseline) was subtracted from post-exposure images. (E): Same data as in D, but maximum change in Tl⁺-dependent fluorescence (at 60 sec post exposure) was plotted against the number of pulses in the train. Note double-logarithmic scale.

DISCUSSION

We have shown that both Δg and transmembrane movement of ions increase with the number of pulses at a set pulse amplitude and repetition rate. The same increase of g can be achieved by applying either a single, high-amplitude USEP, or a train of USEP at lower amplitude. Moreover, by using multiple pulses, we found that the threshold for the USEP effect on Δg is at or below 1.7 kV/cm for 60-ns pulse duration, which is substantially lower than reported earlier using a single USEP [20]. This finding points to the ability of low-amplitude USEP to produce subthreshold membrane lesions, which can add up to produce a detectable Δg increase when multiple pulses are applied. These subthreshold lesions could be actual membrane pores, which are just too small and/or too sparse to affect Δg; however, it could also be some rearrangement of the lipid bilayer that does not involve immediate formation of a pore, but makes the membrane more responsive to the porating effect of the following pulses.

In previous work [20], we found that AD was the universal exposure metric that determines Δg changes after a single USEP of either 60- or 600-ns duration. However, here we demonstrate that this conclusion does not hold true for multiple pulse exposures. This finding can be reasonably explained by the fact that an already permeabilized membrane is less susceptible to the electroporating effect of subsequent pulses in a USEP train. Indeed, if plasma membrane is considered as a simple resistive load in series with other (smaller) loads such as endoplasmic reticulum, nucleus, and other organelles, then the increase in Δg will result in a lower USEP-induced voltage across the plasma membrane, and, consequently, its less effective permeabilization.

This gradual decrease of membrane sensitivity to USEP as the USEP train proceeds can be quantitatively described by a model that treats a train of USEP as a series of single-pulse exposures. In this model, the effectiveness of any pulse in a train depends on: Δg₁ (which denotes the immediate Δg by the first pulse in the train and is determined by AD); and t, which is the time interval after the pulse that allows for gradual membrane resealing and Δg recovery.

Specifically, the Δg by time t after a single pulse exposure and its dependence on the pulse parameters can be expressed as:

$$\mathrm{\Delta }g=\mathrm{\Delta }{g}_1·e^{-\beta t}$$ (1)

$$\mathrm{\Delta }g\propto AD·e^{-\beta t}=(E^2·\tau ·\frac{\sigma }{\rho })·e^{-\beta t}$$ (2)

where β is the recovery coefficient, E is the E-field, τ is the pulse width, σ is the conductivity, and ρ is the solvent density.

Should all pulses in a train have equal efficiency independent of Δg, a pulse in train that comes after n preceding pulses can be written as:

$$\mathrm{\Delta }{g}_{n+1}=\mathrm{\Delta }{g}_n·e^{-\beta T}+\mathrm{\Delta }{g}_1$$ (3)

where Δg_n+1 is the total Δg increase expected immediately after n+1 pulses, Δg_n is the Δg change by n pulses, and T is the time between pulses in the train. Now, the reduction of pulse efficiency with Δg increase can be taken into account as:

$$\mathrm{\Delta }{g}_{n+1}=\mathrm{\Delta }{g}_n·e^{-\beta T}+\mathrm{\Delta }{g}_1·e^{-\alpha \mathrm{\Delta }{g}_n·e^{-\beta T}}$$ (4)

where α is a proportionality coefficient which reflects reduction of the membrane susceptibility to USEP as Δg increases. It is clear that with infinitely long T, Δg_n+1 = Δg₁, because the cell recovers completely from the previous pulse and the effect is the same as with a single pulse exposure. One can also see that if α is zero, then Eq. 4 reverts into Eq. 3, meaning that the effect of individual pulses will be independent from Δg.

As evidenced both by electrophysiological methods (Fig. 2; see also [18]) and by facilitation of the ion transport [16], the membrane recovery is gradual over the course of minutes after exposure. Hence, the extent of recovery over periods shorter than 1 second can reasonably be disregarded. To test our model against the experimental data presented in Figure 4, we assumed that recovery was not significant within the 200-ms intervals between the pulses. We also assumed that recovery was not appreciable between the final pulse of the exposure and the onset of data collection (a time interval of about 5 seconds) as such we did not consider possible contribution of the recovery coefficient β. Therefore, we used the following equation to determine α and Δg₁ values by an iterative least squares algorithm for the best fit with the experimental data:

$$\mathrm{\Delta }{g}_{n+1}=\mathrm{\Delta }{g}_n+\mathrm{\Delta }{g}_1{e}^{-\alpha (\mathrm{\Delta }{g}_n)}$$ (5)

The fit results for 60-ns pulses of 1.7, 3.3, and 6.5 kV/cm are presented in Figure 6A. The best fit value of α, as determined from all simulations, was 0.05 (nS)⁻¹; the respective Δg₁ values for different pulse voltages fell close to the values that were actually measured in experiments with single-pulse exposures (Fig. 6 B). Notice that lower voltages yield Δg₁ below measureable thresholds, but can be estimated with this model.

Fig. 6.

Fitting of the experimental data with a model that treats USEP trains as a series of single-pulse exposures with exponentially diminishing efficiency.

The experimental data are the same as shown earlier in Figs. 3 and 4. The best fit lines in panel A are plotted using Eq. (5) using optimized value of α = 0.05 (nS)⁻¹. Panel B shows that Δg₁ values obtained by the numerical algorithm are close to the values measured in single-pulse exposure experiments. See text for more detail.

The determined value of α is probably a characteristic of a given cell line and Δg measurement protocol, and its impact is seen on the graphs (Fig. 6 B) as gradual decrease of the slope of the best fit curve with increasing number of pulses. Since α is a measure of diminishing efficiency of individual USEP as the pulse train proceeds, the impact of α is greater for pulses of higher amplitude, which manifests as an increased curvature of the best fit line for the highest voltage tested, 6.5 kV/cm.

We believe that the coefficient α is directly related to the ability of charge to build up on the plasma membrane. Therefore, α is likely related to the conductivity of the intra- and extracellular solutions, and we intend to test this hypothesis in future experiments. In addition, we plan to compare the effectiveness of pulse trains delivered at different repetition frequencies in order to establish an empirical value for β for various cell types, and further incorporate it into the above model.