Measurement of admixture proportions and description of admixture structure in different US populations

Abstract

Variation in individual admixture proportions leads to heterogeneity within populations. Though novel methods and marker panels have been developed to quantify individual admixture, empirical data describing individual admixture distributions are limited. We investigated variation in individual admixture in four US populations [European American (EA), African American (AA) and Hispanics from Connecticut (EC) and California (WC)] assuming three-way intermixture among Europeans, Africans and Indigenous Americans. Admixture estimates were inferred using a panel of 36 microsatellites and 1 SNP, which have significant allele frequency differences between ancestral populations, and by using both a maximum likelihood (ML) based method and a Bayesian method implemented in the program STRUCTURE. Simulation studies showed that estimates obtained with this marker panel are within 96% of expected values. EAs had the lowest non-European admixture with both methods, but showed greater homogeneity with STRUCTURE than with ML. All other samples showed a high degree of variation in admixture estimates with both methods, were highly concordant and showed evidence of admixture stratification. With both methods, AA subjects had 16% European and <10% Indigenous American admixture on average. EC Hispanics had higher mean African admixture and the WC Hispanics higher mean Indigenous American admixture, possibly reflecting their different continental origins.

INTRODUCTION

Understanding the genetic structure of populations is of genetic and anthropological interest. It is also of practical importance for the valid control of population stratification in case-control association studies. Each individual in a population has a unique genetic history. Thus, evaluating genetic variation within and between populations has important consequences for both forensic and medical genetics. The United States has three predominant population groups. According to recent estimates of the US census bureau (Table NC-EST2007-03), African Americans (AAs) represent 12.3% of the total US population. This category designates a range of people including those of exclusively African origin with little or no mixed ancestry and people of African descent who have substantial non-African admixture. Hispanics (or Latinos) represent 15% of the total US population and include Mexican Americans, Puerto Ricans, Cubans, and others who speak Spanish, i.e. they are categorized based on language and cultural identity rather than ancestry. These populations may, depending on the particular group sampled, have very different individual admixture proportions (Halder et al., 2008).

The prevalence of many diseases differs between populations and there is evidence that some of the differences reflect group genetic differences -- for example, hypertension and prostate cancer in AAs (Douglas et al., 1996, Hoffman et al., 2001) and diabetes in American Indians (Martinez 1993, Songer and Zimmet 1995) (for a more detailed summary, see Halder and Shriver, 2003, Table 1.). Understanding the genetic structure of populations and exploring biogeographical heterogeneity may yield a better understanding of the genetic processes and, eventually, disease etiology in these populations, thereby decomposing the sources of variation (i.e., environmental, genetic, and gene-environment interactions) that contribute to the disease. Understanding and characterizing such variation will also help the forensic community and efforts can be made to construct regional databases.

Table 1.

δc values for all pair wise comparisons

Markers	AF-EU	AF-IA	EU-IA
CSF1PO	0.232	0.211	0.140
D10S1786	0.470	0.545	0.516
D10S197	0.424	0.307	0.275
D11S935	0.756	0.583	0.337
D12S352	0.283	0.574	0.635
D13S317	0.265	0.519	0.452
D14S68	0.292	0.422	0.225
D15S1002	0.573	0.560	0.405
D16S3017	0.447	0.347	0.530
D16S539	0.181	0.231	0.246
D17S799	0.522	0.668	0.541
D18S51	0.320	0.310	0.204
D19S433	0.244	0.533	0.372
D1S196	0.270	0.337	0.160
D1S2628	0.624	0.479	0.339
D21S11	0.227	0.356	0.215
D22S274	0.339	0.377	0.372
D2S1338	0.447	0.352	0.424
D2S162	0.473	0.599	0.185
D3S1358	0.150	0.299	0.328
D5S407	0.369	0.419	0.371
D5S410	0.516	0.667	0.523
D5S818	0.207	0.510	0.331
D6S1610	0.456	0.517	0.412
D7S2469	0.360	0.359	0.359
D7S640	0.532	0.577	0.450
D7S657	0.682	0.503	0.393
D7S820	0.125	0.429	0.403
D8S1179	0.230	0.402	0.243
D8S1827	0.409	0.534	0.124
D8S272	0.458	0.552	0.428
D9S175	0.494	0.743	0.515
FGA	0.246	0.312	0.264
FY	0.968	0.980	0.012
TH01	0.421	0.483	0.369
TPOX	0.210	0.377	0.233
VWA	0.131	0.333	0.296
Total δ	14.354	17.305	12.626
Average δ	0.388	0.468	0.341

The process of intermixture between populations (or individuals within populations) that have been geographically separated results in a newly admixed population. Different models have been proposed to explain and model the process of admixture (Long, 1991; Pfaff et al., 2001). The two extreme cases are “Hybrid Isolation,” where admixture occurs in a single generation between different ancestral populations, and “Continuous Gene Flow,” where admixture occurs through successive generations between one or more of the ancestral populations and the new admixed population. Contemporary admixed populations usually have histories in which both processes have contributed, thereby creating a compound distribution of individual admixture proportions in the population. The investigation and interpretation of this variation in individual admixture levels within a population are important for modeling population structure and controlling type I and type II errors caused by undetected stratification in genetic association studies.

To study the genetic variation within and between populations, we conducted individual admixture analysis in four US resident populations: EA, AA, and two Hispanic populations from two different regions, referred to henceforth as East Coast Hispanics (EC) and West Coast Hispanics (WC). Although certain assumptions are inherent in the measurement of biogeographical ancestry and admixture, the estimates provide an initial basis for understanding the genetic variability in population samples. Prior literature has shown that substantial variation in individual admixture proportions exist in the AA, EC and WC populations (Bonilla et al., 2003a,b, Reiner et al., 2005, Shriver et al., 2005, Halder et al., 2008). In contrast, EAs are generally assumed to be more homogenous although not devoid of genetic stratification (Bauchet et al., 2007). Using a panel of thirty-seven microsatellites and one SNP marker, which are informative of continental origin, we investigated variation in individual admixture proportions in the four US populations.

METHODS

Populations

Three of the populations studied in this report were recruited at the University of Connecticut Health Center (Farmington) as part of larger studies of the genetics of alcohol and drug dependence and affective disorders. These include unrelated individuals who self-identified as European Americans (EA) (N = 652), African Americans (AA) (N = 228) and Hispanics (identified henceforth as East Coast Hispanics (EC)) (N = 102). Details on sample collection and characteristics have been described previously (Yang et al., 2005a and Luo et al., 2006). Subjects were evaluated using the Structured Clinical Interview for DSM-IV (SCID) and individuals with a primary diagnosis of a major psychotic illness (schizophrenia or schizoaffective disorder) were excluded from analysis. The final sample consisted of 89 unrelated, self-identified Hispanic individuals recruited from Southern California (henceforth called West Coast Hispanics (WC) as part of a previously reported study of affective disorders (Stein et al, 2004). Although detail familial ancestry was not specifically asked, each subject self-identified as belonging to the racial group in which they have been included. Neither were all subjects free of major complex diseases. Since no phenotypes were studied in the current report, subjects were randomly selected from the larger cohorts irrespective of their phenotypic status.

Ancestral allele frequencies and genotypes were ascertained in 59 Spanish, 88 Mexican, and 78 individuals from Sierra Leone, who have been described and used previously for individual admixture estimation (Shriver et al., 2003; Bonilla et al., 2003). These samples served as reference European (EU), Indigenous American (IA), and West African (AF) ancestral groups, respectively. The Mexican sample from Guerrero, Mexico has been shown to have very low European or African admixture (Bonilla, 2003) and was used as a representative IA population. All subjects provided written informed consent and IRB approvals were obtained prior to study initiation.

Genetic markers

The ancestry informative markers (AIMs) used in the present study are the same as those we have previously described (Stein et al, 2004; Yang et al., 2005a,b) and included 36 microsatellites and one SNP (FY; rs2814778). Of the STRs, 15 loci are used in forensic analyses as part of the combined DNA identification system (CODIS: D8S1179, D21S11, D7S820, CSF1PO, D3S1358, TH01, D13S317, D16S539, D2S1338, D19S443, vWA, TPOX, D18S51, D5S818 and FGA). An additional panel of 21 markers was selected from published reports. These markers typically have high allele frequency differences between European and African populations as well as between EA and AA, and in some cases, between Hispanic and Asian populations (Smith et al. 2001) and included the markers D1S196, D1S2628, D2S162, D2S319, D5S407, D5S410, D6S1610, D7S640, D7S657, D8S272, D8S1827, D9S175, D10S197, D10S1786, D11S935, D12S352, D14S68, D15S1002, D16S3017, D17S799, and D22S274. Genotyping was conducted as reported previously (Yang et al., 2005a,b). Some of the current subjects were included in our prior reports but most were genotyped specifically for this study.

Individual admixture estimation

Individual admixture was estimated using both a maximum likelihood (ML) method and a separate Bayesian method as implemented in the program STRUCTURE (Pritchard et al., 2000, Falush et al., 2003). A software program, MLIAE, was written to implement the ML method as previously described (Hanis et al., 1988, Chakraborty and Weiss, 1988). The algorithm computes the probability of observing a marker genotype given ancestral allele frequencies at a locus. Summing over the logs of individual locus probabilities combines information across multiple loci. The admixture proportion that maximizes the probability of obtaining the observed genotype is the ML Estimate (MLE) of ancestry for the individual. Estimates of individual admixture in the EA, AA and two Hispanic samples were calculated under a trihybrid (i.e., k=3) model of admixture between EU, AF and IA populations.

The models in STRUCTURE were set up to incorporate and identify ancestral populations by specifying both the “Usepopinfo” and “Popflag” options and allowing for admixture. Separate models were set up to analyze EA, AA, EC and WC, but each model included 59 Spanish, 88 Mexican, and 78 African ancestral individuals. In addition, allele frequencies were specified as being uncorrelated and a separate ‘alpha’ parameter (that characterizes the distribution of admixture proportions in each individual) was assumed for each population to allow for variation in ancestry proportions among individuals from different populations. The number of subpopulations (K) was specified from 1 to 3. For adequate convergence of the STRUCTURE algorithm, runs of different lengths were simulated. Final runs consisted of 40,000 burnin followed by an additional 80,000 for parameter estimation. For all other options the default parameters were used.

Sample characterization

Allele frequency estimates and exact tests for Hardy Weinberg equilibrium were carried out using Genepop software (Raymond and Rousset, 1995). All statistical analyses (other than those described above) were carried out in SPSS v10. Comparisons between group means were tested using t-tests. The individual admixture distributions between groups were compared using the Kolmogorov-Smirnov test for two samples. Marker information content for ancestry was estimated as the composite δ(δ_c) value, which is an extension of biallelic δ, the difference in allele frequencies of two populations, to a multiallelic situation (Shriver et al., 1977). δ_c is defined as:

$${\delta }_c=1/2\times {\sum }_{i=1}^n\mid f_{iA}-f_{iB}\mid$$

Where f_iA and f_iB are the frequencies of the ith allele in the two populations, A and B, being compared ata locus. We also computed marker informativeness for ancestry estimation, I_n, as defined previously (Rosenberg et al., 2003) using the program Infocalc v1.1 available at Dr. Rosenberg’s website (http://rosenberglab.bioinformatics.med.umich.edu/infocalc.html).

Detection of stratification related to admixture

We used STRUCTURE (Pritchard et al. 2000, Falush et al., 2003) to test for the presence of subpopulations within the sample being studied. STRUCTURE requires as input a predefined number of populations (K); we tested for K=1–3. These STRUCTURE runs did not include subjects from predefined ancestral populations. A model with admixture, uncorrelated allele frequencies, and separate alpha parameters was specified, and the program was run with 30,000 burnin iterations followed by 70,000 iterations for parameter estimation. The values of log Probability of Data for K = 1, 2 and 3 were compared to evaluate the presence of stratification. We also used the Individual Ancestry Correlation test (Shriver et al., 2005), in which the original marker panel is split randomly into two non-overlapping sets of markers (Pfaff et al., 2001). The procedure of randomly splitting markers was repeated 20 times and ancestry was estimated separately with each of the different (20 × 2) sets of markers. Significant correlation between half-sets was used to infer presence of stratification.

Simulation studies

Simulated data sets were generated using an algorithm described previously (Halder et al., 2008). First we simulated 1000 unadmixed individuals from each of the EU, AF and IA ancestral populations. Since each individual is expected to have 100% ancestry from one ancestral group, we compared measured admixture proportions to the expected 100% ancestry from a population and ascertained “population bias” (total ancestry from non-contributing populations, e.g., total non-EU admixture in a simulated individual who is expected to be 100% EU) and the “ancestry bias”(total contribution from one non-contributing population to other populations in the analysis, e.g., the % IA ancestry in simulated 100% EU individuals) of the marker panel.

RESULTS

Allele frequencies and ancestry informativeness of markers

Allele frequencies for all markers in all populations are shown in Supp. Table S1. We have previously reported the allele frequencies of these markers for EU and AF populations (Yang et al., 2005b) and reproduce them here to demonstrate marker δ_c values and compare them to allele frequencies in other populations studied here. All markers within each population were tested for consistency with Hardy Weinberg Equilibrium (HWE) expectations and those not consistent with HWE are indicated in the table. The EU, AF, and IA populations were used to ascertain ancestral allele frequencies for subsequent admixture analyses.

Allele frequency differences (δ_c) between the ancestral populations are shown in Table 1. The total δ_c value for pair-wise comparisons was highest between AF and IA and lowest between the IA and EU. Markers with δ ≥ 0.3 have previously been shown in empirical studies to be particularly useful for ancestry estimation (Parra et al. 1998; Collins-Schramm et al. 2002; Shriver et al. 2003; Bonilla et al. 2004; Bonilla et al. 2004a). The proportion of markers with δ ≥ 0.3 and, was 22/36 for the EU-AF comparison, 33/36 for the AF-IA comparison and 23/36 for the EU-IA comparison. That said, markers were not excluded from the panel if they had δ_c < 0.3 for any one pair-wise comparison and two markers (CSF1PO, D16S539) did have δ_c < 0.3 for all pairwise comparisons. The only SNP in this panel, FY, is an African ancestry-specific marker and shows nearly 100% allele frequency difference between the African and non-African ancestral populations.

Ancestry Informativeness (I_n) of markers assuming a three-way admixture model with equal priors showed I_n values ranged from 0.07 to 0.572 (Supp. Table S2). I_n values within and inclusive of 0.131 and 0.216 correspond to δ of 0.5 and are considered highly informative for ancestry information (Rosenberg et al., 2003). In this panel 27 out of 36 markers are above the lower range of this I_n value (i.e. > 0.131).

Individual admixture proportions in US populations

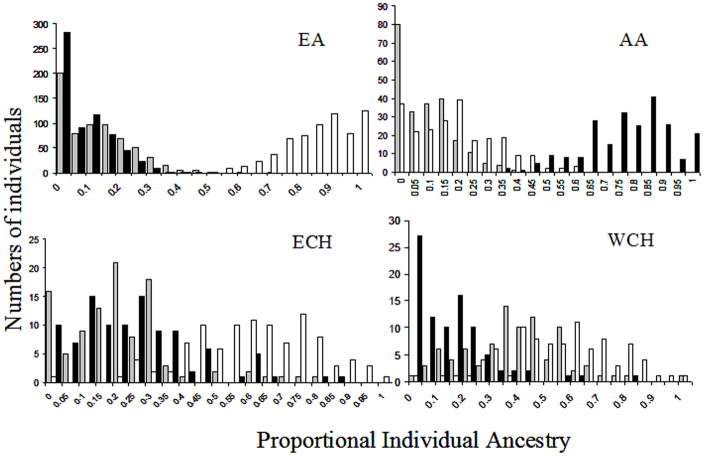
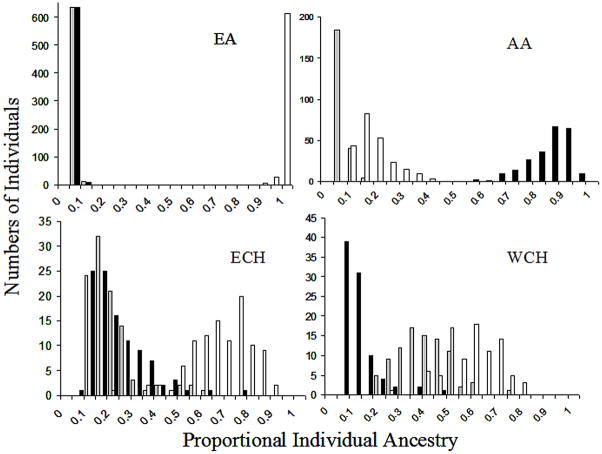
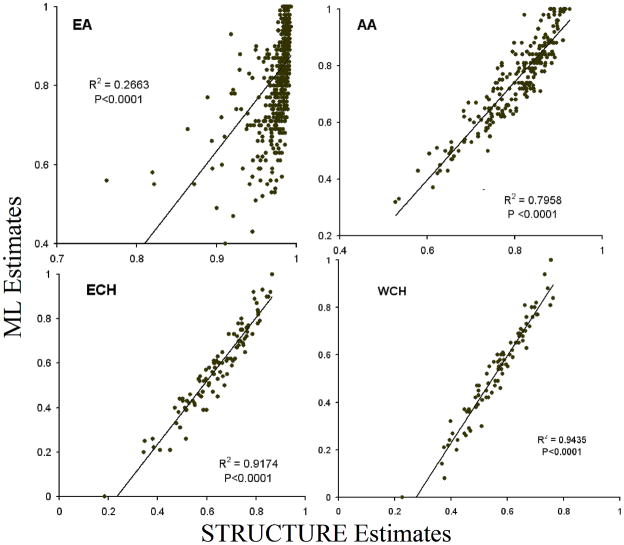
Table 2 shows mean admixture estimates obtained with each method and the correlations between these estimates. Histograms depicting frequency of individual admixture distributions obtained using ML are shown in Figure 1, and those obtained with STRUCTURE are shown in Figure 2. Triangle plots depicting the distribution of individual admixture in each population using ML and STRUCTURE are shown in Supp. Figures S1 and S2. ML and STRUCTURE estimates showed significant correlations and similar trends in all population samples. Figure 3 shows the correlation between ML and STRUCTURE estimates for the ancestral group contributing maximally to a population.

Table 2.

Mean ± Standard Deviations of Estimates of Individual Admixture

Population (N)	ML			STRUCTURE			Correlations
	IA	EU	AF	IA	EU	AF	IA	EU	AF
EA (652)	0.10 ± 0.1	0.84 ± 0.12	0.06 ± 0.07	0.01 ± 0.01	0.98 ± 0.02	0.01 ± 0.02	0.43	0.267	0.214
AA (228)	0.08 ± 0.08	0.17 ± 0.14	0.75 ± 0.15	0.04 ± 0.02	0.16 ± 0.07	0.81 ± 0.08	0.689	0.796	0.841
EC (102)	0.19 ± 0.16	0.59 ± 0.19	0.22 ± 0.18	0.17 ± 0.10	0.65 ± 0.13	0.18 ± 0.12	0.924	0.917	0.914
WC (89)	0.36 ± 0.18	0.53 ± 0.2	0.11 ± 0.14	0.36 ± 0.10	0.56 ± 0.11	0.08 ± 0.07	0.967	0.944	0.926

ML and STRUCTURE means significantly different (P < 0.0001) for all ancestry axes in all populations. P-values for all Spearman’s rank correlation coefficients <0.0001

Figure 1.

Histograms showing the distribution of individual admixture estimates in all four populations using maximum likelihood method. The X axis represents proportional ancestry bins, the Y axis represents number of individuals who have admixture proportions within the designated bins. White bars represent proportional European admixture, black bars represent proportional West African admixture and gray bars represent proportional Indigenous American admixture. EA: European Americans, AA: African Americans, ECH: East Coast Hispanics from CT, WCH: West Coast Hispanics from CA.

Figure 2.

Histograms showing the distribution of individual admixture estimates in all four populations using STRUCTURE. The X axis represents proportional ancestry bins, the Y axis represents number of individuals who have admixture proportions within the designated bins. White bars represent proportional European admixture, black bars represent proportional West African admixture and gray bars represent proportional Indigenous American admixture. EA: European Americans, AA: African Americans, ECH: East Coast Hispanics from CT, WCH: West Coast Hispanics from CA. Compare the tighter clustering in Figure 2 with the clustering in Figure 1.

Figure 3.

Correlations between individual admixture estimates obtained with ML and STRUCTURE for the ancestral group that contributes maximally to a population. STRUCTURE estimates are shown in the X axis and ML estimates are shown on the Y axis. EA: European Americans, AA: African Americans, ECH: East Coast Hispanics from CT, WCH: West Coast Hispanics from CA. Individual European admixture is shown for EA, ECH and WCH; individual West African admixture is shown for AA. Higher correlations are observed in the AA, EC and WC samples compared to the EA sample. All correlations are highly significant.

Both methods detected high mean EU admixture and significant (P < 0.0001) non-EU admixture in the EA sample, indicating that for some of the EA individuals, we were able to detect non-EU admixture. However, mean estimates obtained with the two methods were significantly different (P<0.0001) for each ancestry axis (Table 2). STRUCTURE estimates were more tightly clustered compared to ML estimates (compare Supp. Figures S1 and S2). This discrepancy was also reflected in the lower correlations between estimates obtained with the two methods when compared to correlations observed in AA, EC and WC (Table 2).

Individual admixture estimates showed wider distribution in AA, EC and WC groups, in comparison to the EA sample. Although correlations between estimates obtained with ML and STRUCTURE were higher in these three population samples compared to the EA sample (Table 2, Figure 3), the means were significantly different for all populations across all ancestry groups (Table 2). With both methods, the AA sample had high mean EU and mean AF admixture and much lower but significant (P<0.0001) non-zero IA admixture. In the two Hispanic groups’ mean EU admixture was the highest, with substantial AF and IA admixture (Table 2). The histograms in Figures 1 and 2 further demonstrate that ancestry estimates for the three admixed populations are bound within certain limits of ancestry proportions, for example, ML estimates indicate that 35% of AA show no IA ancestry, but in contrast, using STRUCTURE, 35% of AAs show 0.05 IA ancestry. However, not all individuals who have 0 IA admixture with ML show 0.05 IA ancestry with STRUCTURE.

Despite significant correlations in admixture estimates obtained with the two methods (Figure 3), the absolute values of the estimates for each ancestry axis differed significantly (Table 2). In general, STRUCTURE estimates showed tighter clustering compared to ML estimates (see Supp. Figures S1 and S2). The most striking discrepancies between STRUCTURE and ML estimates were observed in the EA sample, in which the former method yielded results that showed most individuals to have 95% – 100% EU ancestry, whereas ML estimates had a wider range of 50% – 100%.

Difference in admixture proportions between two Hispanic samples

Two-sample t-tests comparing mean admixture proportions showed that IA and AF estimates obtained with both ML and STRUCTURE are significantly different (P<0.0001 for all) between the EC and WC samples (Table 2), and persist after Bonferroni correction is applied to account for multiple corrections. EC had significantly higher AF admixture (ML: 22% in EC vs. 11% in WC; STRUCTURE: 18% in EC vs. 8% in WC), while WC had significantly higher IA admixture (ML: 36% in WC vs. 19% in EC; STRUCTURE: 36% in WC vs. 17% in EC). Although ML estimated EU admixture proportions did not vary between the groups, STRUCTURE estimated EU admixture was significantly higher in EC compared to WC (65% vs. 56%).

We compared the difference in distributions of individual admixture estimates using two-sample Kolmogorov-Smirnov test (Table 3). We rejected the null hypothesis that samples are from the same distribution at a significance level of P = 0.016 (after Bonferroni correction for multiple testing). For the ML estimates, significant differences were observed for AF and IA (P<0.0001 for both), but not for EU (P = 0.195). However, estimates obtained with STRUCTURE show significant differences for all ancestry axes (P <0.0001). Together, these tests indicate that there are significant differences in admixture proportions between EC and WC samples.

Table 3.

Comparing admixture in two Hispanic populations

	t-test (P value)		K-S test (P value)
Admixture Axis	MLE	STR	MLE	STR
EU	2.06 (0.041)	4.88 (<0.0001)	0.1534 (0.195)	0.3262 (<0.0001)
AF	4.76 (<0.0001)	0.769 (<0.0001)	0.3594 (<0.0001)	0.5974 (<0.0001)
IA	−6.62 (<0.0001)	−12.73 (<0.0001)	0.545 (<0.0001)	0.7643 (<0.0001)

Tests for admixture stratification

Results of the Individual Ancestry Correlation Test (IACT) using ML estimates are shown in Table 4. AA, EC and WC samples all show evidence of admixture stratification, with significant correlations observed between estimates obtained with non-syntenic marker panels for the ancestral group that contributes maximally to that sample. However, no evidence of admixture stratification was detected in the EA sample.

Table 4.

Individual ancestry correlation test:

	IA	EU	AF
EA	0.041 (0.3)	0.067 (0.09)	−0.052 (0.187)
AA	0.007 (0.917)	0.13 (0.05)	0.18 (0.006)
EC	0.236 (0.017)	0.276 (0.005)	0.549 (<0.0001)
WC	0.289 (0.006)	0.404 (<0.0001)	0.392 (<0.0001)

Significant values P<0.016 after multiple test correction are shown in bold

Using STRUCTURE, we tested for the presence of subpopulations, as measured by deviations from HWE and linkage equilibrium in the sample, given the genotypes, by specifying models with predefined numbers of subpopulations (K=1, 2 or 3) and not including any ancestral population. In the AA sample, individuals were assigned to 2 subpopulations with greater probability than to 1 or 3 subpopulations. In the other samples, EA, EC, and WC, K= 1 was the best option, indicating no evidence of substructure within them. The implications of these results are discussed later.

Simulations

Using simulation studies, we investigated how precisely this marker panel was able to estimate admixture proportions. First, we simulated genotypes of 1000 unadmixed individuals representing each of the three ancestral populations, EU, AF and IA, based on the observed allele frequencies. Individual admixture estimates of simulated data were ascertained using both ML and STRUCTURE. These simulated individuals were expected to show 100% ancestry from the corresponding ancestral population and any discrepancies with measured admixture estimates provides an indication of the bias inherent in the measurements. Table 5 shows the mean ancestry proportions estimated in the simulated samples using ML, where 63.6% of simulated IA, 57% of simulated EU, and 57.7% of simulated AF individuals showed 100% affiliation with the expected ancestral population. These results were used to compute two estimates of bias associated with this panel and the ML method. “Population Bias” refers to the ancestry estimated from non-contributing populations (e.g., total non-EU ancestry estimated in 100% EU samples). This estimate does not reflect whether such bias can be attributed to one specific non-contributing ancestral population (where more than two ancestral populations are included in the model and can be used to evaluate the reliability of observed estimates in the study samples). “Ancestry bias” is complementary to population bias in that this is a measure of the total contribution from one non-contributing population to other ancestral populations included in the analysis (for example, the total EU ancestry in simulated 100% IA or 100% AF individuals). Both ancestry and population bias was 4% or less for each group in this study, indicating that there is up to a 4% chance of individuals showing ancestry from a population from which they have no contribution when using the current marker panel and ML. Ancestry bias for both IA and EU are also up to 4%, while only 1% for AF. These estimates further demonstrate that this marker set is less able to distinguish between IA and EU populations, compared to AF and non-AF distinctions, a finding that is consistent with the expectations based on the procedure used to select the markers (Yang et al., 2005). With STRUCTURE, the bias estimates are less than 1% in each case (data not shown), indicating that the present marker panel in conjunction with the STRUCTURE algorithm yields more precise estimates.

Table 5.

Estimated ML admixture proportions in simulated ancestral samples:

Population (N)	IA	EU	AF	Population Bias
Indigenous American	0.98 ± 0.05	0.02 ± 0.05	0.004 ± 0.02	0.02 ± 0.06
African	0.02 ± 0.03	0.02 ± 0.04	0.97 ± 0.05	0.04 ± 0.07
European	0.03 ± 0.05	0.97 ± 0. 06	0.01 ± 0. 03	0.04 ± 0.08
Ancestry Bias	0.04 ± 0.08	0.04 ± 0.08	0.01 ± 0.04

DISCUSSION

We used a panel of thirty-six microsatellite markers augmented by one SNP to investigate variation in individual admixture proportions in four US populations. Studies on admixture have typically focused on a single population (e.g., African Americans from different US locations by Parra et al., 1999, Puerto Ricans by Bonilla et al., 2004a, Hispanics from Colorado by Bonilla et al., 2004, African Americans from four US cities by Reiner et al., 2005). Analyzing different populations using the same marker panel and using an admixture model based on known population history of the samples provides an opportunity to evaluate empirically admixture distributions in different US populations and to compare the assignment methods. We observed that individual admixture proportion varies in all populations, with greater variation in populations with a history of continental admixture (i.e., AA, EC and WC). Individual admixture estimates obtained in this study are generally similar to previously reported estimates in these populations (Parra et al., 1999, Bonilla et al., 2004a, 2004b; Reiner et al., 2005; Halder et al., 2008). However, most of these previous studies did not establish the threshold above which computed admixture estimates can be considered reliable. Using simulations, we have established this threshold against which one can compare the observed estimates. We also show that with different estimation methods (i.e. ML vs. STRUCTURE), the threshold may vary, such that we can expect reliable estimates within 99% of expected values with STRUCTURE and within 96% with ML. The estimates obtained with either method are highly correlated. Using two different tests, we detected presence of stratification attributable to admixture in the AA sample. One test also detected presence of admixture-stratification in the EC and WC samples. Although a few EA individuals did show some non-European admixture, neither of the formal tests concluded presence of admixture-stratification in the EA sample.

The marker panel used here is comparable to some AIM panels used previously for individual admixture estimation in terms of information content as measured by total δ_c (Shriver et al., 2003; Bonilla et al., 2004). For instance, Bonilla et al., 2004a used a panel of 36 AIMs where total δ was 11.72 for EU-IA comparison, 14.28 for EU-AF comparison and 16.34 between AF-IA (Bonilla et al., 2004a). In comparison, total δ_c in the present panel is 12.6 for EU-IA comparison, 14.35 for EU-AF comparison, 17.3 for AF-IA comparison. Total information content of the present marker panel, which consists mostly of STRs, is comparable to that of SNP panels used in previous studies (Shriver et al., 2003; Bonilla et al., 2004), and thus provides an alternate panel of comparable power for individual ancestry estimation. Individually, more than 50% of the marker panel is informative for any pair-wise comparison between populations as indicated by the individual marker δ_c values, which are >0.3. Measures of ancestry Informativeness (I_n), indicate that most of the markers are highly informative for ancestry. Finally, the simulation studies have established the lowest threshold above which the admixture estimates obtained should be considered highly reliable. Detailed comparison of this marker panel to previous ones is beyond the scope of this paper. The choice of markers has been optimized for easy amplification and genotyping (as discussed in Yang et al., 2005) and is likely to be a good resource for individual admixture estimation. This panel has less information than some larger SNP-AIM panels, but it can provide good estimates of individual admixture. This marker set has some advantages. Many of the markers are from the standard CODIS panel and have been widely genotyped in several populations (Budowle et al., 2001) while others are from previously published studies (Smith et al., 2001) and are part of standard Marshfield marker panels. Thus, obtaining ancestral allele frequencies from other populations is straightforward. Several existing genotype-phenotype databases (for example, those based on reports from the Framingham Heart, Hypergen, GenNet, and Genoa studies) have all used the Marshfield panel of markers and should already have many of these marker genotypes available. Genotyping the additional CODIS markers included in the current panel may add more value than genotyping an entirely new SNP AIM panel for individual admixture estimation in these samples. With the threshold of accurate admixture estimates now defined by our simulation studies, this panel should prove to be an important resource in population based studies. We chose to use a three-way admixture model comparing EU, AF and IA populations because of the close association among these populations in the United States for as long as five hundred years. While the history of migration and admixture is a well documented and a continuing process in AA, EC, and WC populations, EAs are a more homogeneous group. However, given the close association of the populations in the continental United States, it is likely that some EA individuals have non-European admixture. Indeed, both admixture estimation methods showed low levels of non-European admixture in this sample. The biological significance of this variation or the possible effects that this may have on phenotype-association studies warrants further investigation. An interesting aspect of our results is the difference in admixture estimates between the EC and WC samples. The term “Hispanic” denotes individuals who share a common language rather than a shared geographical origin and includes Mexicans, Cubans, Puerto Ricans, and numerous other South and Central American populations. Depending on the demographic history of the population sampled, the admixture proportions may differ. In our study, the EC sample from Connecticut is more likely to be of Puerto Rican origin and has higher AF admixture compared to the WC sample. In contrast, the WC sample recruited from California has greater Mexican contribution, reflected in higher detected IA admixture compared to the EC sample. These results further illustrate why genetic association studies in different “Hispanic” groups may yield very different results, if the phenotype being tested varies as a function of genetic ancestry.

Individual admixture estimates obtained with STRUCTURE and ML was highly correlated in AA, EC and WC, and to a lesser extent in EA. While correlation in admixture estimates obtained with different methods may be used as an indicator of reliability of these estimates (Shriver et al., 2003; Bonilla et al., 2004a, 2004b; Reiner et al., 2005; Shriver et al., 2005), we also found that the estimates differed significantly based on the method used. This is exemplified in the tighter clustering of STRUCTURE estimates compared to ML estimates (see for instance Supp. Figures S1 and S2), and likely reflects the differences in statistical theories underlying the estimation procedures. Simulation studies have shown that with large sample sizes and large panels of AIMs, Bayesian and ML estimates will be asymptotically equivalent (McKeigue et al., 2005; Tang et al., 2005). But the assumptions underlying each estimation method are different and the results should be interpreted after considering these assumptions. ML relies on pre-specification of the exact ancestral allele frequencies. More precise estimates of ancestry depend on 1) appropriate ancestral populations being specified, 2) use of an adequate sample sizes used to estimate ancestral allele frequencies, 3) use of a complete data set used with few missing genotypes, and 4) use of a sufficiently informative panel of ancestry informative markers. Estimates for each individual depend on the exact markers genotyped in that individual, and since each locus is treated as an independent observation, the information inherent in linked loci cannot be used explicitly (unless haplotypes are modeled and haplotype frequencies are used). The sample size of the admixed population under investigation has no effect on the estimate of any one individual. In contrast, the Bayesian MCMC methods have been proposed to take into account the inherent uncertainty in 1) choice of ancestral populations, i.e., the admixture model assumed, 2) the allele frequency estimates in ancestral populations, and 3) ambiguities arising due to missing data. The STRUCTURE algorithm uses admixed and unadmixed individuals to make inferences for any one individual and simultaneously infers allele frequencies in all populations (admixed and non-admixed) and ancestry proportions in all individuals in the sample. We have included ancestral populations and specified the “Usepopinfo” option to augment the inference. In addition, the Bayesian framework allows individuals of known (e.g., more homogeneous) ancestry to be included in the EA, AA, EC and WC samples for additional information when inferring the ancestry of each unknown individual. The ML estimates for each individual are independent of others in the sample, while other individuals included in the sample influence the STRUCTURE estimates.

The AA, EC and WC samples in our study were smaller than the EA sample and have wider variation in individual admixture estimates. The continuum of admixture estimates is captured by both methods, leading to higher correlations. In the larger EA sample (N = 652), true non-European admixture for most individuals is much lower, which influences the estimates obtained for the few individuals who do have higher non-European admixture. Although we have relatively large numbers of individuals, we used a relatively small marker set, which could also partly explain the discrepancies between the estimates. The convergence of the STRUCTURE algorithm indicates that the observed estimates are the best possible ones, given the data. Just as the ML assumes fixed ancestral allele frequencies, the STRUCTURE algorithm assumes a unimodal Dirichlet prior distribution, for both allele frequencies and ancestry estimates. If the true distributions of these parameters in the samples were different, it would skew the admixture estimates. In our simulation studies too, we observed that the bias with STRUCTURE was lower than that with ML. We speculate that when true variation among individuals in the EA sample being studied is low, the effect of a few individuals who are genetically distant from the majority of individuals (i.e., having higher admixture) is minimized in a larger sample than in a smaller sample. When the sample size is small, including a few individuals who are very different from the others will have a more appreciable effect. However, when there is greater variation in the sample, in this case due to substantial historically documented admixture, the sample size of the admixed population is less of an issue. Other statistical approaches like the Principal Components method may be more suitable for detecting stratification in the European American sample (Paschou et al., 2008).

The differences in statistical procedures also contribute to the different results obtained in EC and WC with the two tests for stratification. Evidence of admixture-stratification in EC and WC was detected only with the IAC test and not with STRUCTURE. Given the known history of admixture in these populations, apparently there exists a continuum in ancestry proportions, as opposed to distinct subgroups. Indeed, plots of admixture estimates (Supp. Figures S1 and S2) show this, using both methods. Using STRUCTURE, evidence of admixture-stratification is detected by deviations from HWE and linkage equilibrium. It is theoretically possible that random mating within the EC and WC samples used here resulted in situations where neither of the assumptions of the algorithm were violated and hence, the program did not detect any evidence for subpopulations. On the other hand, the IAC test examines relative differences between individuals in the population. If ancestry proportions vary substantially within the population, then on average, all regions of the genomes in each individual will reflect this variation. The relative differences between individuals will be retained irrespective of the part of the genome used to infer admixture proportions for each individual. This relative genetic distance between individuals is examined by inferring individual admixture using non-syntenic marker panels. Indeed, previous simulation studies have shown that without admixture-stratification, no association is observed between admixture proportions estimated with different sets of markers (Pfaff et al., 2001). Thus, despite not detecting presence of admixture-stratification using STRUCTURE, variation in individual admixture in AA, EC and WC are indicators of possible confounding in case-control associations if not taken into consideration, since disease risk and prevalence may vary with admixture proportions.

The small amounts of IA ancestry detected in some of the AA individuals may lead to questions about whether this ancestry axis is real or an artifact of the population model. STRUCTURE results showed that a k=2 model is a better fit to the data as opposed to a k=3 model and the IACT tests did not show any stratification along the IA axis. The distinction to be made here is between the population and the individual. While IA ancestry in the overall population may indeed be as low as to appear an artifact (i.e. not detectable by some formal tests), a few individuals could still have significant IA ancestry that is different from their EU ancestry. We have shown that this marker panel is able to distinguish between EU and IA ancestry within the range of error identified by the simulation studies. Given the demographic history of the US and the known cultural histories of these particular populations, low levels of IA ancestry is expected in the general African American population, while for some individuals the IA ancestry could be very high. We found mean IA ancestry in AA to be at least 4% with both methods, which is at the significant threshold for ML estimates and above the threshold for the STRUCTURE estimates. It is possible that the few individuals who showed high IA ancestry contributed to this overall mean. For these specific individuals, this ancestry component is indeed useful to adequately attribute a portion of their genetic heritage to IA ancestry as opposed to EU ancestry. In a population-based study, however, such as admixture mapping, such individuals may not provide any additional information. In such cases the few individuals who have high IA ancestry may either be outliers (and hence ideally be removed from subsequent analysis) or simply not contribute enough information as to substantially alter the results of a genotype-phenotype association or admixture mapping study with a reduced ancestral population model. We have previously demonstrated this phenomenon in a sample of Puerto Ricans (Halder et al., 2008). Since our goal in this study was to quantify individual admixture, we have used the three-population model which we believe to be adequately representative of the underlying demographics.

Choice of ancestral populations included in the analysis has a significant effect on admixture estimates obtained with any statistical method. We have used a sample of Spanish individuals as a representative European ancestral population. While this sample is apparently adequate to analyze the two Hispanic samples, there are clear limitations for the analyses in AA and EA samples when using this Southern European ancestral group. Most obvious European ancestors of EA populations include the British, Irish, German and Italian populations and the most appropriate ancestral EU population would be one that includes representation from these specific European populations. Given less variability among different European populations, this issue is perhaps less important than restricting the variation within the African continent by only using a single AF ancestral group. We used a West African population from Sierra Leone based on the historical contributions of this region to the modern African-American gene pool. Thus, adding more African and European populations would qualitatively enhance the ancestral allele frequency estimates. Nonetheless, the distributions in admixture estimates obtained provide empirical evidence describing variation in individual admixture in different US.

The simulation of unadmixed individuals indicates that the present marker panel easily has sufficient power to distinguish between the three ancestral populations, using either statistical method. In the simulated samples, individual admixture in the West African ancestral sample showed equal variation along both of the non-African axes, whereas in the European and Indigenous American samples variation was greater along the EU-IA axis. This possibly reflects the more recent shared common ancestry between these populations and lower total IA-EU δ_c (since the markers were initially selected to have high African vs. non-African discrimination). While the large sample sizes (N = 1000) may have affected the STRUCTURE estimates, which shows >99% ancestry for each ancestral population, ML, which is unaffected by sample size, shows that there is <5% chance of ancestry bias or population bias using this marker panel. Theoretically, for samples of individuals simulated to have no admixture, all individuals are expected to show 100% ancestry from one population. Observed variations in individual admixture is a function of the ancestry information content of the marker panel and the method used for making inferences. For instance, for a set of 90 SNP markers in which alternate alleles are fixed in different populations, ancestry estimates are observed as expected (i.e. all individual have 100% ancestry from the expected ancestral group using any method of admixture estimation; IH unpublished work), when all individuals who are being studied are from one population and have no history of admixture.

Though the current microsatellite panel has good discriminatory power, it is limited in not having such definitive ancestry information content. Based on computed δ_c levels, this panel compares to some SNP panels reported previously for individual admixture estimation (e.g., Shriver et al., 2003 reported a panel of 34 AIMs with summed δ values of 15.8 (AF-EU), 17.2 (AF-IA) and 12.55 (IA-EU); Bonilla et al., 2004b reported a panel of 35 AIMs with summed δ values of 14.4 (AF-EU), 16.6 (AF-IA) and 11.7 (IA-EU)). However, this measure consolidates information across multiple loci, which can have important consequences. When biallelic SNPs are used, assigning ancestry to an allele is a straightforward process, since frequencies of only two possible alleles have to be considered. In contrast, for multiallelic loci, there is a greater chance that some alleles will be missing in ancestral populations that exist in moderate frequency in the admixed sample, due to stochastic variation. MLE will treat such alleles as missing. In such cases, it may be more efficient to use linked markers in Bayesian MCMC methods (like STRUCTURE), which can incorporate information in linked markers for making inferences of individual ancestry.

In conclusion, this study provides a description of individual admixture distribution in different US populations and shows that individual admixture varies in all populations, more in those with a known recent history of admixture. Such variation may not lead to the creation of distinct subgroups, but rather a continuum of individual admixture proportions that, unless accounted for, is likely to affect case-control associations. Comparisons of the two Hispanic groups further suggest that there is geographic heterogeneity among samples that reflects the demographic histories of the populations. Finally, as the simulations indicate, the marker panel described here can be used reliably for inferring individual admixture proportions in different US populations.