Unidirectional Brownian motion observed in an in silico single molecule experiment of an actomyosin motor

Abstract

The actomyosin molecular motor, the motor composed of myosin II and actin filament, is responsible for muscle contraction, converting chemical energy into mechanical work. Although recent single molecule and structural studies have shed new light on the energy-converting mechanism, the physical basis of the molecular-level mechanism remains unclear because of the experimental limitations. To provide a clue to resolve the controversy between the lever-arm mechanism and the Brownian ratchet-like mechanism, we here report an in silico single molecule experiment of an actomyosin motor. When we placed myosin on an actin filament and allowed myosin to move along the filament, we found that myosin exhibits a unidirectional Brownian motion along the filament. This unidirectionality was found to arise from the combination of a nonequilibrium condition realized by coupling to the ATP hydrolysis and a ratchet-like energy landscape inherent in the actin-myosin interaction along the filament, indicating that a Brownian ratchet-like mechanism contributes substantially to the energy conversion of this molecular motor.

Molecular machines in living organisms are nanometer-sized small systems working robustly and efficiently in the presence of the severely disturbing thermal noises. Furthermore, in the case of the molecular motors, the energy supplied by the hydrolysis of adenosine triphosphate (ATP), which is to be converted to the mechanical work, is only an order of magnitude larger than the thermal energy at room temperature (∼20k_BT), and hence it seems likely that the molecular machines harness the thermal noise, instead of suppressing it as the human-made machines do (1). This distinct feature of the molecular machines should arise from the atomic structures of the constituent proteins, which is reflected in the current focus of interest in the structural aspect of the molecular machines. However, it should be remembered that the structural aspect is not everything but is inseparably linked to the dynamical and energetical aspects. Therefore, a unified description of structure, dynamics, and energetics is the step necessary to understand the molecular-level physical principle of how the molecular machines work.

The actomyosin molecular motor, the system composed of myosin II and actin molecules, is responsible for muscle contraction, and is the most extensively studied molecular motor. It has been shown by single molecule experiments (SME) that a single myosin molecule and an actin filament (polymerized actin) constitute the minimal force-generating unit of this motor (2–4) (see Fig. 1A). Although SME has been a powerful approach to study the dynamical aspect of the force-generating unit (2–4), the limitation of the spatiotemporal resolution of SME has inhibited us from developing the full atomistic picture of the force-generating process. On the other hand, since the currently available high-resolution structures of myosin (5–7) are those obtained in the crystalline environment and in the absence of actin, it remains unclear whether the structural changes inferred from the crystal structures actually occur when the motor is at work (7). While the model structures for the actomyosin complex (8–10) have provided useful information on the actin-myosin interaction, the energetical and dynamical aspects cannot be addressed solely by the structural information. As an approach that unifies the strong points of SME and structural studies, the in silico (computer-based) SME, in which the structural, dynamical, and energetical aspects are collectively taken into account, should play an important role.

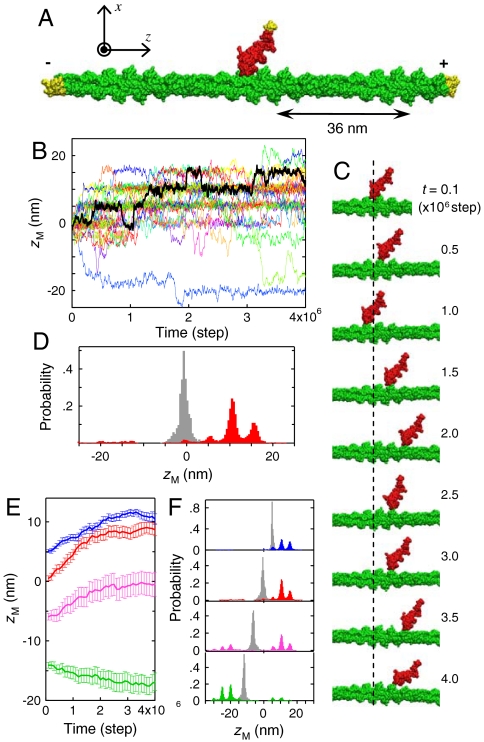
Fig. 1.

Unidirectional Brownian motion observed in the in silico SME. (A) The three-dimensional structure of the actomyosin complex we used as the base structure. Myosin and the actin filament are colored in red and green, respectively. The portions to which restraints are applied were colored in yellow. The long axis of the actin filament was set in parallel to the z axis, and the mass center of the actin filament was set at the origin of the coordinate system. (B) Time courses of the z-position of the mass center of the myosin head, z_M, are shown. Myosin was initially placed near the center of the actin filament (z_M(0) = -0.7 nm). The black line represents a sample time course, the snapshots of which are shown in (C). (D) Probability distributions of z_M are shown for the initial stage (0 ∼ 0.03 × 10⁶ steps; gray) and the final stage (3.7 × 10⁶ ∼ 4 × 10⁶ steps; red). (E) Average time courses in the case of z_M(0) = 4.8 (blue), -0.7 (red), -6.2 (magenta), and -11.7 nm (green). The error bars represent the standard errors. (F) Probability distributions of z_M in the case of z_M(0) = 4.8, -0.7, -6.2, and -11.7 nm (from the top to the bottom; the initial distribution is colored in gray, and the final distribution is colored so as to correspond to E).

The actomyosin molecular motor converts the chemical energy of ATP to the mechanical work in a cyclic manner. In each cycle, myosin hydrolyzes a single ATP molecule and couples this chemical reaction to the physical state transition between the weak and strong actin-binding states (11 and 12). The weak-to-strong actin-binding transition has been thought to play a key role in the force-generation (12). However, when and how the force is generated remains controversial (7 and 13). While it is widely held that the force is generated just after the weak-to-strong transition via the so-called lever-arm mechanism (6), it has been demonstrated that the force-generation occurs during the weak-to-strong transition via a Brownian ratchet-like mechanism (4). This controversy has not yet been settled and the argument about the relative importance of these two mechanisms has been extended beyond the muscular (i.e., myosin II-based) motor to the nonmuscular (myosin V or VI-based) motors (14), and provoked active investigations on the roles of the Brownian motion in molecular motors (15–19), which has also been actively studied theoretically (20–22). Despite these studies, the Brownian ratchet-like mechanism remains elusive, in contrast to the lever-arm mechanism which is so illustrative as is explained in many textbooks of molecular biology and biochemistry.

In this study, in order to provide a clue to resolve the controversy and analyze whether the Brownian ratchet-like motion is indeed possible, we conduct an in silico SME of the muscular (myosin II-based) actomyosin motor system, simulating the in vitro SME of the force-generating unit (2–4), with the focus on the weak-to-strong transition as has been studied theoretically (22). With the in silico SME, we show that the movement of a single myosin molecule is stochastic but has a statistically definite unidirectionality along the actin filament. We further show that this unidirectionality arises from an asymmetric funnel-like energy landscape of the actin-myosin interaction, which forms a ratchet-like landscape with 36 nm (nanometer) periodicity. The asymmetric funnel can be viewed as a “functional funnel,” which would be a general ingenuity for molecular machines to function efficiently and robustly in the presence of the thermal noise.

Results

In Silico Single Molecule Experiment.

In our in silico SME of the actomyosin system, the above mentioned essential aspects have been taken into account: structures of myosin/actin (5, 9, 10, 23), physico-chemical intermolecular interaction energies (24 and 25), and molecular dynamics. In order to observe the large-scale spatio-temporal behavior of the actomyosin system involved in the weak-to-strong transition, we used a coarse-grained representation of structures of myosin/actin, where amino-acid residues are represented by Cα atoms (see Materials and Methods). The actomyosin system we studied consists of a single-headed myosin molecule (subfragment 1 of chicken skeletal muscle myosin) and a 110-nm-long filament of rabbit skeletal actin (Fig. 1A). The actin filament, set in parallel to the z axis, was fixed in space via restraints applied to the terminal protomers. Simulating the setup of the in vitro SME (4), we applied restraints to the tip of the tail domain of myosin in the x and y-directions, and observed the motion of myosin. No external force was applied to myosin in the z-direction, so that myosin would exhibit a free one-dimensional Brownian motion along the actin filament if there were no interaction with the actin filament.

We placed myosin near the center of the actin filament, as shown in Fig. 1A, and observed how myosin behaves. The time course data of the z-position of the mass center of myosin, z_M, shows that myosin did not stay at the initially-placed position (z_M = -0.7 nm) and began to move along the actin filament in a stochastic manner (Fig. 1B). The snapshots for a typical time course data (Fig. 1C) illustrate that myosin exhibited a “sliding” motion along the actin filament (see also Movie S1). Almost all of the time course data shown in Fig. 1B were of this sliding-motion type, and further presented the following striking features: One is the net unidirectionality toward the plus direction, i.e., toward the plus-end of the actin filament. This unidirectionality is unexpected, because no external force was applied to myosin along the actin filament. The other feature is that the motion of myosin was stepwise, the step-width coinciding with the actin monomer size (5.5 nm). These two features, as well as the stochastic nature, are more clearly seen in the probability distribution of z_M (Fig. 1D, see also Fig. S1), indicating that in our in silico SME, myosin exhibited a unidirectional, stepwise Brownian motion along the actin filament. These features bear strong resemblance to those observed in the in vitro SME by Kitamura et al. (4). Our in silico SME further shows that the unidirectionality is dependent on the initial z-position of myosin (Fig. 1E): the net unidirectionality toward the plus-end was observed for z_M(0) = 4.8, -0.7 and -6.2 nm, whereas that toward the minus-end was observed for z_M(0) = -11.7 nm.

One would wonder why the net unidirectionality arises and why it is dependent on the initial z-position. The probability distribution of z_M (Fig. 1F) demonstrates that there are regions where myosin is highly populated, which indicates that myosin had preferential binding regions on the actin filament. Within the z-range displayed in Fig. 1F, two such regions can be found: one located at z ∼ 10 nm and the other at z ∼ -20 nm. The existence of such preferential binding regions immediately solves the above questions: i.e., myosin tends to move toward the nearest preferential binding region. This is exactly what has been observed in the in vitro SME by Steffen et al. (26). Moreover, in our in silico SME, it was found that myosin shows the unidirectionality toward the plus-end even when it is placed at about the midpoint of the two preferential binding regions (see the results shown in magenta in Fig. 1 E and F). Therefore, truly striking is that the unidirectionality toward the plus-end dominates over that toward the minus-end and hence is not canceled out even after averaging over initial z-positions.

Energy Landscape and Asymmetric Funnel.

Then, to elucidate how the asymmetry of the preferential binding regions arises, we investigated the actin-myosin interaction energy. The structural quantity of interest is z_M, so we calculated the average actin-myosin interaction energy as a function of z_M, which we refer to as the “energy landscape” (Fig. 2). The energy landscape perspective has been applied to the study of complex motions of proteins, and spawned fruitful concepts such as “conformational substates (27)” and “folding funnel (28).” The energy landscape for the actin-myosin intermolecular interaction (Fig. 2) was found to present these two features: the “substates” appearing at the intervals of ∼5.5 nm, and an underlying “asymmetric funnel” (see the arrow pairs colored in cyan) with gentler slope toward the plus-end. It is important to note that the energy landscape depicted in Fig. 2, which was obtained using the data in the relaxation (i.e., nonequilibrium) processes where myosin exhibits the unidirectional motion, coincides well with the energy landscapes obtained under the equilibrium condition (Fig. S2). This indicates that the unidirectionality observed here arises from the equilibrium aspect of the energy landscape.

Fig. 2.

Energy landscape along the actin filament. Instantaneous intermolecular potential energies that the actomyosin system experiences during the Brownian motion of myosin were bin-averaged with regard to z_M (with the bin-width Δz_M of 0.2 nm). To probe a wide range of the energy landscape, time course data with varying initial z-positions (z_M(0) = -17.2 ∼ 29.3 nm) were used. A pair of arrows (cyan) is drawn to emphasize the underlying “asymmetric funnel.” The succession of the asymmetric funnels results in a ratchet-like appearance.

In Silico Mutagenesis.

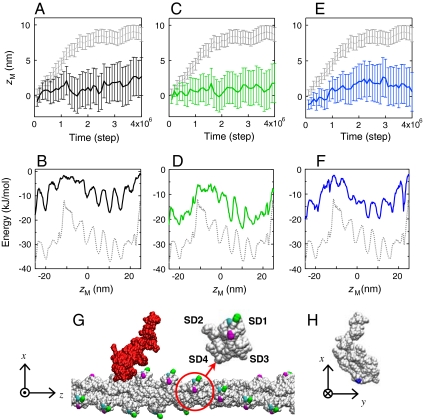
We then scrutinized the energy landscape and the resulting unidirectional Brownian motion by perturbing the actin-myosin interactions, making comparisons with corresponding in vitro experiments. It has been shown by an in vitro motility assay that the myosin’s ability to move an actin filament is diminished as the ionic concentration is increased (29); we therefore examined the effect of the ionic concentration. When the ionic (KCl) concentration was increased from 25 mM to 100 mM, the unidirectionality in the Brownian motion was significantly reduced (Fig. 3A), and myosin sometimes dissociated from the actin filament. These results are consistent with the in vitro motility assay (29) and highlight the critical role of the electrostatic interaction. The reason for the loss of motility is now clearly understood on the basis of the energy landscape (Fig. 3B): The asymmetric funnel is made significantly shallower as the ionic concentration is increased and the actin-myosin electrostatic interaction is weakened.

Fig. 3.

Effects of ionic concentration and amino acid mutations. (A, B) The average time course of z_M and the energy landscape which were obtained at 100 mM KCl are shown, respectively, together with those of the original (at 25 mM KCl; gray dotted line). The error bars represent the standard errors. (C, D) The results for the double mutation D1H/E2H (green) are shown together with those of the wild type actin. (E, F) The results for the charge neutralizing mutation introduced on the lysines in loop 2 of myosin (K640/K641/K642) are shown (blue), together with those of the wild-type myosin. (G) The positions of the mutated residues in actin are depicted: D1/E2 (green), D24/D25(magenta), and E99/E100 (cyan) (The results for D24/D25 and E99/E100 are presented in Fig. S3). An actin protomer (circled) is displayed in a magnified view, with the subdomains (SD1-4) labeled. (H) The positions of the mutated lysines in myosin are shown (blue).

This result arouses further interest as to which amino acid residues are involved in the electrostatic interaction. Motility assays combined with mutagenesis should provide useful information on this problem. As an example, we introduced a double charge reversal mutation into the N terminus (D1H/E2H), and found that the mutation diminishes the unidirectionality in the Brownian motion (Fig. 3C). The single mutation, D1H, yielded an intermediate result between the double mutant and the wild type (Fig. S3). Another double mutant, E99H/E100H, was also found to diminish the unidirectional Brownian motion (Fig. S3). These results are all consistent with the in vitro motility assay (30 and 31), and are clearly understood by the energy landscape shallowing (Fig. 3D and Fig. S3). Thus, these acidic residues, constituting a negatively charged cluster on the surface of subdomain 1 of actin (Fig. 3G), are shown to be involved in the actin-myosin electrostatic interaction. Loop 2 of myosin, on the other hand, has been thought to interact with actin, and the charge neutralizing mutation at the conserved lysines in loop 2 was shown to impair the myosin’s ability to move an actin filament (32). The in silico charge neutralizing mutation introduced into the lysines in loop 2 (K640/K641/K642) showed that these residues are actually involved in the actin-myosin electrostatic interaction (Fig. 3 E and F). The predicted shallowing of the energy landscape should be directly observed in an in vitro single molecule experiment.

Structural Origin of the Ratchet Potential.

Suppose that myosin moves in parallel to the actin filament (Fig. 3G); as myosin moves to the right, lysines in loop 2 (Fig. 3H) become closer to the acidic-residue cluster of the nearest actin protomer, gradually strengthening the electrostatic interaction and making a gentle descent in the energy landscape. As myosin moves further to the right, the nearest accessible acidic-residue cluster is switched to the one in the opposite strand, resulting in a steep ascent in the landscape. In this switching, the acidic residues, D24 and D25, which are located in between the two clusters (Fig. 3G), play an important role: indeed, charge reversal mutation (D24H/D25H) was found to affect the energy landscape (Fig. S3). After the switching and further moving to the right, due to the helical structure of the filament, the identical actin-myosin interface reappears. Note that the asymmetry along the actin filament arises due to the fact that there is no structural symmetry in the actomyosin complex other than the helical symmetry of the actin filament (i.e., there is no reflection symmetry in the charge distribution and resulting electrostatic potential along the long axis of the filament).

However, the above explanation does not hold if the actin filament rotates about its long axis. Indeed, the asymmetric funnel disappeared when the actin filament was allowed to rotate about its long axis (Fig. S4). Although, when the frictional coefficient for the actin filament was increased, as is the case for a filament attached to large beads (2, 3, 26) or glass surface (4), the asymmetric funnel reappeared (Fig. S4). This result reflects that an axial torque accompanies the force generation along the actin filament, as has been observed in the motility assays (33 and 34). On the other hand, when myosin was allowed to change its orientation relative to actin (while the azimuthal orientation about the actin filament was still restricted), the asymmetric funnel and the resulting unidirectional motion remained substantial (Fig. S5); the unidirectional motion toward the plus-end arises (though reduced) even when myosin is rotated 180 degrees about the x axis (Fig. S5), indicating that the polarity of the unidirectional motion is determined by the polarity of the actin filament, in agreement with the in vitro SME (3 and 35).

Discussion

Brownian motion is isotropic under thermal equilibrium, and a net unidirectionality arises only when the system is out of equilibrium. The actomyosin motor works in a cyclic manner, coupling the chemical reaction of ATP hydrolysis, which is maintained out of equilibrium and accompanied by a decrease in Gibbs free energy, to the force-generating physical transition between the weak and strong actin-binding states (11 and 12). To understand the energy-converting mechanism, it is vital to relate the physical process in which we observed the unidirectional Brownian motion to the chemical reaction cycle of ATP hydrolysis.

Since the actin-myosin interaction becomes stronger during the process we observed (“a” in Fig. 4), it is natural that this process is involved in the transition from the weak actin-binding to the strong actin-binding states (11 and 12). The weak-to-strong transition is a fast event occurring on the timescale of milliseconds (4 and 36) (see also Fig. S6 and discussion therein). This transition is triggered by ATP hydrolysis, and during the transition, myosin is supposed to retain the hydrolysis products (ADP and inorganic phosphate (Pi)) (13 and 37) and generate force (13 and 38). The weak-to-strong transition is thought to accompany structural changes of myosin, such as closure of the actin-binding cleft (8–10, 37, 39) and rearrangement of loop 2 (9 and 39). Since our myosin is in the cleft-closed state (see Materials and Methods and Fig. S7), it would be able to get near the strong binding state. However, the accomplishment of the strong binding state (“b” in Fig. 4) may require further induced-fit-like (plastic) structural changes not only in myosin but in actin, including surface loop rearrangements, which are beyond the applicability of the elastic model used in the present study (Fig. S8). It is generally thought that the accomplishment of the strong binding state and the subsequent hydrolysis-products release (13 and 37) induce force-generating lever-arm motion (6, 7, 13, 38, 39). Therefore the force could be generated in two steps (13 and 38) during the weak-to-strong transition: The first step is via the unidirectional Brownian motion we observed here, and the second step, which remains to be studied, is via the structural changes including the lever-arm motion taking place when myosin binds strongly to the actin filament. After the accomplishment of the strong binding state, binding of ATP to myosin causes myosin to dissociate from actin (“c”) (11). Structural changes such as cleft opening (10, 39, 40) and loop 2 rearrangement (39) are thought to be involved in this process. Myosin is then brought into the detached state (E₂ in Fig. 4), where the actin-myosin interaction is so weak that myosin exhibits an almost isotropic Brownian motion (“d”). When ATP is hydrolyzed, the ratchet-like energy landscape (E₁) is turned on (“e”), so that myosin reenters the weak-to-strong transition and goes into the next cycle (“a”’). Note however that the way the above-described key structural changes are induced by the chemical state changes of ATP hydrolysis (i.e., the allosteric mechanism) has not yet been clearly understood, prompting further studies at the molecular level.

Fig. 4.

Schematic view demonstrating how the motion of myosin is associated with ATP hydrolysis. The solid curve, E₁, represents the energy landscape found in our study (see Fig. 2), while the dotted curves, and E₂, represent putative energy landscapes for the strong actin-binding (nucleotide-free) and the detached (ATP-bound) states, respectively. For convenience, different colors are used for the high-energy (magenta) and low-energy (blue) regions. Arrows constitute a possible sequence of myosin motion coupled with ATP hydrolysis: (a) unidirectional, stepwise Brownian motion as found in our study (see Fig. 1) in the presumed ADP·Pi-bound state, (b) transition into the strong binding state upon products (ADP and Pi) release, (c) dissociation from the actin filament upon new ATP binding, (d) essentially isotropic Brownian motion in the ATP-bound state, (e) reentry to E₁ upon ATP hydrolysis (i.e., in the ADP·Pi-bound state).

When E₁ is turned on (“e”), the myosin position (z_M) is randomized as a result of the extensive Brownian motion in “d”, which is essential for the unidirectional motion: Suppose that the probability distribution of z_M has become practically uniform when E₁ is turned on, it then follows that the probability distribution undergoes a gradual change presenting a net forward shift due to the ratchet-like shape of E₁, as has been observed in Fig. 1 E and F where the initially uniform distribution is approximately represented by the set of the evenly-spaced initial distributions (gray distributions in Fig. 1F). Therefore, it is the combination of the ratchet-like energy landscape and the nonequilibrium initial distribution that produces the unidirectional Brownian motion. From the energetical viewpoint, a substantial part of the total free energy of ATP hydrolysis (∼50 kJ/mol under the physiological conditions (41)) is used to forcibly switch the energy landscape from to E₂. Essentially similar theoretical models have been proposed as a flashing ratchet model (20 and 21) or a more realistic energy landscape-based model (22). Our study embodies these theoretical models, indicating that a Brownian ratchet mechanism is likely to contribute substantially to the energy conversion of the actomyosin motor.

The single-headed kinesin, KIF1A, is known to move along the microtubule toward the plus-end with high processivity. Interestingly, it has been shown that this unidirectionality arises during the transition from the weak microtubule-binding to the strong microtubule-binding states (18); the same result has been reported for the conventional kinesin (19). These results imply that the energy landscape for the kinesin-microtubule interaction is asymmetric (with 8-nm periodicity of the microtubule), suggesting that the same Brownian ratchet mechanism as found here is inherent in the kinesin-microtubule system (18). Myosin V moves along the actin filament in a dimeric form with high processivity. A clock-escapement-like mechanism to regulate ADP release has been shown to play a critical role in the high processivity (42–44). In addition, the longer and more positively charged loop 2 of myosin V, which makes the energy landscape for the actin-myosin interaction deeper, would contribute to the high processivity. The asymmetric funnel would also help the detached head of myosin V, which exhibits an extensive Brownian motion (15 and 16), to quickly find the preferential binding site (42). A Brownian ratchet-like mechanism may also contribute to the force generation via a strain-dependent weak-to-strong transition, as has been shown by a recent in vitro SME of myosin VI (17).

From a general point of view, such an asymmetric funnel as found in the present study can be regarded as “functional funnel,” i.e., the energy landscape designed to fulfill functions efficiently and robustly. The functional funnel may be nature’s ingenious mechanism that enables molecular machines to harness the thermal noise, just as the “folding funnel” enables proteins to find their native structures efficiently and robustly via a Brownian search (28).

Materials and Methods

Base Structure of Actomyosin Complex.

Although no crystal structure is available for the actomyosin complex, electron-microscopic (EM) studies (8–10) provide us with a useful frame. In the present study, following the EM models, we prepared the base structure of the actomyosin complex for our in silico single molecule experiment. In the actomyosin complex model proposed by Holmes et al. (10), the actin filament is modeled based on the x-ray diffraction data of the oriented actin-filament fiber and the crystal structure of rabbit skeletal actin monomer (23). By using the protomer structure and its intrafilament alignment of the Holmes et al. model, we prepared a filament composed of 39 actin protomers with 13/6 helical symmetry, resulting in a 110-nm-long actin filament, which was used as the base structure of the actin filament. Missing residues in the protomer were complemented by using MODELLER (45). (Note that the actin filament structure recently refined by Oda et al. (46) gave essentially the same results (see Fig. S7)). The myosin structure in the actomyosin complex has been modeled based on the EM density map of the myosin subfragment 1 (S1) strongly bound to the actin filament (8–10) and the crystal structure of S1 of the chicken skeletal muscle myosin (5). It has been pointed out that the actin-binding cleft of myosin must be closed to fit the crystal structure into the EM density map (8–10). We employed the myosin structure model proposed by Mendelson and Morris (9) for the reason that missing loops of myosin, including loop 2, are complemented. We superimposed this structure onto the higher-resolution EM model by Holmes et al. (10), which was used as the base structure of myosin. In addition, to examine the influence of possible large-scale structural changes within myosin, we studied (i) the myosin structure in the presumed weak actin-binding state in which the actin-binding cleft is partially opened and the lever-arm is raised up (47) and (ii) the effect of enhanced flexibility conferred on the surface loops in the actin-biding region (Fig. S7).

Intra-/Intermolecular Interactions.

To reduce the heavy computational load in conducting the in silico SME, we employed a coarse-grained model: The amino acid residues constituting myosin and the actin filament were treated in a coarse-grained manner as particles whose spatial positions are represented by the corresponding Cα atoms. We hereafter refer to the coarse-grained particle as “CP.” With regard to the intramolecular interaction between CPs, we employed the elastic network model (ENM) (48). ENM was applied to myosin and the actin filament, respectively, using the base structure described above as the reference structure. Note that ENM well reproduces thermal fluctuations exhibited by a protein molecule (48–50) (see also Fig. S8). With regard to the intermolecular interaction between myosin and the actin filament, we employed the electrostatic and van der Waals interactions, since these are the physico-chemical intermolecular interactions of general importance. For the electrostatic interaction, we used the Debye-Hückel potential (24 and 25). Water and ions were incorporated implicitly into the interaction model as the dielectric constant and the Debye screening length. For the van der Waals interaction, we used the 6-12 type Lennard-Jones potential (24 and 25). See SI Text for the energy functions and the accompanying parameters used in the present study.

Molecular Dynamics.

To simulate the actomyosin systems as studied in the in vitro SME (4), we applied spatial restraints to myosin and the actin filament. For myosin, we restricted the motion of the tip of the tail domain (P830 to K843 of the heavy chain and the N-terminal half of the regulatory light chain) by applying harmonic restraints in the x and y directions to each CP in the tip (see Fig. 1A): in the z-direction, no external force was applied to myosin. For actin, we fixed the filament in the coordinate system by applying harmonic restraints in the x, y, and z directions to each CP in the terminal protomers. The reference coordinates for the harmonic restraints were the coordinates in the base structure of the actomyosin complex described above. The restraint strengths were set so that the thermal fluctuations in the restraint-applied direction were reduced to be less than 0.2 nm. We then observed the motion of myosin along the actin filament. As the equation of motion, we employed the Langevin equation (25) to take into account the viscous and random forces exerted by surrounding solvents. For the random force, Gaussian random numbers were generated by the Box-Muller method using the L’Ecuyer’s algorithm with Bays-Durham shuffling (51). The mass was set at 0.11 kg/mol for all CPs, and the temperature was set at 310 K. The viscosity of the surrounding environment was set so that the translational diffusion constant of myosin results in 6.8 nm²/ns, which corresponds to the diffusion in a viscous environment with the viscosity of 7 × 10^-6 Pa·s. This viscosity is two orders of magnitude lower than that of water at 310 K. We used this low viscosity to enhance the diffusional motion of myosin and consequently to save computational time, with the same intention as has been practiced in an earlier simulation study of protein folding (52): It is shown that the time scale of the unidirectional motion increases approximately linearly with the viscosity (Fig. S6), implying that a higher viscosity would merely increase the time scale, even though it should also be remembered that the mechanism might be different at a higher viscosity. The equation of motion was numerically integrated with the time increment of 3.3 × 10^-5 ns, and 4 × 10⁶ step integration was carried out. For each condition, we conducted a total of 64 independent runs.