Abstract
The transfer model implying additivity of the peptide backbone free energy of transfer is computationally tested. Molecular dynamics simulations are used to determine the extent of change in transfer free energy (ΔGtr) with increase in chain length of oligoglycine with capped end groups. Solvation free energies of oligoglycine models of varying lengths in pure water and in the osmolyte solutions, 2M urea and 2M trimethylamine N-oxide (TMAO), were calculated from simulations of all atom models, and ΔGtr values for peptide backbone transfer from water to the osmolyte solutions were determined. The results show that the transfer free energies change linearly with increasing chain length, demonstrating the principle of additivity, and provide values in reasonable agreement with experiment. The peptide backbone transfer free energy contributions arise from van der Waals interactions in the case of transfer to urea, but from electrostatics on transfer to TMAO solution. The simulations used here allow for the calculation of the solvation and transfer free energy of longer oligoglycine models to be evaluated than is currently possible through experiment. The peptide backbone unit computed transfer free energy of −54 cal/mol/M compares quite favorably with −43 cal/mol/M determined experimentally.
Keywords: backbone solvation, free energy, folding, glycine
Introduction
The study of the action of organic osmolytes on protein solutions has revealed many fundamental aspects of protein folding. These small cosolvent molecules can have profound effects on protein stability, e.g. protecting osmolytes destabilize the unfolded state and facilitate protein folding, whereas the nonprotecting osmolyte urea stabilizes the unfolded state and denatures proteins.1 The relationship between osmolytes and protein stability is biologically unique in that many protecting osmolytes have undergone natural selection not only for their effectiveness in regulating cell volume, but also for their ability to stabilize proteins against certain denaturing stresses.2,3
An interesting example of the usage of osmolytes in nature is the counterbalance between the denaturing effects of urea and the protective ability of trimethylamine N-oxide (TMAO). TMAO prevents the denaturation of proteins in the presence of high intracellular concentrations of urea found in such organisms as marine elasmobranches.4,5 The study of TMAO's properties has proved to be useful in providing insight into fundamental aspects of protein stability, as well as providing important concepts involving numerous diseases.6-10
Transfer free energy values for sidechains and peptide backbone, ΔGtr, quantify the thermodynamic consequences of solvating a protein species in a cosolvent solution relative to pure water. Based on the transfer model and experimental ΔGtr for these groups it has been proposed that osmolytes exert their effect on protein stability primarily via the protein backbone.11,12 This provides the basis of a universal mechanism for osmolyte-mediated protein stabilization by protecting osmolytes and destabilization by urea as the protein backbone is shared by all proteins, regardless of side chain sequence.13–15
The evaluation of group transfer free energy values defined the now classic Tanford model for urea-induced protein denaturation.16,17 In that model, the thermodynamic interaction of the side chains with the urea solution gave rise to the long held concept of favorable urea interaction with hydrophobic groups as a driving force in urea's denaturation effect. Recent work corrected the previous measurements for the activities of the model compounds in solution and showed that the strength of the hydrophobic interactions do not change substantially on transfer to urea, and that urea's favorable interaction with the protein backbone is responsible for its denaturing ability.18 Thus, the free energy dependence of protein stability as a function of osmolyte concentration can be predicted if one assumes that the transfer free energies of solvent exposed sidechain and backbone groups on the native and denatured states are additive.18–20
Here, using computational methods, we assess the transfer free energies of the peptide backbone from water to two osmolyte solutions, 2M urea and 2M TMAO. The goal is to evaluate the peptide backbone transfer free energies as a function of chain length of oligoglycine peptides with capped end groups, and determine the extent to which the transfer free energies change in an additive manner with respect to chain length. The use of solvation free energy simulation calculations will also provide insight into the role of the electrostatic and van der Waals components of the transfer free energies, providing a more informative understanding of these empirically derived quantities.19
Results
Our model solutions contain a blocked, acetylglycine amide oligomer (neutral) from 2 to 5 glycines long. These compounds are denoted Gly2–5 below. In addition to an aqueous system, we prepared three component aqueous solutions adding a concentration of 2M TMAO or urea. We note that experimentally, glycine oligomers of 5 and beyond are increasingly difficult to work with due to solubility issues.19
The total solvation free energies and the component contributions from the van der Waals (vdW) and electrostatic terms for the peptide backbone models are shown in Figure 2. For each model, the total solvation free energy in TMAO solution is the most unfavorable solution environment (greatest free energy value), whereas the urea solution is the most favorable (lowest free energy). This is consistent with the notion that urea creates a better solution environment for the peptide backbone,21-23 whereas TMAO is a poorer solvent than water.19
Figure 2.
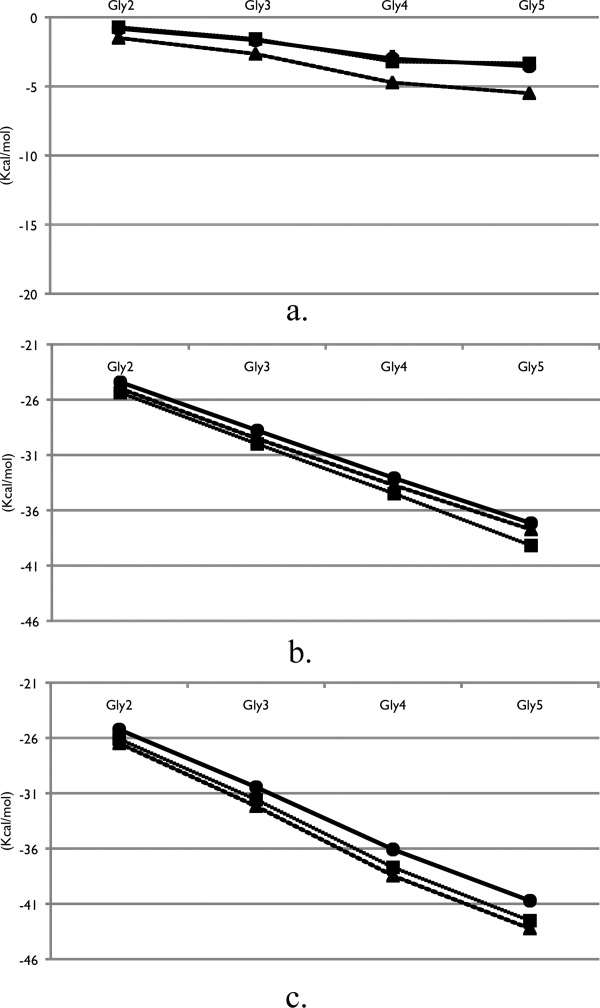
Solvation free energies of the peptide backbone models in pure water (squares), TMAO solution (circles) and urea solution (triangles). (a) vdW component, (b) electrostatic component, and (c) total solvation free energy. Error bars were calculated by separating the data set into three blocks and computing the averages and standard deviations between the different sets.
Components analysis of the total solvation free energy allows for a mechanistic view of the thermodynamic effect of osmolyte solution on the solvation of the peptide backbone. Comparing the three solutions in Figure 2(a) it is clear that urea possesses the most favorable contributions from the vdW component in comparison with water, whereas the TMAO solution and water solution values are essentially equivalent. The electrostatic term for the solvation free energies in Figure 2(b) is significantly greater in magnitude as compared to the vdW term, with water having the most favorable electrostatics and TMAO the least favorable.
Previous simulations utilizing thermodynamic integration and different models have calculated the solvation free energy of a five-residue helical glycine peptide in water to be −37.3 Kcal/mol.24 Though the geometry of the peptide used was helical and the solvation free energy value was obtained by neglecting the end group contributions, there appears to be reasonable agreement with the solvation free energy of the extended form calculated in this study of −42.53 Kcal/mol, which includes end groups. Previous solvation free energy studies have calculated the solvation of glycine in water to be −5.85 Kcal/mol.25 By subtracting the differences between Glyn and Glyn+1 solvation free energies in water, we obtain an average value of −5.48 Kcal/mol increment per peptide unit. Electrostatic calculations of a short alanine peptide computed the electrostatic solvation energy of an internal alanine residue to be −8.51 Kcal/mol,26 which is more favorable than our average electrostatic solvation component of glycine, −4.60 Kcal/mol but used different methodology.
Transfer free energies, ΔGtr, were calculated by subtracting the total solvation free energy and energy components of the peptide backbone in pure water from the corresponding values of the peptide in osmolyte solution and are plotted in Figure 3. The two osmolytes demonstrate differing trends with increasing peptide backbone lengths. The vdW contribution to the transfer of the peptide backbone models from water to TMAO becomes less favorable with increase in number of peptide repeats and is small in magnitude overall. This is in contrast to the total vdW component of the solvation free energies as seen in Figure 2(a), which becomes increasingly favorable with chain length. The trend of the vdW contribution of the transfer into urea solution is similar to that of the total vdW solvation component, in that both ΔGtr and solvation free energies become more favorable with chain length.
Figure 3.
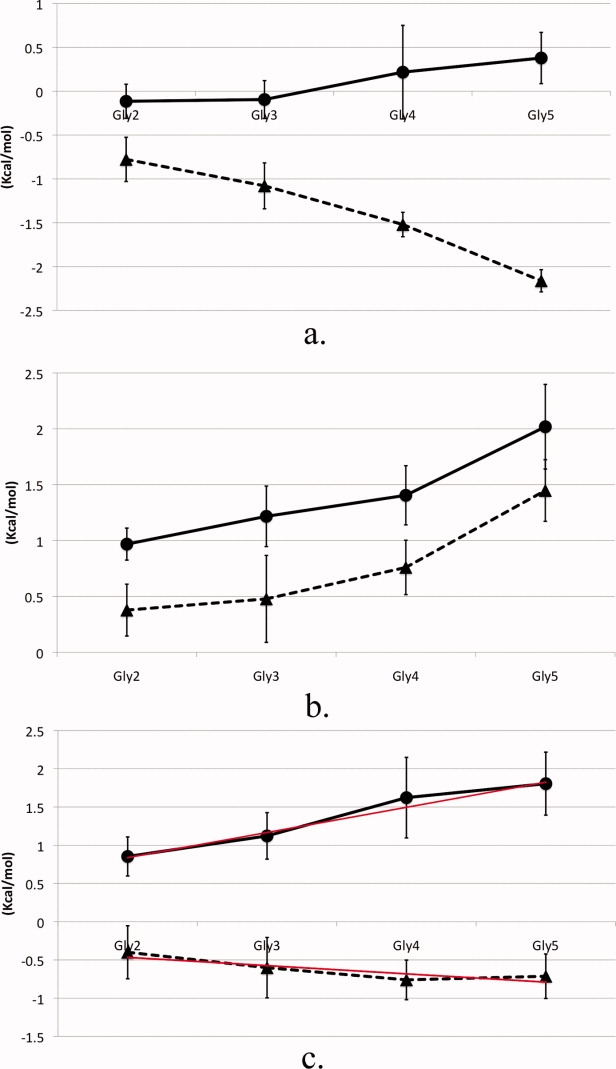
Peptide backbone model calculated ΔGtr of TMAO solution (circles) and urea solution (triangles) from water. (a) vdW component, (b) electrostatic component, and (c) total transfer free energy with trend line (red) determined using weighted least squares fitting. Error bars were calculated by separating the data set into three blocks and computing the averages and standard deviations between the different sets.
Electrostatics dominates the ΔGtr landscape in the case of TMAO but not that of urea. The electrostatic component to the transfer free energy of both solutions has the same sign of the slope and both are unfavorable relative to water [Fig. 3(b)]. For TMAO, this component is significantly more unfavorable compared to urea and has the same trend of decreased favorability with increased peptide length as does the vdW contribution to the transfer into TMAO solution. However, in the transfer of the peptide backbone from water to urea, the vdW and electrostatic free energy components differ in sign [Fig. 3(a,b)]. The total calculated transfer free energies in Figure 3(c), demonstrate a clear linear trend with backbone increment in both osmolyte solutions, illustrating additivity of the transfer free energy for increments of the peptide backbone. In urea, increasing lengths of the peptide backbone progress linearly towards a more energetically favorable solution environment, whereas the opposite trend occurs in TMAO solution. Previously published backbone transfer free energies demonstrated additivity of backbone repeats of lengths two through four;19 here we calculated the transfer free energy of peptides including one unit longer. Our results show additivity of the transfer free energies of the peptide backbone with chain length consistent with experiment.19
We performed a weighted least squares fitting of the total transfer free energies in Figure 3(c) using the propagated errors from our solvation free energy calculations to aid in the fitting. The slope of the fitted line then corresponds to the contribution of the peptide backbone unit to the osmolyte transfer free energy.19 The peptide backbone transfer free energy from water to 2M TMAO solution is 329 cal/mol per mol of backbone unit with an associated error of 32 cal/mol; for transfer from water to 2M urea solution ΔGtr is −108 ± 46 cal/mol. A basic tenet of the linear extrapolation method used extensively in analysis of protein stability is that free energy is a linear function of osmolyte concentration.27 Using this tenet, our computed free energies for glycine backbone transfer from water to 1M urea and water to 1M TMAO of −54 and 165 cal/mol/M respectively, compare favorably with experimentally determined values of −43 and 87 cal/mol/M.19 The comparisons give better agreement for transfer to urea than to TMAO. This is likely due to the fact that the energy function for the urea model was parameterized to give correct chemical activities and therefore chemical potentials, while no such energy function is available at this time for the TMAO model.28
To provide a view of the molecular interactions between solution components and peptide backbone we performed a structural analysis of the solution around the fixed peptide conformations used to calculate the solvation free energies. Figure 4 presents radial pair probability density distribution functions (RDFs) of osmolyte around water in our Gly3 system; the functions were essentially identical in all backbone systems. This quantity measures the ratio of the density of a species (e.g. water) at a particular distance around another (osmolyte) relative to the bulk, thus giving an atomistic description of the relative probability after averaging the orientation of water surrounding the osmolyte. Figure 4(a) gives the RDFs in urea solution. These probabilities are an average over all possible angles for each distance. Significant urea–oxygen to water–hydrogen correlation is observed at the expected hydrogen bonding distance. The association of the water–hydrogen to the urea–oxygen also brings the water–oxygen close to the urea–oxygen as indicated by the corresponding peak in urea–oxygen and water–oxygen curve.29
Figure 4.
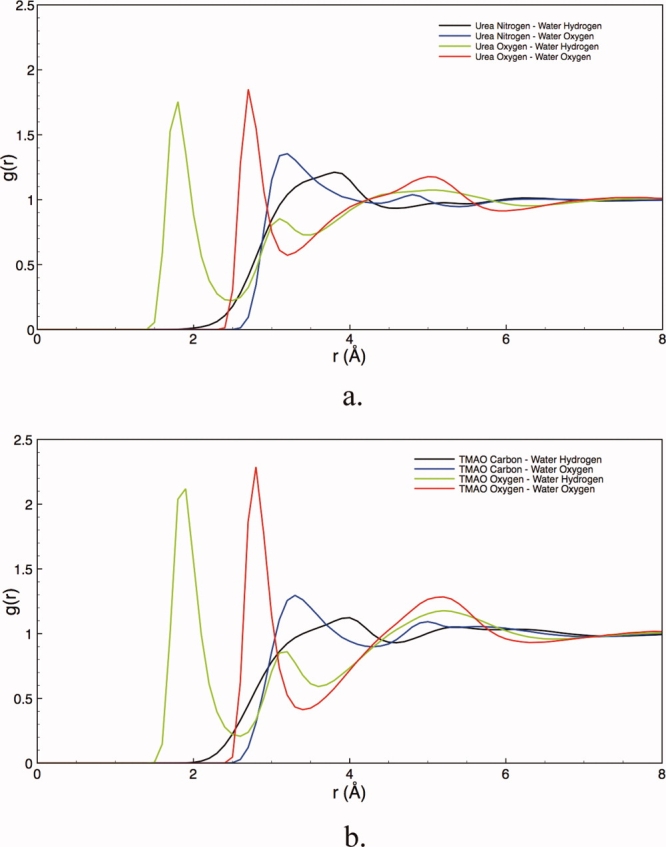
Osmolyte–water radial probability distribution function; (a) urea–water, and (b) TMAO–water. The increase in peak heights in TMAO solution indicates that TMAO coordinates more water than urea.
In Figure 4(b), we show the RDFs between TMAO and water. The TMAO–oxygen to water–hydrogen peak probability occurs at a close distance (again at less than 2.0Å) indicating strong hydrogen bonding. For these models we find that TMAO coordinates more water molecules within its first hydration layer compared to urea. The functions for all of the constituent atoms of TMAO show increased correlations in subsequent solvation layers, as compared to urea. Coupled with the more pronounced first solvation peak, the increase structure in the RDFs for TMAO demonstrate the strong correlation of TMAO with water, as compared to that of urea. The strong hydration of TMAO has been previously demonstrated in both experiments and simulations.30-35 Urea is a nearly ideal solute in aqueous solution (in the molar scale); is smaller and correspondingly shows more modest correlations with water.
Next, we consider the preferential interaction parameter as defined in the Methods section. This parameter gives a thermodynamic view of the distribution of osmolyte in the local region of the peptide backbone as compared to bulk solution. A smaller preferential interaction parameter indicates a deficit of osmolyte molecules as compared to bulk solution. For our calculation of the preferential interaction parameter, we have chosen a local cutoff distance to be 8.0Å beyond which the correlations are no longer strong.36 At this distance, we have included around three hydration layers of the peptide backbone, thus providing a satisfactory view of the overall hydration of the backbone. From Eq. (9) for all linear Glyn systems we see an overall excess of urea molecules in the local region surrounding the backbone models (data not shown). Additionally, the backbone–TMAO interaction parameter for all backbone models is less than that of urea, indicating a decrease in the local concentration of TMAO as compared to urea. For longer repeats of the backbone model the preferential interaction parameter is usually negative indicating a significant decrease in the overall amount of TMAO as compared to bulk solution, but this depends on conformation and is quite noisy. The high relative error seen is common behavior for the preferential interaction parameter as evidenced by the calculations of others,36-38 because the nature of the calculation depends upon the local number fluctuations at increasing distances. The inherent nosiness of the parameter, and the subsequent lack in statistical confidence of the interpretation, caused us to look at shorter ranged events that are less susceptible to artifacts caused by large local number fluctuations.
In Figure 5, we have shown direct interaction events between the peptide backbone and osmolyte molecules defined by collisions. This analysis gives a connection between structure, thermodynamics, and dynamics, which is a result of direct interaction, and focuses on shorter distances than that used to determine the preferential interaction parameter.36 Contact events are defined to be when any atom on the osmolyte molecule is within 3.0Å from any atom on the peptide backbone models. Figure 5(a) presents the average number of contact events for the backbone models in both osmolyte solutions per simulation snapshot. Urea molecules on average have a higher number of contact events with the peptide backbone as compared to TMAO. This is significant that TMAO has more atoms (14) than urea (8), thus allowing for more potential opportunities of contact interactions based upon our definition of a contact although TMAO clearly diffuses slower. As contact events include nonspecific interactions that are less important thermodynamically, we calculated the residence time of these collisions to obtain a separate measure, albeit still nonthermodynamic; this is shown in Figure 5(b). Here we not only see that there are more collisions between urea and peptide backbone than with TMAO, but they occur for a longer period of time. The infrequent TMAO backbone collision/trapping events occur on average for only 10 ps in duration, whereas the urea ones last for about 14 ps. With this, the interpretation of preferential exclusion of TMAO and preferential interaction of urea (in both first and larger hydration layers) are both in agreement with the signs of the transfer free energies in Figure 3(c) and show that the first solvation shell contained much of the information.
Figure 5.
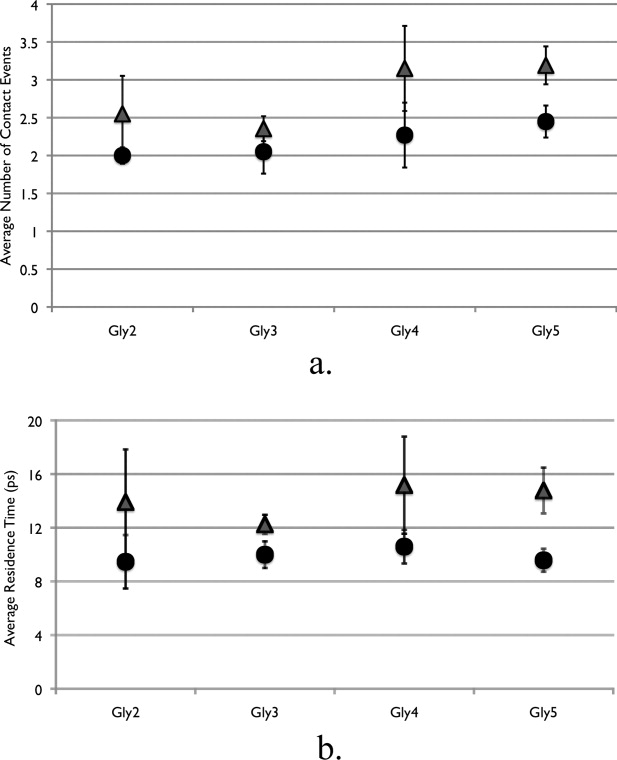
Contact events and residence times for osmolyte and peptide backbone models. (a) Average number of contact events per simulation snapshot. Contact is defined as any osmolyte atom being within 3.0 Å from any solute atom. (b) Average residence time per contact event. Triangles are the peptide backbone in urea solution and circles are the peptide backbone in TMAO solution.
Hydrogen bonding between solution and protein has an important contribution to the overall stability of proteins.15,39,40 By calculating the number of osmolyte and water-hydrogen bonds to the peptide backbone models, and separating them into whether the solution species act as a donor or acceptor, helps to describe the nature in which each species interacts with the peptide backbone model (Table I). As expected, TMAO rarely forms hydrogen bonds with the peptide backbone, whereas urea, on average, forms between one and two hydrogen bonds with the peptide backbone for all backbone conformations. Interestingly, urea serves as a hydrogen bond donor more frequently than it does a hydrogen bond acceptor via its carbonyl group. In TMAO solution, there is a slight increase of water-hydrogen bonds with each peptide backbone model as compared to in urea solution using our rather generous hydrogen bond criterion.41 However, the total solution–peptide hydrogen bond amounts are usually lower in TMAO, which is in part, a result of the lack of interaction of TMAO with the peptide backbone as compared to urea.38 This is analogous to the classic interpretation of experiments by Timasheff that protecting osmolytes are preferentially excluded from the local region of the protein, whereas nonprotecting osmolytes are seen in higher amounts close by.42,43
Table I.
Average Osmolyte and Water-Hydrogen Bonds with Peptide Backbone Models
| a. | TMAO acceptor | Water acceptor | Water donor | Total | |
|---|---|---|---|---|---|
| Gly2 | 0.1 (0.0) | 1.3 (0.1) | 6.0 (0.1) | 7.3 (0.1) | |
| Gly3 | 0.0 (0.0) | 1.6 (0.0) | 7.8 (0.1) | 9.4 (0.1) | |
| Gly4 | 0.1 (0.0) | 1.6 (0.1) | 9.4 (0.3) | 11.1 (0.3) | |
| Gly5 | 0.1 (0.0) | 1.5 (0.0) | 11.5 (0.5) | 13.1 (0.5) | |
| b. | Urea acceptor | Urea donor | Water acceptor | Water donor | Total |
| Gly2 | 0.2 (0.1) | 1.0 (0.4) | 1.3 (0.1) | 5.8 (0.3) | 8.2 (0.1) |
| Gly3 | 0.1 (0.0) | 0.8 (0.2) | 1.5 (0.3) | 7.4 (0.5) | 9.7 (0.9) |
| Gly4 | 0.1 (0.1) | 1.4 (0.4) | 1.3 (0.1) | 7.2 (0.4) | 10.0 (0.0) |
| Gly5 | 0.2 (0.1) | 1.8 (0.3) | 1.6 (0.1) | 11.2 (0.3) | 14.7 (0.1) |
Acceptor denotes the osmolyte or water accepting a hydrogen from the peptide backbone. Donor denotes the osmolyte or water donating a hydrogen to the peptide backbone. a) TMAO solution b) urea solution. Parentheses denote error.
Recent experimental measurements have indicated hydrogen bonding of urea with the NH group of a dialanine peptide, yet urea hydrogen bonding with the carbonyl group of the peptide was not as well resolved.39 However, those authors expected to have significantly more hydrogen bonds between the peptide carbonyl group as opposed to the peptide NH groups,39 a trend that we see in our simulations (Table I). In the literature, we find a scatter of results from different models. Some previous simulations show urea hydrogen bonding with the peptide carbonyl group,22,44,45 whereas others see more significant hydrogen bonding with the peptide amides as opposed to the peptide carbonyl group.46
To provide a further description of the nature of osmolyte and backbone correlations, we have calculated the solvent density profile around the peptide. The densities in Figure 6 correspond to regions of high probability for the particular solvent species to reside. Comparing the TMAO and urea density, we see that in TMAO solution there is less osmolyte density around the peptide backbone as compared to urea. It can be seen that urea occupies the first hydration layer of the peptide backbone models, whereas TMAO resides mostly within the second hydration layer. Concurrent with this decrease in osmolyte density, there is an increase of water density sites along the peptide backbone in TMAO solution.
Figure 6.
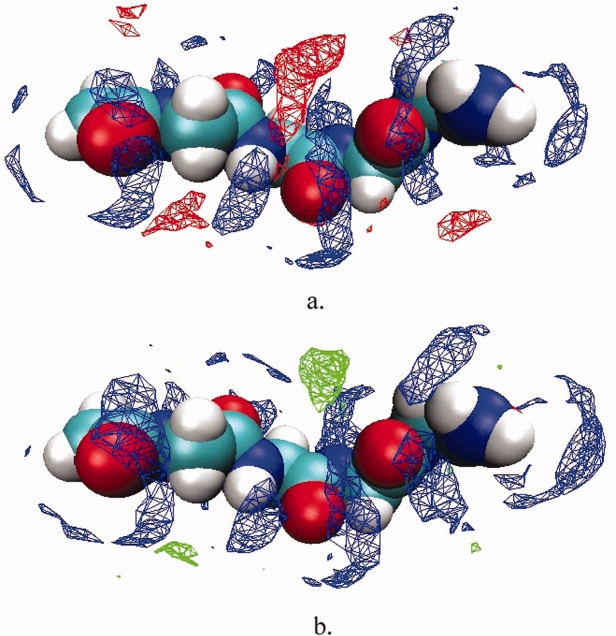
Solvent density profiles for Gly4. Colored regions indicate volumes of high solvent densities. (a) water densities are colored blue, urea is red; (b) water densities are colored blue, TMAO are green.
Discussion
The solvation free energy values presented here are comparable with the limited amount of previous simulation work24,25 and provide important insight into the structural origin of the thermodynamic behavior. The free energies of solvation delineate the thermodynamic differences between protecting and nonprotecting osmolyte solution. Solvation of all the peptide backbone models in urea solution studied here are clearly more favorable than in water solution. Urea provides a better solvent environment for the peptide backbone, giving a computed transfer free of −54 cal/mol/M that compares quite favorably with −43 cal/mol/M determined experimentally.21-23 Similarly, the presence of TMAO creates a more unfavorable environment for enhanced water solvation of the peptide backbone and it strongly interacts with water, normally crystallizing as a dihydrate. All this makes TMAO a comparatively poor solvent for the peptide backbone. A computed glycine backbone transfer free energy of 165 cal/mol/M agrees within a factor of two of the 87 cal/mol/M measured experimentally. The lesser agreement for the TMAO solution compared to urea is likely due to the force field choice, which was not parameterized with respect to TMAO chemical activities as was the urea solution. Nevertheless, the calculated and experimental glycine backbone transfer free energies demonstrate reasonable agreement and account for the features of the protein folding ability of TMAO.15,47,48
We obtained ΔGtr from the simulated solvation free energy differences between 2M osmolytes and pure water. These calculated transfer free energies of the peptide backbone demonstrated additivity of each incremental unit of the peptide backbone corresponding to a nearly constant change in the free energy for these short oligomers. The components of the calculated transfer free energies further emphasize the importance of the vdW interactions in the urea solution. Relative to water, urea has more favorable vdW interactions whereas the vdW component transfer free energy for TMAO is nearly constant with chain length. The electrostatic component to the transfer free energy for both osmolytes are unfavorable compared to water, with TMAO being the more unfavorable. In urea, the magnitude of the vdW component of the transfer free energy is larger than that of the electrostatic component in urea. Therefore, the linear trend of the favorable transfer free energy of increasing backbone units in urea is a result of the increased favorability of the vdW interactions dominating the somewhat unfavorable electrostatic interaction differences. This is not the case for the transfer of the peptide backbone models from water to TMAO. The TMAO solution has no such favorable vdW interactions to balance the unfavorable electrostatic component, as it is roughly equivalent to water. Therefore, in TMAO solution the total transfer free energies of the peptide backbone models are unfavorable and seen to increase linearly with each additional backbone unit.
The contribution of the vdW interactions for urea denaturation has been seen in another recent computational study of the preferential binding of urea to protein.46 Those authors found a shift towards more favorable vdW potential energy of urea within the first solvation shell as compared to the bulk solvent, with no corresponding shift in the electrostatic component.46 The analysis demonstrates that interaction of urea with peptide groups should be described by more than just the electrostatic terms. Though the electrostatic interactions are obviously important for hydrogen bonding to occur within this type of model it is clear that the vdW aspects of these interactions plays an integral role. The alteration of the electrostatic fields and free energies caused by hydrogen bonding of urea to the peptide is not enough to explain the solution differences seen.40,44,45,49 Rather, the accumulation of urea responsible for the strongly thermodynamic favorability of all the peptide backbone models in urea solution is dominated by the favorable vdW component of ΔGtr of the peptide backbone models from water to urea. Correspondingly, the lack of interaction of the protecting osmolyte TMAO with the peptide backbone models results in no such favorable vdW interactions and instead contributes to the overall unfavorable solvation difference of the peptide backbone models for TMAO versus water.
Because molecular simulations do not possess the difficulties concerned with solubility as do experiments, we were able to extend the glycine backbone model to five residues, one more backbone unit than was possible in experiments.19 Thus, we have verified that additivity of the transfer free energy of the peptide backbone in osmolyte solution occurs at still longer lengths of the peptide backbone. From the slope of the transfer free energies of increasing lengths of the oligomer, we obtained ΔGtr per peptide backbone unit repeat in osmolyte solution.19 The transfer free energy of one backbone unit in urea and TMAO possess the expected sign, indicating the qualitative trends of the difference in solvation free energy seen in our simulations with an increase in peptide backbone unit in osmolyte solution.
By analyzing the properties for each of the peptide conformations used to calculate the solvation free energies, we were able to identify significant correlations in the osmolyte-backbone-water tertiary system. At short distances Figure 5(a) describes the number of collision events, and shows that urea comes into contact more often with the peptide backbone than does TMAO. In addition to this increased contact with the peptide backbone by urea, these collisions occur for longer periods of time, indicating stronger correlations. Several previous simulations have demonstrated the direct interaction of urea with peptide or protein22,45,46,50-52 as well as the lack of interaction between TMAO and a cyclic53 and long peptide backbone model.38 Similarly, solution hydrogen bonds with the peptide backbone models demonstrate very little hydrogen bonding of TMAO with the peptide backbone, whereas urea forms about 1/2 hydrogen bond per glycine residue. We see the denaturing osmolyte acting as a hydrogen bond donor with far more frequency than as a hydrogen bond acceptor.22,39
Methods
Each peptide backbone was created in its extended conformation using the CHARMM-27 all atom parameter set41 and subjected to energy minimization using the steepest descent method. The osmolyte solutions consisted of 66 osmolyte molecules and 1614 TIP3P54 water molecules in a cubic simulation box with lengths of 3.8 nm, resulting in 2M osmolyte concentration. Urea force field parameters were obtained from recent work that determined parameters for this model designed to match experimental activities.28 This model of urea has been shown to predict near ideal activity coefficients at concentrations up to 10M in agreement with experiment, whereas another popular urea model deviated significantly from ideality.55 The TMAO parameters were obtained from previously published results.56 For the pure water solutions, 1778 water molecules in a solvation box with 3.8 nm side lengths were used.
For all solutions, each solvent species was initially placed on a lattice sufficiently large to ensure no overlapping of atoms. The lattices of water and osmolyte were allowed to interpenetrate while being energy minimized and shrinking the walls. All systems were then pre-equilibrated using the Extended Systems Program57 for 950 ps using 1 fs time steps whereas reassigning velocities and refining the volume to achieve the target pressure. A full equilibration of the solvent and peptide of 1 ns was carried out using 1 fs time steps for the isothermal–isobaric ensemble (NTP) with target temperature of 300 K and pressure of 1 atm, using the Nosé-Anderson method.58,59
The conformational ensemble of each peptide in solution was characterized using two structural parameters: the radius of gyration and distance between the peptide groups. From these two structural parameters the most probable structure was determined for each peptide backbone model and a representative structure was chosen for solvation free energy calculations. As the structures chosen represent the most sampled ensemble, we acknowledge that we are calculating an approximation to the ensemble-averaged solvation free energy, via the solvation free energy of representative structures that would contribute the most to the ensemble average. The structures for each peptide backbone model are illustrated in Figure 1. Our purpose in using these representative structures was to increase the precision of the solvation free energy values in evaluating the extent of the additivity of the transfer free energies of the peptide backbone. Each structure was initially placed diagonally in the simulation box. Equilibration of the peptide systems was then carried out for 300 ps.
Figure 1.
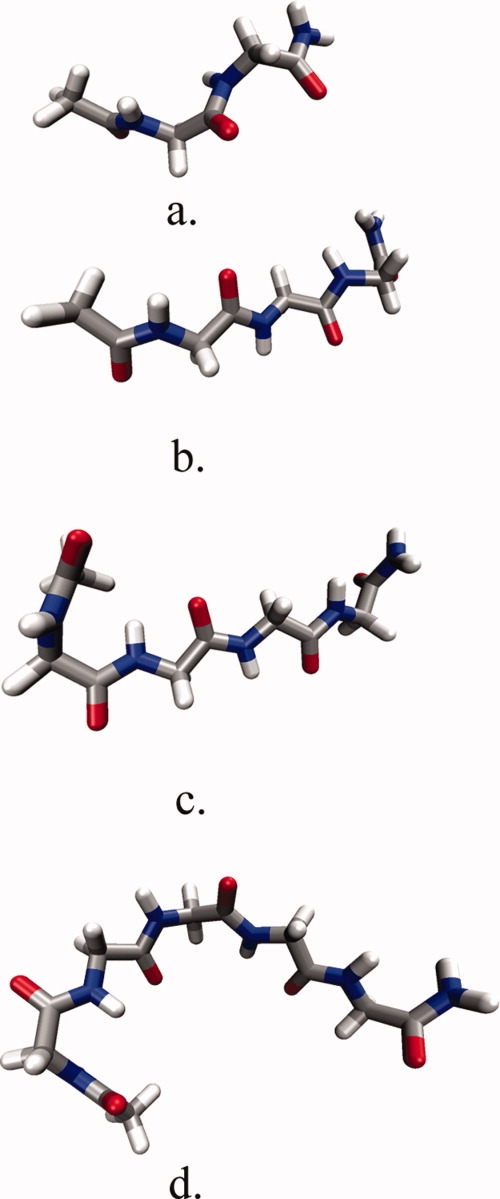
Conformations of peptide backbone models used to calculate solvation free energy. (a) Gly2, (b) Gly3, (c) Gly4, (d) Gly5.
Solvation free energies for our peptide backbone models in solution were calculated using the thermodynamic perturbation method and the Bennett-Pande acceptance ratio method.60,61 This method has been shown to be highly accurate in calculating amino acid side chain analogs62,63 and urea activity coefficients in solution.55 The method, based on the well-known thermodynamic perturbation method, has been detailed elsewhere55,60 so we mention only the basic fundamentals of the method. The free energy between two states of a system, i and j, is defined by the following equation:
| (1) |
Therefore, the free energy difference between two states is determined by calculating the ensemble average of the potential energy differences in one of the states. To bridge the gap between the two states which may be far apart, a coupling parameter, l, is used in which successive steps of l are made in between each state, such that the free energy difference becomes
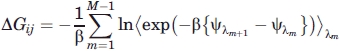 |
(2) |
where i is the starting state and j is the end state, and 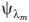 is the potential energy between the peptide and solvent molecules at the λm state.
is the potential energy between the peptide and solvent molecules at the λm state.
The method of lambda exchange, or Hamiltonian exchange, was used to ensure good sampling of our system.64,65 Each lambda parameter is simulated independently, with replica i corresponding to λm. The Hamiltonian for the i-th replica at λm becomes:
| (3) |
with p[i] and q[i] being the momentum and coordinate vectors, respectively, of the i-th replica. K(p[i]) is the kinetic energy in the i-th replica, and 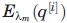 is the potential energy at λm.
is the potential energy at λm.
The vdW component was calculated first, in the absence of the electrostatic coupling. To improve sampling, a soft core potential was used for the calculation of the van der Waals terms,
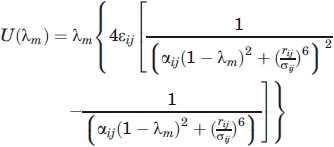 |
(4) |
After the calculation of the vdW contribution, the electrostatic contributions were calculated, with the full vdW contribution in effect, using a simple linear scaling. This widely used method yields components that while path dependent individually are interpretable and of course add up to the path independent state function value of the desired free energy.
We used the following 28 intermediate λ points for the calculation of the vdW component: 0.000, 0.100, 0.150, 0.200, 0.230, 0.255, 0.270, 0.285, 0.300, 0.310, 0.320, 0.330, 0.345, 0.360, 0.380, 0.400, 0.425, 0.455, 0.485, 0.520, 0.560, 0.600, 0.650, 0.700, 0.750, 0.800, 0.900, and 1.000. More points are needed near the peak in the vdW λ sampling, whereas the electrostatics profile is very smooth with respect to λ and so only 11 intermediate λ points were used: 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0.
After 1000 steps a swap between lambda systems is attempted and accepted based upon the probability:
| (5) |
with 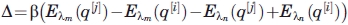 .
.
To maximize numerical precision, the Bennett-Pande acceptance ratio method was used60,61 to calculate the solvation free energy. From
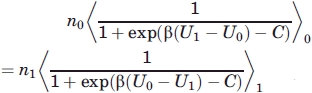 |
(6) |
with
| (7) |
where n0 and n1 are the number of samples in each respective state. Solving for C and defining the number of samples in each state to be equal, the free energy difference becomes
| (8) |
Each component was simulated for 300 ps using the lambda exchange method. To supplement the data obtained from the free energy simulations, the fixed peptide systems were further simulated with the same box dimensions using standard molecular dynamics for 2 ns each so that other solution properties could be gathered.
The preferential interaction parameter provides a relationship between the distribution of cosolvent around a solute species at a particular distance to that of the bulk solution. An excess of cosolvent molecules correlates with a higher preferential interaction parameter with a positive sign, whereas a deficit of cosolvent yields a negative value. The preferential interaction parameter between osmolyte and peptide backbone is defined as:66
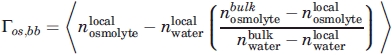 |
(9) |
Because Γ is intrinsically a fluctuation difference it is prone to large levels of noise.
Conclusion
By utilizing the unique advantage of simulations, we have provided molecular insight into the process of additivity and strongly suggest that the interactions between the peptide backbone and osmolyte solution are responsible for the osmolyte-effect on protein stability. There has been confusion over the dominant free energy component of the direct mechanism of interaction between osmolytes and proteins: some have suggested interactions are driven by electrostatics,40,44,45 whereas others have shown a dominant role of vdW interactions.46 From our simulated solvation free energies, and the subsequent highly precise transfer free energy calculations, we are able to decompose the contributions of the dispersion and electrostatic interactions to the free energy of transfer of both protecting and denaturing osmolytes. We have shown that upon the transfer of the peptide backbone models from water to urea, the electrostatic component is actually highly unfavorable. It is in fact the significantly favorable vdW component to the transfer free energy, which causes the total transfer of the peptide backbone from water to urea to be energetically favorable. The favorable dispersion forces are manifested in the direct interaction of urea with the peptide backbone. This is different from the protecting ability of TMAO, in which the free energy of transfer is dominated in magnitude and sign by the electrostatic component. Again, the consequence of the free energy difference can be seen via the lack of interaction of TMAO with the peptide backbone models.
Acknowledgments
We are grateful for the insight, discussions and collegiality provided by Jörg Rösgen and Matthew Auton. The simulations and computations were performed using the Molecular Science Computing Facility at the Environmental Research of the U.S. Department of Energy, located at the Pacific Northwest National Laboratory, and the Pittsburgh Supercomputing Center on the National Science Foundation Teragrid.
References
- 1.Lin TY, Timasheff SN. Why do some organisms use a urea-methylamine mixture as osmolyte? Thermodynamic compensation of urea and TMAO interactions with protein. Biochemistry. 1994;33:12695–12701. doi: 10.1021/bi00208a021. [DOI] [PubMed] [Google Scholar]
- 2.Hochachka PW, Somero GN. Biochemical adaptation. Mechanism and process in physiological evolution. New York: Oxford University Press; 2002. [Google Scholar]
- 3.Yancey P, Clark M, Hand S, Bowlus R, Somero G. Living with water stress: evolution of osmolyte systems. Science. 1982;217:1214–1222. doi: 10.1126/science.7112124. [DOI] [PubMed] [Google Scholar]
- 4.Wang A, Bolen D. A naturally occurring protective system in urea-rich cells: mechanism of osmolyte protection of proteins against urea denaturation. Biochemistry. 1997;36:9101–9108. doi: 10.1021/bi970247h. [DOI] [PubMed] [Google Scholar]
- 5.Yancey PH, Somero GN. Counteraction of urea destabilization of protein structure by methylamine osmoregulatory compounds of elasmobranch fishes. Biochem J. 1979;183:317–323. doi: 10.1042/bj1830317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jia LY, Gong B, Pang CP, Huang Y, Lam DS, Wang N, Yam GH. Correction of the disease phenotype of myocilin-causing glaucoma by a natural osmolyte. Invest Opthalmol Vis Sci. 2009;50:3743–3749. doi: 10.1167/iovs.08-3151. [DOI] [PubMed] [Google Scholar]
- 7.Scaramozzino F, Peterson DW, Farmer P, Gerig JT, Graves DJ, Lew J. TMAO promotes fibrillization and microtubule assembly activity in the C-terminal repeat region of tau. Biochemistry. 2006;45:3684–3691. doi: 10.1021/bi052167g. [DOI] [PubMed] [Google Scholar]
- 8.Nandi P, Bera A, Sizaret P. Osmolyte TMAO converts recombinant a-helical prion protein to its soluble b-structured form at high temperature. J Mol Biol. 2006;362:810–820. doi: 10.1016/j.jmb.2006.07.060. [DOI] [PubMed] [Google Scholar]
- 9.Tatzelt J, Prusiner SB, Welch WJ. Chemical chaperones interfere with the formation of scrapie prion protein. EMBO J. 1996;15:6363–6373. [PMC free article] [PubMed] [Google Scholar]
- 10.Georgescauld F, Mocan I, Lacombe M, Lascu I. Rescue of the neuroblastoma mutant of the human nucleoside diphosphate kinase A/nm23-H1 by the natural osmolyte trimethylamine-N-oxide. FEBS Lett. 2009;583:820–824. doi: 10.1016/j.febslet.2009.01.043. [DOI] [PubMed] [Google Scholar]
- 11.Bolen D, Baskakov I. The osmophobic effect: natural selection of a thermodynamic force in protein folding. J Mol Biol. 2001;310:955–963. doi: 10.1006/jmbi.2001.4819. [DOI] [PubMed] [Google Scholar]
- 12.Liu Y, Bolen DW. The peptide backbone plays a dominant role in protein stabilization by naturally occurring osmolytes. Biochemistry. 1995;34:12884–12891. doi: 10.1021/bi00039a051. [DOI] [PubMed] [Google Scholar]
- 13.Pauling L, Corey RB, Branson HR. The structure of proteins: two hydrogen-bonded helical configurations of the polypeptide chain. Proc Natl Acad Sci USA. 1951;47:205–211. doi: 10.1073/pnas.37.4.205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rose G, Fleming P, Banavar J, Maritan A. A backbone-based theory of protein folding. Proc Natl Acad Sci USA. 2006;103:16623–16633. doi: 10.1073/pnas.0606843103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bolen DW, Rose GD. Structure and energetics of the hydrogen-bonded backbone in protein folding. Annu Rev Biochem. 2008;77:339–362. doi: 10.1146/annurev.biochem.77.061306.131357. [DOI] [PubMed] [Google Scholar]
- 16.Nozaki Y, Tanford C. The solubility of amino acids and related compounds in aqueoues urea solutions. J Biol Chem. 1963;238:4074–4081. [PubMed] [Google Scholar]
- 17.Tanford C. Isothermal unfolding of globular proteins in aqueous urea solutions. J Am Chem Soc. 1964;86:2050–2059. [Google Scholar]
- 18.Auton M, Holthauzen L, Bolen D. Anatomy of energetic changes accompanying urea-induced protein denaturation. Proc Natl Acad Sci USA. 2007;104:15317–15322. doi: 10.1073/pnas.0706251104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Auton M, Bolen DW. Additive transfer free energies of the peptide backbone unit that are independent of the model compound and the choice of concentration scale. Biochemistry. 2004;43:1329–1342. doi: 10.1021/bi035908r. [DOI] [PubMed] [Google Scholar]
- 20.Auton M, Bolen DW. Predicting the energetics of osmolyte-induced protein folding/unfolding. Proc Natl Acad Sci USA. 2005;102:15065–15068. doi: 10.1073/pnas.0507053102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Qu Y, Bolen CL, Bolen DW. Osmolyte-driven contraction of a random coil protein. Proc Natl Acad Sci USA. 1998;95:9268–9273. doi: 10.1073/pnas.95.16.9268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tran HT, Mao A, Pappu RV. Role of backbone-solvent interactions in determining conformational equilibria of intrinsically disordered proteins. J Am Chem Soc. 2008;130:7380–7392. doi: 10.1021/ja710446s. [DOI] [PubMed] [Google Scholar]
- 23.O'Brien EP, Ziv G, Haran G, Brooks BR, Thirumalai D. Effects of denaturants and osmolytes on proteins are accurately predicted by the molecular transfer model. Proc Natl Acad Sci USA. 2008;105:13403–13408. doi: 10.1073/pnas.0802113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Staritzbichler R, Gu W, Helms V. Are solvation free energies of homogeneous helical peptides additive? J Phys Chem B. 2005;109:19000–19007. doi: 10.1021/jp052403x. [DOI] [PubMed] [Google Scholar]
- 25.Gu W, Rahi S, Helms V. Solvation free energies and transfer free energies for amino acids from hydrophobic solution to water solution from a very simple residue model. J Phys Chem B. 2004;108:5806–5814. [Google Scholar]
- 26.Avbelj F, Baldwin RL. Limited validity of group additivity for the folding energetics of the peptide group. Proteins. 2006;63:283–289. doi: 10.1002/prot.20756. [DOI] [PubMed] [Google Scholar]
- 27.Greene RF, Pace CN. Urea and guanidine hydrochloride denaturation of ribonuclease, lysozyme, a-chymotrypsin, and B-lactoglobulin. J Biol Chem. 1974;249:5388–5393. [PubMed] [Google Scholar]
- 28.Weerasinghe S, Smith PE. A Kirkwood-Buff derived force field for mixtures of urea and water. J Phys Chem B. 2007;107:3891–3898. [Google Scholar]
- 29.Kokubo H, Pettitt B. Preferential solvation in urea solutions at different concentrations: properties from simulation studies. J Phys Chem B. 2007;111:5233–5242. doi: 10.1021/jp067659x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sinibaldi R, Casieri C, Melchionna S, Onori G, Segre A, Viel S, Mannina L, De Luca F. The role of water coordination in binary mixtures. A study of two model amphiphilic molecules in aqueous solutions by MD and NMR. J Phys Chem B. 2007;110:8885–8892. doi: 10.1021/jp056897+. [DOI] [PubMed] [Google Scholar]
- 31.Paul S, Patey G. Why tert-butyl alcohol associates in aqueous solution but TMAO does not. J Phys Chem B. 2006;110:10514–10518. doi: 10.1021/jp0609378. [DOI] [PubMed] [Google Scholar]
- 32.Freda M, Onori G, Santucci A. Infrared study of the hydrophobic hydration and hydrophobic interactions in aqueous solutions of tert-butyl alcohol and TMAO. J Phys Chem B. 2001;105:12714–12718. [Google Scholar]
- 33.Fornili A, Civera M, Sironi M, Fornili S. Molecular dynamics simulation of aqueous solutions of TMAO and tert-butyl alcohol. Phys Chem Chem Phys. 2003;5:4905–4910. [Google Scholar]
- 34.Di Michele A, Freda M, Onori G, Paolantoni M, Santucci A, Sassi P. Modulation of hydrophobic effect by cosolutes. J Phys Chem B. 2006;110:21077–21085. doi: 10.1021/jp068055w. [DOI] [PubMed] [Google Scholar]
- 35.Michele A, Freda M, Onori G, Santucci A. Hydrogen bonding of water in aqueous solutions of TMAO and TBA: a near-infrared study. J Phys Chem A. 2008;108:6145–6150. [Google Scholar]
- 36.Baynes BM, Trout BL. Proteins in mixed solvents: a molecular-level perspective. J Phys Chem B. 2003;107:14058–14067. [Google Scholar]
- 37.Athawale MV, Dordick J, Garde S. Osmolyte TMAO does not affect the strength of hydrophobic interactions: origin of osmolyte compatibility. Biophys J. 2005;89:858–866. doi: 10.1529/biophysj.104.056671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hu CY, Lynch GC, Kokubo H, Pettitt BM. Trimethylamine N-oxide influence on the backbone of proteins: an oligoglycine model. Proteins. 2009;78:695–704. doi: 10.1002/prot.22598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lim WK, Rösgen J, Englander SW. Urea, but not guanidinium, destabilizes proteins by forming hydrogen bonds to the peptide group. Proc Natl Acad Sci USA. 2009;106:2595–2600. doi: 10.1073/pnas.0812588106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tobi D, Elber R, Thirumalai D. The dominant interaction between peptide and urea is electrostatic in nature: a MD study. Biopolymers. 2003;68:359–369. doi: 10.1002/bip.10290. [DOI] [PubMed] [Google Scholar]
- 41.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 42.Lee JC, Timaseff SN. The stabilization of proteins by sucrose. J Biol Chem. 1981;256:7193–7201. [PubMed] [Google Scholar]
- 43.Timasheff S. Water as ligand: preferential binding and exclusion of denaturants in protein unfolding. Biochemistry. 1992;31:9857–9864. doi: 10.1021/bi00156a001. [DOI] [PubMed] [Google Scholar]
- 44.O'Brien E, Dima R, Brooks B, Thirumalai D. Interactions between hydrophobic and ionic solutes in aqueous GdnCl and urea solutions: lessons for protein denaturation mechanism. J Am Chem Soc. 2008;129:7346–7353. doi: 10.1021/ja069232+. [DOI] [PubMed] [Google Scholar]
- 45.Das A, Mukhopadhyay C. Urea-mediated protein denaturation: a consensus view. J Phys Chem B. 2009;113:12816–12824. doi: 10.1021/jp906350s. [DOI] [PubMed] [Google Scholar]
- 46.Hua L, Zhou R, Thirumalai D, Berne BJ. Urea denaturation by stronger dispersion interactions with proteins than water implies a 2-stage unfolding. Proc Natl Acad Sci USA. 2008;105:16928–16933. doi: 10.1073/pnas.0808427105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Baskakov I, Bolen DW. Forcing thermodynamically unfolded proteins to fold. J Biol Chem. 1998;273:4831–4834. doi: 10.1074/jbc.273.9.4831. [DOI] [PubMed] [Google Scholar]
- 48.Baskakov I, Wang A, Bolen DW. Trimethylamine-N-oxide counteracts urea effects on rabbit muscle lactate dehydrogenase function: a test of the counteraction hypothesis. Biophys J. 1998;74:2666–2673. doi: 10.1016/S0006-3495(98)77972-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Robinson DR, Jencks WP. The effect of compounds of the urea-guanidinium class on the activity coefficient of acetyltetraglycine ethyl ester and related compounds. J Am Chem Soc. 1965;87:2462–2470. doi: 10.1021/ja01089a028. [DOI] [PubMed] [Google Scholar]
- 50.Caflisch A, Karplus M. Structural details of urea binding to barnase; a molecular dynamics study. Structure. 1999;7:477–488. doi: 10.1016/s0969-2126(99)80064-1. [DOI] [PubMed] [Google Scholar]
- 51.Tirado-Rives J, Orozco M, Jorgensen WL. Molecular dynamics simulations of the unfolding of barnase in water and 8M aqueous urea. Biochemistry. 1997;36:7313–7329. doi: 10.1021/bi970096i. [DOI] [PubMed] [Google Scholar]
- 52.Stumpe MC, Grubmüller H. Interaction of urea with amino acids: implications for urea-induced protein denaturation. J Am Chem Soc. 2007;129:16126–16131. doi: 10.1021/ja076216j. [DOI] [PubMed] [Google Scholar]
- 53.Zou Q, Bennion B, Daggett V, Murphy K. The molecular mechanism of stabilization of proteins by TMAO and its ability to counteract the effects of urea. J Am Chem Soc. 2002;124:1192–1202. doi: 10.1021/ja004206b. [DOI] [PubMed] [Google Scholar]
- 54.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 55.Kokubo H, Rosgen J, Bolen D, Pettitt B. Molecular basis of the apparent near ideality of urea solutions. Biophys J. 2007;93:3392–3407. doi: 10.1529/biophysj.107.114181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kast K, Brickmann J, Kast S, Berry R. Binary phases of aliphatic n-oxides and water: force field development and molecular dynamics simulation. J Phys Chem A. 2003;107:5442–5351. [Google Scholar]
- 57.Pettitt BM. ESP: extended system program. Developed in the Research Laboratory of Prof. B. M. Pettitt at the University of Houston. Houston, TX: 1996. [Google Scholar]
- 58.Andersen HC. Molecular dynamics simulations at constant pressure and/or temperature. J Chem Phys. 1980;72:2384–2393. [Google Scholar]
- 59.Nose S. A unified formulation of the constant temperature molecular dynamics methods. J Chem Phys. 1984;81:511–519. [Google Scholar]
- 60.Shirts M, Pande V. Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J Chem Phys. 2005;122:144107-1:15. doi: 10.1063/1.1873592. [DOI] [PubMed] [Google Scholar]
- 61.Bennett CH. Efficient estimation of free energy differences from Monte Carlo Data. J Comput Phys. 1976;22:245–268. [Google Scholar]
- 62.Shirts M, Pande V. Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. J Chem Phys. 2005;122:1334508-1:12. doi: 10.1063/1.1877132. [DOI] [PubMed] [Google Scholar]
- 63.Shirts M, Pitera J, Swope W, Pande V. Extremely precise free energy calculations of AA side chain analogs: comparison of common molecular mechanics force fields for proteins. J Chem Phys. 2003;119:5740. [Google Scholar]
- 64.Fukunishi H, Watanabe O, Takada S. On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: application to protein structure prediction. J Chem Phys. 2002;116:9058–9067. [Google Scholar]
- 65.Sugita Y, Kitao A, Okamoto Y. Multidimensional replica-exchange method for free-energy calculations. J Chem Phys. 2000;113:6042–6051. [Google Scholar]
- 66.Kang M, Smith PE. Preferential interaction parameters in biological systems by K-B theory and computer simulation. Fluid Phase Equilib. 2007;256:14–19. [Google Scholar]


