Abstract
The role of conformational dynamics in allosteric signaling of proteins is increasingly recognized as an important and subtle aspect of this ubiquitous phenomenon. Cooperative binding is commonly observed in proteins with twofold symmetry that bind two identical ligands. We construct a coarse-grained model of an allosteric coupled dimer and show how the signal can be propagated between the distant binding sites via change in slow global vibrational modes alone. We demonstrate that modulation on substrate binding of as few as 5–10 slow modes can give rise to cooperativity observed in biological systems and that the type of cooperativity is given by change of interaction between the two monomers upon ligand binding. To illustrate the application of the model, we apply it to a challenging test case: the catabolite activator protein (CAP). CAP displays negative cooperativity upon association with two identical ligands. The conformation of CAP is not affected by the binding, but its vibrational spectrum undergoes a strong modification. Intriguingly, the first binding enhances thermal fluctuations, yet the second quenches them. We show that this counterintuitive behavior is, in fact, necessary for an optimal anticooperative system, and captured within a well-defined region of the model's parameter space. From analyzing the experimental results, we conclude that fast local modes take an active part in the allostery of CAP, coupled to the more-global slow modes. By including them into the model, we elucidate the role of the modes on different timescales. We conclude that such dynamic control of allostery in homodimers may be a general phenomenon and that our model framework can be used for extended interpretation of thermodynamic parameters in other systems.
Introduction
Cooperative binding of two or more ligands (protein allostery) is crucial to the function of the majority of proteins. Some aspects of protein allostery are not fully understood, particularly the role of conformational fluctuations. Yet it is now accepted that the fluctuations contribute, or in some cases, even drive, the long-range communication (1–5).
Allostery is a thermodynamic phenomenon. The cooperativity is driven by the free energy differences between the individual binding steps. Traditional views of allostery (6–8), primarily concentrated on the structural changes, ignore the ligand-induced changes in flexibility of the protein. However, both experiments and computer simulations suggest that the backbone structural changes are not sufficient to explain the cooperativity of multiple systems (2,9–12), implying contribution of protein motions to the allosteric effect. Furthermore, general considerations of protein physics suggest that dynamics most likely plays some role in all allosteric proteins (4,13). It is therefore important to address this phenomenon, which has wide potential implications for molecular biology and the drug design within the pharmaceutical industry (5,14,15).
Here we investigate homotropic allostery in homodimers. Proteins with twofold symmetry constitute a large and important group of proteins. Many DNA-binding proteins, antibodies, and receptors are either present in the cell as dimers or are composed of two identical domains (16). Homotropic allostery, where a ligand binding to one protomer affects the protein's affinity for the second, identical ligand associating with the other protomer, is widely present among homodimers (17–22).
Thermal fluctuations of the protein's native environment excite a whole spectrum of internal vibrations. These may contribute to long-range allosteric signaling, principally through slow internal motions. A slow, global mode involves a whole structural unit such as a helix or a domain. Perturbation of such motion therefore directly influences distant protein sites. Fast modes, such as side-chain movements, are typically localized in proteins (23), and consequently only affect a few residues within their localization length. However, they can couple to slow motions and become involved in the communication indirectly (24).
The suggestion to include dynamical changes in the model of allostery came from Cooper and Dryden (13), who demonstrated theoretically that alterations in protein dynamics constitute an alternative mechanism for long-range communication. Hawkins and McLeish (25,26) have expanded their ideas into the form of concrete models of several classes of proteins: DNA and tubulin binding proteins to account for allosteric entropy in rigid dimers and coiled coils, respectively. The Met repressor is an example of a protein in which dynamics can give rise to both entropic and enthalpic contributions to the allosteric free energy (24). Other more recent efforts have focused on identifying sets of linked residues in proteins, the so-called allosteric pathway along which signals are communicated (5,27). Communication can proceed via structural changes and/or altered vibrations of the linked residue. However, these studies concentrate on detecting the pathways rather than the mechanism by which the interaction proceeds.
We would like to understand the role of the motions from both ends of the frequency spectrum in connection with allostery and calculate their possible contribution to the overall allosteric effect. We try to achieve this by combining and refining previous models into a single model that is more complex, which can serve to describe a different class of real systems. Slow modes involve concerted motion of large groups of residues over long timescales that are impossible to capture with current or foreseeable atomistic simulation. Coarse-grained representation of the system is therefore required to gain an insight into the mechanism. Elastic and Gaussian network models (28–30), and other algorithms (31–35) for systematic coarse-graining open the door to simulating systems over longer timescales. They show that residues distant in space can be coupled by changes in the vibrational structure of the protein (33). We coarse-grain systems even further, to describe the motions in an analytic way. Such description, while losing the detail of local structure, has the advantage of providing an intuitive understanding of the possible mechanism of the signal propagation, as well as the ability to reveal and investigate the dynamical parameter space that evolution of protein structure can, in principle, explore. We treat structurally compact parts, such as subdomains, helices, sheets, etc., as rigid or nearly rigid structures. We assume local harmonic potential fields between the structures. An important assumption is that their effective spring stiffness can be altered locally, but not distantly, by a ligand binding. Fast modes are included purely locally, but coupled to the amplitude of slow modes to reflect the consequences of internal protein motions for local structural order (24).
In this article, we first introduce a general model of dynamic homotropic allostery in a homodimer and then test the validity of the theory on a representative homodimer, the catabolite activator protein (CAP). CAP has been recently shown to display negative cooperativity without a significant conformational change upon binding two identical ligands called cAMP (2). Nuclear magnetic resonance (NMR) measurements revealed that CAP's fluctuations undergo a counterintuitive change upon binding, whereby binding of the first cAMP molecule slightly enhanced, and the second completely suppressed, the amplitude of global motions. Application of the model to the CAP system reveals a possible mechanism and internal design of the protein interactions that yield the complex and intriguing allosteric behavior without the requirement of the structural change. In addition, this model is applicable to systems where vibrational changes go hand-in-hand with structural changes, as has been shown on the example of Lac repressor (25).
Model of a Homodimer
Single slow mode
A homodimer in this context is a protein consisting of two identical subunits, each of which binds a ligand. In the first and simplest approximation of the equilibrium dynamics of such protein, we assign one internal breathing mode to each subunit and then elastically couple the subunits. This very simple and coarse-grained model is designed to explore only the qualitative features of dynamic allostery in the system. For the unliganded protein, the internal mode and coupling strength are characterized by spring constants k and kc, respectively. Binding of a ligand is modeled as changes of the spring constants.
We concentrate on the symmetric case where the two ligands and their binding sites are identical. We make two assumptions on the effect of the ligand binding. The first follows from the symmetry of the system and requires that both binding events have the same effect on the spring constant representing the protein. In the second, we assume locality: the effect of binding is not directly propagated to the distant subunit. At this level of model, locality means that ligand binding to one subunit affects only the stiffness of its own internal mode and the coupling to the other subunit, but no direct effect on the internal stiffness of the other subunit. The ligand binding alters chemical bond structure locally and therefore only the spring constants that directly derive from these bonds are likely to change. However, the subunits are elastically coupled and thus the thermal motions of the distant subunit are indirectly modified too, leading to the dynamic allosteric effect. The assumptions are demonstrated in Fig. 1. We define nondimensional parameters describing the effect of substrate binding as follows: the first binding event changes the local subunit spring constant by a factor β and the coupling spring constant by a factor α. Introduction of the second ligand evokes the same alteration in the other subunit.
Figure 1.
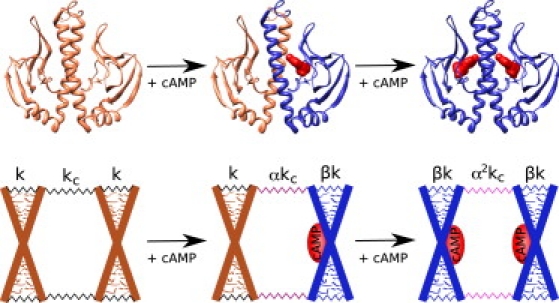
Residues 1–138 of crystallographic structure of CAP (PDB entry 1G6N) binding the ligand cAMP (red) and a sketch of the corresponding coarse-grained model of the system. The large X represents the backbone of one subunit whose one internal mode is simulated by a scissorlike movement of the rods. The little protrusions represent small structures moving fast relative to the slow scissorlike motion of the rods. The internal mode of each subunit and the coupling is defined by the elastic constant k and kc, respectively. The constants are altered upon binding by factors α and β.
The system is mathematically described by a Hamiltonian:
| (1) |
The inertia matrix M is approximately constant during the binding events and therefore can be left out from the subsequent calculations. For the unliganded protein, the elastic part of the Hamiltonian reads
| (2) |
where x1 and x2 are the generalized amplitudes of the internal modes in each of the individual subunits. The partition function of the coarse-grained dimer undergoing structural fluctuations is obtained from the Hamiltonian and reads Z = πkBT/|K|1/2, where kB is the Boltzmann constant. The free energy is then, G = –kBT ln Z. We are only interested in the free energy differences between the ligation states, and therefore all terms that stay constant during the binding can be ignored. We wish to calculate only the dynamic contributions and therefore other contributions such as entropy of desolvation or hydrophobicity of the binding pockets are not included in this calculation.
The requirements for the two constraints of symmetry and locality of binding are implemented by introducing coefficients α and β into the matrix K as illustrated in Fig. 1. The difference between the free energy change of each binding step (ΔΔG) measures the degree of cooperativity, ΔΔG = (G2:1 – G1:1) – (G1:1 – GAPO); 2:1 refers to doubly liganded, and 1:1 to singly liganded, protein. ΔΔG ≠ 0 indicates cooperativity, ΔΔG < 0 corresponds to a positively cooperative system, and ΔΔG > 0 to negatively cooperative system. A larger absolute value of ΔΔG signifies a more cooperative system. The evaluation yields
| (3) |
where the crucial quantity ΔΔG is now expressed using three dimensionless parameters: Kc = kc/k the ratio between the subunit and the coupling spring constant; α, the dimensionless enhancement of the coupling strength on binding; and β, the dimensionless enhancement on the local subunit mode stiffness (Fig. 1). The dimensionless character of the equation is advantageous for the parameterization from experimental results, because only relative changes in the spring stiffness contribute to ΔΔG. We look for areas in the parameter space yielding ΔΔG ≠ 0. To picture the three-parameter space we make two fixed choices in each of two qualitative regimes for the parameter α, and plot ΔΔG as a function of the remaining two parameters (Fig. 2, top).
Figure 2.
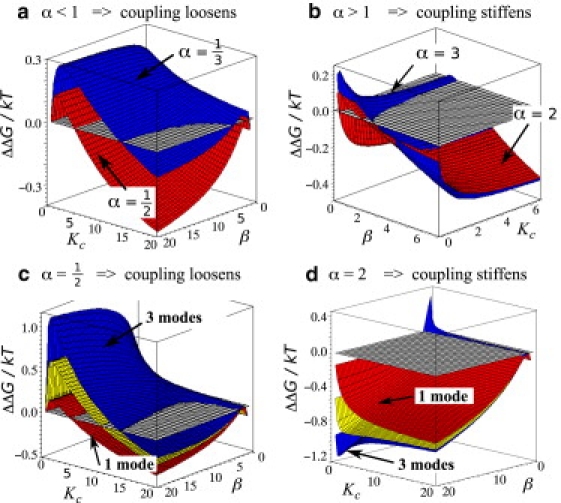
(a and b) Allosteric free energy landscapes for a single slow mode. (c and d) Allosteric free energy landscape for one (blue), two (yellow) and three (red) slow modes. The plane ΔΔG = 0 is shown to highlight the border between positive (ΔΔG < 0) and negative cooperativity (ΔΔG > 0).
The parameter space is divided into two subspaces: α > 1, which corresponds to stiffening of the coupling between subunits on binding of a ligand, and α < 1, which corresponds to coupling loosening. The shape of the ΔΔG landscape is nontrivial for α ≠ 0; regions of positive and negative cooperativity are observed in both subspaces. The qualitative character in the landscape is independent of the choice of the value of α within each subspace, but there are substantial differences between the two subspaces (Fig. 2). In the case in which coupling stiffens, positive or negative cooperativity is achieved by carefully choosing β; if the coupling loosens, Kc becomes the critical parameter instead. The second major difference is that as α tends to 0, ΔΔG becomes more positive. When α > 1, the values in the area where ΔΔG > 0 are slightly enhanced, whereas for larger values of β, the landscapes cross and the system becomes increasingly cooperative (Fig. 2). This suggests that positively cooperative systems are exploring the subspace α > 1, and negatively allosteric system, the subspace α < 1. The borderline case of α = 1 does not result in negative cooperativity for any choice of the remaining parameters.
The allosteric free energy (Eq. 3) is directly proportional to the temperature, implying that the slow mode change gives rise to purely entropic allostery (in the isothermal case).
A good measure of slow mode amplitudes is provided by the mean relative fluctuations 〈(x1 – x2)2〉, which we evaluate for each ligation state as
Four types of behavior are observed:
-
Case 1.
Sequential increase of fluctuation amplitude.
-
Case 2.
Decrease of fluctuation amplitude.
-
Case 3.
Amplified fluctuation, then quenching: Fluctuations are amplified upon the first ligand binding but quenched upon the second binding. The fluctuation amplitude of the doubly liganded state is smaller than that of the unliganded protein.
-
Case 4.
Amplitude increase, then decrease: Increase in the amplitude is followed by decrease; however, the fluctuation amplitude of the doubly liganded state is now larger than that of the unliganded system.
The four types of behavior are mapped onto the allosteric free energy surface in Fig. 3. We observe that for α < 1, all four types of behavior are present for large regions of the parameter space. The most interesting observation, however, is that to maximize negative cooperativity (ΔΔG > 0) the loosening-tightening effect is required (Case 3). In the case of α > 1, the fluctuations tend to be sequentially quenched upon the binding; this is especially the case for a positively cooperative system. However, a negatively cooperative system whose coupling would get stronger upon binding is again likely to display the loosening-tightening effect.
Figure 3.
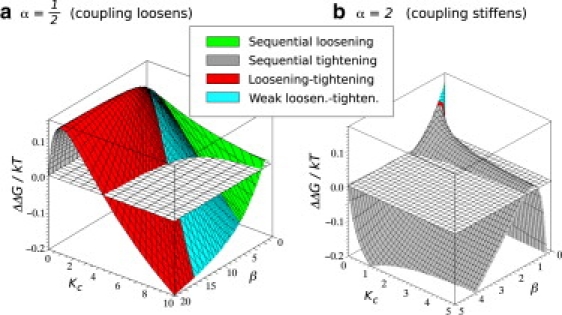
Four regions with different change in fluctuations mapped onto the ΔΔG landscape for α = 1/2 (a) and α = 2 (b). Color code: In the red region, the loosening-tightening effect is observed. The fluctuations of the doubly liganded system are smaller than that of the apo-protein. The blue region is characterized by the weak loosening-tightening effect, whereby the doubly liganded system moves more than the apo-protein, but less than the 1:1 system. The green region is characterized by sequential stiffening of the protein upon binding. In the gray region, each binding increases the fluctuations. The green region for α > 1 is hidden behind the peak in this view.
Even the simplest level of coarse-grained model shows that allosteric effects can arise in coupled dimers purely from spatial fluctuations. The evaluation of the fluctuations demonstrates that the loosening-tightening effect is required to produce strong negative cooperativity, whereas strong positive cooperativity is accompanied by sequential tightening of the system. However, the allosteric free energy is of purely entropic origin and its values of ΔΔG match the generally observed values of few kBT only for limiting cases of parameters tending to 0 or ∞. That represents unphysical conditions and we conclude, as might be expected on physical grounds, that additional modes which are naturally present in the system must take part in the allosteric signaling. These fall into two classes: fast local modes and additional, global, slow modes.
The effect of fast modes on the allostery have been investigated before (24), and it has been shown that the net values of ΔΔG are not amplified but that the free energy is split into compensating entropic and enthalpic parts, which themselves do acquire enhanced absolute values. The effect of including fast modes in the model of a homodimer will be discussed at the end of this section.
Multiple slow modes
We extend our model to include M slow modes per subunit. We assume that the modes are harmonically coupled to each other across the subunits. This corresponds to a Hamiltonian
| (4) |
where xi, j is a coordinate of jth mode on the ith subunit with the respective spring stiffness ki, j. The coupling constants λ[i, j][k, l] are, in principle, different for all modes and can be parameterized from experiments or simulations. At this level, to probe the properties of the model while avoiding a proliferation of arbitrary parameters, we constrain their value by reasonable simplifying assumptions. We set all coupling and internal subunit constants equal to each other for the free symmetric protein, i.e., λ[i, j][k, l] = kc, and ki, j = k, ∀i, j, k, l. The Hamiltonian reduces to
| (5) |
We further assume that, as in the one-mode case, 1), ligand binding affects only the local elastic constants plus the coupling constants; and 2), binding of the ligand to either subunit has the same effect—all internal subunit stiffnesses change by a factor β and coupling constants by a factor α. The resulting Hamiltonian of the apo-protein in matrix form is , where
| (6) |
and δ denotes the Krönecker delta. The matrix K1 of the singly liganded complex has alternating terms βk + α(2M − 1)kc and k + α(2M − 1)kc on the diagonal, and the off-diagonal terms are equal to –αkc. The diagonal terms of the matrix K2 of the doubly liganded complex are βk + α2(2M − 1)kc, the off-diagonal –α2kc. The allosteric free energy is obtained from the partition function as previously described,
| (7) |
Here, ΔΔG is a function of four dimensionless parameters α, β, and Kc and number of modes M. The exact formula depends on the number of modes included and is shown in the Appendix A. The central result is that the free energies are indeed modified with increasing number of slow modes as is shown in Fig. 2.
In particular, this extension confirms that negatively allosteric systems are likely to live in the α < 1 subspace and positively cooperative in α > 1 subspace. In these subspaces, including extra slow modes leads to the amplified allosteric effect in question. In the subspace α > 1, this amplification is observed also in the region with ΔΔG > 0 but is much less pronounced than in the other subspace. ΔΔG values of ±5 kBT are observed for as few as 5–10 slow modes. The values in connection to experiments will be discussed in more detail in the next section.
The fluctuation changes are evaluated in the form of the fluctuation matrix C:
| (8) |
As more slow modes are added to the system, the fluctuation amplitude per mode,
decreases, whereas the total fluctuations,
increase. The comparison of the fluctuations of three ligation states yields again the same four types of behavior as the simple-mode case depending on the parameter choice (Fig. 3). This is observed for any number of modes M. The mapping onto the allosteric free energy landscape results in a picture analogous to that of the simple-mode case, with the four classes of behavior spanning the same regions of the ΔΔG landscape.
Fast modes
In contrast to the slowest modes, fast modes are typically localized (involve only a few atoms) and are therefore unlikely to transmit allosteric signals across large distances by themselves (23). However, they can couple to the slow modes and so become involved in the transmission, modifying its amplitude. Here we draw on previous work (24) to couple several fast modes to the global, slow ones. We can picture the situation as shown in Fig. 1. The slow breathing mode of the subunit is represented as a scissorlike movement of the two rods. Fast motions of smaller structures within the subunit such as side chains are represented as vibrations of little protrusions attached to the rods. Here we derive the results for one slow mode and multiple fast modes, and then generalize the result for multiple slow and fast modes in the next section.
The coupling is based on the idea that the flexibility of the fast modes increases with the amplitude of the slow mode. Physically, local structures are freer to move when their environment is disrupted. We assume therefore that the rigidity of the fast mode depends on the displacement xs of the larger structure within the slow mode. If xs is small, the localized structures are in their native environment, experience a deep, narrow potential, and move only slightly about the equilibrium position. If the slow mode becomes more flexible and thus xs larger, the fast mode environment becomes disrupted, and the corresponding potential becomes flatter. A further physically motivated assumption made is that the fast modes are only coupled to the local slow mode (Fig. 1).
We implement the idea by modifying the Hamiltonian to
| (9) |
where is the Hamiltonian of the slow modes (Eq. 2) and the sum adds up the fast modes. N fast modes are enslaved to each subunit, the ith enslaved mode experiences a potential . If the fast mode is not coupled to the slow mode, its effective potential is the harmonic approximation ; the potential depth and the mode stiffness kf are assumed as in the previous work (24) to be the same for all fast modes. The width and depth of the potential are assumed to be affected by the slow mode in the coupled case. The increased flexibility of the slow mode corresponds to a flatter and wider potential , for which we take the functional parameterization
| (10) |
Here, xs = x1, x2 is the slow mode coordinate, the ith fast mode coordinate, and kv, kf, and kk are coupling constants (given, without loss of generality, the dimensions of a spring constant). The choice of coupling functions is arbitrary; the only requirement is smooth widening and flattening of the potential with increasing |xs|. We repeat the statistical mechanics calculation with the modified Hamiltonian and find
| (11) |
where
| (12) |
The parameters α, β, and Kc define the slow mode during the two binding steps (see Fig. 1).
Including fast modes increases the region of the parameter space α, β, and Kc, yielding ΔΔG > 0. However, the absolute maximal value of ΔΔG is always slightly lower than in the nonenslaved case. The structure of the coupled model is most clearly seen if we make the simplifying choice of A = 0, which would correspond to a system at a fixed special temperature. Now ΔΔG is identical to the nonenslaved case. However, the free energy is now composed of compensating entropic and enthalpic terms. This enthalpic contribution arises naturally from the coupling between the mean energy adopted within the local mode potentials and the amplitude of the global dynamics, and can be calculated by standard application of thermodynamic relations to our model. For isothermic changes,
| (13) |
and thus,
| (14) |
An example: catabolite activator protein (CAP)
To illustrate the utility of our model, we apply it to an example homodimer, the catabolite activator protein (CAP). The transcriptional activator in Escherichia coli, it consists of two identical subunits, each of which binds a small activator called cyclic adenosine monophosphate (cAMP). The cAMP molecules serve as an allosteric activator that greatly increases the CAPs affinity for DNA. The binding of the two cAMP molecules to the protein is itself allosteric and negatively cooperative; the binding of the first cAMP molecule reduces the affinity for the second by nearly two orders of magnitude (36). The distance between the two cAMP ligands is 10 Å (37), excluding electrostatic or any other direct interactions.
Each subunit of CAP is composed of two distinct domains—the cAMP binding domain (residues 1–138) and the DNA binding domain (residues 139–209). The negative cooperativity upon cAMP binding takes place independently of the presence of the DNA binding domain and according to Heyduk et al. (38), becomes even stronger in its absence. Popovych et al. (2) studied the allosteric binding of cAMP in the truncated version of CAP (CAPN, residues 1–138). Their NMR relaxation measurements ruled out ligand-induced conformational change in the binding site of the second ligand but observed a substantial modification in the dynamic behavior. The slow backbone motions (microsecond-to-millisecond timescale) exhibited a nonintuitive pattern whereby binding of the first cAMP molecule slightly enhanced, and the second completely suppressed, the amplitude of these global motions. Fast motions of the backbone on the picosecond-to-nanosecond timescale changed far less than the slow motions. Thermodynamic potentials of the individual binding steps were obtained from calorimetric measurements. The measured positive value of the allosteric free energy ΔΔG = 4.7 kBT confirms negative cooperativity, yet the enthalpic term (ΔΔH = –1.8 kBT) actually favors binding of the second cAMP ligand. Popovych et al. (2) concluded that the strongly unfavorable entropy (TΔΔS = –6.5 kBT) drives the negative cooperativity.
In the previous section, we derived the structure of the allosteric free energy landscape arising from ligand-induced change in slow motions for a coupled dimer. The main assumptions were that the individual ligand bindings have local and identical effect on the slow modes of the protein. To check the validity of these assumptions for the case of CAP, we used the Gaussian network model (29), implemented on the webserver iGNM (http://ignm.ccbb.pitt.edu) (39), to study the lowest normal modes of the protein. All simulations were performed on CAPN; the atomic model was obtained from the crystal structure of the doubly liganded full-length protein (Protein DataBank (PDB) entry 1G6N) by selecting desired residues and stripping off cAMP ligands for the singly liganded and unliganded version.
The evolution of the dynamic behavior is best manifested on the dynamical cross-correlation maps, Λij = 〈ΔRi × ΔRj〉 between residues i and j (Fig. 4). We observe that the two main subunits of CAP are very little correlated in the apo-protein, which implies that subunits move as weakly coupled individual units. cAMP binding strengthens correlation between the central helices and the β-sheet structure of the liganded monomer, confirming that communication between the two subunits does not proceed directly but only through the interface (central helices). The dynamical pattern of the unliganded subunit is approximately unperturbed, which also motivates the assumption we make on the coarse-grained effect of coupling.
Figure 4.
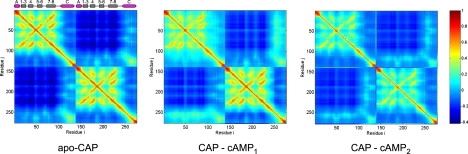
Cross-correlation map, Λij, between residue i and j, for three ligation states of CAPN, obtained from the Gaussian network model implemented on the webserver iGNM. A pair subjected to a fully correlated motion (Λij = 1) is colored dark red, fully anticorrelated motions (Λij) are not present, and moderately correlated motions are colored dark blue. cAMP binding disturbs correlations in the liganded monomer (top-left corner of the middle picture) but introduces correlation between the central helices and the liganded monomer. Binding of the second cAMP reestablishes symmetry in the motion pattern and removes correlations of the central helices to the β-sheet structures. Main parts of the secondary structure of CAP are shown above the APO-CAP map; α-helices are represented as magenta cylinders, and β-sheets as gray rectangles.
From the derived structure of the ΔΔG landscape, we concluded that negative cooperativity can arise in a coupled dimer for a particular choice of parameters. We inferred that for negative cooperativity to arise, the parameter α is most likely to be <1. This corresponds to coupling between subdomains weakening upon the ligand binding. We also found from our exploration of the general model that ΔΔG is maximal when the loosening-tightening effect is present, suggesting that optimal design of a negatively cooperative system displays such a change in fluctuation amplitudes. Experiments have demonstrated that the loosening-tightening effect indeed occurs in CAP during the cooperative binding, strongly supporting our hypothesis (2). In the following, we want to use the remaining experimental results to determine whether the dynamical structure of CAP is captured by our model, and if it is, to further localize CAP in the parameter space and gain further insight into the mechanism of its cooperativity.
We showed that the experimental value of ΔΔG = 4.7 kBT can be recovered by including additional slow modes. To account for the favorable enthalpy change (ΔΔH = –1.8 kBT), we need to add fast modes as reviewed above. Enthalpy has been experimentally found in the CAP system to favor the second ligand binding, which corresponds to ΔΔH < 0. By plotting Eq. 14, we can find the region of the parameter space with negative enthalpy.
The amplitude of the slow mode fluctuations are also identical to the nonenslaved case if A = 0 (Eq. 12). We localize the part of the parameter space with properties matching experimental results, i.e., ΔΔG > 0, ΔΔH < 0, and displaying the loosening-tightening effect upon binding. This area also coincides with high allosteric free energy (see Fig. 5).
Figure 5.
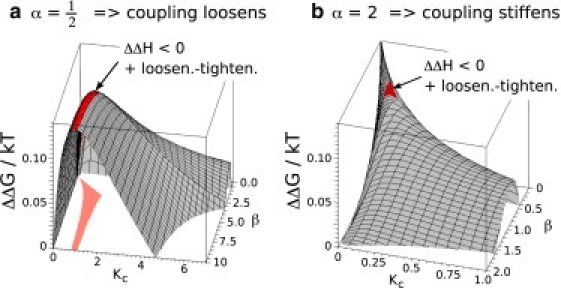
The allosteric free energy landscapes in the case in which a single slow mode is coupled to a set of identical fast modes, for α = 1/2, 2 with the area displaying the loosening-tightening effect plus ΔΔH < 0 highlighted in red. The projection of the area into the Kc-β plane is shown in orange.
Fast fluctuations evaluated from our model cannot be compared directly to the experiment because the NMR experiments only measured fast motions of the backbone. Our model incorporates small structures such as side chains into . A 40-ns molecular dynamics simulation performed by Li et al. (40) does, however, report on the fast motions of the whole molecule. The root-mean-square deviation of the whole structure was found to decrease upon binding. This measure accounts for both side-chain and backbone motions, but is the best guideline available to us. We therefore add the decreasing fast fluctuations to the desired properties of our model. The fast mode fluctuations calculated with our model display a sequential tightening during the two binding steps for β ≳ 1 and sequential loosening for β ≲ 1. Only in the case of α < 1 does the area with ΔΔH < 0 and the loosening-tightening effect stretch to large values of β (Fig. 5). This supports the hypothesis that the coupling between the CAP subunits is weakened upon the ligand binding.
This is a very significant advance. However, we found that the addition of fast modes alone does not capture the experimental magnitudes of ΔΔG. This suggests that multiple slow modes are active in the allosteric effect alongside with the fast modes.
The most complex model we studied is composed of multiple slow and fast modes. The fast potential is assumed to depend on the superposition of the local slow modes, i.e., fast modes on the subunit 1 depend on the displacement . The allosteric free energy was evaluated, but the exact formula is not shown because of its length and complicated dependency on number of slow modes. Analysis of the result shows that the characteristic properties of the one slow mode case are retained. Let us again denote and set A = 0 for simplification. The free energy then equals the free energy of the slow modes only, and is split into enthalpic and entropic parts. The enthalpic part is directly proportional to the number of enslaved fast modes and the region of parameter space with properties matched to experiment, i.e., ΔΔG > 0, ΔΔH < 0, in which the loosening-tightening effect and doubly suppressed fast modes span the ridge of high ΔΔG in the subspace of α < 1 (Fig. 5 a). The doubly suppressed fast modes now completely rule-out the case of α > 1.
It is possible to use the thermodynamic data to constrain both the number of global (slow) and local (fast) modes. Including more slow modes and amplifying the change in coupling constant induced by cAMP binding (choosing the value of α further away from 1) both increase the allosteric free energy. The experimental observations may be quantitatively recovered for the highly suggestive value of six global modes (M = 6), α = 1/4, β = 8, and Kc = 1/2. The number of fast modes N can be fitted from the value of ΔΔH = 1.8 kBT. The form of the derived equation for ΔΔH is preserved from the one slow mode case (Eq. 14), i.e., . We estimate the value of to be ≲kBT. For kBT and M = 6, α = 1/4, β = 8, and Kc = 1/2, we need 15 fast modes per subunit to recover the ΔΔH value. For a smaller value of kBT, also consistent with the data and identical remaining parameters only three fast modes (N = 3) are required.
As noted in the case of the Lac dimer (25), there are six mutual global modes of motion between two internally rigid domains (three relative translations, three relative rotations), suggesting that each monomer of CAP is composed of two semirigid subunits. This is confirmed by Gaussian network model simulations in which the β-sheet structure and the long central helix (C-helix) are observed to move as semirigid bodies. Their relative motion is also evident from the correlation maps. The β-sheets of each domain are highly correlated with each other and the small uncorrelated islands in the pattern correspond to the long β-hairpin that moves fast on its own. The mobility of the structure (data not shown) increase with the increasing distance from the central helix, demonstrating that the structure moves with respect to the nearly stationary helices that are uncorrelated with the rest of the domain.
The intersubunit coupling is provided by the long C-helices. The role of the helices has been studied by Heyduk et al. (38) and it was found that when the DNA binding domain and the helix are missing, cAMP binding still occurs with the same affinity as in the full version of CAP, although the binding is noncooperative. This corresponds to the case when coupling is not modified upon binding (α = 1) and no cooperativity occurs. When, on the other hand, the helix is present, but the DNA binding domain is removed, the binding is tighter and more anticooperative than in the complete CAP. Popovych et al. (41) showed that cAMP binding introduces a coil-to-helix transition in the untruncated version of CAP, where residues 125–136 are turned from a random coil in apo-CAP to α-helix in the liganded CAP. The α-helices in the coiled-coil conformation interact more strongly than the random coils. This transition might therefore act against the coupling loosening present in the truncated version and might, therefore, reduce the strength of the cooperativity.
The parameter set of the minimal quantitative coarse-grained model is underdetermined by current experimental data. It is, however, still possible to conclude that the number of fast modes enslaved by the CAP dimer has a range between a few and a few tens, a physically reasonable range.
Summary and Conclusions
We have attempted to add to the understanding of the allostery of coupled dimers by constructing a simple but intuitive coarse-grained model based on the basic thermodynamic principles of ligand binding and protein dynamics. We derived a model that describes the propagation of the allosteric signal in a coupled dimer purely via slow global motions. We have shown that such a model can account for positive and negative allostery. This is achieved by fine-tuning of three parameters.
The parameter space is naturally divided into two subspaces (α > 1 and α < 1), each of which supports a different type of cooperativity. In the subspace where coupling becomes stronger upon binding (α > 1), the system is very likely to be positively cooperative. In the opposite case, when the coupling becomes weaker upon binding (α < 1), the remaining parameters would need to reach unphysical values if a significant positive cooperativity were to occur.
The relative fluctuations were evaluated for the homodimer and four distinct types of responses to the consecutive binding were found. When mapped onto the allosteric free energy landscape, predictions can be made as to what type of response is likely to occur for different types of cooperativity. An anticooperative system is expected to display a loosening-tightening effect whereas the fluctuation amplitudes of a positively cooperative protein are most likely to be suppressed by each binding.
The model containing one slow mode only is very instructive; however, the magnitudes of the allosteric free energy are significantly smaller than in real systems. We therefore speculated that more slow modes are active in the allosteric signaling. We extended our model to include the extra modes and indeed found that values of ΔΔG are noticeably amplified. Values of several kBT corresponding to common biological systems were recovered for 5–10 slow modes. The character of the relative fluctuations was preserved from the single mode model.
We then validate our approach on a test case homodimer: the catabolite activator protein (CAP). We focused on explaining the internal mechanism and the origin of the thermodynamic parameters measured in experiments. From the findings of the first section we knew that slow, global modes are responsible for the free energy value but on their own produce a purely entropic effect. The value of ΔΔG increases with the number of slow modes involved. To account for the compensating enthalpic and entropic parts, fast modes were added to the system using the method of Hawkins and McLeish (24). Fast modes, despite being localized, can contribute to the allosteric signaling as enslaved by the slow modes. They are responsible for splitting the free energy coming from change in dynamics into enthalpic and entropic parts. The extent of this split is determined by the number of enslaved fast modes; the larger the number of fast modes, the larger the compensating enthalpic and entropic terms.
According to experiments and simulations, the overall change in enthalpy ΔΔH < 0 and fast fluctuations decrease during the two binding steps. These results, along with the loosening-tightening effect displayed by the slow modes, were captured by the full model containing multiple slow and fast modes. It also enabled us to localize CAP in the model's parameter space. The examination of the allosteric free energy landscapes suggests that α < 1, i.e., the coupling between subunits becomes softer upon cAMP binding. The other requirements overlap in a small region of the parameter space highlighted in red in Fig. 5 a. This region covers a narrow strip of the free energy landscape with the highest values of ΔΔG, a feature that is preserved also when multiple slow modes are introduced. Furthermore we recover observed calorimetric values quantitatively in the case of six global and ∼10–20 fast modes per subunit. The case of six internal modes is very suggestive, because there are six mutual global modes of motion between two internally rigid domains (three relative translations, three relative rotations). The CAP subunits do indeed contain two principal units (the long α-helix and the β-sheet structure) as demonstrated by performing a GNM simulation. It should not prove excessively difficult to identify these structures experimentally even though NMR measurements are currently mapped onto spatial, rather than modal, dynamics. In addition, the change in fluctuations seems to be optimized for the maximum anticooperative effect.
We elucidated the effect, puzzling at first sight, in which binding of two identical ligands to a completely symmetric dimer has entirely different consequences. We have also shown that a change in protein dynamics can produce a nonzero enthalpy change and suggested how measured thermodynamic parameters can be interpreted. They indicate how many slow and fast modes are being harnessed for the allostery and how the local stiffnesses change. The importance of the coupling between the subunits of a dimer has been highlighted, and the different extent of cooperativity in both truncated and complete versions of CAP has been explained.
Employing our model as an analytical tool of current experimental data allows us to make new predictions and to suggest new experiments. Specifically we expect to find that coupling between subunits weaken on cAMP binding, that two structures dominate the global dynamics, and ∼10–20 local structures couple to the global fluctuations. However, the exact determination of the parameters relies on either new analysis of available data or new experimental and/or computer simulation results.
Appendix A
Evaluation of Eq. 7 yields the allosteric free energy for M slow modes per subunit
| (15) |
Acknowledgments
We thank Peter Olmsted for useful discussions.
This work was supported by the Engineering and Physical Sciences Research Council (UK).
References
- 1.Kern D., Zuiderweg E.R. The role of dynamics in allosteric regulation. Curr. Opin. Struct. Biol. 2003;13:748–757. doi: 10.1016/j.sbi.2003.10.008. [DOI] [PubMed] [Google Scholar]
- 2.Popovych N., Sun S., Kalodimos C.G. Dynamically driven protein allostery. Nat. Struct. Mol. Biol. 2006;13:831–838. doi: 10.1038/nsmb1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yonetani T., Laberge M. Protein dynamics explain the allosteric behaviors of hemoglobin. Biochim. Biophys. Acta. 2008;1784:1146–1158. doi: 10.1016/j.bbapap.2008.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tsai C.J., del Sol A., Nussinov R. Allostery: absence of a change in shape does not imply that allostery is not at play. J. Mol. Biol. 2008;378:1–11. doi: 10.1016/j.jmb.2008.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Goodey N.M., Benkovic S.J. Allosteric regulation and catalysis emerge via a common route. Nat. Chem. Biol. 2008;4:474–482. doi: 10.1038/nchembio.98. [DOI] [PubMed] [Google Scholar]
- 6.Monod J., Wyman J., Changeux J.P. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 7.Koshland D.E., Némethy G., Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1966;5:365–385. doi: 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- 8.Freire E. The propagation of binding interactions to remote sites in proteins: analysis of the binding of the monoclonal antibody D1.3 to lysozyme. Proc. Natl. Acad. Sci. USA. 1999;96:10118–10122. doi: 10.1073/pnas.96.18.10118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jardetzky O. Protein dynamics and conformational transitions in allosteric proteins. Prog. Biophys. Mol. Biol. 1996;65:171–219. doi: 10.1016/s0079-6107(96)00010-7. [DOI] [PubMed] [Google Scholar]
- 10.Clarkson M.W., Gilmore S.A., Lee A.L. Dynamic coupling and allosteric behavior in a nonallosteric protein. Biochemistry. 2006;45:7693–7699. doi: 10.1021/bi060652l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jusuf S., Loll P.J., Axelsen P.H. Configurational entropy and cooperativity between ligand binding and dimerization in glycopeptide antibiotics. J. Am. Chem. Soc. 2003;125:3988–3994. doi: 10.1021/ja027780r. [DOI] [PubMed] [Google Scholar]
- 12.Harris S.A., Gavathiotis E., Laughton C.A. Cooperativity in drug-DNA recognition: a molecular dynamics study. J. Am. Chem. Soc. 2001;123:12658–12663. doi: 10.1021/ja016233n. [DOI] [PubMed] [Google Scholar]
- 13.Cooper A., Dryden D.T. Allostery without conformational change. A plausible model. Eur. Biophys. J. 1984;11:103–109. doi: 10.1007/BF00276625. [DOI] [PubMed] [Google Scholar]
- 14.Gunasekaran K., Ma B., Nussinov R. Is allostery an intrinsic property of all dynamic proteins? Proteins Struct. Funct. Bioinf. 2004;57:433–443. doi: 10.1002/prot.20232. [DOI] [PubMed] [Google Scholar]
- 15.Liu J., Nussinov R. Allosteric effects in the marginally stable von Hippel-Lindau tumor suppressor protein and allostery-based rescue mutant design. Proc. Natl. Acad. Sci. USA. 2008;105:901–906. doi: 10.1073/pnas.0707401105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Alberts B., Johnson A., Walter P. Garland Science; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- 17.Chaiancone E., Vecchini P., Antonini E. Dimeric and tetrameric hemoglobins from the mollusk Scapharca inaequivalis. J. Mol. Biol. 1981;152:577–592. doi: 10.1016/0022-2836(81)90270-9. [DOI] [PubMed] [Google Scholar]
- 18.Strater N., Hakansson K., Lipscomb W.N. Crystal structure of the T state of allosteric yeast chorismate mutase and comparison with the R state. Proc. Natl. Acad. Sci. USA. 1996;93:3330–3334. doi: 10.1073/pnas.93.8.3330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yang X., Lee W.H., Elkins J.M. Structural basis for protein-protein interactions in the 14-3-3 protein family. Proc. Natl. Acad. Sci. USA. 2006;103:17237–17242. doi: 10.1073/pnas.0605779103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Muralidhara B.K., Negi S.S., Halpert J.R. Dissecting the thermodynamics and cooperativity of ligand binding in cytochrome P450eryF. J. Am. Chem. Soc. 2007;129:2015–2024. doi: 10.1021/ja066303w. [DOI] [PubMed] [Google Scholar]
- 21.Eaton A.K., Stewart R.C. The two active sites of Thermotoga maritima CheA dimers bind ATP with dramatically different affinities. Biochemistry. 2009;48:6412–6422. doi: 10.1021/bi900474g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tsai C.J., Del Sol A., Nussinov R. Protein allostery, signal transmission and dynamics: a classification scheme of allosteric mechanisms. Mol. Biosyst. 2009;5:207–216. doi: 10.1039/b819720b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Micheletti C., Lattanzi G., Maritan A. Elastic properties of proteins: insight on the folding process and evolutionary selection of native structures. J. Mol. Biol. 2002;321:909–921. doi: 10.1016/s0022-2836(02)00710-6. [DOI] [PubMed] [Google Scholar]
- 24.Hawkins R.J., McLeish T.C. Coupling of global and local vibrational modes in dynamic allostery of proteins. Biophys. J. 2006;91:2055–2062. doi: 10.1529/biophysj.106.082180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hawkins R., McLeish T. Coarse-grained model of entropic allostery. Phys. Rev. Lett. 2004;93:098104. doi: 10.1103/PhysRevLett.93.098104. [DOI] [PubMed] [Google Scholar]
- 26.Hawkins R., McLeish T. Dynamical allostery of protein α-helical coiled-coils. J. R. Soc. Interface. 2005;3:125–138. doi: 10.1098/rsif.2005.0068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Smock R.G., Gierasch L.M. Sending signals dynamically. Science. 2009;324:198–203. doi: 10.1126/science.1169377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tirion M.M. Large amplitude elastic motions in proteins from single-parameter, atomic analysis. Phys. Rev. Lett. 1996;77:1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- 29.Bahar I., Atilgan A.R., Erman B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997;2:173–181. doi: 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- 30.Hinsen K. Analysis of domain motions by approximate normal mode calculations. Proteins Struct. Funct. Genet. 1998;33:417–429. doi: 10.1002/(sici)1097-0134(19981115)33:3<417::aid-prot10>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- 31.Pan H., Lee J.C., Hilser V.J. Binding sites in Escherichia coli dihydrofolate reductase communicate by modulating the conformational ensemble. Proc. Natl. Acad. Sci. USA. 2000;97:12020–12025. doi: 10.1073/pnas.220240297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Atilgan A.R., Durell S.R., Bahar I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001;80:505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ming D., Wall M.E. Allostery in a coarse-grained model of protein dynamics. Phys. Rev. Lett. 2005;95:198103. doi: 10.1103/PhysRevLett.95.198103. [DOI] [PubMed] [Google Scholar]
- 34.Gohlke H., Thorpe M.F. A natural coarse graining for simulating large biomolecular motion. Biophys. J. 2006;91:2115–2120. doi: 10.1529/biophysj.106.083568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Moritsugu K., Smith J.C. Coarse-grained biomolecular simulation with REACH: realistic extension algorithm via covariance Hessian. Biophys. J. 2007;93:3460–3469. doi: 10.1529/biophysj.107.111898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Heyduk T., Lee J.C. Escherichia coli cAMP receptor protein: evidence for three protein conformational states with different promoter binding affinities. Biochemistry. 1989;28:6914–6924. doi: 10.1021/bi00443a021. [DOI] [PubMed] [Google Scholar]
- 37.Passner J.M., Schultz S.C., Steitz T.A. Modeling the cAMP-induced allosteric transition using the crystal structure of CAP-cAMP at 2.1 Å resolution. J. Mol. Biol. 2000;304:847–859. doi: 10.1006/jmbi.2000.4231. [DOI] [PubMed] [Google Scholar]
- 38.Heyduk E., Heyduk T., Lee J.C. Intersubunit communications in Escherichia coli cyclic AMP receptor protein: studies of the ligand binding domain. Biochemistry. 1992;31:3682–3688. doi: 10.1021/bi00129a017. [DOI] [PubMed] [Google Scholar]
- 39.Yang L.-W., Rader A.J., Bahar I. oGNM: online computation of structural dynamics using the Gaussian network model. Nucleic Acids Res. 2006;34(Web Server issue):W24–W31. doi: 10.1093/nar/gkl084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Li L., Uversky V.N., Meroueh S.O. A computational investigation of allostery in the catabolite activator protein. J. Am. Chem. Soc. 2007;129:15668–15676. doi: 10.1021/ja076046a. [DOI] [PubMed] [Google Scholar]
- 41.Popovych N., Tzeng S.-R., Kalodimos C.G. Structural basis for cAMP-mediated allosteric control of the catabolite activator protein. Proc. Natl. Acad. Sci. USA. 2009;106:6927–6932. doi: 10.1073/pnas.0900595106. [DOI] [PMC free article] [PubMed] [Google Scholar]


