Structural Hierarchy Governs Fibrin Gel Mechanics

Abstract

Fibrin gels are responsible for the mechanical strength of blood clots, which are among the most resilient protein materials in nature. Here we investigate the physical origin of this mechanical behavior by performing rheology measurements on reconstituted fibrin gels. We find that increasing levels of shear strain induce a succession of distinct elastic responses that reflect stretching processes on different length scales. We present a theoretical model that explains these observations in terms of the unique hierarchical architecture of the fibers. The fibers are bundles of semiflexible protofibrils that are loosely connected by flexible linker chains. This architecture makes the fibers 100-fold more flexible to bending than anticipated based on their large diameter. Moreover, in contrast with other biopolymers, fibrin fibers intrinsically stiffen when stretched. The resulting hierarchy of elastic regimes explains the incredible resilience of fibrin clots against large deformations.

Introduction

Fibrin is the main structural protein in blood clots, which stop bleeding and serve as scaffolds to promote wound repair (1). Upon vascular injury, fibrin polymerizes to form a fibrous gel that can withstand the forces exerted by flowing blood and by embedded cells (2,3). Fibrin gels are among the most resilient polymer gels in nature (4,5). They stiffen strongly when deformed and thereby become increasingly resistant to further deformation (3,6–10). Fibrin clots can survive shear and tensile strains of up to 300% (4,5). This remarkable elastic behavior appears to be crucial for the biological function of blood clots. Abnormalities in the structure of fibrin or in its assembly can lead to bleeding or thrombosis, which are both associated with changes in clot mechanics (11). However, the molecular basis of the extraordinary resilience of fibrin clots is still unresolved (12).

Fibrin clots are composed of fibers that appear stiff and straight when viewed by atomic force microscopy (Fig. 1 A). Based on their appearance and on their large diameter (typically 80 nm or more (13)), the fibers are often believed to behave as rigid rods with negligibly small thermal fluctuations (5,7,14,15). The persistence length characterizing the distance over which the fibers are straight is expected to be in the millimeter-range, assuming that they possess a homogeneous elasticity (see Note S1 in the Supporting Material). Various models indicate that cross-linked networks of rigid fibers should stiffen under shear, because the shear aligns the fibers and thereby causes a transition from a soft elastic regime dominated by fiber bending to a stiffer elastic regime dominated by fiber stretching (16–18). Although experimental studies indeed show that fibers align when fibrin gels are sheared (7) or stretched (5,15), there is no evidence that this alignment is the cause of the strain-stiffening behavior of fibrin gels. In fact, there are structural clues that fibrin fibers are unlikely to be homogeneously elastic, as required by the models.

Figure 1.

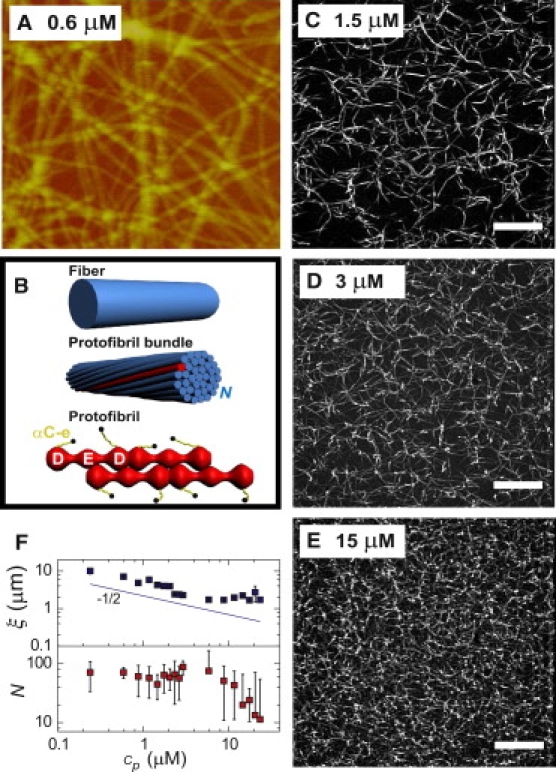
Structural properties of fibrin gels. (A) Atomic force microscopy shows a homogeneous network of thick and straight fibers (5 × 5 μm area). (B) Fibrin fibers have a hierarchical architecture: fibers (top) are bundles of protofibrils (middle), which consist of two half-staggered strands of fibrin monomers with αC-extensions (αC-e) protruding from the surface (bottom). (C–E) Confocal microscopy demonstrates that fibrin gels are homogeneous over a large range of protein concentrations. Scale bars, 10 μm. (F) (Top panel) The mesh size of fibrin gels estimated from confocal images decreases as the square-root of protein concentration (symbols), consistent with the expectation for homogeneous networks of fibers of constant diameter (solid line). (Bottom panel) Concentration dependence of the number of protofibrils per fiber N, measured by turbidimetry.

Fibrin fibers are bundles consisting of dozens of protofibrils (Fig. 1 B, middle), which themselves are composed of two half-staggered strands of fibrin monomers (Fig. 1 B, bottom) (19,20). The monomers in turn consist of three pairs of polypeptide chains, designated Aα, Bβ, and γ, folded into a central E-region and two distal D-regions (21). Fibrin fibers thus have a complex, hierarchical structure. They are furthermore known to contain almost 80% water (22–24). This open internal structure may make the fibers more flexible than previously assumed, because the flexibility of a bundle is sensitive to the degree of coupling between the constituent protofibrils. The bundle will only behave as a simple elastic beam if the coupling is tight. The persistence length l_p will then increase quadratically with bundle size N, reaching a few millimeters for typical values of N (see Note S1 in the Supporting Material). If the protofibrils are not tightly coupled, however, the fibers will be much more flexible than anticipated by the elastic beam limit. In the limit of complete decoupling, the bending stiffness will show a weaker, linear increase with N (25). Coupling between fibrin protofibrils is normally mediated by long, carboxy-terminal extensions of the Aα-chains that protrude from the protofibril surface (26–29) (Fig. 1 B, bottom). These chains are mainly unstructured and rather flexible (29,30), suggesting that the protofibrils may be loosely coupled. Based on this structural evidence, we study the rheology of fibrin gels with the aim of identifying the possible role of this flexibility.

Here we report that the bundlelike structure of fibrin fibers is responsible for the strong strain-stiffening response and exceptional resilience of fibrin gels. We measure the fiber persistence length by optical tweezer microrheology and find that the fibers behave as flexible, loosely coupled bundles of protofibrils. We show that fibrin clots stiffen in two distinct stages when sheared, first by stretching out of fiber fluctuations, between network cross links followed by stiffening of the fibers themselves. This intrinsic fiber nonlinearity makes fibrin gels unique among biopolymer networks, in which nonlinearities are commonly associated with network structure (16,31–33). We propose a new model that accounts for network and fiber nonlinearities and explains the elasticity of fibrin clots over the entire range of strains.

Materials and Methods

Network reconstitution

Human fibrinogen and α-thrombin were obtained from Enzyme Research Laboratories (Swansea, UK) and chemicals were purchased from Sigma-Aldrich (Zwijndrecht, NL). Fibrinogen solutions were made in a buffer of pH 7.4 containing 20 mM HEPES, 150 mM NaCl, and 5 mM CaCl₂. The protein concentration range was 0.1–8 mg/mL, with 1 mg/mL equivalent to 2.94 μM or a fiber length density per volume ρ = 6.1 × 10¹¹ m⁻². Polymerization and cross-linking was initiated by adding 0.5 U/mL thrombin. The networks were cross-linked by fibrinoligase (FXIIIa) (present in the fibrinogen stock solution) at a constant molar ratio of FXIIIa to fibrinogen. We checked by gel electrophoresis that γ-monomers were fully converted to γ-dimers, and α-monomers were fully converted to α-polymers. Consistent with this observation, we did not find (within experimental error) any further increase of the elasticity when we added up to 150 U/mL extra FXIIIa. This evidence suggests that the fibrin gels are maximally cross-linked.

Network visualization

Alexa488-labeled fibrinogen (Invitrogen, Breda, NL) was mixed with unlabeled fibrinogen in a molar ratio of 1:4. Samples were polymerized for 4 h at 37°C and imaged with a spinning disk confocal microscope (Leica Microsystems, Heerbrugg, Switzerland) using a 100×/1.3 NA objective, 488 nm laser, and cooled electromagnetic charge-coupled device camera (C9100; Hamamatsu Photonics, Hamamatsu City, Japan). Image stacks were obtained by scanning through the z direction in increments of 0.1 μm with a piezo-driven objective. Images were band-pass filtered and maximum intensity projections were made in ImageJ (http://rsbweb.nih.gov/ij/). The mesh size ξ was calculated from binarized images (34).

Determination of fiber size

Fiber diameters and mass-length ratios were measured by turbidimetry (see Note S2 in the Supporting Material). Data points are averages over three measurements. A more direct measurement of the fiber diameter, but in a dried state, was made by atomic force microscopy. Samples were polymerized on mica surfaces in a moist 37°C atmosphere. After rinsing with water and drying with nitrogen, samples were imaged in tapping mode using a Dimension V Scanning Probe Microscope and silicon cantilevers (Veeco, Plainview, NY).

Rheology

Rheology was performed with a stress-controlled rheometer (Physica MCR 501; Anton Paar, Graz, Austria). Samples were polymerized at 37°C between a steel cone and plate (40-mm diameter, 1°). Drying was prevented by coating the sample edge with mineral oil and maintaining a moist atmosphere. Networks reached a constant stiffness after ∼3 h. The linear shear modulus G^∗ was obtained by applying an oscillatory strain with amplitude γ = 0.5% and frequency ω = 0.06-38 rad/s and measuring the sinusoidal stress response, σ(ω) = G^∗γ(ω), where G^∗ = G′ + iG″. The in-phase modulus G′ is the elastic modulus, while the out-of-phase modulus G″ is the viscous modulus. The high-strain regime was probed by prestressing the sample with a steady stress σ₀, and superposing a small stress oscillation of amplitude | δσ₀ | < 0.1 σ₀. The stress-dependent tangent modulus follows from the oscillatory strain response, K^∗ = δσ₀/δγ₀. K′ was independent of frequency and of the waiting time in the prestressed state, demonstrating that the prestress did not cause viscous flow. Data represent averages of three measurements.

Microrheology

Fibrin networks were polymerized in the presence of strongly adherent polystyrene particles with a diameter of 1 μm. Particles in the gel interior were weakly trapped using a laser with wavelength of 1064 nm (35). Their thermal position fluctuations were detected by a quadrant photodiode at a sampling rate of 195 kHz and converted to shear moduli using linear response theory (36). There was no evidence of anisotropy in the particle fluctuations, suggesting that they reflect the local rheology rather than fiber motion (see Note S3 in the Supporting Material).

Results and Discussion

Fiber structure and mechanics

We assembled fibrin gels from purified human fibrinogen under near physiological conditions. The gels were enzymatically cross-linked by fibrinoligase (FXIIIa), which provides molecular bonds both within and between fibers (37,38). Addition of thrombin to a solution of fibrinogen causes spontaneous polymerization into thick, straight fibers with diameters of ∼100 nm (Fig. 1 A). The networks are homogeneous and isotropic over a wide range of fibrinogen concentrations, as revealed by fluorescence microscopy (Fig. 1, C–E). The mean distance between filaments progressively decreases as the fibrinogen concentration is raised. The average mesh size decreases with the square-root of fibrinogen concentration, c_p (Fig. 1 F, top), as expected for homogeneous networks of fibers with a constant diameter.

We first investigated whether the fibers within the gels exhibit any thermal bending fluctuations. To measure fiber fluctuations and their rheological consequences in situ, we used optical microrheology. Polystyrene particles were embedded within a fibrin gel and held in a weak optical trap created with a focused laser beam (Fig. 2 A, bottom-right). We observed the thermal fluctuations of the trapped particles with a quadrant photodiode in the back focal plane of the microscope objective. Using linear response theory, the shear modulus of the gel was calculated from the particle fluctuations (36). Fibrin gels are viscoelastic materials, which store deformation energy, as quantified by the elastic modulus G′, but also dissipate energy, as quantified by the viscous modulus G″. At frequencies <1000 rad/s, G′ (solid squares in Fig. 2 A) is larger than G″ (open squares in Fig. 2 A), indicating that fibrin gels are predominantly elastic. However, at frequencies >1000 rad/s, G″ dominates the response. The shear modulus at these high frequencies reflects the stress response of single filaments. G″ increases as a power-law in frequency with an exponent of 0.8 ± 0.01. This exponent is consistent with the ω^3/4 scaling predicted for semiflexible polymers (35,39–41), whereas it differs substantially from the linear scaling expected for stiff polymers. The data therefore strongly suggest that the fibers fluctuate.

Figure 2.

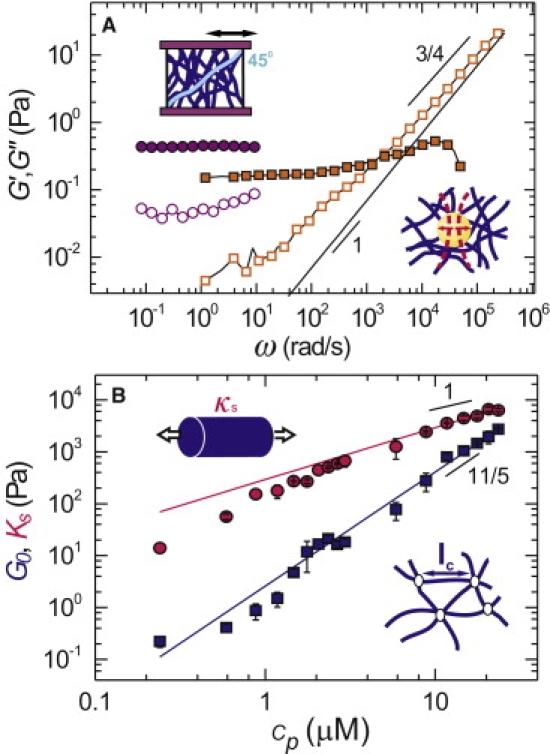
Low-strain rheology of fibrin gels. (A) Frequency dependence of the elastic (solid symbols) and viscous (open symbols) moduli for a network of 0.6 μM fibrin, measured by rheometry (circles) and microrheology (squares). Solid line shows the viscous modulus of the solvent. (Upper inset) The bulk rheology is measured by applying a small, oscillatory shear stress to a fibrin gel between two plates of a rheometer. (Bottom inset) The local rheology is measured by microrheology: a probe sphere inside the fibrin gel is held by an optical tweezer (dotted red lines). Its thermal fluctuations are tracked with a quadrant photodiode and converted to shear moduli using linear response theory. (B) The low-strain plateau modulus G₀ (blue squares) agrees with an entropic model of semiflexible fibers (blue line) with one adjustable parameter, the distance l_c between cross links (bottom inset). The high-strain plateau modulus K_s (red circles) agrees with a single-fiber stretching model (red line) with one adjustable parameter, the fiber stretch modulus κ_s (upper inset).

The persistence length of the fibers can, in principle, be calculated from the amplitude of the particle fluctuations in the high-frequency regime. The microrheology analysis used to compute G′ and G″ assumes that the beads measure the bulk viscoelastic modulus. The amplitude of G″ then suggests a fiber persistence length of 60 μm (Eq. S2 in Note S3, Supporting Material). However, because the probe particles are similar in size to the mesh size, it is not obvious that they measure bulk rheology. Because they adhere to the fibers, it is possible that the bead fluctuations instead directly reflect transverse fluctuations of the fibers. These fluctuations are characterized by the same 3/4 exponent in either time or frequency as G″ (42). Within this framework, the amplitude of the bead fluctuations we observe are consistent with a persistence length of 20 μm. We believe, however, that our microrheology measurements measure network rheology rather than fiber fluctuations. Such fiber fluctuations would be expected to be anisotropic, contrary to our observations. Moreover, the apparent elastic modulus measured by microrheology is close to the bulk modulus. In any case, our measurements clearly indicate the presence of significant thermal bending fluctuations, and both interpretations are consistent with a persistence length of the order of tens of μm. This is 100-fold less than the millimeter-sized persistence length expected for homogeneous fibers (see Note S1 in the Supporting Material). We hypothesized that this discrepancy is due to the bundlelike architecture of the fibers. The effective persistence length of a bundle of N protofibrils is sensitive to the compliance of the cross links between protofibrils, especially for large N (25). To assess the bundle size in situ, we performed turbidimetry on fibrin gels. This technique probes the fibers in their native, hydrated state, in contrast to atomic force microscopy. Both the mass-length ratio and the diameter of the fibers can be calculated from the wavelength dependence of the turbidity (see Fig. S1 A and Note S2 in the Supporting Material). The mass-length ratio was 1 × 10¹³ Da/cm and independent of fibrin concentration up to 10 μM (Fig. S1 B). As protofibrils have a mass-length ratio of 1.5 × 10¹¹ Da/cm (19), the fibers contain, on average, 65 protofibrils (Fig. 1 F, bottom). This implies a fiber persistence length of 1.5 mm for tightly bound protofibrils and 33 μm for loosely bound protofibrils. The latter value agrees well with the microrheology data. In support of the idea that the protofibrils may be loosely coupled, we note that according to turbidimetry the bundles are very open structures, with a diameter close to 90 nm (Fig. S1 C) and protein density of only 0.28 g/cm³ (Fig. S1 D).

Low-strain mechanics of fibrin gels

Microrheology provides measurements of the local gel rheology on the scale of the probe particle size. For probe particles that are similar in size to the mesh size, as is the case here, the local rheology usually differs somewhat from the bulk rheology (36). To obtain more quantitative measurements of the low-frequency rheology, we performed rheometry using a rotational rheometer with cone-and-plate geometry. We applied a small oscillatory stress to a fibrin gel with the top plate and measured the resulting network strain (Fig. 2 A, upper-left). Consistent with microrheology (squares in Fig. 2 A), rheometry shows that the fibrin gels are predominantly elastic at low frequency (circles in Fig. 2 A). G′ is independent of frequency (solid circles) and at least 100-fold larger than G″ (open circles). This indicates that the fibrin gels behave as nearly-perfect elastic solids. The networks remain solidlike even when subjected to a shear stress for 20 min (Fig. S2), indicating negligible sliding of protofibrils or fibers (37,38).

The concentration dependence of the low-frequency elasticity provides another way to distinguish between models of semiflexible and rodlike polymers. The elastic modulus in the elastic plateau region, G₀, increases by four orders of magnitude, from 0.1 to 2000 Pa, when the protein concentration is raised 100-fold, from 0.2 to 24 μM (blue squares in Fig. 2 B). The increase follows a power-law in concentration with an exponent of 2.3, similar to other reports (37,38,43,44). This scaling agrees well with the c^11/5-scaling predicted (and observed) for semiflexible polymers such as actin, where the elasticity is dominated by entropic stretching of the thermally bent polymers (32,33). In contrast, a smaller exponent of 2 is expected for rodlike polymers that bend when the network is sheared (45,46). As the difference between these exponents is rather small, we also tested more quantitatively whether the fibers behave as semiflexible polymers by comparing the data with a theoretical model (32). The modulus for a densely cross-linked network of semiflexible polymers that strains uniformly is G₀ = 6ρk_BTl_p²/l_c³, where ρ is the total fiber length per volume, k_B is Boltzmann's constant, and T is absolute temperature. We can calculate ρ from the measured fiber mass-length ratio and the molar concentration of fibrin. The mesh size ξ = (1/ρ)^1/2, calculated from ρ, is consistent with the measured mesh size (line in Fig. 1 F, top). The cross-link distance l_c is proportional to the distance between filament entanglements, l_e ∼ l_p^1/5ρ^−2/5 (32,33). Assuming that the fibers are loose protofibril bundles with l_p = 33 μm, we find excellent agreement of the experimental data with the entropic model over the entire range of polymer concentrations (blue line in Fig. 2 B). We used only a single free parameter, namely the prefactor between l_c and l_e. We found a best-fit value of 0.35, and values of l_c close to ξ. This indicates that the gels are densely cross-linked, consistent with their branched structure (12).

If the fibrin fibers are semiflexible, the network elasticity should remain linear until the shear straightens out the thermal slack of polymer segments between cross links (32,33). The critical strain γ_c where nonlinearity sets in should thus decrease with increasing polymer concentration. In contrast, γ_c will increase with concentration for rodlike polymers, as nonlinearity will set in when the shear aligns the polymers and buckles the polymer segments between cross links (17). One can therefore distinguish between rodlike versus semiflexible polymer behavior by measuring the concentration dependence of γ_c. We subjected the fibrin gels to a steady prestress σ₀, and measured the tangent modulus K′ by superposing a small oscillatory stress. K′ always increases strongly above a critical stress σ_c (Fig. 3, bottom). The corresponding critical strain decreases with increasing polymer concentration, consistent with the entropic model and contrary to the model of rodlike polymers (squares in Fig. 4 A). Again, we can make this test more quantitative by comparing the data with the entropic model, which predicts γ_c = l_c/3l_p (32). The concentration dependence of γ_c agrees well with the predicted c_p^2/5 scaling (line in Fig. 4 A). The values of γ_c are a factor-4 lower than the predicted values (using the same assumptions for l_c and l_p as before). Similarly, there is a fourfold difference between the calculated and measured critical stress (Fig. 4 B, blue line and blue symbols, respectively). The small numerical discrepancy with the data suggests that strain-stiffening is postponed by a slight degree of nonaffine bending or rotation of filaments (47). Still, the agreement is rather good, thus providing independent evidence that the fibrin fibers are loose protofibril bundles.

Figure 3.

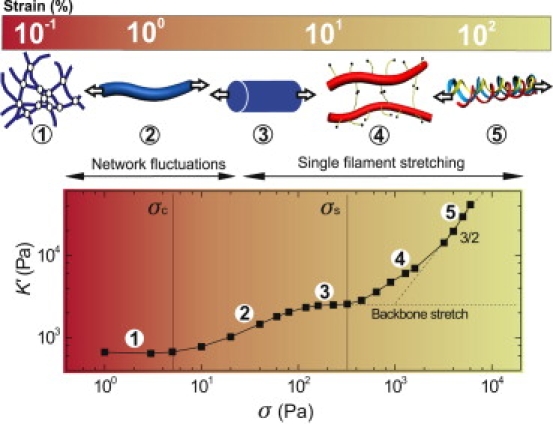
High-strain mechanics of fibrin gels. (Top) Increasing levels of shear strain (bar) induce a sequence of distinct elastic regimes. (Bottom) Typical stress-stiffening behavior of a fibrin gel (9 μM). The color coding of the background indicates the transition from a regime dominated by entropic elasticity at the network level (red) to a regime dominated by entropic elasticity at the fiber level (green). The initial, linear network stiffness reflects thermal fluctuations of the fibers (regime 1). Strains of a few percent pull out the thermal slack from fiber segments between cross links, leading to network stiffening (regime 2). Even larger strains cause fiber stretching, resulting in a second linear regime (regime 3). The elastic modulus would remain constant for fibers with a linear stretch modulus (dashed line). Instead, the modulus increases again (regime 4), indicating stretching of flexible regions within the fibers. The increase is consistent with the σ^3/2 response expected for wormlike chains (dashed line). Forced-unfolding of fibrin monomers may start before network rupture (regime 5).

Figure 4.

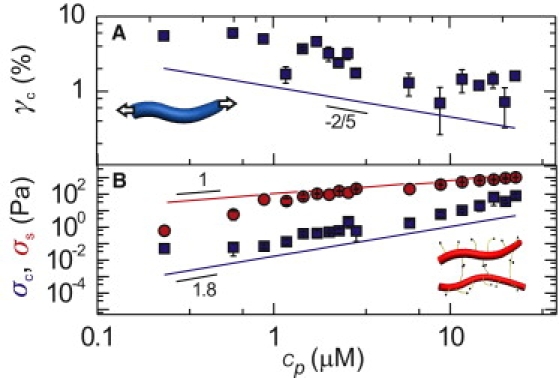
Strain-stiffening transitions of fibrin gels. (A) Critical strain characterizing the onset of the first strain-stiffening regime (regime 2), compared with a model (line) that assumes entropic stretching of fibers (Inset). (B) Critical stress characterizing the onset of the first strain-stiffening regime (regime 2, blue squares) and the onset of the second strain-stiffening regime (regime 4, red circles). Solid lines indicate model predictions for entropic stretching of fibers (blue line) and of loose protofibril bundles (red line and inset).

The persistence length compatible with the rheology data is internally consistent with that obtained by laser tweezer microrheology. However, the value of 30–60 μm is smaller than values reported previously. A recent study using tweezers to actively bend fibrin fibers within a clot reported a Young's modulus of 14.5 MPa for ligated fibrin fibers with a diameter of 270 nm, suggesting that l_p was ∼1 m (14). Two other studies tracking thermally induced transverse fiber fluctuations within clots using a fast camera (48) and dynamic light scattering (49) reported l_p at ∼20–40 cm, but the fiber diameter and mass-length ratio were not reported. The latter two studies did find a power-law exponent of 3/4 for the bending fluctuations characteristic of semiflexible polymer behavior, consistent with our results. There are several factors that make it difficult to make a direct comparison between our study and the previous reports. Firstly, fibrin assembly is known to be highly sensitive to ionic strength, pH, the presence/concentration of certain ions (such as calcium), thrombin concentration, and temperature (13,50–52). In addition, the presence of other proteins (likely present in the plasma but not in our reconstituted clots) can affect assembly. The assembly conditions can affect fiber mass-length ratio and diameter and fiber branching. However, even fibers with apparently the same structure can differ in protein packing density or in the degree of lateral binding between protofibrils within the fibers. Changes in lateral association between protofibrils can strongly affect fiber persistence length; sliding would, for instance, tend to lower l_p. Secondly, the hierarchical bundlelike structure of fibrin fibers implies that the measured persistence length may depend on the length-scale and timescale on which it is probed. Our optical tweezer method probes the fibers on short length- and timescales (frequencies of 1–100 kHz), whereas the previous reports probed l_p at lower frequencies of 3 Hz (14), 100 Hz (49), or up to 1 kHz (48). We conclude that it is crucial in future to perform a detailed study of the variation of fiber persistence length with assembly conditions, using a combination of different techniques (at different spatiotemporal resolutions).

High-strain mechanics of fibrin gels

We next tested whether signatures of a loose bundle structure are present in the rheology of fibrin gels at high strains, where fibers are subject to large tensile forces. The stiffness exhibits at least four distinct stress regimes (Fig. 3, bottom). There is an initial linear regime (regime 1), followed by a rise in stiffness (regime 2), a second linear regime (regime 3), and finally a second stiffening regime (regime 4). The network ruptures at a maximum stress σ_max, labeled as regime 5. The rupture stress is nearly 1000-fold larger than σ_c across the entire concentration range (Fig. S3). The maximal stiffening relative to G₀ decreases from a factor 300 for the sparsest network to a factor 20 for the densest network (Fig. S4). Remarkably, the stress-stiffening curves are repeatable during many consecutive stress sweeps, even when the stress is increased almost to the breakage point (Fig. S5 A). Moreover, we observe no hysteresis between upward and downward stress sweeps (Fig. S5 B).

Although the linear elastic response of the fibrin gels is consistent with an entropic model, the nonlinear response deviates strongly from this model. The model predicts an increase of elasticity with stress as σ^3/2 (33). However, this is valid only if the polymers are inextensible, whereas fibrin fibers are known to be extensible (4). To test whether fiber stretching can explain the high-strain response of fibrin gels, we rescaled the stress-stiffening curves for different fibrin concentrations by the density of protofibrils, Nρ. Note that this scaling accounts for the changing bundle size above 10 μM fibrinogen (Fig. 1 F, bottom). If the elasticity is governed by single-fiber mechanics, the rescaled data should fall on a single curve. As shown in Fig. 5 A, rescaling indeed leads to data collapse onto one curve with a linear regime (regime 3) followed by a strain-stiffening regime (regime 4). The corresponding plateau modulus K_s (Fig. 2 B, red circles) and critical stress σ_s (Fig. 4 B, red circles) increase linearly with fiber concentration. Altogether, this suggests that the high-strain gel response is governed by single fiber mechanics, and that the fibers are intrinsically nonlinear in their response to stretch.

Figure 5.

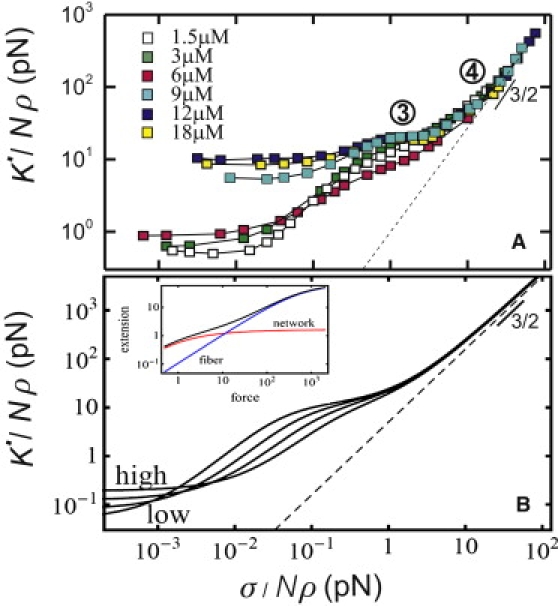
Intrinsic nonlinear stretch modulus of fibrin fibers. (A) Stress-stiffening curves measured for different polymer concentrations, rescaled by protofibril density. The data collapse onto a mastercurve at large strain, where the network elasticity is governed by stretching of fibers with a nonlinear stretch modulus. The stiffening is consistent with the response of a wormlike chain (dashed line). (B) Stress-stiffening curves predicted for fibrin concentrations of 0.3 (low), 1, 3, and 9 (high) μM. (Inset) The fibers are modeled as loose, parallel arrays of protofibrils that fluctuate independently over a length l₀ = 0.1 μm between cross links to the rest of the fiber. The model combines entropic elasticity of the fibers between network cross links (red line), and intrinsic fiber nonlinear stretching due to entropic elasticity of the protofibrils (blue line). The extension (or compliance) of these two contributions add (black line).

The linear stretch modulus of the fibers can be estimated from K_s. For an aligned network of fibers with stretch modulus κ_s, K_s can be approximated as 1/8 ρκ_s (see Note S4 in the Supporting Material). The rheology data are consistent with κ_s = 11 nN (red line in Fig. 2 B). This corresponds to a stretch modulus of 170 pN per protofibril, close to previously reported values of 50–100 pN for protofibril gels polymerized from fish fibrinogen (31). For fibrinogen gels with concentrations below 2 μM, the data depart from the predicted stiffness. This may be due to a small degree of nonaffinity, but we also note that stress-stiffening curves for dilute gels do not show a pronounced plateau (Fig. S4). The nonlinear stretching of the fibers can have several origins. One possibility is suggested by the loose bundle structure of the fibers. Let us consider a fibrin bundle as a parallel array of protofibrils that fluctuate independently over a length l₀ between cross links to the rest of the fiber. The stretch modulus of this bundle for small extensions will be given by 90 k_BTl_p²/l_c³, where l_p is the protofibril persistence length (0.5 μm (6,31)). The measured stretch modulus of 170 pN corresponds to l₀ = 80 nm, meaning that the protofibrils are cross-linked to the rest of the bundle at least at every other αC-chain given that each fibrinogen monomer has a length of 46 nm. The protofibril bundle should stiffen once the thermal slack of flexible protofibril segments between cross links is pulled out. This occurs at a critical force τ = π²k_BTl_p²/l₀², which is 3 pN for l₀ = 80 nm. This number agrees well with the experimental value of ∼2.5 pN that can be read off from Fig. 5 A.

The predictions of this model, including both the initial network elasticity (regimes 1 and 2) and the fiber stretching response (regimes 3 and 4) for l_p = 0.5 μm and l₀ = 0.1 μm are shown in Fig. 5 B. Curves are shown for four different fibrinogen concentrations between 0.3 (low) and 9 (high) μM. This model accounts well for the distinct elastic regimes observed in our experiments, particularly for dense networks.

The first strain-stiffening transition is dominated by the entropic force-extension relation of the whole fiber (sketched as red line in Fig. 5 B, inset) due to long wavelength bending fluctuations of the fiber as a whole (32,53,54). In addition to this compliance, we also allow for an extension of the contour length of the fiber (31,55) (blue line in Fig. 5 B, inset). These two effects can be thought of as (nonlinear) springs in series and the full extension is the sum of these two contributions, shown by the black line. As noted above, for the extensional response we model the fiber as a loose bundle of protofibrils that act as springs in parallel. The semiflexible nature of the protofibrils leads to a characteristic 3/2-scaling of network stiffness with stress (32,33) (dashed line in Fig. 5 B). This is consistent with the experimental data in regime 4 (dashed line in Fig. 5 A). Such entropic stretching is expected to be fully reversible, like that shown in our experiments (Fig. S5).

Although the loose bundle model appears to describe the measured gel elasticity well, it requires several assumptions because microscopic parameters such as the cross-link distance, cross-link affinity, and cross-link compliance are unknown. It is also possible that other flexible regions within the fibers cause the intrinsic fiber nonlinearity. For instance, the αC-regions might elongate under fiber extension. Recent stretching experiments on fibers composed of fibrinogen from different species that differ in the length of their αC-regions showed that the maximum elongation increased with the length of the αC-region (56). Because these mainly unstructured regions have a small persistence length in the nanometer-range, stretching should also be characterized by an entropic force-extension relation and 3/2 scaling of stiffness with stress. Alternatively, flexible regions may be created by forced-unfolding of fibrin monomers, as suggested by x-ray diffraction studies on fibrin gels under tensile load (5,57). The principal unfolding elements are the coiled-coils connecting the E-region to the distal D-regions, as shown by stretching of single molecules (58,59) and protofibrils (5,58). To test whether forced unfolding can explain the observed stress-stiffening behavior, we estimate the force experienced by fibers from the macroscopic shear stress. The average force per fiber at the onset of fiber stiffening is 500 pN, or 1–10 pN per protofibril (open squares in Fig. 6 B). This is far less than the average value of 130 pN required to unfold protofibrils (though this number is rate-dependent) (58). The maximum force per protofibril just before network rupture is 10–40 pN, still less than required for unfolding (solid squares in Fig. 6 B). The maximum extensional strain per fiber is ∼175% (a little over half of the shear strain in Fig. 6 A), which is less than the 300–500% strains reported for single fibers (4,56). The onset of the nonlinear regime 4, however, occurs for strains substantially smaller than 100%. Moreover, the reversibility of the stress-stiffening curves is not expected when molecular unfolding occurs (58,59). We therefore consider it unlikely that forced unfolding can account for the second strain-stiffening regime. Perhaps unfolding starts at strains close to γ_max (regime 5 in Fig. 3). However, the network probably breaks before unfolding is completed. The rupture stress σ_max increases more strongly with concentration than the linear increase expected if the network strength is governed by breakage of fibers (Fig. S3). This indicates that the network strength is limited by the strength of fiber-fiber contacts (60).

Figure 6.

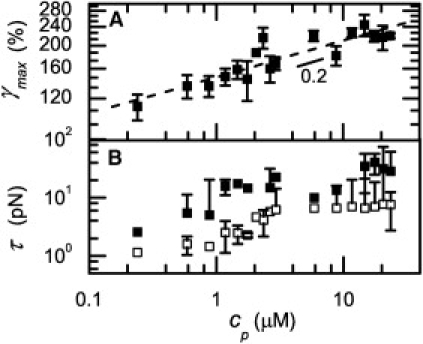
Rupture behavior of fibrin gels. (A) The rupture strain (symbols) increases weakly with fibrin concentration according to a power-law with exponent 0.2 (dashed line). (B) Tension per protofibril calculated from the shear stress where the second strain-stiffening regime starts (open symbols) and from the stress where the network ruptures (solid symbols).

Conclusions

The major finding of this work is that the bundlelike structure of fibrin fibers accounts for the remarkable elastic properties of fibrin gels, as summarized in Fig. 3. The fibers behave as loosely cross-linked bundles of protofibrils with a built-in stretch-stiffening response. This structure leads to a rich elastic response that reflects stretching of thermal fluctuations of fibers between network cross links (regimes 1 and 2) followed by stretching of flexible regions within the fibers (regimes 3 and 4). From the rheology data alone it is not possible to identify exactly which molecular regions cause the intrinsic nonlinearity of the fibers. The protofibrils themselves are likely candidates, but the αC-regions or unfolded molecular regions may also contribute. It appears that the clots break before the monomers are fully unfolded (regime 5). This is in apparent contrast to a recent study of fibrin gels under tensile load, where gel stiffening was accompanied by molecular unfolding (5). However, our study addresses a complementary regime of lower strains, enabling us to observe a hierarchy of mechanical regimes that precedes molecular unfolding. We note that there are potentially differences between gel shearing and gel extension. It would therefore be interesting to perform direct measurements of the molecular structure of fibrin monomers in fibrin gels under shear, to prove to what degree molecular unfolding occurs. A promising avenue is to combine mechanical testing with small angle x-ray scattering, as was reported for gels under tensile load (5). Another promising avenue to achieve a molecular level understanding is to perform single-fiber-stretching experiments at smaller forces than hitherto probed.

Our results indicate that the αC regions play an important role in controlling the extensibility and mechanical resistance of human fibrin clots. Interestingly, while these regions mediate lateral associations between protofibrils in normal clots, they are actually not necessary for lateral association. Fibrin monomers whose αC regions are removed by proteolytic digestion still assemble into striated fibers that form coarse clots that are similar in appearance to normal clots but more fragile (26). There are also several clotting disorders (dysfibrinogenemias) involving mutations or truncations of fibrinogen in the carboxy-terminal region of its α-chain (reviewed in (29)), which likely lead to changes in clot mechanics. Indeed, clots of recombinant fibrin with truncated αC regions showed plasticity due to slippage of protofibrils (27). A true molecular-scale understanding of fibrin clot mechanics will require an in-depth study of the role of the αC regions as well as that of other molecular domains mediating lateral association, such as the knob-hole interactions (61,62) and γ-γ cross links (27,63). It will be interesting to perform similar nonlinear rheology studies as ours on proteolytically modified fibrin (26), recombinant fibrin with truncated α-chains (27), fibrin from other species (differing in length of the αC region (56)), and variant fibrin from human patients with dysfibrinogenemias (such as Caracas II, Marburg, or Dusart) (29). Based on our findings, we predict that these fibrin clots will be less extensible and more fragile than normal human fibrin clots.

Our study demonstrates that supramolecular assembly is a powerful strategy to build fibrous networks that are incredibly resistant to breakage. Supramolecular assembly is a widely used principle in biopolymers. However, few biopolymers are as extensible as fibrin. An archetypal example of a hierarchical biopolymer is collagen, which provides tensile strength to soft tissues. Collagen fibers can withstand large tensile loads but rupture at strains <50% because the monomers are inextensible and tightly bundled (64). Cytoplasmic intermediate filaments do match the elasticity and extensibility of fibrin fibers, but these filaments consist of tightly bundled subunits that, similar to fibrin, can unfold upon stretching (57,65). Fibrin thus has an extra hierarchical level of structure that provides additional mechanical resilience. Our data reveal molecular design principles that allow blood clots to recover reversibly from large shear forces. This may help us to understand how mutations or pathological alterations in fibrin change the resilience of clots, which can cause hemorrhage or thromboembolism (11). Specifically, our work sheds light on the molecular mechanism by which mutations or truncations of fibrinogen in the carboxy-terminal region of its α-chain lead to dysfibrinogenemias (29). Moreover, our findings suggest a new design concept for resilient synthetic materials with potential applications in drug delivery and tissue repair (66,67).

Supporting Material

Three equations, four notes, and five figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00205-5.