Abstract
Two de novo protein design frameworks are applied to the discovery of new compstatin variants. One is based on sequence selection and fold specificity, whereas the other approach is based on sequence selection and approximate binding affinity calculations. The proposed frameworks were applied to a complex of C3c with compstatin variant E1 and new variants with improved binding affinities are predicted and experimentally validated. The computational studies elucidated key positions in the sequence of compstatin that greatly affect the binding affinity. Positions 4 and 13 were found to favor Trp, whereas positions 1, 9, and 10 are dominated by Asn, and position 11 consists mainly of Gln. A structural analysis of the C3c-bound peptide analogs is presented.
Introduction
Compstatin is a synthetic 13-residue cyclic peptide that inhibits the cleavage of C3 to C3a and C3b in the human complement system and thus hinders complement activation. It is cyclized by a disulfide bond between Cys2 and Cys12. Compstatin is a novel drug candidate identified through the screening of a phage-displayed random peptide library with C3b, a proteolytically activated form of complement C3, and was later truncated to its present 13-residue form without loss of activity (1). Although complement activation is part of normal inflammatory response, inappropriate complement activation can cause host-cell damage, which is the case in >25 pathological conditions, including autoimmune diseases, stroke, heart attack, Alzheimer's disease, and burn injuries (2). Compstatin has shown highly promising results in numerous clinically relevant trials (1,3–10).
De novo design of compstatin variants aims at acquiring the sequences corresponding to the best inhibitors to C3 and thus the most potent drugs for diseases related to inappropriate complement activation (11–15). Recent review articles on de novo protein design present the advances and challenges (16,17). Morikis et al. (13) studied compstatin sequences using rational design, experimental combinatorial design, and computational combinatorial design. A number of compstatin variants with known experimental relative activities are presented in Table S1 in the Supporting Material. The activities are relative to the native compstatin sequence.
The rational design of compstatin yielded an analog with a fourfold higher activity than the native compstatin (18). Using experimental combinatorial design, another compstatin analog with fourfold increased activity was found (peptide No. 6). In this design, the hydrophobic cluster and the β-turn were kept, with the novel introduction of Trp at position 9 (19). The introduction of this second Trp suggests that Trp ring stacking may be important for the compstatin activity. The computational combinatorial design of compstatin gave several analogs of compstatin with higher activity than the native (11). These included peptides with an 11-fold and 16-fold higher activity (peptides No. 7 and No. 8, respectively) along with an extremely potent analog with 45-fold higher activity (peptide No. 9, from here on referred to as variant E1) (20). The computational design identified another position (position 4) where an aromatic ring could be placed to enhance ring stacking and activity. In this case, Tyr was present in position 4 with Trp present in position 7. In addition, Mallik et al. (20) studied compstatin analogs with nonnatural amino acids.
Methods
Design template
The crystal structure of compstatin variant E1 in complex with complement component C3c, recently elucidated by Janssen et al. (21) (Protein DataBank (PDB) code: 2QKI), was used as the design template. They performed the work on C3c instead of the whole C3 protein itself because C3c crystals are easier to obtain and they diffract at a higher resolution than those of C3. The structure of C3c complexed with the compstatin variant E1 is shown in Fig. S1 in the Supporting Material.
As revealed by the structure, the binding site of the compstatin variant on C3c is at macroglobulin domains 4 and 5. Because this is not confirmed as the actual binding site of the compstatin variant E1 on C3, we only employ the structure of the compstatin variant E1 in the C3c-compstatin complex as the design backbone template for our de novo design of the inhibitor (see Fig. 1). We believe this is the best model for C3-compstatin variant E1 interaction we can obtain thus far in the open literature. Both chains G and H correspond to the compstatin variant E1 in the PDB file of the structure of C3c-compstatin E1 complex. As we found that both chains are highly structurally similar with an atom-to-atom root mean-square deviation of 0.405 Å, we only used chain G as the template for designing new compstatin variants. In addition, the free compstatin structure was used (PDB code: 1A1P) for comparison to the native compstatin sequence.
Figure 1.
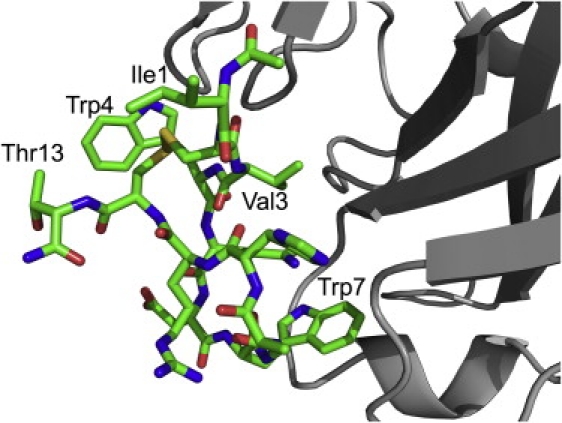
A closeup view of the structure of compstatin variant E1 (ICVWQDWGAHRCT) in Fig. S1. It constitutes the design template for our de novo design of the inhibitor.
Mutation set
As the disulfide bridge was found to be essential for aiding the formation of the hydrophobic cluster and prohibiting the termini from drifting apart, both residues Cys2 and Cys12 were maintained. In addition, because the structure of the type-I β-turn was not found to be a sufficient condition for activity, the turn residues were fixed to be those of the parent compstatin sequence; namely Gln5-Asp6-Trp7-Gly8. In fact, when stronger type I β-sequences were constructed, which was supported by nuclear magnetic resonance (NMR) data indicating that these sequences provided higher β-turn populations than compstatin, these sequences resulted in lower or no activity (18). For similar reasons, Val3 was maintained throughout the computational experiments.
Based on the structural and functional characteristics of those residues involved in the hydrophobic cluster, positions 1, 4, and 13 were allowed to select only from the hydrophobic amino acid set (A,F,I,L,M,W,V,Y). In addition, this set included Threonine for position 13 to allow for the selection of the wild-type residue at this position. Thr is partially hydrophobic because it has a methyl group and partially polar because it has a hydroxyl group. For positions 9, 10, and 11, all residues were allowed, except for Cysteine and Tryptophan. This mutation set leads to a problem with complexity 3.0 × 106.
De novo design based on fold specificity calculations
We first calculated the fold specificities of compstatin variants complexed with C3c using our two-stage de novo design framework (11,12,14,22,23). A graphical overview of the design process is depicted in Fig. 2. The first stage produces a rank-ordered list of amino acid sequences with the lowest energies in a flexible design template by solving an integer programming sequence selection model (11,12,14,24). The second stage calculates the specificities of the sequences to the fold based on the full atomistic force field either through 1), the ASTRO-FOLD approach (25–34) and deterministic global optimization (35–41); or 2), the AMBER force field via a novel NMR structure refinement method (16,22).
Figure 2.
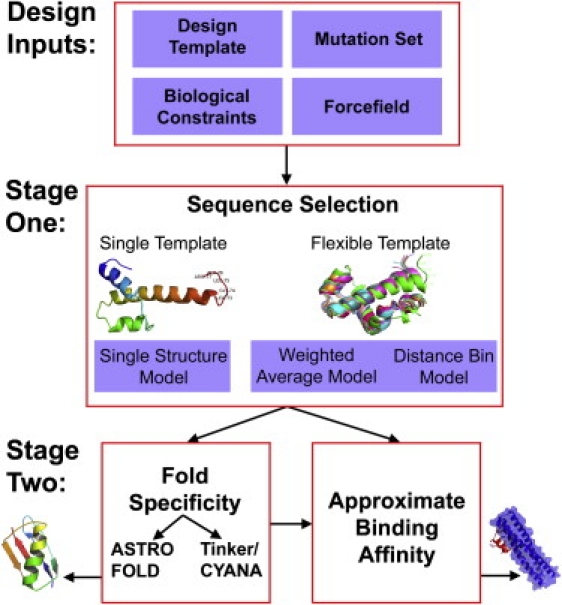
Overview of the de novo design framework.
The de novo protein design framework
Stage one: sequence selection
As the design backbone template has only one structure, the basic sequence selection model (14) was used for obtaining amino acid sequences with the lowest energies in the fold, although Fung et al. (14) have presented other optimization models for flexible templates with multiple protein structures. The basic model is an integer linear programming model of the form
| (1) |
Set i = 1, …, n defines the number of amino acid positions along the backbone. At each position i, there can be a set of mutations represented by j{i} = 1, …, mi, where, for the general case mi = 20 ∀ i. The equivalent sets k ≡ i and l ≡ j are defined, and k > i is required to represent all unique pairwise interactions. Binary variables yij and ykl are introduced to indicate the possible mutations at a given position. Specifically, variable yij will be one if position i is occupied by amino acid j, and zero otherwise. Similarly, variable ykl will assume the value of one if position k is taken by amino acid l, and the value of zero otherwise. The composition constraints in the formulation require that there is exactly one type of amino acid at each position. Energy parameters Eikjl indicate the pairwise interaction between amino acid j at position i and amino acid l at position k and were calculated using the centroid-centroid force field of Rajgaria et al. (42).
Using Eq. 1, we generated 1000 low energy sequences for which we calculated the fold specificities in stage two.
Stage two: fold specificity calculations
The method described in Fung et al. (22) was used to generate an ensemble of several hundred conformers for each of the 1000 sequences using CYANA 2.1 (43,44) and TINKER (45). The conformers are within the upper and lower bounds on the Cα-Cα distances and dihedral angles obtained from the native structure. The energies of the conformers for each sequence and the native sequence were used to calculate the fold specificity (see Supporting Material). A workflow of stage two, detailing the programs used and the number of structures that are input and output in each step, is given in Fig. S2.
De novo design based on approximate binding affinity ranking metric
The design of compstatin variants was also done using a novel de novo design framework based on an approximate binding affinity (K∗) ranking metric. This novel de novo design framework also consists of two stages. The first stage solves an integer programming sequence selection model to generate a rank-ordered list of amino acid sequences with the lowest energies (11,12,14,24). The second stage ranks the sequences based upon approximate binding affinities. This second stage is more applicable when the design template consists of a complex. Stage two of the novel design framework utilizes programs from the Rosetta++ package (47–49) for the necessary structure and docking prediction and ensemble generation. Fig. 2 shows an overview of the novel de novo design framework.
The novel de novo protein design framework
Stage one: sequence selection
Stage one is the same as the one used in the de novo design based on fold specificity calculations.
Stage two: approximate binding affinity calculation
A novel approach to approximating the binding affinity of protein-ligand complexes has been introduced by Lilien et al. (50). The approximate binding affinity, K∗, is given by Eq. 2, where qPL is the partition function of the protein-ligand complex, qP is the partition function of the free protein, and qL is the partition function of the free ligand:
| (2) |
The partition functions are defined in Eq. 3, where sets B, F, and L contain the rotamerically based conformations of the bound protein-ligand complex, the free protein, and the free ligand, respectively. En is the energy of conformation n, R is the gas constant, and T is the temperature:
| (3) |
Because K∗ uses the Boltzmann probability distribution, it satisfies the Ergodic hypothesis and can be proved to approximate the true binding affinity, KA. K∗ will equal KA if K∗ is calculated using exact partition functions. For an enzyme/ligand system, the true binding affinity is defined in Eq. 4. At equilibrium, the chemical potentials μi of the complex, free protein, and free ligand sum to zero (Eq. 5). By expressing the chemical potential in terms of indistinguishable particles (Eq. 6) and substituting this into Eq. 5, we obtain Eq. 7. Thus, the true binding affinity can be expressed as a ratio of the individual species partition functions. The more accurate the partition functions, the better KA is approximated:
| (4) |
| (5) |
| (6) |
| (7) |
Fig. S2 provides a graphical depiction of the steps needed to calculate K∗ and further details can be found in the Supporting Material. First, three-dimensional structures of each sequence are generated using RosettaAbinitio (47,51,52). For each sequence, 1000 peptide structures are generated. The structures are then clustered based upon their ϕ- and ψ-angles using OREO (53, P. A. DiMaggio, S. R. McAllister, C. A. Floudas, X. J. Feng, J. D. Rabinowitz, and H. A. Rabitz, unpublished). This groups together similar structures. An average structure from each of the 10 largest clusters, plus the overall lowest energy structure, are selected for docking. RosettaDock (48,55,56) is used to dock each of the 11 peptide structures to the target protein. For each docking run, 1000 docked conformers are generated. Finally, RosettaDesign (49) is used to generate the rotamerically based conformation ensembles using the peptide structures from RosettaAbinitio, the complex structures from RosettaDock, and the crystal structure of the target protein as input structures for the free peptide, complex, and free protein ensembles, respectively. Solvation effects are incorporated implicitly in the energy functions that are used to drive each of the modeling steps (sequence selection, structure prediction, docking, etc.). The Rosetta programs use the Lazaridis-Karplus solvation model (57), which is based on a Gaussian-shaped solvent exclusion.
The free peptide ensemble consists of 22,000 total structures (set L). One-hundred-and-ten starting structures are obtained by selecting the 10 lowest-energy structures from each of the 10 largest clusters plus the 10 overall lowest-energy structures obtained from RosettaAbinitio. For each starting structure, 200 rotamer conformers are generated, giving a final ensemble of 22,000 structures. The ensemble incorporates both backbone flexibility (by using 110 different backbone starting structures) and rotamer flexibility (by generating 200 rotamer conformers per starting structure).
The complex ensemble also consists of 22,000 total structures (set B). Again, 110 starting structures are used, this time by selecting the 10 lowest-energy docked conformers from the 11 docking runs per sequence. Two-hundred rotamer conformers are generated per starting structure. Flexibility is taken into account by the various peptide backbone structures used (11 different backbones total), the various docked conformations (10 per peptide backbone), and the rotamer conformers for each starting structure.
The free protein ensemble consists of only 2000 total structures (set F). Because the target protein is so large (>1000 residues), it is computationally infeasible to predict backbone structures. Therefore, the crystal structure of the protein is used as the only starting structure and 2000 rotamer conformations are generated.
For the stage two calculations, we are not attempting to compare our predicted K∗ values with actual experimental binding affinities, but instead are using it as a ranking metric to sort the sequences from stage one to elucidate better binders. In fact, it is difficult to precisely compare the values of K∗ to experimental binding affinities because K∗ is unitless. The partition functions themselves are unitless.
Results
Results for both stage one (run 1) and the top 10 sequences with the highest fold specificities from stage two are shown in Table S2 and Table 1, respectively.
Table 1.
Top 10 sequences from stage one with the highest fold specificities (Run 1)
| Sequence | Sequence selection rank | Fold specificity rank | Approximate binding affinity rank | Position |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K∗ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||||
| NCV-2 | 756 | 2 | 1 | 4.31 × 10−02 | I | C | V | W | Q | D | W | G | R | N | N | C | W |
| NCV-10 | 809 | 10 | 2 | 3.30 × 10−02 | V | C | V | W | Q | D | W | G | R | V | N | C | W |
| NCV-3 | 392 | 3 | 3 | 3.83 × 10−04 | L | C | V | W | Q | D | W | G | Q | M | R | C | W |
| Variant E1 | n/a | n/a | 4 | 5.78 × 10−06 | I | C | V | W | Q | D | W | G | A | H | R | C | T |
| NCV-5 | 684 | 5 | 5 | 4.10 × 10−07 | W | C | V | W | Q | D | W | G | R | N | N | C | W |
| NCV-1 | 833 | 1 | 6 | 3.55 × 10−07 | V | C | V | W | Q | D | W | G | Q | M | R | C | W |
| NCV-8 | 867 | 8 | 7 | 9.69 × 10−08 | I | C | V | W | Q | D | W | G | Q | I | R | C | W |
| NCV-7 | 671 | 7 | 8 | 6.26 × 10−09 | F | C | V | W | Q | D | W | G | Q | M | R | C | W |
| NCV-4 | 659 | 4 | 9 | 3.51 × 10−10 | I | C | V | W | Q | D | W | G | Q | V | R | C | W |
| NCV-9 | 343 | 9 | 10 | 8.01 × 10−11 | I | C | V | W | Q | D | W | G | Q | R | N | C | W |
| NCV-6 | 539 | 6 | 11 | 6.88 × 10−11 | L | C | V | W | Q | D | W | G | Q | R | N | C | W |
| Native | n/a | n/a | 12 | 4.27 × 10−12 | I | C | V | V | Q | D | W | G | H | H | R | C | T |
Mutations are indicated in boldface.
The following suggested mutations versus the native sequence of compstatin are observed from the sequences predicted based on fold specificities: I1(V/L/I), V4W, H9(Q/R), H10(M/N/V/R), R11(R/N), and T13W. The preference of Trp at positions 4 and 13 is dominant. Notice that the Trp at position 4 is already present on compstatin variant E1, which corresponds to 45-fold improvement in potency over the native compstatin (20). As for position 13, a mutation to Val was experimentally validated to be preferred (11,46), whereas a more hydrophobic amino acid of Trp might lead to even higher potency. The suggested mutations of H9(Q/R) and H10(M/N/V/R) have not been experimentally tested. For positions 1 and 11, the fold specificity results suggest it might be favorable to keep the native residues.
Before using the sequences generated from stage one, stage two of the novel design framework was tested on sequences from the previous designs of compstatin (Table S1). The goal was to predict, correctly, whether the compstatin variant binds better or worse than the native. For all partition function calculations, the sets B and L consisted of 22,000 configurations, and the set F consisted of 2000 configurations.
The approximate binding affinity model is successful because it provides theoretical predictions on binding, which have been experimentally validated using surface plasmon resonance (SPR) binding studies. Although the theoretical algorithm ranks the predicted analogs with respect to the native peptide, this ranking is only approximate and depends on the theoretical details and parameterization of the algorithm and the calculation setup. In addition, the theoretical predictions are based on binding of compstatin analogs to C3c, whereas the SPR studies are performed with the whole C3. Thus, the success of the algorithm lays in its ability to predict any new sequences with binding abilities. Further optimization of the predicted sequences by incorporating nonnatural amino acids (20) is expected to increase binding affinities.
Of the sequences in Table S1, peptide Nos. 6, 7, 8, and 9 were correctly predicted to be better binders than the native, and peptide Nos. 2 and 4 were correctly predicted to be worse binders than the native. Peptide Nos. 1 and 3 were incorrectly predicted to be better binders than the native. There could be two reasons for this discrepancy. One is that the experimental relative activity is based upon IC50 data. IC50 is a measure of the concentration of the peptide required to obtain 50% inhibition of the target protein. This is not the same as binding affinity, although the two are related. The relationship between binding affinity and IC50 also depends upon the concentration of the substrate or ligand and the Hill coefficient. There can be cases where a ligand has a higher binding affinity (or lower KD, inverse of binding affinity), but a higher IC50 when compared to another ligand (58). Furthermore, the computational predictions and SPR data are on binary systems, whereas any immunological assay, in vitro or in vivo, are on nonbinary systems, involving inhibitions of pathways or reactions. Therefore, we cannot expect the data from binary systems to correlate exactly with data from nonbinary systems. The second reason for the discrepancy is that the rotamer sampling is simply not high enough. If the rotamer space could be perfectly sampled, the prediction of K∗ would be exact. This, however, is computationally demanding. Our method is also limited by the accuracy of the energy functions used in the various Rosetta programs. Although these are some of the best protein prediction and docking methods available, any inherent limitations translate into our calculations.
Looking closer at the sequences in Table S1, variant E1 has two mutations compared to the native (i.e., V4W and H9A), and exhibits a 45-fold higher potency than the native compstatin (20). The sequences proposed by Klepeis et al. (11,12) show up to a 16-fold improvement in activity over the native compstatin. Peptide No. 7 has three mutations (i.e., V4Y, H9F, and T13V), whereas peptide No. 8 has two mutations (i.e., V4Y and H9A) compared to the native sequence. It is important to emphasize that the key common element is the presence of a hydrophobic and aromatic amino acid in position 4.
Approximate binding affinities of high-fold specificity sequences were calculated to compare the ranking based upon fold specificity and the ranking based upon approximate binding affinities. Table 1 shows the K∗ results. In comparing the two ranking metrics, we find no correlation, yet the sequences with high fold specificities are all predicted to be better binders than the native sequence. All of the designed sequences exhibit a higher binding affinity than the native, and three of them, variants NCV-2, NCV-10, and NCV-3 have higher approximate binding affinities than variant E1. Variant NCV-2 has five mutations (V4W, H9R, H10N, R11N, and T13W). Variant NCV-10 has six mutations (I1V, V4W, H9R, H10V, R11N, and T13W). Variant NCV-3 has five mutations (I1L, V4W, H9Q, H10M, and T13W). The mutations among the 10 variants are extremely similar. In all cases, positions 4 and 13 were mutated to Trp and positions 9–11 were mainly mutated to a set of polar amino acids. Note the consistency in position 9 (either Q or R) for these sequences and the dominance of Asn in position 11. Many combinations of polar amino acids at these positions are possible and examples of structural analyses are given in Fig. S3 and Fig. S4. These sequences are similar to variant E1 in position 4 and contain the same dominance in positions 9–11 of polar amino acids. Variant E1 also maintains the native Thr in position 13, while the 10 variants changed this residue to Trp.
Based upon these observations, the sequence selection model (stage one) was run again, generating sequences with mutations allowed only in positions 1, 9, 10, and 11. Positions 9, 10, and 11 were allowed to select from the hydrophilic amino acids (G,N,Q,H,K,R,D,E,S,T,P), while position 1 was allowed to select from all amino acids. Trp was specified in positions 4 and 13 and positions 2–3, 5–8, and 12 were kept the same as in the native. Two-thousand sequences were generated in total. Table S2 shows preferred amino acid mutations (run 2) for each position.
Table 2 shows a selection of sequences from stage one for which approximate binding affinities were calculated. The sequences are ranked accordingly.
Table 2.
Top sequences from stage one with the highest approximate binding affinities (Run 2)
| Sequence | Sequence selection rank | Approximate binding affinity rank | K∗ | Position |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||||
| SQ027 | 40 | 1 | 3.38 × 10+01 | W | C | V | W | Q | D | W | G | T | N | R | C | W |
| SQ100 | 159 | 2 | 8.45 × 10+00 | W | C | V | W | Q | D | W | G | Q | T | Q | C | W |
| SQ087 | 214 | 3 | 4.26 × 10−02 | N | C | V | W | Q | D | W | G | K | K | Q | C | W |
| SQ072 | 166 | 4 | 1.31 × 10−02 | D | C | V | W | Q | D | W | G | Q | N | Q | C | W |
| SQ077 | 185 | 5 | 3.07 × 10−03 | G | C | V | W | Q | D | W | G | G | N | Q | C | W |
| SQ040 | 102 | 6 | 4.48 × 10−04 | Q | C | V | W | Q | D | W | G | T | N | Q | C | W |
| SQ098 | 238 | 7 | 3.46 × 10−04 | K | C | V | W | Q | D | W | G | N | N | K | C | W |
| SQ017 | 50 | 8 | 6.78 × 10−05 | N | C | V | W | Q | D | W | G | H | N | K | C | W |
| SQ025 | 69 | 9 | 4.27 × 10−05 | N | C | V | W | Q | D | W | G | S | N | Q | C | W |
| SQ086 | 210 | 10 | 1.10 × 10−05 | Q | C | V | W | Q | D | W | G | Q | N | Q | C | W |
| Variant E1 | n/a | 11 | 5.78 × 10−06 | I | C | V | W | Q | D | W | G | A | H | R | C | T |
| SQ023 | 59 | 12 | 6.73 × 10−07 | N | C | V | W | Q | D | W | G | E | N | Q | C | W |
| SQ024 | 65 | 13 | 4.35 × 10−07 | S | C | V | W | Q | D | W | G | N | N | Q | C | W |
| SQ059 | 144 | 14 | 1.50 × 10−07 | D | C | V | W | Q | D | W | G | T | N | K | C | W |
| SQ055 | 133 | 15 | 2.95 × 10−08 | P | C | V | W | Q | D | W | G | N | K | Q | C | W |
| SQ046 | 112 | 16 | 2.06 × 10−08 | P | C | V | W | Q | D | W | G | N | N | Q | C | W |
| SQ088 | 213 | 17 | 1.11 × 10−08 | G | C | V | W | Q | D | W | G | K | N | Q | C | W |
| Native | n/a | 18 | 4.27 × 10−12 | I | C | V | V | Q | D | W | G | H | H | R | C | T |
Mutations are indicated in boldface.
Upon closer examination of the 16 sequences, the mutations chosen for two of the four positions are rather conserved. Position 10 exhibited 13 mutations to Asn and two to Lys. Position 11 exhibited 12 mutations to Gln and three mutations to Lys. Positions 1 and 9 showed more variability in the amino acids chosen, but in each case, there was one dominant amino acid. The dominant amino acid in positions 1 and 9 was Asn, with four of the 16 sequences choosing that amino acid in each position. However, the two best sequences show a mutation of Trp in position 1. These sequences exhibit four Tryptophans. Among the 10 sequences that outperformed variant E1, position 10 exhibited seven mutations to Asn. Position 11 exhibited seven mutations to Gln and two mutations to Lys. Position 1 showed more dominance for Asn, with three of the 10 sequences choosing that amino acid, whereas position 9 showed less dominance for Asn, with only one out of the 10 sequences choosing that amino acid.
The effect of different docking programs was also examined and was found to have no effect on the final K∗ ranking. Further details can be found in the Supporting Material.
Experimental binding studies of select sequences
Three of the designed sequences were selected for synthesis and determination of experimental binding using SPR. The experiments were carried out using the biosensor Biacore X100 (Biacore, Piscataway, NJ). The native compstatin, variant E1, SQ027, SQ086, and SQ059 were synthesized and immobilized on the sensor chip. Table S4 provides the amino acid sequences that were synthesized. Eight polyethylene glycol blocks, followed by K-biotin, were added to the amino acid sequences for Biacore. Seven different concentrations of C3 were used during the experiment: 1600 nM, 800 nM, 400 nM, 200 nM, 100 nM, 50 nM, and 25 nM. The KD values were extracted by simultaneous fitting of the 0–800 nM data. The 1600 nM were not used because they showed some evidence of saturation. The data from the experiments were fit to three models: 1:1 binding model, two-state reaction model, and a heterogeneous ligand model. The experimental bindings (KD) are reported in Table 3. Values of KD for using both the two-state reaction model and the 1:1 binding model are also reported. Based on our selection criteria for the quality of the fits (Rmax values, χ2 values, and visual inspection of the fits and residuals), the two-state reaction model is more appropriate to describe the data. In Table 3, we also include the simplest 1:1 binding model for comparison.
Table 3.
Experimental binding results and stage two ranking for four compstatin variants and the native compstatin
| Sequence | Approximate binding affinity rank | KD (M) | Model |
|---|---|---|---|
| Variant E1 | 11 | 0.19 × 10−06 | Two-state reaction |
| 0.23 × 10−06 | 1:1 binding | ||
| SQ059 | 14 | 0.74 × 10−06 | Two-state reaction |
| 0.45 × 10−06 | 1:1 binding | ||
| SQ027 | 1 | 0.76 × 10−06 | Two-state reaction |
| 0.51 × 10−06 | 1:1 binding | ||
| SQ086 | 10 | 0.99 × 10−06 | Two-state reaction |
| 0.50 × 10−06 | 1:1 binding | ||
| Native | 18 | 1.26 × 10−06 | Two-state reaction |
| 0.81 × 10−06 | 1:1 binding |
KD is the inverse of the binding affinity, KA, so a lower value indicates a better binder. Based upon the experimental data in Table 3, all four compstatin variant sequences bind better to C3 than the native compstatin.
Effect of sampling on K∗ rank
Further computational experiments were performed on SQ059, SQ086, SQ027, and variant E1 to investigate the effect of sampling on the K∗ rank. These higher sampling runs increased the number of peptides generated using RosettaAbinitio from 1000 to 5000 and the number of docked conformers generated using RosettaDock from 1000 to 5000. The ranking obtained using the higher sampling is variant E1 > SQ086 > SQ059 > SQ027. This nearly matches the experimental ranking, with only SQ086 out of order.
Discussion
Computational findings
Two de novo protein design frameworks were presented and applied to the design of novel compstatin variants.
Approximate binding affinity calculations were first applied to a number of compstatin variants with known relative activities compared to the native compstatin. Although most of the sequences were correctly predicted to be better or worse binders than the native compstatin, two of the sequences were not correctly predicted. As stated earlier, this could be due to the fact that the relative activities are based upon IC50 data, not binding affinity data, and although there is a correlation between IC50 and binding affinity, they are not an exact match. The incorrect predictions may also point out some current limitations in the framework. The better we are able to sample the conformation space, the better we can approximate the binding affinity.
Approximate binding affinities of 10 sequences with high fold specificities were calculated to see how functional these well-folded peptides are. Looking at Table 1, one sees that every one of the designed sequences is ranked higher than the native, with three of them (variants NCV-2, NCV-10, and NCV-3) ranking higher than variant E1. However, sequences with higher fold specificities do not necessarily have higher approximate binding affinities than those with lower fold specificities. Therefore, fold specificity calculations do not necessarily capture how functional a designed peptide or protein will be, making the K∗ ranking a good measure for validating the designed sequences.
Computational studies of the design of compstatin have elucidated a number of key positions in the sequence that greatly affect the binding of compstatin to C3c. These studies identify Trp in positions 4 and 13. This is consistent with the results found by Morikis et al. (13), indicating that ring stacking and π-cation interactions may be important for compstatin activity. Based upon these results, a second design of compstatin was performed. Stage one generated 2000 sequences, allowing mutations only in positions 1, 9, 10, and 11, and fixing positions 4 and 13 as Trp. Stage two calculations show that of the 16 sequences presented all are ranked higher than the native compstatin.
The dependence of the ranking on the docking program used was investigated by redoing the approximate binding affinity calculations using another docking program, HADDOCK. Whether we used RosettaDock or HADDOCK, we still obtained the same ranking for the sequences, showing the independence of the overall framework on the particular docking program used.
Three sequences were selected for synthesis and experimental validation of the binding affinity using Biacore X100. The experimental results validate that the predicted sequences are better binders than the native.
Finally, the effect of higher sampling on the three designed sequences selected for experimental validation and variant E1 was examined, showing that the sampling does indeed affect the final ranking, and that higher sampling ranks the sequences closer to the experimental rank. It should be noted that even though higher sampling leads to an increase in the computational requirement, it achieves the goal of elucidating better binders than the native sequence.
Structural analysis of the C3c-bound compstatin variants
We have performed structural analysis of compstatin variants with higher predicted binding affinities in complex with C3c. Fig. S3 shows the best binders from a selected 10 predictions of Table 2, using the structures of the complexes and the structures of the individual compstatin variants. The selected 10 predictions correspond to approximate binding affinities in the range 1.11 × 10−08 – 4.62 × 10−02 (Table 2). There is a consensus binding site in the β-chain of C3c, with small positional variability (Fig. S3 A). The consensus binding site is similar to that of the E1 variant, observed in the crystal structure (21). Interestingly, there is orientational and conformational variability, within the consensus binding site, in the selected 10 predictions of compstatin variants. The orientational variability is shown in Fig. S3, A and B, and the conformational variability is shown in Fig. S3, C and D. These variabilities are not unusual in binding. As Boehr and Wright (59) point out, according to conformational selection hypothesis, before binding the protein-ligand partners exist as ensembles of conformations in dynamic equilibria. Conformational selection involves interactions of low-population and high-energy conformers (60). Positional, orientational, and conformational variabilities are in line with this model. Indeed, for a family of peptides with variable binding affinities, owed to small sequence differences, it is the physicochemical properties of the replaced amino acids that contribute to differences in conformational selection and the equilibrium of the bound conformation.
Fig. S4 shows a complete analysis of positional, orientational, and conformational variabilities for the top 10 iterations that led to the selected 10 binders. The relative topologies of the selected 10 variants with respect to the binding site in C3c are depicted in Fig. S3 A and their relative topologies with respect to each other are depicted in Fig. S3, A and B. The conformational variability includes random coil conformations (three structures), β-hairpins (two structures), and helical conformations (five structures) (Fig. S3, C and D). Fig. S5 provides a Ramachandran plot analysis of the secondary structures. In the two β-hairpin conformers and in the random coil region of at least one helical conformer a Type I β-turn is present in the segment Gln5-Gly8, as was the case of free compstatin in solution and several of its analogs in free state (18–20,61). Shifted β-turns are also present in the three random coil conformers. Shifted or fused β-turns are also consistent with NMR spectra of free compstatin analogs (18,20). A Type I β-turn is present in the structure of free E1 variant (20) but absent in the structure of the E1 variant complexed with C3c (21). The helical conformations are short involving one or two helical turns (Fig. S3 D). All five helical conformations involve the second-half of the peptide sequences (Fig. S3 D), which is consistent with the observation from previous NMR studies that Alanine at position 9 introduces helical propensity (13,18,20). Two of the helical conformations also involve a segment close to the N-terminal. The helical conformations are stabilized by backbone-backbone (i, i+3) and (i, i+4) hydrogen bonds, which is consistent with the presence of 310- or α-helices. There are two 310-helical turns in two structures, one alone and another in combination with an α-helical turn, the remaining being α-helical turns. The β-hairpin conformations are stabilized by the presence of up to four interstrand backbone-backbone hydrogen bonds. Other fortuitous hydrogen bonds involving backbone or side chains are also present in some structures.
It is possible that the backbone conformation and orientation is dictated by the specific intermolecular side-chain interactions, rather than an intrinsic structural propensity. This is not unexpected, because free peptides in solution are flexible and form ensembles of interconverting conformers (13,18,20,61–67). Binding occurs through conformational selection of one free peptide conformation, not necessarily of lowest free energy, followed by induced fit within the binding site. The latter involves side-chain rearrangements for both peptide and target protein, possibly small backbone motions, and exclusion of solvent molecules from the binding interface. Conformational interconversion has been observed before for parent compstatin using molecular dynamics (64), involving the same conformations as here: coil, β-hairpin, and helical. Actually, the calculated motional amplitudes for interconversion were very small, 0.1–0.4 Å. The same applied on free energies, which were ∼2–11 kcal/mol, corresponding to gaining or losing approximately three hydrogen bonds.
We have performed a side-chain analysis for the selected 10 compstatin variants in search for dominant sidechain-sidechain intra- and intermolecular interactions that may stabilize internally the peptides structures and the peptide-C3c complexes. We focused first on the three Tryptophans, which represent a novel finding of this article (to our knowledge), and we extended our analysis to all side chains. Fig. S6 shows the binding sites from the best binders of the selected 10 compstatin variants (Table 2), focusing on interactions of Trp4, Trp7, and Trp13 with C3c amino acids within 3.5 Å. A complete analysis, not only of the three Tryptophans but also of the other side chains within 5 Å, is given in Table S5. The choice of 3.5 Å and 5 Å was to identify salt bridges or medium-range ionic interactions. Multiple interactions are present within 5 Å, involving hydrophobic contacts, interactions between the Tryptophan ring π-electron system and positive or negative charges of basic or acidic C3c side chains, and hydrogen bonds. Although there are no obvious consensus side-chain contacts, there are compensatory effects involving the three Tryptophans. For example, when one Tryptophan does not participate or has reduced contacts with C3c, another Tryptophan has increased contacts with C3c. This type of compensation may explain the slight variation of the consensus binding site and the orientational and structural variability of the selected 10 compstatin variants.
The role of Trp4 is variable and depends on the peptide sequence and the optimal physicochemical contacts it makes with C3c. These involve hydrophobic clustering against C3c amino acids and occasionally hydrogen-bonding and π-cation interactions. The structural analysis of Fig. S3 and Fig. S4 suggests a wealth of possible physicochemical interactions, depending on the specific peptide sequences, secondary and tertiary structures, and side-chain conformations. This is expected, given that the specifics of the sequence are responsible for binding variability.
Table S6 presents an intermolecular hydrogen-bond analysis. There are two-to-five intermolecular hydrogen bonds per compstatin variant-C3c complex, which is comparable to the five intermolecular hydrogen bonds in the E1 variant (PDB code: 2QKI (21)), calculated with the same hydrogen-bond definition criteria (Table S6). Persistent hydrogen bonds throughout our analysis of the selected 10 binders involve Trp4 (five structures and E1 variant) and amino acid at position 1 (four structures and E1 variant). Hydrogen bonds involving the side chain of Trp13 are observed in two structures. It should be noted that Trp7 does not participate in hydrogen-bonding in our analysis, although it shows a hydrogen bond in the E1 variant. Overall, our analysis shows 20 intermolecular hydrogen bonds involving compstatin variant side chains and 12 involving backbone, with backbone or side-chain partners in C3c. Persistent amino acids of interaction on the C3c side are Arg455 and Arg458 (five structures each).
Fig. S7 presents an analysis of intramolecular side-chain conformational variability and intramolecular side-chain contacts.
Overall, our data suggest that there is neither fixed conformation nor fixed lock-and-key binding site-peptide complex. This may be indicative of weak binding. Weak binding may be supported by the absence of a C3c binding cavity and by the fact that only 40% of the surface of the E1 variant is buried in the crystal structure (21). According to experimental data, the binding of compstatin to C3c is much weaker than to C3b and C3 (3). For example, the binding of parent compstatin to C3c was found to be 74-fold lower than to C3 and the binding mechanism was proposed to be different based on experimental data (i.e., involving biphasic binding and local conformational changes (3)). A structural analysis of the best binders of Table 1 demonstrates two docking hits with alternative binding sites, but the majority of the variants bind within the consensus binding site (Fig. S8). Although hits with nonsignificant statistical meaning are not unusual in docking studies, the possibility of alternative binding sites may not be excluded. The presence of active analogs with conformational and orientational variability and compensatory binding effects owed to the presence of the three Tryptophans may be the novelty of our data. This type of variability cannot be identified using static crystallographic structures.
Supporting Material
Six tables and eight figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00222-5.
Supporting Material
Acknowledgments
C.A.F. gratefully acknowledges financial support from the National Science Foundation (grant No. CTS-0496691), the National Institutes of Health (grants No. R01 GM52032 and No. R24 GM069736), and the United States Environmental Protection Agency (EPA grant No. R 832721-010). Although the research described in the article has been funded in part by the EPA's STAR program (grant No. R 832721-010), it has not been subjected to any EPA review and therefore does not necessarily reflect the views of the Agency, and no official endorsement should be inferred.
References
- 1.Sahu A., Kay B.K., Lambris J.D. Inhibition of human complement by a C3-binding peptide isolated from a phage-displayed random peptide library. J. Immunol. 1996;157:884–891. [PubMed] [Google Scholar]
- 2.Sahu A., Lambris J.D. Structure and biology of complement protein C3, a connecting link between innate and acquired immunity. Immunol. Rev. 2001;180:35–48. doi: 10.1034/j.1600-065x.2001.1800103.x. [DOI] [PubMed] [Google Scholar]
- 3.Sahu A., Soulika A.M., Lambris J.D. Binding kinetics, structure-activity relationship, and biotransformation of the complement inhibitor compstatin. J. Immunol. 2000;165:2491–2499. doi: 10.4049/jimmunol.165.5.2491. [DOI] [PubMed] [Google Scholar]
- 4.Soulika A.M., Khan M.M., Lambris J.D. Inhibition of heparin/protamine complex-induced complement activation by Compstatin in baboons. Clin. Immunol. 2000;96:212–221. doi: 10.1006/clim.2000.4903. [DOI] [PubMed] [Google Scholar]
- 5.Nilsson B., Larsson R., Lambris J.D. Compstatin inhibits complement and cellular activation in whole blood in two models of extracorporeal circulation. Blood. 1998;92:1661–1667. [PubMed] [Google Scholar]
- 6.Schmidt S., Haase G., Peltroche-Llacsahuanga H. Inhibitor of complement, Compstatin, prevents polymer-mediated Mac-1 up-regulation of human neutrophils independent of biomaterial type tested. J. Biomed. Mater. Res. A. 2003;66A:491–499. doi: 10.1002/jbm.a.10031. [DOI] [PubMed] [Google Scholar]
- 7.Fiane A.E., Mollnes T.E., Lambris J.D. Compstatin, a peptide inhibitor of C3, prolongs survival of ex vivo perfused pig xenografts. Xenotransplantation. 1999;6:52–65. doi: 10.1034/j.1399-3089.1999.00007.x. [DOI] [PubMed] [Google Scholar]
- 8.Mollnes T.E., Brekke O.L., Lambris J.D. Essential role of the C5a receptor in E. coli-induced oxidative burst and phagocytosis revealed by a novel lepirudin-based human whole blood model of inflammation. Blood. 2002;100:1869–1877. [PubMed] [Google Scholar]
- 9.Klegeris A., Singh E.A., McGeer P.L. Effects of C-reactive protein and pentosan polysulphate on human complement activation. Immunology. 2002;106:381–388. doi: 10.1046/j.1365-2567.2002.01425.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sahu A., Morikis D., Lambris J.D. Compstatin, a peptide inhibitor of complement, exhibits species-specific binding to complement component C3. Mol. Immunol. 2003;39:557–566. doi: 10.1016/s0161-5890(02)00212-2. [DOI] [PubMed] [Google Scholar]
- 11.Klepeis J.L., Floudas C.A., Lambris J.D. Integrated computational and experimental approach for lead optimization and design of compstatin variants with improved activity. J. Am. Chem. Soc. 2003;125:8422–8423. doi: 10.1021/ja034846p. [DOI] [PubMed] [Google Scholar]
- 12.Klepeis J.L., Floudas C.A., Lambris J.D. Design of peptide analogs with improved activity using a novel de novo protein design approach. Ind. Eng. Chem. Res. 2004;43:3817–3826. [Google Scholar]
- 13.Morikis D., Soulika A.M., Lambris J.D. Improvement of the anti-C3 activity of compstatin using rational and combinatorial approaches. Biochem. Soc. Trans. 2004;32:28–32. doi: 10.1042/bst0320028. [DOI] [PubMed] [Google Scholar]
- 14.Fung H.K., Taylor M.S., Floudas C.A. Novel formulations for the sequence selection problem in de novo protein design with flexible templates. Optimiz.Meth. Softw. 2007;22:51–71. [Google Scholar]
- 15.Floudas C.A., Fung H.K., Zhang L. Overcoming the key challenges in de novo protein design: enhancing computational efficiency and incorporating true backbone flexibility. In: Mondiani R., editor. Modeling of Biosystems: An Interdisciplinary Approach. Springer Verlag; Heidelberg, Germany: 2007. [Google Scholar]
- 16.Fung H.K., Welsh W.J., Floudas C.A. Computational de novo peptide and protein design: rigid templates versus flexible templates. Ind. Eng. Chem. Res. 2008;47:993–1001. [Google Scholar]
- 17.Floudas C.A., Fung H.K., Rajgaria R. Advances in protein structure prediction and de novo protein design: a review. Chem. Eng. Sci. 2006;61:966–988. [Google Scholar]
- 18.Morikis D., Roy M., Lambris J.D. The structural basis of compstatin activity examined by structure-function-based design of peptide analogs and NMR. J. Biol. Chem. 2002;277:14942–14953. doi: 10.1074/jbc.M200021200. [DOI] [PubMed] [Google Scholar]
- 19.Soulika A.M., Morikis D., Lambris J.D. Studies of structure-activity relations of complement inhibitor compstatin. J. Immunol. 2003;171:1881–1890. doi: 10.4049/jimmunol.171.4.1881. [DOI] [PubMed] [Google Scholar]
- 20.Mallik B., Katragadda M., Lambris J.D. Design and NMR characterization of active analogues of compstatin containing non-natural amino acids. J. Med. Chem. 2005;48:274–286. doi: 10.1021/jm0495531. [DOI] [PubMed] [Google Scholar]
- 21.Janssen B.J.C., Halff E.F., Gros P. Structure of compstatin in complex with complement component C3c reveals a new mechanism of complement inhibition. J. Biol. Chem. 2007;282:29241–29247. doi: 10.1074/jbc.M704587200. [DOI] [PubMed] [Google Scholar]
- 22.Fung H.K., Floudas C.A., Morikis D. Toward full-sequence de novo protein design with flexible templates for human β-defensin-2. Biophys. J. 2008;94:584–599. doi: 10.1529/biophysj.107.110627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Taylor M.S., Fung H.K., Floudas C.A. Mutations affecting the oligomerization interface of G-protein-coupled receptors revealed by a novel de novo protein design framework. Biophys. J. 2008;94:2470–2481. doi: 10.1529/biophysj.107.117622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fung H.K., Rao S., Rendl F. Computational comparison studies of quadratic assignment like formulations for the in silico sequence selection problem in de novo protein design. J. Comb. Optim. 2005;10:41–60. [Google Scholar]
- 25.Klepeis J.L., Floudas C.A. Free energy calculations for peptides via deterministic global optimization. J. Chem. Phys. 1999;110:7491–7512. [Google Scholar]
- 26.Klepeis J.L., Floudas C.A., Lambris J. Predicting peptide structures using NMR data and deterministic global optimization. J. Comput. Chem. 1999;20:1354–1370. [Google Scholar]
- 27.Klepeis J.L., Floudas C.A. Ab initio prediction of helical segments in polypeptides. J. Comput. Chem. 2002;23:245–266. doi: 10.1002/jcc.10002. [DOI] [PubMed] [Google Scholar]
- 28.Klepeis J.L., Floudas C.A. Prediction of β-sheet topology and disulfide bridges in polypeptides. J. Comput. Chem. 2003;24:191–208. doi: 10.1002/jcc.10167. [DOI] [PubMed] [Google Scholar]
- 29.Klepeis J.L., Floudas C.A. Ab initio tertiary structure prediction of proteins. J. Glob. Optim. 2003;25:113–140. [Google Scholar]
- 30.Klepeis J.L., Pieja M.T., Floudas C.A. A new class of hybrid global optimization algorithms for peptide structure prediction: integrated hybrids. Comput. Phys. Commun. 2003;151:121–140. [Google Scholar]
- 31.Klepeis J.L., Pieja M.T., Floudas C.A. A new class of hybrid global optimization algorithms for peptide structure prediction: alternating hybrids and applications for Met-encephalin ad melittin. Biophys. J. 2003;84:869–882. doi: 10.1016/S0006-3495(03)74905-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Klepeis J.L., Floudas C.A. ASTRO-FOLD: a combinatorial and global optimization framework for Ab initio prediction of three-dimensional structures of proteins from the amino acid sequence. Biophys. J. 2003;85:2119–2146. doi: 10.1016/s0006-3495(03)74640-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Klepeis J.L., Wei Y., Floudas C.A. Ab initio prediction of the three-dimensional structure of a de novo designed protein: a double-blind case study. Proteins. 2005;58:560–570. doi: 10.1002/prot.20338. [DOI] [PubMed] [Google Scholar]
- 34.McAllister S.R., Mickus B.E., Floudas C.A. Novel approach for α-helical topology prediction in globular proteins: generation of interhelical restraints. Proteins. 2006;65:930–952. doi: 10.1002/prot.21095. [DOI] [PubMed] [Google Scholar]
- 35.Adjiman C.S., Dallwig S., Floudas C.A. A global optimization method, α BB, for general twice-differentiable constrained NLPs. I. Theoretical advances. Comput. Chem. Eng. 1998;22:1137–1158. [Google Scholar]
- 36.Androulakis I., Maranas C., Floudas C.A. Alpha BB: a global optimization method for general constrained nonconvex problems. J. Glob. Optim. 1995;7:337–363. [Google Scholar]
- 37.Adjiman C., Androulakis I., Floudas C.A. A global optimization method, αBB, for general twice-differentiable constrained NLPs. II. Implementation and computational results. Comput. Chem. Eng. 1998;22:1159–1179. [Google Scholar]
- 38.Androulakis I., Maranas C., Floudas C.A. Prediction of oligopeptide conformations via deterministic global optimization. J. Glob. Optim. 1997;11:1–34. [Google Scholar]
- 39.Floudas C.A., Pardalos P.M. State-of-the-art in global optimization—computational methods and applications—preface. J. Glob. Optim. 1995;7:113. [Google Scholar]
- 40.Esposito W.R., Floudas C.A. Global optimization in parameter estimation of nonlinear algebraic models via the error-in-variables approach. Ind. Eng. Chem. Res. 1998;37:1841–1858. [Google Scholar]
- 41.Esposito W.R., Floudas C.A. Deterministic global optimization in nonlinear optimal control problems. J. Glob. Optim. 2000;17:97–126. [Google Scholar]
- 42.Rajgaria R., McAllister S.R., Floudas C.A. Distance-dependent centroid-to-centroid force fields using high-resolution decoys. Proteins. 2008;70:950–970. doi: 10.1002/prot.21561. [DOI] [PubMed] [Google Scholar]
- 43.Güntert P., Mumenthaler C., Wüthrich K. Torsion angle dynamics for NMR structure calculation with the new program DYANA. J. Mol. Biol. 1997;273:283–298. doi: 10.1006/jmbi.1997.1284. [DOI] [PubMed] [Google Scholar]
- 44.Guntert P. Automated NMR structure calculation with CYANA. J. Mol. Biol. 2004;278:353–378. doi: 10.1385/1-59259-809-9:353. [DOI] [PubMed] [Google Scholar]
- 45.Ponder J. Department of Biochemistry and Molecular Biophysics, Washington University School of Medicine; St. Louis, MO: 1998. TINKER, Software Tools for Molecular Design. [Google Scholar]
- 46.Floudas C.A., Fung H.K. Mathematical modeling and optimization methods for de novo protein design. In: Rigoutsos I., Stephanopoulos G., editors. Systems Biology. Vol. II. Oxford University Press; Oxford, UK: 2007. [Google Scholar]
- 47.Rohl C.A., Strauss C.E.M., Baker D. Protein structure prediction using ROSETTA. Methods Enzymol. 2004;383:66–93. doi: 10.1016/S0076-6879(04)83004-0. [DOI] [PubMed] [Google Scholar]
- 48.Gray J.J., Moughon S., Baker D. Protein-protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J. Mol. Biol. 2003;331:281–299. doi: 10.1016/s0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
- 49.Kuhlman B., Baker D. Native protein sequences are close to optimal for their structures. Proc. Natl. Acad. Sci. USA. 2000;97:10383–10388. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lilien R.H., Stevens B.W., Donald B.R. A novel ensemble-based scoring and search algorithm for protein redesign and its application to modify the substrate specificity of the gramicidin synthetase A phenylalanine adenylation enzyme. J. Comput. Biol. 2005;12:740–761. doi: 10.1089/cmb.2005.12.740. [DOI] [PubMed] [Google Scholar]
- 51.Lee M.R., Baker D., Kollman P.A. 2.1 and 1.8 Å average Cα RMSD structure predictions on two small proteins, HP-36 and S15. J. Am. Chem. Soc. 2001;123:1040–1046. doi: 10.1021/ja003150i. [DOI] [PubMed] [Google Scholar]
- 52.Rohl C.A., Baker D. De novo determination of protein backbone structure from residual dipolar couplings using ROSETTA. J. Am. Chem. Soc. 2002;124:2723–2729. doi: 10.1021/ja016880e. [DOI] [PubMed] [Google Scholar]
- 53.DiMaggio P.A., McAllister S.R., Rabitz H.A. Biclustering via optimal re-ordering of data matrices in systems biology: rigorous methods and comparative studies. BMC Bioinformatics. 2008;9:458. doi: 10.1186/1471-2105-9-458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Reference deleted in proof.
- 55.Daily M.D., Masica D., Gray J.J. CAPRI rounds 3–5 reveal promising successes and future challenges for RosettaDock. Proteins. 2005;60:181–186. doi: 10.1002/prot.20555. [DOI] [PubMed] [Google Scholar]
- 56.Gray J.J., Moughon S.E., Baker D. Protein-protein docking predictions for the CAPRI experiment. Proteins. 2003;52:118–122. doi: 10.1002/prot.10384. [DOI] [PubMed] [Google Scholar]
- 57.Lazaridis T., Karplus M. Effective energy function for proteins in solution. Proteins: Struct. Funct. Gen. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 58.Barlow R.B., Bond S.M., McQueen D.S. Antagonist inhibition curves and the measurement of dissociation constants. Br. J. Pharmacol. 1997;120:13–18. doi: 10.1038/sj.bjp.0700865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Boehr D.D., Wright P.E. Biochemistry. How do proteins interact? Science. 2008;320:1429–1430. doi: 10.1126/science.1158818. [DOI] [PubMed] [Google Scholar]
- 60.Lange O.F., Lakomek N.-A., de Groot B.L. Recognition dynamics up to microseconds revealed from an RDC-derived ubiquitin ensemble in solution. Science. 2008;320:1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 61.Morikis D., Assa-Munt N., Lambris J.D. Solution structure of Compstatin, a potent complement inhibitor. Protein Sci. 1998;7:619–627. doi: 10.1002/pro.5560070311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Merutka G., Morikis D., Wright P. NMR evidence for multiple conformations in a highly helical model peptide. Biochemistry. 1993;32:13089–13097. doi: 10.1021/bi00211a019. [DOI] [PubMed] [Google Scholar]
- 63.Morikis D., Lambris J.D. Structural aspects and design of low-molecular-mass complement inhibitors. Biochem. Soc. Trans. 2002;30:1026–1036. doi: 10.1042/bst0301026. [DOI] [PubMed] [Google Scholar]
- 64.Mallik B., Lambris J.D., Morikis D. Conformational interconversion in compstatin probed with molecular dynamics simulations. Proteins. 2003;53:130–141. doi: 10.1002/prot.10491. [DOI] [PubMed] [Google Scholar]
- 65.Mallik B., Morikis D. Development of a quasi-dynamic pharmacophore model for anti-complement peptide analogues. J. Am. Chem. Soc. 2005;127:10967–10976. doi: 10.1021/ja051004c. [DOI] [PubMed] [Google Scholar]
- 66.Tamamis P., Skourtis S.S., Archontis G. Conformational analysis of compstatin analogues with molecular dynamics simulations in explicit water. J. Mol. Graph. Model. 2007;26:571–580. doi: 10.1016/j.jmgm.2007.03.014. [DOI] [PubMed] [Google Scholar]
- 67.Zhang L., Morikis D. Solution structure of a bent α-helix. Biochemistry. 2007;46:12959–12967. doi: 10.1021/bi701252n. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


