A theoretical framework for gene induction and experimental comparisons

Abstract

Ligand-mediated gene induction by steroid receptors is a multistep process characterized by a dose–response curve for gene product that follows a first-order Hill equation. This behavior has classically been explained by steroid binding to receptor being the rate-limiting step. However, this predicts a constant potency of gene induction (EC₅₀) for a given receptor-steroid complex, which is challenged by the findings that various cofactors/reagents can alter this parameter in a gene-specific manner. These properties put strong constraints on the mechanisms of gene induction and raise two questions: How can a first-order Hill dose–response curve (FHDC) arise from a multistep reaction sequence, and how do cofactors modify potency? Here we introduce a theoretical framework in which a sequence of steps yields an FHDC for the final product as a function of the initial agonist concentration. An exact determination of all constants is not required to describe the final FHDC. The theory predicts mechanisms for cofactor/reagent effects on gene-induction potency and maximal activity and it assigns a relative order to cofactors in the sequence of steps. The theory is supported by several observations from glucocorticoid receptor-mediated gene induction. It identifies the mechanism and matches the measured dose–response curves for different concentrations of the combination of cofactor Ubc9 and receptor. It also predicts that an FHDC cannot involve the DNA binding of preformed receptor dimers, which is validated experimentally. The theory is general and can be applied to any biochemical reaction that shows an FHDC.

In ligand-mediated gene induction, the amount of gene expressed depends on the amount of ligand present. Thus, the specific shape and properties of the dose–response curve of gene induction, which is of crucial importance for development, differentiation, and homeostasis in many biological systems, provide a quantitative means for probing the gene-induction process. In many cases, the dose–response curve in gene induction obeys a sigmoidal curve, but not all sigmoidal curves have the same shape. For example, a dose–response curve obeying a first-order Hill equation or function (Hill coefficient equal to 1) goes from 10 to 90% of maximum activity over an 81-fold change in ligand concentration, whereas only a 9-fold change is required in a second-order Hill function, which thus has a different shape (Fig. S1). (A first-order Hill function is sometimes called a Michaelis–Menten function.) Depending upon the shape of the dose–response curve, the responsiveness of gene induction to the same variation in ligand concentration will differ greatly. In addition to the shape, the position or potency [i.e., concentration required for 50% of maximal response (EC₅₀)] and maximum activity (A_max) of the dose–response curve are required to specify the amount of gene expressed for a given amount of ligand. Despite the vital role that the dose–response curve plays in biological systems, the mechanisms that determine its shape and position remain poorly understood. Therefore, a better understanding of the control and shape of the dose–response curve may provide insights into the gene-induction process.

Steroid-mediated gene induction provides an excellent system for investigating basic questions about gene induction and dose–response curves. The current model is that steroids enter the cell by passive diffusion and bind to intracellular receptors that can be predominantly cytoplasmic, as for glucocorticoid receptors (GRs), or nuclear, as for estrogen receptors. After a poorly understood step called activation, the receptor-steroid complex binds as a dimer with high affinity to biologically active DNA sequences [called hormone response elements (HREs)] to recruit additional transcriptional cofactors and modify the rates of transcription of nearby genes by the RNA polymerase complex. Glucocorticoids are an important class of steroids because they affect almost every cell and tissue in the body and are used to treat a variety of conditions, including asthma, autoimmune diseases, and cancer (1). In most experiments, the observed dose–response curves closely match a first-order Hill function. This is the dose response for the actual amount of protein product measured, not the receptor occupancy or an initial reaction rate. The addition of various cofactors can shift the EC₅₀ and A_max yet preserve the shape of the dose–response curve (2–4). The fact that the multiple steps between ligand-receptor binding and translation to protein can yield a first-order Hill dose–response curve (FHDC) that can change position is remarkable. Here we develop a theoretical framework for a ligand-regulated gene-induction process that predicts the shape, position, and maximum activity of these dose–response curves. The theory is based on modeling the gene-induction process as an arbitrarily long sequence of complex-forming steps or reactions. A set of stringent but biologically plausible constraints that yield an FHDC arises from the theory. The theory is mathematically tractable in that it manages the parameter explosion of mathematical modeling by generating formulas for the FHDC with a small number of parameters that can be applied quantitatively to data. Although here it is applied specifically to glucocorticoid-induced gene expression, our paradigm is applicable to any general biochemical pathways that exhibit FHDCs.

Model

Obtaining FHDCs.

The basic principles of our theory can be demonstrated in some simple examples. In steroid-receptor-regulated gene induction, the ligand binds to an intracellular receptor. The receptor-ligand complex then associates with DNA to initiate a series of transcriptional and translational processes (see Fig. S2 for an example of a reaction sequence). The classic explanation for an FHDC is that receptor-ligand binding is the rate-limiting step (5). For example, consider the reaction 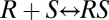, for a receptor R and a ligand S. If the reaction obeys mass-action kinetics, then in equilibrium the concentrations obey 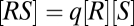, where q is the affinity or association constant and square brackets indicate concentration. By mass conservation, 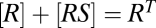, where R^T is the total receptor concentration. Solving the concentration and conservation equations gives the classic FHDC relationship between the complex and the free-ligand concentration,

where A_max = R^T and EC₅₀ = 1/q are both constants. If this receptor-ligand reaction is the rate-limiting step for gene induction, then the concentration of gene product can be assumed to be proportional to [RS]. However, experiments show that EC₅₀ and A_max are not constant and can be changed by cofactors that act downstream of ligand-receptor binding (6), thereby ruling out the classic explanation. Thus, we are left with two questions: How can an FHDC arise for multiple reaction steps, and how can A_max and EC₅₀ be controlled by cofactors?

In the gene-induction process, the receptor-steroid complex undergoes an activation step (or steps) culminating in binding to DNA, which is followed by multiple other steps such as the binding of transcription factors and the recruitment of polymerase (Fig. S2). These steps are envisaged as the building of larger and larger complexes (7). However, considering just two steps of such a sequence, for example, 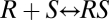and 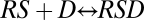(where D represents DNA), does not generally lead to an FHDC for the product [RSD] in terms of [S], which can be seen as follows. The dose–response curve is computed by combining the concentration equations [RS] = q₁[R][S] and [RSD] = q₂[RS][D] with the mass-conservation equations [R] + [RS] + [RSD] = R^T, [D] + [RSD] = D^T, to eliminate [R], [D], and [RS], and obtain an equation for [RSD] and [S]. The resulting equation is quadratic [RSD], ruling out an FHDC (SI Section 1). Including additional complex-forming reactions does not alleviate this problem but makes the resulting equation even more complicated. An FHDC can exist if the resulting equation is linear in [RSD] (bilinear in [S] and [RSD]).

Hence, a sequence of complex-building reactions does not yield an FHDC in general because of the presence of quadratic and other nonlinear terms. However, the quadratic term does not exist if [RSD] can be disregarded or is of negligible value in the conservation equation for [R] (i.e., if [R] + [RS] + [RSD] = R^T can be replaced by [R] + [RS] = R^T). In this case, the two reactions 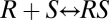and 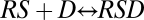“decouple” and can be solved independently to yield Eq. 1 (with q = q₁) and 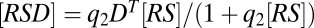. Combining the two equations then yields the FHDC

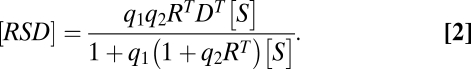This property that the combination of two FHDCs results in another FHDC has been used previously (8, 9). Here we show how this property, which arises because the FHDC is in the family of Möbius or fractional linear transforms and forms a group under function composition (SI Section 2), can be generalized to any set of complex-forming biochemical reactions and allows us to derive a formula for the dose–response curve for an arbitrarily long reaction sequence. We consider the biological conditions under which this can occur below. We also note that the expressions for 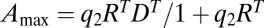and 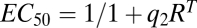indicate that they can now be altered by factors downstream of receptor-steroid binding.

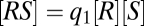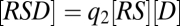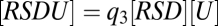This FHDC property can also be exploited in diverse ways, which is seen by adding a third reaction, , where U is a cofactor such as Ubc9. The concentration equations for the three reactions are now , , and , and the mass-conservation equations are 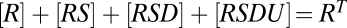, , 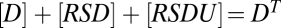and 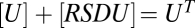. The equation giving [RSDU] as a function of [S] is quartic (SI Section 1) and hence does not yield an FHDC. 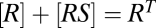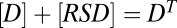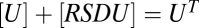However, if downstream products in the conservation equations can be disregarded as before, such that , , and , then the three reactions decouple and [RSDU] has an FHDC with respect to [S]. Alternatively, if the conservation equations obey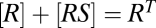, , 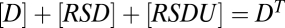and 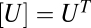, then this yields a different FHDC. This second scenario could occur, for example, if the concentration of factor D were much smaller or limited compared with the other factors, and thus the reaction 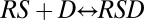acts like a steady-state analog of a rate-limiting step, which we term the concentration-limiting step (CLS).

Biological Conditions Leading to an FHDC.

The theory hinges on having much smaller concentrations of downstream complexes than either upstream complexes or downstream cofactors. Small downstream concentrations of complexes could arise if cofactors and complexes only act transiently but produce a lasting response. For example, in the second scenario, if the second and third reactions were of the form and D′ + U ⇔ D* + U, where D′ and D* are different states of D, then the same mass-conservation equations would result, leading to an FHDC for final product [D*] with respect to [S]. Possible biological mechanisms are that a cofactor could bind transiently to DNA but affect the DNA state (e.g., methylation, ubiquitination, uncoiling, untwisting, etc.), facilitate the binding of another cofactor, or alter the mRNA state during translation (6, 10, 11). Considerable experimental evidence has been advanced in support of transient binding (dubbed “hit and run”) of GR to endogenous genes (12, 13). We show below how these concepts can be applied to a sequence of complex-forming reactions in a general gene-induction process.

General Theory.

Consider a sequence of n binary reactions of the form 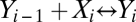, where i = 1, 2,…, n, is an index for a reaction. Let Y₀ be the ligand, X₁ be the receptor, and Y₁ be the receptor-ligand complex. We call the subsequent X variables activators or cofactors and the Y variables products. The reactions need not be reversible; they only should reach a stationary or a steady state. Hence, any number of the reactions could be irreversible with decay, that is, 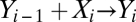and 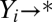, or be transient (hit and run), e.g. 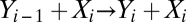. For mass action, the steady-state concentrations obey 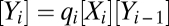and mass conservation implies 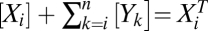for i = 1, 2,…, n. The n association constants 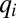and the n total concentrations X_i^T are free parameters. The concentration and conservation equations consist of 2n equations in 2n + 1 unknowns. The equation governing [Y_n] as a function of [Y₀] is a high-degree polynomial, for which [Y_n] is not in general a first-order Hill function of [Y₀].

As shown in the examples above, an FHDC can arise if some of the downstream terms in the conservation equations are zero or very small (automatically satisfied for hit and run). It can be shown mathematically that the general form for the mass-conservation equations to ensure an FHDC has the form

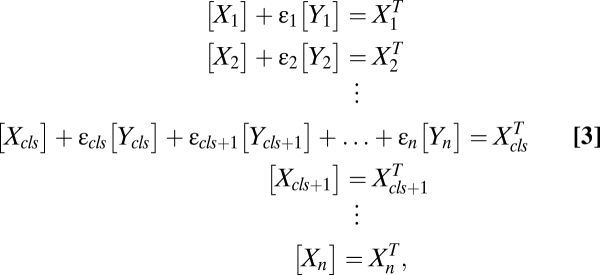where 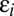is 1 or 0, indicating the presence or absence of [Y_i] in the equations. Step cls is the general definition of the CLS (introduced above). In this step, the concentration of factor X_cls is small compared with the concentration of the other activators. Hence, all terms appear in its conservation condition. For all steps after the CLS, the free concentration of any activator is equal to its total concentration. Hence, the location of the CLS can move by adding or removing varying amounts of activators. The CLS also need not exist for all situations.

For reactions obeying the steady-state concentration equations and mass conservation (Eq. 3), the equations can be solved exactly using the group property of the fractional-linear transformation (SI Section 2) to obtain a formula for the dose–response curve,

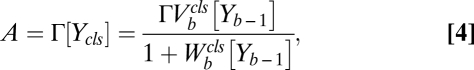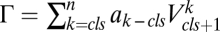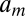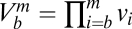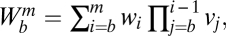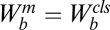where A is the activity of the gene and , where are positive constants, , and , for 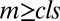. We use the convention 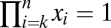if 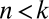. The factors v_i and w_i have explicit formulas listed in Table 1. These factors specify the action of the cofactor at step i and take different forms depending on location with respect to the CLS. As is evident from comparison with Eq. 1, 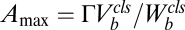and EC₅₀ = 1/W_b^m. If the sequence of reactions does not have a CLS then A has the same formula as Eq. 4, except that cls is the index for the last reaction of interest and 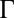is a positive constant.

Table 1.

Values for v_i and w_i for activator and inhibitor at position i before, at, or after CLS

Position	Activator	Activator with inhibitor
Before CLS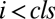
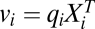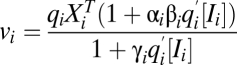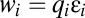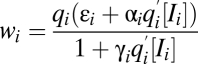At CLS	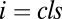vi same as before CLS	vi same as before CLS
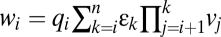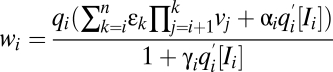After CLS	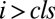vi same as before CLS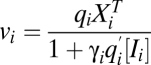

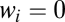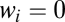Eq. 4 depends on 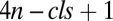free parameters, namely the 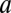, , 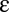q, and 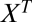parameters, and the choice of these parameters specifies a model for the data. In general, all of these parameters and even the number of steps will be unknown. However, the formula is useful because the number of effective parameters necessary to specify a model can be reduced because any sequence of steps collapses or “telescopes” into a single first-order Hill function with an effective A_max and EC₅₀. The result is that there are now only three effective “steps” to consider (before, at, or after the CLS), which reduces the possible parametric models that can explain a given experiment to a small number involving a finite set of cofactors. One also does not need to know a priori whether there even is a CLS. By applying the different possible models to the data, the existence of a CLS can be inferred. The CLS could be located experimentally by finding the cofactor that affects the dose–response curve in the appropriate manner for the CLS, as predicted by the theory. The reaction sequence also has a “modular” structure in that reactions, or a sequence of reactions, can be inserted, deleted, or combined without affecting the FHDC. Arbitrarily complex reaction sequences that maintain first-order Hill form can be constructed in this way. Thus, different genes could mix and match different pieces of the reaction sequence and all have FHDCs but with different A_max and EC₅₀.

Incorporation of Inhibitors.

We have only considered activators so far. However, it is known that inhibitors, which act by reducing the concentration or efficacy of activators or products, can affect gene induction (10, 11). The reaction scheme for an inhibitor I_i acting at step i that preserves FHDC form is

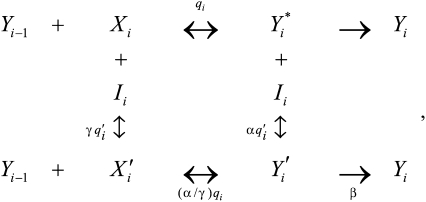
where the parameters obey 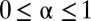, , 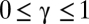and 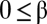. The case of 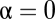is called competitive inhibition, 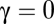is called uncompetitive inhibition, 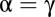is called noncompetitive inhibition, 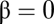is called linear inhibition, and 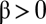is called partial inhibition. Although I is called an inhibitor, its actions need not be inhibitory or repressive on the final activity. For example, if 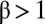, I can be activating because it diverts the output from a lower-yield product to a higher-yield one. The dependence of 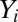and 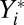on Y_i−1 is derived in SI Section 3 (following refs. 10 and 11) by solving the concentration and mass-conservation equations to obtain formulas for factors v_i and w_i, which specify the actions of the inhibitor on the activator at step i and are listed in Table 1. Inhibitory steps can be inserted anywhere in the reaction sequence before the CLS, but only competitive inhibitors can occur after the CLS.

Results

Application to Steroid-Mediated Gene Induction.

To demonstrate the utility of our theory, we have applied it to steroid-receptor-mediated gene induction, where an FHDC has been observed experimentally. When a cofactor is added, A_max and EC₅₀ of the dose–response curve can increase, decrease, or not change (4). Mechanisms for these various combinations can be predicted using Eq. 4 expressed in a form so that the inhibitor [I_i] or activator 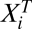concentrations are visible (SI Section 4). Leaving out the combination of both not changing, we have experimentally observed seven of the eight remaining scenarios that are listed in Table 2 along with the predicted mechanisms. Although these suggested mechanisms are not unique (some of the scenarios are consistent with multiple mechanisms; see also SI Section 5), the predictions are consistent with previous results (6), as described below.

Table 2.

Effect of cofactors on A_max and EC₅₀

Amax	EC50	Cofactors and context	Mechanism and position
Decrease	Decrease	CBP (with GR) (3), NCoR (with PR) (17)	(L and U) or (A after CLS)
Decrease	Increase	GMEB2, NCoR (with GR) (43), CPT, H8, DRB (with high GR and Ubc9) (6)	(C or L) before or at CLS
Decrease	No change	DRB, H8 (with high GR), VPA (with high GR and Ubc9) (6)	(P and U) before CLS
Increase	Decrease	TIF2 (with GR) (2, 3), Ubc9 (with high GR) (6, 14)	A before or after CLS
Increase	Increase	Not observed but predicted	C after CLS
Increase	No change	TSA, VPA, Ubc9 (with low GR) (6, 14)	A at or after CLS
No change	Decrease	SRC-1 (with GR) (3)	A after CLS
No change	Increase	TIF2 siRNA (with GR) (30)	L or C anywhere

A, activator; I, inhibitor; L, linear inhibitor; P, partial inhibitor; C, competitive inhibitor; U, uncompetitive inhibitor.

Quantitative Predictions for Ubc9.

To uniquely identify a mechanism, the set of parameters specifying a model must be estimated directly from the data. We show this for the unusual capacity of the comodulator Ubc9 to cause different responses in transiently transfected cells depending upon the concentration of steroid receptor (6, 14, 15). (Experimental methods are in SI Section 8.) To generate numerous data points for an exacting test of our model, we used six different steroid (Dex) concentrations to define the dose–response curves for four levels of GR with three amounts of Ubc9 (Fig. 1). With low levels of GR, Ubc9 increases the A_max of luciferase activity while perturbing EC₅₀ marginally. At higher receptor concentrations, there is a less proportional increase in A_max and a greater decrease in EC₅₀. In all cases, an FHDC is always seen. In addition to extracting parameters to specify a mechanism, applying Eq. 4 to the data of Fig. 1 also gives an independent test of the model. We first must reexpress Eq. 4 so that three factor concentrations (steroid, receptor, and Ubc9) are visible in the formula (SI Section 4). However, whereas the steroid and receptor are assumed to appear in the first reaction, it is not known where Ubc9 appears. Hence, we must consider the possibility that it is before, at, or after a possible CLS. Recall that the CLS represents the step for which the cofactor has the smallest concentration compared with the other cofactors. The case of no CLS has the same formula as Ubc9 appearing before the CLS. The applicable formula has the form (SI Section 4)

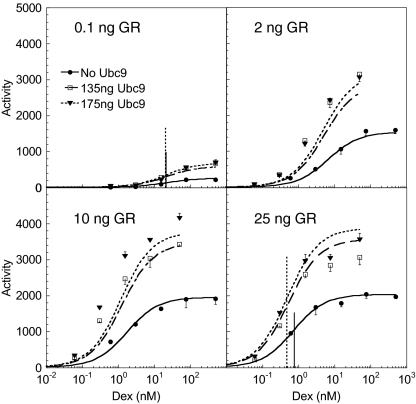
Fig. 1.

Theoretical versus observed dose–response curves with different amounts of GR and Ubc9. The induction by Dex of transiently transfected GREtkLUC reporter and different amounts of GR (0.1, 2, 10, and 25 ng GR plasmid) ± Ubc9 plasmid in CV-1 cells was determined. Solid circle, 0 ng Ubc9; open square, 135 ng Ubc9; solid triangle, 175 ng Ubc9 (error bars, SD for triplicates). The vertical line indicates the EC₅₀ for the dose–response curve with the same line style.

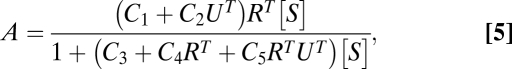where A represents the luciferase activity, U^T denotes the total Ubc9 concentration, R^T equals the total steroid-receptor concentration, [S] is the free-steroid concentration, which we assume is approximated by the total steroid concentration, and the C parameters (given in Table S1) differ depending on where Ubc9 acts. Table S1 shows that if Ubc9 acts at the CLS (i.e., it is the concentration-limiting step), then it cannot affect EC₅₀, so we can rule that possibility out. We fit Eq. 5 to the complete dataset of multiple doses of S, R, and Ubc9. Fig. 1 shows that the model captures the data fairly well, thereby reinforcing the validity of the model. The fitting algorithm and estimated parameter values are in SI Section 6. Given the parameters, we can predict where Ubc9 acts. The model fit finds the ratio of C₁/C₂U^T ∼ 1. If Ubc9 acts before the CLS, then this ratio implies that the endogenous to exogenously applied Ubc9 ratio in the cell is near 1 (U_T = 0 implies there is no exogeneous Ubc9). However, quantitative reverse transcription–PCR measurements give a ratio of ∼100, which rules out this possibility. Thus, we conclude that Ubc9 is an activator that acts after the CLS, as was hypothesized previously (14, 15).

GR Monomer Versus Dimer Binding to DNA.

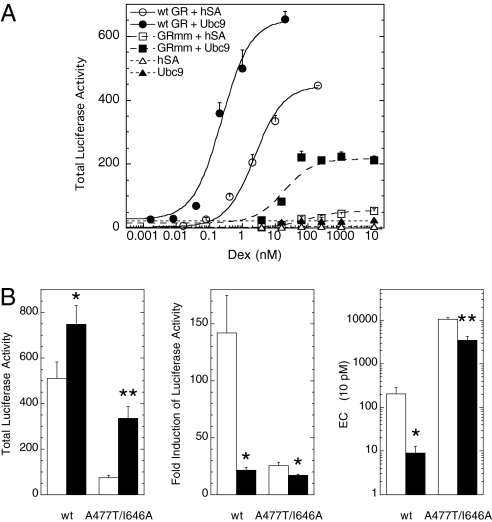
In the prevailing model of steroid hormone action, preformed dimers of receptor-steroid complex bind to the biologically active HREs of target genes (7, 16). However, our theory predicts that such a cooperative step will destroy the FHDC. Thus, in those cases where a steroid produces an FHDC, our theory predicts that GR dimerization cannot be a necessary step for gene induction and vice versa (see SI Section 7 for a theoretical justification). In support of our theory, recent NMR studies show conformational changes in DNA-bound dimers occurring after the DNA binding of monomeric receptor (18). Furthermore, experiments with both steroid receptors (19–22) and helix-loop-helix zipper transcription factors (23, 24) strongly suggest that the majority of receptor binding to HREs occurs not by preformed dimers but by monomers that then form dimers on the DNA. To further examine this issue, we performed new experiments. We looked at the activity of several known dimerization-defective mutants (GR A477T, R479D, and D481R) (21, 25), plus a new double mutant (GR A477T/I646A) with a mutation in the dimerization domains of both the DNA-binding domain and ligand-binding domain (26). Each mutant is expressed at equivalent levels (Fig. S3), is active, and yields an FHDC (Fig. 2A). We then find that Ubc9 increases the A_max (while decreasing the fold induction) and decreases the EC₅₀ of each mutant, similar to that seen with the wild-type GR (Fig. 2B and Fig. S4). We therefore conclude that defects in GR dimerization do not prevent GR transactivation or the modulatory activity of Ubc9, as predicted by our theory.

Fig. 2.

Modulatory activity of Ubc9 is maintained with dimerization-defective GR mutants. (A) Dose–response curves of wild type (wt GR; circles), double mutant (GRmm; squares), and empty vector (no GR; triangles) with added hSA or Ubc9 (open and closed symbols, respectively). (B) The induction properties with Dex of CV-1 cells transiently transfected with GREtkLUC reporter and wild-type or double mutant GR (A477T/I646A) plasmids ± Ubc9 plasmid were determined as in Fig. 1. The average values (n = 5; ±SEM) were plotted. *P < 0.05, **P ≤ 0.005 versus no Ubc9.

Discussion

We have described a theoretical framework for ligand-mediated gene induction that was applied specifically to glucocorticoid hormone action but is applicable to any biochemical pathway that exhibits an FHDC. The theory produces a formula for the FHDC describing how the A_max and the EC₅₀ can change and yields mechanistic insights that are not obtainable with the common practice of examining just A_max (Table 1). The theory shows that any number of first-order steps of arbitrary complexity telescope into a single expression, with an effective A_max and EC₅₀, consisting of just three steps that are before, at, or after a CLS. The steps involved need not be reversible as long as they reach steady state or equilibrium. An FHDC-preserving reaction sequence has a modular structure in that reactions can be inserted, deleted, or combined. In fact, different genes could possibly mix and match different pieces of the reaction sequence and all have FHDCs but with different A_max and EC₅₀.

Our theory yields valuable information and testable hypotheses even when the precise steps of action are unknown. Despite minimal initial experimental constraints, the theory accounted for all of the different combinations of changing A_max and EC₅₀ that have been observed experimentally. The validity of the theory is further supported by its successes in explaining how steps well downstream of ligand binding can alter the A_max and EC₅₀ (6, 27). The theory defines a CLS, which is an equilibrium/steady-state analog of the rate-limiting step. One property of the CLS is that products from all steps after it can be summed directly and still preserve an FHDC. As shown in Table 1, the theory makes specific predictions of both biochemical mechanism of cofactor action and site of action relative to the CLS. For example, Table 1 predicts that the changes in A_max and EC₅₀ of gene induction by high concentrations of GR upon addition of Ubc9 result from Ubc9 functioning as an activator before or after the CLS. Other experiments then restricted the possible mechanisms to Ubc9 acting as an activator downstream of the CLS, providing confirmation for our previous hypothesis of Ubc9 acting downstream of GR and a rate-limiting step (14). One also does not need to know a priori whether there is a CLS. The CLS could be located by finding a cofactor that affects the dose–response curve, as predicted by the theory.

A stringent test for application of our theory is the invariance of an 81-fold change between 0.1 and 0.9 of maximal induction under all conditions. More generally, the fold change between a fraction p and 1 − p of maximal induction is (1 − p)²/p². This does not hold for a general complex-forming sequence of reactions. Additionally, we note that the first-order Hill function is the only Hill function that preserves its form when substituted into itself (i.e., forms a group under function composition). Higher-order Hill functions will be driven to a “switch-like” activation curve with the inclusion of more such steps, whereas lower-order ones will be driven to a flat activation curve (Fig. S1). Thus, any reaction scheme that is not described by our theory would be unlikely to produce the 81-fold change.

Another critical test of the model came with its prediction that appreciable DNA binding of preformed receptor dimers, which is widely believed to occur, cannot be necessary for steroid-induced gene expression in all situations. This does not mean that steroid receptors never bind to HREs as preformed dimers. Indeed, examples of non-FHDCs could indicate steps like receptor dimers or other cooperative behaviors that break the FHDC. Instead, our model says that the observation of an FHDC uniquely restricts the mechanism for receptor regulation of the observed gene to one that does not require preformed dimers. We show that three GR mutants with documented low to negligible binding as dimers to DNA, plus a combination double mutant that would be expected to be even less capable of dimer formation, are all still active with A_max and EC₅₀ values that are modulated by exogenous Ubc9, as described by the model (Fig. 2 and Figs. S3 and S4). These and previous results of others suggest that the initial binding to biologically active DNA sequences involves predominantly GR monomers, as opposed to preexisting dimers, when the dose–response curve obeys first-order Hill form.

Although the studies of the current report are all with the transiently transfected reporter GREtkLUC, we have observed FHDCs with several endogenous genes for GR-mediated induction and repression (27–30). However, dose–response curves with other endogenous genes and/or other conditions (28) indicate non-FHDCs, which could serve as a valuable screen for systems where additional factors/processes contribute to the overall control of gene expression in a manner that violates the conditions of the theory. Our theory also does not include the effects of biomolecular fluctuations due to small numbers of molecules. We hypothesize that the mean concentrations should not be strongly affected because the regime under which our theory operates is near linear, implying that correlations arising from fluctuations should not be too deleterious. However, fluctuations will imply that the variance of the gene product could be nonnegligible, and this could affect downstream systems that depend on the expressed protein. An analysis with fluctuations could be formulated with the chemical master equation. Our theory could also potentially be useful in synthetic biology (31, 32), where precise control of the amount of gene product is desired. Our theory demonstrates that an exact determination of all rate constants of synthetic reactions is not necessary for an accurate description of the final dose–response curve, because there are only a few effective parameters that need to be tuned and these parameters can compensate for other possibly unknown parameters. The modularity also implies that tuning of the dose–response curve could be achieved by inserting or deleting a small number of synthetic modules to adjust EC₅₀ or A_max as required.

Considerations of EC₅₀ are of major importance in intact organisms, as seen with ecdysone regulation of Drosophila embryo development (33), GR concentration in glucocorticoid-induced apoptosis of mouse thymocytes (34), the role of coactivators in the pituitary resistance to thyroid hormone syndrome (35), and gene-selective responses in human peripheral blood mononuclear cells (30). An FHDC implies that changes in factor concentration act like a rheostat to give a continuum of responses (2, 4, 36, 37), which suggests that gene expression by steroid receptors during development, differentiation, and homeostasis employs differential control, as seen with other transcription factors and morphogens (38–41). This rheostat model is fully compatible with the many observations that the binding of steroid receptors and transcription factors is rapid and readily reversible (12, 13, 42). Indeed, the rapid binding of steroid receptors is a consequence of FHDC and a prediction of our theoretical framework.