DNA bending induced by carbocyclic sugar analogs constrained to the north conformation

Abstract

DNA bending caused by introduction of carbocyclic sugars constrained to the north conformation was studied using explicit solvent molecular dynamic (MD) simulations. The native Drew-Dickerson (DD) dodecamer and its three modifications containing north carbocyclic sugars in the 7^th (T7*), 8^th (T8*) or both 7^th and 8^th (T7T8*) nucleotide positions were examined. Introduction of the carbocyclic sugar results in A-form conformations for the α, β, χ, ζ, and sugar pucker backbone parameters in the modified nucleotides. Increased steric repulsion between the sugar and its parent base in the modified oligonucleotides impacts the roll and cup dinucleotide step parameters, increasing the bending of the oligomer axis. Increased buckling of the substituted nucleotides disrupts the usual stabilizing base stacking interactions. The level of overall bending depends on the number and position of carbocyclic sugars introduced in the DNA sequence. Single sugar substitutions are unable to induce substantial bending due to the neighboring unmodified nucleotides counterbalancing the distortion. Significant bending can, however, be induced by two consecutive north sugars (T7T8*), which is in agreement with experimental results. The modified oligomers populate a wide range of bend angles, indicating that they maintain flexibility in the bent state. The present results suggest that insertion of carbocyclic sugars into DNA or RNA duplexes can be used to engineer bending of the duplexes without impacting the electrostatic or chemical properties of the phosphodiester backbone, thereby serving as excellent tools for experimental elucidation of nucleic acid structure-function relationships.

INTRODUCTION

DNA is often required to bend when it interacts with proteins^1,2. Such bending ensures its proper packing into nucleosomes^3-5 as well as regulation of expression of specific genes^6-8. Certain DNA duplex sequences such as AT tracts can be intrinsically bent⁹, but usually DNA strands are observed to be straight for lengths up to 50 nm, with an average bend of the axis of up to 1 radian¹⁰. A recent study on the free energy of DNA bending estimated the electrostatic contribution of phosphate-phosphate interactions to be only about 30%, suggesting that other interactions also play an important role in DNA bending¹¹. A study of the rotational decay times of a 100 basepair DNA oligomer, in which a section of one strand was replaced by 24 non-covalently bound N⁶-methyladenines, indicated that 90% of the rigidity of the DNA is due to base stacking¹².

Changes in the DNA bending axis can occur at a sharp angle (DNA bound to the catabolic activator protein CAP^13,14 or PurR repressor¹⁵) or they can be gradual (DNA wrapped around histones^3-5). The role played by repeating sequence motifs in the bending of DNA around histone proteins^16-19 suggests the importance of intrinsic bending capacity of the histone-bound DNA sequences. Other studies suggest that DNA bending in nucleosomes is due to phosphate charge neutralization by positively charged amino acids in the histone proteins²⁰. An important question regarding nucleosomal DNA therefore is whether the DNA preorganizes itself into a bent conformation or whether histone protein binding induces the bending.

DNA duplexes bound to proteins often show repuckering of the deoxyribose sugar rings at the bend or kink junctions, mostly involving changes from the south (S = C2′-endo) conformation seen in the dominant B-form to the north (N = C2′-exo, C3′-endo) conformation seen in the A-form^{21,22 23-25}. Amongst sugar modifications, carbocyclic sugar moieties^26,27 have the advantage of being able to constrain the sugar to either the north or south conformation, which can be used to probe the effects of sugar pucker on bending susceptibility. In a recent study, inclusion of carbocyclic sugars constrained to be in the north conformation into the well-studied Drew-Dickerson dodecamer (DD, CGCGAATTCGCG)^28-33 was shown to lead to increased bending of the DD duplex³⁴. North carbocyclic sugars introduced individually into positions 7 or 8 or simultaneously in both positions, all increased bending of the oligonucleotide with greater bending occurring in the disubstituted species. However, the questions of whether bending is associated with a local kink or due to a more gradual curve in the DNA axis and whether it is linked to changes in DNA flexibility still remain unanswered. Use of carbocyclic sugars as experimental tools in DNA structure-function studies would be helped greatly by understanding the atomic details of their impact of DNA bending.

All-atom MD simulations with explicit solvent are currently the best available method to analyze such specific atomistic details involving localized chemical or structural molecular perturbations of oligonucleotides as well as other biological macromolecules³⁵. The mechanism by which carbocyclic sugars alter the binding of the cognate DNA sequence to the cytosine-5-methyltransferase from HhaI was previously elucidated using MD simulations of carbocyclic modified DNA in conjunction with experimental studies³⁶. In the present study, MD simulations were carried out on the native DD along with three modified oligomers, T7*, T8*, T7T8*, where north carbocyclic sugars have been introduced into the T7, T8, or T7 and T8 nucleotides, respectively. The results from the simulations are analyzed to characterize the local determinants of the bending induced by the introduction of the north constrained sugars.

Methods

MD simulations were carried out for the four sequences (DD=native, T7*, T8*, T7T8*) using the program CHARMM³⁷ with the CHARMM27 force field parameters for nucleic acids^38,39, previously determined north carbocyclic sugar parameters³⁶, the TIP3P water model⁴⁰ implemented in CHARMM, and published sodium parameters⁴¹.

The protocol for the MD simulations was as follows: Starting from a canonical B conformation obtained from the program Quanta (Accelrys, Inc.), the DNA structures were generated within CHARMM and minimized in the gas phase for 100 steepest descent (SD) steps. The duplexes were then overlaid onto a pre-equilibrated solvent box containing water and sodium, such that there was at least 8 Å of solvent around the DNA oligomers. Overlapping sodiums or waters with oxygen atoms within 1.8 Å of the oligomer non-hydrogen atoms were deleted, and the number of sodiums adjusted to maintain electrical neutrality by adding them at random positions or deleting those farthest from the solute as required. Periodic boundary conditions were applied using the images generated by the CRYSTAL module⁴² in CHARMM, using orthorhombic symmetry with box sizes of 62x37x37 Å. Treatment of nonbond interactions involved the calculation of long-range electrostatic interactions with Particle Mesh Ewald (PME)⁴³. Real space and Lennard-Jones interaction cutoffs of 10 Å were used and the nonbond interaction lists were heuristically updated to 15 Å. The screening kappa parameter was set to 0.35 and the LJ interactions were smoothed over 8 to 10 Å via force switching⁴⁴. The systems were then minimized for 500 steepest-descent (SD) steps followed by 500 steps of Adopted Basis Newton-Raphson (ABNR) while keeping 2.0 kcal/mol⁻¹ A⁻¹ mass-weighted harmonic restraints on the oligomer non-hydrogen atoms. While maintaining the harmonic restraints, 20 ps of constant volume, isothermal (NVT) dynamics were carried out to allow the water and ions to equilibrate around the DNA. To the final structures from these simulations a geometrical harmonic distance restraint of 3 Å and 50 kcal/mol⁻¹ A⁻¹ was applied to the central hydrogen bond N1-N3 of the terminal CG base pairs maintaining the Watson-Crick (WC) distances; these restraints were maintained throughout the production simulations. The systems were then further equilibrated with 50 ps of NVT dynamics with harmonic restraints on the solute followed by 500 steps of SD and 500 steps of ABNR minimization. Production dynamics were performed for 20 ns in the isobaric, isothermal (NPT) ensemble⁴⁵ at 300 K with the Leapfrog integrator using SHAKE⁴⁶, a 0.002 ps integration step with overall translation and rotation of the system removed every 100 integration time steps. Coordinate sets were saved every 5 picoseconds from the final 15 ns of the trajectories for analysis. Averages were obtained by calculating the block averages over every 1 ns, with the final reported values being the average of these 15 block averages along with the associated standard error. Each 1 ns block is assumed to be an independent sample of the MD trajectory which allows for the calculation of statistical parameters⁴⁷. When relative values are presented, the native sequence without any modified sugars (DD) is used as reference.

The values of calculated bend angles depend on the algorithm and the reference frame used. The helical parameters and the curvature of the DNA oligomers, excluding the terminal base pairs, were analyzed with Curves 5.3^{48 49} using a minimized curvilinear axis and fitting the base pairs. For comparison, the bend angle was also calculated using Madbend⁵⁰, which has been shown to eliminate artificial bending angles that occur in Curves due to the presence of slide⁵¹.

Results

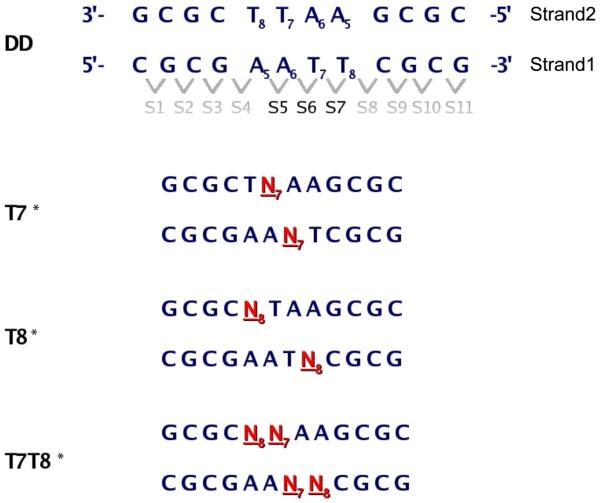
Schematic diagrams of the four oligomers studied (DD, T7*, T8*, T7T8*) are shown in Figure 1. The three modified oligomers contain north carbocyclic sugars with their cyclopropyl moieties pointing towards the minor groove (Figure 2). T7* contains a carbocyclic sugar at position 7 (N₇) of each complementary strand, resulting in a total of two modified sugars at base step 6 (Figures 1 and 2). T8* contains a carbocyclic sugar at position 8 (N₈) in each strand, resulting in one modified sugar at base step 5 and one modified sugar at base step 7. T7T8* contains two carbocyclic sugars in each strand at position 7 (N₇) and 8 (N₈), resulting in one modified sugar at base step 5, two at base step 6, and one at base step 7.

Figure 1.

Sequences and nomenclature of the studied DNA duplexes. The native sequence (DD) shows the numbering scheme for the nucleotides, individual strands and base pair dimer steps. Modified north sugars are shown in red.

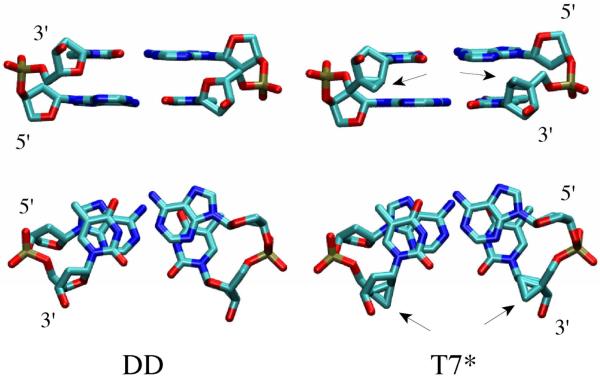
Figure 2.

Structures of base A6 and T6 that comprise base step 6 in the DD and T7 oligomers in the initial B-DNA canonical conformation. Arrows indicate the location of the north carbocyclic sugar. Upper and lower panels are approximately orthogonal views of the same structures.

Global Structure and base pairing

All DNA oligomers maintain an overall B-form conformation as shown by the Root Mean Square Distances (RMSD) in Table 1, which is calculated for all non-hydrogen atoms except those in the terminal base pairs. T7T8*, with its four north carbocyclic sugars, has the greatest deviation in RMSD from the canonical B-form conformation and the lowest RMSD from A-DNA. Changes in the RMSD values of the central segments (bases 5-8) are similar to the changes seen for the oligomers (bases 2-11), underscoring the contribution of the north sugars. The central segment of T7T8* has the greatest deviation from the B-form and the smallest from the A-form , While the central segments of DD, T7* and T8* maintain a B-form conformation, T7T8* seems a mixture of both A- and B-forms. Interestingly, there is no significant increase in the deviations from the B-DNA conformation for T7* and T8* with respect to DD.

Table 1.

Average Root Mean Square Distances (RMSD) of each oligomer from its canonical A-and B-forms. Results for two heavy atom segments, one including bases 2-11 and the other the four central bases 5-8 are shown.

		RMSD vs A-DNA		RMSD vs B-DNA
		Average	S.E.	Average	S.E.
Bases 2-11
DD	5-20ns	4.17	0.15	2.14	0.14
T7*	5-20ns	4.38	0.12	2.17	0.11
T8*	5-20ns	4.22	0.12	2.29	0.11
T7T8*	5-20ns	3.72	0.24	2.83	0.24
Central Bases 5-8
DD	5-20ns	3.07	0.14	1.87	0.12
T7*	5-20ns	3.25	0.10	1.92	0.08
T8*	5-20ns	3.18	0.11	2.03	0.09
T7T8*	5-20ns	2.74	0.20	2.45	0.19

RMSD in Å. Averages and Standard Errors (S.E.), over the last 15 ns of the MD simulations.

The pyrimidine-purine N1-N3 base pair distances shown in Table 2 indicate that the presence of the north carbocyclic sugars does not significnantly disrupt Watson-Crick (WC) interactions in DNA double helix. The adenine-thymine N6-O4 distances of the central 4 base pairs with north carbocyclic sugar substitutions are also maintained near those of their unmodified counterparts in the DD sequence. These distances are, however, slightly longer and show larger standard errors than those in DD. These larger standard errors, also seen in the RMSD values in Table 1, could be due to greater flexibility associated with slight WC base pair distortions caused by the carbocyclic sugars. Thus, the presence of the north carbocyclic sugars thus causes only small perturbations of WC base pairing.

Table 2.

Average Watson-Crick interaction distances between the pyrimidine N1 and purine N3 atoms and the adenine N6 and thymine O4 atoms.

	DD		T7*		T8*		T7T8*
	N1-N3	S.E.	N1-N3	S.E.	N1-N3	S.E.	N1-N3	S.E.
C1	2.99	0.01	2.99	0.01	2.99	0.00	3.00	0.01
G2	2.98	0.01	2.99	0.01	2.99	0.01	2.99	0.01
C3	2.98	0.01	2.98	0.01	2.98	0.01	2.98	0.01
G4	2.97	0.01	2.97	0.01	2.99	0.01	2.99	0.01
A5	2.95	0.01	2.98	0.01	2.91	0.01	2.93	0.01
A6	2.94	0.01	2.94	0.04	2.95	0.02	2.95	0.01
T7	2.94	0.01	2.93	0.01	2.95	0.01	2.94	0.01
T8	2.95	0.01	2.98	0.01	2.91	0.01	2.92	0.01
C9	2.96	0.01	2.97	0.01	2.98	0.01	2.99	0.01
G10	2.97	0.01	2.98	0.01	2.98	0.01	2.97	0.01
C11	2.99	0.01	3.00	0.01	2.99	0.01	2.99	0.01
C12	2.99	0.01	2.99	0.01	3.00	0.01	2.99	0.01
	N6-O4	S.E.	N6-O4	S.E.	N6-O4	S.E.	N6-O4	S.E.
A5	3.00	0.04	2.96	0.02	3.17	0.05	3.09	0.04
A6	3.08	0.05	3.24	0.17	3.06	0.04	3.11	0.07
T7	3.10	0.05	3.23	0.10	3.05	0.02	3.18	0.08
T8	2.99	0.02	2.97	0.02	3.18	0.05	3.09	0.03

Distances in Å and S.E. is the standard error.

DNA Bending

Introduction of north carbocyclic sugars has been shown to increase bending of the modified DNA oligomers³⁴. Since the precise bend angle value for specific DNA oligomer geometries depends on the method used to calculate it, in the present MD simulations, the bend angle was determined using two different approaches. In the first approach, the Curves program was used to fit and minimize a curvilinear global axis to the DNA duplex. In the second approach, the Madbend program was used to calculate the bend angle based on a reference point in the middle the duplex (i.e. step 6 in Figure 1). The results reported in Table 3 show that there is an increase in the bend angle with increasing sugar modifications from DD to T7T8* as determined by both approaches. For the unmodified DD structure, the calculated bend angle range of 14-16°, is consistent with the experimentally determined value of 10°⁵², when the estimated experimental variation range of 3-5° is taken into account³⁴.

Table 3.

Averages of the overall bend angle for the oligomers.

	Curves (f=t, m=t)		Madbend (break=6.5)
	Average	S.E.	Average	S.E.
DD	13.7	2.0	16.4	2.6
T7*	14.0	1.5	16.1	1.4
T8*	15.0	1.8	18.9	2.3
T7T8*	19.8	3.3	27.8	5.1

Angles in degrees. Averages and standard errors, S.E. over the last 15 ns of the simulations.

Assuming a bend angle value of 10° for DD, experimental estimates of bending based on residual dipolar coupling are 19.8°, 14.9° and 24.4° for T7*, T8* and T7T8*, respectively³⁴. The bend angles calculated from the present MD simulations for T8* and T7T8* are in good agreement with experiment, while the bending in T7* is underestimated. Given the differences in methodologies between the present MD simulations and the experimental study, in which the data was collected in dilute aqueous liquid crystalline media (20mg/ml Pf1), the picture of DNA bending obtained from both studies is quite consistent.

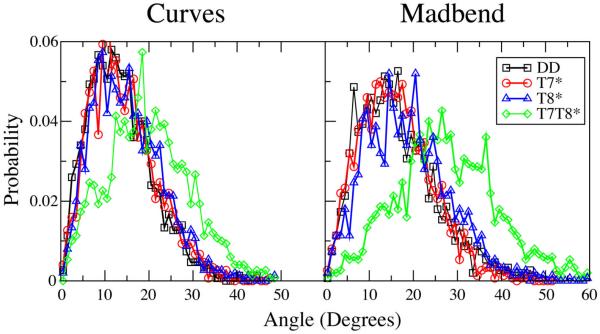
To further characterize these changes in DNA bending, the probability distributions of bend angles obtained from both the Curves and Madbend analysis are plotted in Figure 3. The T7* and T8* distributions are similar to that of DD, with only a slight shift towards larger values. In T7T8*, the bend angle distribution shows a greater shift towards larger bend angles. The broad range of bend angle distributions for all four oligomers indicates that the presence of the modified sugars does not lead to “rigidly” bent structures, but leads to changes in the sampling of bend angles leading to the increased bend angle average values.

Figure 3.

Probability distributions of the bending angles obtained with Curves (left panel) and Madbend (right panel).

Local structural parameters

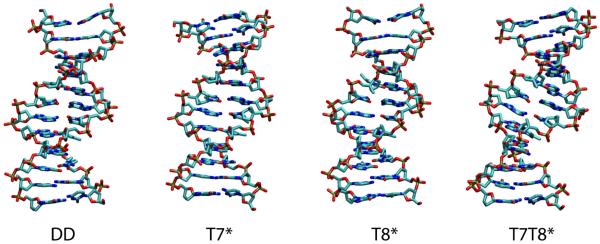
DNA bending can be caused by significant kinks localized at specific base steps, or small additive changes over several base steps, or a combination of both. The snapshots of the structures at 20 ns shown in Figure 4 illustrate how the distinction between these two possibilities is not necessarily obvious by visual inspection alone. It is of interest to see whether additional analysis of local DNA structural parameters such as backbone dihedrals, sugar puckering or helical parameters^53,54 calculated using Curves can reveal the nature of the bend introduced by the north carbocyclic sugars.

Figure 4.

Snapshots of the four simulated structures at 20ns

Helical Parameters (roll, rise and cup)

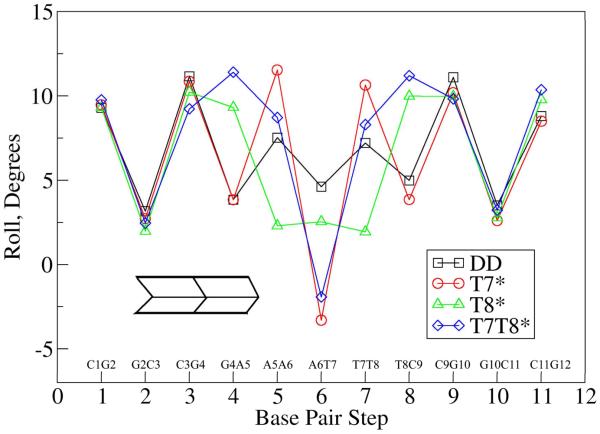
Roll is a rotational helical parameter that measures the angle between the planes of two consecutive WC base pairs. It can describe DNA bending^48,49 and is a part of the slide-roll-twist degree of freedom found in a study of base pair stacking interactions in X-ray structures^55,56. Figure 5 summarizes the average local roll values between base pair steps for the four oligomers. There are no significant differences between roll values for native DD and the substituted oligomers in the three terminal base steps, which suggest that the changes in bending are localized in structural changes in the substituted central bases (AATT) and/or the junction between them and the terminal (CGCG) segments. T7* maintains its similarity to DD further from the terminus than the other two substituted oligomers. The roll values for base steps 4 and 8 are very similar for T7* and DD (about 4-5°), while T8* and T7T8* show roll values greater than 9° at these base steps. In T7T8*, the two north carbocyclic sugar substitutions cause roll values at four base steps (4, 5, 7, and 8) to be more positive than DD. At the central base step 6 (A₆-T₇), the T7* and T7T8* oligomers both show negative roll values that are compensated for by the large positive roll values on the neighboring base steps 5 and 7. There is a difference of more than 10 ° in the roll values between the central base step 6 and its neighboring base steps 5 or 7 for the T7* and T7T8* oligomers. This difference is about 5° in the native DD oligomer, and about 1° in the T8* oligomer. The negative roll of the central base step in T7* and T7T8* suggests a local bend into the minor groove. However, the Madbend global roll values for the entire oligomer were 8.6, 7.3, 11.4 and 22.4° for DD, T7*, T8* and T7T8*, respectively. These positive global roll values suggest that the overall bending is towards the major groove, which is consistent with experimental observations.³⁴

Figure 5.

Average local roll values at each base pair step for the four oligomers.

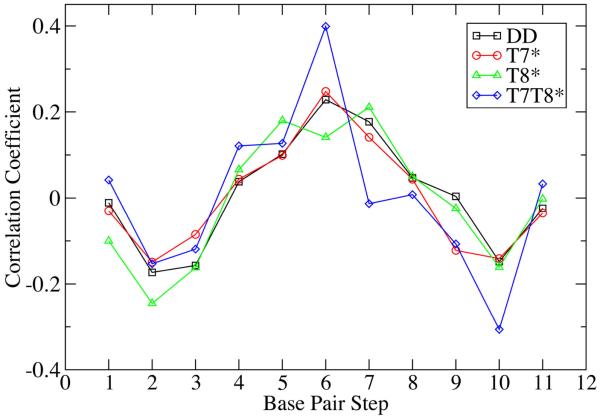
Variation in the differences between roll for neighboring base steps in each oligomer may be related to observed differences in their respective bend angles. To better quantify the contribution of the individual roll values to the overall duplex bending, correlation coefficients between roll and bending angle were calculated as a function of base step (Figure 6). The roll/bend correlation coefficient values are not large (between −0.4 and +0.4), but they are similar for the 4 systems, suggesting commonalities among the four oligomers. The roll of the central base step has a positive correlation with bending in all four oligomers, with T7T8* showing the largest correlation at this position. The correlation in three of the four systems is lower at the neighboring steps (5 and 7) than the central base step, the exception being T8*, where the correlation at the central step is slightly higher. The roll of the terminal base steps (1 and 11) shows no correlation with bending; however, the penultimate base steps (2 and 10) typically show negative correlation suggesting that roll changes at these steps may compensate for bending associated with roll changes at the central base steps. This roll analysis suggests that overall oligomer bending may be primarily due to localized geometric changes in the central base step (or three central base steps) rather than a more gradual bending distributed over many base steps

Figure 6.

Correlation between local roll values for the base steps and the overall bend angles of the oligomers from the Madbend analysis.

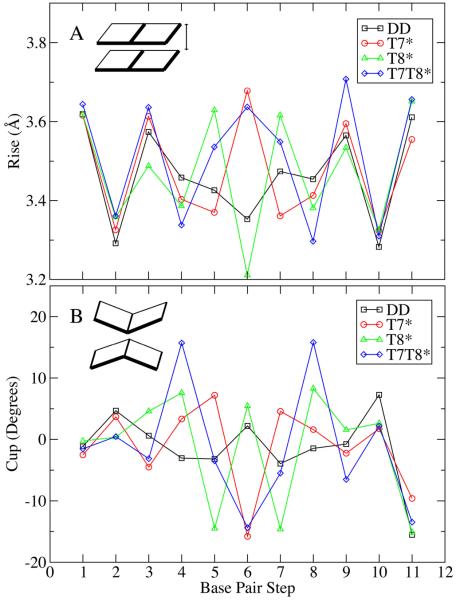
Rise is a helical parameter describing the distance between the planes of two consecutive base pairs⁴⁸ and is correlated to buckling⁵⁷. Figure 7A shows the rise values for all the base steps in the four oligomers studied. In T7*, where two modified sugars are present in base step 6, the rise values for base step 6 are greater than those in the native DD. In T8*, where the modified sugars are present in base steps 5 and 7, the rise of these base steps is greater, while the rise in base step 6 with no modified sugar is compressed. All three central base steps have modified sugars and show greater rise in T7T8* than in DD, with the double substituted base step 6 showing higher rise than the single substituted base steps 5 and 7. The rise value analysis shows that the presence of north carbocyclic sugars increases the distance between adjacent base pairs.

Figure 7.

Average rise (A) and cup (B) values as a function of base step.

Cup is a helical parameter that quantifies the difference in buckle between consecutive base steps. ⁵⁸ As illustrated in Figure 7B, if buckling causes shorter distances between the center of base pairs, the geometry corresponds to a positive cup value. Negative cup values correspond to increased distances between the center of stacked base pairs due to buckling. In T7* and T7T8*, the presence of the cyclopropyl groups at base step 6 (Figures 1 and 2) leads to buckling that separates the base pairs in that base step, yielding a negative cup value. In T8*, the presence of the carbocyclic sugar at base step 5 and 7, also causes these base steps to exhibit a more negative cup value. The presence of the north carbocyclic sugars evidently results in the basepairs buckling away from the bases attached to the cyclopropyl group containing sugar. This effect could be due to steric repulsion between the north carbocyclic sugars and neighboring DNA moieties or due to changes in backbone dihedrals associated with the presence of the carbocylic sugar³⁴.

Backbone dihedrals and sugar pucker

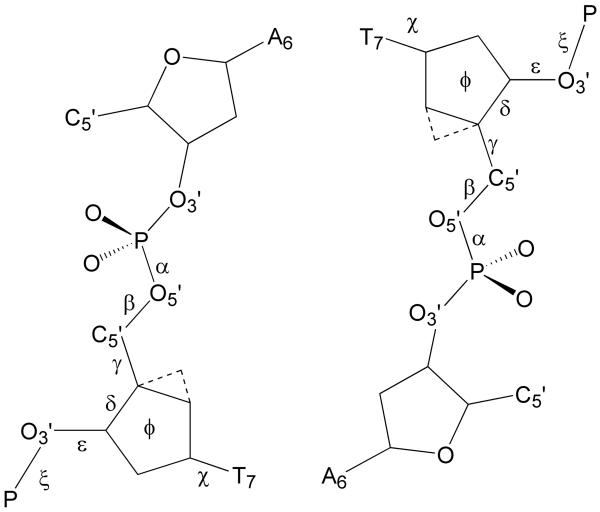
Figure 8 illustrates the IUPAC nomenclature for standard dihedrals in the DNA backbone. Since no significant dihedral perturbations are present other than in the central four nucleotides and the averages for these nucleotides for both strands are similar (Table S1 of the supplemental information), for simplicity, only values corresponding to strand 1 are reported in Table 4. The dihedrals χ and δ are omitted because, for north carbocyclic sugars, they are locked in an A-form conformation with the dihedral distributions for χ centered around 206-214° (A-form value=206°)³⁸ while the distributions for δ are centered around 73-78° (A-form value=83°)(data not shown). In the unmodified positions, χ and δ mostly adopt B-form conformations, but they do sample A-form conformations, particularly at the central base step 6 in DD. This is in agreement with NMR data indicating a south/north sugar equilibrium in B-DNA, dominated by the south conformation^23-25.

Figure 8.

Illustration of the dihedral nomenclature used for dihedrals at the individual nucleotides presented in Table4 and Table S1 of the supporting information.

Table 4.

Average local backbone dihedral values for the central 4 nucleotides in Strand 1.

	α	β	γ	ε	ζ
DD
A5	299	174	51	186	255
A6	297	177	51	189	263
T7	300	167	53	189	262
T8	302	172	52	192	252
T7*
A5	300	179	49	189	257
A6	296	167	52	188	256
T7	278	158	81	205	286
T8	298	172	65	191	258
T8*
A5	300	168	52	185	250
A6	299	179	49	189	261
T7	301	167	50	190	255
T8	278	155	81	211	281
T7T8*
A5	298	172	50	188	256
A6	294	167	51	189	259
T7	277	159	80	205	291
T8	279	171	71	208	278
A-DNA a	291	175	57	205	287
B-DNA a	298	168	51	187	262

^aFrom reference ³⁸.

A survey of crystallographic data, the modal values for α, β, γ, ε and ζ are 291, 175, 57, 205, and 287° for A-DNA and 298, 168, 51, 187, and 262° for B-DNA, respectively³⁸. In DD, the α dihedrals are centered around 300°. In the presence of a modified sugar, the α average falls between 277° and 279°, closer to the A-form value of 291°. Similar changes from B-form values to A-form values occur in ε and ζ resulting in a rotation of the phosphate group. The lack of complete conversion to an A-form conformation is indicated by two observations: the rise in the modified oligomers does not correspond to A-DNA, and not all dihedrals assume A-form values. The β dihedral averages for most north carbocyclic sugars become smaller and sample a more limited range of conformations in the presence of the modified sugars. For the γ dihedral in north carbocyclic sugars, there is an increase from about 50-60° to about 80° (A-form value = 57°). North carbocyclic sugars also increase the γ dihedral values of the next base pair step to about 65° (T7* in Table 4 and Table S1 of the Supplemental Information). These changes in β and γ are consistent with previous observations based on surveys of crystal data and quantum mechanical calculations⁵⁹.

These dihedral differences between DD and the modified oligomers indicate that specific local changes of the phosphate backbone are caused by the presence of north carbocyclic sugars. Along with the RMSD data in Table 1, they indicate that inclusion of more than one modified sugar into DNA leads to a localized conversion to an A-form conformation. This transition also does not significantly impact helix stability, as the melting free energy based on differential scanning calorimetry becomes less favorable by only 1 kcal/mol upon going from DD to T7T8*⁶⁰. North carbocyclic sugar introduction into DNA may therefore be used to control the extent of DNA bending without large structural perturbations or destabilization of the DNA.

Sugar puckering

In the present study, the pseudorotation angle (P) parameter^61-63 is used to classify the sugar pucker conformation as follows: the north sugar pucker conformation (N) includes the P values from −36° to 36° (C2′exo and C3′endo) and the south sugar conformation (S) includes values between 108° to 180° (C1′exo and C2′endo). Table 5 includes the percentage of each (N, S) population for both DNA strands in the four oligomers averaged over the last 15 ns of the MD simulations. The north carbocyclic sugars are clearly limited to the N conformation (P values in bold). An NMR study on DD indicates the C1, C3, T7, C9, C11 and G12 sugars sample the north conformation significantly⁵². The present MD simulation results for DD show substantial sampling of the north conformation for C3, A6, T7, and C9 sugars. The terminal sugars C1, C11, and G12 are dominated by the south conformation, which could be related to their water-exposed nature or the N1-N3 distance restraints imposed on these terminal base pairs in the present study.

Table 5.

Population percentage of north and south conformations for sugars in each complementary strand of the four DNA oligomers

	DD		T7*		T8*		T7T8*
	N	S	N	S	N	S	N	S
DNA1:
C1	3	87	2	85	3	85	3	85
G2	0	90	0	91	0	90	0	91
C3	11	70	19	60	15	67	13	71
G4	0	85	1	82	3	79	5	74
A5	4	83	0	85	1	90	0	88
A6	5	86	10	87	0	87	18	76
T7	5	66	98	0	3	80	98	0
T8	5	83	0	95	97	0	93	0
C9	23	65	10	79	34	60	1	88
G10	0	86	0	86	0	83	4	80
C11	4	82	8	78	5	80	6	79
G12	0	88	0	88	1	89	4	85
DNA2:
C1	3	84	3	86	4	82	4	84
G2	0	88	2	87	1	89	4	85
C3	12	71	12	71	15	66	3	81
G4	3	84	0	84	0	83	6	73
A5	0	88	0	86	0	90	0	90
A6	23	68	12	86	4	85	29	65
T7	18	56	97	0	6	77	98	0
T8	2	88	0	95	97	1	94	0
C9	22	66	16	74	29	64	12	78
G10	1	85	2	86	0	84	0	84
C11	4	83	8	77	7	78	6	79
G12	0	89	2	86	1	88	1	89

N indicates P between −36° to 36°, and S indicates P between 108° to 180°

For the modified oligomers, there appears to be only a minimal influence of the constrained sugars on the puckering of surrounding sugars. With T7* and T7T8*, there is an increase in the population of the north conformation for the WC partner of T7 (i.e. A6); however, this does not occur in T8* (with A5) and in T7T8* for A5. In addition, there appears to be little effect of the constrained sugar on adjacent sugars in the same strand. These results indicate that the A-form conformation induced by the north constrained sugars is only local and does not propagate to remote areas in the DNA double helix.

Steric Interactions

Analysis of the cup parameter shown in Figure 7B suggested that steric interactions could differ for the north carbocyclic sugars as compared to the usual deoxyribose sugar, due to the enforced north pucker conformation and the presence of the extra cyclopropyl moiety. To investigate this possibility, the average interaction energies between the sugars and surrounding atoms were obtained from the trajectories and compared to those in the oligomers generated in the B-form prior to dynamics (Table 6). The trajectory averages and initial B-form conformation for DD show a strong attractive energy between the unmodified sugar and the base attached to it ranging from −40.5 to −45.3 kcal/mol. In all the constrained sugars (bold in Table 6) in the B-form conformation prior to the simulation, there is a repulsive interaction with the base of approximately +5 kcal/mol, which, upon relaxation during the MD simulation, becomes slightly attractive (−0.4 to −2.6 kcal/mol).

Table 6.

Interaction energies (kcal/mol) between the sugar atoms of thymine 7 and 8 with backbone, base or neighboring sugar atoms

	T7			T8
	B-DNA	Average	S.E.	B-DNA	Average	S.E.
Sugar-Backbone
DD	43.4	39.4	5.9	43.5	40.6	5.9
T7*	27.1	14.8	2.0	43.5	36.5	2.9
T8*	43.4	43.3	4.8	27.4	17.4	1.5
T7T8*	27.1	16.3	2.4	27.4	13.0	1.3
Sugar-Base
DD	−40.6	−44.9	2.5	−40.6	−44.1	1.8
T7*	5.4	−1.8	1.1	−40.6	−40.5	1.3
T8*	−40.6	−45.3	1.4	5.7	−0.4	1.5
T7T8*	5.4	−2.6	1.4	5.7	−1.6	1.6
Sugarn-Sugarn+1
DD	−1.3	−3.6	1.5	−1.3	−5.2	1.0
T7*	−1.4	1.7	1.0	−1.3	−4.8	1.2
T8*	−0.0	0.8	0.6	−0.7	2.3	0.5
T7T8*	0.0	−0.4	0.4	−0.7	2.2	0.5

n refers to the base number, B-DNA energies are based on the canonical structures prior to dynamics

This less favorable interaction between the modified sugars and the base is, to some extent, balanced by interactions between the sugar and the backbone. In DD, the interaction energy of the sugar with the backbone atoms is repulsive for the B-form DD conformer and remains equally repulsive during the MD simulations. This appears to be due to the proximity of sugar O4′ and backbone O5′ atoms. The interaction energies of the modified sugars with the backbone atoms are less repulsive in the initial structures and become even less repulsive during the simulation by more than 10 kcal/mol. Modified sugars do not have the O4′ atom but have the C1S carbon atom in its place. The average distances in unmodified sugars between O4′ and O5′ is 3.0 Å (std. error < 0.15), while the average distance between the C1S atom and O5′ is 3.2 Å (std. error < 0.15). The enforced north pucker in the modified sugars, reflected in δ dihedral changes, seems to reposition the sugar away from the backbone. Loss of favorable interactions between the sugar and the base are thus compensated by reduction in repulsion between the sugar and backbone atoms. The changes in the helicoidal parameters roll and cup resulting in intrinsic DNA bending due to the carbocyclic sugars may be caused by this change in the balance between sugar-base and sugar-backbone interactions.

Solvation

DNA structure can be significantly impacted by its solvation⁶¹. Replacement of the sugar ether oxygen by a cyclopropyl group in the carbocyclic sugars could affect the solvation structure around the DNA oligomer. To quantify such changes in solvation, the number of water oxygens within 3.5 Å of different moieties of DNA were counted for the four central nucleotides in the DNA oligomer (Table 7). The 3.5 Å cutoff value incorporates the first hydration shell in the bulk water probability distribution⁶⁴. The introduction of the cyclopropyl moiety in the modified sugars results in the reduction of one hydrating water molecule. A simultaneous decrease in the hydration number of both sugar oxygen and base atoms indicates that the missing water molecule interacts with both these regions in DD. The total change in the hydration number of the modified duplexes is not significant. The decreases at nucleotides 7 and 8 in T7* and T7T8* are compensated by increases in nucleotide 9, while the changes for nucleotides in T8* are quite small. It is difficult to estimate the precise contribution of this change in solvation to DNA bending. The present results suggest a small effect; however, a more significant role for the changes in water structure on the DNA bending and dynamics cannot be excluded.

Table 7.

Relative average number of hydrating water oxygens within a 3.5 Å cutoff for the 4 central base positions in strand 1. Values are averaged over the last 15 ns of simulation and are shown as differences from the values corresponding to the DD oligomer.

	Full Nucleotide	Base	C8 or C6	Minor Groove	Major Groove	Sugar O or C*	Ester O3′	Ester O5′	O−
6
DD	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
T7*	−0.3	0.0	0.1	−0.4	0.3	−0.1	0.0	0.1	−0.1
T8*	−0.6	−0.7	0.0	0.0	0.0	0.1	0.1	0.0	−0.2
T7T8*	−0.4	−0.2	0.1	−0.3	0.2	−0.2	0.0	0.2	0.0
7
DD	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
T7*	−0.3	−0.9	−0.3	−0.2	0.2	−0.9	0.1	−0.1	−0.3
T8*	0	0.0	0.0	−0.2	−0.1	0.0	0.0	0.0	0.1
T7T8*	−0.6	−1.1	−0.3	−0.2	0.1	−0.9	0.2	−0.1	−0.2
8
DD	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
T7*	−0.7	−0.5	−0.1	0.1	0.1	−0.1	0.2	−0.2	−0.1
T8*	0.3	−0.7	−0.3	−0.2	0.0	−1.2	0.1	0.2	0.0
T7T8*	−0.4	−1.1	−0.3	0.2	0.1	−1.0	0.1	0.0	0.2
9
DD	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
T7*	1.9	0.4	0.0	0.1	0.0	−0.1	0.1	0.0	0.7
T8*	−0.5	−0.3	−0.1	0.0	−0.1	0.0	0.1	−0.1	0.1
T7T8*	1.1	0.2	−0.2	0.1	−0.1	−0.1	0.3	0.0	0.5

O⁻ indicates the anionic phosphate oxygens.

CONCLUSIONS

The present MD simulations of the native DD and three modified oligomers containing north carbocyclic sugars provide a detailed picture of the impact of introduction of constrained sugars on DNA bending and flexibility. The north carbocyclic sugars enhance bending, which is more pronounced when two adjacent positions in each strand contain the modified sugars. The modified DNA is not rigidly bent, instead a wide conformational distribution with larger bend angles is populated. The bending is also not gradual, it results from A-form conformations in a B-form duplex causing a localized kink with altered base stacking.

The presence of the bulkier modified carbocyclic sugar increases steric repulsion between the sugar and the base, which is reflected in changes in the roll and cup base step parameters. Increased bending of the oligomer axis is accompanied by greater roll of the base pairs near the modified sugars. Buckling of the substituted nucleotides suggests disruption of the stabilizing stacking interactions that rigidify the DNA duplex. The marginally increased base step flexibility seen in the distribution of bend angles and population of A-form conformations in adjacent backbone torsions occurs in all the modified oligomers. In the monosubstituted duplexes, however, compensating conformational changes in the adjacent nucleotides minimize the distortion introduced by the modified sugars, thereby diminishing the overall bending of the modified DNA duplex.

Systematic control over the intrinsic bending ability of DNA can be a valuable experimental asset in the investigation of multiple biological processes that require DNA bending. The present quantification of the precise structural perturbations caused by the presence of constrained north carbocyclic sugars in a DNA duplex is expected to facilitate such rational engineering of intrinsic DNA bends. Future studies are required to determine the impact of carbocyclic sugars constrained to be in the south conformation on stabilization of the B-form in DNA duplexes, which may offer enhanced tuning capacity in the engineering of specific bent states of DNA in the structure-function studies of DNA-protein interactions.