RNA pseudoknots: folding and finding

Abstract

RNA pseudoknots are important for function. Three-dimensional structural information is available, insights into factors affecting pseudoknot stability are being reported, and computer programs are available for predicting pseudoknots.

Introduction and context

RNA pseudoknots are important for many functions [1-3]. Pseudoknots are formed by pairing between bases in a loop region and complementary bases outside the loop (Figure 1). That is, for any base pairs i-j and k-l, i<j, k<l, and i<k, there are cases in which i<k<j<l. A two-loop nomenclature was initially used, but 30.9% of pseudoknots now listed in PseudoBase [4] have an additional loop, so the three-loop nomenclature from Brierley et al. [1] is more generally applicable (Figure 1). Loop 2 typically has zero or one nucleotide, whereas loops 1 and 3 and the stems are more variable (Table 1).

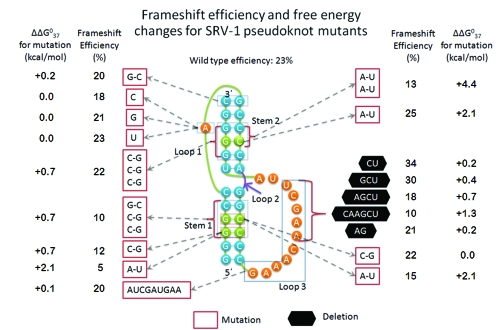
Figure 1. Simian retrovirus-1 (SRV-1) mutants’ frameshift efficiency [49-51] and their predicted free energy changes for the mutations.

A three-loop nomenclature is used for the pseudoknot. The free energy changes are predicted by coupling the individual nearest neighbor model [37] with a statistical polymer model [21,22], neglecting tertiary interactions.

Table 1. Three-dimensional structures of short pseudoknots.

Type of Organism or RNA	RNA	Function	Method	PDB #	Ref.	Size, nts	Stem 1, bps	Loop 1, nts	Stem 2, bps	Loop 2, nts	Loop 3, nts	Coaxial stack or bend
Mammalian retrovirus		Ribosomal frameshifting										Coaxial stack
	Simian retrovirus-1 (SRV-1)		NMR	1E95	[51]	36	6	1	6	0	12
	Mouse mammary tumor virus (MMTV)		NMR	1KPD	[56]	32	5	2	6	1	8
				1KAJ	[57]
				1RNK	[58]
Plant Luteoviridae viruses	Beet western yellow virus (BWYV)		X-ray	437D	[5]	26	5	2	3	1	7	Bend
				1L2X	[9]
	Sugarcane yellow leaf virus (ScYLV)		NMR	2AP0	[8]	28	5	2	3	1	9
				1YG4	[2]
	Potato leaf roll virus (PLRV)		X-ray	2A43	[7]	26	4	2	3	1	9
	Pea enation mosaic virus (PEMV)		NMR	1KPY	[6]	33	5	2	3	1	7
Human	Telomerase RNA	Telomere maintenance	NMR	1YMO	[3]	46	6	8	9	0	8	Slight bend
				2K96	[43]
Plant virus (tymovirus) 3′ NCR	Turnip yellow mosaic virus (TYMV)	t-RNA like	NMR	3PHP	[59]	23	3	4	5	0	3	Coaxial stack
				1A60	[60]
Bacteria	Aquifex aeolicus tmRNA	Trans-translation	NMR	2G1W	[61]	21	4	1	3	1	5	Bend

bps, base pairs; NCR, non-coding region; NMR, nuclear magnetic resonance; nts, nucleotides; PDB, Protein Data Bank; Ref., reference.

Major recent advances

Folding of pseudoknots

Quite a few three-dimensional (3D) structures have been determined for isolated pseudoknots of fewer than 50 nucleotides (Table 1). Some tertiary interactions are conserved in particular classes and are essential for biological activity [2,3]. Examples include a quadruple-base interaction in pseudoknots from Luteoviridae viruses [2,5-9] and triplexes in telomerase RNA [3] and in viral mRNA that undergo -1 frameshifting [10]. Structures of natural pseudoknots bound to small molecules are being reported [11-13], and structures of larger RNAs are revealing long-range pseudoknots [14-20].

The stability of RNA pseudoknots is a key factor determining structure-function relationships [10] and is important for predicting RNA structure [21-32]. Thermodynamic measurements have started appearing [3,33-36].

A statistical polymer model for loops [21,22] coupled with the INN-HB (Individual Nearest Neighbor-Hydrogen Bonding) model for stems [37] allows estimates of the stability of small pseudoknots. Coaxial stacking of the two stems can be included, although this is not always observed in 3D structures [5]. Contributions from tertiary interactions between the loops and stems are neglected because little is known about their thermodynamics.

Mechanical unfolding of single molecules by optical tweezers [10,38,39] reveals that frameshifting efficiency is highly related to the mechanical stability of pseudoknots, as suggested from cryoelectron microscopy [40] and prediction by a statistical polymer model [41]. Single-molecule experiments also indicate that pseudoknot folding and unfolding at low forces are stepwise [42] and that the presence of Mg²⁺ stabilizes the pseudoknot more than hairpins [39]. A better understanding of pseudoknot thermodynamic and mechanical stability and of folding dynamics will help reveal structure-function relationships [43].

Finding pseudoknots

Finding pseudoknots by computationally folding RNA sequences is a difficult problem. Because of computational cost, most of the popular dynamic programming algorithms for predicting the lowest free energy structure do not allow pseudoknots. With state-of-the-art knowledge, finding the lowest free energy structure with pseudoknots takes an exponentially increasing amount of time as the sequence gets longer; that is, the problem is NP-complete [23,24].

To predict low free energy structures with pseudoknots, roughly four different practical approaches are used by available programs. The first approach is to apply stochastic methods either to simulate folding pathways or to sample structures [25,26,44]. With these algorithms, structures are revised according to an element of chance and new pairs that are pseudoknotted with existing pairs can be added. A variation on this theme follows a folding pathway to find low free energy structures but is deterministic in its choices of stems [27]. The second approach is to use a dynamic programming algorithm in which the possible topologies of the predicted structures are limited [28-30]. The possible topologies predicted by a number of different programs have been examined [31]. A third approach is to assemble structures from component base pairs using a graph-theoretic approach [45,46]. A fourth approach is to iteratively build structures using algorithms that cannot predict pseudoknots with a single iteration [47,48]. The Nuclear magnetic resonance (NMR)-Assisted Prediction of RNA Secondary Structure (NAPSS) algorithm is an iterative approach that includes constraints from simple NMR experiments to improve predictions [32].

A number of the programs cited above either require multiple homologous sequences or are capable of using them to find a conserved structure [44-46,48]. These programs should be more accurate at structure prediction than those that use a single sequence because of the additional information available in the multiple sequences. For example, pairs that are not conserved in the set of sequences can be excluded from the final structure.

A recent benchmark of the accuracy of structure prediction using single sequences provides guidance for choosing a program [47]; Table 2 lists programs available for free. For 12 RNA sequences of 210 nucleotides or longer, a pathway folding algorithm [25] had the highest accuracy. The iterative approaches also performed similarly and were time-efficient [47,48].

Table 2. Available programs for secondary structure prediction including pseudoknots.

Program name	Website
HotKnots [47]	http://www.cs.ubc.ca/labs/beta/Software/HotKnots/
hxmatch [46]	http://www.tbi.univie.ac.at/papers/SUPPLEMENTS/HXMATCH/
ILM [48]	http://cs.utsa.edu/~jruan/Software.html
KineFold [26]	http://kinefold.curie.fr/
pknotsRG [29]	http://bibiserv.techfak.uni-bielefeld.de/pknotsrg/
SimulFold [44]	http://people.cs.ubc.ca/~irmtraud/simulfold/
vsfold5 [27]	http://www.rna.it-chiba.ac.jp/~vsfold/vsfold5/

This table provides a list of programs that are available for free and can make predictions on a desktop computer for sequences that are up to at least 200 nucleotides long. Note that hxmatch is designed to find conserved structures for sequences in a multiple alignment and that ILM can be run with one sequence or with an alignment of multiple sequences. SimulFold works on a set of homologous sequences and infers the sequence alignment. KineFold and vsfold5 are available as web servers. pknotsRG is available for use on a web server or for download.

Future directions

Predictions of the occurrence and stabilities of pseudoknots can be improved. The best-performing program tested by Ren et al. [47] predicted only 57% of known canonical base pairs, and only 39% of the predicted pairs were in the known structures. New insights into the structures and stabilities will suggest computational simplifications for existing strategies and improve approximations of stabilities. New methods to find pseudoknots conserved in multiple sequences and to incorporate more experimental data will restrain folding space. Finding more pseudoknots will likely expand the types of functions known for pseudoknots. Increased understanding of the sequence dependence of pseudoknot stabilities can improve comparisons with functional studies. For example, the relative frameshifting efficiencies of simian retrovirus-1 (SRV-1) pseudoknot and its mutants [49,50] qualitatively correlate with their predicted relative stabilities (Figure 1, revised from [51]). The exception is mutant U11A34, which is predicted to be less stable than the wild-type pseudoknot but shows higher efficiency of frameshifting. This could result from an additional tertiary interaction if a U11A34/A7 base triple is formed. Such comparisons can suggest new experiments.

Future work can also resolve current ambiguities. For example, there is disagreement about the role of pseudoknot stability in human telomerase RNA. The pseudoknot domain may act as a molecular switch [52], in which the pseudoknot and the stem 1 hairpin have nearly equal stability [34], or only the pseudoknot conformation may be important for function [53]. A two-base mutation destabilizing the human telomerase pseudoknot is found in some patients with the inherited disease dyskeratosis congenita [54]. A theoretical calculation suggests that folding kinetics of the pseudoknot may determine activity [55]. There is much more to be revealed about the roles of pseudoknots and their modus operandi.

Abbreviations

3D

three-dimensional

INN-HB

individual nearest neighbor-hydrogen bonding

NAPSS

nuclear magnetic resonance (NMR)-assisted prediction of RNA secondary structure

NMR

nuclear magnetic resonance

SRV-1

simian retrovirus-1

Competing interests

The authors declare that they have no competing interests.

The electronic version of this article is the complete one and can be found at:http://f1000.com/reports/b/2/8