Abstract
We study spontaneous dynamics and signal transduction in a model of active hair bundle mechanics of sensory hair cells. The hair bundle motion is subjected to internal noise resulted from thermal fluctuations and stochastic dynamics of mechano-electrical transduction ion channels. Similar to other studies we found that in the presence of noise the coherence of stochastic oscillations is maximal at a point on the bifurcation diagram away from the Andronov-Hopf bifurcation and is close to the point of maximum sensitivity of the system to weak periodic mechanical perturbations. Despite decoherent effect of noise the stochastic hair bundle oscillations can be synchronized by external periodic force of few pN amplitude in a finite range of control parameters. We then study effects of receptor potential oscillations on mechanics of the hair bundle and show that the hair bundle oscillations can be synchronized by oscillating receptor voltage. Moreover, using a linear model for the receptor potential we show that bi-directional coupling of the hair bundle and the receptor potential results in significant enhancement of the coherence of spontaneous oscillations and of the sensitivity to the external mechanical perturbations.
I. INTRODUCTION
Spontaneous rhythmic activity was observed in peripheral auditory and vestibular sensory systems comprised of sensory cells coupled to primary afferent neurons through chemical synapses. Examples include spontaneous mechanical oscillations of hair bundles in auditory hair cells [1–7]; spontaneous voltage oscillations of receptor potential of saccular hair cells [8–10]; pacemaker-like firing of vestibular afferent neurons [11]. Spontaneous receptor oscillations were also documented in peripheral electrosesnory systems [12–14].
Sensory hair cell is the first stage in conveying the mechanical stimuli into the electrical signals. Using the mechanically gated ion channels on stereocilia, a hair cell converts deflection of its hair bundle into the changes of the membrane potential. Spontaneous stochastic oscillations with amplitudes much larger than expected for mere thermal fluctuations and whose response to weak stimuli breaks the fluctuation-dissipation theorem indicate an active process in which the hair bundle generates motion by itself, battling viscous drag from surrounding fluids [7]. Active hair bundle motion contributes to the amplification of weak mechanical signals, sharpens frequency response and is responsible for the phenomenon of otoacoustic emission [15–17]. Experimental and modeling studies have shown that spontaneous hair bundle oscillations are mediated by two main processes that need to be present together to provide self-sustained oscillations (i) negative differential stiffness, providing a positive feedback and leading to mechanical instability and (ii) adaptation processes due to calcium-controlled molecular motors, providing negative feedback [7, 18–23]. Several studies suggested that the hair bundle operates on a verge of an Andronov – Hopf bifurcation, providing extreme sensitivity and sharp selectivity to external mechanical perturbations [19, 24–26].
Less understood is a functional role of spontaneous voltage oscillations documented in experiments with the saccular hair cells of lower vertebrates [8–10]. These oscillations are mediated by basolateral potassium and calcium ion channels and observed as a large (10 – 70 mV) amplitude oscillations of the receptor potential. Indeed, variations of membrane potential may strongly influence the mechanics of hair bundles via a reverse electro-mechanical transduction [20, 27–29]. The authors of Refs. [8–10] hypothesized that the receptor potential oscillations may contribute to the active amplification and sharpening of frequency response in hair cells. A receptor voltage resonator coupled to active bundle motion was recently proposed as a possible mechanism of self-tuning [22].
In this paper, we focus on the role of hair bundle oscillations and on effects of receptor potential oscillations in shaping the system’s response to external mechanical stimuli using a computational model. Several computational models were developed to account for spontaneous hair bundle oscillations. Models developed in [19, 21–23, 30] describe a hair bundle as a single object whose elasticity is mediated by adaptation processes and by transduction ion channels. Detailed finite element model of hair bundle mechanics [31, 32] was used to examine the possibility of high frequency oscillations in mammalian outer hair cells in Ref. [33]. Here we use a model developed in Ref. [21]. A simplified version of this model was used in Refs. [23, 30]. We modified the model in two ways: (i) we added periodic oscillations of the membrane potential to study the electro-mechanical sensitivity of the hair bundle motion to externally modulated receptor potential; (ii) we introduced a linear resonator model for the receptor potential coupled to the hair bundle to study effects of reverse electro-mechanical transduction on the coherence of spontaneous oscillations and on the sensitivity of hair bundles to weak mechanical stimuli. In addition to the sensitivity measure used in the previous studies we employ nonlinear synchronization analysis to quantify phase locking and frequency entrainment of the stochastic hair bundle motion by weak external periodic force and by receptor potential oscillations.
The paper is organized as follows. Sec. II introduces the hair bundle model and discusses it’s deterministic dynamics. Spontaneous stochastic oscillations and response to periodic mechanical force are studied in Sec. III. In Sec. IV we introduce periodic perturbation of receptor potential and re-analyze spontaneous dynamics and responses to mechanical stimuli.
II. HAIR BUNDLE MODEL AND DETERMINISTIC DYNAMICS
A model of spontaneous hair bundle oscillations was proposed in [21] based on detailed in vitro experiments with bullfrog sacculus. These cells are sensitive to linear motion of the head. Below we briefly describe the model using the same notation as in [21]. In the model a hair bundle is represented as an elastic object comprised from stereocilia which move as a whole in a viscous fluid. The variable x(t) represents the position of the tip of the bundle. The hair bundle is subjected to a drag force, λẋ; elastic forces from extension or compression of gating springs connecting individual stereocilia with the gates of MET channels, FGS; an elastic force arising from the stereocilia pivots FSP; and an external force, Fext. The nonlinearity in the model stems from the forces exerted by the gating springs, FGS. The hair bundle is composed of NGS transduction elements each with a spring attached to the gate of single MET ion channel. The gating springs lie in parallel with one another, and characterized by the stiffness κGS. The combined elastic force from the gating springs is FGS = NGSκGSγl, where γ relates the shearing motion between stereocilia to the motion of the hair bundle tip, and l is the extension of individual gating spring. The extension l of the gating spring is influenced by opening of the MET channel and by adaptation processes which move insertional plaque of the MET channel up and down along stereocilia. Opening of the MET channel shortens the gating spring by an amount d, while the adaptation results in shortening by an amount xA. As a result the total extension of the gating spring is l = γx − xA − pod + xC, where po is the probability of the MET channel to be opened and xC is the resting extension of the spring when the MET channel is closed. A two-state kinetic model is used to describe the gating of the MET channels, τṗo = p∞ − po, where τ = 1 msec and p∞ is the equilibrium value of po, which depends nonlinearly on x and xA (see below). The adaptation involves two competing processes: the gating spring pulling downward and the molecular motors pulling upward on the insertional plaque of the MET channels. Both processes are influenced by the concentration of calcium ions, [Ca2+]. The rate of adaptation pulling downward increases with [Ca2+], while the rate of adaptation due to pull from the molecular motors decreases with [Ca2+]. In the model both rates are assumed to interpolate linearly between 0 and maximum values Cmax, Smax in proportion to the probability of calcium binding at the adaptation site, pM. The stiffness of the gating spring is affected by fast reclosure of transduction channel due to calcium entrance. In the model gating springs are comprised of two elements in series: a tip link with the stiffness κTL and a reclosure element with the stiffness κRE, giving the overall stiffness, κGS = κTLκRE / (κTL +κRE). While the stiffness of the tip link, κTL is constant, the stiffness of the reclosure element, κRE, changes linearly between a maximal and minimal values in proportion to the probability of Ca2+ binding at the reclosure element, pRE: κRE = (1 − pRE)(κRE,max − κRE,min) + κRE,min. The model’s equations are,
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Eq. (1) describes the position of the bundle tip. The last two terms, −βLKSF x and Fext stand for an external mechanical load, characterized by the stiffness KSF, and the external force, respectively; βL is a dimensionless control parameter characterizing the strength of the external load. Eq.(2) governs the adaptation variable xA. Eq.(3) is the kinetic equation for the open probability of transduction channel with the equilibrium value,
| (7) |
where ΔE is the change of the free energy of the MET channel when it switches from open to close states in the absence of the gating spring and T is the temperature. Eqs. (4) and (5) describe the probabilities of Ca2+ binding to the adaptation site (4) and to the reclosure element (5). [Ca2+]M, RE are Ca2+ concentrations at these sites. Ca2+ enters through the MET channel and its concentrations at the adaptation site, [Ca2+]M, and at the reclosure element, [Ca2+]RE are determined with the Goldman-Hodgkin-Katz equation [34] resulting in,
| (8) |
where [Ca2+]O = 0.25 mM is extracellular Ca2+ concentration, rM,RE are the distances from the channel to adaptation motors and to reclosure element, respectively; Vm is the membrane potential of the hair cell; qe is the elementary charge; PCa is Ca2+ permeability of the MET channel and DCa is the diffusion coefficient of Ca2+ in water. In Eq.(8) α is a dimensionless control parameter, related to calcium sensitivity parameter used in a model proposed in Ref.[23]. Notice that according to Eq.(8) [Ca2+] at the adaptation and reclosure sites depends on the receptor potential Vm. Dimensionless parameters α and βL were used as a control parameters of the model. The values of other parameters were fixed and are listed in Table 1 of Ref. [21].
Local bifurcations of the model Eqs.(1–8) were studied using a software package CONTENT [35]. For the parameters values used in this study the model exhibits two types of steady-state solutions: equilibrium points and limit cycles. Bifurcation diagram of the equilibrium points on the parameter plane (α, βL) in Fig. 1(a) shows a line of the supercritical Andronov-Hopf (AH) bifurcations. For a fixed value of external load parameter βL, there are two supercritical AH bifurcations as external [Ca2+] varies. For small α < 0.58 (low [Ca2+]O) the MET channels are mostly opened and the hair bundle is in the equilibrium position. For large α the MET channels are mostly closed and the system is again at equilibrium. At the first AH bifurcation point of small α0 a small limit cycle is born [Fig. 1(b,c)]. In a very narrow parameter α range its amplitude increases as (α − α0)1/2 and its frequency is nearly constant. Small increase in α results in sudden jump of the amplitude to much higher values [Fig. 2(a)], corresponding to a large excursion of the phase trajectory [Fig. 1(b,c)]. Such a transition is often observed in slow-fast systems which possess drastically different characteristic time scales and refers to the existence of so-called canard trajectory which explodes to a large amplitude limit cycle in a narrow range of the control parameter [36]. The canard explosion dramatically slows down oscillations. Fig. 2(b) shows that the frequency of small-amplitude oscillations drops abruptly 3 times at the canard explosion points. Further increase of α results in oscillations with gradually increasing frequency, but with decreasing amplitude until the limit cycle bifurcates to the equilibrium state via second AH bifurcation. The external mechanical load results in a shrinking of the oscillating region and in overall increase of the frequency of oscillations. The canard explosion disappears for βL > 0.7. For large βL, the passive stiffness overwhelms the negative stiffness resulting in disappearance of the limit cycle oscillations. Thus, the frequency and the amplitude of oscillations depends drastically on the control parameters in the vicinity of the first AH bifurcation.
FIG. 1.
(Color online) (a): Bifurcation diagram of the model. Solid line shows the Andronov-Hopf bifurcation. Shaded area corresponds to the existence of periodic solution (limit cycle). (b): Hair bundle position versus time before (grey line), near (dotted blue line), and after (black line) canard explosion. (c) Phase portrait corresponding to the time traces of panel (b). (d): Magnified region of the phase space showing small-amplitude cycles. The values of control parameter α are indicated in the figure legend, βL = 0 on panels (b) and (d).
FIG. 2.
Amplitude (a) and frequency of the limit cycle as a function of the control parameter α for the indicated value of βL. α0 is the value of control parameter α at which the first Andronov-Hopf bifurcation occurs for a given βL.
III. SPONTANEOUS HAIR BUNDLE OSCILLATIONS AND RESPONSE TO PERIODIC FORCE
The deterministic model Eqs.(1–8) was extended to take inevitable fluctuations into consideration. Here we consider two sources of internal noise. The first source results from the Brownian motion of viscous fluid surrounding hair bundles. This leads to additional term η(t) in the r.h.s of Eq.(1),
| (9) |
modeled as Gaussian white noise with the autocorrelation function 〈η(t)η(0)〉 = 2kBTλδ(t). The second noise source stems from stochastic dynamics of transduction channels, which can be approximated as [37]
| (10) |
where ξ(t) is a Gaussian white noise with the autocorrelation function . Note that this second type of noise is state-dependent, as its intensity depends on the phase variables of the model through p∞. All other sources of fluctuations such as fluctuating forces acting on motors considered in [23] are neglected. The model equations (1–8) with the modification mentioned above were simulated using the Euler method with the time step of 10−3 msec.
A. Spontaneous oscillations
We first show that the stochastic version of the model reproduces experimental results of Ref.[21]. In experiments the influence of Ca2+ was studied using iontophoresis. Correspondingly we varied the parameter α in a step- or ramp-like manner as shown in Fig. 3: when the external [Ca2+] increases, the oscillations go faster and are of smaller amplitude [Fig. 3(a)]. Decreasing the external [Ca2+] leads to an opposite effect [Fig. 3(b)]. Relative low or high external [Ca2+] prohibits oscillations. These results are consistent with experimental observations (Fig. 6 of Ref.[21]). Noise has significant effect on the hair bundle dynamics. For example, for low [Ca2+] below the value of the first AH bifurcation internal noise induces oscillations [Fig. 3(b)]. With the increase of external load (parameter βL) the frequency of oscillations increases and their amplitude decreases [Fig. 3(c)] (compare with Fig. 8 of Ref.[21]).
FIG. 3.
Effect of the external Ca2+ concentration α (a,b) and the external load βL (c) on spontaneous hair bundle oscillations. (a) α was ramped linearly from 0.8 to 1.5 in 1200 msec. (b) Step-like reduce of α from 0.8 to 0.55 for 1200 msec. (c) Step-like increase of βL form 0 to 1.0 for fixed α = 0.8.
The power spectral density (PSD) of the hair bundle position is shown in Fig. 4(a). For α < 0.58, i.e. for the parameter value prior to the first AH bifurcation, the hair bundle shows low-frequency erratic relaxation oscillations induced by internal noise [Fig. 3(b)]. Thermal noise smears out any signature of small-amplitude limit cycle observed in this parameter region in the deterministic system. Consequently, the PSD has a broad peak at low frequency. With the increase of α the natural frequency of hair bundle oscillations increases and oscillations become more coherent, as indicated by the narrower peaks in Fig. 4(a). However, with further increase of α the hight of the spectral peak decreases and its width increases, indicating the approach to the second AH bifurcation. We characterized the coherence of spontaneous oscillations with the quality factor defined as the ratio of peak frequency, f0, to the width of the spectral peak at the level of half maximal power. The parameter dependencies of the quality factor, Q, and the characteristic frequency, f0 are shown in Fig. 4(b,c). The quality factor attains a maximum value at α ≈ 0.7, which is located in between of two AH bifurcations and corresponds to the average open probability 〈po〉 ≈ 0.5. Increasing the external load leads to faster and less coherent oscillations. This is consistent with the results of Refs.[23, 38, 39].
FIG. 4.
(Color online) Spectral properties of spontaneous hair bundle oscillations. Power spectral densities (PSD) of hair bundle motion for βL = 0.5 and for the indicated values of parameter α (a). The quality factor (b) and the characteristic frequency (c) of spontaneous hair bundle oscillations versus α for the indicated values of the parameter βL.
B. Signal amplification and synchronization
The response of the model to a periodic external force, Fext = F0 cos(2πfst), was quantified with two approaches. In the first approach we estimated the response function of the system. Time-dependent average 〈x(t)〉 of periodically stimulated hair bundle was calculated by averaging over an ensemble of 100 realizations of x(t) each 100 sec long. The sensitivity function was calculated as χM = |X(fs)|/F0, where |X(fs)| is the absolute value of the first Fourier harmonic of 〈x(t)〉 [23]. The sensitivity shows a peak at the characteristic frequency of the hair bundle oscillations and demonstrates the effect of compressive nonlinearity: the sensitivity saturates for small amplitudes of external force, decreases according to a power law for intermediate amplitudes and saturates again for large values of F0 [23]. This is illustrated in Fig. 5(a) for different values of α. The characteristic frequency and the quality factor of spontaneous oscillations depend crucially on α [Fig. 4(b,c)]. As a result, the sensitivity to weak external force possesses a global maximum on the parameter plane (fs, α) shown in Fig. 5(b).
FIG. 5.
(Color online) (a) The mechanical sensitivity of the hair bundle χM versus the amplitude of external force F0 for the indicated values of the parameter α and βL = 0.5. The frequency of external force, fs, was tuned to the characteristic frequency of spontaneous oscillation (fs = f0), also indicated in the figure legend. (b) Contour plot of the mechanical sensitivity for various values of α and fs. Other parameters are: F0 = 0.1 pN and βL = 0.5.
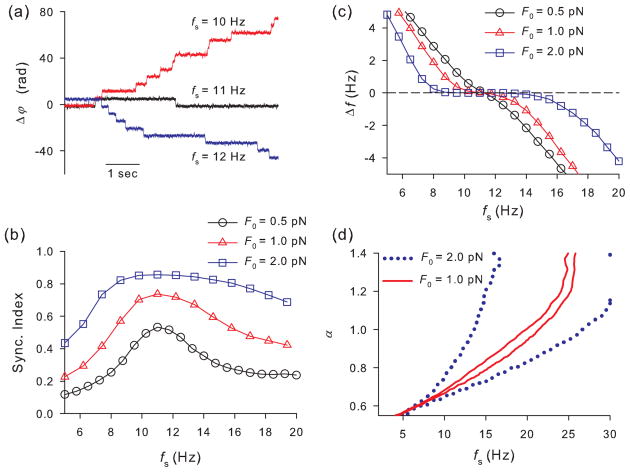
The mechanical sensitivity does not provide information about the phase locking and frequency entrainment. Thus, in our second approach we calculated the instantaneous phase of the hair bundle position, φ(t), and the phase lag between the hair bundle position and the external force, Δφ(t) = φ(t) − 2πfst using the Hilbert transform [40]. Phase locking corresponds to a constant value of Δφ(t). However, due to noise the phase difference fluctuates, Δφ(t), and can be represented as a Brownian motion in a tilted periodic potential [41]. The tilt of such a potential is determined by the mismatch between the frequencies of the hair bundle oscillator and the external force. In the presence of noise synchronization is never perfect. Instead, long-lasting small-scale fluctuations of Δφ(t) around the potential minima are interrupted by large-scale transitions over the potential barriers. This stochastic synchronization is illustrated in Fig. 6(a) where phase locking epochs of nearly constant phase difference lasting for many periods of external force are interrupted by abrupt 2π phase slips. The strength of phase locking is characterized by the synchronization index, Γ2 = 〈cos(Δφ)〉2 + 〈sin(Δφ)〉2, where the averaging is taken over time [40]. The synchronization index changes from 0 (absence of synchronization) to 1 (perfect synchronization) and is shown in Fig. 6(b). Synchronization becomes significant for strong enough external force, F0 ≥ 1 pN, so that the mean frequency of the hair bundle, fb = 〈φ̇〉/2π, is entrained by the external periodic force in a finite region of parameter values. This is illustrated in Fig. 6(c), where the frequency difference, Δf = fb − fs, is shown as a function of fs. The synchronization region where Δf is close to 0 extends for up to 8 Hz for F0 = 2 pN. Nevertheless, the synchronization index is smaller than 1 in this region [Fig. 6(b)], indicating the existence of phase fluctuations. Since the characteristic frequency of the hair bundle oscillator is governed by the parameter α we present a region of frequency entrainment on the parameter plane (fs, α) for two values of the signal amplitude [Fig. 6(d)]. The synchronization region is narrower for small values of α, where the system is closer to the first AH bifurcation. In this region large-amplitude relaxation oscillations appeared through the canard explosion are strongly affected by thermal noise resulting in low phase coherence. With the increase of α towards the second AH bifurcation the amplitude of oscillations decreases [Figs. 2(a) nd 3], so that the external force merely suppresses intrinsic hair bundle oscillations leading to a wider range of frequency entrainment.
FIG. 6.
(Color online) Phase synchronization of the hair bundle oscillations by the external periodic force. (a) Instantaneous phase difference, Δφ(t) = φ(t) − 2πfst, for the indicated values of the driving frequency, fs. Other parameters are F0 = 1 pN, α = 0.7 and βL = 0.5. (b) Synchronization index versus the driving frequency. Other parameters are the same as in panel (a). (c) The frequency difference, Δf = fb − fs versus the driving frequency for the indicated values of the driving amplitude, F0. Other parameters are the same as in panel (a). (d) Regions of synchronization within which |Δf| ≤ 0.05 Hz on the parameter plane (fs, α) for F0 = 1 pN (red, solid line) and F0 = 2 pN (blue, dotted line).
IV. INFLUENCE OF RECEPTOR VOLTAGE OSCILLATIONS
The characteristic frequency and the coherence of spontaneous hair bundle oscillations depend crucially on Ca2+ concentration at the adaptation sites which is controlled by the parameter α in the model. Ca2+ entry through the MET channels indeed depends on the electrical potential of the cell, Vm, as expressed by the Goldman-Hodgkin-Katz equation (8). Depolarization of the cell decreases [Ca2+] at the adaptation sites, while hyperpolarization leads to an increase of [Ca2+], which in turn affect the rates of adaptation (Eqs. 2,4–6). Thus, variations of the receptor potential may strongly affect the hair bundle motion through the phenomenon of reverse electro-mechanical transduction [3]. Bullfrog saccular hair cells are known to exhibit the phenomenon of electrical resonance whereby the receptor potential shows dumped oscillations being knocked by a pulse of injected current [42]. Moreover, spontaneous self-sustained oscillations of the receptor potential were observed experimentally in [8–10]. To explore the effects of receptor potential oscillations on mechano-electrical transduction we used two approaches. In the first approach we modulated the receptor voltage periodically and characterized reverse electro-mechanical transduction. In the second approach we used a linear model for underdamped electrical oscillations coupled to the hair bundle model and characterized effect of such coupling on the mechanical sensitivity of the hair bundle.
A. Sensitivity to external receptor potential modulation and electro-mechanical synchronization
The receptor potential Vm in Eq.(8) was modulated periodically as Vm(t) = Ṽm + V0 cos(2πfvt), where Ṽm = −55 mV is the constant component of the potential used in the previous sections of the paper, V0 is the modulation amplitude, and fv is the frequency of modulation. We calculated the electro-mechanical sensitivity as χv = |X(fv)|/V0, where |X(fv)| is the absolute value of the first Fourier harmonic of 〈x(t)〉. Similarly to mechanical sensitivity, the electro-mechanical sensitivity is nearly constant for a weak modulation (V0 ≤ 5 mV) and decreases with further increase of V0 [Fig. 7(a)]. However, for larger values of V0 in the physiological range V0 ≤ 80mV [10] no saturation of the electro-mechanical sensitivity was observed. The electro-mechanical sensitivity displays the resonance with respect to variations of the voltage frequency: χv is maximal at fv matching the frequency of the spontaneous hair bundle oscillations f0. Similarly to the mechano-electrical sensitivity [Fig. 5(b)] the sensitivity to weak external voltage oscillations possesses a global maximum on the parameter plane (fV, α) shown in Fig. 7(b). These results indicate a rather strong sensitivity and selectivity of the hair bundle to external voltage variations with 1–2 nm per mV.
FIG. 7.
(Color online) Sensitivity of the hair bundle to the periodic modulation of the receptor potential. (a) The electro-mechanical sensitivity χv versus the amplitude of voltage modulation, V0, for the indicated values of α and fv. (b) Contour plot of the electro-mechanical sensitivity χv for various values of α and fv. Other parameters are: V0 = 5 mV and βL = 0.5.
For V0 ≥ 10 mV the external voltage oscillations lock the hair bundle oscillations. This electro-mechanical synchronization is shown in Fig. 8. The mean frequency of the hair bundle oscillations is entrained by the voltage modulation in a finite range of fv [Fig. 8(a)]. We note that the modulation amplitudes of 20 – 35 mV resulting in a wide synchronization region [Fig. 8(b)] correspond well to 40 – 75 mV values of peak-to-peak amplitudes of the receptor potential oscillations measured in [10].
FIG. 8.
(Color online) Phase synchronization of the hair bundle oscillations by the external voltage modulation. (a) The frequency difference, Δf = fb − fv, versus the modulation frequency, fv, for the indicated values of the modulation amplitude, V0. (b) Region of synchronization within which |Δf| ≤ 0.05 Hz on the parameter plane (fv, V0). Other parameters are the same as in Fig. 7.
B. Linear resonator model for the receptor potential oscillations
Oscillatory and resonant properties of the receptor potential are mediated by K+ and Ca2+ ion channels in the basolateral membrane of a hair cell [8, 42–45]. Several Hodgkin-Huxley - type models were developed to account for electrical resonance [42] and self-sustained oscillations of the membrane potential [8, 9]. Instead, here we use a simplified description of the receptor potential as a linear resonator developed in [46]. The equation for the membrane potential reads,
| (11) |
where Cm is the capacitance of the cell membrane, β0 and k0 are effective damping and “stiffness”, respectively which are related to parameters of basolateral ionic currents, ωv is the natural frequency, . I0 is a constant current which may represent either external command current or a current from support cells [47]. Since the MET channels are not ion specific, the MET current in effect is similar to the leakage current. The leakage conductance enters in both the damping, β0, and “stiffness”, k0, coefficients of Eq.(11) [46]. The MET current is given by It = gtpoVm, where gt is the maximal combined conductance of transduction channels (i.e. when all MET channels are opened), po is the open probability of the MET channels [48]. Upon introduction of the MET current, the coefficients β0 and k0 are modified as: β = β0 + gtpo and k = k0 + ωvgtpo. Introducing the quality factor of the resonator in the absence of the MET current, Qv = ωvCm/β0, we arrive to the following equation for Vm:
| (12) |
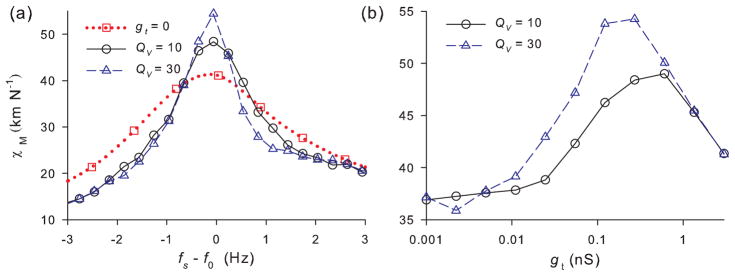
where σ is a dimensionless coefficient defined as σ = gt(Cmωv)−1. We required that the receptor potential oscillates about an equilibrium value close to −55 mV used in the preceding sections by setting V0 as V0 = Ṽm − I0 [(1 + 0.5σ)ωvCm]−1, where Ṽm = −55 mV. Notice, that the increase of the MET conductance (increase of po) raises the damping in the linear resonator model (12) and thus lowers its quality factor. In the following we use Cm = 14 pF for the cell membrane capacitance [8] and I0 = 10 pA. The maximal conductance of the MET channels of bullfrog sacculus ranges from 0.08 to 2.48 nS [48]. The quality factor of the electrical resonator, Qv, its natural frequency, ωv = 2πfv, and the maximal MET conductance, gt are then the parameters of the linear electrical resonator model. Combining Eq.(12) with the hair bundle model Eqs.(1–10) results in bi-directional mechano-electrical and electro-mechanical coupling. The maximal MET conductance, gt, plays the role of the coupling strength. For gt = 0, the receptor potential is at its equilibrium value, Ṽm = −55 mV. A representative example of the time courses of the hair bundle position and the receptor potential is shown in Fig. 9. The voltage resonator tuned to the characteristic frequency of the hair bundle oscillations filters out noise, leading to a sharper peak in the power spectrum of the hair bundle motion [Fig. 10(a)]. The dependence of the hair bundle Q-values on the coupling strength is non-monotonous [Fig. 10(b)] for small values of gt the amplitude of the voltage oscillations is small and the effect of electro-mechanical coupling is small as well. Consequently, the coherence of the mechanical oscillations is close to the case of the fixed receptor potential. On the other hand, the increase of gt results in decrease of the quality factor of linear resonator. As a result, there is an optimal coupling strength at which the coherence of the hair bundle oscillations is maximal. Sharpening of the peak in the power spectrum of spontaneous oscillations results in a sharper response to the external periodic force. Fig. 11 shows calculations of the mechanical sensitivity, χM to the external force, Fext = F0 cos(2πfst). With the electrical resonator coupled to the hair bundle the response to the external mechanical force becomes significantly sharper [Fig. 11(a)]: with the receptor potential fixed the quality factor of the mechanical sensitivity tuning curve is ≈ 3.2 and increases to 6.1 for the coupled system with QV = 10. Similarly to the quality factor [Fig. 10(b)], the mechanical sensitivity possesses a maximum versus the MET conductance, shown in Fig. 11(b).
FIG. 9.
The hair bundle position x(t) (upper trace), and the receptor potential VM (t) (lower trace) for the combined model Eqs.(1–8) and Eq.(12). The parameters are α = 0.7, βL = 0.5, Qv = 30, fv = 10.5 Hz and gt = 0.12nS.
FIG. 10.
(Color online) (a) Power spectral density (PSD) of the hair bundle position for the indicated values of the MET conductance, gt. Other parameters are the same as in Fig. 9. (b) Quality factor of the hair bundle oscillations versus the MET conductance for the indicated Q-values of the electrical resonator. Other parameters are the same as in Fig. 9.
FIG. 11.
(Color online) Mechanical sensitivity, χM, of the hair bundle coupled to the electrical resonator. (a) χM versus the frequency detuning, fs − f0, for the indicated values of Qv. The natural frequency of the electrical resonator was equal to the frequency of the spontaneous hair bundle oscillations, fv = f0 = 10.5 Hz. The MET conductance gt is 0.3 nS for Qv = 10 (circles, solid line) and 0.2 nS for Qv = 30 (triangles, dashed line). The amplitude of the external force F0 = 0.1 pN. (b) χM versus the MET conductance for fv = fs = 10.5 Hz and the indicated values of Qv. Other parameters are the same as in Figs. 9,10.
V. CONCLUSION
We have studied spontaneous oscillations and response dynamics of ciliary bundles of sensory hair cell using numerical simulations. The original model used in this study was proposed in Ref. [21] to account for spontaneous hair bundle oscillations observed in in-vitro experiments with isolated bullfrog saccular hair cells. The model incorporates differential negative stiffness of the hair bundle and two adaptation mechanisms (due to adaptation molecular motors and due to fast reclosure of transduction channels) to account for self-sustained oscillations. Adaptation rates are controlled by the concentration of Ca2+ ions at the adaptation sites. We first performed bifurcation analysis of the model using external [Ca2+] as the control parameter. For the parameters values used in Ref. [21] we found that the system possesses single stable equilibria for both low and high [Ca2+]. Transitions to periodic self-sustained oscillations occur through the supercritical Andronov–Hopf bifurcations (Fig. 1). Interestingly, transition to the self-sustained oscillations from low [Ca2+] is accompanied by a canard explosion. Before the canard explosion, but after the Andronov–Hopf bifurcation, a small-amplitude limit cycle exists in exponentially narrow range of the control parameter. Small increase of the parameter results in explosion of this limit cycle resulting in low-frequency large-amplitude relaxation oscillations whose frequency depends crucially on the control parameter. Indeed, thermal noise completely washes out these small-amplitude oscillations, so that they can be hardly detected in the time traces or in the power spectrum of the hair bundle motion.
Spontaneous dynamics of stochastic model resembles experimental data and is very similar to modeling results of [23]. Consistent with Ref.[23] we found that the coherence of spontaneous oscillations quantified by the quality factor is maximal for a value of the control parameter at which the open probability of transduction ion channels is close to 0.5. This parameter value is away from both Andronov–Hopf bifurcations.
We then explored response of the stochastic hair bundle model to the periodic external force. Besides the mechanical sensitivity function, which characterizes the amplification of external signal and tuning of the system used in previous studies, we employed a synchronization analysis to characterize instantaneous phase locking and frequency entrainment. We showed that despite large fluctuations induced by thermal noise the spontaneous hair bundle oscillations can be phase synchronized by periodic external force with amplitude as small as 1 pN, corresponding to ≈ 10 nm amplitude of mechanical stimulation displacement. This is consistent with the experimental results (Fig. 1 in Ref. [6]).
Tuning of a hair cell can be provided by resonant properties of basolateral membrane which comprises various K+ and Ca2+ ion channels, responsible for the phenomenon of electrical resonance [42] and for a large (10 – 70 mV) amplitude spontaneous oscillations of receptor potential [8–10]. The receptor potential is a crucial parameter in the model, since its variations affect Ca2+ entrance through the transduction channels and consequently the adaptation dynamics. Thus a model for hair cell can be constructed from two compartments: (i) a mechanical compartment of the hair bundle and (ii) an electrical compartment describing dynamics of the receptor potential. These compartments are coupled bi-directionally [27]. The mechano-electrical coupling is realized through the mechano-electrical transduction current which tends to depolarize the hair cell. The electro-mechanical coupling is due to the influence of the receptor potential on intracellular Ca2+ concentration which in turn controls the hair bundle dynamics. In this paper we simplified the consideration by assuming that variations of the receptor potential affect Ca2+ concentration locally, i.e. at the locations of adaptation motors and reclosure elements. First, we explored the reverse electromechanical transduction by changing the receptor potential periodically. We found that the external periodic modulation of the receptor potential entrains the hair bundle oscillations for the ranges of the modulation strength consistent with the values of amplitudes of spontaneous voltage oscillations documented in Ref. [10]. Second, we used a simple linear model to describe resonant properties of basolateral membrane. Similar approach was used in [22] to explain a possible mechanism of self-tuning whereby the hair bundle always operates on the verge of the Andronov–Hopf bifurcation. In that study the voltage compartment was used to mediate a background Ca2+ concentration in stereocilia via Ca2+ current through the basolateral ion channels. Our scenario is different in that the receptor potential affect Ca2+ current through the mechano-electrical transduction channels. With the quality factor of the electrical resonator higher than that of the hair bundle compartment we showed that bi-directional coupling enhances the coherence of spontaneous hair bundle oscillations, as compared to the case with a fixed receptor potential. Consequently, the mechano-electrical sensitivity is enhanced by the electrical resonator and displays a sharper tuning (Fig. 11).
Recently the authors of Ref.[49] showed that mechanical coupling of the hair bundles synchronizes their spontaneous motion leading to dramatic enhancement of the coherence of spontaneous oscillations and of the mechanical sensitivity to weak external forces. The mechanism proposed here may contribute to further suppression of noise-induced fluctuations and thus to additional enhancement of hair cells sensitivity and selectivity. Indeed, the linear resonator model for receptor potential is a severe simplification. In particular, it does not allow to consider self-sustained voltage oscillations which are characterized by large amplitudes and high coherence. Consequently one can expect mutual synchronization of the hair bundle and voltage oscillations. A detailed Hodgkin-Huxley -type model for the receptor potential [8, 10] along with a model for Ca2+ homeostasis in stereocilia [50] can be employed to account for the interaction of the active hair bundle motion and the self-sustained receptor oscillations.
Acknowledgments
The authors thank Michael Zaks and Andrey Shilnikov for valuable discussions. This work was supported by National Institutes of Health Grant No. DC05063 and by the Biomimetic Nanoscience and Nanotechnology program of Ohio University. L.H was supported by the China Scholarship Council.
Contributor Information
Lijuan Han, School of Science, Beijing Institute of Technology, Beijing 100081, People’s Republic of China and Department of Physics and Astronomy, Ohio University, Athens, OH 45701, USA.
Alexander B. Neiman, Department of Physics and Astronomy, Ohio University, Athens, OH 45701, USA
References
- 1.Crawford A, Fettiplace R. J Physiol. 1985;364:359. doi: 10.1113/jphysiol.1985.sp015750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Howard J, Hudspeth A. PNAS. 1987;84:3064. doi: 10.1073/pnas.84.9.3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Denk W, Keolian RM, Webb WW. J Neurophysiol. 1992;68:927. doi: 10.1152/jn.1992.68.3.927. [DOI] [PubMed] [Google Scholar]
- 4.Benser M, Marquis R, Hudspeth A. J Neurosci. 1996;16:5629. doi: 10.1523/JNEUROSCI.16-18-05629.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Martin P, Hudspeth A. PNAS. 1999;96:14306. doi: 10.1073/pnas.96.25.14306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Martin P, Hudspeth A. PNAS. 2001;98:14386. doi: 10.1073/pnas.251530498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Martin P, Hudspeth A, Jülicher F. PNAS. 2001;98:14380. doi: 10.1073/pnas.251530598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Catacuzzeno L, Fioretti B, Perin P, Franciolini F. J Physiol. 2004;561:685. doi: 10.1113/jphysiol.2004.072652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jrgensen F, Kroese ABA. Acta Physiol Scand. 2005;185:271. doi: 10.1111/j.1365-201X.2005.01495.x. [DOI] [PubMed] [Google Scholar]
- 10.Rutherford MA, Roberts WM. J Neurosci. 2009;29:10025. doi: 10.1523/JNEUROSCI.1798-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Goldberg JM. Exp Brain Res. 2000;130:277. doi: 10.1007/s002210050033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Clusin WT, Bennett MV. J Gen Physiol. 1979;73:685. doi: 10.1085/jgp.73.6.685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lu J, Fishman HM. Biophys J. 1995;69:2458. doi: 10.1016/S0006-3495(95)80116-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Neiman AB, Russell DF. J Neurophysiol. 2004;92:492. doi: 10.1152/jn.00742.2003. [DOI] [PubMed] [Google Scholar]
- 15.Hudspeth A. Neuron. 2008;59:530. doi: 10.1016/j.neuron.2008.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Manley GA. J Neurophysiol. 2001;86:541. doi: 10.1152/jn.2001.86.2.541. [DOI] [PubMed] [Google Scholar]
- 17.Manley GA. Hear Res. 2009;255:58. doi: 10.1016/j.heares.2009.05.009. [DOI] [PubMed] [Google Scholar]
- 18.Martin P, Mehta AD, Hudspeth AJ. PNAS. 2000;97:12026. doi: 10.1073/pnas.210389497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Choe Y, Magnasco MO, Hudspeth AJ. PNAS. 1998;95:15321. doi: 10.1073/pnas.95.26.15321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ricci A, Crawford A, Fettiplace R. J Neurosci. 2002;22:44. doi: 10.1523/JNEUROSCI.22-01-00044.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Martin P, Bozovic D, Choe Y, Hudspeth A. J Neurosci. 2003;23:4533. doi: 10.1523/JNEUROSCI.23-11-04533.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vilfan A, Duke T. Biophys J. 2003;85:191. doi: 10.1016/S0006-3495(03)74465-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nadrowski B, Martin P, Jülicher F. PNAS. 2004;101:12195. doi: 10.1073/pnas.0403020101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Eguiluz VM, Ospeck M, Choe Y, Hudspeth AJ, Magnasco MO. Phys Rev Lett. 2000;84:5232. doi: 10.1103/PhysRevLett.84.5232. [DOI] [PubMed] [Google Scholar]
- 25.Camalet S, Duke T, Jülicher F, Prost J. PNAS. 2000;97:3183. doi: 10.1073/pnas.97.7.3183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Risler T, Prost J, Jülicher F. Phys Rev E. 2005;72:016130. doi: 10.1103/PhysRevE.72.016130. [DOI] [PubMed] [Google Scholar]
- 27.Denk W, Webb WW. Hear Res. 1992;60:89. doi: 10.1016/0378-5955(92)90062-r. [DOI] [PubMed] [Google Scholar]
- 28.Ricci A, Crawford A, Fettiplace R. J Neurosci. 2000;20:7131. doi: 10.1523/JNEUROSCI.20-19-07131.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bozovic D, Hudspeth A. PNAS. 2003;100:958. doi: 10.1073/pnas.0337433100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tinevez JY, Jülicher F, Martin P. Biophys J. 2007;93:4053. doi: 10.1529/biophysj.107.108498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nam JH, Cotton JR, Grant W. Biophys J. 2007;92:1918. doi: 10.1529/biophysj.106.085076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Beurg M, Nam JH, Crawford A, Fettiplace R. Biophys J. 2008;94:2639. doi: 10.1529/biophysj.107.123257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nam JH, Fettiplace R. Biophys J. 2008;95:4948. doi: 10.1529/biophysj.108.138560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hille B. Ionic Channels of Excitable Membranes. Sinauer Associates Inc; 1984. [Google Scholar]
- 35.Kuznetsov Y. ftp://ftp.cwi.nl/pub/CONTENT.
- 36.Glendinning P. Stability, Instability and Chaos: An Introduction to the Theory of Nonlinear Differential Equations. Cambridge University Press; 1994. [Google Scholar]
- 37.Fox RF, Lu YN. Phys Rev E. 1994;49:3421. doi: 10.1103/physreve.49.3421. [DOI] [PubMed] [Google Scholar]
- 38.Clausznitzer D, Lindner B, Jülicher F, Martin P. Phys Rev E. 2008;77:041901. doi: 10.1103/PhysRevE.77.041901. [DOI] [PubMed] [Google Scholar]
- 39.Jülicher F, Dierkes K, Lindner B, Prost J, Martin P. Eur Phys J E. 2009;29:449. doi: 10.1140/epje/i2009-10487-5. [DOI] [PubMed] [Google Scholar]
- 40.Pikovsky A, Rosenblum M, Kurths J. Synchronization: a universal concept in nonlinear sciences. Cambridge University Press; 2003. [Google Scholar]
- 41.Stratonovich RL. Topics in the Theory of Random Noise. Gordon and Breach; New York: 1963. [Google Scholar]
- 42.Hudspeth A, Lewis R. J Physiol. 1988;400:275. doi: 10.1113/jphysiol.1988.sp017120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hudspeth A. Hear Res. 1986;22:21. doi: 10.1016/0378-5955(86)90070-5. [DOI] [PubMed] [Google Scholar]
- 44.Hudspeth A, Lewis R. J Physiol. 1988;400:237. doi: 10.1113/jphysiol.1988.sp017119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Eatock RA, Hutzler MJ. Ann N Y Acad Sci. 1992;656:58. doi: 10.1111/j.1749-6632.1992.tb25200.x. [DOI] [PubMed] [Google Scholar]
- 46.Ashmore J, Attwell D. Proc R Soc Lond B. 1985;226:325. [Google Scholar]
- 47.Corey DP, Hudspeth AJ. J Neurosci. 1983;3:942. doi: 10.1523/JNEUROSCI.03-05-00942.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Holton T, Hudspeth A. J Physiol. 1986;375:195. doi: 10.1113/jphysiol.1986.sp016113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dierkes K, Lindner B, Jülicher F. PNAS. 2008;105:18669. doi: 10.1073/pnas.0805752105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lumpkin EA, Hudspeth AJ. J Neurosci. 1998;18:6300. doi: 10.1523/JNEUROSCI.18-16-06300.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]