Summary
Rigorous statistical evaluation of the predictive values of novel biomarkers is critical prior to applying novel biomarkers into routine standard care. It is important to identify factors that influence the performance of a biomarker in order to determine the optimal conditions for test performance. We propose a covariate-specific time-dependent PPV curve to quantify the predictive accuracy of a prognostic marker measured on a continuous scale and with censored failure time outcome. The covariate effect is accommodated with a semiparametric regression model framework. In particular we adopt a smoothed survival time regression technique (Dabrowska, 1997) to account for the situation where risk for the disease occurrence and progression is likely to change over time. In addition, we provide asymptotic distribution theory and resampling-based procedures for making statistical inference on the covariate specific positive predictive values. We illustrate our approach with numerical studies and a dataset from a prostate cancer study.
Keywords: Biomarker evaluation, Negative predictive value, Positive predictive value, Semi-parametric survival analysis
1. Introduction
The utility of novel molecular markers and clinical information for predicting disease risk and future prognostic outcome has great potential for advancing treatment and management decisions. In the Pacific Northwest Prostate Cancer SPORE (Specialized Program of Research Excellence), a cohort of patients diagnosed with prostate cancer (PC) are under follow-up for clinical outcomes. Information on biomarkers such as serum prostate-specific antigen (PSA) at diagnosis and genotype data on single nucleotide polymorphisms (SNPs) have been collected. One goal of the study is to identify biomarkers that can predict PC-specific mortality so that treatment options can be tailored to the individual. In this setting there are two key prognostic questions. First, should a test be taken by a patient to predict his/her prognosis? Second, given a patient has the test, what is the probability that a poor outcome will be realized in the near future based on the test result?
The first prognostic question may be addressed with retrospective accuracy characterized by correct classification rates such as the true positive fraction (TPF) and true negative fraction (TNF). Traditionally for a marker measured on a continuous scale, denoted by Y, measured concurrently with the disease outcome D, its discrimination potential can be summarized with the receiver operating characteristic (ROC) curve. The ROC curve is a plot of the TPF, P(Y > c|D = 1) against the false positive fraction (FPF), P(Y > c|D = 0) for all possible values c, where D = 1 indicates the presence of disease. These summaries reflect how well the test results reflect the true outcome, and they are crucial for evaluating the public health implications of clinical guidelines. Extending the traditional cross-sectional concept of ROC curve to accommodate the censored failure time outcome has been an area of active research for the past decade (e.g., Etzioni et al. (1999); Heagerty et al. (2000); Cai and Pepe (2002); Heagerty and Zheng (2005), for review, see Pepe et al. (2008)).
Physicians and individual patients are often most concerned with disease prediction given their clinical status data. Thus the prospective accuracy such as positive predictive values (PPV) and negative predictive values (NPV) are critical in addressing the second prognostic question. When data from a prospective cohort are available, calculation of PPV and NPV is usually performed. In contrast to research on retrospective accuracy, statistical methods for prospective accuracy have not been well developed, especially when a continuous marker is measured and the outcome is followed prospectively from a cohort study. The two prospective accuracy summaries are traditionally defined for a dichotomous test Y as
To accommodate a continuous marker, Moskowitz and Pepe (2004b) proposed to define PPV(v) = P{D = 1|F(y) ≥ v} and NPV(v) = P{D = 0|F(y) < v}, where F is the cumulative distribution function of Y in the population. Analogous to the idea of an ROC curve for thresholding the continuous marker values, they consider the PPV curve, a plot of PPV(v) versus v, for 0 < v < 1, where subjects with marker values exceed the vth percentile of the population are regarded as having a positive test. The consideration of v rather than the raw marker values as the x-axis of the PPV curve is appealing. First, it provides a common scale for comparing multiple markers with raw values measured on different scales. Second, it highlights the need for considering both predictive probability and marker distribution in the targeted population when evaluating the predictive accuracy of the marker.
Zheng et al. (2008) considered extending the PPV curve concept to a setting where disease status is not measured concurrently with the test and the time to event can be censored. Specifically, they consider disease status as a function of time, D(t) = 1(T < t) for a clinical event time T. Consequently PPV and NPV were time-dependent functions of the form
A time-dependent PPV curve at a predictive time t is then defined as a plot of PPV(t, v) versus v for v in an open interval of (0, 1). Therefore the x-axis of a PPV curve shows the proportion of subjects testing positive when a positive test is defined by exceeding the threshold corresponding to the vth percentile of Y in the population: Y ≥ F−1(v), whereas the y-axis of a PPV curve shows the risk of developing an event by time t for subjects who satisfy the positivity criterion. Zheng et al. (2008) focuses on a class of nonparametric PPV curve estimators and their associated indices that provide a natural way for handling censored event outcomes and involve little parametric assumption. The methods are useful for evaluating individual PPV curves and comparing PPV curves.
In this article we focus on the statistical method for evaluating factors that may influence the predictive accuracy of a continuous biomarker. In practice there are many variables that can affect the accuracy of a marker, such as a subject’s age, gender, or body mass index (BMI). For example PSA levels tend to increase with age, and older patients may have a higher risk of prostate cancer progression depending upon treatment. It is likely that the predictive performance of PSA can be altered by these confounding variables. Marker performance may also depend on the means by which a biomarker-based test is administered or varying protocols between different institutions participating in the study. For example, variations in the timing for collecting and processing biological specimens should be considered. Furthermore, the heterogeneous nature of the disease will often affect the performance of the test. Gleason score is a PC aggressiveness index. A biomarker such as PSA could have differential performance in predicting prognosis in patients with a high Gleason score as compared to those in a low Gleason score group. Genetic studies will often identify new genotypes that give rise to sub-populations differing in their disease susceptibility, and the performance of PSA among these sub-populations may be substantially different. When the performance of a biomarker among sub-populations may be substantially different from the general population, covariate-specific PPV curve should be considered. It provides a graphical tool for investigating the impact of these confounding factors on the predictive performance of the marker, and therefore helps to identify appropriate sub-populations with effective test performance.
A broad range of questions can be addressed with covariate-specific PPV curves, in a regression model framework. It can be used to characterize the simultaneous or independent effects of covariates on predictive accuracy and to compare tests with regard to predictive accuracy while controlling for potential confounding variables. Using a test indicator as a covariate in the model permits more efficient comparison of two tests. Finally, it may provide a way to evaluate the incremental values of a new test, for example by examining whether the new test is predictive beyond previously identified prognostic information.
Statistical methods for incorporating covariate effects into PPV analysis are limited. One approach to incorporating covariate effects into time-dependent predictive values has been suggested by Moskowitz and Pepe (2004a) for a binary marker Y, where Y = 1 indicating a positive test result. For PPVz(t) = P (T < t|Y = 1, Z = z), they considered a standard Cox proportional hazards model only for individuals who test positive, and model
in which β1 quantifies the difference in positive predictive accuracy between two levels of covariate Z. However, the idea is not directly applicable to continuous markers. The nonparametric time-dependent PPV curve estimators considered in Zheng et al. (2007) are quite flexible in specifying the relationship between a continuous marker Y and clinical event T, but it can be difficult to handle multiple covariates. In this article, we extend the method of the time-dependent PPV curve studied by Zheng et al. (2008) to the estimation of covariate-specific PPV curves. Similar to Moskowitz and Pepe (2004b), we will accommodate the covariate effects in a regression framework, but we will seek to preserve the flexible relationship between biomarker and event time that accommodated by the nonparametric PPV curve estimators in Zheng et al. (2008).
A formal definition of the covariate-specific PPV curve is given in Section 2. We describe two alternative estimation procedures and characterize their large sample properties in Section 3 and 4, respectively. The finite sample performance is investigated in Section 5, and in Section 6 we illustrate the method by analyzing a prostate cancer dataset. A discussion of the potential extensions of current work is given in section 7.
2. The model
Consider a setting where one is interested in determining the effect of Z on the predictive accuracy of a continuous marker Y. In particular, we have a prospective study where each subject indexed by the subscript i is followed over time for a clinical event, and measured along with a marker Yi at the baseline and other covariates Zi. We let FY|z(y) = P (Y < y|Z = z) denote the conditional distribution function and . Let Ti denote the event time for the ith subject. Due to censoring, instead of observing Ti, we observe the bivariate vector (Xi, Δi), where Xi = min(Ti, Ci), Δi = I(Ti ≤ Ci) and Ci is the censoring time for the ith subject. Data for analysis consist of n independent and identically distributed copies of (Xi, Δi, Yi, Zi) for i = 1, …, n. For censoring, we require the standard assumption that Ci is independent of Ti conditional on Yi and Zi. Since a biomarker threshold value is used for clinical decision making, for covariate-specific PPV curves it is desirable to have the assumption that risk P(T < t|Y = y, Z = z) be a monotonic function of y given z. However note that the validity of the proposed procedures for the covariate specific PPV and NPV curves do not require the monotonicity assumption. By convention we assume that larger values of the marker Y are associated with higher risks at each level of Z.
2.1 Covariate-specific PPV curves
We define a time-dependent covariate-specific PPV curve for a prediction time t as a plot of
versus v, for v in an open interval of (0,1). In contrast to a PPV curve that ignores covariates, the x-axis of a covariate-specific PPV curve displays among the subgroups who share the same covariate values z the fraction of subjects testing positive, when a positive test is defined by exceeding the threshold corresponding to the vth percentile of Y in the subpopulation: Y ≥ cz(v). The y-axis indicates the risk of event by time t among the subgroup of subjects who share the same covariate values z, and who test positive based on some positivity criterion. Time dependent covariate-specific NPV curves can be similarly defined, with
Observe that the differences among PPVz(t, v) at different values of Z may be due to several factors. For example, if the absolute risk of event varies with covariates Z, naturally one may expect that the predictive accuracy may also vary with Z. On the other hand, even if a covariate Z itself is not predictive of risk whereas Y is, variations in the distributions of Y across Z may also lead to distinctly separate covariate specific PPV curves. Therefore it is important to investigate the covariate effects on the predictive accuracy of Y, even for a covariate that does not appear to be associated with disease progression. By inspecting covariate-specific PPV and NPV curves, one can discover the extent to which the covariates Z influence the predictive accuracy of Y. If PPV curves representing different covariate levels are different across v at a fixed time point t, one may conclude that in practice we indeed need to take Z into consideration when evaluating the predictive accuracies of Y. Note also that a covariate-adjusted PPV is dependent on the average disease risk of the subgroup. To gauge the predictive performance of the marker, in the covariate-specific PPV curve, we can add horizontal lines that correspond to the marginal event time probabilities P(T < t|Z = z) ≡ PPVz(t, 0). These serve as the benchmark PPV curves for completely uninformative markers. Markers with PPV curves that rise more steeply and reach higher levels compared with the horizontal lines can be deemed informative.
3. Estimation
A simple approach for estimating the covariate-specific PPV curves is to fit an individual PPV curve using only data with Z = z. The procedure developed in Zheng et al. (2008) can be directly applied. However, such a subgroup analysis can not accommodate continuous covariates and may not be feasible due to sparseness of data. We therefore consider here flexible regression based procedures to accommodate more general structures of Z.
Observe that the covariate-specific PPV curve can be written as
The estimation of PPVz(t, v) requires the specification of (1) the conditional distribution of Y given Z = z, FY|z(·); and (2) the conditional survival function Sy,z(t) = P (T ≥ t|Y = y, Z = z).
To estimate FY|z(·), if Z is a discrete variable with only a few levels, one can simply consider empirical distribution
For multiple covariates or continuous variables, we will adopt the semi-parametric regression quantile method of Heagerty and Pepe (1999). Specifically, it specifies biomarker Y as a function of Z with a location-scale model: Yi = γTZi + exp(κTZi)εi, where the standardized error εi has mean 0 and variance 1 with unspecified distribution. The unknown regression parameters γ and κ may be estimated based on quasi-likelihood methods as discussed in Heagerty & Pepe (1999). Let γ̂ and κ̂ denote the respective estimators of γ and κ. The distribution function of a marker given Z can be estimated using the empirical distribution function based on the standardized residual (Heagerty & Pepe, 1999). The procedure is more efficient than the conditional empirical estimator mentioned above, it allows for continuous covariates, and yet it is flexible as it does not make a distributional assumption about the residual εi. The semiparametric location-scale estimator of FY|z(·) is
| (3.1) |
The other key quantity is the conditional survival function Sy,z(t) = P (T < t|Y = y, Z = z). Some deliberation is required in order to properly capture the relation between Y, Z and T. We provide details of two alternative estimating procedures below.
3.1 Estimating Sy,z(t) using Cox proportional hazards model
In order to estimate the absolute risk function Sy,z(t), we first turn to a standard tool for analyzing survival data, the Cox proportional hazards model (Cox, 1972),
| (3.2) |
where is the cumulative baseline hazard function. Under the Cox model assumption, the survival function can be consistently estimated by
where α̃ and β̃ are the maximum partial likelihood estimators of α0 and β0 respectively, and
is the Breslow estimator of Λ0(t) and Ni(u) = I(Xi ≤ u)Δi.
A plug-in estimator for PPVz(t, v) based on the conditional survival probability is
| (3.3) |
where . The approach has two advantages. First, the maximum partial likelihood based estimator will be most efficient when the assumption of a proportional hazards model holds. Second, it is easy to implement with standard software.
3.2 Estimating Sy,z(t): a more flexible approach
It is often anticipated in biomarker studies that the effects of markers may be time-varying and/or non-linear. As a result, the standard proportional hazards assumption may not be satisfied. For example, it is generally observed in HIV studies that the predictive capacity of CD4 cell counts on time to HIV infection among sero-converters tend to be stronger early in time, however the effect wanes over time (Zheng and Heagerty, 2005). Mis-specification of T|Y can have a substantial impact on estimating the PPV curve (Zheng et al., 2008). A more flexible specification of the relationship between T, marker value Y and covariates Z would be useful in practice. In the absence of covariates, Zheng et al. (2008) considered a nonparametric kernel estimator for P(T ≥ t|Y), which results in a more robust PPV estimator. To extend such a non-parametric procedure to incorporate covariates, we propose to preserve the non-parametric form of the functional relationship between T and Y, but cast the effects of other time-constant covariates within a regression model framework. This motivates the consideration of a “smoothed Cox regression model” by Dabrowska (1997),
| (3.4) |
This model, while allowing possibly a complex non-linear effect of Y on T, can easily accommodate multiple continuous covariates. Note that interactions between Y and Z can be accommodated by adding additional covariates that corresponding to the interaction terms in the parametric part of the model. The estimator β̂ can be obtained as the maximizer of the following (pseudo) smoothed profile likelihood:
where , and Kh(y) = K(y/h)/h. Here K is a symmetric kernel density function, with h = h(n) → 0 as the bandwidth. To alleviate the computational burden Dabrowska (1997) suggested considering a simpler form of the profile likelihood:
The maximizer of Ĉ*(β) was shown to be asymptotically equivalent to β̂. Subsequently, the conditional survival function Sy,z(t) = P (T ≥ t|Y = y, Z = z) under the smoothed Cox regression model can be estimated as
where . Again, a plug-in estimator of PPVz(t, v) is given by
| (3.5) |
4. Inference
4.1 Inference on covariate effects
In order to test whether a covariate has a significant impact on predictive accuracies, we consider an omnibus test to test the joint hypotheses:
at every (t, v) and for all z1 and z2, where z1 and z2 are different covariate values that define subpopulations under investigation. Suppose we use the semiparametric location-scale model as specified in model (3.1) for the distribution of the marker. We show in Web Appendix A that under a proportional hazards regression model as specified in model (3.2), H0 holds if and only if H̃0: α0κ0 = 0 and β0 = −α0γ0 holds. Thus, the covariate effect could be tested by simultaneously testing . A χ2 test could be constructed based on the asymptotic distribution of the corresponding estimates. When the assumption of a proportional hazards model does not hold, and the distribution of the disease process is specified as a smoothed Cox regression model (model (3.4)), we can show that testing H0 is equivalent to testing β0 = γ0 = κ0 = 0. A χ2 test can be derived using the variance-covariance matrix of all parameters involved. In practice, one can first test the proportional hazards assumption in the failure time model, then select the appropriate χ2 test to test whether predictive accuracies vary by different values of the covariate.
4.2 Inference about individual points on a PPV curve
To make inference about PPVz(t, v), we derived asymptotic properties of the proposed estimators. We first show in the Web Appendix B that
almost surely and
is asymptotically equivalent to a sum of independent and identically distributed (i.i.d) terms,
, where ζi(t, v, z) is defined in Web Appendix B. Furthermore, we show by the functional central limit theorem of Pollard (1990) that the process 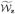 (t, v) converges weakly to a mean zero Gaussian process in (t, v). Similarly, we show in the Appendix that
almost surely and
is asymptotically equivalent to a sum of i.i.d.,
, and converges weakly to a mean zero Gaussian process, where ξi(t, v, z) is defined in the Appendix.
(t, v) converges weakly to a mean zero Gaussian process in (t, v). Similarly, we show in the Appendix that
almost surely and
is asymptotically equivalent to a sum of i.i.d.,
, and converges weakly to a mean zero Gaussian process, where ξi(t, v, z) is defined in the Appendix.
To construct point-wise and simultaneous confidence intervals for PPVz(t, v), we follow a resampling procedure that was considered in Park and Wei (2003), Cai et al. (2005) and Zheng et al. (2008). Specifically, to approximate the distributions of 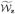 (t, v) and
(t, v) and 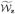 (t, v), we first generate independent standard normal random variates {
, i = 1, … n}, for j = 1, …, J. Let
when approximating
(t, v), we first generate independent standard normal random variates {
, i = 1, … n}, for j = 1, …, J. Let
when approximating 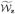 (t, v), and
when approximating
(t, v), and
when approximating 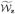 (t, v), where ζ̂i(t, v, z) and ξ̂i(t, v, z) are the respective empirical counterparts of ζi(t, v, z) and ξi(t, v, z). Then for any t, v and z, one can estimate the corresponding variance with
. A 100(1 − α)% confidence interval for PPVz(t, v), for example, based on
, can be constructed as
(t, v), where ζ̂i(t, v, z) and ξ̂i(t, v, z) are the respective empirical counterparts of ζi(t, v, z) and ξi(t, v, z). Then for any t, v and z, one can estimate the corresponding variance with
. A 100(1 − α)% confidence interval for PPVz(t, v), for example, based on
, can be constructed as
where for a pointwise confidence interval, dα is the 100(1 − α/2)th percentile of the standard normal distribution. To construct simultaneous confidence intervals for PPVz(t, v) for any given t and z and v ∈ {va, vb}, we find dα from the J samples such that
5. Simulation
We conduct numerical studies to assess the performance of the estimators under several scenarios. We first consider their finite sample performance using a moderate sample size of n = 500 and then a larger sample of n = 2000. We consider the case when the hazard of failure depends on the marker Y and a single covariate Z through the proportional hazards model of the form: . We generate the censoring time from a uniform distribution with mean 10. This yields a censoring rate of 25% approximately. The covariate Z is a binary random variable from a Bernoulli distribution with probability equal to 0.5. The marker Y is generated from a conditional normal distribution with mean 0.5Z and variance 1. We estimate PPV values for Z = 0, 1 at t = 7 and v = 0.1, 0.3, 0.5, 0.7, 0.9. We evaluate the performance of PPVz(t, v) estimators: using the Cox regression model and using the smoothed Cox regression model. The smoothing bandwidth for is taken to be h = n−1/3c, with c equal to the standard deviation of Y. FY|z is evaluated using the conditional empirical distribution. In addition, since Z is binary, it is possible in this case to estimate the covariate-specific PPV curves by calculating the PPV curve at each level of Z. We therefore are also able to obtain nonparametric PPV curve estimators based on the Zheng et al. (2008) using subsets with given levels of Z. Consequently, we also compare the performance of the non-parametric estimator and the proposed semi-parametric estimator obtained by the regression modeling framework. Results are presented in Table 1. All estimators show negligible bias, and the analytic standard errors track the empirical standard deviations well. The coverage probabilities of the pointwise confidence intervals are close to the nominal 95% level with the exception of when the sample size is small and v is close to 1 for . Improved performance is observed for a larger sample size. As expected, achieves smaller bias and better efficiency than , however is still more efficient than the nonparametric estimator . The phenomenon is more pronounced at larger values of v. Similar results are observed with different censoring rates (data not shown).
Table 1.
Simulation Results: Estimates (Est.), Standard Errors (SE), Means of the Standard Error Estimators ( ), and the 95% Coverage Probabilities (95% cov) under Cox Regression Models
| z = 0 | z = 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| v = 0.1 | v = 0.3 | v = 0.5 | v = 0.7 | v = 0.9 | v = 0.1 | v = 0.3 | v = 0.5 | v = 0.7 | v = 0.9 | ||
| PPVz (t, v) | 0.35 | 0.40 | 0.46 | 0.54 | 0.69 | 0.57 | 0.64 | 0.71 | 0.80 | 0.91 | |
| n = 500 | |||||||||||
|
| |||||||||||
| Est. | 0.35 | 0.40 | 0.46 | 0.54 | 0.68 | 0.57 | 0.64 | 0.71 | 0.79 | 0.90 | |
| SE | 0.03 | 0.03 | 0.04 | 0.04 | 0.05 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | |
| 0.03 | 0.03 | 0.04 | 0.04 | 0.05 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | ||
| 95% cov | 0.95 | 0.95 | 0.95 | 0.94 | 0.93 | 0.95 | 0.95 | 0.94 | 0.94 | 0.94 | |
|
| |||||||||||
| Est. | 0.35 | 0.40 | 0.46 | 0.53 | 0.66 | 0.56 | 0.63 | 0.70 | 0.77 | 0.87 | |
| SE | 0.03 | 0.03 | 0.04 | 0.05 | 0.06 | 0.03 | 0.03 | 0.04 | 0.04 | 0.05 | |
| 0.03 | 0.03 | 0.04 | 0.05 | 0.06 | 0.03 | 0.03 | 0.04 | 0.04 | 0.05 | ||
| 95% cov | 0.94 | 0.94 | 0.94 | 0.93 | 0.93 | 0.94 | 0.93 | 0.93 | 0.92 | 0.92 | |
|
| |||||||||||
| Est. | 0.35 | 0.41 | 0.46 | 0.54 | 0.67 | 0.57 | 0.64 | 0.71 | 0.79 | 0.88 | |
| SE | 0.03 | 0.04 | 0.05 | 0.06 | 0.10 | 0.03 | 0.04 | 0.04 | 0.05 | 0.06 | |
| n = 2000 | |||||||||||
|
| |||||||||||
| Est. | 0.35 | 0.40 | 0.46 | 0.54 | 0.69 | 0.57 | 0.64 | 0.71 | 0.80 | 0.91 | |
| SE | 0.01 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | |
| 0.01 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | ||
| 95% cov | 0.96 | 0.96 | 0.95 | 0.95 | 0.96 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | |
|
| |||||||||||
| Est. | 0.35 | 0.40 | 0.46 | 0.54 | 0.68 | 0.57 | 0.64 | 0.71 | 0.79 | 0.89 | |
| SE | 0.01 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | |
| 0.01 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | ||
| 95% cov | 0.95 | 0.95 | 0.95 | 0.94 | 0.95 | 0.94 | 0.94 | 0.93 | 0.94 | 0.93 | |
|
| |||||||||||
| Est | 0.35 | 0.40 | 0.46 | 0.54 | 0.68 | 0.57 | 0.64 | 0.71 | 0.79 | 0.90 | |
| SE | 0.02 | 0.02 | 0.02 | 0.03 | 0.05 | 0.02 | 0.02 | 0.02 | 0.03 | 0.03 | |
We also investigate the robustness of the two estimators under two scenarios. We first consider a model of the form λ(t) = (2Y +1.5Y2 +3Z}/10, but fit a mis-specified Cox model ignoring the quadratic term for . In the second scenario, for the ith subject Yi is from a mixture of the log-normal distribution: log(Yi) = 0.5Zi+ρi, where ρ and Z are random variates from standard normal and Bernoulli with probability equal to 0.5, respectively. In addition, T is simulated with a hazard function of the form λ(t) = exp{log(t + 1)Y + 1.5Z}. Since the effect of Y on T varies as a function of t, a Cox regression model assuming proportional hazards for Y would likely fail. As shown in Table 2, we found that in both cases, based on misspecified Cox regression models yield substantial biases and much greater mean squared errors (MSEs), compared with . Therefore although appears to be the method of choice when the proportional hazards assumption is valid, there is still an advantage for considering for its robustness. This aspect is important especially when formal checking of survival regression models has not become a routine in practice.
Table 2.
Estimates (Est.), Standard Errors (SE) and Mean Squared Errors (MSE) under Two Simulated Regression Models
| z = 0 | z = 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| v = 0.1 | v = 0.3 | v = 0.5 | v = 0.7 | v = 0.9 | v = 0.1 | v = 0.3 | v = 0.5 | v = 0.7 | v = 0.9 | ||
| Model I | |||||||||||
| PPVz(t, v) | 0.39 | 0.44 | 0.52 | 0.66 | 0.92 | 0.69 | 0.74 | 0.82 | 0.92 | 0.99 | |
|
| |||||||||||
| Est. | 0.41 | 0.47 | 0.53 | 0.61 | 0.74 | 0.73 | 0.79 | 0.85 | 0.91 | 0.97 | |
| SE | 0.03 | 0.04 | 0.04 | 0.05 | 0.06 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 | |
| MSE×103 | 1.74 | 2.09 | 1.68 | 5.09 | 35.45 | 2.46 | 3.30 | 1.61 | 0.81 | 1.23 | |
|
| |||||||||||
| Est. | 0.39 | 0.44 | 0.52 | 0.64 | 0.88 | 0.68 | 0.73 | 0.81 | 0.91 | 0.99 | |
| SE | 0.03 | 0.03 | 0.04 | 0.05 | 0.06 | 0.03 | 0.03 | 0.03 | 0.03 | 0.01 | |
| MSE×103 | 0.81 | 1.12 | 1.65 | 2.83 | 4.89 | 0.87 | 1.05 | 1.18 | 1.01 | 0.12 | |
| Model II | |||||||||||
| PPVz(t, v) | 0.61 | 0.64 | 0.69 | 0.77 | 0.93 | 0.80 | 0.84 | 0.89 | 0.95 | 1.00 | |
|
| |||||||||||
| Est. | 0.61 | 0.62 | 0.64 | 0.68 | 0.76 | 0.80 | 0.81 | 0.84 | 0.88 | 0.95 | |
| SE | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | |
| MSE×103 | 0.25 | 0.64 | 2.53 | 8.80 | 28.22 | 0.22 | 1.01 | 3.12 | 6.29 | 3.08 | |
|
| |||||||||||
| Est. | 0.61 | 0.64 | 0.68 | 0.76 | 0.91 | 0.80 | 0.84 | 0.89 | 0.95 | 0.99 | |
| SE | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |
| MSE×103 | 0.24 | 0.29 | 0.38 | 0.52 | 0.77 | 0.19 | 0.21 | 0.22 | 0.21 | 0.10 | |
6. Example: PSA for Prostate Cancer Prognosis
Prostate cancer is a major health problem in aging men. The disease is unique in that it manifests in two forms with no clear distinction: an aggressive form, and an indolent form, which develops slowly over many years and does not pose a threat to the patient’s life. Many patients with indolent prostate cancer are subjected unnecessarily to invasive procedures that may lead to important side effects and significant morbidity. One of the goals of our prostate cancer research is to identify novel markers, used in combination with other existing markers and clinical factors, for improved predictions of prostate cancer prognosis. Since PSA has been used as a prognostic marker in the past, it is a crucial first step to evaluate the predictive performance of PSA-based criteria for treatment decisions in our population. Specifically, our cohort consists of 752 incident PC cases who were diagnosed at ages 40–64 years in 1993–1996 and who are followed for disease progression and survival. We include 671 patients with PSA measures prior to prostate cancer primary treatment in our analysis. By the time the data are analyzed, 124 patients are deceased and the median followup time among patients alive is 12 years. Pre-treatment PSA (logarithm transformed throughout this section) is a strong predictor for all-cause mortality, with an unadjusted hazard ratio of 1.58 [95% CI: 1.39, 1.8].
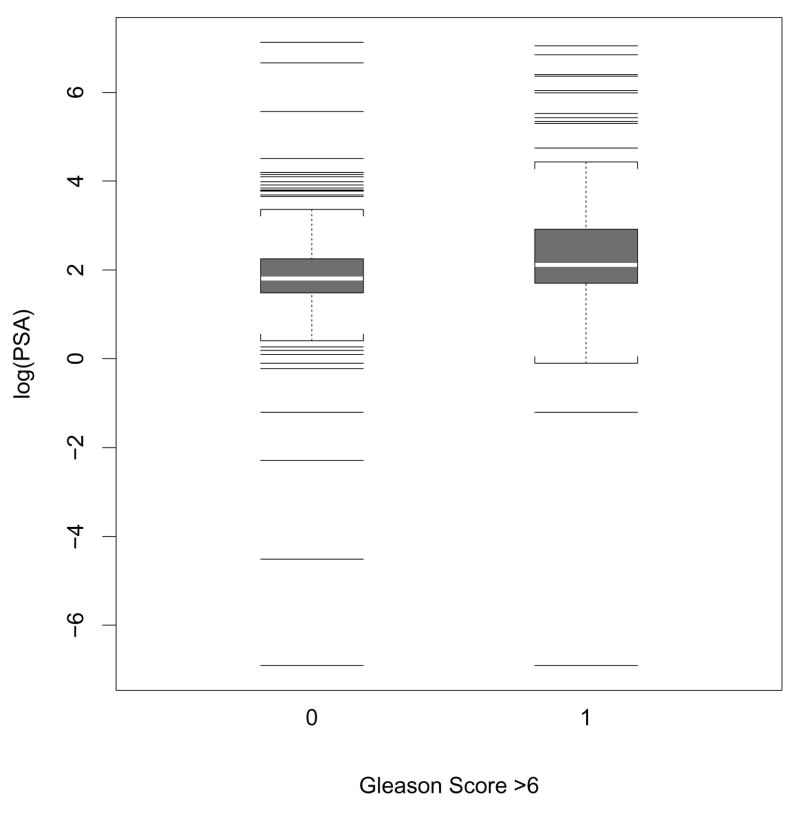
One question of interest is whether the predictive performance of PSA is affected by other characteristics such as tumor grade. For example, do PPV curves for PSA differ between groups of patients with low grade (i.e., Gleason score ≤ 6) and moderate to high grade (i.e., Gleason score ≥ 7)? Figure 1 shows the distributions of log-transformed pre-treatment PSA for both the low grade and moderate to high grade patients. Although the mean of PSA appears to be slightly higher for the high grade group, the two distributions are essentially overlapped. This implies that a positive test based on PSA would likely include both low and high grade patients. We use covariate-specific PPV curves to address this question, considering both estimators that are based on the ordinary Cox proportional hazards model or the smoothed Cox regression model. To calculate we fit a proportional hazards model of the form λ(t|Y, Z) = λ0(t)exp{αlog(PSA) + βI(grade=high)}. For we fit a smoothed hazards model of the form λ(t|Y, Z) = λ0{t, log(PSA)}exp{βI(grade=high)} with the smoothing bandwidth h = cn−1/3, using the standard deviation of the logarithm of PSA for c. FY|z is estimated empirically. Similar estimates for the effect of Gleason score are observed: exp(β̂) = 1.90[95% CI: 1.33, 2.67], and 1.77 [95% CI: 1.22, 2.57], respectively from the two models. This indicates that for patients who test positive at a given threshold based on their PSA values, the averaged risk of death is higher if they have moderate or high grade PC than if they have low grade PC. There does not appear to be significant interaction between PSA and cancer grade from either of the models: the corresponding estimated hazard ratios are 1.13[95% CI: 0.84, 1.43] and 1.07[95% CI: 0.82, 1.40], respectively.
Figure 1.
Box plot shows the distributions of log-transformed PSA values from low grade (Gleason score ≤ 6), and moderate to high grade (Gleason score > 6) prostate cancer patients.
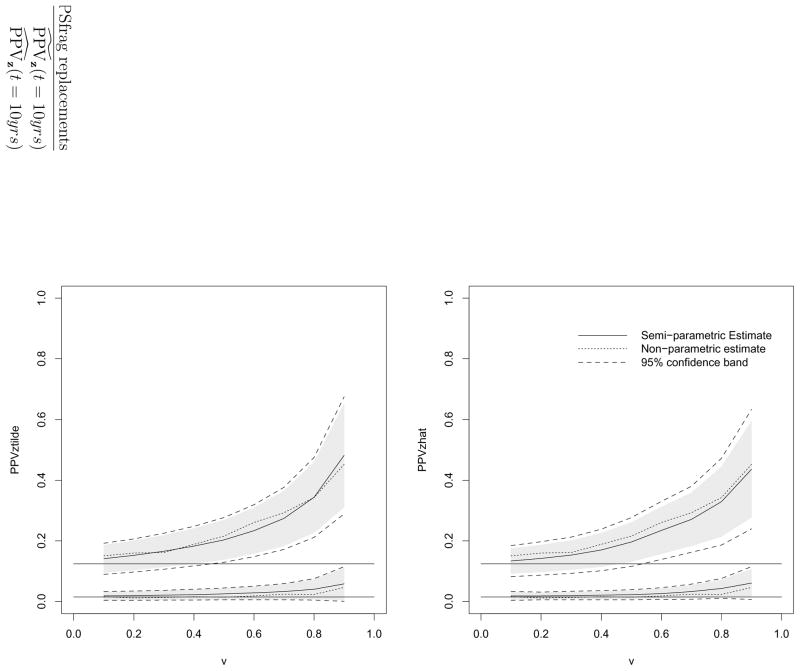
The estimated PPV and NPV for different groups at t=10 years and their estimated 95% confidence intervals and simultaneous confidence bands are shown in Tables 3 and 4, respectively. For comparison we also calculated the corresponding PPV and NPV using the nonparametric estimators introduced in Zheng et al. (2008), using the data from each covariate group separately. The estimator is the most flexible as it does not involve any parametric assumptions about the failure time and either PSA or Gleason score. The estimates from the two semiparametric approaches agree well with those from the nonparametric procedure, suggesting that the assumptions used in the semiparametric models work well in this sample. The efficiencies of the two semiparametric models are comparable; as expected, the nonparametric estimators are relatively less efficient. Since NPVs for both groups do not appear to vary much over the entire range of PSA values we focus presentation below only on PPV. The covariate-specific PPV curves for v ranging from 0.1 to 0.9 from the proposed procedures are displayed in Figure 7. It appears that for low grade PC patients the averaged 10-year PC mortality risk stays at a very low level across a wide range of PSA values used as positivity criteria for defining a positive test. The averaged risk for 10-year mortality among these whose PSA values are at the top 10% of this subpopulation is only about 6% ( , 95% CI: [0.01, 0.12]). In contrast, for the subpopulation of patients with moderate to high grade cancer, the PPV curve increases relatively more steeply, an indication that PSA is quite informative at identifying patients with elevated risk of death by 10 years in this subpopulation. For example, at v = 0.1, the corresponding is 0.15 (95% CI: [0.09, 0.18]), whereas equals 0.44 (95% CI: [0.28, 0.60]) at v = 0.9. In other words, PSA is a more useful marker in helping patients with moderate or high grade tumors to make treatment decisions. Such information may be helpful for urologists to determine how many patients are eligible for more aggressive treatment based on both PSA and Gleason scores. For example, if patients with a 10-year mortality risk of at least 30% are eligible for an aggressive therapy, we may opt to only administer the treatment to those with high grade cancer and PSA values in the top 30% of the subpopulation. In contrast, if only the crude PPV curve is considered (as illustrated in Figure 1), we would use the same PSA threshold for these two groups. Nevertheless, those eligible patients with low Gleason scores would in fact have a very low risk of death within 10 years and therefore would not really benefit from the treatment. We conclude that covariate-specific PPV curves in this case indeed lead to more informed treatment decisions.
Table 3.
Estimates (95% confidence intervals) and [95% confidence bands] of PPVz(t, v) at t = 10 years with various sample percentile (v) in the PC SPORE study.
| v = 0.1 | v = 0.3 | v = 0.5 | v = 0.7 | v = 0.9 | ||
|---|---|---|---|---|---|---|
| Low grade PC: Gleason score ≤ 6 | ||||||
| ĉz(v)* | 2.7 | 4.7 | 6.1 | 8.5 | 16.4 | |
|
|
0.02(0.00, 0.03) [0.00, 0.03] | 0.02(0.01, 0.04) [0.00, 0.04] | 0.03(0.01, 0.04) [0.01, 0.04] | 0.03(0.01, 0.06) [0.01, 0.06] | 0.06(0.00, 0.11) [0.00, 0.12] | |
|
|
0.02(0.01, 0.03) [0.00, 0.03] | 0.02(0.01, 0.03) [0.01, 0.03] | 0.02(0.01, 0.04) [0.01, 0.04] | 0.03(0.01, 0.05) [0.01, 0.06] | 0.06(0.02, 0.11) [0.01, 0.12] | |
|
|
0.02(0.01, 0.03) [0.00, 0.04] | 0.01(0.00, 0.03) [0.00, 0.04] | 0.02(0.00, 0.04) [0.00, 0.05] | 0.02(0.01, 0.06) [0.00, 0.08] | 0.05(0.01, 0.14) [0.00, 0.17] | |
| Moderate to high grade PC: Gleason score > 6 | ||||||
| ĉz(v) | 4.2 | 5.9 | 8.3 | 15.8 | 51.1 | |
|
|
0.14(0.10, 0.19) [0.09, 0.19] | 0.17(0.11, 0.22) [0.11, 0.23] | 0.20(0.14, 0.27) [0.13, 0.28] | 0.28(0.18, 0.36) [0.17, 0.38] | 0.48(0.31, 0.65) [0.29, 0.68] | |
|
|
0.13(0.09, 0.18) [0.08, 0.18] | 0.15(0.10, 0.20) [0.09, 0.21] | 0.20(0.13, 0.26) [0.12, 0.28] | 0.27(0.18, 0.36) [0.16, 0.38] | 0.44(0.28, 0.60) [0.24, 0.63] | |
|
|
0.15(0.11, 0.20) [0.10, 0.21] | 0.16(0.11, 0.22) [0.10, 0.24] | 0.22(0.15, 0.30) [0.13, 0.32] | 0.29(0.19, 0.40) [0.16, 0.44] | 0.45(0.26, 0.62) [0.21, 0.66] | |
: PSA threshold values.
Table 4.
Estimates (95% confidence intervals) and [95% confidence bands] of NPVz(t, v) at t = 10 years with various sample percentile (v) in the PC SPORE study.
| v = 0.1 | v = 0.3 | v = 0.5 | v = 0.7 | v = 0.9 | ||
|---|---|---|---|---|---|---|
| Low grade PC: Gleason score ≤ 6 | ||||||
| ĉz(v)* | 2.7 | 4.7 | 6.1 | 8.5 | 16.4 | |
|
|
1.00 (0.00, 1.00) [0.94, 1.00] | 0.99 (0.94, 1.00) [0.93, 1.00] | 0.99 (0.96, 1.00) [0.97, 1.00] | 0.99 (0.97, 1.00) [0.97, 1.00] | 0.99 (0.97, 1.00) [0.97, 1.00] | |
|
|
0.99 (0.99,1.00) [0.99, 1.00] | 0.99 (0.98,1.00) [0.98, 1.00] | 0.99 (0.98,1.00) [0.98, 1.00] | 0.99 (0.98,1.00) [0.98, 1.00] | 0.99(0.98, 1.00) [0.98,1.00] | |
|
|
0.98 (0.92, 1.00) [0.90, 1.00] | 0.98 (0.96, 1.00) [0.96, 1.00] | 0.98 (0.97, 0.99) [0.96, 1.00] | 0.98 (0.97, 0.99) [0.97, 0.99] | 0.98 (0.97, 0.99) [0.97, 0.99] | |
| Moderate to high grade PC: Gleason score ≥ 7 | ||||||
| ĉz(v) | 4.2 | 5.9 | 8.3 | 15.8 | 51.1 | |
|
|
0.96 (0.63, 1.00) [0.59, 1.00] | 0.94 (0.80, 0.99) [0.78, 1.00] | 0.94 (0.85, 0.99) [0.84, 1.00] | 0.94 (0.87, 0.97) [0.87, 1.00] | 0.90(0.86, 0.94) [0.85, 0.96] | |
|
|
0.96(0.94,0.99) [0.94,0.99] | 0.95(0.92,0.98) [0.92,0.98] | 0.94 (0.91, 0.97) [0.91, 0.97] | 0.93 (0.90, 0.96) [0.89, 0.96] | 0.90(0.87, 0.94) [0.86, 0.95] | |
|
|
1.00 (0.79, 1.00) [0.67, 1.00] | 0.94 (0.83, 0.98) [0.78, 0.99] | 0.94 (0.89, 0.98) [0.87, 0.98] | 0.93 (0.88, 0.96) [0.87, 0.97] | 0.90 (0.85, 0.93) [0.83, 0.94] | |
: PSA threshold values.
7. Discussion
When applying novel biomarkers into routine standard care, it is important to consider risk threshold to ensure that medical decisions are satisfying at the individual patient level. It is also important to identify factors that influence the performance of a biomarker in order to determine the optimal or suboptimal conditions or populations for test performance. By understanding the effects of the biomarker on different subgroups, intervention can be targeted for those individuals most likely to benefit, at a reasonable expense with nominal risk of complications. The covariate-specific time-dependent PPV curve provides a novel way to carry out this task.
We develop a regression model framework to accommodate the covariate effect when quantifying time-dependent predictive accuracies. Existing methods often fail to account for the fact that risk for disease occurrence and progression is likely to change over time. Such a limitation is critical given that model checking for failure time data has not become a routine practice. By adopting a smoothed survival time regression technique, we provide estimating procedures that will be broadly applicable to many biomarker study settings. Our procedures are simple yet meaningful for clinical practice, amenable to the complex covariate structure, and flexible in its assumption about the underlying model and censoring mechanism. Other flexible modeling approaches can also be considered. One natural choice is the Cox model with time-varying coefficients, which offers greater robustness than the proportional hazards model while retaining the loglinear relationship between the baseline hazard and the marker. This model can be applied in a parametric version, going back to Cox (1972), or in a nonparametric version, as described by Tian et al. (2005) and other authors. General model checking procedures can be helpful for selecting a parsimonious model.
The proposed covariate-specific PPV curve is developed for the setting where a test is administered and subjects are classified into being tested positive and negative based on . Therefore the assumption of a monotonic function for P(T < t|Y = y, Z = z) is imposed to reflect the rationale for classifying subjects as short term or long term survivors based on the binary classification rule. In practice, to ensure the monotonicity of the estimated risk function when the underlying true risk is expected to be increasing, one may construct such a monotone estimate by considering various isotonic regression techniques (Friedman and Tibshirani (1984); Bloch and Silverman (1997); Hall and Huang (2001)). However inference procedure may need to be modified to reflect the constrained inference. A simpler remedy is to replace Λ̂y(t) with , which does not alter the asymptotics of the proposed estimates (Lin et al., 1999; Peng and Huang, 2007).
Research on time-dependent PPV curves can be extended in a number of directions. First, once factors that may have a substantial impact on the accuracy of a clinical prediction are identified, a natural next step might be seeking a new algorithm for incorporating other factors by combining multiple factors into a new test. In our PC application it is of great interest to decide whether new markers (e.g., SNPs) provide significant improvement in predictive accuracy when combined with standard variables (pre-operative PSA, Gleason score, clinical stage) for predicting PC mortality. Statistical procedures for deriving and evaluating a new combinatory rule for improved predictive accuracy for this setting are yet to be developed. Second, the analysis of time-to-event data is often complicated by the presence of competing risk. In the prostate cancer example, invasive procedures are only necessary for individuals with aggressive forms of the disease (i.e., those who are at risk of dying from rather than dying with prostate cancer). Therefore the most important outcome when considering PC-related treatment is PC-specific death. Deaths due to other causes are competing risk events. Characterizing the predictive accuracy of a marker on different causes of failures, might allow more rational or cost-effective use of specific medical or surgical treatment strategies. Statistical methods that accommodate competing risk events are subjects of current development.
Supplementary Material
Figure 2.
Estimated PPV curves (left panel: ; right panel: ) and 95% confidence intervals and bands for v ∈ (0.10, 0.90) and at t = 10 years after diagnosis in PC study. Solid lines: estimates of PPVz(t, v); dotted lines: nonparametric estimators of crude PPV(t, v). Dashed lines: 95% simultaneous confidence bands. Shaded areas: 95% confidence intervals. The horizontal lines correspond to the marginal event time probabilities P(T < 10 years|low grade) and P(T < 10 years|moderate to high grade).
Acknowledgments
The authors thank Dr. David Zucker for several suggestions that have greatly improved the article. This research was supported by grant U01-CA86368, P01-CA053996 and R01-GM079330 awarded by the National Institutes of Health.
Appendix
Throughout we assume that the joint density of T, C and Y is twice continuously differentiable and W = (Y, ZT)T belongs to a compact set ΩW. We consider v ∈ [pl, pu] ⊂ (0, 1) and t ∈ [τ1, τ2], where τ1 and τ2 are pre-determined constants such that P (X < τ1) > 0 and P(X > τ2) > 0. In addition, we assume that , is bounded away from 0 for y ∈ [cz(pl), cz(pu)]. For F̂Y|z(y), without loss of generality, we assume that
| (A.1) |
where 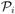 (y, z) =
(y, z) =  (y, z, Xi, Δi, Yi, Zi) for some function
(y, z, Xi, Δi, Yi, Zi) for some function  that is bounded for (y, z) ∈ ΩW with total variation bounded by a constant. Under a semi-parametric location model,
, which satisfies (A.1). The consistency and weak convergence of
can be established through standard empirical processes theory. The derivations can be found in Web Appendix B. We next outline derivations for the asymptotic properties of
and also refer to the Web appendix C for detailed justifications.
that is bounded for (y, z) ∈ ΩW with total variation bounded by a constant. Under a semi-parametric location model,
, which satisfies (A.1). The consistency and weak convergence of
can be established through standard empirical processes theory. The derivations can be found in Web Appendix B. We next outline derivations for the asymptotic properties of
and also refer to the Web appendix C for detailed justifications.
We require the same conditions as specified in Dabrowska (1997) and the bandwidth h is chosen such that nh2 → ∞ and nh4 → 0 as n → ∞. It follows from Dabrowska (1997) that supt,y|Λ̂y,z(t) − Λy,z(t)| = op(n−1/4) and , where , ℐ(β) is the limit of , and is the limit of .
The uniform convergence of Λ̂y,z(t), together with the uniform consistency of F̂Y|z(y) and cz(v), and Lemma A.3 of Bilias et al (1997), implies the uniform consistency of . Now, to derive the large sample distribution for , we write
where and
To approximate the distribution of 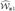 (t, v), we again invoke Lemma A.3 of Bilias, Gu and Ying (1997) and use the fact that supt,y|Λ̂y,z(t) − Λy,z(t)| + supy|F̂Y|z(y) − FY|z(y)| + supv|ĉz(v) − cz(v)| = op(n−1/4) to obtain
(t, v), we again invoke Lemma A.3 of Bilias, Gu and Ying (1997) and use the fact that supt,y|Λ̂y,z(t) − Λy,z(t)| + supy|F̂Y|z(y) − FY|z(y)| + supv|ĉz(v) − cz(v)| = op(n−1/4) to obtain
Now, it follows from the asymptotic expansions for Λ̂y,z(t) given in Dabrowska (1997) that
where Ay(s) = E{Ni(s)|Yi = y}dP(Yi ≤ y)/dy is the limit of N̂y(s), π̂y(u) = π̂y (u, β0), πy(u) = πy(u, β0), ℬz(t, y) is evaluated at β = β0, and . It follows that
Now, by a change variable and assuming that nh4 = op(1),
Therefore, , where
On the other hand, the process 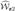 (t, v) can be approximated by
as for
(t, v) can be approximated by
as for 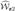 (t, v). Hence,
, where ξi(t, v, z) = ξi1(t, v, z) + ζi2(t, v, z). This, together with a functional central limit theorem, implies that
(t, v). Hence,
, where ξi(t, v, z) = ξi1(t, v, z) + ζi2(t, v, z). This, together with a functional central limit theorem, implies that 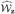 (t, v) converges weakly to a zero-mean Gaussian process.
(t, v) converges weakly to a zero-mean Gaussian process.
Footnotes
Web Appendices referenced in Sections 4 and Appendix are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.
References
- Bloch DA, Silverman BW. Monotone discriminant functions and their applications in rheumatology. Journal of the American Statistical Association. 1997;92:144–153. [Google Scholar]
- Cai T, Pepe MS. Semiparametric receiver operating characteristic analysis to evaluate biomarkers for disease. Journal of the American Statistical Association. 2002;97:1099–1107. [Google Scholar]
- Cai T, Tian L, Wei L. Semiparametric Box-Cox power transformation models for censored survival observations. Biometrika. 2005;92:619–32. [Google Scholar]
- Cox DR. Regression models and life-tables (with discussion) Journal of the Royal Statistical Society, Series B, Methodological. 1972;34:187–220. [Google Scholar]
- Dabrowska DM. Smoothed Cox regression. The Annals of Statistics. 1997;25:1510–1540. [Google Scholar]
- Etzioni R, Pepe M, Longton G, Hu C, Goodman G. Incorporating the time dimension in receiver operating characteristic curves: A case study of prostate cancer. Medical Decision Making. 1999;19:242–251. doi: 10.1177/0272989X9901900303. [DOI] [PubMed] [Google Scholar]
- Friedman J, Tibshirani R. The monotone smoothing of scatterplots. Technometrics. 1984;26:243–250. [Google Scholar]
- Hall P, Huang LS. Nonparametric kernel regression subject to monotonicity constraints. The Annals of Statistics. 2001;29:624–647. [Google Scholar]
- Heagerty P, Zheng Y. Survival model accuracy and roc curves. Biometrics. 2005;61:92–105. doi: 10.1111/j.0006-341X.2005.030814.x. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ, Lumley T, Pepe MS. Time-dependent ROC curves for censored survival data and a diagnostic marker. Biometrics. 2000;56:337–344. doi: 10.1111/j.0006-341x.2000.00337.x. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ, Pepe MS. Semiparametric estimation of regression quantiles with application to standardizing weight for height and age in US children. Applied Statistics. 1999;48:533–551. [Google Scholar]
- Lin DY, Sun W, Ying Z. Nonparametric estimation of the gap time distributions for serial events with censored data. Biometrika. 1999;86:59–70. [Google Scholar]
- Moskowitz C, Pepe M. Quantifying and comparing the accuracy of binary biomarkers when predicting a failure time outcome. Statistics in Medicine. 2004a;23:1555–1570. doi: 10.1002/sim.1747. [DOI] [PubMed] [Google Scholar]
- Moskowitz C, Pepe M. Quantifying and comparing the predictive accuracy of continuous prognostic factors for binary outcomes. Biostatistics. 2004b;5:113–127. doi: 10.1093/biostatistics/5.1.113. [DOI] [PubMed] [Google Scholar]
- Park Y, Wei LJ. Estimating subject-specific survival functions under the accelerated failure time model. Biometrika. 2003;90:717–23. [Google Scholar]
- Peng L, Huang Y. Survival analysis with temporal covariate effects. Biometrika. 2007;94:719–733. [Google Scholar]
- Pepe M, Zheng Y, Jin Y, Huang Y, Parikh C, Levy W. Evaluating the ROC performance of markers for future events. Lifetime Data Analysis. 2008;14:86–113. doi: 10.1007/s10985-007-9073-x. [DOI] [PubMed] [Google Scholar]
- Pollard D. Empirical processes: theory and applications. Institute of Mathematical Statistics; 1990. [Google Scholar]
- Tian L, Zucker D, Wei L. On the Cox model with time-varying regression coefficients. Journal of the American Statistical Association. 2005;100:172–183. [Google Scholar]
- Zheng Y, Cai T, Pepe M, Levy W. Time-dependent predictive values of prognostic biomarkers with failure time outcome. Journal of the American Statistical Association. 2008;103:362–368. doi: 10.1198/016214507000001481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Heagerty P. Partly conditional survival model for longitudinal data. Biometrics. 2005;61:379–391. doi: 10.1111/j.1541-0420.2005.00323.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.