Diffusion of the Reaction Boundary of Rapidly Interacting Macromolecules in Sedimentation Velocity

Abstract

Sedimentation velocity analytical ultracentrifugation combines relatively high hydrodynamic resolution of macromolecular species with the ability to study macromolecular interactions, which has great potential for studying dynamically assembled multiprotein complexes. Complicated sedimentation boundary shapes appear in multicomponent mixtures when the timescale of the chemical reaction is short relative to the timescale of sedimentation. Although the Lamm partial differential equation rigorously predicts the evolution of concentration profiles for given reaction schemes and parameter sets, this approach is often not directly applicable to data analysis due to experimental and sample imperfections, and/or due to unknown reaction pathways. Recently, we have introduced the effective particle theory, which explains quantitatively and in a simple physical picture the sedimentation boundary patterns arising in the sedimentation of rapidly interacting systems. However, it does not address the diffusional spread of the reaction boundary from the cosedimentation of interacting macromolecules, which also has been of long-standing interest in the theory of sedimentation velocity analytical ultracentrifugation. Here, effective particle theory is exploited to approximate the concentration gradients during the sedimentation process, and to predict the overall, gradient-average diffusion coefficient of the reaction boundary. The analysis of the heterogeneity of the sedimentation and diffusion coefficients across the reaction boundary shows that both are relatively uniform. These results support the application of diffusion-deconvoluting sedimentation coefficient distributions c(s) to the analysis of rapidly interacting systems, and provide a framework for the quantitative interpretation of the diffusional broadening and the apparent molar mass values of the effective sedimenting particle in dynamically associating systems.

Introduction

In the last decade, sedimentation velocity analytical ultracentrifugation (SV) has reemerged as a powerful technique for the study of interacting macromolecules. It has unique potential for the detection of size, shape, composition, and thermodynamic equilibrium constants of complexes in slow or rapid chemical equilibrium with their free constituent species. In particular, SV is well suited to address the often most difficult problem of establishing the number and stoichiometry of multiple coexisting complexes, and to determine the reaction scheme. At the same time, the hydrodynamic and spectral resolution provides the virtue of SV being relatively robust against the presence of many kinds of impurities and aggregates. The technique has been reviewed, for example, in references (1–5).

SV has a long history spanning almost a century of theoretical and practical application to protein interactions. Driven by increased interest in the study of protein interactions, the last decade brought many significant advances, especially in the computational modeling of SV. The underlying partial differential equation (PDE) of SV, the Lamm equation, can now be solved sufficiently fast and precise so that it can be used for fitting by nonlinear regression of experimental raw data sets on ordinary laboratory computers. This brought the modern techniques of directly and globally fitting the equations for the sedimentation/diffusion/reaction PDE of certain reaction schemes to experimental data (6–9), as well as the determination of diffusion deconvoluted, high-resolution sedimentation coefficient distributions (10), size-and-shape distributions (11), and multisignal sedimentation coefficient distributions for multicomponent systems (12).

Despite this computational progress, many phenomena have remained less well understood on a biophysical level. As has been pointed out by Gilbert and Jenkins already 50 years ago, systems of interconverting species with instantaneous reactions on the timescale of sedimentation migrate very differently from populations of noninterconverting species (13), in ways perhaps unexpected and nonintuitive (14). Of course, any behavior is captured in the solutions to the partial differential equations of sedimentation, but this alone is insufficient for understanding the mechanisms of coupled transport. It also does not help us to understand rules for how the system parameters relate to each other when the system is exhibiting a certain phenomenology. However, such knowledge is important in the development of robust experimental designs and methodology for data analysis, and, in particular, to fully exploit the unique potential of SV in the study of multicomponent interactions.

To this end, we have recently introduced the effective particle theory (EPT) that explains, in a simple physical picture, the basic rules that govern the formation of sedimentation boundary patterns of multicomponent mixtures (i.e., the division of the sedimenting system into a slowly migrating single-component undisturbed boundary and a rapidly migrating reaction boundary containing a mixture of all species) (15). EPT highlights, for the first time, the existence of a phase transition in parameter space, where the singularity occurs that the entire reacting system sediments in a single boundary, the latter sedimenting with a velocity unequal to any of the species' velocities. When crossing this phase transition line, the constituent of the slow boundary switches. EPT also describes how the asymmetry of the individual free species' velocities translates into an asymmetry of this phase transition line in the parameter space of loading concentrations. EPT provides simple quantitative expressions for the amplitudes and velocities of all boundary components, as well as the phase transition. This facilitates data analysis approaches based on modeling the isotherms of boundary patterns as a function of loading concentration (15,16), and enables the extension of this approach to more complex interaction schemes. The experimental observables of SV across the parameter space of loading concentrations, as predicted by EPT, as well as the molecular mechanism of coupled reaction and sedimentation for given parameters, can be visualized in the effective particle explorer tool of the software SEDPHAT (a biophysical data analysis software for interacting systems (17)).

However, with its basis in considerations of mass balance of the reaction boundary, EPT is only concerned with the sedimentation coefficients and amplitudes of the sedimentation boundaries. It does not address the questions of the detailed boundary shape. In particular, the diffusive properties of the reaction boundaries constitutes an area that has, so far, remained comparatively poorly explored. Yet, it is of high practical interest, as deconvolution of diffusion affords highly increased hydrodynamic resolution. Again, the basic computational recipe provided by the sedimentation/diffusion/reaction PDE equations provides a rigorous predictive tool for the evolution of concentration gradients given a certain parameter set, but it does not satisfactorily explain the relationships between the observables throughout the parameter space of loading concentrations. In particular, the set of Lamm PDEs of reacting systems does not define the magnitude of the average diffusion coefficient of the reaction boundary, or the variation across the reaction boundary from this average value.

The constant bath approximation, originally developed by Krauss et al. (18) and later rediscovered by Urbanke et al. (19), predicts that reaction boundaries diffuse with a single, weight-average diffusion coefficient. This is consistent with the observation that c(s) distribution of noninteracting species (10) can model concentration profiles from reacting systems remarkably well (9). Even though qualitatively the results of the constant bath theory are very good, and the accuracy of the predicted sedimentation coefficients is excellent, the predictions for the diffusion coefficient are less successful (9). Further, the constant bath approximation cannot be applied well throughout the whole parameter space of loading concentrations (9) due to the neglect of cosedimentation of both free components in the reaction boundary.

This work explores a different approach to arrive at an approximate analytical expression for the diffusion properties of the reaction boundaries. It is physically motivated, and exploits the relationships arising in EPT to approximate the concentration gradients in the reaction boundary. We show that this compares well with best-fit diffusion coefficients to reaction boundaries from exact solutions of the sedimentation/diffusion/reaction PDE. Finally, the consequences for diffusional deconvolution with sedimentation coefficient distribution c(s) and size-and-shape distributions are discussed.

Theory

Let us consider a bimolecular reaction of A + B ↔ AB in instantaneous equilibrium characterized by the mass action law c_AB = Kc_Ac_B with association equilibrium constant K (or equilibrium dissociation constant K_D = 1/K). Let us choose the nomenclature of A and B such that A is the slower sedimenting species. The initial loading concentrations of A and B are c_Atot,0 and c_Btot,0, respectively, and are uniform throughout the sample cell.

Lamm equations

The propagation of the system after start of centrifugation at the angular velocity ω is given by the Lamm PDE, which can be written generally as

$$\frac{{\partial }_{c_k}}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}\left[c_k{s}_k{w}^2{r}^2-D_k\frac{{\partial }_{c_k}}{\partial r}r\right]=q_k,$$ (1)

with k denoting the species A, B, and AB, s_k and D_k the species' sedimentation and diffusion coefficients, and c_k(r,t) the local radial and time-dependent concentration of the species (14). The value q_k denote the reaction fluxes that have the constraint from mass conservation q_A = q_B = −q_AB. The absence of hydrodynamic nonideality (i.e., a concentration-dependence of s_k and D_k) is assumed in the following. Equation 1 can be solved numerically with the software SEDPHAT for given parameter sets, but this does not further illuminate the physical processes of sedimentation.

For rapid self-associating systems, to simplify the Lamm PDE and to eliminate the reaction fluxes, it is customary to condense all species' equations into a single PDE in terms of total local concentration and concentration-dependent, locally weight-averaged sedimentation coefficient and gradient-average diffusion coefficient, respectively. It is possible to express the Lamm PDE of heterogeneous associations similarly in terms of constituent concentrations c_Atot(r,t) = c_A(r,t) + c_AB(r,t) and c_Btot(r,t) = c_B(r,t) + c_AB(r,t),

$$\begin{array}{l}\frac{\partial c_{\text{Atot}}}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}\left[s_{\text{Atot}}\left(c_{\text{A}},c_{\text{B}}\right)c_{\text{Atot}}{\omega }^2{r}^2-D_{\text{Atot}}\left(c_{\text{A}},c_{\text{B}}\right)\frac{\partial c_{\text{Atot}}}{\partial r}r\right]=0\\ \frac{\partial c_{\text{Btot}}}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}\left[s_{\text{Btot}}\left(c_{\text{A}},c_{\text{B}}\right)c_{\text{Btot}}{\omega }^2{r}^2-D_{\text{Btot}}\left(c_{\text{A}},c_{\text{B}}\right)\frac{\partial c_{\text{Btot}}}{\partial r}r\right]=0\end{array}$$ (2)

with the local weight-average sedimentation and gradient average diffusion coefficients

$$\begin{array}{l}{s}_{\text{Atot}}\left(c_{\text{A}},c_{\text{B}}\right)=\frac{s_{\text{A}}+c_{\text{B}}K{s}_{\text{AB}}}{1+c_{\text{B}}K},\\ D_{\text{Atot}}\left(c_{\text{A}},c_{\text{B}}\right)=\frac{D_{\text{A}}+D_{\text{AB}}K\left[c_{\text{B}}+c_{\text{A}}\frac{\partial c_{\text{B}}}{\partial r}{\left(\frac{\partial c_{\text{A}}}{\partial r}\right)}^{-1}\right]}{1+K\left[c_{\text{B}}+c_{\text{A}}\frac{\partial c_{\text{B}}}{\partial r}\left(\frac{\partial c_{\text{A}}}{\partial r}\right)\right]},\end{array}$$ (3)

and the symmetrical expressions

$$\begin{array}{l}{s}_{\text{Btot}}\left(c_{\text{A}},c_{\text{B}}\right)=\frac{s_{\text{B}}+c_{\text{A}}K{s}_{\text{AB}}}{1+c_{\text{A}}K},\\ D_{\text{Btot}}\left(c_{\text{A}},c_{\text{B}}\right)=\frac{D_{\text{B}}+D_{\text{AB}}K\left[c_{\text{A}}+c_{\text{B}}\frac{\partial c_{\text{A}}}{\partial r}{\left(\frac{\partial c_{\text{B}}}{\partial r}\right)}^{-1}\right]}{1+K\left[c_{\text{A}}+c_{\text{B}}\frac{\partial c_{\text{A}}}{\partial r}\left(\frac{\partial c_{\text{B}}}{\partial r}\right)\right]}\end{array}$$ (4)

(note that a detailed derivation is in the Supporting Material). A typical set of concentration gradients evolving during the sedimentation of an interacting system is shown in Fig. 1 A. The boundary pattern exhibits a division into an undisturbed boundary that consists entirely of either free A or free B, and the reaction boundary that exhibits coupled migration of all free and complex species (13,15).

Figure 1.

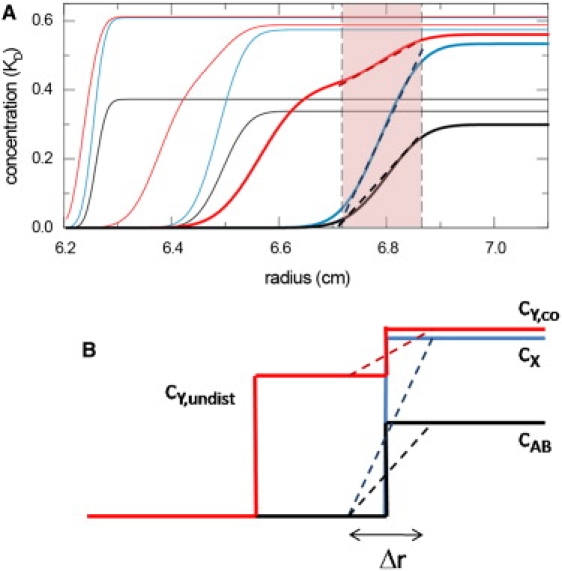
Schematic representation of the concentration gradients in the reaction boundary. (A) Concentration profiles of free A (100 kDa, 7 S, red), free B (200 kDa, 10 S, blue), and complex (13 S, black) species during the sedimentation of the interacting system A + B ↔ AB in the limit of instantaneous reaction, for the conditions at equimolar loading concentrations at K_D shown in (9). For clarity, only the concentration profiles from time-points 300 s and 1500 s (thin lines) and 3000 s (bold lines) are superimposed. The vertical dashed lines and the range highlighted in red indicate the radial range that covers 10–90% of the reaction boundary at 3000 s. The dotted diagonal lines are linear approximations of the gradients in the reaction boundary. (B) Schematics of the boundary structure described in EPT, with the division of the secondary component into the undisturbed boundary with concentration c_Y,undist and the cosedimenting free fraction c_Y,co, as well as the concentration of the free species of the dominant component c_X and the complex c_AB in the reaction boundary. All quantities c_Y,undist, c_Y,co, c_X, and c_AB, as well as the question of which component plays the role of dominant and secondary component X and Y, are analytically predicted in EPT as a function of loading concentration, equilibrium constant, and all species s values. We may assign a finite boundary width Δr to the reaction boundary, and approximate it as a constant gradient.

Effective particle theory

The propagation of the undisturbed boundary is trivial, except for the question which component provides this undisturbed boundary, and the question of the concentration in the undisturbed boundary. In EPT (15), this component is denoted the secondary component, abbreviated as Y, and the component that is not secondary is termed dominant, and abbreviated as X. Y is equal to A for c_Btot,0 < c^∗_Btot,0 and Y is equal to B for c_Btot,0 > c^∗_Btot,0, with the phase transition

$$c_{\text{Btot},0}^{\ast }\left(c_{\text{Atot},0}\right)=c_{\text{Atot},0}+\frac{\left(s_{\text{B}}-s_{\text{A}}\right)}{2K\left(s_{\text{AB}}-s_{\text{B}}\right)}\left(1+\sqrt{1+\frac{4c_{\text{Atot},0}K\left(s_{\text{AB}}-s_{\text{B}}\right)}{\left(s_{\text{AB}}-s_{\text{A}}\right)}}\right)\text{.}$$ (5)

The undisturbed boundary vanishes at the phase transition point c_Btot,0 = c^∗_Btot,0. The concentration of the undisturbed boundary is

$$c_{\text{Y},\text{undist}}=c_{\text{Ytot},0}-c_{\text{AB}}\left(1+\frac{\left(s_{\text{AB}}-s_{\text{Y}}\right)}{K{c}_{\text{Y}}\left(s_{\text{AB}}-s_{\text{Y}}\right)+\left(s_{\text{X}}-s_{\text{Y}}\right)}\right)\text{.}$$ (6)

The reaction boundary contains mixtures of free X and complex AB at the initial equilibrium concentration (i.e., cosedimenting c_X,co = c_X,0), as well as free Y at the concentration c_Y,co = c_Y,0 – c_Y,undist . They sediment as an ergodic system, where the fractional time molecules X and Y spend being bound or free are equal to their population fractions, and such that the time-average velocities of molecules X and Y are equal, assuming a value

$$s_{\text{A}\cdots \text{B}}=\frac{c_{\text{X}}{s}_{\text{X}}+c_{\text{AB}}{s}_{\text{AB}}}{c_{\text{X}}+c_{\text{AB}}}\text{.}$$ (7)

This can be illustrated best in a movie (20). EPT is only concerned with the total fluxes arising from the sedimentation of the reaction boundary and the undisturbed boundary, and the concentration profiles are thus approximated as step-functions, as illustrated in Fig. 1 B. EPT does not make statements regarding the boundary shape or diffusion.

Diffusion coefficients of the reaction boundary

If the components are instantaneously linked by the mass-action law at all times, it should be possible to approximate the diffusive broadening of the reaction boundary by a single diffusion coefficient of the system, D_A…B. We expect that both components contribute to diffusion, and that the magnitude of D_A…B is weighted by each component's fluxes. Thus, it is hypothesized that the average diffusion coefficient should take the form of a gradient average

$$D_{\text{A}\cdots \text{B}}=\frac{D_{\text{Xtot}}\partial c_{\text{X}}/\partial r+D_{\text{Ytot}}\partial c_{\text{Y}}/\partial r}{\partial c_{\text{X}}/\partial r+\partial c_{\text{Y}}/\partial r}\text{.}$$ (8)

It is noted that exact expressions for D_Atot and D_Btot are available in Eqs. 3 and 4. Their evaluation requires knowledge of the concentration gradients ∂c_A/∂r and ∂c_B/∂r, similar to Eq. 8.

We can make use of the knowledge of the concentration differences in EPT to approximate the concentration gradients. As visualized by the dotted lines in Fig. 1 A, a linear concentration increase across a radial range Δr may serve at least as a first approximation. This leads to ∂c_X/∂r ≈ c_X,0/Δr, ∂c_Y/∂r ≈ (c_Y,0 – c_Y,undist)/Δr, and ∂c_XY/∂r ≈ c_AB/Δr. Inserted in Eqs. 3, 4, and 8, the boundary width Δr cancels out, and yields

$$D_{\text{A}\cdots \text{B}}\approx \frac{c_{\text{X},0}\frac{D_{\text{X}}{c}_{\text{X},0}+D_{\text{AB}}{c}_{\text{AB}}}{c_{\text{X},0}+c_{\text{AB}}}+\left(c_{\text{Y},0}-c_{\text{Y},\text{undist}}\right)\frac{D_{\text{Y}}\left(c_{\text{Y},0}-c_{\text{Y},\text{undist}}\right)+D_{\text{AB}}{c}_{\text{AB}}}{\left(c_{\text{Y},0}-c_{\text{Y},\text{undist}}\right)+c_{\text{AB}}}}{c_{\text{X},0}+\left(c_{\text{Y},0}-c_{\text{Y},\text{undist}}\right)}\text{.}$$ (9)

One may further use the Svedberg equation to define an “apparent molar mass” of the effective particles in the reaction boundary of

$$M_{\text{A}\cdots \text{B}}=\frac{s_{\text{A}\cdots \text{B}}RT}{D_{\text{A}\cdots \text{B}}\left(1-\overline{\upsilon }\rho \right)}\text{.}$$ (10)

Sedimentation coefficient distributions

The sedimentation coefficient distribution c(s) describes the evolution of the experimental signal profiles a(r,t) as a superposition of Lamm equation solutions χ₁(s,M,r,t) of noninteracting species (10),

$$a\left(r,t\right)\cong \int c\left(s\right){\chi }_1\left(s,M\left(s\right),r,t\right)ds,$$ (11)

where M(s) is usually calculated as a function of s value following the power-law

$$M\left(s\right)\approx k\left({\left(f/f_0\right)}_w,\rho ,\eta \right)s^{3/2},$$ (12)

and typically fit with the average frictional ratio (f/f₀)_w as an adjustable fitting parameter (21), although other relationships are possible and available in the ultracentrifugal data analysis software SEDFIT (17).

Analogously, the size-and-shape distribution is

$$a\left(r,t\right)\cong \int c\left(s,M\right){\chi }_1\left(s,M,r,t\right)dsdM,$$ (13)

although it is usually calculated in a more convenient form of c(s,f/f₀) (11).

Both Eqs. 11 and 13 are discretized and phrased into a linear least-squares problem for the calculation of the distribution. High-resolution distributions can be calculated conveniently on desktop computers, using established computational tools that yield a mathematically well-defined best-fit solution for this linear least-squares fit (22). As the analysis is ill posed, it must be combined with regularization techniques to avoid detail not warranted by the data. All data analysis was done with the software SEDFIT, using maximum entropy or Tikhonov regularization. (Note that Eq. 13 can generally not be solved accurately with Demeler's 2DSA method (23), which may be considered a heuristic approach motivated by Eq. 13, as shown in (22).)

Results

The performance of the approximation Eq. 9 was by calculating exact Lamm equation solutions via Eq. 1 for a variety of conditions, and by extracting estimates for the diffusion coefficients from these boundary profiles. In the absence of hydrodynamic nonideality, this can be accomplished through fitting the concentration profiles with the c(s) model.

Broadening of the reaction boundary arises not only from diffusion, but also from the heterogeneity of the sedimentation coefficient distribution, as predicted in the asymptotic boundaries by Gilbert-Jenkins theory (13). Even though the range of s values is very narrow, except for conditions close to the phase transition line (15) (see below), the exquisite sensitivity of SV to the polydispersity of s values makes this an important contribution. The polydispersity of the s values in the reaction boundary can be captured by modeling the concentration profiles with a continuous c(s) distribution across the range from approximately s_B to s_AB.

Polydispersity results in exponentially time-dependent broadening of the boundary. This is independent of the diffusive, i.e., the $\sqrt{t}$-dependent, component of the reaction boundary broadening. The latter can be extracted by adjusting a signal-average frictional ratio of the c(s) distribution to its best-fit value (see below). The undisturbed boundary is modeled as a discrete species with sedimentation parameters of the free component Y predicted from EPT. For conditions where the c(s) peak of the reaction boundary is resolved from the discrete species of the undisturbed boundary, integration of c(s) then provides a value for s_A⋯B. Together with s_A⋯B, the best-fit frictional ratio implies an estimate of the average molecular weight as well as the average diffusion coefficient (via the Svedberg equation), which may be taken as estimates of D_A⋯B, and M_A⋯B, and be compared with the approximations Eqs. 7, 9, and 10, respectively.

The test-system used was that of a 40-kDa, 3.5 S molecule A rapidly interacting with a 60-kDa, 5.0 S molecule B, to form a 100-kDa, 6.5 S complex. The sedimentation profiles were predicted for a 10-mm solution column at 50,000 rpm, and signals a(r,t) = ɛ_Ac_A(r,t) + ɛ_Bc_B(r,t) + ɛ_ABc_AB(r,t) were calculated in 10 min time-intervals, using signal increments that would be typical with the interference optical detection for these molecules. The parameter space of loading concentrations was explored along different trajectories of equimolar concentrations and titration series of constant A or constant B, respectively. The results of the simulated experiments are shown in Figs. 2 and 3, where the circles depict the values derived from the fit of the simulated sedimentation data (PDE solution), and the solid lines depict the isotherms predicted by Eqs. 7, 9, and 10, respectively. It should be noted that there is no adjustable parameter in the solid lines.

Figure 2.

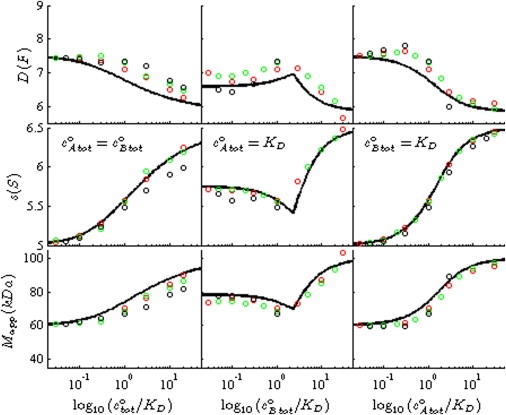
Testing the observed diffusional spread of the reaction boundary for a dependence on the detection of different species. Shown here are diffusion coefficient D_A⋯B (top row), sedimentation s_A⋯B (middle row), and apparent molar mass M_A⋯B (bottom row), observed in the reaction boundary (circles), in comparison with the corresponding predictions of Eqs. 7, 9, and 10, respectively (solid lines). To determine the data points for the reaction boundary parameters, exact Lamm PDE solutions were calculated for a molecule A of 40 kDa, 3.5 S rapidly interacting with a molecule B of 60 kDa, 5.0 S to form a 100 kDa, 6.5 S complex, sedimenting at 50,000 rpm in a 10-mm solution column, for equimolar dilution series (left column), a titration of A with varying B (middle column), and a titration of B with varying A (right column). The signal profiles were fitted (excluding the back-diffusion region) with a combination of a Lamm equation solution for a discrete noninteracting species describing the undisturbed boundary and a c(s) distribution describing the reaction boundary. Where the c(s) peak could be well resolved from the discrete species, it was integrated to determine the average diffusion coefficient D_A⋯B, sedimentation coefficient s_A⋯B, and apparent molar mass values M_A⋯B. Shown in red are simulations using extinction coefficients that would be realistic for interference optical detection (ɛ_A = 110,000 fringes × M⁻¹ cm⁻¹, ɛ_B = 165,000 fringes × M⁻¹ cm⁻¹, and ɛ_AB = 275,000 fringes × M⁻¹ cm⁻¹). In green are shown data obtained from simulations with invisible A, as may be possible in the selective absorbance optical system (ɛ_A = 0, ɛ_B = 165,000 OD × M⁻¹ cm⁻¹, and ɛ_AB= ɛ_B). In black is shown an unphysical simulation of a system with invisible complex (ɛ_A = 110,000 fringes × M⁻¹ cm⁻¹, ɛ_B = 165,000 OD × M⁻¹ cm⁻¹, and ɛ_AB= 0). The theoretical isotherms are independent of the species' signal increments, and have no adjustable parameters.

One basic prediction from the derivation above is that the values for s_A⋯B, D_A⋯B, and M_A⋯B should be independent of the species' signal increments. This is at variance with the results from Gilbert-Jenkins theory that the contributions of the free components A and B to the asymptotic boundaries are not proportional to each other (13). This dilemma motivates a test of the extent of a dependence of the observed diffusion coefficients in the reaction boundary on the species signal contributions.

To this end, different situations were simulated with different assumptions on the species' signal increments, with the results shown in Fig. 2. In red is shown the realistic simulation with signal increments for all species as would be observed for refractive-index sensitive interference optics in a current analytical ultracentrifuge. Green shows the data that are obtained when A does not contribute to the signal, solely using contributions of the larger species and the complex. The opposite extreme is simulated in the data shown in black, which emphasizes the small species A and B by applying conditions where, artificially, ɛ_AB is set to zero. If the individual species were to migrate in the reaction boundary with significantly different diffusional spread, the resulting data (red, green, and black circles) would diverge. However, it can be discerned from Fig. 2 that the values obtained are quite similar. Furthermore, the values follow closely the prediction of the isotherm Eqs. 7, 9, and 10, respectively. D_A⋯B is slightly systematically underestimated; however, the deviation is ∼10% or better.

Whether Eq. 9 is of the correct functional form to provide good approximations for the average diffusion coefficients can be explored by variation of the parameters D_A, D_B, and D_AB in the simulated Lamm equation solutions. The values that can be probed are not limited to physically reasonable values, but instead may cover extreme or even physically impossible values, that solely reflect the mathematical structure of the Lamm PDE solutions in relation to Eq. 9. The results of this set of simulation experiments is shown in Fig. 3. Data points in red recapitulate the results for the simulations under standard conditions as shown in Fig. 2. Blue circles show the results when A is diffusing much stronger (setting M_A = 10 kDa, at unchanged s_A = 3.5 S, M_B = 60 kDa, M_AB = 70 kDa, and otherwise standard parameters), green circles show the results when B is diffusing much stronger (setting M_B = 35 kDa, at unchanged s_B = 5.0 S, M_A = 40 kDa, M_AB = 75 kDa, and otherwise standard parameters), and finally, magenta circles show the results when D_AB becomes very large (by setting M_AB = 40 kDa, at unchanged s_AB = 6.5 S, M_A = 40 kDa, M_B = 60 kDa, and otherwise standard parameters). Again, the isotherms predicted by Eqs. 7, 9, and 10, indicated by the solid lines, have no adjustable parameters and there is no fit involved. They are in very good agreement with the PDE-derived data, indicating that Eq. 9 captures at least the most essential contributions to the diffusive broadening of the reaction boundary.

Figure 3.

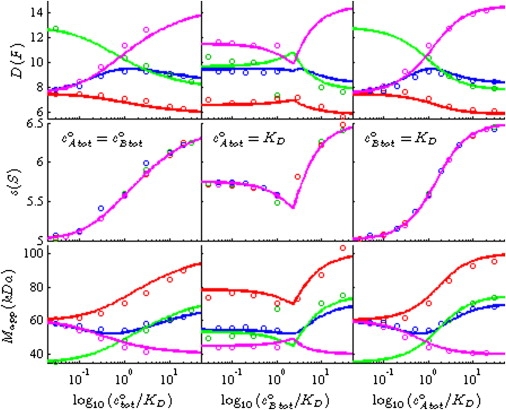
Probing the diffusive properties of the reaction boundary for different systems. The presentation is analogous to Fig. 2: the circles indicate the values extracted via c(s) from the Lamm PDE solutions (using standard interference optical signal increments of ɛ_A = 110,000 fringes × M⁻¹ cm⁻¹, ɛ_B = 165,000 fringes × M⁻¹ cm⁻¹, and ɛ_AB = 275,000 fringes × M⁻¹ cm⁻¹), and the solid lines are the isotherms predicted by Eqs. 7, 9, and 10 for diffusion coefficient D_A⋯B (top row), sedimentation s_A⋯B (middle row), and apparent molar mass M_A⋯B (bottom row), respectively. In red are shown the results for the standard conditions for a molecule A of 40 kDa, 3.5 S rapidly interacting with a molecule B of 60 kDa, 5.0 S to form a 100 kDa, 6.5 S complex. Blue, green, and magenta depict analogous simulations under conditions that are unphysical, but probe extreme values for species' diffusion coefficients: a 10-kDa molecule A (blue); a 35-kDa molecule B (green), and a 40-kDa complex (magenta).

With Eq. 10 it is possible to inspect the apparent molar mass values of the reaction boundary M_A⋯B as a function of loading concentrations. In particular, it is instructive to compare M_A⋯B with the molar mass of the complex M_AB, and with the weight-average mass of the entire system M_w (as it would be measured, for example, in certain sedimentation-equilibrium analysis models). The isotherms M_A⋯B/M_AB(c_Atot,0,c_Btot,0) and M_A⋯B/M_w(c_Atot,0,c_Btot,0) are shown in Fig. 4, A and B, respectively. Not surprisingly, M_A⋯B is always between the mass of the complex and the weight-average mass of the entire system. It attains asymptotically the mass of the complex for conditions where the reaction is saturated with excess A and/or excess B, in parallel with the isotherms of s_A⋯B approaching the s value s_AB of the complex (as shown in Fig. 5 in (15)). On the other hand, M_A⋯B is close to the weight-average mass of all species in the loading mixture when the loading concentrations are near the phase transition line, where the undisturbed boundary vanishes. We note that M_A⋯B is not equal to the weight-average molar mass of the material in the reaction boundary, even though the relative difference is <5% for the particular conditions of Fig. 2 (data not shown).

Figure 4.

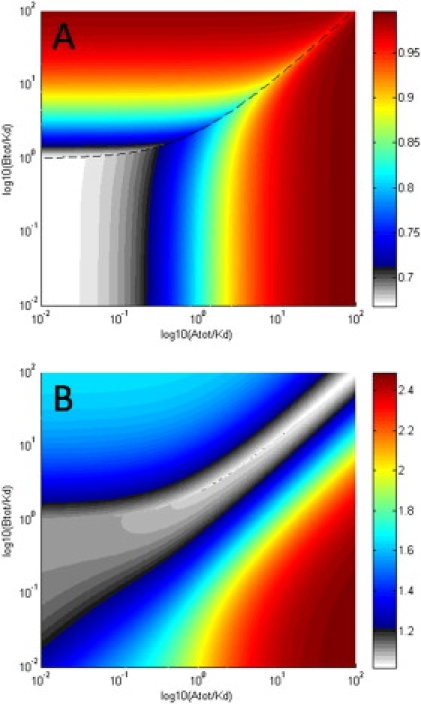
Isotherms of the apparent molar mass M_A⋯B in the parameter space of total loading concentrations, as predicted by Eq. 10. Shown are the ratios M_A⋯B/M_AB(c_Atot,0,c_Btot,0) (A) and M_A⋯B/M_w(c_Atot,0,c_Btot,0) (B), for the system of Fig. 2, in a contour plot with the color temperature scale as indicated on the right. The phase transition line of the sedimenting system is indicated by the black dashed line.

Figure 5.

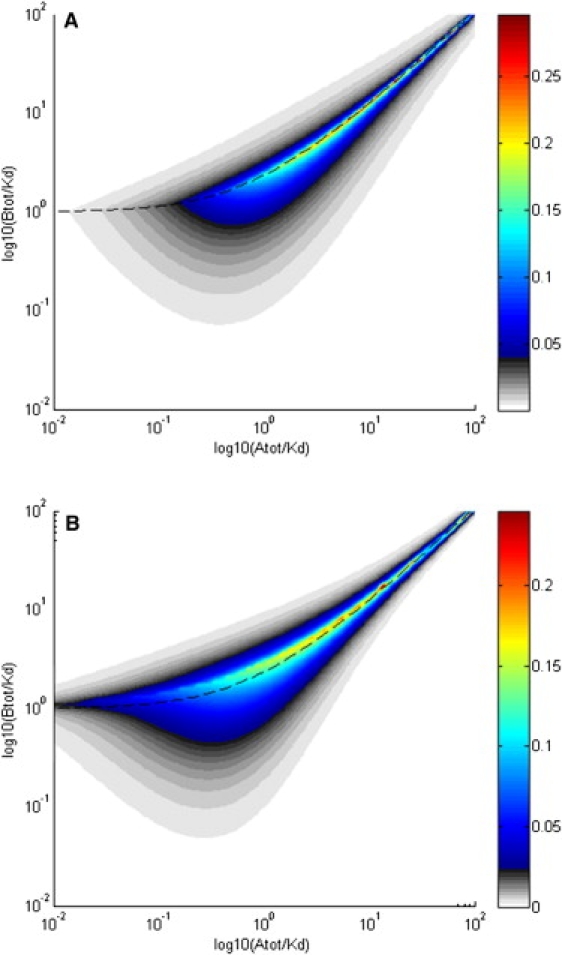
Polydispersity of the reaction boundary. (A) Estimate for the variation of the diffusion coefficient across the reaction boundary, as a function of loading concentration. Shown are values of $\left(D_{\text{A}\cdots \text{B},\text{max}}-D_{\text{A}\cdots \text{B}}\right)/D_{\text{A}\cdots \text{B}}$ using the color temperature scale on the right, where D_A···B,max is estimated for the trailing edge of the reaction boundary. High values > 0.1 are located in a very narrow band along the phase transition line (shown as dashed line) for concentrations c_A > K_D. (B) Polydispersity of the sedimentation coefficients based on the asymptotic boundaries $d\widehat{c}/dv$ from Gilbert-Jenkins theory (13). Plotted are the relative width $\left(v_{\max }-v_{\min }\right)/{\overline{v}}_{GJ}$ with ${\overline{v}}_{GJ}=\int v\left(d\widehat{c}/dv\right)dv/\int \left(d\widehat{c}/dv\right)dv$, where $d\widehat{c}/dv$ was calculated with the numerical method described by Gilbert and Gilbert (29), using a division of 10,000 concentration values, and v_max and v_min are the upper and lower limit of s values for which $d\widehat{c}/dv$ > 0.

In addition to the average diffusion coefficient D_A⋯B across the reaction boundary, we can ask the question how large the local variation of the diffusion coefficient might be, considering that the boundary shape will create regions of different gradients (hence different gradient averages). After all, the boundaries are not linear, as approximated above. Some preliminary estimates are possible based on the observation that the concentration profiles of all species in the reaction boundary take roughly similar shape (for example, in Fig. 1 A, compare the shapes of the thick red and blue lines in the highlighted region). Although this observation is not entirely accurate, it does permit an initial estimate of the range of diffusion coefficients arising at positions in the boundary. To this end, we may apply the parameterization c_X′ = kc_X,0 and (c_Y,0 – c_Yundist)' = k(c_Y,0 – c_Y,undist) with $k\left[0,1\right]$, which explores, in a rough approximation, the regions of decreasing slopes in the trailing end of the reaction boundary. When inserted into Eq. 9, a limiting value for k=0 can be found, which provides an estimate for the maximal diffusion coefficient D_A···B,max in the trailing edge of the reaction boundary. In Fig. 5 A, this information has been presented in the form of the relative change (D_A···B,max – D_A···B)/D_A···B as a function of loading concentration. Even though a considerable spread of diffusion coefficients between the average value D_A···B and the maximum value D_A···B,max may be encountered, the region of >10% variation (plotted in cyan and warmer colors) extends very narrowly along the phase transition line. For most of the parameter space, the relative variation with this estimate appears to be <5%.

It is interesting to compare this with the relative variation of s values in the reaction boundary, as predicted by the asymptotic boundaries in Gilbert-Jenkins theory (13) (denoted as diffusion-free velocity distributions $d\widehat{c}/dv$, customarily using the symbol v to denote the constant sedimentation velocity in linear geometry). The relative variation of s in the reaction boundary may be assessed by comparing the width and average of the asymptotic velocity distribution predicted by Gilbert and Jenkins, i.e., $\left(v_{\max }-v_{\min }\right)/{\overline{v}}_{GJ}$, where ${\overline{v}}_{\text{GJ}}=\int v\left(d\widehat{c}/dv\right)dv/\int \left(d\widehat{c}/dv\right)dv$. This is shown in Fig. 5 B across the parameter space for the same system as Fig. 2 and Fig. 5 A. (Similar results are obtained when considering the central second moment instead of the maximum spread, which is approximately a factor of two smaller than the maximum spread; data not shown). For the s values, similar to the D values, significant polydispersity is encountered exclusively in a narrow region close to the phase transition line for concentrations c_Atot,0 > K_D.

Discussion

The diffusional properties of the reaction boundary formed during the sedimentation of rapidly interacting species is a problem of long-standing interest in analytical ultracentrifugation. Even though the Lamm PDE of the interacting system predicts the evolution of the concentration profiles of all species, this alone is not completely satisfactory or sufficient for the optimal planning and evaluation of SV experiments on rapid protein interactions.

Current numerical algorithms and abundant computational resources on desktop computers make routine direct fitting of Lamm PDE solutions of interacting systems to experimental data possible (6–9,24). However, the overwhelming majority of studies in the literature does not apply this approach. This may be attributed to the high susceptibility of the sedimentation boundaries to trace impurities and macromolecular heterogeneity that impede the fit of PDE solutions (9). (An analogous case is the common difficulty of fitting discrete species models to noninteracting mixtures, which is rarely possible, in contrast to the fit of sedimentation coefficient distributions c(s) that can account for trace imperfections, which is very successfully applied in the literature (25).) In addition, the process of establishing the reaction scheme by comparing the performance of various alternate hypothesized Lamm PDE models would be very cumbersome. For this reason, alternative, more flexible and robust approaches must be developed for the data interpretation of interacting systems in SV.

Perhaps most importantly, when the Lamm PDEs are used solely as computational recipes, they do not explain the relationship between the physical sedimentation and concentration parameters that generate certain features in the concentration profiles. Similarly, while they generate near-exact concentration profiles for the set of underlying simulation parameters, they do not allow generalizing of observables to different parameter sets, and an overview across the parameter space of loading concentrations, for example, would have to be assembled point-by-point. This impedes optimal experimental design and robust data analysis. A comprehensive overview of the observables as a function of Lamm PDE parameters has not yet been reported, and, therefore, major general features of the phase behavior of rapidly interacting systems in SV have been overlooked (see below).

With regard to the sedimentation boundary patterns exhibited by rapidly reacting bimolecular systems, this problem was addressed recently by EPT (15). In EPT, physically based rules provide simple analytical relationships that describe, in excellent approximation, the sedimentation boundary patterns of the system across the parameter space. Briefly, EPT distinguishes a dominant component, which exists exclusively in the reaction boundary, from the secondary component, which provides the undisturbed boundary. Both components must exhibit the same time-average s value in the reaction boundary. This condition is sufficient to predict quantitatively the composition, amplitudes, and s values of all sedimentation boundaries.

EPT also revealed an asymmetrically shaped phase transition line in the parameter space, where the role of dominant and secondary component switches. At the phase transition, anomalous sedimentation behavior exists (in that there is only one single boundary at an s value intermediate to all species), which is naturally explained in EPT by the requirement for all molecules to exhibit the same time-average s value (20). EPT allows us to answer, with simple analytical relationships, nontrivial questions such as: when does the supernatant concentration (i.e., the undisturbed boundary) reflect a good approximation of the concentration unbound ligands? and When does the loading composition at the transition point reflect the complex stoichiometry?

In this work, we made use of the new analytical predictions from EPT regarding the magnitudes of the concentration differences across the boundaries, to explore from a new angle the problem of diffusion in the reaction boundary. When the Lamm PDE is expressed in constituent concentrations, gradient average diffusion coefficients naturally appear for each component. They can be approximated by linearized gradients across the boundary, and can be further combined into a gradient average diffusion coefficient of all components. We have shown that the resulting analytical expression, which relates all sedimentation, diffusion, and concentration parameters, describes well the overall diffusional spread of the reaction boundary, D_A⋯B,. In conjunction with the sedimentation coefficient of the reaction boundary from EPT, s_A⋯B, it may be used to define operationally, via the Svedberg equation, an apparent molar mass M_A⋯B of the effective particle. Not surprisingly, the resulting values are between the weight-average molar mass of the complete system and the molar mass of the complex, and are often close to the weight-average molar mass of all species in the reaction boundary.

Further, this approach enables us to obtain a rough estimate of the heterogeneity of the diffusion coefficients in the reaction boundary. Interestingly, it closely mirrors the polydispersity of sedimentation coefficients in the asymptotic boundary predicted by Gilbert-Jenkins theory. Perhaps contrary to conventional wisdom, both exhibit quite low degrees of polydispersity under most conditions, with the exception of a narrow band of concentrations close to the phase transition region at concentrations >K_D. This may be explained by the fact that under conditions far from the phase transition line, the high concentration of the undisturbed boundary leads to an offset of concentrations of the secondary component across the reaction boundary. This greatly diminishes the range of fractional saturation of the dominant component, which governs the polydispersity of both s values and D values. We believe it is essentially this phenomenon that was already captured in the constant bath approximation for the special case of very dissimilar-sized molecules at conditions of excess small binding partner (9), and led there to the perhaps surprising conclusion that the evolution of the reaction boundary may be approximated rather well with a single sedimentation and a single diffusion coefficient.

To illustrate the performance of this and other data analysis models, we have simulated examples for Lamm PDE solutions with different degree of expected polydispersity. Fig. S1 (see Supporting Material) shows data under condition of equimolar c_Atot = c_Btot = 0.2 K_D, an example for conditions where heterogeneity should only be a few percent; Fig. S2 shows conditions of c_Atot = c_Btot = K_D, which is an intermediate case; and Fig. S3 shows data for c_Btot = 3 K_D and c_Atot = 1.5 K_D at the phase transition line by EPT in the region of relatively strong polydispersity.

For all cases, the root-mean-square deviation (RMSD) of a two-discrete-species model (one species for the undisturbed and one for the reaction boundary) is ∼≤2%. However, the D values for the reaction boundaries, and implicitly the M values, are strongly affected by the polydispersity. This is not surprising, given the well-known susceptibility of the boundary spread to heterogeneity. Obviously, any imperfection that real data may exhibit would further bias the best-fit values from such a discrete model.

Arguably the most important consequence of the reaction boundaries exhibiting normal and relatively homogeneous diffusion properties is the possibility of diffusional deconvolution. The study of boundary s values and their isotherms does not rely on boundary shapes, but instead relies only on the mass transport accompanying the sedimentation boundaries. This mass transport can be measured in the plateau region, and relates to the integral over the reaction boundaries, rather than their shape (15,26,27). Nevertheless, the diffusional deconvolution is often a crucial advantage in identifying the boundary components and resolving signal contributions from impurities and aggregates.

Deconvolution of diffusion can be achieved, for example, by approximating the sedimentation signal as a superposition of Lamm PDE solutions of noninteracting species with a continuous distribution of s values and D values. In the c(s) method, the two are linked by a scaling law D(s) with an adjustable parameter, typically using the average frictional ratio f/f₀ (10,21). Empirically, many applications of SV to interacting systems in the literature have already illustrated that the diffusional deconvolution afforded by the c(s) sedimentation coefficient distribution works very well also when applied to sedimentation data of rapidly reacting systems, and can yield remarkably high quality of fits (25). This can be understood by considering that over the small range of s values and D values encountered in the reaction boundary, the exact scale relationship D(s) is not very important. We note that the apparent frictional ratio f/f₀ implied by a literal interpretation of D_A⋯B and M_A⋯B, as if they were molecular parameters, is not physically meaningful, and assumes slightly smaller values than those of the free and complex species. (For this reason, a c(s) approach where the s axis is segmented with different f/f₀ values attributed to different regions, may be warranted to account separately for the undisturbed and possibly other clearly visible boundaries; a variety of such models are implemented in SEDFIT and SEDPHAT.)

In all cases of Fig. S1, Fig. S2, and Fig. S3, the fit with c(s) in the standard form, with an adjustable frictional ratio parameter, is very good although not perfect. With values of ∼1% or better, the RMSD is approximately a factor two better than a discrete model. Due to the ill-posed nature of the distribution analysis, the sedimentation coefficient distribution does not exactly follow the asymptotic boundary shapes predicted by Gilbert-Jenkins theory (shown as blue area patches), but they were shown to be highly consistent when using Bayesian regularization (28). Close to the phase transition, even the standard maximum entropy regularization can lead to the qualitatively correct bimodal reaction boundary shape. As already shown in Fig. 3, the implicit c(M) values of the reaction boundary peaks (using the conversion of c(s) to c(M) based on a fitted f/f₀ parameter of the reaction boundary) follow closely the expected values of Eqs. 9 and 10.

The size-and-shape distribution, most conveniently expressed as c(s,f/f₀), promises an even more detailed analysis accounting for polydispersity in both s and D. However, additional peaks arise at s values and f/f₀ values that are not predicted by the theory (Fig. S1 D, Fig. S2 D, and Fig. S3 D). The RMSD is improved by another factor two relative to the c(s) analysis, but the additional flexibility of the size-and-shape distribution model seems to extract features more detailed than warranted by the quality of the approximations above for rapidly interacting systems. These features are well defined, but other than the integrals over the undisturbed and reaction boundary features being measures of the mass balance, and the resulting relationship to the overall weight-average s value s_w and the average s value of the reaction boundary s_A⋯B, respectively, they currently do not appear to be usefully interpretable.

In conclusion, diffusional deconvolution and analysis of the reaction boundary spread appears to be conducted best with the c(s) method. This work sheds further light on the relationship of the sedimentation coefficient distributions with the theoretically expected asymptotic boundaries and EPT, and clarifies the meaning of the M values encountered with the reaction boundaries in the transformation of c(s) to c(M). Because the spread of the sedimentation coefficient distribution is generally small, there will be little influence from using different scaling laws in c(s), as long as they have in some form an adjustable parameter for the magnitude of diffusion.

Conceptually, it should be possible to fit isotherms of M_app values extracted from the reaction boundary of experimental data of rapid interacting multicomponent systems to the theoretical expressions of M_A⋯B(c_Atot,c_Btot) based on Eqs. 9 and 10 to analyze binding constants. This would give an additional isotherm data set with independent information that could be fit globally with appropriate interaction models, in conjunction with the isotherm of s_A⋯B(c_Atot,c_Btot), s_w(c_Atot,c_Btot), and the boundary amplitudes a_undist(c_Atot,c_Btot) and a_react(c_Atot,c_Btot) introduced previously (16) and implemented in SEDPHAT. However, at this point it seems that the generally very high precision of s values and the robustness of measuring the amplitudes of the multimodal boundaries would provide superior information, and perhaps not too much would be gained in terms of further diminishing the uncertainty of the derived estimate of the binding constant.

Another useful aspect of the framework presented here is that it can support important qualitative conclusions about the nature of the reaction. Knowing, for example, that the M_A⋯B value of the reaction boundary is very close to the complex molar mass under conditions of 10-fold excess of c_Atot or c_Btot over K_D (Fig. 4) may provide an indicator for the complex stoichiometry. The theoretical approach presented here should be straightforward to generalize to multisite binding, similar to the constant bath theory and EPT.

Supporting Material

Seven equations and three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00329-2.