Evolvability and Single-Genotype Fluctuation in Phenotypic Properties: A Simple Heteropolymer Model

Abstract

Experiment showed that the response of a genotype to mutation, i.e., the magnitude of mutational change in a phenotypic property, can be correlated with the extent of phenotypic fluctuation among genetic clones. To address a possible statistical mechanical basis for such phenomena at the protein level, we consider a simple hydrophobic-polar lattice protein-chain model with an exhaustive mapping between sequence (genotype) and conformational (phenotype) spaces. Using squared end-to-end distance, R_N², as an example conformational property, we study how the thermal fluctuation of a sequence's R_N² may be predictive of the changes in the Boltzmann average 〈R_N²〉 caused by single-point mutations on that sequence. We found that sequences with the same ground-state (R_N²)₀ exhibit a funnel-like organization under conditions favorable to chain collapse or folding: fluctuation (standard deviation σ) of R_N² tends to increase with mutational distance from a prototype sequence whose 〈R_N²〉 deviates little from its (R_N²)₀. In general, large mutational decreases in 〈R_N²〉 or in σ are only possible for some, though not all, sequences with large σ values. This finding suggests that single-genotype phenotypic fluctuation is a necessary, though not sufficient, indicator of evolvability toward genotypes with less phenotypic fluctuations.

Introduction

The study of protein evolution entails ascertaining how changes in a protein's amino acid sequence lead to changes in its biological functions (1). Biological functions of proteins, in turn, are often intimately related to their conformational structures. Thus, to address principles of protein evolution, the mappings between sequences and structures in various simplified heteropolymer models have been investigated. Using explicit—albeit highly coarse-grained—representations of the protein chain with physics-inspired interactions (see, e.g., (2–16)), these modeling efforts have led to significant advances (reviewed in (17,18)). Because the folded nature of many proteins are crucial for their functions, explicit-chain models of protein evolution to date have focused primarily on the mapping from sequences to their ground-state (lowest-energy) conformations that represent the folded native structures of globular proteins. In these analyses, the role of excited-state conformations (those with energies higher than that of the ground state) is only subsidiary and a structure is seen as encodable (5) or designable (6) only if it is the unique ground-state conformation of a sequence.

Recent developments, however, have revealed a more central evolutionary role for excited-state conformations that are accessible by thermal fluctuation. In the study of RNA evolution, it is well known that a sequence can assume a variety of energetically favorable shapes (19). Likewise, it is recognized that excited-state populations of proteins might serve “promiscuous” biological functions (20,21) and thus be subject to a selection process that can speed up evolution (22–24) and reviewed in (25,26)). This perspective is in line (20) with the energy landscape picture of protein folding (27–30), the observation of in vivo phenotypic variations modulated by molecular chaperones (31), as well as the notion that broadened phenotypic fluctuations among individuals with the same genotype can be a successful evolutionary strategy under severe selective environments (32). Accordingly, it is more appropriate to view sequence-to-structure mapping as one that takes each sequence to a structural distribution that encompasses all conformations (23), rather than one that matches each sequence solely to its ground-state conformation(s). Depending on the sequence and its environment, a sequence's structural distribution can be dominated by one conformation, as for globular proteins under folding conditions, or it can favor many conformations simultaneously, as for intrinsically disordered proteins (33–35).

To what extent, then, is a single genotype's evolvability predetermined by its phenotypic fluctuation (26,36)? At the level of protein molecules, evolvability is the propensity of an amino acid sequence or a population of sequences to develop new structural/functional features by perturbatively changing the original sequence(s). Here, genotype is identified with the amino acid sequence and phenotype corresponds to the structural or functional properties of the sequence. Sato et al. (37) and Yomo et al. (38) addressed single-sequence evolvability by using artificial evolution (39,40) of mutants of a green fluorescent protein (GFP) in bacteria. By monitoring the variance of fluorescence intensity among clones (bacteria with the same amino acid sequence for the GFP) and selecting for large increases in this trait (41), they found that the largest possible increase in fluorescence intensity caused by mutation on a genotype (a particular amino acid sequence for the GFP) is well correlated with the variance of fluorescence intensity exhibited by that genotype (37). This observation suggests that the largest achievable evolutionary change on a phenotypic property by mutation may be governed by the extent of fluctuation of that property in the original parent genotype. Inspired by this discovery, here we explore biophysical principles that may underlie such a phenomenon.

Fig. 1 illustrates the question we aim to address. Starting with two sequences (represented by the black and red solid circles) that have the same average value for a conformational (structural) property, Fig. 1 shows a hypothetical relationship between variations in sequence space (top and bottom) and variations in conformational space (middle). Variation in the structural distribution encoded by a sequence is expected to be smooth—at least on average—with respect to change in sequence (23). Based on this premise, Fig. 1 stipulates, hypothetically, that the sequence depicted as a red solid circle and has a broad distribution in a conformational property is likely to have a single-point mutant (e.g., red triangle) with a larger shift in the average value of that property than the corresponding shifts achieved by single-point mutants (e.g., blue square) of the sequence with a narrower distribution to begin with (solid circle). As commented by Sato et al. (37), such a correlation between increased single-genotype phenotypic fluctuation and increased evolvability is reminiscent of the fundamental relationship between fluctuation and dissipation in statistical physics (42) because, by analogy, enhanced evolvability may be viewed as reduced resistance to phenotypic change.

Figure 1.

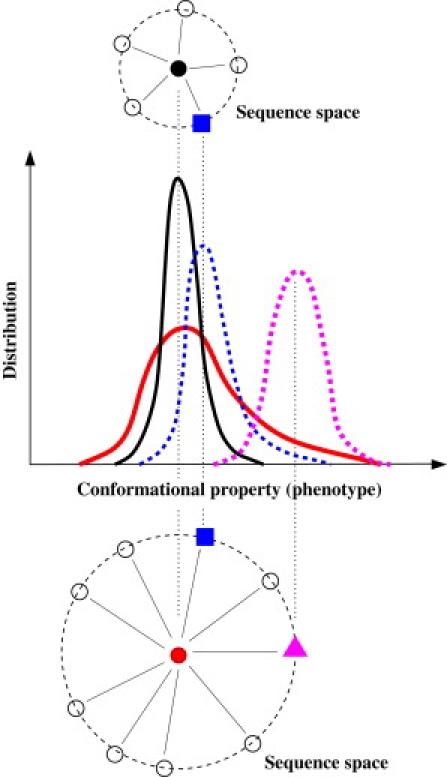
Schematic of how single-genotype phenotypic fluctuation might correlate with evolvability. Top and bottom are parts of the sequence space, wherein single-point substitutive mutations are represented by solid lines and a dashed circle is used to indicate unit Hamming distance (a single substitution) from a center sequence (black or red circle). The middle plot shows distributions of a hypothetical conformational property for four of the sequences (marked by vertical dotted lines and color coding). Other sequences are depicted as black open circles.

The scenario in Fig. 1 is intuitive, but the extent to which it is physically viable for protein chains remains to be assessed. Approximate analytical formulations have provided insights into the fluctuation-evolvability question (37,43) (see below) as well as whether evolvability is a selectable trait (44). However, as has been demonstrated in the study of protein folding (45), explicit-chain modeling is indispensable for evaluating whether assumptions made in analytical formulations of protein evolution are physically plausible. We adopt the simple exact HP (hydrophobic-polar) lattice model (28) for this task, as in our previous studies of evolutionary questions (9,11,15,23). Using this extremely coarse-grained and thus computationally tractable construct (17), the present effort is an essential complement to analytical approaches.

Here, we choose to study the squared end-to-end distance, $R_N^2$, as an example of a conformational property that exhibits thermal fluctuations. Although not directly related to biological function in general, $R_N^2$ is useful for a first test of principle because its average, 〈$R_N^2$〉, is experimentally accessible by fluorescence resonance energy transfer (see, e.g., (46)). Other measures of conformational geometry such as chain compactness and radius of gyration may also be studied, but we do not pursue them here. In view of the experimental advances on artificial evolution of random amino acid sequences (47), our consideration is not restricted to unique or low-degeneracy sequences (9). By extending our attention to all random sequences, we also explore how selection on 〈$R_N^2$〉 might, as a side effect, lead to changes in ground-state degeneracy. Our analysis demonstrates that evolvability of 〈$R_N^2$〉 indeed correlates with fluctuation in $R_N^2$, in a manner somewhat similar to that envisioned by analytical theory (37). However, our results also reveal richer, unanticipated features. These include a marked difference between selecting for increasing 〈$R_N^2$〉 versus selecting for decreasing 〈$R_N^2$〉, the detail of which will be described below.

Model and Method

A reduced two-letter alphabet (5,48) is used in the HP model to mimic the attractive interactions among nonpolar amino acid residues (28) (Fig. 2). We adopt the HP model for evolutionary studies because it captures general trends of the sequence-to-structure mapping for real proteins (49,50), notwithstanding the model's insufficiency for detailed protein energetics (45,51). HP and other lattice models with reduced alphabets are useful for rationalizing properties of disordered protein conformations as well (4,52–54).

Figure 2.

Squared end-to-end distance $R_N^2$ of HP model chains on square lattices. The example in panels a and b shows a g = 2 sequence (H residues: solid circles; P residues: open circles) in two conformations with different $R_N^2$ values. (a) One of this sequence's two ground-state conformations. The other ground-state conformation (not shown) also has ($R_N^2$)₀ = 1. (b) This is an unfolded conformation. (c) Normalized distribution of $R_N^2$ of an example g = 1 sequence HPHPHPPHPHPPHPPHHH at ɛ = 0 (solid circles) and ɛ = –5 (open squares). Note that only discrete $R_N^2$ values of 1, 5, 9, … are allowed by the lattice model (circles and squares); lines through the symbols are merely a guide for the eye. (d) ΔG_f (in units of k_BT) as a function of ɛ. Solid circles show ΔG_f averaged over all sequences that can make at least one HH contact (261,088 sequences with h_N > 0); open circles show ΔG_f averaged over the 6,349 g = 1 sequences in our model.

As in our previous studies (9,11,15,23), model protein chains are configured as self-avoiding walks on the two-dimensional square lattice. A favorable energy ɛ (< 0) is assigned to each hydrophobic-hydrophobic (HH) contact; thus a conformation with h HH contacts has energy ɛh. The ground state of a sequence is the collection of conformations each of which has the largest number (denoted as h = h_N) of HH contacts that the sequence can achieve. The number of such conformations is the ground-state degeneracy g. We denote the $R_N^2$ value of a ground-state conformation by ($R_N^2$)₀. On the square lattice, the possible $R_N^2$ values (see illustrations in Fig. 2, a and b) are given by $R_N^2$ = x² + y² where x and y are nonnegative integers, x + y is restricted to be odd (even) when n is even (odd), and 0 < x + y ≤ n – 1. As before (9,11,15,23), here we use chains with length (number of residues) n = 18, for which there are 39 possible $R_N^2$ values (1,5,9,…289) among the 5,808,335 conformations that are not related by rigid rotations and mirror reflections. Short two-dimensional HP model chains are appropriate for mimicking the ratio between the numbers of surface and interior residues in real globular proteins (28) and are apparently adequate for rationalizing their hydrophobic patterns (49).

For each of the 2¹⁸ HP sequences in our model, we obtain by exact enumeration the number of conformations as a joint function, g(h, $R_N^2$), of h and $R_N^2$

$$P\left(R_N^2\right)=\frac{\sum _{h=0}^{h_{\text{N}}}g\left(h,R_N^2\right)\exp \left(-\varepsilon h/k_{\text{B}}T\right)}{\sum _{R_N^2}\sum _{h=0}^{h_{\text{N}}}g\left(h,R_N^2\right)\exp \left(-\varepsilon h/k_{\text{B}}T\right)},$$ (1)

which is the distribution of $R_N^2$, where k_B is the Boltzmann constant and T is absolute temperature. To simplify notation, ɛ is given in units of k_BT below. When ɛ becomes more negative, P($R_N^2$) becomes more dominated by the average value, $\overline{{\left(R_N^2\right)}_0}$, of ($R_N^2$)₀ among its ground-state conformation(s). For g = 1, $\overline{{\left(R_N^2\right)}_0}$ reduces to a single value of ($R_N^2$)₀. An example showing the variation of P($R_N^2$) with ɛ is provided in Fig. 2 c. In this example, because ground-state ($R_N^2$)₀ = 1, P($R_N^2$) for ɛ = –5 is sharply peaked at $R_N^2$ = 1. The distribution of $\overline{{\left(R_N^2\right)}_0}$ over all 2¹⁸ sequences is shown in Fig. S1 in the Supporting Material.

Information about ground-state thermodynamic stability in our model is provided in Fig. 2 d, showing averages, over sequences, of the free energy of folding,

$$\Delta G_{\text{f}}=-k_{\text{B}}T\ln \left[\frac{g\left(h_{\text{N}}\right)\exp \left(-\varepsilon h_{\text{N}}\right)}{\sum _{h=0}^{h_{\text{N}}-1}g\left(h\right)\exp \left(-\varepsilon h\right)}\right],$$ (2)

where

$$g\left(h\right)=\sum _{R_N^2}g\left(h,R_N^2\right)$$

is the density of states (9). The data indicate that ɛ ≤ –5 is required, on average, for ground-state dominance (ΔG_f < 0). The Boltzmann-weighted average of squared end-to-end distance

$$\langle R_N^2\rangle =\sum _{R_N^2}{R}_N^{2}P\left(R_N^2\right)$$ (3)

is computed for each sequence by using Eq. 1. Averages for other functions of h and $R_N^2$ are similarly defined. Fluctuation of $R_N^2$ is characterized by its standard deviation

$$\sigma =\sqrt{{\langle \left(R_N^2-\langle R_N^2\rangle \right)}^2\rangle }\text{.}$$ (4)

By definition, σ has the same dimension ([length]²) as $R_N^2$, both of which are expressed in units of squared lattice bond length. Fig. S2 provides the ɛ-dependence of 〈$R_N^2$〉 and σ for two sets of sequences to be analyzed below. Each is a net of unique (g = 1) sequences interconnected by single-point H → P or P → H substitutive mutations. Results in Fig. S2, a and c, are for a neutral net in which all sequences encode for the same ($R_N^2$)₀ = 1 ground-state conformation (9,55), whereas those in Fig. S2, b and d, are for a net in which all sequences encode for ground-state conformations with ($R_N^2$)₀ = 9. The latter ($R_N^2$)₀ = 9 net is not a neutral net in the original definition (9) because sequences in this net can encode for different ground-state conformations, although this net may be viewed as neutral, insofar as ($R_N^2$)₀ is concerned.

Results and Discussion

To address the relationship between evolvability and single-genotype phenotypic fluctuation in the context of our model, we ask: To what extent can σ of a sequence predict the change in 〈$R_N^2$〉 among the sequence's single-point mutants?

We first inspect the relationship between σ and 〈$R_N^2$〉 for all sequences. When the HH attraction is weak (Fig. 3, left column), a single correlation covers all sequences. This trend follows from the fact that more-compact conformations tend to have smaller $R_N^2$ values (e.g., whereas the compact conformations that can be uniquely encoded by g = 1 sequences have $R_N^2$ ≤ 29, the maximum possible $R_N^2$ among all conformations is 289). Therefore, sequences with thermodynamically more stable ground states tend to have somewhat less open conformations and thus smaller 〈$R_N^2$〉 values even under a weakly favorable ɛ. Conformational fluctuations of these sequences tend to be less because of their higher thermodynamic stability; hence a general correlation between 〈$R_N^2$〉 and σ in Fig. 3, a and c.

Figure 3.

Boltzmann average of a conformational property and its thermal fluctuation. Shown here are scatter plots of 〈$R_N^2$〉 and σ at ɛ = –1 (a and c) and ɛ = –5 (b and d) for various sets of sequences, as follows. Data points in panels a and b for 6349 unique (g = 1) sequences are plotted in black, red, green, light blue, magenta, blue, and orange, respectively, for ($R_N^2$)₀ = 1, 5, 9, 13, 17, 25, and 29. Data points in c and d for 19,309 g ≥ 1 sequences each with only one uniform ($R_N^2$)₀ value for its ground-state conformation(s) are plotted using the same color code for ($R_N^2$)₀ as that in panels a and b. This set of sequences includes those in panels a and b. Plotted in gray in panels c and d are data points for the other 2¹⁸–19,309 = 242,835 sequences in the model, each with more than one ($R_N^2$)₀ value among its g > 1 ground-state conformations.

The situation under stronger folding conditions is quite different (Fig. 3, right column). Whereas a decrease in σ with a more negative ɛ value is expected because stronger HH attractions reduce conformational fluctuations, Fig. 3, b and d, show that the relationship between σ and $R_N^2$ is complex under conditions favorable to folding. Two noteworthy features emerge:

• 1.Instead of dispersing widely under weakly folding conditions at ɛ = –1, sequences with the same uniform ground-state ($R_N^2$)₀ (plotted in the same color) now cluster together for ɛ = –5 in Fig. 3, b and d.
• 2.At ɛ = –5, a funnel-like variation of σ with 〈$R_N^2$〉 develops for each set of sequences with ($R_N^2$)₀ = 1, 5, 9, 13, 17 (each set shown in a different color) such that as σ decreases toward ≈ 0, deviations of 〈$R_N^2$〉 from ($R_N^2$)₀ also decreases toward ≈0, with ($R_N^2$)₀ acting like an attractor. This pattern applies to the g = 1 sequences (Fig. 3 b) that have been used to model natural globular proteins (9) as well as sequences that have multiple ground-state conformations sharing the same ($R_N^2$)₀ (plotted in black and in color in Fig. 3 d).

The emergence of these features suggest that the general formula

$${\langle x\rangle }_{a+\Delta a}-{\langle x\rangle }_a=b\left(\Delta a\right){\left({\sigma }_x^2\right)}_a$$ (5)

proposed by Sato et al. (37) to relate change in the average of a variable x with variance (${\sigma }_x^2$)_a of x may apply to each of the funnel-like clusters in Fig. 3, b and d. Following Sato et al. (37), the left-hand side in Eq. 5 is the change in the average of x induced by a change a → a + Δa in a parameter a related to x. On the right-hand side of Eq. 5, b is a constant independent of a and (${\sigma }_x^2$)_a is the variance of x before the a → a + Δa change (37). We test the applicability of Eq. 5 to our model system by setting the variable x to our $R_N^2$ and identifying Δa as a unit change in mutational (Hamming) distance (from a reference sequence) caused by a single-point H → P or P → H mutation. Using this formulation, we aim to ascertain the extent to which changes in 〈$R_N^2$〉 caused by single-point mutations in our model can be determined by σ.

Such an analysis requires information on the model sequences' mutational connections, which we will investigate below. Although mutational connectivity is not included in Fig. 3, the appearance of a curved-funnel pattern for each set of sequences with the same ($R_N^2$)₀ in Fig. 3, b and d (black and color dots) already suggests that their behaviors might, to an extent, conform to Eq. 5. The curved-funnel shapes indicate that the magnitude of horizontal change in 〈$R_N^2$〉 from one sequence to the next is larger for sequences with larger σ-values located higher up in the funnels. This behavior would be similar to that described by Eq. 5 if we assume that changing from one sequence to a neighboring sequence in Fig. 3, b and d, corresponds roughly to an a → a + Δa process, with b(Δa) > 0 or b(Δa) < 0 depending on whether the change in sequence results in a positive or negative change in 〈$R_N^2$〉. Fig. 3, b and d, show two classes of behaviors in this regard. For sequences with uniform ($R_N^2$)₀ = 1 (black dots), the funnel is one-sided because 〈$R_N^2$〉 < 1 is impossible in the model. For sequences with uniform ($R_N^2$)₀ in the range 5 ≤ ($R_N^2$)₀ ≤ 17, the funnels are two-sided because for these cases, $R_N^2$ < ($R_N^2$)₀ is possible for some excited-state conformations. Funnel-like organization for sequences with uniform ($R_N^2$)₀ > 17 is not easily discerned because the number of such sequences is small: There are 156 g = 1 sequences for ($R_N^2$)₀ = 17 but only 3 g = 1 sequences each for ground-state ($R_N^2$)₀ = 25 and ($R_N^2$)₀ = 29. The scatter of gray dots in Fig. 3 d shows that funnel-like organization is not apparent for g > 1 sequences with nonuniform ($R_N^2$)₀.

In view of the suggestive trends in Fig. 3, we now address directly our model's conformity, or lack thereof, with Eq. 5. We first focus on two networks of sequences interconnected by single-point H → P or P → H mutations (Figs. 4 and 5). Such networks are of interest as models for studying evolution within a sequence subspace whereby mutations that take sequences outside the network are lethal (9) or, in Maynard Smith's terminology, not “meaningful” (1). In other words, the restrictive conditions for defining the protein network in such models, e.g., the g = 1 requirement, are seen as necessary for the survival of the organism in which the protein operates. As an example, Fig. 4 studies the same neutral net of 48 g = 1 sequences as that in Fig. S2, a and c. Biologically, the situation for this net may correspond to one in which the presence of a specific protein structure in sufficiently high concentration (which would not be possible if g > 1) is necessary for survival. As another example, Fig. 5 studies an extended net of sequences with a uniform ground-state ($R_N^2$)₀ = 9. This situation may correspond to one in which a high concentration of structures possessing 〈$R_N^2$〉 values within a narrow range around ($R_N^2$)₀ is necessary for survival. For each net, we identify a prototype sequence as the sequence with maximum mutational stability in that it has the maximum number of single-point mutants within the given net (9).

Figure 4.

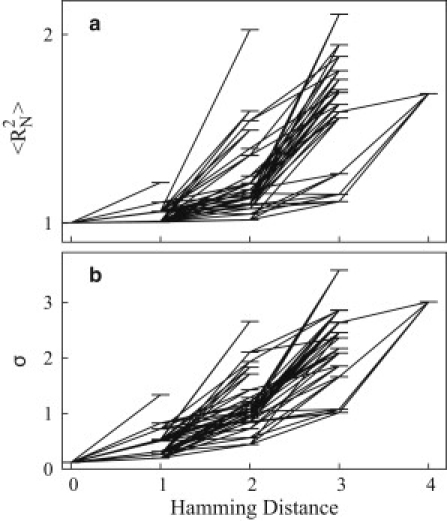
Generalization of the superfunnel paradigm. Funnel-like organization of variation of 〈$R_N^2$〉 (a) and σ (b) with Hamming distance (number of single-point mutations) from the prototype sequence. Results shown are for the 48 g = 1 sequences in the HP model neutral net described in the text. Horizontal lines indicate the sequences' 〈$R_N^2$〉 and σ-values computed at ɛ = –5. Inclined lines connect pairs of sequences that are single-point mutants of each other, as in the original superfunnel drawing in Fig. 2a of Bornberg-Bauer and Chan (9). The relationship between 〈$R_N^2$〉 and σ for the sequences here and those in Fig. 5 are provided by Fig. S3.

Figure 5.

Funnel-like organization of variation of 〈$R_N^2$〉 and σ in an extended net for ($R_N^2$)₀ = 9 (ɛ = –5). Hamming distance is from a prototype sequence with the maximum number of 10 single-point mutants in the net. Data plotted in black in panels a and b are for the 52 g = 1 sequences studied by Fig. S2, b and d; those plotted in light blue are for 83 g > 1 sequences in an extended net containing a total of 135 sequences for which every ground-state conformation has ($R_N^2$)₀ = 9. Mutational connections between g = 1 sequences are in black, those involving g > 1 sequences are in light blue. The plotting convention in panels a and b is otherwise the same as that in Fig. 4. (c) Average ground-state degeneracy as a function of Hamming distance.

Under conditions favoring folding, the organizations of both 〈$R_N^2$〉 and σ in Fig. 4 resemble the superfunnel pattern of native stabilities for the same neutral net (Fig. 2a of Bornberg-Bauer and Chan (9)). The role of the prototype sequence in a sequence-space superfunnel for evolution is analogous (9) to that of the native structure in a conformational-space funnel for protein folding (27,29,56). Here, we find that the prototype sequence is also the sequence that has the minimum 〈$R_N^2$〉 as well as the minimum fluctuation σ. This trend means that selecting for a mutant with a smaller 〈$R_N^2$〉 would most likely lead to a mutant with a reduced σ as well, and vice versa. Essentially all 99 mutational connections in Fig. 6 have positive slopes and thus are funnel-like (9,13,15): The number of connections accompanying a decrease in Hamming distance with a decrease in 〈$R_N^2$〉 and σ are, respectively, 97 and 99.

Figure 6.

Correlation between conformational fluctuation and mutational effect. All results shown are for ɛ = –5. Panels a–c are for the g = 1, ($R_N^2$)₀ = 1 sequences in Fig. 4. Panels d–f are for the ($R_N^2$)₀ = 9 sequences in Fig. 5, with data involving g > 1 sequences plotted in light blue. Each data point in panels a and d represents a sequence. Each data point in panels b, c, e, and f represents a mutation, showing the σ-value of a given sequence and the change, Δ〈$R_N^2$〉, in the Boltzmann average 〈$R_N^2$〉 resulting from a mutation on that sequence. Scatter plots in b and e (middle column) and in c and f (right column) are for mutations that change the Hamming distance, respectively, by –1 and by +1 in Fig. 4 or Fig. 5. The curves in panels b and e show the theoretical expression $\sigma =C\sqrt{|\Delta \langle R_N^2\rangle |}$ obtained by least-square fitting our model data to σ² = C²|Δ〈$R_N^2$〉|, with C = 3.26 for panel b and C = 5.0 and 4.2 (in units of lattice bond length), respectively, for the Δ〈$R_N^2$〉 < 0 and Δ〈$R_N^2$〉 > 0 data points in panel e. The Pearson correlation coefficients are, respectively, r = 0.85, 0.82, and 0.28.

Fig. 5 shows the largest net of g = 1 sequences with ($R_N^2$)₀ = 9 and its extension to include g > 1 sequences with the same uniform ($R_N^2$)₀ = 9. The g = 1 net covers two different ground-state conformations, whereas the entire extended net covers a total of 11 different ground-state conformations. The prototype sequence has an 〈$R_N^2$〉 value very close to 9 (Fig. 5 a). It also has the minimum σ among the sequences in this net (Fig. 5 b). The population of g > 1 sequences is concentrated in the middle range of Hamming distances from the prototype sequence (Fig. 5 c). As expected from the two-sided funnel patterns in Fig. 3, b and d, Fig. 5 a shows that as Hamming distance decreases, the 〈$R_N^2$〉 value for the prototype sequence is approached both from above and from below. Both of these tendencies are concomitant with a unified trend of decreasing σ (Fig. 5 b). There are a total of 272 mutational connections in the extended net in Fig. 5, 86 of which are between g = 1 sequences. We define a funnel-like connection for 〈$R_N^2$〉 as one that accompanies a decrease in Hamming distance with a decrease in the absolute value of the difference between the sequence's 〈$R_N^2$〉 and that of the prototype sequence. Such a connection can have either a positive or a negative slope. A funnel-like connection for σ is defined as for Fig. 4 above and always has a positive slope. Most of the connections in Fig. 5 are funnel-like in this regard: In Fig. 5 a, 219:272 = 80.5% of the connections for the extended net, and 70:86 = 81.4% of the connections between g = 1 sequences satisfy the above funnel-like criterion. Likewise, in Fig. 5 b, 241 (88.6%) of all connections and 82 (95.3%) of the g = 1 connections are funnel-like. These percentages of funnel-like connections in Fig. 5 are high but not as high as the 98.0% or 100% for the neutral net in Fig. 4, indicating that there is more sequence-space ruggedness (9) in Fig. 5. Nonetheless, the general superfunnel-like organization in Fig. 5, a and b, implies that selecting for a mutant with a smaller σ in this net would most likely shorten the Hamming distance from, and reduce the difference in 〈$R_N^2$〉 with the prototype sequence.

Each of the nets in Figs. 4 and 5 thus represents a funnel-like organization centered around a prototype sequence with the least fluctuation σ in $R_N^2$. It follows from previous analyses of the effect of sequence-space topologies on evolutionary dynamics (9,17,57) that such an organization entails a tendency for the minimum-σ prototype sequence to achieve a higher steady-state evolutionary population than any other sequence in the same net. Are the mutational changes in 〈$R_N^2$〉 in these nets governed by σ as in Eq. 5? We address this question in Fig. 6. Mirroring the overview in Fig. 3, b and d, the σ-versus-〈$R_N^2$〉 scatter plot in Fig. 6 a for the ground-state ($R_N^2$)₀ = 1 neutral net shapes like a one-sided funnel, whereas that in Fig. 6 d for the ($R_N^2$)₀ = 9 net shapes like a two-sided funnel. We next consider mutational changes, Δ〈$R_N^2$〉, in the two nets. Here, Δ〈$R_N^2$〉 is the 〈$R_N^2$〉 value of the mutant sequence after the mutation minus that of the original sequence before the mutation. Following the formulation of Sato et al. (37), Δ〈$R_N^2$〉 is plotted against the σ-value of the original sequence before the mutation.

Fig. 6 separates the mutations into two classes: Those that move toward (namely b and e); and those that move away (namely, c and f) from the prototype sequence. Our results show a marked difference between them. Whereas mutations toward the prototype sequence exhibit a reasonable conformity to Eq. 5 (see fitted curves), no similarity with Eq. 5 is discernible for mutations that move away from the prototype sequence (largely random scatter) in Fig. 6, c and f. In Fig. 6, b and e, the C ∼ b(Δa) values for the fitted curves are similar although they are not identical. Moreover, in Fig. 6 e, the HP model data for the Δ〈$R_N^2$〉 < 0 mutations fit significantly better with Eq. 5 than those for the Δ〈$R_N^2$〉 > 0 mutations. Because an overwhelming majority of the mutations that move away from the prototype sequences in Figs. 4 and 5 increase fluctuation σ, the different behaviors for the two classes of mutations in Fig. 6 suggest that the relation in Eq. 5 is more likely to be viable for protein mutations toward more ordered conformations (with smaller σ-values) but less likely to hold for mutations toward more disordered conformations (with larger σ-values). In light of this asymmetry, it is noteworthy that in the original artificial evolution experiment on mutants of a GFP in bacteria (37,38), Eq. 5 was verified for mutations that increase fluorescence intensity but was not tested for mutations that decrease fluorescence intensity.

Thus, although the

$$\sigma =C\sqrt{|\Delta \langle R_N^2\rangle |}$$

relation stipulated by Eq. 5 fits reasonably with mutations toward the prototype sequences in a net, the data in Fig. 6 also exhibit substantial scatter. To further assess the viability of the idea behind Eq. 5, we now take a global view by considering all 18 × 2¹⁸ single-point mutations in our model (Fig. 7). These mutations include, but are not restricted to, those in the relatively small networks in Figs. 4–6. Now, we assess the evolvability of 〈$R_N^2$〉 of every sequence by performing all 18 possible H → P or P → H substitutions on it to identify the mutation that leads to the largest possible decrease in 〈$R_N^2$〉 (minimum Δ〈$R_N^2$〉, steepest descent) and the mutation that leads to the largest increase in 〈$R_N^2$〉 (maximum Δ〈$R_N^2$〉, steepest ascent). The resulting scatter plots of σ with these minimum and maximum Δ〈$R_N^2$〉 values for all sequences are shown, respectively, in Fig. 7, a and b.

Figure 7.

Phenotypic fluctuation and evolvability. Δ〈$R_N^2$〉 is the change in a sequence's 〈$R_N^2$〉 as a result of a single-point mutation, and Δg is the corresponding change in ground-state degeneracy. Data shown are computed at ɛ = –5 for all 2¹⁸ sequences in the model. The scatter plots a and c are for mutations that achieve the largest possible decreases (steepest descent) in 〈$R_N^2$〉; scatter plots b and c are for mutations that achieve the largest possible increases (steepest ascent) in 〈$R_N^2$〉. The lines in panel a are the approximate boundaries of the distribution discussed in the text. In panels c and d, mutations that cause no change in ground-state degeneracy are marked by the vertical line at Δg = 0. In panel a, the data points lining up horizontally at σ = 35.4 are for the h_N = 0 sequences. Note that some h_N = 1 sequences have σ-values larger than that of the h_N = 0 sequences; e.g., an h_N = 1 sequence that allows an HH contact between positions 2 and 17 has σ = 37.3.

The two scatter plots are dramatically different. Because of how the mutations are chosen above, it is not surprising that Δ〈$R_N^2$〉 < 0 for almost all steepest-descent mutations and Δ〈$R_N^2$〉 > 0 for almost all steepest-ascent mutations. What is striking, however, is that a correlation between σ and Δ〈$R_N^2$〉 exists for the steepest-descent mutations in Fig. 7 a but no meaningful correlation is observed for the steepest-ascent mutations in Fig. 7 b. This asymmetry between Fig. 7, a and b is similar to that in Fig. 6 between the two classes of mutations moving in opposite directions with respect to the prototype sequence. A reason for the similar trends may be that in Fig. 6, 〈$R_N^2$〉 decreases for most mutations toward the prototype sequence whereas 〈$R_N^2$〉 increases for most mutations away from the prototype sequence, even though the steepest-descent and steepest-ascent mutations in Fig. 7 were not constructed with respect to any prototype sequence.

For the steepest-descent mutations in Fig. 7 a, large decreases in 〈$R_N^2$〉 are possible only for sequences with large fluctuations in $R_N^2$. Fig. 7 a shows clearly that the magnitude of the mutational change Δ〈$R_N^2$〉 is limited by σ of the original sequence. The trend may be summarized, very roughly, by the inequalities Δ〈$R_N^2$〉 > –4.8σ for σ ≲ 3 (Δ〈$R_N^2$〉 ≳ –13) and Δ〈$R_N^2$〉 > –1.2σ –10 for σ ≳ 3 (Δ〈$R_N^2$〉 ≲ –13). (Note that Δ〈$R_N^2$〉 and σ have the same [length]² unit.) However, Fig. 7 a also shows that having a large σ, per se, is not sufficient to guarantee a sequence's ability to achieve a large mutational decrease in 〈$R_N^2$〉. For σ ≲ 15, Δ〈$R_N^2$〉 for different sequences may take virtually any value within a range from Δ〈$R_N^2$〉 ≈ 0 to the approximate lower bounds delineated above. For σ ≳ 15, the largest Δ〈$R_N^2$〉 values become negative, roughly satisfying the inequality Δ〈$R_N^2$〉 < –1.2σ + 17.6. This trend indicates that for each of these sequences with larger fluctuations in $R_N^2$, at least one mutant can bring about an appreciable decrease in 〈$R_N^2$〉, although the magnitude of that decrease may still be substantially smaller than –Δ〈$R_N^2$〉 ≈ 1.2σ + 10.

In stark contrast, the steepest-ascent mutations in Fig. 7 b do not show any of the above-described or other correlative features between σ and Δ〈$R_N^2$〉. This lack of correlation means that a sequence's fluctuation in $R_N^2$ alone is not predictive of its evolvability to another sequence with a larger 〈$R_N^2$〉. Fig. 7, c and d, show further that the changes in ground-state degeneracy g for the steepest-descent and steepest-ascent mutations are also very different. Steepest-descent mutations tend to decrease ground-state degeneracy, and in this respect making the sequence more similar to natural globular proteins. For the data in Fig. 7 c, the median and average values of Δg are, respectively, –28 and –2.6 × 10⁴. This trend means that selecting for a mutant with smaller 〈$R_N^2$〉 would likely yield, as a byproduct, a mutant that also has fewer ground-state conformations. Such coevolution of various properties of the same sequence may be viewed as a single-genotype analog of the hitchhiking effect (58). Steepest-ascent mutations, however, tend to lead to large increases in ground-state degeneracy. For the data in Fig. 7 d, the median and average values of Δg are, respectively, +282 and +2.2 × 10⁵. It will be instructive to explore how the lack of correlation between fluctuation and evolvability among the steepest-ascent mutations in Fig. 7 b might be related to the more rugged conformational landscapes (27–29) entailed by the Δg > 0 increases in Fig. 7 d.

To ascertain the robustness of the trend we observed, we have also investigated the relationship between σ and Δ〈$R_N^2$〉 for all single-point mutations at ɛ = –2, –3, and –4 (detailed results not shown). In addition, we have also studied single-point mutations with steepest descents (maximum decreases) and steepest ascents (maximum increases) in fluctuation σ (Fig. S4). In all of these other studies, a level of correlation between σ and Δ〈$R_N^2$〉 similar to that in Fig. 7 a was observed for mutations with steepest descents in either Δ〈$R_N^2$〉 or σ. However, as in Fig. 7 b, no correlation was observed for corresponding mutations with steepest ascents.

We have also generalized the interpretation of Eq. 5 to consider the relationship between Δ〈$R_N^2$〉 and the standard deviation of $R_N^2$ of the mutated sequence (denoted as σ(final)) instead of σ for the original sequence. For the results in Fig. 6, b, c, e, and f, changing the variable σ to σ(final) amounts to swapping Fig. 6 b with c, swapping Fig. 6 e with f, and changing the sign of Δ〈$R_N^2$〉. It is clear from the existing results in Fig. 6 that after these changes the same data would indicate a correlation of σ(final) with Δ〈$R_N^2$〉 for mutations away from the prototype sequence (especially those leading to an increase in both σ and 〈$R_N^2$〉) but not for mutations toward the prototype sequence. For the steepest-descent and steepest-ascent results in Fig. 7 for all sequences, although the scatter plots for σ(final) (Fig. S5) are not exact mirror images of those for σ, they nonetheless show a degree of correlation of σ(final) with steepest-ascent mutations toward larger 〈$R_N^2$〉 (Fig. S5 b) but not with steepest-descent mutations toward smaller 〈$R_N^2$〉 (Fig. S5 a). This behavior thus follows a trend similar to that for σ(final) deduced above for the ($R_N^2$)₀ = 1 and ($R_N^2$)₀ = 9 nets in Fig. 6. Therefore, our results suggest in general that for a pair of sequences that differ by one single-point substitutive mutation, the magnitude of the difference Δ〈$R_N^2$〉 between the sequences of the pair tends to correlate with the larger but not with the smaller of the two σ-values for the two sequences.

Taken together, our results indicate consistently that conformational fluctuation of a sequence is correlated with evolvability of that sequence toward a mutant with decreased conformational fluctuation (smaller σ, more order); but the extent of conformational fluctuation by itself is not predictive of a sequence's evolvability toward a mutant with increased conformational fluctuation (larger σ, less order). Therefore, it appears that the fluctuation-response idea of Sato et al. (37) is applicable, with caveats, for protein mutations toward more ordered conformational states; but the idea may not be so applicable for protein mutations toward more disordered conformational states.

Conclusions

Using a simple exact model of the mapping between protein sequence and structure, we have now characterized several statistical mechanical aspects of the relationship between evolvability and single-genotype phenotypic fluctuation, which was modeled as conformational fluctuation of a single model protein sequence. Biological functions of proteins are often related to conformational fluctuations (59). For single-domain cooperatively folding proteins (51), native conformational fluctuation is often small (60), perhaps to guard against harmful aggregation. For larger proteins, however, conformational flexibility is often critical for function (59). Here, we have verified that a simple formula proposed by Sato et al. to relate fluctuation and response (37) can indeed provide a semiquantitative rationalization for the correlation between evolvability and fluctuation among the mutations that move sequences toward the prototype sequence of a superfunnel (9) (Fig. 6). At the same time, the present explicit-chain modeling has also revealed subtle, unanticipated aspects of the fluctuation-evolvability relationship. Our results suggest that significant single-genotype phenotypic fluctuation is, in general, a likely requirement for a sequence's evolvability to other sequences with less phenotypic fluctuations. However, not every sequence with significant single-genotype phenotypic fluctuation is highly evolvable. Although single-genotype phenotypic fluctuation is an indicator of evolvability toward more conformational order, single-genotype phenotypic fluctuation per se is not predictive of evolvability toward less conformational order. These asymmetric behaviors deserve more future theoretical attention; and it would be extremely interesting to inquire experimentally whether a similar asymmetry exists in the evolution of real polypeptides.

Supporting Material

Five figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00326-7.