Abstract
F1-ATPase is a rotatory molecular motor fueled by ATP nucleotides. Different loads can be attached to the motor axis to show that it rotates in main discrete steps of 120° with substeps of ∼80° and 40°. Experimental data show the dependence on the mean rotational velocity ω with respect to the external control parameters: the nucleotide concentration [ATP] and the friction of the load γL. In this work we present a theoretical analysis of the experimental data whose main results are: 1), A derivation of a simple analytical formula for ω([ATP], γL) that compares favorably with experiments; 2), The introduction of a two-state flashing ratchet model that exhibits experimental phenomenology of a greater specificity than has been, to our knowledge, previously available; 3), The derivation of an argument to obtain the values of the substep sizes; 4), An analysis of the energy constraints of the model; and 5), The theoretical analysis of the coupling ratio between the ATP consumed and the success of a forward step. We also discuss the compatibility of our approach with recent experimental observations.
Introduction
The cell is a complex system that is out of equilibrium. To maintain such a state and fulfill its tasks, the cell needs a continuous income and outcome of matter and energy. Molecular motors are the machinery in charge of performing such functions. No matter how small the motor is, it must obey the laws of physics in addition to those of chemistry to perform the task it has evolved to do. Moreover, these motors perform this work successfully despite the highly noisy media in which they live.
To perform these tasks, molecular machines must obtain energy from the hydrolysis of nucleotides such as ATP or from the membrane electrochemical potential. For instance, kinesin is a molecular protein delivering vesicles in the cell using microtubules as tracks. Kinesin transforms the ATP hydrolysis energy into translational motion. Kinesin is a linear motor (1) but rotatory motors also exist, such as bacterial flagellar motor (2) or F0F1-ATP synthase (3).
In particular, the F0F1-ATP synthase is a complex machine composed of two main rotatory units (F0 and F1) that act as two coupled motors. Both units F0 and F1 are joined through the central γ-shaft, which transmits the rotatory motion between them (3). When the F0 motor dominates the motion, it transforms a proton gradient into a rotatory motion that is used by the F1 motor part to catalyze ATP synthesis out of its hydrolysis products. Furthermore, in the reverse way, the F1 can perform the opposite task of hydrolyzing ATP and transmitting the mechanical motion to the F0, which acts now as an ion transmembrane pump. Moreover, the F1 can be isolated to study the mechanical properties of the rotation induced by the ATP hydrolysis process. This is designated “F1-ATPase”. We are interested in this setup. The experimental situation for our study is described below.
Our quantitative study is focused on the extensive amount of experimental data from the F1 obtained from the thermophilic bacterium PS3. The extension to F1 motors from other organisms (4,5) can be performed by pursuing the same methodology as presented here.
In the experimental setup, different loads are attached to a bulge in the γ-shaft (6), and their rotation angle can be measured with laser dark-field microscopy, enabling us to obtain data for a wide range of different dissipative loads γL and nucleotide concentrations [ATP] (4,7,8). The experimental output is a series of trajectories of the rotational angle of the load, which can be identified with the rotational angle of the motor axis θ(t). From this information the mean angular velocity can be obtained. This empirical information and data from some of the more-recent studies in the literature (9–12) constitute the starting point of our study.
Short time experimental observations show that the motion of the load is discretized in single main steps of one-third of a turn (7),
coinciding with the conformational symmetry of the F1 unit (formed by a cycle of three αβ-subunits). The steps are separated by ATP dwell waiting times in which the shaft does not advance. It is thus accepted that the γ-shaft has one steady state in each αβ-subunit and that the hydrolysis of one ATP induces a conformation change of the pair αβ with the final result of one step, Δθ0, of the γ-shaft (13). Moreover, experiments with higher resolution reveal that each step is divided in two consecutive substeps of ∼80° and ∼40° (8,14). This fact implies that two different dynamical stroke processes occur. The values of these empirical torques are of special relevance for an appropriate choice of the model.
By using longer time trajectories, the mean angular velocity of the load can be calculated as
This allows us to obtain the dependence relation between the mean velocity with friction of the load γL or the ATP concentration (1). Two important facts are observed in experimental data when varying the friction of the load: For loads below a certain value, the velocity of the motor saturates, whereas for larger loads, the velocity is independent of [ATP]. The velocity relation with [ATP] follows a Michaelis-Menten law behavior, as expected from its enzymatic nature: for low values of ATP concentration, the velocity is proportional to it and it saturates at high values (8). Moreover, in the low [ATP] regime, the velocity does not depend strongly on the friction of the load. This is a signature of dissipative torques. A different dependence is observed for conservative forces as those in kinesin experiments (15).
In addition, another set of recent experiments gives extra experimental information. The hydrolysis free energy of the ATP has been used as a control parameter (9). In these experiments, the value of the free energy is observed to affect the dwell times. This result supports the enzymatic nature of the dwell times. Other experiments have been performed by using assisting or hindering conservative torques that show strong effect in both mean velocity and dwell time (10,11).
In this article, we will take into account all these experimental facts to propose a theoretical physico-chemical model. The structure of it is the following. In the next section, we perform a deterministic analysis of the most relevant mechanisms, which gives a preliminary but very reliable predictive information to interpret the experimental data and to support an analytical basis of the mechanico-chemical steps involved. With this information, a flashing ratchet model is proposed that returns a proof of the substep sizes and torques. Then the stochastic complete model is solved by using numerical simulations with emphasis in the energy balances and the error rates. Finally, we draw the conclusions.
Deterministic analytical approach
The experimental data can be classified in two sets: the short timescale measures in which the step-by-step movement of the shaft is observed; and the long timescale data that shows the mean velocity relation. These sets of results are not independent. Our theoretical analysis of the short-time behavior leads to the prediction of the long-time behavior.
Mean angular velocity prediction
We initially consider only the total angular step of one-third of a turn, Δθ0 = 2π/3. As this value is fixed by the biochemical structure of the motor, the final mean velocity ω of the shaft will be determined by an estimation of the time intervals ti of the different processes involved to perform this step (16):
| (1) |
Although the number of possible ti could be large, we will consider here a minimum set of three: an internal time t0; the dwell time t1; and the mechanical time tmech.
The first time value, t0, is an internal independent time that has to be estimated from experimental data. This time includes all the intrinsic times of the motor (such as catalytic dwells) that do not depend on the ATP concentration.
The second time value, t1, is the ATP dwell time (i.e., the time for the ATP to reach the empty catalytic site of the motor). It is inversely proportional to the ATP concentration:
| (2) |
The addition of both times t0 and t1 is responsible for the Michaelis-Menten behavior of the motor. It can be understood in terms of a minimum dwell time t0 for the ATP saturation regime and a simple dependence on [ATP] through the affinity constant kMM. Due to the enzymatic nature of these times, they will be referred to herein as “chemical times”.
As there is no net movement of the shaft during the chemical times, the parameters t0 and kMM can be extracted from the experimental information of the dwell times in the rest state, by fitting a Michaelis-Menten dependence, following the same procedure as in Yasuda et al. (8). The parameter values obtained are t0 = 2 ms and kMM = 17 μM.
The remaining process is the power stroke involved in the mechanical motion along the angular step Δθ0 that lasts a time tmech. To find an expression for tmech, it is necessary to characterize the dynamics of the shaft. Assuming that there is a tight coupling between motor and load (we will check this assumption below), and that molecular motors live in a very small Reynolds number medium (no inertial contribution is considered), the angular velocity ωmech of the load under a torque τ follows that
| (3) |
where γ0 is the effective internal friction of the shaft and γL the friction of the load. The motor torque exerted on the shaft is approximated by
| (4) |
where ΔGATP is the available free energy from the ATP hydrolysis. From Eqs. 3 and 4, we find that the mechanical time is
| (5) |
The present time classification, in terms of chemical and mechanical times, is based on dwell and stepping times and is not intended for the separation of the mechanical and chemical mechanisms of the motor. Indeed, mechanical and chemical regimes are always mixed and have to be addressed at the same time.
Now we are ready to write a simple but explicit expression for the mean velocity (Eq. 1) as a function of the external control variables: γL and [ATP],
| (6) |
This explicit formula is the first analytical result of this article. Parameters t0 and kMM are taken directly from experimental data in Yasuda et al. (8). The choice of a value for the friction parameter γ0 needs an explanation. Although the value of the friction of the load can be calculated (4,7) and the value of the ATP hydrolysis energy is delimited, the value for the friction coefficient of the shaft is not well known and should be estimated from experimental data. In Yasuda et al. (8) the velocity versus the friction of the load (Fig. 1 a) shows a saturating regime or plateau for γL < 0.001 pN nm s. This limit corresponds to the situation in which the friction of the shaft is larger than the friction of the load (γ0 ≫ γL), and therefore, variations of the friction of the load can be neglected. On the other hand, for high values of the friction of the load, γL > 0.1 pN nm s, a log-log relation is found between the velocity and the friction of the load. This is the zone in which the friction of the shaft can be neglected over the friction of the load (γL ≫ γ0). Therefore, a value for the friction of the shaft is expected between 0.001 and 0.01 pN nm/s. A better refinement of these values can also be obtained by fitting our analytic formula versus experimental data (see Table 1). These parameter values are in agreement with the estimated values of Yasuda et al. (8). In Fig. 1 we can see that our analytical expression matches well with experimental data.
Figure 1.
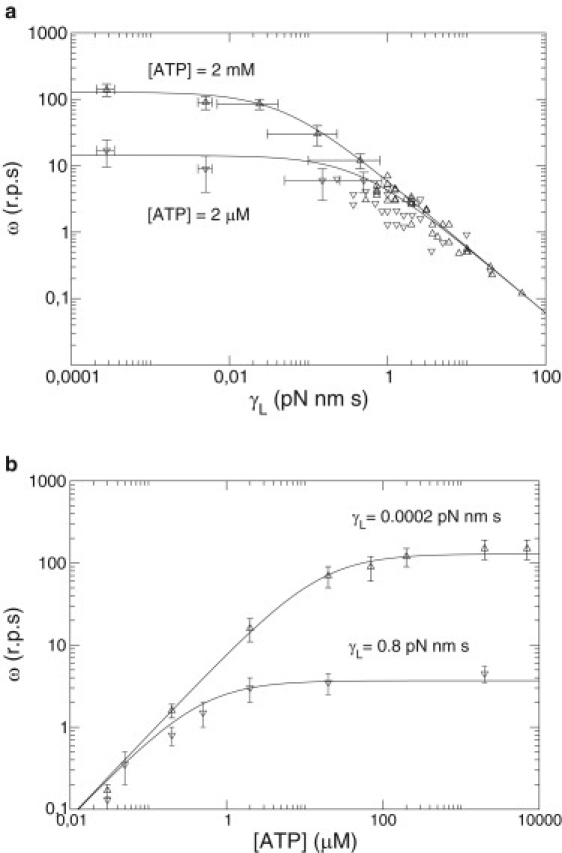
Mean angular velocity ω (revolutions per second) of the F1 motor versus experimental control parameters: load friction γL and ATP concentration. Experimental data (triangles) scanned from figures of Yasuda et al. (8), and derived from deterministic theoretical prediction (Eq. 6) (line). (a) Velocity-versus-load for two ATP concentrations. (b) Velocity-versus-[ATP] for two load frictions.
Table 1.
Parameters used for the comparison between the deterministic analysis (Eq. 6) and the experimental data (8)
| Model parameters | Symbol | Fit value |
|---|---|---|
| Chemical internal time | t0 | 0.0023 s |
| ATP affinity constant | kMM | 18 μM |
| Shaft friction coefficient | γ0 | 0.005 pN nm s |
| ATP hydrolysis energy | ΔGATP | 80 pN nm |
The mechanical torque predicted by this description returns the commonly used value τ ≃ 40 pN nm for ΔGATP ≃ 80 pN nm.
Substeps
A more-accurate time observation of the experimental trajectories reveals that the main discrete step of 120° is divided in two correlative substeps of sizes ∼80–90° and ∼40–30°, respectively (8,14).
The substepping mechanism can be related with two different energetic steps. In the first substep, associated with the ATP binding and hydrolysis, a deformation of the catalytic zone of the β-domain appears and the shaft advances ∼80°, whereas in the second substep, associated with the release of the chemical products, part of the hydrolysis energy, probably stored in elastic form, is recovered now by completing the second substep of ∼40° (8,13). This interpretation is compatible with the analysis performed in Hirono-Hara et al. (11).
The presence of two substeps implies that the mechanical time (Eq. 5) should be divided in two subintervals, tmech1 and tmech2, one for each stroke. Following the previous dynamical analysis (Eq. 4), the torque of each step may be written as
| (7) |
where E1, 2 and Δθ1, 2 are the energies and angles of each substep respectively, and the following constraints have been used,
| (8) |
The dynamics of the shaft needs a more detailed description of the motor. The experimental data of single trajectories point out that there are at least two main regimes of the motor: a relaxed or steady-state regime that corresponds to the regime in which there is no ATP in the catalytic site; and an excited state in which the ATP reaches the motor (where it is hydrolyzed) and the motor obtains the energy required to advance one step. These two states can be described by a flashing ratchet mechanism. This type of approach has been frequently used in theoretical models of molecular machines (17–19). As we will show, the substep phenomenology emerges naturally for the flashing ratchet description in which two advancing torques appear.
The relaxed or steady-state potential VR(θ, n) (see Fig. 2, top) is a symmetric ratchet with three minima in a whole turn, and at the nth step is
| (9) |
Figure 2.
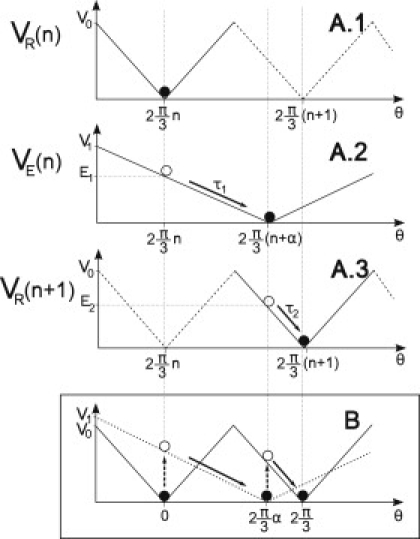
Dynamics of the two-states flashing ratchet model. (A1, A2, and A3) Detailed dynamics along the complete nth step. The step involves two flashes of the potential that perform two different strokes. The nth step starts when the motor switches the relaxed state potential VR(θ, n) (A1) to the excited state potential VE(θ, n) (A2) so VE(θ, n) produces a torque τ1 that moves the shaft to the minimum of VE(n), therefore performing the first substep. The length of the first substep is determined by the parameter α (0.5 < α < 1). After this substep, the motor switches the potential from VE(θ, n) (A2) to VR(θ, n + 1) (A3) so VR(θ, n + 1) produces a torque τ2 that moves the shaft to the minimum of VR(θ, n + 1), completing the second substep. The step is then finished and the shaft rests in the next minimum until a new excitation. In the scheme, the shaft is represented by a solid circle in the steady states and by an open circle in the transient ones. Solid lines show the potential acting on the γ-shaft in the corresponding state, and dashed lines indicate the periodicity of VR. (B) Merger of panels A1, A2, and A3 for a compact visualization of the whole step including the relaxed (solid line) and the excited (dotted line) potentials. Initial minimum is chosen at θ = 0, allowing us to compare angular distances. Along the step, this is equivalent to chose n = 0. Dashed arrows indicate potential switching.
The excited potential VE(θ, n) (see Fig. 2, middle) is a local potential that depends on the corresponding step index n of VR,
| (10) |
In Fig. 2 the flashing ratchet mechanism over one step is presented with the two conformations of the effective motor potential, indicating that the two substeps and parameters are also involved. The first substep and its torque takes place after the transition from VR(θ, n) to VE(θ, n). The second substep and its torque occurs after the transition from VE(θ, n) to VR(θ, n + 1), completing the whole step. The key point in this model is parameter α, which controls the first substep size, Δθ1 = αΔθ0 = α2π/3, where 0.5 < α < 1. Although its value is approximately known from experimental data, we present a theoretical derivation of it here.
Here, for the sake of simplicity, we will present the analysis of a particular case in which the values V0 = V1 and ΔGATP are fixed. This assumption reduces the number of free parameters and the calculation becomes analytically tractable. (In Section S1 of the Supporting Material, we present the analysis of a more-general case, i.e., V0 ≠ V1(ΔGATP), which illuminates the relation of the model parameters with ΔGATP. That analysis furnishes also the prediction that the substep length does not depend very much on the value of ΔGATP—thus remaining in a range close to the one predicted by the case V0 = V1.)
From the previous Eqs. 7–10 we see that torques, substeps, and the potential parameter V0 are related by
| (11) |
| (12) |
and by imposing the necessary energetic constraint (Eq. 8), one obtains
| (13) |
Under these circumstances the only free parameter in the system is α, which will determine the length of the substeps and their associated torques. It is expected that, due to evolution, molecular machines have to run in an optimal regime compatible with the physical constraints of the system. As there are more internal processes than the ones considered here, we postulate that the optimum regime will correspond to a maximum in the total mechanical time. This condition will favor the energy transduction from chemistry to mechanics.
The total mechanical time tmech can be evaluated as
| (14) |
To find the value αM (for the parameter α) that maximizes the mechanical time, we impose
obtaining the maximum time condition
| (15) |
giving the solution
which corresponds to a maximum with angular substeps,
(see Fig. 3). These values are in agreement with the angles found experimentally. This is an important result of the model, as the theoretical values found do not depend, in this particular case, on any parameter of the model such as the friction or the energy input.
Figure 3.
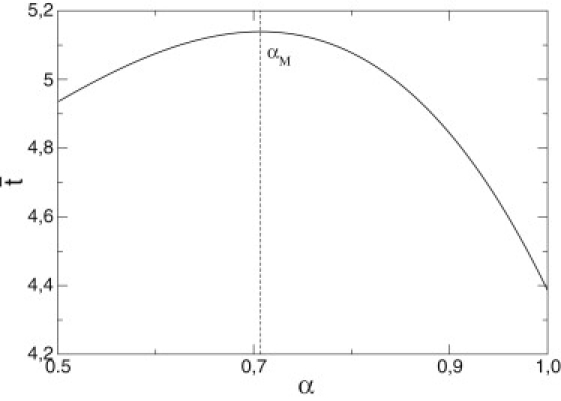
Dimensionless mechanical time , as a function of the parameter α. It shows a maximum for αM ∼ 0.71 (dashed line), which corresponds to a substep angle of ∼85°.
From this description there are now two different torques acting in the model whose magnitude depends on the ATP hydrolysis energy and the substep angle, obtaining τ1 ≃ 27 pN nm and τ1 ≃ 65 pN nm, respectively, for a ΔGATP ≃ 80 pN nm. For other F1 motors from other organisms, similar torque values are expected because they only depend on ΔGATP and the substep sizes.
Experimental measures on the excited potential are available through the study of the ADP-inhibited conformation. The ADP-inhibited conformation corresponds with the state where the first substep is completed but the system is unable to flash to the relaxed potential. Experimental measures on the ADP-inhibited conformation angular potential (11) show that it matches up very well with the excited potential used, and also presents an average torque smaller than 40 pN nm. There are also experiments in the literature showing that the torque is not constant along the whole step, but instead has a defined angular distribution (20) oscillating at ∼30 and 70 pN nm. Our theoretical result is also in agreement with the low stall forces that were measured in experiments by Watanabe-Nakayama et al. (10), as it is only needed to oppose the smaller of the two torques to stall the motor. (However, due to a conservative hindering force, quantification of this latter argument does need to be contrasted with the inhibition (21).)
The stochastic complete model
When the position of the load is observed in the experiments, it presents large fluctuations. These fluctuations make it difficult to appreciate all the substepping phenomenology. Nevertheless, substeps can be observed for low [ATP] and small loads. Here we will present a stochastic model that exhibits this randomness, and whose results compare better with experimental data.
As it is usual in theoretical descriptions of molecular motors based in flashing ratchet potentials, we start with a Langevin equation in the overdamped limit. The equation is written for the two degrees of freedom of our system: the rotation angle of the shaft θ, and the rotation angle of the bead ϕ, which is the measured variable (see Fig. 4). Both variables are treated as separate entities because the shaft's bulge is not rigid (12). The joining potential of both units has been chosen to be a harmonic potential of stiffness κ,
| (16) |
Figure 4.
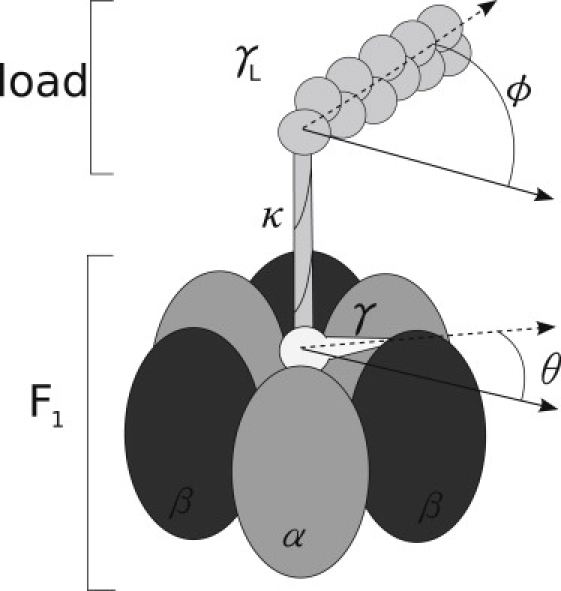
Scheme of the F1ATPase motor and the attached load with the main variables and parameters used in the models.
The equations of motion are
| (17) |
where γ0 and γL are the friction parameters of both variables; κ is the stiffness of the harmonic coupling between the shaft and the load; and ξ(t) and ξL(t) are Gaussian, and are white thermal noises that are fulfilled by the relations
| (18) |
| (19) |
All the dynamics are determined by the flashing ratchet potential VR, E (introduced in Eqs. 9 and 10, and in Fig. 2), which acts directly on the shaft. As our interest here is to analyze the experiments with a dissipative load, we have not considered a conservative torque in the expressions in Eq. 17 (although it can be included).
The movement of the load is governed by the forces transmitted by the shaft through the linking term κ(θ − ϕ). The rigid shaft-load limit can be recovered by setting θ − ϕ = 0, which reduces the system to a one-variable problem,
| (20) |
with a new noise correlation,
| (21) |
which is equivalent to the equation used above for the deterministic guess, but with an additional white noise term, and an effective friction coefficient γeff ≡ γ0 + γL.
For a full representation of the model, we need to propose the values of the mean times tR and tE that the system spends in the relaxed and excited states, respectively. The time in the rest state tR has two contributions: the ATP dwell time s for a new ATP binding event; and the mechanical time tmech 2 of the second substep once the excitation is finished. This is
| (22) |
The dwell time s is a stochastic process with a mean value of t1 (Eq. 2). As the probability to absorb an ATP molecule is time-independent, the ATP dwell time probability distribution follows an exponential behavior of
| (23) |
The time tmech 2 needed to complete one of the mechanical processes cannot be defined quite as straightforwardly due to its complex mechano-chemistry. A constant time to make the process may be expected if related with the set of coupled reactions needed to perform the step (13). A reasonable time for this process corresponds to the deterministic mechanical time previously obtained in Eq. 14. Therefore, the excitation does not finish when the shaft reaches the energy minimum of the substep but when the time to perform the process finishes. In this interpretation, mechanical and chemical times are not independent, but instead, mixed in the ratchet states, as it is found experimentally (10,11).
By following the same analysis, it is found that the time the motor spends in the excited state tE involves two subintervals: the mechanical time tmech 1 to perform the first stroke; and the catalytic time t0. It is
| (24) |
These subintervals are plotted in Fig. 5. As in the previous case, the mechanical time tmech 1 is evaluated according to the expressions given by the deterministic analysis in Eq. 14.
Figure 5.

Simulated trajectory fragment in which the different characteristic time lapses are indicated. The figure also differentiates the times where the excited potential VE is active (shaded zones) from the times where the relaxed potential VR is active (nonshaded zones). For the sake of a better visualization, particular parameter values used are [ATP] = 2 μM and γL = 0.1 pN nm. For this case the characteristic timescales are of the same order.
In this model the source of stochasticity is twofold: the thermal noises affecting the trajectories of the shaft and the load; and the ATP waiting time s, which follows an exponential distribution (see Eq. 23).
Numerical simulation results
Taking these definitions into account, we have to proceed now with the explicit details of the simulation algorithm. Stochastic equations describing the complete model (Eq. 17) have been numerically simulated. Stochastic trajectories have been obtained by using a Heun method (22) for the numerical integration of the Langevin equations in a particular system state.
In Fig. 5, a complete step is plotted. The numerical trajectories are very similar to the experimental ones. We can see two differentiated regimes: the strokes during the advancing steps; and the plateaus during the dwell chemical activity.
The behavior of the mean velocity numerically obtained (Fig. 6) is very similar to the one predicted by the deterministic prediction (Eq. 6). However, the stochastic model fits better to experimental data for large values of the load (Fig. 7). For these values, the system exhibits missing events and the coupling ratio is <1. These missing events can be considered theoretically in the deterministic analysis obtaining a relation between coupling ratio and load friction. This calculation is presented in the next subsection.
Figure 6.
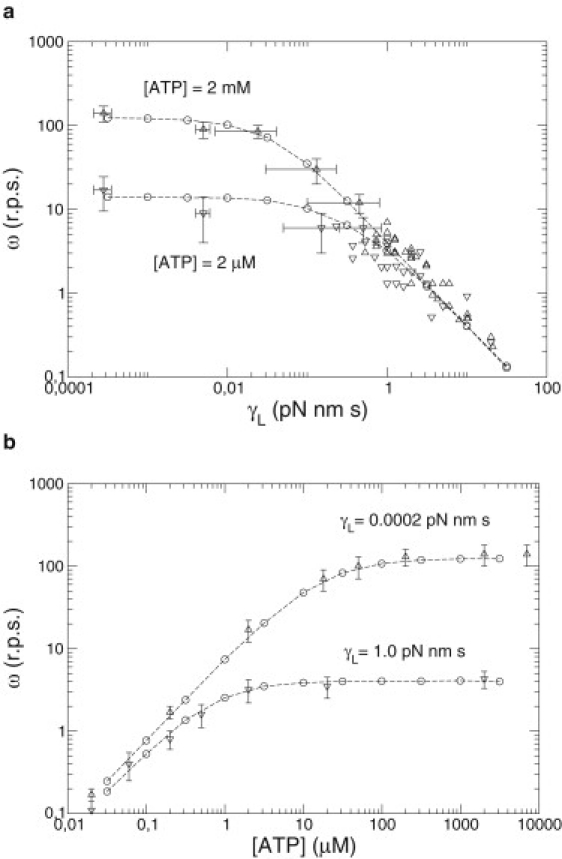
Mean angular velocity ω of the stochastic F1 motor. Experimental data (triangles) scanned from figures of Yasuda et al. (8) and derived from numerical simulations of the stochastic model (Eq. 17) (circles). (a) Velocity-versus-load friction for two different ATP concentrations. (b) Velocity-versus-[ATP] for two different load frictions. Dashed lines connect the numerical points.
Figure 7.
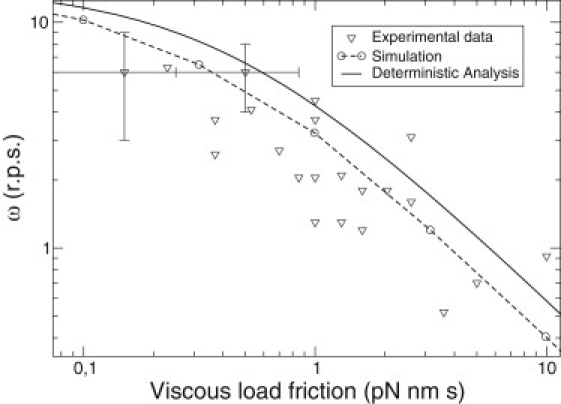
Magnified views of Figs. 1a and 6a to enable comparison of the results of the deterministic analysis, the stochastic simulations, and the experimental results for large values of the load. Dashed lines connect the simulation results.
In the simulation, a value of ΔGATP = 90 pN nm for the hydrolysis energy has been used, which is a little higher than that of the deterministic fit. For this new value the two torques are slightly increased, obtaining τ1 = 30 pN nm and τ2 = 73 pN nm.
Recent experiments show that the stiffness of the shaft is ∼750 pN nm (12). In our simulations, we observe that the performance of the motor does not depend on the flexibility of the shaft for κ > 200 pN nm (see section S3 in the Supporting Material), which justifies the simplification in Eq. 20. For the simulation, a value of κ = 500 pN nm was chosen for this parameter regime.
It is worth discussing here the energetics of the model. The energy transduced from the chemical energy of an ATP molecule into motion of the shaft in the model can be evaluated in each integration step ti of the simulation from the equations of motion, using the equation
| (25) |
In Fig. 8, it is observed that the energy is supplied to the motor in two stages, corresponding with the two torques of the system. Furthermore, we observe that the energy supplied by the ATP is consumed independently of the success of the step, so there is also energy consumption for missing steps. This follows from the dissipative and random nature of the system.
Figure 8.
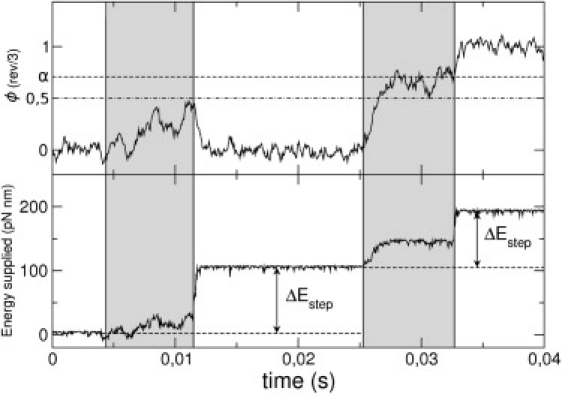
Numerical simulation of a trajectory of the load showing two ATP hydrolysis processes where the excited potential VE duration is marked by shaded zones. The first excitation results in a failed step, whereas the second results in a successful one. (Top) Angular trajectory of the load ϕ(t). When the excitation begins, the excited potential tries to perform the first substep driving the shaft to the minimum of VE (dashed line), but if the shaft does not exceed the angular position of the maximum of the relaxed state VR (dot-dashed line) at the end of the excitation, the shaft returns to the initial minimum of VR. (Bottom) Energy transferred during the evolution. Parameter values used: [ATP] = 2 μM and γL = 0.1 pN nm s.
An analytical approach to the coupling ratio
Let us now analyze the relation between an ATP consumed and a successful step: failed steps reduce the coupling ratio of the motor. For viscous friction of loads <0.01 pN nm, the coupling ratio of the motor is constant and near to 1, i.e., each ATP consumed corresponds to a successful step. However, there is a reduction of the coupling ratio for larger loads, in the zone where the mismatches with the deterministic guess are larger (Fig. 7). This is a clear signature of the inclusion of fluctuations in the model.
These failures happen mostly at the relaxation of the potential, upon switching from the excited to the rest potential, if the γ-shaft is not able to arrive on time to the next relaxed dip (Fig. 8). This occurs mainly for large values of the friction of the load, when the dynamics of the system shaft-load is slow. Thus, considering that this is the only source of failure, an approximation for the coupling ratio can be obtained which is an upper limit for the coupling ratio. This can be computed by solving the corresponding Fokker-Planck equation for the evolution of the probability distribution of the load during an excitation. The coupling ratio can be computed as the fraction of the distribution probability of the shaft that has surpassed the maximum of the relaxed potential when the excitation finishes (Fig. 9). Under this assumption, our analytical prediction for the coupling ratio CR(γL) is
| (26) |
with
| (27) |
where cr0 is an estimation of the maximum coupling ratio, and and are an estimation of the average and variance of the position of the shaft at the beginning of the stroke, respectively. (The value of the constant cr0, the dependence of and with the friction of the load, and the explicit details of the derivation of these expressions, are indicated in Section S2 in the Supporting Material.)
Figure 9.
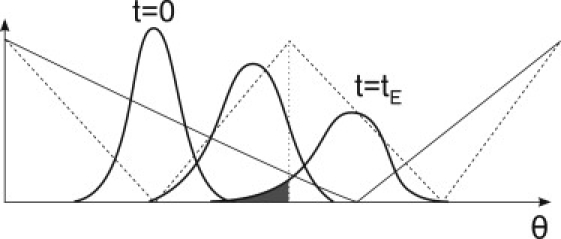
Scheme for the evolution of the probability distribution function of the shaft during an excitation. The shaded portion of the tail of the distribution at a time tE has been considered to be the probability to fail the excitation and fall back to the previous rest state. (Solid straight lines) VR; (dashed lines) VE.
We see in Fig. 10 that CR(γL) is a good predictor for the coupling ratio of the motor for all values of the friction. This result is interesting, as it constitutes an analytical approximation for the velocity of the motor which includes stochastic effects.
Figure 10.
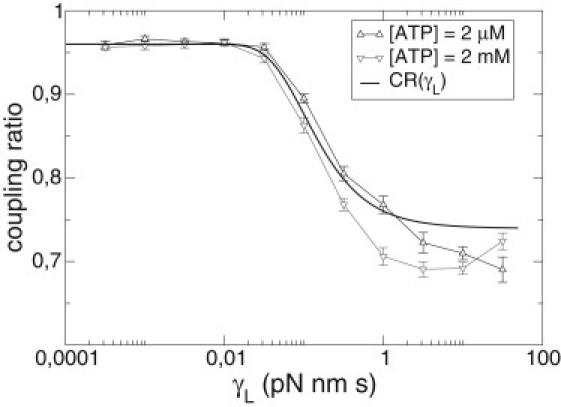
Results for the theoretical predicted coupling ratio (thick line) versus the viscous friction of the load for different ATP concentrations. (Triangles joined by lines) Numerical simulation data.
Conclusions
Using the experimental information of the F1-ATPase molecular motor from the thermophilic bacterium PS3, we have proposed a simple calculation tool and a ratchet flashing model to interpret experimental data. Our approach can be applied to other motors of the same family such as those of Escherichia coli (4) by changing specific values of t0, kMM, and γ0. These values will imply different mechanical times, but the stroke values have to be very similar, because they are related to ΔGATP and Δθ0 (which are common to both motors).
In a first approach, we have presented a deterministic analytical calculation to obtain a generic formula for the angular velocity ω([ATP], γL). This expression fits in quite well with the experimental data and gives information about the relevance of the different parameters of the system and their main variables: ATP concentration and load friction.
In a second approach, we have developed a two-state ratchet model that reproduces the experimental substep sizes directly from minimization arguments independently of the magnitude of the variables involved in the problem. Despite the simplicity of the model, it is interesting to see how the introduction of different mechanical substeps is able to explain the appearance of different torques during one step; this is compatible with the energetics of the hydrolytic process.
A more-inclusive model was then proposed, introducing the thermal fluctuations, excitation, and relaxation rates of the ratchet potential, and the stiffness of the joint between the load and the shaft. Thermal fluctuations were introduced by means of a Langevin force, while the rates were found by relating the different times of the motor with the nature of the different processes involved in one step. For this model, a better fit with the experimental data was found, especially for large values of the load when failed steps are observed. We also performed a study of the failed steps obtaining an analytical approximation for the coupling ratio of the motor.
Finally, our approach has a predictive power that can stimulate new experiments for this motor (for example, in determining the substep sizes dependence of ΔGATP and the particular values of the torques associated with each substep).
Supporting Material
Three sections, two figures, and 19 equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00279-1.
Supporting Material
Acknowledgments
We thank M. Ibanes for a critical reading of the manuscript.
We acknowledge financial support from projects No. FIS2009-13360-C03-01 (Ministerio de Educación y Ciencia of Spain) and No. 2009SGR14 (Generalitat de Catalunya), and R.P.-C. acknowledges grant No. FPU-AP2007-00987 (Ministerio de Ciencia e Innovación of Spain).
References
- 1.Block S.M., Asbury C.L., Lang M.J. Probing the kinesin reaction cycle with a 2D optical force clamp. Proc. Natl. Acad. Sci. USA. 2003;100:2351–2356. doi: 10.1073/pnas.0436709100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Berg H.C. The rotary motor of bacterial flagella. Annu. Rev. Biochem. 2003;72:19–54. doi: 10.1146/annurev.biochem.72.121801.161737. [DOI] [PubMed] [Google Scholar]
- 3.Yoshida M., Muneyuki E., Hisabori T. ATP synthase—a marvelous rotary engine of the cell. Nat. Rev. Mol. Cell Biol. 2001;2:669–677. doi: 10.1038/35089509. [DOI] [PubMed] [Google Scholar]
- 4.Spetzler D., York J., Frasch W. Microsecond timescale rotation measurements of single F1-ATPase molecules. Biochemistry. 2006;45:3117–3124. doi: 10.1021/bi052363n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gibbons C., Montgomery M.G., Walker J.E. The structure of the central stalk in bovine F1-ATPase at 2.4 Å resolution. Nat. Struct. Biol. 2000;7:1055–1061. doi: 10.1038/80981. [DOI] [PubMed] [Google Scholar]
- 6.Noji H., Yasuda R., Kinosita K. Direct observation of the rotation of F1-ATPase. Nature. 1997;386:299–302. doi: 10.1038/386299a0. [DOI] [PubMed] [Google Scholar]
- 7.Yasuda R., Noji H., Yoshida M. F1-ATPase is a highly efficient molecular motor that rotates with discrete 120° steps. Cell. 1998;93:1117–1124. doi: 10.1016/s0092-8674(00)81456-7. [DOI] [PubMed] [Google Scholar]
- 8.Yasuda R., Noji H., Itoh H. Resolution of distinct rotational substeps by submillisecond kinetic analysis of F1-ATPase. Nature. 2001;410:898–904. doi: 10.1038/35073513. [DOI] [PubMed] [Google Scholar]
- 9.Muneyuki E., Watanabe-Nakayama T., Noji H. Single molecule energetics of F1-ATPase motor. Biophys. J. 2007;92:1806–1812. doi: 10.1529/biophysj.106.097170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Watanabe-Nakayama T., Toyabe S., Muneyuki E. Effect of external torque on the ATP-driven rotation of F1-ATPase. Biochem. Biophys. Res. Commun. 2008;366:951–957. doi: 10.1016/j.bbrc.2007.12.049. [DOI] [PubMed] [Google Scholar]
- 11.Hirono-Hara Y., Ishizuka K., Noji H. Activation of pausing F1 motor by external force. Proc. Natl. Acad. Sci. USA. 2005;102:4288–4293. doi: 10.1073/pnas.0406486102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sielaff H., Rennekamp H., Junge W. Domain compliance and elastic power transmission in rotary F0F1-ATPase. Proc. Natl. Acad. Sci. USA. 2008;105:17760–17765. doi: 10.1073/pnas.0807683105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Oster G., Wang H. Rotary protein motors. Trends Cell Biol. 2003;13:114–121. doi: 10.1016/s0962-8924(03)00004-7. [DOI] [PubMed] [Google Scholar]
- 14.Shimabukuro K., Yasuda R., Yoshida M. Catalysis and rotation of F1 motor: cleavage of ATP at the catalytic site occurs in 1 ms before 40° substep rotation. Proc. Natl. Acad. Sci. USA. 2003;100:14731–14736. doi: 10.1073/pnas.2434983100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Visscher K., Schnitzer M.J., Block S.M. Single kinesin molecules studied with a molecular force clamp. Nature. 1999;400:184–189. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 16.Ciudad A., Sancho J.M. A unified phenomenological analysis of the experimental velocity curves in molecular motors. J. Chem. Phys. 2008;128:225107. doi: 10.1063/1.2937452. [DOI] [PubMed] [Google Scholar]
- 17.Astumian R.D., Bier M. Fluctuation driven ratchets: molecular motors. Phys. Rev. Lett. 1994;72:1766–1769. doi: 10.1103/PhysRevLett.72.1766. [DOI] [PubMed] [Google Scholar]
- 18.Jülicher F., Ajdari A., Prost J. Modeling molecular motors. Rev. Mod. Phys. 1997;69:1269–1282. [Google Scholar]
- 19.Reimann P. Brownian motors: noisy transport far from equilibrium. Phys. Rep. 2002;361:57–265. [Google Scholar]
- 20.Pänke O., Cherepanov D.A., Junge W. Viscoelastic dynamics of actin filaments coupled to rotary F-ATPase: angular torque profile of the enzyme. Biophys. J. 2001;81:1220–1233. doi: 10.1016/S0006-3495(01)75780-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ciudad A., Sancho J.M. External mechanical force as an inhibition process in kinesin's motion. Biochem. J. 2005;390:345–349. doi: 10.1042/BJ20042092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Garcia-Ojalvo J., Sancho J. Springer-Verlag; Berlin: 1999. Noise in Spatially Extended Systems. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


