Bidirectional Transport by Molecular Motors: Enhanced Processivity and Response to External Forces

Abstract

Intracellular transport along cytoskeletal filaments is often mediated by two teams of molecular motors that pull on the same cargo and move in opposite directions along the filaments. We have recently shown theoretically that this bidirectional transport can be understood as a stochastic tug-of-war between the two motor teams. Here, we further develop our theory to investigate the experimentally accessible dynamic behavior of cargos transported by strong motors such as kinesin-1 or cytoplasmic dynein. By studying the run and binding times of such a cargo, we show that the properties of biological motors, such as the large ratio of stall/detachment force and the small ratio of superstall backward/forward velocity, are favorable for bidirectional cargo transport, leading to fast motion and enhanced diffusion. In addition, cargo processivity is shown to be strongly enhanced by transport via several molecular motors even if these motors are engaged in a tug-of-war. Finally, we study the motility of a bidirectional cargo under force. Frictional forces arising, e.g., from the viscous cytoplasm, lead to peaks in the velocity distribution, while external forces as exerted, e.g., by an optical trap, lead to hysteresis effects. Our results, in particular our explicit expressions for the cargo binding time and the distance of the peaks in the velocity relation under friction, are directly accessible to in vitro as well as in vivo experiments.

Introduction

The complex internal structure of biological cells depends, to a large extent, on active transport by molecular motors moving along microtubules and actin filaments (1). Large-scale transport in cells is typically achieved by the cooperation of several motors, as recently shown both from the experimental (2–6) and the theoretical points of view (7–10). Moreover, transport in cells is often bidirectional, with cargos alternating between movements toward the microtubule plus end, driven, e.g., by kinesin-1 motors, and movements toward the microtubule minus end, driven by dynein motors. A central challenge is to understand how these opposing motors are coordinated (11–13). We have recently shown that the observed patterns of bidirectional movement can be explained by a stochastic tug-of-war, in which antagonistic motors exert pulling forces on each other (14–16). Indeed, two recent experimental studies provide direct evidence for this mode of motor interaction (17,18). The basic mechanism underlying fast bidirectional transport in a tug-of-war is provided by an instability arising from the force-dependent unbinding of the motors from the filament (14,15,19). Similar instabilities were also proposed to play a role in oscillations of muscle fibers (20,21), of the mitotic spindle (22), and of chromosomes in mitosis (23). In this article, we extend the analysis of our tug-of-war model to address cargo processivity, as well as the motion of the cargo in the presence of external forces as caused by cytoplasmic friction or by the action of an optical trap.

The processivity of a bidirectionally moving cargo is related to the time during which the cargo stays bound to the filament and the times during which it moves into each direction. Because these timescales determine the spatio-temporal distribution of cargos in the cell, they are crucial for the biological function of bidirectional transport, and are a prominent target of cellular regulation (11,12,24–28) as well as the focus of experimental studies of bidirectional transport (11,12,24–28). Our new results for these important quantities show that the motor parameters are optimized for bidirectional cargo transport, leading to fast bidirectional motion and enhanced diffusion. Furthermore, we present an explicit expression for the binding time of a cargo transported by two teams of motors, which shows that the binding time increases roughly exponentially with the motor numbers, similar to a cargo transported by only one team (2–4,8). This result is not obvious, as the motors are engaged in a tug-of-war and thus tend to pull each other off the filament, thereby reducing the cargo's binding time.

We then extend our theory to include external forces. We find that frictional forces, as imposed by the crowded and viscous cytoplasm (29), lead to peaks in the velocity distribution. External forces exerted by an optical trap can lead to hysteresis. Both predictions are accessible to experiments.

Theory for Stochastic Tug-of-War

In this section, we briefly review the main features of the stochastic tug-of-war between molecular motors as introduced in our previous work (14,15). A more detailed account can be found in Section S1 in the Supporting Material.

Description of single motor behavior

A single motor binds to the filament, walks along it, and unbinds from it stochastically with force-dependent rates derived from single molecule experiments. A motor that is bound to the filament unbinds from it with the unbinding rate (8,14)

$$\epsilon \left(F\right)={\epsilon }_0\exp \left[F/F_d\right],$$ (1)

which increases exponentially with the load force F, the force-scale being the detachment force F_d. The velocity of a single filament-bound motor decreases with the load force. The precise shape of the force-velocity-curve depends on the experimental conditions, such as the ATP concentration or the geometry of the linkage of the motors to the cargo (30,31), as discussed in Section S1 in the Supporting Material. For simplicity, the force-velocity curve is taken to decrease linearly from the forward velocity ν_F at zero load force to zero velocity at the stall force F_s. For superstall load forces, the motor moves backward very slowly (30), as characterized by the small backward velocity ν_B ≪ ν_F. Finally, an unbound motor binds to the filament with the load-independent rate π₀. The parameter values used for the plus-motor kinesin-1 and the minus-motor cytoplasmic dynein are summarized in Table S1. Both motors species can be characterized by three dimensionless parameters, with very similar values for both motor species:

$$\begin{array}{l}\text{Desorption}\text{constant}K\equiv {\epsilon }_0/{\pi }_0\simeq 0.2,\hfill \\ \text{Stall}/\text{detachment}\text{force}\text{ratio}f\equiv F_s/F_d\simeq 2,\text{and}\hfill \\ \text{Backward}/\text{forward}\text{velocity}\text{ratio}\nu \equiv {\nu }_B/{\nu }_F\simeq 0.01\text{.}\hfill \end{array}$$ (2)

Tug-of-war model

We now consider a cargo transported by one team of N₊ plus and another team of N₋ minus motors, as described by the single motor parameters in Eq. 2. Typically, the numbers N₊ and N₋ lie in the range of 1–10 motors (11). While being firmly attached to the cargo, the motors bind to and unbind from the filament in a stochastic fashion. Therefore, the number of motors that are bound to the filament fluctuates (see Fig. 1 a). As only the bound motors can exert force on the cargo, the cargo motion is determined by the numbers n₊ and n₋ of bound plus and minus motors, with 0 ≤ n₊ ≤ N₊ and 0 ≤ n₋ ≤ N₋. These numbers (n₊, n₋) change when a single motor binds or unbinds. The rates for these binding and unbinding events and the motion of the cargo are obtained using the following two simplifying assumptions:

Figure 1.

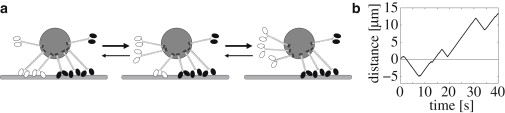
Example for tug-of-war. (a) A cargo with a total number of N₊ = 4 (solid) plus and N₋ = 3 (open) minus motors is pulled by a fluctuating number of motors. Only three of the (N₊ +1)(N₋ +1) = 20 possible configurations of (n₊, n₋) are shown. (b) The trajectory of a cargo transported by four kinesin and three dynein motors with parameters as in Table S1 exhibits stochastic switching between fast plus and fast minus motion.

Assumption 1

When bound to the filament, the motors interact because 1), opposing motors generate load forces; and 2), same-directional motors share this load.

Assumption 2

When bound to the filament, all motors move with the same velocity, which is equal to the cargo velocity.

These assumptions neglect a possible unequal distribution of the load force as well as interference between same-directional motors, as reported recently (6). Inclusion of such effects in our tug-of-war model is possible, and leads only to quantitative rather than qualitative changes of our results (see Section S4 in the Supporting Material).

Cargo motility

The above model exhibits complex cargo motility patterns ((14,15), and see this article's Section S1 and Movie S1 in the Supporting Material). Here we focus on the case of cargo transport by strong motors with high stall/detachment force ratios f = F_s/F_d > 1, such as for kinesin-1 and dynein (see Eq. 2). In this case, the cargo exhibits stochastic switching between fast plus and fast minus motion, as shown in Fig. 1 b. Most of the time only motors of one type are bound to the filament, because cargo states in which both motor types are bound are destabilized by an unbinding cascade. Indeed, when both types of motors are bound, the motors exert high forces onto each other. Because the unbinding rates, as determined by Eq. 1, increase exponentially with the load force, the motors pull each other off the filament. When one team becomes predominant, an unbinding cascade quickly leads to the complete unbinding of the weaker team (as illustrated in Fig. 1 a) for a minus motor unbinding cascade. The remaining team can now pull the cargo without any opposition, so that the cargo undergoes fast motion. The direction of motion persists until stochastic motor unbinding and binding events swap the predominance of the motor teams. In total, the cargo exhibits stochastic switching between fast plus and fast minus motion, as shown in Fig. 1 b.

Bidirectional Dynamics: Run, Switch, and Binding Times

An important property of a single molecular motor is its processivity, which is related to the binding time, i.e., to the time a motor stays bound to the filament. Because a motor such as kinesin-1 walks at a rather constant speed into one direction, its binding time equals the time the motor moves into this direction. For a bidirectionally moving cargo, one has to distinguish several quantities related to processivity.

First, we define the binding time as the time period between cargo binding to and cargo unbinding from the filament, i.e., the time period during which the cargo remains continuously bound to the filament. This binding time has also been called dwell time, walking time, or unbinding time. Note that the motor movement during the binding time can include several cargo runs into both plus and minus directions.

Then, we define the plus run time as the time interval from the beginning to the end of a single plus run, i.e., until minus motion or a pause begins. Note that this is different from the plus switch time, the time from the beginning of plus motion until the beginning of minus motion, which can be longer because of possible intermediate pauses.

We denote the average binding time, plus run time, and switch time by Δt_b, t_R,₊ and t_S,₊, respectively; and the distances covered during the plus run or switch time are the plus run or switch length, respectively.

The average plus-run velocity ν_R,₊ and switch velocity ν_S,₊ are defined as quotients of the corresponding length- and timescales.

Analogous quantities are defined for minus-directed motion. Note that the precise values of these quantities are very sensitive to the experimental resolution (see Section S3 in the Supporting Material), which one has to bear in mind when comparing theory and experiment as well as different experiments.

The run, switch, and binding times play important roles in intracellular transport, as they determine the spatio-temporal distribution of bidirectional cargos in the cell. The binding time corresponds to the time during which the cargo is actively moved by molecular motors, while an unbound cargo diffuses passively in the cytoplasm. The run and switch times as well as the corresponding length scales determine the cargo's directionality, because a bidirectional cargo can achieve net transport if its runs in one direction are, on average, longer than the runs in the other direction. The run times and lengths are therefore the target of cellular regulation, as has been observed for the directional regulation of mitochondria in axons (24), of melanosomes during dispersion and aggregation (26), of lipid-droplets during embryo development (25), and of virus targeting during entry and egress (27).

Parameter dependence of different timescales

In this section, we investigate the dependence of the cargo dynamics on the single motor parameters. We focus on the run, switch, and binding times for the symmetric tug-of-war between equal numbers N = N₊ = N₋ of plus and minus motors with identical parameters. In this case, the indices + (plus) and − (minus) can be omitted for the motor parameters as well as for the run and switch times.

Motor forces

As shown in Fig. 2 a, the binding times decrease with the motor force ratio f = F_s/F_d, while the run and switch times increase with this ratio. For strong motors with a force ratio f larger than a crossover value f_∗ ≃ 4, all times become independent of f. Because active bidirectional transport requires both long binding times and long run times, there is a tradeoff between having strong motors with long run and switch times and having weak motors with long binding times. The force ratio f ≃ 2 of biological motors (see Eq. 2) indicates that long run and switch times seem to be more important to biological function than long binding times. One reason to ensure long run and switch times could be that binding times might be increased anyway by molecular crowding in the cytoplasm, as discussed in Cargo Binding Times below. The biological force ratio of f ≃ 2 also lies somewhat below the crossover value f_∗ ≃ 4: the motor forces are just large enough to produce sufficiently long run and switch times, but small enough to remain sensitive to a change in motor parameters. Such a force ratio will be useful for cellular regulation.

Figure 2.

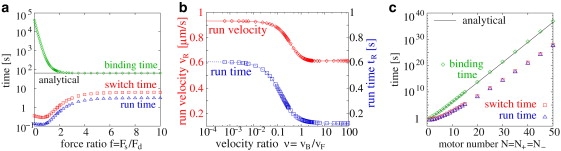
(Color) Symmetric tug-of-war of N plus and N minus motors. (a) Dependence of the average run time t_R (blue triangles), switch time t_S (red squares), and binding time Δt_b (green diamonds) on the stall to detachment force ratio f = F_s/F_d for N = 4. (b) The average run time t_R (blue squares) and velocity ν_R (red diamonds) strongly decreases at a backward/forward velocity ratio ν = ν_B/ν_F ≃ 0.1 for N = 4. (c) The average run time t_R (blue triangles), switch time t_S (red squares), and binding time Δt_b (green diamonds) increase exponentially with the motor number N = N₊ = N₋. The analytical expression (Eq. 3, solid lines in a and c) reproduces the binding times for large f. Motor parameters for kinesin as in Table S1 were used, except for variation of the stall force F_s in panel a and of the slope ν_B/F_s of the superstall force-velocity-relation in panel b.

The binding times decrease with increasing f, because larger motor forces increase the motor unbinding rates (1) and therefore the probability to reach the unbound state with no motors bound. The run and switch times, on the other hand, increase with the force ratio f, as motors of the losing team can hardly gain a foothold against a strong winning team: They rip off quickly under the high generated forces. Fluctuations which lead to a switch of the winning team are therefore unlikely, leading to longer run and switch times. For very large force ratios f > f_∗ ≃ 4, unbinding happens rather fast so that the run and switch times become independent of the precise value of f.

For very low force ratios f, the cargo exhibits the no-motion motility state (0) in which it pauses most of the time (see Section S1 in the Supporting Material for details). When the force ratio f is increased, the cargo passes the (−0+) motility state of fast bidirectional motion with pauses for $f\simeq 1$, which shows up as a shallow minimum in the run and switch times, to reach the (−+) motility state of fast bidirectional motion for large f (see Fig. 2 a). The run and switch times are therefore experimentally accessible fingerprints of the cargo motility state.

Backward motion

Most biological motors walk backward only reluctantly, i.e., they move backward only slowly and only under high load forces, as expressed in the small backward/forward velocity ratio ν = ν_B/ν_F = 0.01 (see Eq. 2). When two motor teams are engaged in a tug-of-war, the motors of the losing team have to walk backward and, because they do this only reluctantly even under high load forces, block the motion of the forward moving winning motors very strongly. On the other hand, if ν is large, the losing motors walk backward easily, complying with the winning motors. At first sight, it seems that high values of ν would enhance cargo motion, and that the small velocity ratio $\nu \simeq 0.01$ is unfavorable. However, as shown in Fig. 2 b, the run times and velocities are larger for biological velocity ratios ν < 0.1 than for large ν > 0.1.

The reason for this counterintuitive behavior is that motors with a high tendency to block motion, i.e., with small velocity ratio ν, cause a large cargo force when they actively pull on a cargo that moves into the opposite direction. Because the motor unbinding rate (1) increases exponentially with the force, this high force triggers an unbinding cascade of the losing motors until only the winning motor type is bound, as described in Theory for Stochastic Tug-of-War. This leads to the large run velocities ν_R in Fig. 2 b, which are almost equal to the velocity ν_F = 1 μm/s of the motors without opposing forces. Furthermore, because of the high load forces, losing motors literally have difficulties to gain a foothold: they get ripped off rather fast. Therefore, once a motor species has won the tug-of-war, it determines the cargo direction for a long time, leading to the large run times in Fig. 2 b. In the opposite case of compliant motors with high velocity ratio ν, the effect of the unbinding cascade is weaker, leading to a high probability of states with both motor types bound, low velocities, and fast directional switching.

In summary, in contrast to naive expectations, a small superstall backward velocity is favorable for fast bidirectional cargo transport, in agreement with the small backward/forward velocity ratios well below 0.1, as observed for biological motors.

Processivity enhancement by motor teams

We now investigate the dependence of the run, switch, and binding times on the number of motors on the cargo.

Cargo binding times

In vivo, cargos typically stay on track for several minutes—much longer than the average binding time of a single motor, which is ∼1 s. In Klumpp and Lipowsky (8), it has been shown theoretically that the binding time of a cargo transported by several motors of one species increases exponentially with the motor number, and that can therefore reach several seconds or minutes for transport by 2–5 motors. This result is reproduced in Fig. 3 a (line with N₋ = 0), and is consistent with in vitro experiments on cargo transport by several motors of one type (2–4). The reason for the increase of the binding times is that the cargo, when attached to the filament by more than one motor, stays close to the filament even when one motor unbinds, and this motor then has the chance to rebind to the filament. This kind of processivity enhancement has also been observed if the cargo is tethered to the filament by a passive, i.e., nondirectional, motor (32–34). When plus and minus motors pull on the cargo, the effect on the binding time is not obvious. There are several motors connecting the cargo to the filament, which should increase the binding time, but the motors perform a tug-of-war and therefore tend to pull each other off the filament, which should decrease the binding time.

Figure 3.

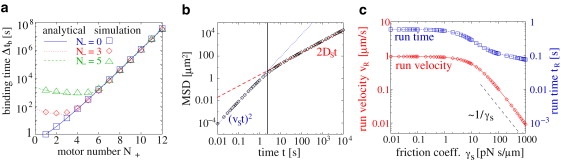
(Color) (a) The cargo binding time Δt_b (symbols) increases with the numbers N₊ of kinesins and N₋ of dyneins, and is well approximated by Eq. 3 (lines). Motor parameters are as in Table S1. (b and c) Symmetric tug-of-war of four plus and four minus motors with kinesin parameters as in Table S1. (b) The mean-square displacement MSD (points) increases with time t as (ν_St)² (blue dotted line) for small t and as 2D_St (red dashed line) for large t. The values for D_S, ν_S, and the crossover time (vertical line) are given in the text. (c) The average run time t_R (blue squares) and run velocity ν_R (red diamonds) decrease as a function of γ_s with a sharp reduction for γ_s ≃ 10 pNs/μm. For large γ_s, the run velocity decreases ∼1/γ_s as given by Eq. 5.

In our model, a cargo can unbind from the filament when it reaches the state (n₊, n₋) = (0, 0) with neither plus or minus motors bound to the filament. For the case of strong motors with large stall/detachment force ratio f = F_s/F_s, such as kinesin and dynein, the binding time can be estimated as

$$\Delta t_{\text{b}}\left(N_{+},N_{-}\right)\simeq \frac{{\left(1+\frac{{\pi }_{0+}}{{\epsilon }_{0+}}\right)}^{N_{+}}+{\left(1+\frac{{\pi }_{0-}}{{\epsilon }_{0-}}\right)}^{N_{-}}-2}{N_{+}{\pi }_{0+}+N_{-}{\pi }_{0-}},$$ (3)

(see Section S2 in the Supporting Material). This expression turns out to be a very good approximation for cargos transported by motors with high force ratios f = F_s/F_d (see Fig. 2, a and c, as well as Fig. 3 a). As predicted by Eq. 3, the binding times increase exponentially with the numbers N₊ of plus and N₋ of minus motors on the cargo (see Fig. 2 c and Fig. 3 a). The tug-of-war leads to a reduction of the binding time of a cargo transported by N₊ plus and N₋ minus motors compared to a cargo pulled by N₊ + N₋ motors of one type, but the binding time of a cargo with N₊ plus and N₋ minus motors is larger than that of a cargo with only N₊ plus or only N₋ minus motors (see Fig. 3 a). In total, the transport by two teams of opposing motors can lead to large binding times in the minute range already for small motor teams: The binding times for the transport by N = N₊ = N₋ = 1, 2, 3, 4, and 5 kinesins and dyneins are 2.1 s, 8.3 s, 36 s, 3.0 min, and 15 min, respectively. These times are much larger than the binding time of ∼1 s of a single motor, and are sufficient to cover distances of tens of micrometers before unbinding, as required for cellular transport. The binding times are also much larger than the times between directional changes, which are of the order of seconds. Therefore, on these timescales characteristic of bidirectional motion, cargo unbinding can often be neglected.

Until now, we have assumed that a cargo unbinds immediately upon reaching the state (0, 0) with no motors bound. Just after the last motor has unbound, the cargo is still as close to the filament as if tethered by motors, so that its rebinding rate is described by N₊π₀₊ + N₋π₀₋ (see Eq. S7), involving the same single motor binding rates π₀₊ and π₀₋ as in the case of a bound cargo. This means that the average time for rebinding is 1/(N₊π₀₊ + N₋π₀₋), which for a cargo with four kinesins and four dyneins equals 0.04 s. This is to be compared to the time the cargo needs to diffuse away from the filament a distance x = 0.1 μm of the order of the motor size. For a cargo of diameter R = 0.5 μm with diffusion constant

$$D=k_{\text{B}}T/\left(6\pi \eta R\right)$$ (4)

at room temperature with k_BT = 4 pN·nm, the diffusion time is only ½x²/D ≃ 0.01 s in water with viscosity η = 1 mPa·s. Thus, a cargo reaching the state (0, 0) is very likely to diffuse away from the filament. However, in the crowded and viscous cytoplasm, diffusion of a cellular cargo may be slowed down considerably, leading to an effective viscosity which is 100–1000 times that of water, depending on the cargo size (see, e.g., (29)). Therefore motors attached to an in vivo cargo have ∼1–10 s to rebind to the filament before the cargo has diffused away, so that in vivo cargos rarely unbind from the track on typical experimental timescales.

Run and switch times

Fig. 2 c shows that the average run and switch times in the symmetric tug-of-war grow exponentially with the number N = N₊ = N₋ of plus and minus motors on the cargo for large N. The scale of this exponential increase is the same as for the exponential increase of the binding time as given by Eq. 3 (see Fig. 2 c). The switch times increase from several seconds for <5+5 motors to minutes for 10+10 motors, and reach enormous times already for ∼20+20 motors. Stochastic switching between plus and minus motors is therefore an effect of small motor numbers (see also (7)). The switch times describe the times for the transition between the plus and minus motion maxima of the probability p(n₊, n₋) to have n₊ bound plus and n₋ bound minus motors (see Section S1 in the Supporting Material). The exponential increase of these transition times is reminiscent of spontaneous symmetry-breaking in equilibrium statistical physics. It therefore strongly indicates that the transition between the two fast-motion maxima represents a nonequilibrium phase transition in the limit of large motor numbers.

Enhanced diffusion

On short timescales, the bidirectional motion is directed ballistic motion either into the plus or into the minus direction. Thus, for short times, the mean-square displacement grows quadratically with time according to (ν_St)² (see Fig. 3 b). The switch velocity ν_S = x_S/t_S = 0.9 μm/s is very close to the single motor velocity ν_F = 1 μm/s, which means that motion in one direction is rather fast even if pauses are included.

On large length- and timescales, the bidirectional motion resembles diffusion in one dimension: the cargo travels back and forth stochastically (see Fig. 1 b). For a symmetric tug-of-war between an equal number of plus and minus motors with identical parameters, there is no net motion even on large length- and timescales. In the latter case, cargo motion can be viewed as a two-state random walk, where one state describes plus and the other minus motion. For large times, the mean-square displacement grows linearly with time according to 2D_St, where the effective diffusion coefficient D_S can be calculated from the average t_S and variance σ_S² of the switch time distribution as D_S = σ_S²ν_S²/(2t_S) (35). This random walk approximation provides a good description for the mean-square displacement of bidirectional cargo motion for large times, as illustrated in Fig. 3 b for a cargo pulled by four plus and four minus motors with kinesin parameters. In this case, the diffusion coefficient is D_S = 1 μm²/s, which is of the same order of magnitude as for a cargo of radius R = 0.5 μm in water, but 100–1000 times larger than the diffusion coefficient 10⁻²–10⁻³ μm²/s for a cargo in the crowded and viscous cytoplasm (compare this to the discussion below Eq. 4). For large motor numbers N = N₊ = N₋, the diffusion coefficient grows exponentially with N (not shown). Bidirectional transport by two motor teams therefore leads to enhanced diffusion, which could be important for cargos in search of their destination, or for cargos which must be distributed over the whole cell such as mitochondria or pigment granules (11,17,26). Enhanced diffusion can also be observed in vitro with a single species of motors but randomized filament direction (36).

The crossover time between the ballistic and the diffusive regime can be estimated as 2D_S/ν_S², and equals 2.4 s for the parameters of Fig. 3 b. The diffusion enhancement thus becomes important already on timescales of a few seconds, which is a reasonable timescale for cellular transport. Such a transition from superdiffusive motion at short timescales to diffusive motion at large timescales has been observed for intracellular bidirectional transport (37,38).

Response to External Forces

In our tug-of-war model, the opposing motors exert forces on each other. These forces are responsible for a dynamic instability that leads to a large probability of having only one motor type bound at a given time. In such a state, the motors do not feel any force, because no opposing motors are bound. In this section, we investigate the effect of external forces, i.e., nonmotor forces, exerted by the cargo's hydrodynamic friction or by an optical trap. These forces act on the motors even in the absence of bound opposing motors, and therefore affect the cargo motility during fast plus and minus motion. This leads to interesting effects such as peaks in the velocity distribution, and hysteresis. The detailed calculations that incorporate frictional and external forces in our tug-of-war model are described in Section S5 in the Supporting Material.

Viscous environments

In this section, we discuss the effect of the hydrodynamic friction force of the cargo-motor complex. For the length- and timescales of bidirectional cargo transport, the friction force F_St of a cargo moving at velocity ν_c can be described by Stokes' law, F_St = γ_s v_c = 6πηR v_c. Here, the friction coefficient γ_s characterizes the strength of the frictional force, and is proportional to the viscosity η of the surrounding solution and to the cargo size R.

Fig. 3 c shows the effect of friction on the run times and run velocities. Small friction γ_s < 1 pNs/μm has negligible effects. For larger friction, cargo motion is slowed down as expected. Furthermore, the additional frictional force on the motors increases the motor unbinding rate (see Eq. 1). Therefore, winning motors drop off more easily, and opposing motors can take over more quickly, which leads to a decrease in the run times.

As discussed in Theory for Stochastic Tug-of-War, a cargo transported by strong motors such as kinesin or dynein is pulled by only one type of motors most of the time. If only plus motors are actively pulling, the cargo velocity is given by

$${\nu }_c\left(n_{+},0\right)={\nu }_{F+}/\left[1+{\gamma }_{\text{s}}{\nu }_{F+}/\left(n_{+}{F}_{s+}\right)\right]\approx n_{+}{F}_{s+}/{\gamma }_{\text{s}}$$ (5)

for 0 ≤ n₊ ≤ N₊ (see Section S5.1 in the Supporting Material). The approximation in Eq. 5 holds for large friction γ_s. When no friction is present, the cargo moves with the single plus motor velocity, ν_c(n₊, 0) = ν_F+, independent of the number n₊ of active plus motors. Likewise, for a frictionless cargo which is pulled by minus motors only, the cargo velocity is ν_c(0, n₋) = ν_F−, independent of the value of n₋. This leads to the velocity distribution of Fig. 4 a with only three peaks at ν_c = ν_F+, ν_F−, and ${\nu }_c\simeq 0$, the latter corresponding to all states with both n₊ > 0 and n₋ > 0.

Figure 4.

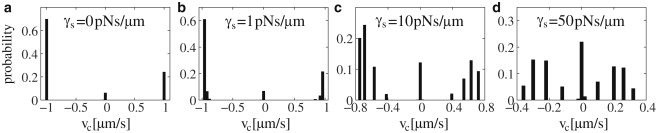
Distributions of the cargo velocity ν_c (solid bars) for the tug-of-war of four kinesins and four dyneins, with parameters as in Table S1, for various Stokes friction coefficients γ_s: (a) Without friction, the cargo either moves with the single motor velocity ±1 μm/s, or pauses. (b–d) With increasing friction, each of the two peaks at ±1 μm/s is divided up into four peaks, which become equidistant for very large friction. The locations of the peaks are given by Eq. 5.

When friction is present, it acts as a load force on the motors even in states where only one motor type is bound. Because same-directional motors share the load force, a cargo with a larger number of active plus motors moves faster, and the cargo velocity depends on n₊ even for states in which no minus motor is bound (see Eq. 5). Therefore, the split up into N₊ and N₋ peaks, respectively, which correspond to the states (n₊, 0) with 1 ≤ n₊ ≤ N₊, and (0, n₋) with 1 ≤ n₋ ≤ N₋, respectively (see Fig. 4, b–d). For very large friction γ_s ≳ 50 pNs/μm, these peaks become integer multiples of F_s+/γ_s (see Eq. 5). For lower friction values, the separation of the maxima of the velocities is smaller than F_s+/γ_s and decreases with n₊ (see Eq. 5). Large friction also leads to an increase of the peak at zero velocity: i.e., increased pausing of the cargo (see Fig. 4).

Now let us consider typical experimental values for the Stokes friction coefficient γ_s. In most in vitro experiments, the cargo moves in aqueous solution with viscosity η = 1 mPa·s. For a typical cargo size R ≃ 1 μm, the friction coefficient is γ_s ≃ 10⁻² pNs/μm, leading to a frictional force F_St ≃ 10⁻² pN for a velocity ν_c ∼1 μm/s. This is negligible compared to typical motor forces of several pN, and should therefore have no significant effect on cargo motion. This is indeed the case (see Fig. 3 c and Fig. 4). Therefore, cargo friction can be neglected in in vitro experiments.

However, as discussed after Eq. 4, the cytoplasm may have an apparent viscosity which is 100–1000 times larger than the viscosity of water (29,39). This leads to friction coefficients γ_s ≃ 1–10 pNs/μm and forces F_St ≃ 1–10 pN of the order of motor forces. This is sufficient to reduce cargo velocity and run length (see Fig. 3 c) and to obtain peaks in the velocity distribution (see Fig. 4). For sufficiently large friction, these peaks can be used to determine the numbers N₊ of plus and N₋ of minus motors on the cargo, and also to estimate the stall forces of the motors or the friction coefficient of the cargo. This has indeed been done for various bidirectionally moving cellular cargos (28,39–41). Note, however, that peaks in the velocity distribution are only expected if the cytoplasmic friction, which depends both on the cargo size and the cell type, is large enough. In addition, low experimental resolution and large noise levels may smear out the individual peaks, leading to broad peaks. Indeed, some cellular cargos display broad peaks rather than several peaks for each direction of motion (27,42).

Tug-of-war in an optical trap

The motion of motor-driven cargos under external forces can be studied by using an optical trap. In the constant-force feedback mode, the trap exerts a fixed force F_ext on the moving cargo (43). Our sign convention is that positive force opposes plus motion, while negative force opposes minus motion.

Fig. 5 shows the force-velocity-relation of a cargo transported by four plus and four minus motors with kinesin parameters, i.e., the average cargo velocity as function of a constant external force F_ext. If F_ext = 0, the tug-of-war is symmetric, so that the average cargo velocity 〈ν_c〉 equals zero. However, a nonzero external force changes the balance of plus and minus motors: A positive force does not only slow down plus-motion, but also makes plus runs shorter and less probable because of faster plus-motor unbinding. Therefore, the velocity changes abruptly to fast minus velocities already for small forces F_ext ≳ 1 pN. For large positive forces (compared to the motor forces), the external force dominates and makes the minus motors win the tug-of-war, so that the cargo moves almost exclusively into the minus direction with high velocity. If the force is negative, the plus motors win, and the cargo moves quickly into the plus direction.

Figure 5.

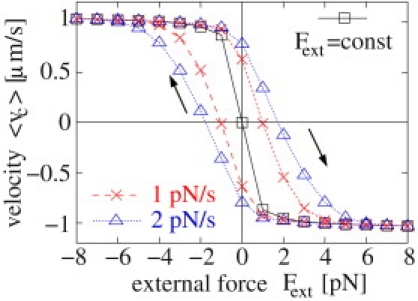
The trajectory-averaged cargo velocity 〈ν_c〉 exhibits a hysteresis loop when the external force F_ext is varied at a relatively fast rate of 2 pN/s (blue triangles). The loop becomes smaller for slower force change rate 1 pN/s of F_ext (red crosses), and vanishes when the system is allowed to reach the stationary state, i.e., for a constant force F_ext = const (black squares). The cargo is transported by four plus and four minus motors with kinesin parameters as in Table S1.

If the external force F_ext is varied in time, the reaction of the cargo depends on how fast this variation occurs: If the force is varied too quickly, the motors do not have enough time to adjust to the new force balance. To investigate this, we varied the force F_ext by an amount of +1 pN from −8 pN to +8 pN, and by −1 pN from +8 pN to −8 pN, every 0.5 s (rate 2 pN/s) or every 1 s (rate 1 pN/s). This force variation leads to a hysteresis of the average cargo velocity (see Fig. 5). For large negative forces, the external force dominates the motor forces, and the cargo moves into the plus direction with high velocity. If the force is now increased from this negative value to zero and then to positive values, it finally assists the minus motors strongly so that they will take over and make the cargo move into the minus direction. If the external force is varied sufficiently fast, the cargo will not switch direction when the external force changes sign, but slightly later, because the takeover from plus to minus motors takes some time. In the same way, when reducing the external force from large positive to large negative values, the directional switch from net-minus to net-plus motion does not occur for zero external force but for negative force. This leads to a hysteresis loop in the cargo velocity (see Fig. 5). This loop becomes smaller when the force change rate is reduced, because then the num-bers of active motors have more time to adjust to the external force. The loop vanishes for infinitely slow force change, i.e., for constant external force at each force value.

Our prediction of a hysteresis loop of the cargo velocity could be easily checked in optical trapping experiments. The external force could be varied by increasing the power of the optical trap stepwise. Depending on the time delay between the increment steps, the average cargo velocity should exhibit a hysteresis loop of varying size. Alternatively, one could study the influence of an optical trap with fixed position on the cargo's back-and-forth movements, which can be viewed as spontaneous oscillations. Increasing the trap stiffness would then lead to a modification of these oscillations and to a reduction of the average switch time, i.e., the oscillation period. A similar coupling to elastic elements, provided by cytoskeletal filaments, has been used to explain mitotic spindle oscillations (22). The interplay of motors and filaments can also lead to oscillatory behavior if the motors bend the filaments (K. Baczynski, M. J. I. Müller, R. Lipowsky, and J. Kierfeld, unpublished).

Summary and Discussion

We have theoretically shown how bidirectional cargo transport arises from a stochastic tug-of-war between two opposing teams of molecular motors. In our theory, the motors are coupled via the mechanical interaction with their common cargo. We have focused on the biologically relevant cargo transport by strong motors with large stall/detachment force ratio, such as kinesin-1 or cytoplasmic dynein. Cargos transported by two opposing teams of such strong motors exhibit stochastic switching between fast plus and fast minus motion, as observed experimentally. The fast bidirectional motion reflects a dynamic instability arising from the nonlinear force-dependence of the single-motor unbinding rate. This instability leads to unbinding cascades of one type of motor, so that there is a high probability of having only the opposing motor type active at a given time. Switching occurs when the stochastic motor unbinding and rebinding leads to an exchange of the winning and losing motor teams.

In experiments, bidirectional transport is typically characterized by run times, run lengths, and run velocities for each direction (11,12,24–28). We have therefore described our predictions for these quantities. For biologically relevant parameter ranges, the run times and run lengths are of the order of seconds and micrometers, as observed experimentally (11,12,24–28). Our theory implies that the unintuitively small superstall backward velocity and the large stall/detachment force ratio f are, in fact, favorable for cellular transport, as they lead to fast bidirectional motion and to high sensitivity even to small changes in the motor parameters. The latter property is useful for cellular regulation, which might directly change the motor properties via signaling cascades. Indeed, cellular regulation often leads to changes in the run length (24–27).

Some cargos, such as mitochondria or pigment granules, do not require net transport but need to be distributed over the whole cell. For these cargos, active bidirectional motion can serve as a mechanism for enhanced diffusion. Indeed, the effective active diffusion constant of a bidirectional cargo is ∼1 μm²/s, which is of the same order of magnitude as the passive diffusion constant of a μm-sized cargo in aqueous solution, but much larger than that in the cytoplasm (29,39). Therefore, active bidirectional motion provides a mechanism to overcome slow cytoplasmic diffusion.

In vivo, cargos are often observed to stay on track for several minutes, in contrast to the average binding time of a single motor of ∼1 s. It has been shown that the binding time of cargos transported by several motors of one type increases exponentially with the motor number (2–4,8). Here we have shown that this is also true if the cargo is transported by two teams of motors that are engaged in a tug-of-war (see Eq. 3, an equation that can be tested by in vitro experiments). For example, a cargo carried by four kinesins and four dyneins stays bound to the track for >2 min, which allows them to cover distances of >100 μm without unbinding. In vivo, these times and distances may be even larger because the cargo may rebind before diffusing away in the crowded cytoplasm.

In this crowded environment of the cell, frictional forces may be quite large. In the stochastic tug-of-war described here, frictional forces lead to smaller velocities, and to peaks in the velocity distribution (see Fig. 4), as have been observed experimentally (28,39–41). The number and location of these peaks can be used to estimate the number of motors on the cargo and their stall forces via Eq. 5. We have also investigated the effect of a time-dependent external force, which leads to hysteresis as illustrated in Fig. 5. This effect is accessible to optical trapping experiments.

Supporting Material

Thirty-eight equations, three figures, one table, and one movie are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00315-2.