Robust approaches to quantitative ratiometric FRET imaging of CFP/YFP fluorophores under confocal microscopy

SUMMARY

Ratiometric quantification of CFP/YFP FRET enables live-cell time-series detection of molecular interactions, without the need for acceptor photobleaching or specialized equipment for determining fluorescence lifetime. Though popular in widefield applications, its implementation on a confocal microscope, which would enable subcellular resolution, has met with limited success. Here, we characterize sources of optical variability (unique to the confocal context) which diminish the accuracy and reproducibility of ratiometric FRET determination, and devise practical remedies. Remarkably, we find that the most popular configuration, which pairs an oil objective with a small pinhole aperture, results in intractable variability that could not be adequately corrected through any calibration procedure. By quantitatively comparing several imaging configurations and calibration procedures, we find that significant improvements can be achieved by combining a water objective and increased pinhole aperture with a uniform-dye calibration procedure. The combination of these methods permitted remarkably consistent quantification of subcellular FRET in live cells. Notably, this methodology can be readily implemented on a standard confocal instrument, and the dye calibration procedure yields a time savings over traditional live-cell calibration methods. In all, identification of key technical challenges and practical compensating solutions promise robust subcellular ratiometric FRET imaging under confocal microscopy.

INTRODUCTION

Fluorescence Resonance Energy Transfer (FRET) is a powerful tool that enables the detection of molecular proximity between suitable GFP-color mutants (e.g., CFP/YFP), when situated within ~100 angstroms of each other. The ability to distinguish proximity on this scale is remarkable because it substantially exceeds the resolution of traditional diffraction-limited fluorescence microscopy (Lakowicz, 2006). Coupled with the widely accessible approach of tagging proteins of interest with these GFP variants, FRET has become a standard tool for investigating molecular interactions, and has found widespread use in many branches of science. Although many elegant approaches can be used to measure FRET (e.g., acceptor photobleaching and fluorescence lifetime imaging), quantitative ratiometric strategies that rely on straightforward determinations of fluorescence intensity may frequently be the method of choice for live-cell FRET imaging. In particular, these ratiometric methods, which include three-cubed FRET (Gordon et al., 1998, Erickson et al., 2001, Erickson et al., 2003a, Erickson et al., 2003b) and E-FRET (Zal & Gascoigne, 2004), offer several practical advantages. First, these ratiometric approaches give the true FRET efficiency, which quantifies the fraction of excited donor molecules whose energy is transferred to an acceptor molecule via resonance (Lakowicz, 2006). Importantly, this unitless measurement has universal meaning, because this metric is independent of the instrumentation used. Second, since FRET efficiency depends on the fractional binding between interacting partners, cell-to-cell variation in expression enables resolution of binding curves, wherein the initial slope of the curve specifies a relative dissociation constant K_d,EFF, and the maximal FRET efficiency can be used to estimate molecular distance and/or conformation (Erickson et al., 2001, Erickson et al., 2003a). Third, these ratiometric methods are non-destructive in that they do not require photobleaching of acceptor or donor molecules. This simplifies time-series FRET, wherein each time point measurement is self-contained, and thereby insensitive to the creation, destruction, or subcellular reallocation of fluorescent molecules within the living cell (Wallrabe & Periasamy, 2005). Finally, ratiometric methods can be readily performed in most laboratories, as they do not require specialized equipment for determining fluorescence spectra or lifetime.

Though powerful, three-cubed FRET depends on accurate knowledge of two key spectral parameters to correct for crosstalk between YFP and CFP (Erickson et al., 2001, Erickson et al., 2003a), which are schematized in Fig. 1A. R_A,YFP characterizes the shape of the YFP excitation spectrum at 442 and 515 nm (Fig. 1A, top), which corrects for the small amount of YFP that is excited when optimally exciting CFP at 442 nm. R_D,CFP characterizes the shape of the CFP emission spectrum at 535 and 480 nm (Fig. 1B, bottom), which is used to subtract the crosstalk of CFP emission that overlaps with YFP's peak emission at 535 nm. Of note, other ratiometric methods, such as E-FRET (Zal & Gascoigne, 2004, Gordon et al., 1998) utilize the same spectral parameters (with different names). Though Fig. 1B idealizes the definition of R_A,YFP and R_D,CFP by displaying pure spectra for the fluorophores themselves, experimentally determined versions of these parameters would additionally incorporate the imperfect spectral properties of the instrument. Thus, the values of these constants depend critically on the particular microscope used, and laborious calibration using live cells expressing YFP or CFP is required to calibrate each apparatus. Unfortunately, the reproducibility of these `constants' depend on the stability of the optical system. In our hands, these spectral parameters are relatively stable on a widefield fluorescence microscope over the course of many weeks. However, on a confocal microscope, such stability has been elusive, both in our hands and in the experience of many in the field (van Rheenen et al., 2004). In our particular case, ordinary use of an Olympus FV300 confocal microscope, with a 60x oil objective and the recommended pinhole aperture of 100 μm (1 Airy unit), resulted in dramatic fluctuations in R_A,YFP and R_D,CFP over the course of weeks, and perhaps even during a single day (data not shown). This experience is common among commercially available confocal platforms. Though it was possible to somewhat compensate for such fluctuations by re-calibrating each day with live cells, such calibrations were prohibitively time consuming, and the end results were not nearly as reliable as from widefield imaging. Here, we characterize the key sources of this variability, and outline simple measures to correct for them. Using these guidelines, we can now routinely exploit the superior z-sectioning of a confocal microscope to resolve subcellular quantitative three-cubed FRET measurements, while achieving reproducibility on-par with widefield imaging. The methodology does not require any specialized equipment, eliminates time-consuming daily calibration using live cells, and should be applicable to any quantitative ratiometric application on a confocal microscope (Chen et al., 2006, Gordon et al., 1998, Miyawaki et al., 1997, Vanderklish et al., 2000, Wallrabe & Periasamy, 2005, Hoppe et al., 2002). As such, this study furnishes a significant practical advance for confocal FRET imaging.

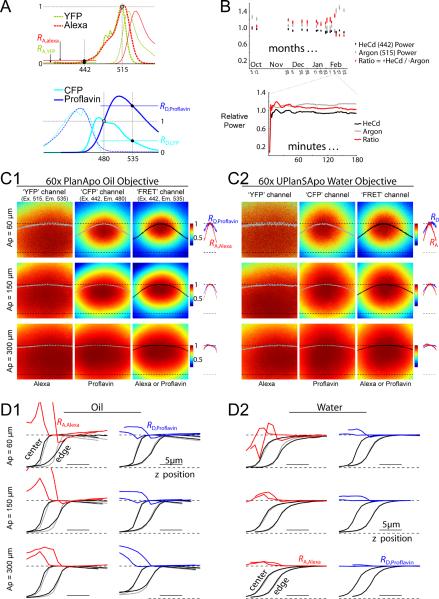
FIGURE 1.

Sources of optical variability. (A) Excitation (dashed curves) and emission (solid curves) spectra of GFP-color mutants and synthetic dyes. Excitation spectra of YFP and Alexa (top, dashed) are normalized to their values at 515 nm, enabling convenient depiction of R_A, which is defined as the excitation at 442 nm divided by excitation at 515 nm. Emission spectra of CFP and Proflavin (bottom, solid) are normalized to their values at 480 nm, enabling convenient depiction of R_D, which is defined as emission at 535 nm divided by emission at 480 nm. (B) Laser power fluctuations over the time course of months (top) and minutes (bottom). HeCd 442 power (black) and Argon 515 power (gray). Fluctuations in the ratio of 442 nm to 515 nm power (red) gauge fluctuations in R_A. (C) Typical dye images at a single z-position, showing x-y intensity profiles. The images in (C1) were taken with a 60× oil objective, and the images in (C2) were taken with a 60× water objective. For each objective, the three columns show different excitation/emission channels used for three-cubed FRET. The rows show pinhole apertures of 60, 150, and 300 μm. Each image is normalized, and color-mapped (see color scale bars). Solid curves across the image (gray or black) correspond to the intensity profile along the x-dimension through the center of the field. R_A,Alexa (red) and R_D,Proflavin (blue) profiles along the x-dimension are shown to the right of the corresponding images. For curves, upper and lower dashed curves show unity and zero levels. (D) Dye intensity profiles along the z-dimension. In each of the twelve plots, curves to the left correspond to z-profiles taken at the center of the x-y field of view, whereas curves to the right correspond to z-profiles at the edge of the x-y field of view, as labelled at top left in panel D1. R_A,Alexa (red curves in the left columns of panels D1 and D2) is the ratio of the FRET channel (black curve) divided by the YFP channel (gray curve) obtained from imaging Alexa dye. R_D,Proflavin (blue curves in the right columns of panels D1 and D2), is the ratio of the FRET channel (black curve) divided by the CFP channel (gray curve) obtained from imaging Proflavin dye. Each curve is normalized. Panel D1 corresponds to a 60× oil objective, and panel D2 corresponds to a 60× water objective. The three rows correspond to pinhole apertures of 60, 150, and 300 μm.

MATERIALS AND METHODS

Molecular biology

CFP, YFP, and CFP-YFP (high-efficiency dimer) were as described (Erickson et al., 2001, Erickson et al., 2003a). The high-efficiency dimer with a nuclear export signal (CFP-YFP-NES) was made by directly inserting a 10 amino-acid oligonucleotide sequence coding for NES into the C-terminal end of CFP-YFP via digest and ligation with BsrGI and NotI sites. The NES sequence was ctaccaccgcttgagagacttactcttgat (LPPLERLTLD). The low-efficiency dimer with a nuclear localization signal (YFP-CFP-NLS) was made by fusing EYFP-KID (YKID) and KIX-ECFP-NLS (KIXCN), which were a kind gift from M. Montminy (Mayr et al., 2001). YKID was PCR amplified and cloned into pcDNA3 between BamHI and EcoRV, with an additional XbaI preceding EcoRV. KIXCN was then PCR amplified and cloned into the previous product using XbaI and EcoRV sites, with a linker containing four glycines (G4) introduced prior to KIX. The final product was (BamHI)-EYFP-KID-(XbaI)-G4-KIX-ECFP-NLS-(EcoRV).

Preparation of dyes

100 mg of Proflavine hemisulfate salt hydrate (SIGMA P2508) was mixed with 1 mL ddH₂O, vortexed, then centrifuged to remove undissolved particles. This stock solution was pH-buffered to 7.0 with 10 mM HEPES, and a 1:20 dilution into HEPES-buffered water was used for imaging. Alexa 514 was prepared by overnight reaction of 1 mg Alexa 514 succinimidyl ester (Molecular Probes A30002) with 980 μL of ddH₂O (pH = 10.0 with NaOH), which was then brought to a volume of 1 mL and pH-buffered to 7.0 with 10 mM HEPES. A 1:100 dilution into HEPES-buffered water was used for imaging. All solutions were stored in the dark at 4°C and were stable for many months. For imaging, we placed a 20 μL droplet of dye in the center of a 3.5 cm culture dish with integral No. 0 or 1.5 glass coverslip (MatTek). To minimize evaporation, we added 50 μL droplets of water to the four corners of the dish, and covered the dish with parafilm. Dye samples were freshly prepared and imaged at the start and end of each imaging session.

Tissue culture

HEK293 cells were thinly plated onto 3.5 cm culture dishes with integral No. 0 or 1.5 glass coverslip bottoms (MatTek) and transiently transfected with FuGene 6 (Roche Molecular Biochemicals). One to two days later, the cells were washed, bathed in HEPES-buffered Tyrode's (pH 7.35), and imaged as described in Fig. 2A.

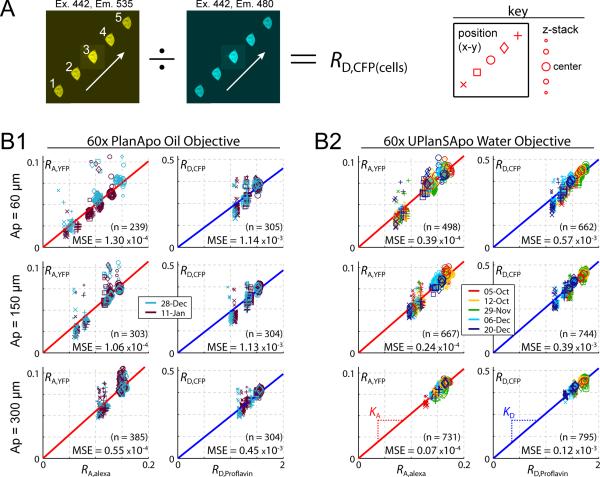
FIGURE 2.

Predicting R_A,YFP and R_D,CFP from R_A,Alexa and R_D,Proflavin. (A) Experimental protocol used to sample cell-based constants over the entire field of view. Each cell was moved to 5 locations across the x-y imaging field. At each location a z-stack of images was obtained. R_D,CFP (example at left) or R_A,YFP was calculated for each image from the ratio of ROI-averaged intensities of two channels. For each cell, this yielded values of R_A,YFP or R_D,CFP at five x-y locations, and at eleven z-positions (center position ± 10 μm, with 2 μm step size). The key (right) explains the conventions used in the scatter plots below. (B) Correlation between cell-based and dye-based ratios. Panel B1 uses an oil objective; panel B2 uses a water objective. The three rows correspond to pinhole apertures of 60, 150, and 300 μm from top to bottom. The size and shape of each data point follows the key convention shown on the far right of panel A, and the color corresponds to the date of the experiment (legends). Laser-fluctuation was normalized using Eq. 1 throughout. Number of data points (n) and mean square deviation from the best-fit line (MSE) are shown.

Fluorescence measurements and analysis

Fluorescence measurements were made on an Olympus Fluoview FV300 confocal laser scanning microscope, with an Olympus PlanApo 60x Oil objective (NA 1.40), and an Olympus UPlanSApo 60x Water objective (NA 1.20). Excitation light was generated with a Helium-Cadmium (HeCd) Laser (442 nm) operated at 1% of maximum power, which corresponds to ~7 μW at the objective; and with an Argon Laser (515 nm) operated at 0.2% of maximum power, corresponding to ~1 μW at the objective. The following Olympus optical filters were used: 442/515 nm excitation splitter (FV-FCV); 515 nm CFP/YFP emission splitter (FV-515CH); 465–495 nm CFP bandpass filter (FV-480BP); and 520–550 nm YFP bandpass filter (FV-535BP). Both dye and cell recordings were preceded by a dark-current image (taken with lasers off), which was subtracted from corresponding images prior to any subsequent analysis. To maximize signal to noise while preventing image intensity clipping, the high-voltage (HV) and/or Gain settings were sometimes changed. For example, in determining R_A,YFP and R_A,Alexa (= FRET channel divided by YFP channel), it was difficult to get an accurate measurement of the FRET channel given the same gain settings used for the much brighter YFP channel. Since both measurements utilize the same photomultiplier tube (PMT), we found that we could improve signal to noise if the gain was increased by a factor of 5 for the FRET channel. Similarly, dim cells, with lower expression levels, required the use of higher HV values. To account for these changes, we standardized all measurements with the following formula:

$$I_{\mathrm{standard}}=I_{\mathrm{raw}}\cdot {(600∕\mathrm{HV})}^{7.7}\cdot (1∕\mathrm{Gain})$$

where I_raw is the dark-subtracted intensity, and the exponent value of 7.7 was experimentally confirmed for each PMT. Thus HV = 600 volts and Gain = 1 could be thought of as `standard' settings. I_standard is the predicted intensity that would be obtained if these standard settings were used. Following HV/Gain standardization, laser fluctuation correction was performed according to Eq. 1 of the ensuing Results section, unless otherwise noted. The custom real-time laser monitoring system consisted of a beam splitter (Chroma) which diverted ~1% of the laser light (prior to the steering galvonometers) into an external PMT (Hamamatsu). To operate in the linear range of this PMT, neutral density filters (Thorlabs) were used to reduce the signal by a factor of 100. The choice of a PMT for laser monitoring enabled compatibility with proprietary A/D circuitry and software. Two PMTs (laser monitoring and brightfield imaging) shared a single A/D channel, and were switched via a custom circuit. All analysis was performed with custom MATLAB software.

RESULTS

Ratiometric imaging of FRET under confocal microscopy can be most challenging when quantitative precision is required, owing to factors less prevalent on a widefield scope. Four main confounding factors were found to predominate in the confocal context, as summarized in Fig. 1: (1) Fluctuations in laser power; (2) Week-to-week drift in optical alignment; (3) Aberrations across the x-y imaging field; and (4) Aberrations along the z-axis. We elaborate on each of these sources of optical variability, and then advance practical means to overcome these challenges.

Fluctuations in laser power

Unlike a widefield microscope, which typically uses a single excitation source, a confocal instrument uses a set of independent lasers for each excitation wavelength. Lasers are notorious for power fluctuations, so we reasoned that independent fluctuations in separate lasers may be a significant source of variability. This would be particularly relevant for R_A,YFP, which is the ratio of YFP excitation at 442 nm (HeCd laser) versus 515 nm (Argon laser). To counteract such variability, we customized our microscope to enable simultaneous laser power monitoring during fluorescent imaging. This revealed uncorrelated power fluctuations in HeCd 442 (Fig. 1B, black) and Argon 515 (gray), evident over the course of months (top), and over the course of minutes (bottom). The ratio of these two laser outputs (red) gauges the fluctuations in R_A,YFP caused by laser power instability. Dramatic fluctuations in this ratio (~50%) occurred over the course of months. Also, significant fluctuations occurred within a single day, which were largest when the lasers were first turned on, and diminished to ~5% after 30–60 minutes of warm-up. Daily re-calibration of R_A,YFP would correct for the ~50% fluctuations from day to day, however, correction of the ~5% fluctuation within a day would require real-time laser monitoring.

Because we operate in the low-excitation regime, the degree to which fluorophores are excited, and the intensity of their fluorescence output, are linearly proportional to laser intensity. Thus, by simultaneously recording laser power, P(t), and fluorescence intensity, I(t), we could correct for laser fluctuations with the following simple relation:

$$I_{\mathrm{norm}}\left(t\right)=I\left(t\right)\cdot P_{\mathrm{norm}}∕P\left(t\right)$$ (1)

where I_norm(t) is the normalized (corrected) fluorescence intensity, and P_norm is a constant value. For convenience, we set P_norm equal to the average laser power measured when the system was first built, however, the actual value of P_norm is unimportant so long as it is never changed. Note that P(t), may vary considerably from P_norm over weeks and months.

Drift in optical alignment and aberrations across the x-y imaging field

Despite correcting for laser power fluctuations, our determinations of live-cell FRET continued to vary considerably from day to day. To eliminate the possible contribution of cellular variability, we selected two synthetic dyes as convenient standards, both dyes with spectra similar to YFP and CFP. Fig. 1A shows the excitation (dashed curves) and emission (solid curves) spectra of YFP and Alexa 515 (top), and of CFP and Proflavin (bottom), demonstrating the spectral similarity between the GFP-variants and the synthetic dyes. We reasoned that imaging a uniform sample of solubilized dye would enable isolation of the optical properties of the microscope. Moreover, if the optical properties of the instrument depend only on the excitation and emission wavelengths used, and not on physical properties of the sample, these uniform dyes could facilitate rapid daily calibration, because R_A,Alexa and R_D,Proflavin should be linearly proportional to R_A,YFP and R_D,CFP, respectively, via slope parameters independent of optical alignment and aberration (Fig. 1A).

Imaging these dyes revealed that not only would R_A and R_D values vary on a daily basis, but that these values would change enormously across the x-y axes of the imaging field, owing to substantial `field curvature' particularly prevalent with the blue excitation (442 nm) required for CFP (Spring et al., 2004). For example, imaging the dyes with the oil objective (Fig. 1C1) resulted in images that were brighter in the center of the field than at the edges. Here, each image corresponds to a particular combination of confocal pinhole aperture (`Ap'), excitation/emission wavelength (`channel'), and calibrating dye (Alexa or Proflavin). Color-coded intensities across each field are shown in a normalized format, with a value of unity at the center (red), and lesser values at the periphery (cooler colors; cyan ~ 0.5) indicating field curvature. The curvature of the FRET channel could be measured with either dye, and both dyes yielded identical results (not shown) indicating that field curvature was a property only of the instrumentation. Field curvature was also quantified by the dome-shaped curves (gray or black) plotted across each image; these curves report intensity along a horizontal line through the image center, with unity and zero levels marked by upper and lower dotted lines, respectively.

Though field curvature could be expected, the extent of this effect was rather surprising. Notably, these x-y aberrations could not be eliminated, even after repeated professional realignment of the system, so the distortions were inherent to the system. The source of this large curvature became apparent by observing how the field curvature depended on the excitation and emission wavelengths (Fig. 1C). The `YFP channel' (left column), measured with Alexa dye, had the least curvature. The `CFP channel' (middle column), measured with Proflavin, had significantly more curvature; and the `FRET channel' (right column) had the most curvature. Overall, then, the larger curvature in the CFP and FRET channels could be attributed to the excitation at blue (442 nm) versus yellow (515 nm) wavelengths, coupled with commerical objectives typically optimized for longer visible wavelengths (van Rheenen et al., 2004). One remedy became apparent by noting that the degree of curvature was more pronounced for smaller pinhole apertures (upper rows) than for larger apertures (lower rows). A similar result was obtained with the water objective (Fig. 1C2). Thus, by using somewhat larger confocal apertures, the curvature could be somewhat flattened.

An important consequence of the wavelength-dependent field curvatures, as described above, is that the ratios R_A,Alexa and R_D,Proflavin must also be non-uniform across the x-y field. This outcome is shown explicitly by the red and blue curves, shown to the right of the images (Figs. 1C1 and 1C2). The red curve plots R_A,Alexa along a horizontal line through the image center; this curve is calculated as the FRET channel profile (right column, black) divided by the YFP channel profile (left column, gray). The x-axis spans the entire image width, but is compressed for compactness. Note also that R_A,Alexa is here shown in normalized format, with unity and zero levels marked by upper and lower dotted lines, respectively. Likewise, the blue curve plots R_D,Proflavin (far right, blue), calculated as the FRET channel profile (right column, black) divided by the CFP channel profile (middle column, gray). Field curvature for these ratios was more pronounced for R_A,Alexa than R_D,Proflavin, and both had more curvature at smaller pinhole apertures (top rows). Although the oil objective profiles were more elliptical in nature, the overall degree of curvature was similar for the oil (Fig. 1C1) and water (Fig. 1C2) objectives.

Beyond enabling characterization of field curvature effects on crosstalk terms R_A and R_D, the imaging of calibrating dyes furnished practical meansto correct for these x-y distortions, as follows. Firstly, we now align the confocal pinhole daily by maximizing the image of these uniform dyes at the beginning of each experiment. Once done, this adjustment should not be repeated, because field curvature profiles can be shifted by realigning the confocal pinhole. Secondly, certain optical elements, such as beam splitters and mirrors, needed to be mechanically reinforced, as a small degree of mechanical instability in these components resulted in perturbations of the curvature profiles over the course of a day. Finally, complete two-dimensional profiles of R_A,Alexa and R_D,Proflavin could be readily obtained on a daily basis (from ratios of entire images), and these profiles could in principle fully compensate for substantial x-y variations in R_A and R_D, as will be validated later in the Results.

Aberrations in the z-dimension

Before turning to such validation, we characterized a still more serious source of variability in quantifying FRET, namely axial aberrations along the z-dimension. To appreciate this issue, whole-field z-stack images of the calibrating dyes were collected. We characterized these z-stack images at two different x-y locations: at the center of the image, and at the top-right corner (i.e., the `edge') of the field. This analysis revealed significant z-aberrations for the oil objective, especially when small pinhole apertures were used. For example, Fig. 1D1 (top, left) shows Alexa z-profiles obtained with an oil objective and the smallest pinhole aperture of 60 μm. The black and gray curves respectively display the z-intensity profiles for the FRET and YFP channels, with the z section being underneath the sample towards the left, and increasingly deep into the dye sample towards the right. The curves labelled `center' and `edge' were obtained at the image center and edge. Taking the ratio of black (FRET channel) and gray (YFP channel) relations then gave the z-dependent profiles for R_A,Alexa (red curves), with the left and right profiles corresponding to the image center and edge. A similar analysis is shown for Proflavin (Fig. 1D1, top, right), where R_D,Proflavin (blue curve) is the ratio of the FRET channel (black curve) divided by the CFP channel (gray curve). The analysis for larger confocal apertures are shown in the middle and bottom rows.

Closer inspection of the results (Fig. 1D1) revealed that the intensity profiles (black and gray curves) peaked near the dye-coverslip interface, and diminished at deeper z-positions. The diminishing intensity at deeper z-positions is due to spherical aberration, which arises from a mismatch in the refractive index between oil and the aqueous environment of the sample (Spring et al., 2004, Török et al., 1997). Importantly, our results also emphasized that the degree of spherical aberration was wavelength-dependent, such that R_A,Alexa and R_D,Proflavin varied as a function of z-position, with progressively larger deviations at greater imaging depth (red and blue curves). This was most pronounced at smaller confocal pinhole apertures (top rows) and towards the edge of the field of view. By contrast, intensity profiles for the water objective (Fig. 1D2, black and gray curves) were flat at deep z positions, indicating less spherical aberration, and R_A,Alexa and R_D,Proflavin were similarly invariant at deeper z-positions (red and blue curves). The elimination of spherical aberration was an expected advantage of the water objective, since it eliminates the mismatch in index of refraction inherent with oil (Spring et al., 2004).

Beyond the effects of spherical aberration to produce deviations at deeper z-positions (towards the right end of curves), we observed a more serious challenge at the interface between the dye and the coverslip. Here, there was a large and erratic variability in R_A,Alexa and R_D,Proflavin profiles, evident as sizeable fluctuations towards the left end of corresponding red and blue curves. We call this phenomenon `chromatic z-misregistration' because at different wavelengths of light, the intensity profiles are mismatched in their rise positions and slopes. For example, this misregistration is evident in the top left image of Fig. 1D1, wherein the rising phase of black and gray curves do not superimpose. Taking the ratio of such curves yields the erratic fluctuations in R_A,Alexa and R_D,Proflavin (red and blue curves) at intensity boundaries. This type of aberration was far more pronounced at small pinhole apertures, and significantly more pronounced with the oil objective. Overall, the best configuration was to pair a water objective with a pinhole aperture of 300 μm (3 Airy units): here the zmisregistration was minimal, with R_A,Alexa and R_D,Proflavin remaining nearly constant over all z-positions, including the dye-coverslip interface (Fig. 1D2, bottom row, red and blue curves are nearly flat). Identification of this optimal configuration ultimately proved critical for robust FRET quantification on a daily basis.

Before describing methods for actual quantification of CFP/YFP FRET, we mention a final consideration regarding the aberrations characterized above. In theory, these distortions could be somewhat minimized by optimizing the choice of coverslip thickness. In fact, all of the characterization in Fig. 1 (C, D) pertains to a No. 0 coverslip, which maximizes working distance while incurring some potential theoretical mismatch with the objectives used. In practice, however, the use of a thicker No. 1.5 coverslip, which was theoretically better matched to our objectives, yielded identical, if not inferior x-y and z aberrations. This was demonstrated by replicating the entire analysis in Figs. 1C and 1D using a No. 1.5 coverglass (Fig. S1, Supplementary Information). From a practical standpoint, then, we henceforth employed No. 0 coverslips, so as to maximize working distance, while incurring no added distorting factors.

Use of dyes to predict R_A/R_D values

Given the four sources of variability delineated above (Fig. 1), we turned to explictly validating the use of synthetic dyes to rapidly compensate for these variability factors over different locations in the field of view, and over time. We imaged both the dyes as above, and cells expressing either YFP or CFP, with the goal of predicting cell-based spectral constants (R_A,YFP and R_D,CFP), from dye-based constants (R_A,Alexa and R_D,Proflavin).

At the start of each session, the confocal pinhole was aligned by centering the CFP and FRET field curvature profiles (while imaging Proflavin), and the pinhole was subsequently held fixed for the remainder of the session. Uniform droplets of Proflavin and Alexa were then imaged (as in Figs. 1C, D) at the start and again at the end of the session. These images were compared to verify that alignment did not drift, and we excluded data sets wherein significant alignment drift occurred (this happened only once over the course of several months imaging). To sample the aberrations across the x-y field with cells, we manually moved each cell (expressing either YFP or CFP) to five x-y locations (Fig. 2A, left), and z-stack imaged the cell at each location. The data were later analyzed by drawing an ROI within each cell and taking the average ROI intensity for each image. For cells expressing YFP, we divided the FRET channel by the YFP channel, yielding R_A,YFP. For cells expressing CFP, we divided the FRET channel by the CFP channel, yielding R_D,CFP (Fig. 2A, left). Corresponding dye ratios (using Alexa or Proflavin) were calculated by mapping ROI coordinates onto dye images from that session, yielding a corresponding value of R_A,Alexa or R_D,Proflavin for each cell, at each x-y location, and each z-position. The ROI mapping procedure was exact with regard to x-y coordinates, however, the mapping in z was only approximate.

Fig. 2B shows the resulting data. For either the oil objective (Fig. 2B1) or the water objective (Fig. 2B2), the left column shows the correlation between R_A,YFP and R_A,Alexa, and the right column shows the correlation between R_D,CFP and R_D,Proflavin. The pinhole aperture is larger for lower rows. Each data point corresponds to a single cell, situated at a single x-y location, and imaged with a single z-slice. The color of each data symbol represents the day of the experiment (Fig. 2B, legends); the shape represents the x-y location within the field (Fig. 2A, right) from bottom-left to top-right (x, □, ○, ◊ +); and the symbol size is largest for a z position in the middle of the cell, and smaller at higher and lower z-positions (Fig. 2A, right). For each subplot in Fig. 2B, a best-fit line, constrained through (0,0) was fit to the data. The scatter was characterized by the mean square error (MSE), which is the average squared vertical deviation from the best-fit line. The relationships between R_A,YFP and R_A,Alexa, and between R_D,CFP and R_D,Proflavin had the highest degree of scatter for the oil objective, and for small apertures (Fig. 2B1, top rows). The tightest correlation, exhibiting a more than tenfold reduction in scatter, was obtained by combining a water objective with an aperture of 300 μm (Fig. 2B2, bottom row). Indeed, the dye calibration strategy works remarkably well for this configuration, which exhibits all forms of distortion (Fig. 1C2, right bottom, showing x-y field curvature, daily alignment drift) except for z-dependent aberrations, which are minimal in this case (Fig. 1D2, right bottom). Thus, the dye calibration method seems to correct well for x-y field-curvature, and day-to-day alignment drift, but less well for z-dependent aberrations. This assessment is further consistent with the correlation between the extent of z-dependent aberration in other configurations (Fig. 1D), and the degree to which dye calibration fails to predict R_A,YFP and R_D,CFP.

Based on these results, we concluded that the water objective clearly outperformed the oil objective, and larger pinhole apertures outperformed small apertures. Given the tight correspondence between cell- and dye-based measurements (Fig. 2B2, bottom row), we could accurately determine live-cell spectral constants based on easily obtainable dye recordings, as follows. For any given x-y location:

$$R_{\mathrm{A},\mathrm{YFP}}(x,y)=K_{\mathrm{A}}\cdot R_{\mathrm{A},\mathrm{Alexa}}(x,y),\text{and}{R}_{\mathrm{D},\mathrm{CFP}}(x,y)=K_{\mathrm{D}}\cdot R_{\mathrm{D},\mathrm{Proflavin}}(x,y)$$ (2)

where K_A and K_D are the slopes in Fig. 2B2 (bottom row). For our setup, we obtained K_A = 0.535 and K_D = 0.26. These values should only depend on excitation/emission wavelengths, and should not be influenced by factors that affect signal intensity due to variability in optical alignment or variable aberrations across the imaging field. Since the wavelengths of excitation and emission are highly reproducible with lasers and emission filters, these equations should hold over very long periods of time. Also, if dye measurements are made each day, Eq. 2 will account for day-to-day fluctuations in laser power. In all, methods utilizing Eq. 2 promise to eliminate the need for painstaking calibration with live cells.

Robust FRET achieved

We could then test for the reliability of utilizing Eq. 2 to measure three-cubed FRET in live cells expressing control molecules with known FRET efficiencies. For the following data, we exclusively used the water objective with an aperture of 300 μm. FRET Ratio (Erickson et al., 2001, Erickson et al., 2003a) was calculated by

$$FR=\frac{I_{\mathit{cell},\mathit{FRET}}-R_{\mathit{D},\mathit{CFP}}\cdot I_{\mathit{cell},\mathit{CFP}}}{R_{A,\mathit{YFP}}\cdot I_{\mathit{cell},\mathit{YFP}}}$$ (3)

$$FR=\frac{I_{\mathit{cell},\mathit{FRET}}-\underset{\overbrace{\left(K_D\cdot I_{\mathit{proflavin},\mathit{FRET}}∕I_{\mathit{proflavin},\mathit{CFP}}\right)}}{\overset{R_{D,\mathit{CFP}}}{}}\cdot I_{\mathit{cell},\mathit{CFP}}}{\underset{R_{A,\mathit{YFP}}}{\overset{\underbrace{\left(K_A\cdot I_{\mathit{alexa},\mathit{FRET}}∕I_{\mathit{alexa},\mathit{YFP}}\right)}}{}}\cdot I_{\mathit{cell},\mathit{YFP}}}$$ (4)

Here, I_cell,FRET, I_cell,CFP, and I_cell,YFP are average intensity values within an ROI of a cell for the FRET, CFP, and YFP channels, respectively. I_{proflavin,FRET}, I_{proflavin,CFP}, I_alexa,FRET and I_alexa,YFP are the ROI-matched dye intensity values from the same session. Eqs. 3–4 are essentially the same as the original three-cubed FRET equation (Erickson et al., 2001), except a third spectral crosstalk parameter is eliminated, since its value was nearly zero under the laser excitation used on our confocal microscope. Eq. 4 is identical to Eq. 3, with the spectral constants explicitly substituted by Eq. 2. The effective FRET efficiency (E_EFF) is linearly proportional to FR by the following relation (Erickson et al., 2001):

$$\begin{array}{cc}\hfill E_{\mathrm{EFF}}& =E_{\max }\cdot A_{\mathrm{b}}=(FR-1)\cdot \frac{{\epsilon }_{\mathrm{YFP}}\left({\lambda }_{\mathrm{CFP}\mathrm{excit}}\right)}{{\epsilon }_{\mathrm{CFP}}\left({\lambda }_{\mathrm{CFP}\mathrm{excit}}\right)}\cdot 100\%\hfill \\ \hfill E_{\mathrm{EFF}}& =E_{\max }\cdot A_{\mathrm{b}}=(FR-1)\cdot \frac{{\epsilon }_{\mathrm{YFP}}\left({\lambda }_{\mathrm{CFP}\mathrm{excit}}\right)}{{\epsilon }_{\mathrm{CFP}}\left({\lambda }_{\mathrm{CFP}\mathrm{excit}}\right)}\cdot 100\%\hfill \end{array}$$ (5)

where E_max is the FRET efficiency that would be seen if all acceptor (YFP) molecules were bound to a single donor (CFP) molecule; A_b is the fraction of acceptor molecules bound; and ε_YFP(_{λCFP exit}) and ε_CFP(_{λCFP exit}) are the molar extinction coefficients of YFP and CFP at the CFP-excitation wavelength (in our case _{λCFP exit} = 442 nm). Thus, E_EFF can be readily calculated from FR if the ratio of molar extinction coefficients is known. Two points merit emphasis. First, in the absence of acceptor/donor binding interaction, A_b = 0, E_EFF = 0, and FR = 1. This can be experimentally verified with a negative FRET control (i.e. co-expressing YFP and CFP as separate molecules). Second, the ratio of molar extinction coefficients can either be determined directly via spectrofluorometric measurements, or by measuring FR for a positive FRET control with known maximal FRET efficiency (E_max). For the latter approach, CFP-YFP dimers would serve as ideal control molecules, since A_b = 1, and thus E_EFF = E_max. Both approaches have previously given the same value of ε_YFP(_{λCFP exit})/ε_CFP(_{λCFP exit}) = 0.095 (Erickson et al., 2001), and this value further yields consistent FR-based estimates of E_max for the CFP/YFP Ca²⁺ sensor yellow cameleon 2 (Erickson et al., 2001, van Rheenen et al., 2004). Thus, we use this value of 0.095 in the upcoming sections to convert between FR and E_EFF, according to Eq. 5.

Fig. 3A (top row) shows FRET calculations for cells expressing a known CFP-YFP dimer with high FRET efficiency, serving as a positive FRET control. The bottom row concerns cells co-expressing CFP and YFP as separate molecules, which serve as negative controls (bottom row). Each subplot shows the calculated FR (left axis) and the calculated E_EFF (right axis), plotted against I_cell,CFP. The color, size, and shape of the data points are as in Fig. 2B. In the first column (Fig. 3A, left), neither laser nor dye correction was performed, and FR was calculated with Eq. 3 holding R_A,YFP and R_D,CFP constant (values were set to the average obtained in Fig. 2B2, bottom row). The second column (Fig. 3A) is similar to the first, except laser correction was performed according to Eq. 1. In the third column, laser correction was not performed, but dye correction was used according to Eq. 4. Finally in the fourth column, both laser and dye correction were used. Within each subplot, two measures of scatter are shown. First, the total variance of the data (average squared deviation from mean FR value) is shown (Var). Second, the mean-square error from a constrained best-fit linear relation (black line) is shown (MSE). As will be elaborated in the Discussion, these linear relations likely account for subtle contributions of collisional FRET, which increases with higher expression of fluorescent molecules (Stratton et al., 2004, Erickson et al., 2003b, Forster, 1949, Fung & Stryer, 1978).

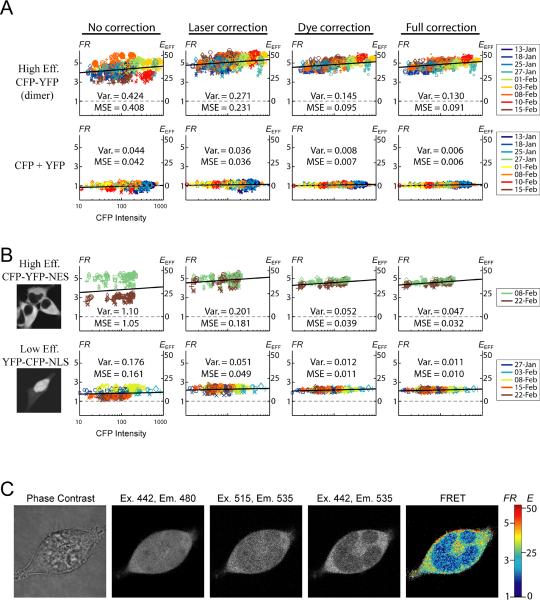
FIGURE 3.

Robust FRET determination in live cells. (A–B) Scatter plots of FR (left axis) and E_EFF (right axis) versus CFP intensity. Top row of (A) is for a high-efficiency CFP-YFP dimer; bottom row of (A) is for CFP and YFP expressed as separate molecules. Top row of (B) is for high-efficiency CFP-YFP-NES; bottom row of (B) is for low-efficiency YFP-CFP-NLS. First column uses no correction. Second column uses only laser correction (Eq. 1). Third column uses only dye correction (Eq. 4). Fourth column uses both laser and dye correction. Symbol color, size, and shape as in Fig. 2B. Two measures of scatter are shown. Var. is the mean-square deviation from the average FR. MSE is the mean-square deviation from the best-fit collisional FRET relation (black line). The slopes of these relations were constrained, as elaborated in the Discussion, to the following values: high-efficiency CFP-YFP: 0.18; CFP + YFP: 0.03; high-efficiency CFP-YFP-NES: 0.18; low-efficiency YFP-CFP-NLS: 0.04. (C) Subcellular FRET within a cell co-expressing CFP-YFP-NES and YFP-CFP-NLS. Phase contrast image (first column), CFP channel (second column), YFP channel (third column), FRET channel (fourth column) are shown. The calculated FR (fifth column) is applied directly to the image, and uses both laser and dye correction.

Without correction (Fig. 3A, first column), FR calculations were highly scattered. Though laser correction alone (second column) yielded some reduction in scatter, a dramatic improvement was obtained with dye correction alone (third column), which nearly matched the scatter for full correction (fourth column). Since dye correction implicitly accounts for day-to-day fluctuations in laser power, the minor improvement between columns three and four represents the small amount of laser instability during a single session, which did not seem to be significant. Importantly, the reproducibility obtained over many weeks with either the fully corrected method (fourth column) or dye-corrected method (third column) was onpar with our widefield setup. It is also worth noting that the uncorrected method (first column), which used a water objective with an aperture of 300 μm, was far superior to our initial attempts using an oil objective with an aperture of 100 μm, which were far more widely scattered (data not shown).

Some final points of validation merit emphasis. First, the fully corrected CFP + YFP data (Fig. 3A, bottom right) agrees well with the expectations for a negative control (i.e., FR = 1 and E_EFF = 0). Second, the FRET efficiency of the high-efficiency CFP-YFP dimer (Fig. 3A, top row) has been previously determined to be 42% using an independent FRET method (Erickson et al., 2001). This value agrees well with our results (Fig. 3A, top right plot, right y-axis), where E_EFF is calculated via Eq. 5 using the published ratio of molar extinction coefficients.

Subcellular FRET

Encouraged by the cell-averaged results of Fig. 3A, we sought to realize the potential of confocal microscopy to resolve subcellular FRET interactions. To begin, we generated test molecules with varying FRET efficiency, targeted to different subcellular locations. Fig. 3B shows the subcellular localization of two such constructs (far left images). The top row shows the same high-efficiency CFP-YFP dimer as in the top row of Fig. 3A, except here it is tagged with a nuclear export signal (NES), which restricts the molecule to the cytoplasm. The bottom row shows a lower-efficiency YFP-CFP dimer tagged with a nuclear localization signal (NLS), which enriches nuclear over cytoplasmic concentration. The scatter plots in Fig. 3B use the same analysis as in Fig. 3A. Note the drastic reduction in FR variability for the CFP-YFP-NES construct from the first to the fourth column (Fig 3B, top row). This data were taken on two separate days, between which something drastic changed in the instrument. Nevertheless, our simple correction techniques yielded exceptionally robust results, enabling clear resolution of FRET efficiency for the two constructs when expressed individually (Fig 3B, right column).

To test the methodology further, we co-expressed the two constructs, with the aim of distinguishing different FRET efficiencies in subcellular locations of the same cell (Fig. 3C). The first image (left) is the phase-contrast channel, the middle three show the three fluorescence channels, and the last (right) shows FR calculated with Eq. 4 applied directly to the fluorescence images. All images employ laser correction according to Eq. 1, and thus the final image is analogous to the full-correction method. The calculated FR (Fig. 3C, far right) yielded a reliable measure of subcellular FRET, in accord with the cell-averaged values obtained in Fig. 3B. The low-efficiency NLS construct had a FR ~2 for both the cell-average data (Fig. 3B, bottom row, right) and the image (Fig. 3C, right, nucleus). The high-efficiency NES construct had a FR ~4.5 for the cell-average data (Fig. 3B, top row, right), and a slightly lower FR ~4 in the image (Fig. 3C, right, cytoplasm). This slight reduction in apparent cytoplasmic FR likely reflects imperfect nuclear targeting of the NLS construct (Fig. 3B, bottom left image). Overall, the reproducibility obtained was on-par with that of widefield fluorescence methods, but of course the spatial resolution here is far superior as expected of a confocal microscope.

Spatial Resolution

Though the results of Fig. 3 demonstrate robust FRET determinations, the use of a large pinhole aperture may raise concerns as to the tradeoff in spatial resolution. In particular, the thickness of an optical slice in confocal microscopy would increase as the pinhole aperture is increased. To address this concern, we quantitatively compared the axial resolution obtained with different pinhole apertures (Fig. 4). To generate this data, Alexa 514 was adsorbed onto the surface of an acid-washed No 1.5 cover glass. Excess dye was rinsed away, leaving dye only at the surface of the glass, with non-fluorescent aqueous solution above. Z-stack images of this sample were then taken with three different pinhole apertures using the water objective. The normalized fluorescence, as a function of z-position, is plotted. Axial slice thickness can be quantitatively estimated by measuring the z-width corresponding to half-maximum intensity of these profiles. The measured axial slice thickness was ~1 μm for small pinhole apertures (60 and 150 μm pinholes). For the large 300 μm pinhole aperture, the axial slice thickness increased to ~ 2 μm. Thus, the use of a large pinhole aperture reduces z-resolution only by a factor of two, as compared to conventional small-pinhole apertures. For many applications, this is a reasonable tradeoff, given the roughly five-fold reduction in variance of the spectral constants (compare the top and bottom rows of Fig. 2B2). Furthermore, via noise analysis of Eq. 3, we estimate that this five-fold improvement in stability of the spectral constants would correspond to a roughly 30-fold improvement in stability of FRET efficiency calculations.

FIGURE 4.

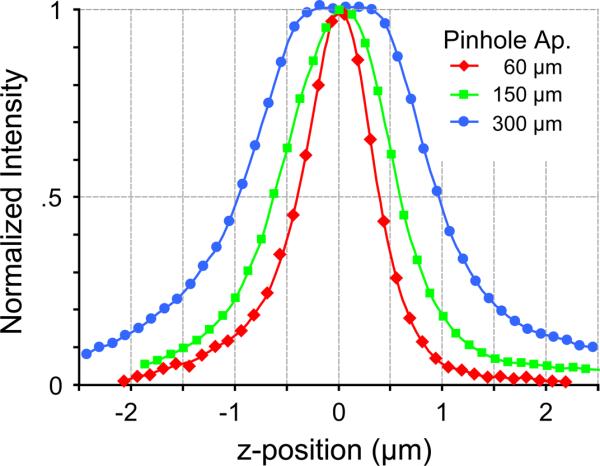
Effect of pinhole aperture on axial resolution. Axial intensity profiles of a sample in which Alexa 514 is adsorbed onto a cover glass surface. The normalized fluorescence, as a function of z-position, is plotted for three different pinhole apertures using the water objective.

This preservation of axial resolution with a larger pinhole aperture (Fig. 4) has been previously characterized (Cox & Sheppard, 2004), and here can be further appreciated by qualitative aspects of the images in Fig. 3. In particular, even with a large aperture of 300 μm (3 Airy units), the image is qualitatively still confocal in nature, and subcellular organization is clearly resolved. The nucleus and cytoplasm are clearly distinguished in the images in Figs. 3B–C, and even cytoplasmic invaginations into the nucleus are clearly distinguished in high spatial detail (Fig. 3C). There is no discernible blurring of the subcellular boundaries, or noticeable contamination from structures above or below the plane of focus.

DISCUSSION

Quantifying ratiometric FRET can be challenging on a confocal microscope. Variability in the required calibration constants (R_A, R_D) arise from fluctuations in laser power, optical alignment drift, aberrations across the x-y imaging field, and aberrations along the z-dimension. Some of these sources of distoration have been previously described (van Rheenen et al., 2004). In their work, van Rheenen and colleagues used a 63× oil objective with a small pinhole aperture, and proposed several techniques to counteract the aberrations, such as adjusting the focus between image acquisitions to correct for differences in axial excitation profiles of the two lasers. Ultimately, these correction techniques were insufficient, leading the authors to devise a protocol in which cells co-expressing CFP and YFP were co-cultured with cells expressing only CFP or only YFP. Under this regime, if all three types of cells were found in close proximity to one another, then the CFP-only and YFP-only cells could be used to estimate R_A and R_D. These estimates would then be used to calculate sensitized emission in the neighboring cell which contains both CFP and YFP. Though clever, this approach has practical limitations. First, it would be quite rare to encounter three cells with the right expression levels within a single field of view. Second, the cells may be at the edges of the field of view, and thus be subject to different degrees of aberration. Third, this approach suffers from unreliable estimates of the spectral constants, given that the neighborhood estimates of R_A and R_D are calculated from single cells (i.e. averaging over a population of cells is not possible). Finally, such an approach would in general prove comparatively time consuming, especially in terms of cell preparation.

A key contribution of the present work is the comprehensive comparison of oil versus water objectives, and of pinhole apertures of different sizes. We found that a water objective combined with a large pinhole aperture clearly outperformed the standard configuration which employs an oil objective and small pinhole aperture. Importantly, with the commonly used oil configuration, synthetic dyes could not accurately account for aberrations observed in live cells (Fig. 2B1, top row). This may seem perplexing: how could the microscope optical properties be different for cells versus dyes, considering that they are both aqueous in nature? An answer to this question can be gleaned from Fig. 1D, which characterizes the microscope optics as a function of z-position, and in response to intensity boundaries (i.e. the dye-coverslip interface). Two key principles can be discerned. First, because it is difficult to accurately register cell images to dye images along the z-dimension, any z-dependent aberration would be very difficult to correct. Second, cells contain non-uniform fluorescence due to subcellular structures, which may mimic the intensity boundaries seen at the dye-coverslip interface, whereas the dyes are completely uniform. For the oil objective, and for small apertures (Fig. 1D1, top row), optical aberrations near intensity boundaries were highly unpredictable due to chromatic z-misregistration, and together with the z-dependent spherical aberration, made it nearly impossible to calibrate. These anomalies were nearly absent when a water objective with an aperture of 300 μm was used (Fig. 1D2, bottom row). Once these enigmatic z-dependent artifacts were eliminated, the dyes were able to robustly correct for all other aberrations along the x-y plane, as well as for day-to-day fluctuations in alignment and laser power. Specifically, the use of Eq. 2 in the dye calibration allows for precise correction for x-y aberrations at any x-y coordinate, which would not be the case with corrections based on nearby calibrating cells in the van Rheenen method (van Rheenen et al., 2004). As an additional benefit to this practical approach, the larger pinhole aperture allows more light to be collected, yielding a higher signal-to-noise ratio, without significantly degrading the ability to resolve subcellular structures.

A final concern for accurate determination of CFP/YFP FRET is the likely contribution of collisional FRET between fluorophores on separate molecules (Forster, 1949, Fung & Stryer, 1978). A first issue concerns the effect of fluorophore concentration: sensitized emission of YFP owing to collisional FRET will increase with heightened concentrations of donor CFP, whereas this effect disappears at vanishingly small concentrations of fluorophore. For plasmid-mediated expression levels of CFP/YFP constructs in mammalian cells (typically less than ~50 μM (Miyawaki & Tsien, 2000)), a low fluorophore concentration regime applies, wherein FRET efficiency depends almost linearly upon CFP concentration (Erickson et al., 2003b). In fact, the small positive slopes of the plots of FRET efficiency versus CFP intensity (Figs. 3A and 3B) likely reflect such an effect (Stratton et al., 2004). A second consideration is that the slope of the relation between collisional FRET and free donor concentration should increase with a larger Forster radius R₀ (Erickson et al., 2003b, Fung & Stryer, 1978). This additional effect is consistent with the slightly larger slope for the high-efficiency CFP-YFP dimer (Figs. 3A and 3B, top row), compared to that for CFP and YFP expressed as separate molecules (Fig. 3A, bottom row). Here, the effective R₀ of the CFP-YFP dimer may be larger, because the CFP fused to YFP within a dimer could serve as an additional collisional energy transfer collector for the cognate YFP. Specifically, this intra-dimer CFP could be excited via intermolecular homo-FRET from other CFP molecules, followed by intra-molecular FRET to the cognate YFP. Given this theoretical foundation, we constrained the slopes of the linear relations in Figs. 3A and 3B (black lines) such that any two constructs with identical R₀ had the same slope (see Fig. 3 legend). Overall, one must consider these effects in interpreting the meaning of aggregate FRET determinations. In particular, the extrapolated FRET efficiency at low CFP intensity best reflects intramolecular FRET, exclusive of collisional FRET.

In summary, we devised simple guidelines to compensate for the sources of FRET variability inherent to confocal microscopy. First, a water objective with a pinhole aperture of ~3 Airy units should be used. Second, pinhole alignment should be done with the guidance of a uniform-intensity dye, and all optical components should be stabilized to minimize alignment drift during the course of an imaging session. Third, whole-field images of Proflavin and Alexa 514 dyes should be taken at the start and end of each recording session. These images enable accurate prediction of the spectral constants, R_D,CFP and R_A,YFP, as a function of position, without the need for laborious calibration using live cells. In addition, comparison of the images taken at the start and end of the session can validate the alignment stability. Fourth, real-time monitoring of lasers to normalize power fluctuations during the course of a session may help, but are not absolutely necessary because the dyes implicitly correct for day-to-day laser fluctuations. Finally, lasers should be allowed to warm up about an hour prior to use, especially if real-time laser monitoring is not used. In all, the simple guidelines outlined here allow the power of ratiometric FRET to be simply attained under confocal microscopy, enabling time-series molecular interactions to be quantitatively examined with subcellular resolution.