The Effects of Load on E-Selectin Bond Rupture and Bond Formation

Abstract

Molecular dissociation rates have long been known to be sensitive to applied force. We use a laser trap to provide evidence that rates of association may also be force-dependent. We use the thermal fluctuation assay to study single bonds between E-selectin and sialyl Lewis^a (sLe^a), the sugar on PSGL-1 to which the three selectins bind. Briefly, an E-selectin-coated bead is held in a laser trap and pressed with various compressive loads against the vertical surface of a bead coated with sLe^a. The time it takes for a bond to form is used to calculate a specific two-dimensional on-rate, ${\mathit{\text{k}}}_{\text{on}}^{\text{o}}$. We observe an increase in ${\mathit{\text{k}}}_{\text{on}}^{\text{o}}$ with increasing compressive force, providing single molecule evidence that on-rate, in addition to off-rate, is influenced by load. By measuring bond lifetimes at known tensile loads, we show that E-selectin, like its family members L- and P-selectin, is capable of forming catch bonds. Our data support a reverse Bell model, in which compressive forces lower the activation energy for binding. Load-dependent on-rates may be a general feature of all intermolecular bonds.

Introduction

The selectins are a family of transmembrane adhesion molecules responsible for the initial capture of flowing leukocytes by the vessel wall, as well as the subsequent rolling of leukocytes along the endothelial surface. The selectin family is comprised of L-selectin, found on most leukocytes, P-selectin, expressed primarily on activated endothelial cells as well as activated platelets, and E-selectin, found on activated endothelium. The most common selectin ligand is P-selectin glycoprotein ligand-1 (PSGL-1), a dimeric glycoprotein found on the surface of both leukocytes and the endothelium. E-selectin/PSGL-1 binding has been shown to be crucial for leukocyte tethering under flow.⁶⁰ Selectin/ligand bonds must possess on-rates high enough to form bonds between a stationary endothelial cell and a rapidly moving leukocyte, and off-rates high enough for the rapid bond dissociation necessary for leukocyte rolling. Rolling rates on the three types of selectins vary greatly, suggesting the molecules do not share the same kinetic properties.^39,44 The underlying molecular kinetics responsible for leukocyte rolling have been investigated primarily in L- and P-selectin,^{10,20,26,29,34,42,43,48,58,61} while single molecule studies of E-selectin kinetics remain few.^20,48,51

L- and P-selectin have been shown to form catch-slip bonds with PSGL-1.^29,43 Catch–slip bonds are bonds that initially increase in lifetime with increasing force, and subsequently decrease in lifetime when a critical force is reached. The existence of catch bonds was first proposed by Dembo⁹ in 1988, but they were not observed experimentally until recent years.^17,29,54 Though catch bonds have been found in such diverse molecules as the actin–myosin system,¹⁷ integrin-mediated adhesion,²⁴ and bacterial fimbria,⁵⁴ their properties have been most widely investigated at the single molecule level using bonds between selectins and their corresponding ligands. Though bonds between P-selectin and PSGL-1²⁹ and L-selectin and PSGL-1⁴³ behave as catch–slip bonds, E-selectin has not been shown to form such bonds with any of its ligands. This is perhaps due to the fewer⁵⁶ and less well defined ligands for E-selectin, causing it to be the least studied member of its family.

A recent flow chamber study³⁴ suggested that like the rates of bond rupture, the rate of L-selectin/PSGL-1 bond formation may be a function of force. This complements an earlier study showing that increasing contact stress, while controlling for contact area, results in higher intrinsic rates of bond formation for bonds between β₂-integrins and intercellular adhesion molecule-1 (ICAM-1).⁴⁶ The authors attributed this to microvillus compression, but a direct increase in molecular binding rate is certainly a possibility.

Here, we use an optical trapping system to study single bonds between E-selectin and sialyl Lewis^a (sLe^a), a sugar on PSGL-1 to which the three selectins bind. The sialyl Lewis sugars (sLe^a and sLe^x) of PSGL-1 are known to be recognized by E-selectin^23,27,37 and evidence suggests that their affinity for E-selectin is stronger than that for either L- or P-selectin.⁵⁵ We observe for the first time clear evidence that E-selectin is capable of forming catch bonds with one of its ligands. We also find that the intrinsic rate of bond formation between E-selectin and sLe^a is enhanced by compressive load. Our laser trap method allows us to observe multiple bonds rupturing sequentially, enabling us to directly determine which of these binding events are in fact single bonds. We present simple physical models to explain how on-rate can be influenced by compressive force, and relate these to the catch bond phenomenon.

Methods

Bead Preparation

Chimeric recombinant human E-selectin (R&D Systems, Minneapolis, MN, USA) was covalently coupled to 0.92 μm carboxylated polystyrene beads (Bangs Laboratories, Fishers, IN, USA) using carbodiimide crosslinking.⁵ First, 12.5 μL (10% solids) beads were suspended in 1 mL of 50 mM MES, pH 6.1 (MES activation buffer). Beads were washed by centrifugation 3× with 1 mL MES activation buffer and resuspended in 50 μL MES activation buffer following the final wash. Next, 500 μL of 200 mM NHS, followed by 500 μL of 4% (w/v) EDAC, was added while mixing. This was allowed to react for 30 min at room temperature on a circular rotator. Beads were then washed twice with 1 mL of 50 mM MES, pH 7.4 (MES coupling buffer) and were resuspended in 100 μL MES coupling buffer following the final wash. The desired amount of E-selectin was added to the beads and they were rotated overnight at 4 °C. Beads were then washed twice with 1 mL of MES coupling buffer and resuspended in 1 mL of 0.1 M ethanolamine, followed by rotation for 30 min at room temperature. Beads were then washed twice with 1 mL of “flow cell buffer” (150 mM NaCl, 25 mM Imidazole, 1 mM CaCl₂, 1 mM NaN₃, pH 7.4), resuspended in 1 mL of flow cell buffer with 0.5% Tween-20 for blocking, and rotated at room temperature for 1 h. Beads are stored at 4 °C.

Trapping Protocol

Selectin-ligand association kinetics have traditionally been studied in three-dimensional (solution) experiments, where at least one species of the receptor– ligand pair is in solution.²¹ Leukocyte binding to the vessel wall is approximately two-dimensional, with a receptor confined to the plane of the leukocyte membrane and a ligand confined to the plane of the endothelial cell membrane. Thus 2-D kinetic constants are perhaps more appropriate than the 3-D kinetic constants. While previous studies have examined the load-dependent 2-D off-rates of selectin/PSGL-1 binding,^10,29 only a few studies to date have attempted to directly measure 2-D on-rates for any selectin interaction.^7,8,48 We used a variation on one of these assays⁷ to measure the time to bond formation, from which 2-D on-rates are directly calculated; our variation used a laser trap transducer rather than a biomembrane force probe.

The laser trap used in these studies is described elsewhere,¹⁶ except that a 1090 nm fiber laser was used (SP25C, SPI, Santa Clara, CA, USA). Trap stiffness and sensitivity were determined by step response and power spectral density methods.⁵⁰

Coverslips were prepared as described^15,17 by spraying a suspension of ∼3 μm glass beads (Polysciences, Warrington, PA, USA) onto a 22 × 22 mm² glass coverslip and then coating with a thin layer of nitrocellulose. An 18 × 18 mm² glass coverslip was then used to assemble a 25 μL flow cell. Streptavidin (MP Biomedicals, Solon, OH, USA) was incubated at the desired concentration in the flow cell for 15 min at room temperature. The flow cells were then blocked with 1% Tween-20 overnight at 4 °C to reduce nonspecific interactions. The desired concentration of sialyl Lewis^a–PAA–biotin (GlycoTech, Gaithersburg, MD, USA) was then incubated in the flow cells for 15 min at room temperature. E-selectin-coated beads were sonicated to minimize aggregation, diluted in flow cell buffer, and added to the flow cell.

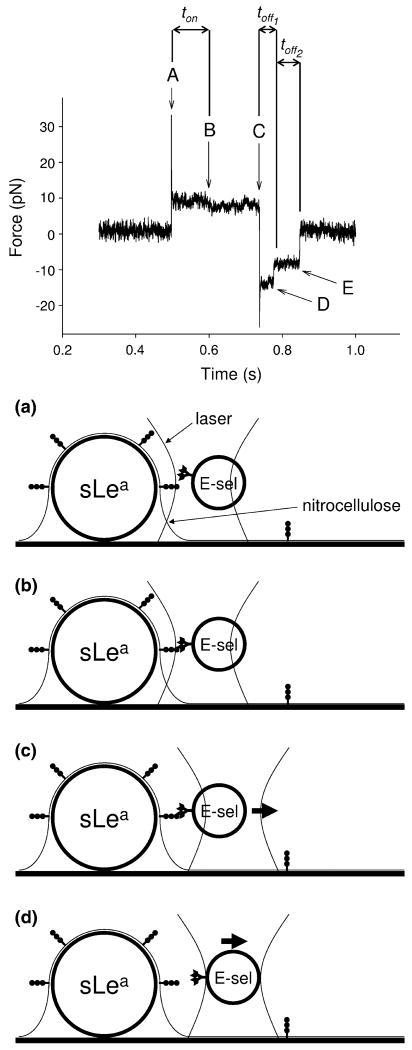
An E-selectin-coated bead was then trapped and brought into contact with a sLe^a-coated bead on the surface of the flow cell (Fig. 1a). Note that the laser is typically moved closer to the sLe^a-coated bead than necessary to bring the receptor and ligand molecules on opposing bead surfaces within binding range, thus generating a compressive load between the beads. The beads were held in contact for a sufficiently long time to form a bond (Fig. 1b). The trapped bead was then stepped away from the stationary bead (Fig. 1c), applying a load to any bond or bonds that had formed until bond rupture (Fig. 1d). The trap data were analyzed as follows. When the trapped bead was initially brought into contact with the stationary bead (Fig. 1a), there was a characteristic mean and variance of the signal determined by noise and overlap of the laser with the stationary bead. When a bond formed between receptor and ligand on opposing bead surfaces (Fig. 1b), there was a small shift of the signal mean and a change in variance. The shift of the signal mean is presumably due to interacting receptor/ligand pairs not being centered within the contact area prior to binding. Bond formation thus results in the trapped bead moving slightly out of trap center. The change in variance is a result of the trapped bead being tethered to the stationary bead once a bond has formed. These measurable changes allowed the time to bond formation (t_on) to be measured. When the trapped bead was stepped away (Fig. 1c), the signal shifted to a new baseline and the laser exerted a near-instantaneous force on the bead, while the receptor–ligand bond effectively prevented the bead from moving to the new trap position. When the bond broke (Fig. 1d), the bead moved toward the trap center and the signal returned to baseline. This allowed us to definitively say if a bond indeed formed between molecules on the opposing bead surfaces. The load applied to the bond and the lifetime of the bond (t_off) under the applied load could be measured. If multiple bonds formed, it was possible to observe the rupture of each individual bond separately (Fig. 1d, e). This allowed us to state with some confidence whether an individual event was due to a single bond or multiple bonds. Upon stepping the trapped bead toward the stationary bead, we compared the known distance the laser was displaced to the measured displacement of the trapped bead. This allowed us to measure how much compressive force was being exerted when the beads were brought together.

FIGURE 1.

Experimental setup and representative laser trap data of a bond event. Letters in the data trace correspond with similarly lettered panels in the experimental setup diagrams. The trapped bead is stepped toward the stationary bead (a), a bond forms (b), the trapped bead is stepped away from the stationary bead (c), a bond ruptures (d), and if there was a second bond present, a second bond ruptures (e). Measurements of t_on and t_off are used to determine on-rate and off-rates, respectively. In the case of multiple bonds, the lifetime of the n_th bond is designated t_offn.

Protein Site Density Determination

The site density of E-selectin on microspheres was determined by time-resolved fluorescence detection of Eu-labeled streptavidin (PerkinElmer Wallac, Turku, Finland).^18,49 Beads were prepared as described previously. They were resuspended in biotinylated anti-E-selectin antibody (HAE-1f, Ancell Corporation, Bayport, MN, USA) at 10 μg/mL in flow cell buffer and incubated on ice for 1 h. After three washes in flow cell buffer, beads were resuspended in Eu-streptavidin at 100 ng/mL in PBS and incubated on ice for 1 h. Beads were then washed five times with flow cell buffer, resuspended in DELFIA enhancer solution (PerkinElmer), and aliquoted into a 384-well plate. After 5 min of incubation at room temperature, the time resolved fluorescence was measured at 355 nm excitation and 615 nm emission with a detection interval of 50–1450 μs on a BMG spectrofluorometer.

The total streptavidin (active and inactive) site density on the flow cell surface was measured by incubation of known concentrations of Eu-streptavidin for 15 min at room temperature in flow cells made with a nitrocellulose-coated coverslip. After washing with five volumes of PBS, 100 μL of DELFIA enhancer solution was simultaneously injected and removed from each flow cell. The solution was transferred to a 384-well plate and the time resolved fluorescence was measured as described previously. The site density of active streptavidin and sLe^a on the flow cell surface was determined by the rate of enzymatic production of a chemiluminescent signal by biotinylated alkaline phosphatase (biotin-AP, New England BioLabs, Ipswich, MA, USA). Briefly, streptavidin at various concentrations was incubated for 15 min at room temperature in flow cells made with a nitrocellulose-coated coverslip. After washing with five volumes of flow cell buffer, flow cells were blocked by overnight incubation of 1% 40 kDa polyvinylpyrrolidone (PVP) at 4 °C. sLe^a was then incubated for 15 min at room temperature in one flow cell at each streptavidin concentration. Flow cells were washed with 5 vol of PBS and biotinylated alkaline phosphatase at 10 μg/mL was then incubated in each flow cell for 1 h at room temperature. After washing with 5 vol of PBS, chemiluminescent substrate with 5% enhancer by volume was added (Invitrogen, Calsbad, CA, USA). Flow cells were immediately imaged for 30 min with 1 min exposures on an Alpha Innotech FluorChem 8900 imager. The density of biotin binding sites was found for flow cells with and without the addition of sLe^a, and the difference between the two values indicated the site density occupied by sLe^a–PAA molecules.

Results

Sequential Bond Ruptures Can Be Observed in Real-Time

A problem that plagues many experimental systems built to study single intermolecular interactions is ascertaining whether one is actually observing single molecules or bonds. The presence of multiple bonds is a concern as most force spectroscopy methods are incapable of definitively distinguishing them from bonds that are truly between a single receptor–ligand pair. A common method of inferring single bonds based on Poisson's law of small numbers is to argue that when a low frequency of test cycles results in a binding event, a very low percentage of these binding events should be multiple bonds.⁶² Other methods employed to argue that single bonds are being measured include looking at how adhesion frequency varies with protein site density,⁸ fitting tether lifetime data from flow chamber studies to the equations of single-bond kinetics,^{1,2,6,40,41,44} looking for quantal behavior in measurements of low number molecular interactions,^2,12 and looking for binding events that have the kinetic and mechanical properties on the order of magnitude of those that can be predicted or inferred.⁸ None of these methods are able to discern the presence of single bonds on datum-by-datum basis.

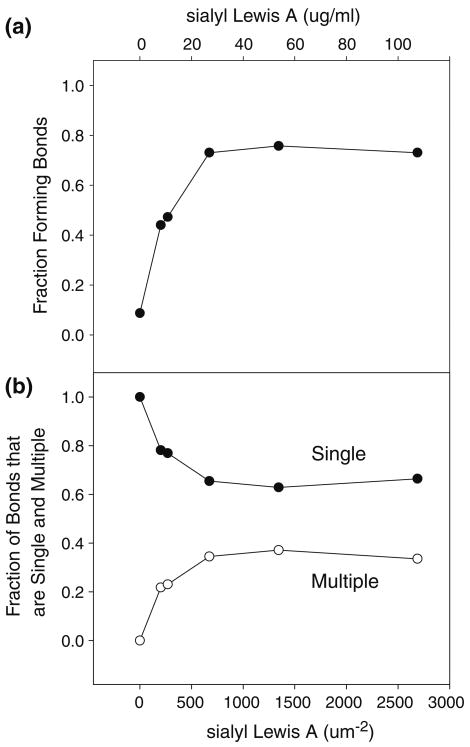
The method utilized here allowed us to accurately determine the presence and frequency of single bond events, and, in the event of multiple bonds, the number of bonds comprising each multiple bond. We saw that the fraction of bonds that are multiple bonds increased with increasing sLe^a concentration (Fig. 2b), suggesting the bonds were specific receptor–ligand bonds. The fraction of total contacts that form a bond (Fig. 2a) did not reach 1, suggesting that the E-selectin-coated surface was not saturated with protein. If a receptor– ligand interaction is comprised of multiple bonds, we were able to observe the dissociation of each individual bond (Fig. 1).

FIGURE 2.

(a) The fraction of bead contacts forming bonds (●) as a function of sLe^a concentration (top x-axis) and sLe^a site density (bottom x-axis). (b) The fraction of bonds that are single bonds (●) and multiple bonds (○) as a function of sLe^a concentration and sLe^a site density.

Bonds Between E-Selectin and sLe^a Exhibit Catch–Slip Behavior

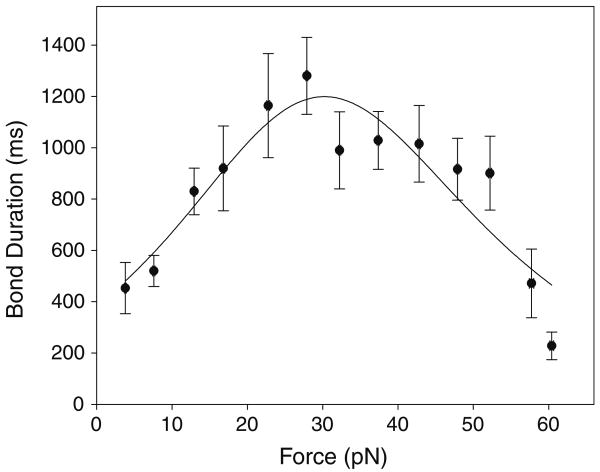
The lifetime of E-selectin/sLe^a bonds was measured over a range of applied loads using a laser trap (Fig. 1). An E-selectin-coated bead was held in the laser trap and brought into contact with a stationary target bead that was coated with sLe^a. The trapped bead was then stepped away from the target, applying a load to any bond (or bonds) that had formed. Bond lifetime and applied load were measured for a total of ∼1200 bonds. As can be seen in Fig. 3, single bond lifetimes increased with increasing load, characteristic of a catch bond, until reaching a maximum at a force of 30 ± 14 pN (propagated from the individual fitted parameter errors). Above 30 pN, bond lifetimes decrease with increasing load, characteristic of a slip bond. The critical force was obtained by fitting the data with a two-pathway model for catch–slip adhesion,³⁵

FIGURE 3.

Bond lifetime as a function of applied load for single bonds. Data is fit by the two-pathway model for catch–slip adhesion. Error bars indicate standard error of the mean.

$$1/t(f)=k_{\text{c}}^{\text{o}}{e}^{x_{\text{c}}f/k_{\text{B}}T}+k_{\text{s}}^{\text{o}}{e}^{x_{\text{S}}f/k_{\text{B}}T},$$ (1)

where t(f) is the mean bond lifetime at force f, $k_{\mathrm{c}}^{\text{o}}$ and $k_{\mathrm{s}}^{\text{o}}$ are the dissociation constants for unbinding through the catch and slip pathways, respectively, x_c and x_s are the transition state distances for unbinding through the catch and slip pathways, respectively, f is the applied load, T the absolute temperature, and k_B the Boltzmann constant. The critical force of 30 pN is nearly identical to the catch–slip transition force reported for P-selectin/PSGL-1 bonds in both AFM and flow chamber experiments,²⁹ but less than the ∼50 pN transition force observed for L-selectin/PSGL-1 bonds in AFM and biomembrane force probe (BFP) experiments, and L-selectin/sLe^x bonds in BFP experiments.^26,43 The measured E-selectin/sLe^a bond lifetime at the transition force is 1.2 s, similar to that seen by others for P-selectin/PSGL-1 bonds,²⁹ and significantly longer than the lifetimes seen for L-selectin/PSGL-1 and L-selectin/sLe^x bonds.^26,43

2-D On-Rates Are Enhanced by Compressive Force

We studied directly the effects of compressive force on the rate of bond formation between E-selectin and sLe^a. An E-selectin-coated bead was brought into contact with a stationary target bead that was coated with sLe^a. When a bond formed between receptor and ligand on opposing bead surfaces, there was an appreciable shift of the signal mean and a change in variance (Fig. 1) that allowed the time to bond formation (t_on) to be measured, from which an apparent 2-D on-rate (k_on) was calculated. Upon stepping the trapped bead away from the stationary bead, comparing the known distance the laser was stepped to the measured displacement of the bead allowed us to measure how much compressive force was being exerted on opposing bead surfaces. A similar method of detecting bond formation has been reported previously in conjunction with a biomembrane force probe⁷ rather than a laser trap, though no attempt was reported to measure compressive force.

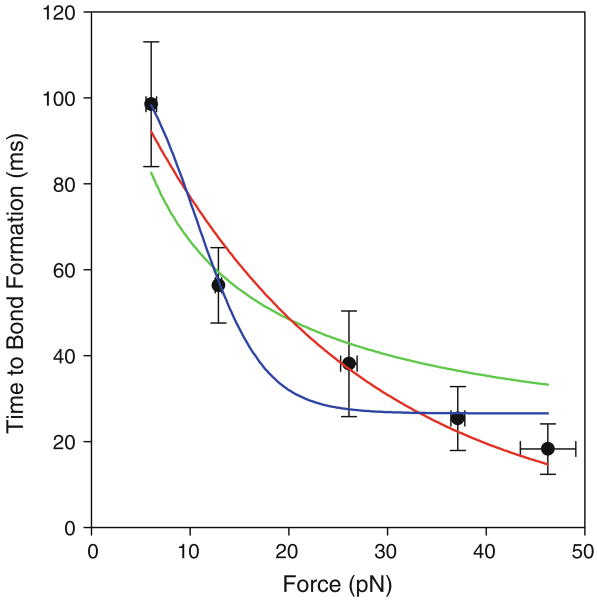
As seen in Fig. 4, t_on decreases with increasing compressive force, showing that force does indeed increase the rate of bond formation. In fact, t_on decreases approximately fivefold as the inward load increases from 6 to 46 pN. This corresponds to a similarly large change in the specific 2-D on-rate, ${\mathit{\text{k}}}_{\text{on}}^{\text{o}}$, calculated as $k_{\text{on}}^{\text{o}}={(t_{\text{on}}{m}_{\text{r}}{m}_{\text{l}}{A}_{\text{c}})}^{-1}$, where m_r and m_l are the site densities of receptor and ligand, respectively, on opposing bead surfaces, and A_c is the bead interaction area. Using our measured E-selectin site density of 1641 μm⁻², the sLe^a–PAA site density of 2687 μm⁻², and interaction area of 0.325 μm², ${\mathit{\text{k}}}_{\text{on}}^{\text{o}}$ ranges from 7.1 × 10⁻⁶ μm²/s at a compressive force of 6 pN to 3.8 × 10⁻⁵ μm²/s at 46 pN.

FIGURE 4.

Time to bond formation (t_on) as a function of compressive force. Data fit by two-state conformational change model (blue line), tilting energy landscape model (red), and surface layer deformation model (green). Error bars indicate standard error of the mean.

Discussion

We show that E-selectin, like L- and P-selectin, forms catch bonds with at least one of its ligands. We also present the first direct evidence that compressive load increases the association rates of single receptor– ligand pairs. These combined effects—increasing rates of association with compressive load, and decreasing rates of dissociation with tensile load—suggest a new aspect of force-enhanced adhesion.

Catch–slip behavior has been established for bonds of both P- and L-selectin^29,43 with PSGL-1, but has not previously been observed for any E-selectin bonds. The single molecule studies that have previously been conducted with E-selectin^20,51 find no evidence of a catch pathway, and instead analyze data in the context of the traditional Bell model³ for force-induced dissociation, which predicts that bond lifetimes decrease exponentially with applied load. The fact that our values for critical force and maximum bond lifetime are similar to those seen for P-selectin catch bonds, but different from those seen for L-selectin, is not surprising as P- and E-selectin serve similar roles on the endothelial surface. Catch bonds and the catch–slip transition are thought to be important in mediating leukocyte adhesion and subsequent rolling. It has been shown that a minimum shear stress is often necessary for leukocytes to tether and roll on selectins,^1,11,25 a concept known as the shear threshold phenomenon. This shear threshold effect may be important in preventing undesired leukocyte adhesion and aggregation in slow flow vessels.^29,61 It has been speculated that catch bonds may be the underlying cause of the shear threshold phenomenon, whereby bond lifetimes are too short to support rolling at low shear stresses, while high shear stresses slow bond dissociation at the trailing edge to allow rolling. Indeed, evidence for this was recently shown for L- and P-selectin using adhesive dynamics simulations.⁴ Our data suggest that the lack of a consistent display of a shear threshold for rolling on E-selectin is not the result of an inability for E-selectin to form catch bonds.

Our adaptation of the recently published thermal fluctuation assay⁷ allowed it to be used with a laser trap to measure the time to bond formation, from which 2-D on-rates were directly calculated. Our specific 2-D on-rate of 7.1 × 10⁻⁶ μm²/s for the lowest value of compressive load is equivalent to an effective on-rate, $A_{\text{c}}{k}_{\text{on}}^{\text{o}}$, of 2.3 × 10⁻⁶μm⁴/s, which is somewhat lower than the effective on-rate of 5.1 × 10⁻⁵ μm⁴/s found by others for L-selectin/PSGL-1 bonds.⁷ This lower on-rate may be due to differences in ligand, as the initial tethering rate of sLe^x microspheres to E-selectin has been shown to be lower that that of PSGL-1 microspheres,⁶³ though an even lower effective on-rate was recently found for E-selectin/PSGL-1 bonds using an E-selectin lacking consensus repeats.⁴⁸

The apparent sensitivity of this on-rate to compressive force is intriguing. While it is accepted that molecular rates of dissociation are impacted by force, the question of whether the rate of association may be influenced by force has largely been ignored. It has been shown that attachment of platelets to the endothelium occurs in orientations that are predicted to result in compression along the bond being formed.³⁰ It has also been observed that increasing contact stress, while controlling for contact area, results in higher intrinsic rates of bond formation for bonds between β₂-integrins and intercellular adhesion molecule-1 (ICAM-1).⁴⁶ The authors attributed this to microvillus compression, but a more fundamental increase in binding rate is certainly a possibility. Evidence for a selectin/ligand on-rate that is enhanced by load was recently seen in a flow chamber study in which the authors observe an amplification of L-selectin binding rates to PSGL-1 by shear-induced compressive forces.³⁴ Our data lends further support to this being an intrinsic property of at least some selectins.

Physical Mechanisms

We considered four possible physical mechanisms to explain load-dependent on-rates. One possibility is that there are two E-selectin conformations whose distribution is determined by force, with each conformation having a distinct association rate. Another potential mechanism is that force is causing the molecules to bind faster by tilting the energy landscape and thus reducing the activation energy for binding. Alternatively, force may be increasing the interaction area by deforming the molecular layers on the bead and/or flow cell surface. Finally, one might postulate that force is causing a reduction in Brownian motion such that the trapped bead is spending a greater fraction of time with its surface molecules within binding range of the molecules on the opposing bead surface.

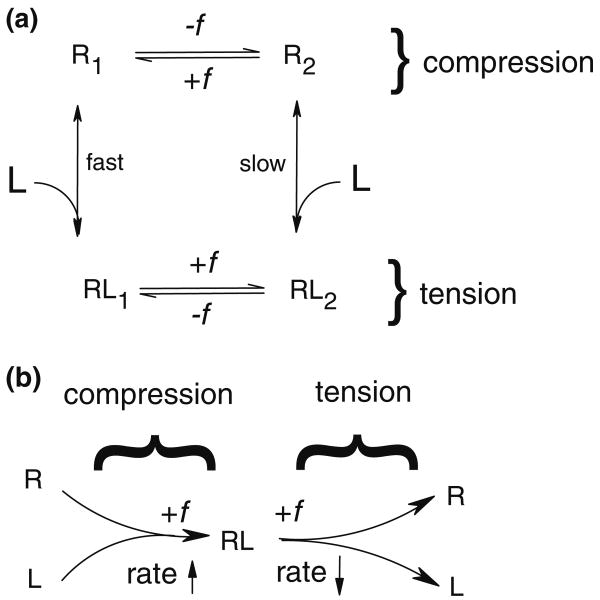
First we consider the conformational change model. This model assumes the existence of two E-selectin conformations with different association rates, such that compressive load generates a conformational change in E-selectin, biasing it toward the state with a faster binding rate. P-selectin has been shown to have two conformations, closed- and open-angle, each with a different angle between the lectin and EGF domains.⁴⁵ The structures suggest that the lectin domain can pivot about the EGF domain in a hingelike fashion. The EGF domains of L- and E-selectin have a similar hinge region but with an Asn at residue 138 rather than a Gly, allowing for an additional hydrogen bond between Tyr37 and Asn138.^14,45 It has been shown how force-induced conformational changes between the two hinge states can regulate the kinetics of L-selectin association and dissociation with PSGL-1 and 6-sulfo-sLe^x.²⁶ Tensile force shifts the molecular equilibrium toward the open-angle state, which is postulated to lower off-rate by allowing the ligand to slide across the lectin domain as preexisting interactions dissociate, leading to the catch bond phenomenon. We envision compressive force between the two surfaces generating a conformational change in the hinge region of E-selectin, converting the molecule to a state with a faster rate of association. This can be viewed as an extension of a two-state catch bond model to include different binding pathways for each state. As can be seen in Fig. 5a, we have modified the two-state allosteric model⁵³ to include two unbound states, R₁ and R₂. The application of a compressive load favors unbound state R₁, which has a faster rate of association. We describe the association pathways of our model by fitting t_on as a function of compressive load, f, using the parallel sum of two different association rates, as follows. Let the overall k_on = k_fastz_fast + k_slowz_slow where k_fast and k_slow are the specific 2-D on-rates for the fast and slow association pathways, respectively, and z_fast and z_slow are the fractions of receptors in the fast- and slow-binding states. z_fast + z_slow = 1. The equilibrium distribution between the two states is given by a Boltzmann distribution modified by force, as in Bell³:

FIGURE 5.

(a) A schematic for the load-dependent association model integrated into the two-state model. Compressive force shifts the equilibrium of unbound receptors to conformational state R₂, which has a faster association rate than state R₁. Tensile force shifts the equilibrium of bound complex to state RL₂, which has a slower dissociation rate than state RL₁. In the compressive regime (top half of figure), +f indicates compressive force, while in the tensile regime, +f indicates tensile force. (b) A schematic for the reverse Bell model. Compressive force increases the rate at which bonds form, while tensile force decreases the rate at which bonds rupture.

$$z_{\text{fast}}(f)/z_{\text{slow}}(f)=exp((-\Delta E+f{x}_{\delta })/k_{\text{B}}T),$$ (2)

where ΔE is the energy difference between the two states and x_δ represents the transition state distance between them. If z is z_slow at zero load, algebraic rearrangement gives

$$z_{\text{fast}}(f)=1/(1+K_{\text{eq}}exp(-f{x}_{\delta }/k_{\text{B}}T)),$$ (3)

where K_eq = z/(1 − z). Our model assumes rapid equilibrium between the two unbound states relative to force application, the rate of binding, and the rate of unbinding. This two-pathway association model fits our data only when z > 0.98, and with large parameter errors. We therefore set z = 0.99, which minimizes the parameter errors, and fitted the data (Fig. 4) with a k_slow of 6.0 ± 0.9 × 10⁻⁶ μm²/s, a k_fast of 2.6 ± 0.6 × 10⁻⁵ μm²/s, and an x_δ of 1.2 ± 0.2 nm. The ratio of k_fast to k_slow is 4.3, meaning that molecules in the conformation favored by force bind 4.3-fold faster than molecules in the low-force conformation. Both association rate values are reasonable when compared to that measured directly in this study (7.1 × 10⁻⁶ μm²/s) and when converted to an effective on-rate and compared to that determined by others for L-selectin/PSGL-1 bonds (5.9 × 10⁻⁵ μm²/s). The transition state distance of 1.2 nm is reasonable given the 0.4 nm movement in the direction of tensile force found for the transition between the open and closed conformation in molecular dynamics simulations.⁴⁷ The high fraction of receptors in the slow-binding state at zero force that is necessary for this model to fit our data is a point of concern, as molecular dynamics simulations have found L-selectin to exhibit a stable closed angle conformation 70% of the time.²⁶ Additionally, the extended conformation state seen at equilibrium in this model is thought to be a high affinity state,³⁶ thus one would expect selectin-ligand bonds to form readily at low or no force; this is not the case.²⁵

We next consider the possibility that force is causing a direct enhancement of binding rate by forcing the receptor and ligand together once they have aligned stereospecifically with one another (Fig. 5b). This would require the opposing binding sites to be approximately opposite one another prior to force application. Force will then compress the binding sites together, effectively tilting the energy landscape to reduce the activation energy for binding, and thus allowing the receptor and ligand to bind more rapidly. This is analogous to the Bell model for force-induced dissociation,³ but with the energy landscape tilting in the opposite direction.

$$k_{\text{on}}(f)=k_{\text{on}}^{\text{o}}exp(f\cdot x_{\gamma a}/k_{\text{B}}T),$$ (4)

where k_on(f) is the load-dependent on-rate, ${\mathit{\text{k}}}_{\text{on}}^{\text{o}}$ is the unloaded on-rate, f the applied load, x_γa the characteristic bond length of association, k_B the Boltzmann constant, and T the absolute temperature. This model fits our data well (Fig. 4), and yields a ${\mathit{\text{k}}}_{\text{on}}^{\text{o}}$ of 5.7 ± 0.6 μm²/s and an x_γ of 0.19 ± 0.03 nm. The value of ${\mathit{\text{k}}}_{\text{on}}^{\text{o}}$ is similar to but slightly larger than that found for bonds between E-selectin and E-selectin ligand-1 (ESL-1) by surface plasmon resonance.⁵⁹ The value of x_γa is comparable to values previously reported for the dissociation characteristic bond length for L- and P-selectin,^{13,19,41,42,44} though this need not be the case because our measurement approaches the transition state from the unbound, rather than the bound state. A limitation of this model is that the receptor and ligand must already be stereospecifically aligned as the compressive force is applied. At any given instant in time the compressive force may not fully manifest at the binding interface; this is the inevitable result of thermal fluctuations in the system, and finite rigidities of the receptors and ligands. Nonetheless, the time-averaged energy landscape for bond formation should be “tilted inward” under compressive force.

A third possible physical mechanism is that compressive force causes an increase in interaction area, and thus the number of potential binding sites, by deforming the surface-adsorbed layer of molecules on the bead and/or flow cell. For example, the likelihood of bond formation between β₂-integrins on neutrophils and ICAM-1 has been shown to increase linearly with contact area,⁴⁶ though the present experiments use beads that are much less compressible than cells. To determine whether a similar mechanism was feasible to explain our data, we fit a molecular compression model to the t_on vs. f data. This allowed us to determine the bulk moduli and/or molecular stiffnesses that would be required for the increase in interaction area necessary to generate the observed decrease in t_on with increasing inward load. Briefly, using expressions for the compression of two spheres in contact,^22,57 the contact radius, a, was calculated as

$$a={(3f{R}^{\ast }/4E^{\ast })}^{1/3},$$ (5)

where f is the applied force, and R* and E* are the equivalent contact curvature and equivalent elastic modulus, respectively. The parameters R* and E* are calculated as

$$1/R^{\ast }=(1/R_1+1/R_2)$$ (6)

and

$$1/E^{\ast }=(1/E_1+1/E_2),$$ (7)

where R₁ and R₂ are the radii of the contacting spheres, E₁ and E₂ are the Young's moduli of the two spheres, and the effect of the Poisson's ratio is minimal. From this, the inward displacement, d, of opposing points on the two spheres was calculated as

$$d=(a^2/R^{\ast }).$$ (8)

The contact area of each sphere⁴² was found as

$$A_x=2\pi r_x{h}_x$$ (9)

where h_x is the height of the cap on sphere x, and r_x is the radius of the sphere. Given a bond that is assumed to be parallel to the x-axis, the cap height for one sphere⁴² is found as

$$h_2=r_2+\frac{1}{2}\left(\frac{r_1^2-r_2^2}{r_1+r_2-l}+l-r_1-r_2\right)$$ (10)

and the second cap height is given by h₁ = l − h₂, where the bond length l = l_o − d, where l_o is the original bond length. The total contact area, A_c = A₁ + A₂, is then used to model t_on as

$$t_{\text{on}}={(k_{\text{on}}{m}_{\text{r}}{m}_1{A}_{\text{c}})}^{-1}$$ (11)

where E* and k_on are fitted parameters. Fitting this model to our t_on vs. f data yields a k_on of 3.1 ± 0.3 × 10⁻⁶ μm²/s and an E* of 152 ± 752 Pa. This model, with large parameter errors, does not fit the data nearly as well as the two pathway association model (Fig. 4). Additionally, the value of E* does not seem reasonable; assuming the surface layer undergoing compression on each bead is of similar stiffness, E₁ and E₂ are both equal to 304 Pa. This is outside the range of any possible modulus for a continuous surface layer of Tween-20, nitrocellulose, or polystyrene, which are more likely to be of GPa magnitude.^28,32,38 Considering the possibility that the modulus is due to individual E-selectin and sLe^a–PAA molecules being compressed, we used the equation E = kn(L/A_s) to calculate the molecular stiffness, k, that would be necessary to generate the modulus value determined by the model, where n is the number of molecules in the interaction area, L is the molecule length, and A_s is the surface area taken up by each molecule based on the measured site densities. For E-selectin and sLe^a–PAA this yields a k of 1.6e⁻⁵ and 1.3e⁻⁵ pN/nm, respectively. These values are far below experimental measurements of single molecule stiffness. In fact, P-selectin/PSGL-1 complexes have been shown to have a molecular stiffness of 5.3 pN/nm,¹³ many fold larger than that calculated using the compression model. Furthermore, we find that the fraction of bonds that are multiple bonds does not increase with increasing compressive force, suggesting that the number of available receptor/ligand molecules and therefore the contact area is not increasing.

A final possibility is that compressive force is reducing Brownian motion of the trapped bead by simply pushing it against the stationary bead, such that it spends a greater fraction of time within a range that allows its surface molecules to bind to those on the opposing bead surface. This seems unlikely as the standard deviation of bead fluctuation, σ, calculated as

$$\sigma =\sqrt{k_{\text{B}}T/\alpha },$$ (12)

where α is the trap stiffness, is only 6.5 nm, many fold smaller than the ∼55 nm combined length of the receptor and ligand. The compressive force is likely also reducing rotational Brownian motion; however, this is unlikely to lead to a large increase in association rate, and may in fact decrease association rate as the receptor and ligand are able to cover a smaller volume per unit time in their search for a binding partner.

Significance

The one model with which our data are fully consistent is the “reverse Bell model,” where compressive force causes a direct enhancement of binding rate by lowering the activation energy of bond formation. If this model is indeed correct, all bonds should exhibit load-dependent on-rates regardless of whether they are also catch bonds. This physical mechanism is likely to depend on the relative orientation of the molecular binding sites, a complex situation that may depend on the orientation of the molecules with respect to the surfaces to which they are bound. The molecules used in our system are not especially rigid and thus it is difficult for us to say how we would expect binding sites to be oriented.

Though the particular two-state conformational change model presented here seems unlikely, a mechanism involving a conformational change of the hinge region should not be ruled out. Some have pointed out that many of the molecules found to exhibit catch–slip behavior contain similar hinge regions,^26,36,52 lending further credence to this possibility. It would be exciting to perform similar tests with selectin mutants that have a modified hinge region to test how the molecules' ability to change lectin-EGF hinge angle affects its binding rate at the single molecule level. Further investigations should examine the relationship between association and dissociation to determine how binding and unbinding pathways are related and how these pathways respond to force.

The localization of PSGL-1 on the tips of neutrophil microvilli³¹ suggests that the effects of these structures on the tensile and compressive forces of adhesion³³ must be considered. The implications of having both a load-dependent association and dissociation rate are intriguing, particularly potential effects on the kinetics of cell capture and rolling. Bonds at the leading edge of a rolling cell may be more likely to form prior to rupture of the initial load-bearing bond at the trailing edge, promoting continued rolling and shorter skips along the surface. Load-dependent association may even play a role in the shear threshold effect, as higher shear increases compressive load, resulting in increased tethering. A detailed knowledge of load dependent kinetics is vital to understand this and other phenomena, and are crucial for the further development of leukocyte adhesion cascade simulations.