Distribution of Fitness Effects Caused by Single-Nucleotide Substitutions in Bacteriophage f1

Abstract

Empirical knowledge of the fitness effects of mutations is important for understanding many evolutionary processes, yet this knowledge is often hampered by several sources of measurement error and bias. Most of these problems can be solved using site-directed mutagenesis to engineer single mutations, an approach particularly suited for viruses due to their small genomes. Here, we used this technique to measure the fitness effect of 100 single-nucleotide substitutions in the bacteriophage f1, a filamentous single-strand DNA virus. We found that approximately one-fifth of all mutations are lethal. Viable ones reduced fitness by 11% on average and were accurately described by a log-normal distribution. More than 90% of synonymous substitutions were selectively neutral, while those affecting intergenic regions reduced fitness by 14% on average. Mutations leading to amino acid substitutions had an overall mean deleterious effect of 37%, which increased to 45% for those changing the amino acid polarity. Interestingly, mutations affecting early steps of the infection cycle tended to be more deleterious than those affecting late steps. Finally, we observed at least two beneficial mutations. Our results confirm that high mutational sensitivity is a general property of viruses with small genomes, including RNA and single-strand DNA viruses infecting animals, plants, and bacteria.

MUTATIONAL fitness effects are relevant to many evolutionary processes. For instance, they determine the fraction of mutations that evolves neutrally (Ohta 1992), the amount of genetic variation at the mutation–selection balance (Haldane 1937), processes of fitness decay, such as Muller's ratchet (Butcher 1995), mutational meltdown (Lynch et al. 1993), or lethal mutagenesis (Bull et al. 2007), the ability of organisms to fix beneficial mutations and evolve novel functions (Wagner 2005), or the origin of sex and recombination (Peck et al. 1997; de Visser et al. 2003). Considerable progress has been made in characterizing mutational fitness effects using model organisms or studying genetic variation in natural populations (Eyre-Walker and Keightley 2007). For instance, mutation–accumulation experiments suggest that the average effect of spontaneous deleterious mutations is 1% or lower (Kibota and Lynch 1996) in Escherichia coli, while roughly 90% of engineered gene knockouts are viable (Baba et al. 2006) and transposon insertions reduce fitness by 3% or less on average (Elena et al. 1998). In yeast, mutation–accumulation and chemical mutagenesis experiments have shown that mutations reduce fitness by 1–4% on average in diploid strains (Zeyl and de Visser 2001; Szafraniec et al. 2003; Joseph and Hall 2004). In nematodes most mutations have fitness effects lower than 1% (Keightley and Caballero 1997; Davies et al. 1999), in Drosophila the average effect of mutations ranges from 0.5 to 3.5% (Mukai et al. 1972; Ohnishi 1977; Fernández and López-Fanjul 1996; Fry et al. 1999), and, in humans, most segregating amino acid substitutions have fitness effects lower than 10% (Eyre-Walker and Keightley 2007).

Although mutation–accumulation studies provide valuable information about the average effects of deleterious mutations, their power to infer the entire distribution of mutational effects, including neutral and lethal mutations, is more limited. Also, excluding bias due to selection can be problematic, and the precise location and nature of each mutation is often unknown. On the other hand, studies based on engineering mutations have been generally restricted to large deletions or insertions, which are probably infrequent in nature compared to point mutations. A direct and powerful approach that helps us to solve these difficulties consists of introducing single-nucleotide substitutions by site-directed mutagenesis. Due to their small genome sizes, viruses are excellent systems for achieving this goal. In previous work, this technique has been used for studying mutational fitness effects in several RNA viruses (Sanjuán et al. 2004; Carrasco et al. 2007; Domingo-Calap et al. 2009). However, less is known for DNA viruses—but see Domingo-Calap et al. (2009). Here, we use this approach to characterize the distribution of mutational fitness effects in the bacteriophage f1, an inovirus of the bacteriophage m13 clade, making two important improvements over previous work: first, the number of mutations tested is higher (100) and second, the contribution of experimental error to the observed distribution is explicitly accounted for. We show that one-fifth of single-nucleotide substitutions are lethal, while viable ones reduce fitness by 11% on average and can be described by a heavy-tail two-parameter distribution such as the log-normal. Interestingly, the fraction of beneficial mutations is unexpectedly high. We also compare the average effects of different mutation types and of mutations affecting different genes.

MATERIALS AND METHODS

Bacteriophage and cells:

Bacteriophage f1 and E. coli C strain IJ1862 (Bull et al. 2004) were originally obtained from James J. Bull (University of Texas). We adapted the phage to our laboratory conditions by performing 80 serial passages at high population sizes as follows: exponentially growing IJ1862 cells at an optical density of OD₆₀₀ = 0.15 were inoculated with ∼10⁵ particle forming units (pfu) in 0.5 ml of LB medium, incubated in agitation (650 rpm) at 37° in a Thermomixer 24-tube shaker (Eppendorf), and harvested after approximately 2 hr, which corresponded to the late exponential growth phase of the virus (∼10⁹ pfu/ml). Cells were removed by centrifugation and supernatants were aliquoted, stored at −70°, and titrated using LB medium solidified with soft agar (a single cycle of freeze–thawing did not noticeably reduce the viral titer). Initial and final titers were used to calculate growth rates and to adjust sampling times for the next passage accordingly. No significant changes in growth rate were observed during the 80 passages. A single plaque from passage 80 was isolated and used to infect a large culture of IJ1862 cells. Viruses from the supernatant of this culture were stored in several aliquots at −70° and used as the reference virus (wild type) in all fitness assays, whereas the cell pellet was used to isolate the circular double-strand replicative form of the viral DNA using a plasmid isolation kit (Roche). This DNA was used as template for the site-directed mutagenesis reactions. Using a well-adapted phage minimizes the fraction of beneficial mutations and increases the genetic stability of the virus during plaque growth and fitness assays.

Site-directed mutagenesis:

Full-length PCR amplicons were obtained from 500 pg of template DNA using Phusion high-fidelity DNA polymerase (New England Biolabs) and a pair of contiguous, divergent, 5′-phosphorylated primers, one of which carried the desired nucleotide substitution. The cycling conditions were 2 min at 98° (initial denaturation), 30 cycles of 30 sec at 98°, 30 sec at 68°, and 4 min at 72°, and a final extension step of 10 min at 72°. The calculated fraction of PCR products carrying nondesired mutations is 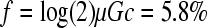, where μ = 4.4 × 10⁻⁷ per base per round of copying is the error rate of the enzyme provided by the manufacturer, G = 6386 is the genome size, and c = 30 the number of PCR cycles. Since primers are contiguous and divergent, PCR products consist of a linear, full-length, genomic DNA. These products were circularized using the Quick T4 ligase (New England Biolabs) and IJ1862 competent cells were transfected by the heat-shock method (42°, 30 sec) in the presence of 100 mm CaCl₂. The transfected cells were immediately plated and four individual plaques of each mutant were picked after 20 hr of incubation at 37°, resuspended in LB, and stored at −70°. PCR was performed directly from the resuspended plaques using Phusion DNA polymerase. To check the presence of the mutation and that no additional mutations appeared in the flanking region (∼500 nt), PCR products were column purified and sequenced using mutagenesis primers that annealed near the target site. Once the mutation was verified, three resuspended plaques were titrated and mixed in equal amounts for fitness assays. Mixing three plaques minimizes the effects of potential additional mutations resulting from PCR errors. Additional details about the site-directed mutagenesis protocol can be found elsewhere (Sanjuán 2010).

Fitness assays:

Approximately 10⁵ pfu were inoculated (t₀) into 0.5 ml of LB medium containing exponentially growing IJ1862 cells at an optical density OD₆₀₀ = 0.15 and harvested after 2 hr 5 min (t₁) of incubation in agitation (650 rpm) at 37°. Cells were removed by centrifugation and supernatants were stored at −70°. Previous assays showed that the viral titer increases exponentially within this interval. Titers at times t₀ and t₁ were determined and the growth rate (r) was calculated as the increase in log-titer per hour. Relative fitness (W) was defined as the growth rate ratio and the relative fitness effect as s = W − 1. Each mutant was assayed in three independent experimental blocks. Three additional blocks were performed for a subset of mutants showing fitness values slightly below 1.0 and for all mutants showing W > 1. In each block, 18 mutants and six wild-type replicates were assayed simultaneously. The relative fitness of mutant i was calculated as W_i = r_i / 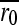, where 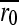is the average of the six wild-type determinations of the block. This cancels out potential block or day effects. However, using the 108 available W₀ = r₀/ 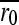values, we detected a significant effect of the position within the block. To minimize this problem, the position of each mutant was changed in each assay. Also, since the bias was roughly linear with the position number, we used the 108 W₀ values to interpolate position effects and to correct W_i values accordingly. Corrected values (reported in the text) were used for inferring the distribution of mutational fitness effects and for testing the effect of each individual mutation. For this latter purpose, we also performed ANOVA tests using uncorrected s-values, accounting for the position within the block as a covariate in the model. This alternative approach yielded the same numbers of neutral, deleterious, and beneficial mutations.

Lethality tests:

For some mutants, transfection yielded an anomalously low number of plaques (<5 vs. typically >100 for the other mutants). Further, the few clones recovered were nonmutant and thus most likely derived from the template DNA. If this result was repeated, the mutant was classified as a candidate lethal. For these cases, we first performed direct sequencing of the mutagenesis PCR product for the region flanking the target site to verify that the target mutation was present and that no additional changes appeared. Second, we designed primers identical to those used for each mutagenesis reaction except that they did not carry the target substitution (control primers), and we repeated the protocol exactly as above for the mutagenesis and control reactions in parallel using the reference, nonmutated DNA as template in both cases. In all cases, the number of plaques obtained from similar amounts of DNA was much higher (>100-fold on average) for controls than for true mutants, thus confirming lethality (supporting information, Figure S1).

Quantification of experimental error:

Several precautions were taken to minimize the frequency at which nondesired mutations appeared: (i) the template DNA used for all mutagenesis was obtained from a plaque-purified virus to minimize its genetic variation; (ii) we used a high-fidelity DNA polymerase; and (iii) the region flanking the target substitution was sequenced. Further, as mentioned above, to reduce the potential impact of nondesired mutations, three plaques of each mutant were mixed prior to fitness assays. To quantify the error of the method, we obtained 45 clones by the same procedure used for obtaining the mutants, except that the PCR primers did not carry any substitution and measured their fitness relative to the wild type. If the method was fully accurate, all these control clones should be selectively neutral (s = 0). Only one clone had a significant fitness defect and sequencing revealed the presence of a small insertion in the primer region. After removing this single case, the mean fitness value of the controls was 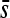= −0.0041 with variance 0.0008, standard deviation 0.0275, and range −0.0513–0.0585. The means and variances of mutational fitness effects reported in the text were obtained after subtracting the control mean and variance from the total means and variances.

Maximum-likelihood inference of the distribution of mutational fitness effects:

Each experimentally observed s-value is determined by the joint action of mutational fitness effects and measurement error. The 44 s-values from the control assays used to calibrate the error (see above) were accurately modeled (r² = 0.992) by a normal distribution with mean −0.0041 and standard deviation 0.0272. Consistently, a Shapiro–Wilk test indicated that normality could not be rejected for these data (P = 0.5549). We convoluted model distributions for mutational fitness effects (exponential, gamma, beta, log-normal, or Weibull) and the above normal to calculate the likelihood of each experimental observation s_i given the model as 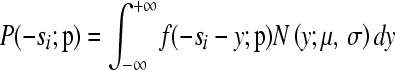, with μ = 0.0041 and σ = 0.0272, where f is the probability density function (pdf) of the model distribution, 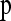the parameters of the model, and N the pdf of the normal distribution (the minus preceding s_i was introduced to make the variable positive for deleterious mutations). Alternatively, instead of using the normal distribution, f could be summed over the 44 control data values, an approach that yielded very similar results. The parameters of the model were estimated by maximum likelihood and the total log-likelihood was used to compare models. Distributions defined within the range [0; ∞] were truncated at 1 and normalized accordingly. This correction was not needed for the beta distribution, which is defined in the same range as −s for nonbeneficial mutations. To obtain a standard measure of the goodness of fit of each model, we calculated the correlation coefficient between the cumulative distribution function (cdf) of the maximum-likelihood model and the cdf of the data.

RESULTS

Fitness of single-nucleotide mutants:

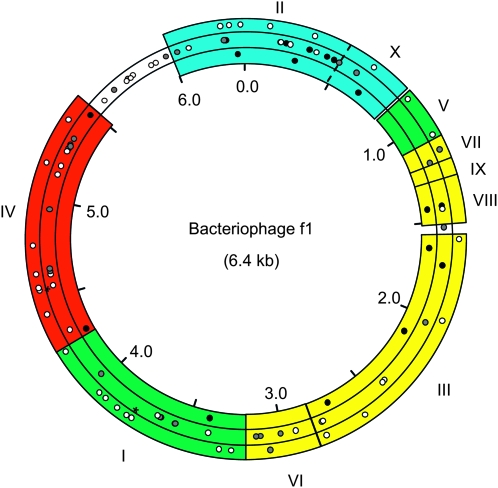
We obtained 100 viral clones by site-directed mutagenesis, each carrying a different nucleotide substitution (Figure 1). The mutated sites were chosen at random and, consequently, changes were spread through all the genome. Ninety belonged to coding regions and 10 to intergenic regions. Although the substituted nucleotide was not random (most changes were to A), mutations were probably representative of a random set: 70 were transversions and 30 transitions and, among the 90 mutations affecting coding regions, 51 produced amino acid substitutions (missense mutations), 9 produced premature amino acid chain termination (nonsense mutations), and 30 were synonymous. Among the 51 missense mutations, 29 changed the polarity of the amino acid (hydrophobic, polar, positively charged, or negatively charged), 10 replaced an aromatic amino acid by an acyclic one or vice versa, and 23 changed the size of the amino acid. Fifteen of the 51 missense mutations affected genes involved in replication, 8 affected maturation genes, 13 affected encapsidation genes, and 15 affected the extrusion gene. These four functions can be more broadly classified as early (replication) and late (maturation, capsid, and extrusion) steps of the infection cycle.

Figure 1.—

Diagram of the f1 genome showing the 100 single-nucleotide substitutions created by site-directed mutagenesis. Gene names (roman numbers) and genome positions are indicated. Colors indicate broad functional categories (blue, replication; green, particle maturation; yellow, capsid; red, extrusion). Additional details about the function of each gene can be found elsewhere (Calendar 2006). Briefly, protein II nicks the viral DNA to allow replication priming, protein X results from in-frame translation of gene II and is required for single-strand DNA accumulation, protein V binds to DNA and collapses the circular genome into a flexible rod, proteins VII and IX are small coat proteins located at the tip of the virion, protein VIII forms the cylinder containing the viral DNA, proteins III and VI are located at the tail of the virion and are involved in termination of virion assembly, protein I is an inner membrane protein that hydrolyzes ATP and promotes capsid morphogenesis, and protein IV forms a channel in the outer membrane to allow virion extrusion. Thinner, noncolored, areas denote intergenic regions, which constitute 9% of the genome. Mutations falling at coding regions are shown in three concentric rings according to whether they are synonymous (outer), missense (central), or nonsense (inner). Open, shaded, and solid circles represent neutral, significantly deleterious, and lethal mutations, respectively. Two significantly beneficial mutations are shown with asterisks. Significance levels were adjusted to 0.05 for multiple tests.

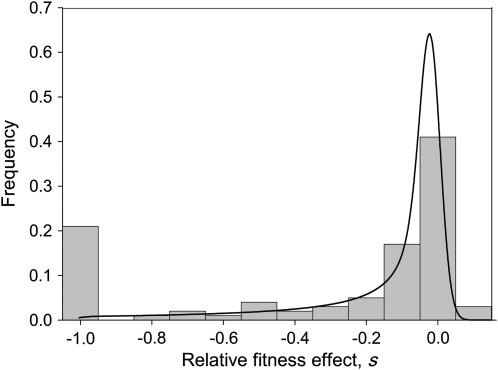
The observed distribution of fitness effects for the 100 mutations is shown in Figure 2. Twenty-one mutations were lethal according to the lack of infectivity of the viral DNA. Fitness assays of the 79 nonlethal mutants indicated that 35 were significantly deleterious (P < 0.05), 39 did not significantly deviate from neutrality, and 5 were significantly beneficial. After applying the sequential Bonferroni correction to control the false discovery rate for multiple tests of the same hypothesis (Benjamini and Hochberg 1995), 24 deleterious and 2 beneficial mutations (C3748A and T4541A) remained, whereas 53 did not deviate significantly from neutrality. The mean fitness effect of all viable mutations was 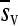= −0.107 with variance V(s_v) = 0.037. After removing the two significantly beneficial mutations, 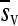= −0.111 and V(s_v) = 0.037.

Figure 2.—

Distribution of fitness effects caused by single-nucleotide substitutions in bacteriophage f1. The frequency histogram of the 100 mutations is shown. Note that the fitness effect of lethal mutations is s = −1. The effect of each individual mutation is provided in Table S1. Shown superimposed is the best-fitting probability density function for viable, nonbeneficial mutations (a log-normal distribution with the parameter values shown in Table 3).

All synonymous mutations were viable and their effects did not deviate from neutrality on average (Table 1; Mann–Whitney test: P = 0.910) although two (6.7%) were significantly deleterious after correcting for multiple tests (C1161A and G3077A, with s-values −0.102 and −0.114, respectively). All mutations at intergenic sites were also viable but tended to be deleterious (P = 0.013). Missense mutations were strongly deleterious (P < 0.001) and 12/51 (24%) were lethal, including 9 that changed the amino acid polarity. The latter were more harmful (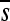 = −0.454, including lethals) than those not changing the amino acid polarity ( 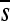= −0.262; P = 0.027). Similarly, acyclic to aromatic substitutions (or vice versa) were more deleterious ( 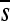= −0.601) than the rest of missense mutations ( 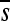= −0.315; P = 0.032). However, fitness effects were apparently the same regardless of whether the mutation changed the size of the amino acid (P = 0.335). Finally, all nonsense mutations were lethal.

TABLE 1.

Mutational fitness effects (s) for different kinds of mutations

	Meana	Variancea	Numbera	Lethal fraction (%)
Missense	0.371	0.164	51	24
Synonymous	0.003	0.002	30	0
Intergenic	0.138	0.036	10	0
Nonsense	1.000	0.000	9	100
Total	0.294	0.163	100	21

^aFor all mutations (including lethals).

Lethal mutations occurred in most genes and thus appeared to be homogeneously spread throughout the genome. However, a more careful examination shows that missense mutations affecting replication genes were more likely to be lethal (7/15) than those affecting other genes (5/36; Fisher exact test, P = 0.026). Consistently, the average effect of mutations tended to be more deleterious if initial steps of the infection cycle were affected (Table 2; Spearman correlation, N = 4, P < 0.05). It is also noteworthy that the two significantly beneficial mutations produced amino acid replacements in the proteins encoded by genes I and IV, which are involved in maturation and extrusion, respectively.

TABLE 2.

Mutational fitness effects (s) of missense mutations for different functional categories

	Genes	Meana	Variancea	Numbera	Lethal fraction
Replication	II, X	0.535	0.214	15	47%
Maturation	I, V	0.362	0.205	8	25%
Capsid	III, VI, VII, VIII, IX	0.305	0.130	13	15%
Extrusion	IV	0.270	0.113	15	7%
Total		0.371	0.164	51	24%

^aFor all mutations (including lethals).

Distribution of mutational fitness effects:

We sought to infer the statistical properties of the distribution of mutational fitness effects (excluding lethal and beneficial mutations) by fitting several model distributions to the data. We used a maximum-likelihood procedure, in which the likelihood of each observation given the model was calculated by taking into account measurement error (see materials and methods). The simplest case considered was the exponential distribution, which has a single parameter. This distribution fit the data reasonably well (Table 3), but we also considered two-parameter models, starting with the gamma distribution, which is a generalization of the exponential. A likelihood-ratio test indicated that the use of this more complex model was justified by the significantly improved fit (χ² = 47.38, P < 0.001). We considered three additional two-parameter distributions: the beta, the log-normal, and the Weibull distributions (Table 3). The total log-likelihoods of the four models were similar and all fit the observed cumulative density function with a precision above 99%. However, the log-normal and the Weibull distributions, which have heavier tails, were slightly better than the gamma or beta. The maximum likelihood estimates of the log-normal parameters gave a predicted average mutational effect of 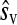= −0.122 and variance 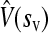= 0.041. The corresponding inferred probability density function is shown in Figure 2.

TABLE 3.

Statistical models describing mutational fitness effects for 77 viable, nonbeneficial, mutations

Model	Probability density functiona	Parameter estimatesb	Log-likelihoodc	Goodness of fitd
Exponential		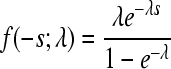λ = 8.144 (6.867;9.564)	35.11	0.957
Gamma		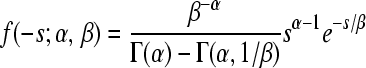α = 0.344 (0.276;0.425)	58.80	0.993
		β = 0.387 (0.262;0.676)
Beta		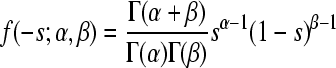α = 0.315 (0.257;0.385)	58.35	0.992
		β = 2.265 (1.661;3.017)
Log-normal		μ = −2.895 (−3.848;−0.916)	60.97	0.994
		σ = 3.473 (2.550;4.691)
Weibull		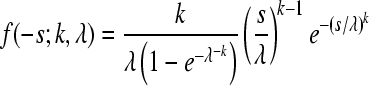λ = 0.079 (0.049;0.161)	60.32	0.994
		k = 0.440 (0.358;0.530)

^aThe constraint 0 ≤ −s ≤ 1 was imposed (0 < −s ≤ 1 for the Log-normal) and probability density functions were normalized accordingly.

^bObtained by maximum likelihood, accounting for experimental error; confidence intervals correspond to an increase of one log-likelihood unit.

^cCalculated from probability densities. Since the latter can be larger than 1, the log-likelihood can be positive.

^dSquared correlation coefficient (r²) between the observed and predicted cumulative distribution functions.

DISCUSSION

Previous work has shown that the distribution of mutational fitness effects can vary across species (Eyre-Walker and Keightley 2007), implying that results from a given model system cannot be readily extrapolated to distantly related groups and that more empirical information is therefore needed. Here, we have carried out a detailed characterization of the fitness effects of single-nucleotide substitutions in a filamentous single-strand DNA phage. It is interesting to see how these data compare to those obtained with other viruses using the same method. In vesicular stomatitis virus (VSV), tobacco etch virus (TEV), and bacteriophage Qβ, more than one-third of single-nucleotide substitutions are lethal, while nonlethal ones reduce fitness by 10–13% on average (Sanjuán et al. 2004; Carrasco et al. 2007; Domingo-Calap et al. 2009; Sanjuán 2010). A recent study has shown that, in the DNA bacteriophage ΦX174, the lethal fraction is 20% and the mean effect size of viable ones is 13% (Domingo-Calap et al. 2009). The results obtained with ΦX174 are very similar to the ones obtained with f1 despite that fact that these are two phylogenetically unrelated single-strand DNA phages. Also, the constancy of average fitness effect size across RNA and ssDNA viruses (10–13%) is remarkable (Sanjuán 2010). Interestingly, the lethal fraction is lower in f1 and ΦX174 than in the RNA viruses VSV, TEV, or Qβ, yet still remarkably high. The comparison with nonviral systems is more problematic because of the variety of methods used and the different types of mutations tested in each study. Despite this limitation, previous work has established that RNA and single-strand DNA viruses show low tolerance to mutation compared with organisms such as E. coli, Caenhorhabditis elegans, Drosophila melanogaster, and others (Elena et al. 2006). This is consistent with the fact that small and compact genomes as those of many viruses encode few or no mechanisms of robustness at the molecular level as, for example, alternative metabolic pathways, genetic redundancy, or modularity (Wagner 2005; Elena et al. 2006).

We have classified viable mutants as deleterious, neutral, or beneficial according to whether their fitness values significantly deviates from that of the wild type. However, it is difficult to distinguish mutations of small effect from strictly neutral ones. Even after performing additional replicates for small-effect mutants, most effect sizes lower than 0.05 were not significantly different from zero. It is also noteworthy that, since neutrality depends not only on the selection coefficient but also on the effective population size (Kimura 1983; Ohta 1992), determining s-values and modeling their statistical distribution is probably more informative than classifying mutations as deleterious or neutral on the basis of their selection coefficient. Concerning the shape of the distribution, viable mutations of small effect are more abundant than those of large effect in all biological systems examined so far (Elena et al. 1998; Davies et al. 1999; Sanjuán et al. 2004; Cowperthwaite et al. 2005; Poon and Chao 2005; Baba et al. 2006; Carrasco et al. 2007; Eyre-Walker and Keightley 2007; Domingo-Calap et al. 2009; Sanjuán 2010). A very simple model that captures this essential feature is the exponential distribution, but the conclusion emerging from several studies is that the observed coefficients of variation are larger than predicted by this model and that the observed distributions tend to have sharper peaks and heavier tails. These properties are better accounted for by the log-normal or the Weibull distributions. Another point worth mentioning is that in all previous studies, the contribution of experimental error to the shape of the observed distribution was unaccounted for, whereas here this has been made possible by carrying out appropriate controls and implementing a more powerful statistical analysis.

We found that 2 of the 100 mutations examined were significantly beneficial even after correcting for multiple tests. As discussed above, the actual fraction might be higher, since mutations of small effect are difficult to detect. High fractions of beneficial mutations have been reported previously in a low-fitness artificial recombinant of VSV (4%) or in debilitated mutation–accumulation lines of bacteriophage ΦX174 (18%) (Sanjuán et al. 2004; Silander et al. 2007). Not surprisingly, these populations can undergo rapid adaptive or compensatory evolution but, in contrast, our f1 genotype had been maintained at high population sizes under the same laboratory conditions for 80 passages without experiencing significant changes in fitness. Other previous estimates of the fraction of beneficial mutations in DNA genomes for moderately well adapted genotypes are 1–2% in bacteriophage ΦX174 (Silander et al. 2007), <0.5% in E. coli (Elena et al. 1998), and 3% in yeast after correcting for multiple tests (Thatcher et al. 1998). In light of these data, we speculate that in DNA microorganisms, adaptive evolution is mainly limited by mutational supply, as opposed to RNA viruses. In the latter, failure to reach the evolutionary optimum might be more often caused by an excessive mutational load rather than by a poor supply of beneficial mutations. Consistently, recent work with bacteriophage T7 strongly suggests that artificially increasing the mutation rate results in faster adaptation (Springman et al. 2009). Therefore, the roughly constant mutation rate of 0.003 per genome and round of copying found in most microorganisms (Drake 1991; Drake et al. 1998) might be generally suboptimal in terms of adaptation.

Finally, our results can also help elucidate other basic evolutionary questions. For instance, the neutral theory of molecular evolution (Kimura 1983), as well as adaptive evolution models based on extreme value theory (Orr 2003), depend critically on the relative abundance of deleterious, neutral, and beneficial mutations.