Comparative mouse brain tractography of diffusion magnetic resonance imaging

Abstract

Diffusion magnetic resonance imaging (dMRI) tractography can be employed to simultaneously analyse three-dimensional white matter tracts in the brain. Numerous methods have been proposed to model diffusion-weighted magnetic resonance data for tractography, and we have explored the functionality of some of these for studying white and grey matter pathways in ex vivo mouse brain. Using various deterministic and probabilistic algorithms across a range of regions of interest we found that probabilistic tractography provides a more robust means of visualizing both white and grey matter pathways than deterministic tractography. Importantly, we demonstrate the sensitivity of probabilistic tractography profiles to streamline number, step size, curvature, fiber orientation distribution, and whole-brain versus region of interest seeding. Using anatomically well-defined cortico-thalamic pathways, we show how density maps can permit the topographical assessment of probabilistic tractography. Finally, we show how different tractography approaches can impact on dMRI assessment of tract changes in a mouse deficient for the frontal cortex morphogen, fibroblast growth factor 17. In conclusion, probabilistic tractography can elucidate the phenotypes of mice with neurodegenerative or neurodevelopmental disorders in a quantitative manner.

Introduction

Understanding developmental or pathological changes in white matter tracts in animal models can lead to a better understanding of neural development and degeneration. At present, tracers or promoter-driven reporter genes such as green fluorescent protein are used as markers of brain connectivity or fiber tracts (reviewed by Kotter, 2007; Morecraft et al., 2009). These methods typically require two-dimensional analysis of a single tract and do not lend themselves to quantitative assessment of connectivity changes. Diffusion magnetic resonance imaging (dMRI) tractography can be employed to simultaneously delineate multiple cerebral white matter tracts in three-dimensions and to identify possible alterations in connectivity. Diffusion MRI tractography is the process of integrating voxel-by-voxel orientations into a pathway that connects distant brain regions, and has been well described in the following reviews: Mori and van Zijl (2002), Jones et al., (2008), Seunarine and Alexander (2009), Jones (2009) and Behrens and Jbabdi (2009).

Diffusion tractography is influenced by the anatomical preparation, data acquisition scheme, data processing (e.g. tensor, multiple tensor, non-tensor), tractography algorithm and tracking parameters. Fixed, ex vivo, dissected brain provides ideal tissue integrity by preserving anatomy and permitting diffusion measurements with comparatively little time constraint, thereby allowing data acquisition at the microstructural level. From this type of experiment, fractional anisotropy (FA) and mean diffusivity permit the selection of regions of interest (ROI) and the calculation of their means and standard deviation (Pierpaoli and Basser, 1996). FA provides a means of quantifying white matter differences following dMRI, but doesn’t provide directional information about the white matter tracts. Directional information about fiber orientation can be generated from incorporation of the principal Eigen vector of the diffusion tensor. These data can be represented as colour-coded FA maps. Tractography integrates diffusion directions to produce a path through the data, which is often represented as a streamline The streamline propagates automatically through the vector field of a sample space along the path where the diffusion is least hindered and from this, additional metrics such as streamline length and number can be obtained (e.g. Ding et al., 2003; Correia et al., 2008). Importantly, the strategies for achieving this propagation can vary greatly according to the algorithm applied.

Diffusion MRI has been used with rodent brain previously (e.g. Mori et al., 1999; Xue et al., 1999; Song et al., 2005; Wang et al., 2006; Boretius et al., 2009; Leergaard et al., 2010). Some of these studies have used dMRI to identify and characterize neuropathologies, including three-dimensional structures of tract abnormalities such as Probst bundles (Ren et al., 2007). With the exception of Leergaard et al. (2010), these studies have, for the most part, used older tractography methods and have not attempted to compare different approaches.

Our aim was to investigate the suitability of current tractography approaches and tractography parameters for generating streamline information from dMRI of an ex vivo mouse brain. We acquired dMR images using a diffusion weighted three-dimensional spin echo sequence and a high-field strength magnet. Next, we aimed to determine the appropriate representation of the diffusion orientations and then applied deterministic and probabilistic tractography to assess the requirement of a measure of uncertainty in the streamline propagation. We compared two tractography software packages that have been used previously – TrackVis (Wang et al., 2007), which performs deterministic tractography, and FSL (Behrens et al., 2007), which performs probabilistic tractography. In addition to these established software packages, we explored tractography using the more recently developed software package MRtrix, which allows for both deterministic and probabilistic tractography (Tournier et al., 2007). Using FSL and MRtrix, we extended our study to include measures of pathways that traverse grey matter regions, such as those that connect the cortex and thalamus. Furthermore, we demonstrated that these tractography approaches could be used to identify subtle tract changes in the Fibroblast growth factor 17 knockout mouse (Fgf17^−/−), which has a hypoplastic frontal cortex.

Methods

Mice

All mice were housed and handled in accordance with the Institutional Animal Care and Use Committee of the University of California, San Francisco. Three adult Fgf17^−/− (knockout, KO) mice and three Fgf17^+/+ age- and sex-matched controls were generated by mating heterozygotes (Fgf17^+/−) (Xu et al., 2000). Mice were anaesthetized and transcardially perfused with 0.1 M Phosphate Buffered Solution (PBS) followed by 4% paraformaldehyde (PFA). Heads were immersed in 4% PFA for a further 24 h, then washed for 24 h in PBS. At this point, heads were transported to the University of Queensland for experimentation. The brain was dissected and immersed for a further 3 days in PBS before imaging.

Diffusion MRI

Diffusion-weighted (DW) magnetic resonance images were acquired of adult mouse brains (n=6) immersed in Fomblin Y-VLAC oil (Y06/6 grade, Solvay, USA), using a 16.4 Tesla vertical bore, small animal MRI system (Bruker Biospin, Rheinstetten, Germany; ParaVision v5.0) and a 15 mm linear, surface acoustic wave coil (M2M, Brisbane, Australia). Three-dimensional DW spin-echo sequences were acquired using the following parameters: TR/TE 400/22.8 ms; imaging resolution, 0.1×0.1×0.1 mm (uninterpolated) and a signal average of 1. Each dataset was composed of two low diffusion weighted images (b = 0 s/mm2) and thirty high diffusion weighted (b = 5000 s/mm2) images with encoding gradient (δ/Δ = 2.5/14 ms) vectors uniformly distributed using the electrostatic approach (Jones et al., 1999). Total imaging time was 32 h. Preliminary data, not shown here, indicated that high angular resolution diffusion imaging (HARDI) modeling of diffusion-weighted imaging in 64 or 48 directions provided no distinct advantage in tractography information, but did increase acquisition time substantially.

Tractography Software

Three software packages, which are freely available to the research community, were tested. The main differences between the tractography software packages are summarized in Table 1.

Table 1.

Differences between the tractography software packages.

	TrackVis	MRtrix	FSL
FOD	Qball	CSD	Bayesian & ARD
tracking	deterministic	deterministic or probabilistic	probabilistic
seeding	whole brain	whole brain or ROI	ROI
step size	variable	fixed *	fixed *
turning angle	angle (step)	curvature (step and angle)	angle
thresholds	angle, mask, streamline length	FOD, streamline length	anisotropy

ARD, automatic relevance determination.

^*amenable by user

TrackVis (v0.4.4; Wang et al., 2007; www.trackvis.org) allows real-time 3D visualization and analysis of fiber tract data created by Diffusion Toolkit (Wang et al., 2007). For TrackVis, reconstruction was generated according to DTI or HARDI/Qball modeling and the Spherical Harmonic Basis method (Tuch, 2004; Hess et al., 2006). From FA and mean diffusivity generated by Diffusion Toolkit, second-order Runge-Kutta (Basser et al., 2000) and a modified version of fiber assignment by continuous tracking (referred to simply here as FACT; Mori et al., 1999; Kreher et al., 2005) were performed.

MRtrix (v0.2.7, www.nitrc.org/projects/mrtrix) uses constrained spherical deconvolution (CSD) to estimate the fiber orientation distribution (FOD; Tournier et al., 2007). Tractography can be based on the diffusion tensor model (not assessed) or multi-fiber CSD, with deterministic (based on the method by Conturo et al., 1999) or probabilistic (Behrens et al., 2003; Parker et al., 2003) streamline tracking approaches. Default preprocessing parameters were used for CSD (i.e. maximum harmonic order lmax = 6).

The FMRIB Software Library (FSL, Release 4.1; Smith et al., 2004; Behrens et al., 2007; Jbabdi et al., 2007; Woolrich et al, 2009; www.fmrib.ox.ac.uk/fsl) uses a Bayesian framework with automatic relevance determination (ARD) to generate the FOD, and probabilistic tractography. In contrast with TrackVis and MRtrix, FSL does not output individual streamlines, but presents streamline-density maps or visitation maps, i.e. a map showing the number of streamlines traversing each imaging voxel.

Representation of streamlines, colour maps and FA maps

Nomenclature and neuroanatomy were assigned using the Mouse Brain Atlas in Stereotaxic Coordinates (Franklin and Paxinos, 1997). For consistent representation amongst tractography programs, results are shown using an FA map overlay. Unless otherwise indicated, FA map overlays are at the level of the anterior commissure when representing horizontal or axial information, or at the midline when representing sagittal information. For coronal views, FA maps are at the level of the ROI. When describing ROIs, colour-coded FA maps were used to allow visualisation of the heterogeneous diffusion directions apparent within the ROI (Supp. Fig. 1). Colour-coded FA maps correspond to the following orientations: red, medial-lateral; blue, dorsal-ventral; and green, rostral-caudal. Streamlines are represented by a colour-coded scheme based on ROI/population. AC streamlines present in the supplementary data are color-coded based on their orientation. Streamlines are shown in 3D while FA maps are in 2D. For the purposes of this study, the following distinction is made between seed and waypoint ROIs (see also Table 1). Seed ROIs are regions where tractography streamlines originate. In the case of TrackVis, the seed ROI is the entire brain (wholebrain). In the case of MRtrix, the seed ROI can be a selected region or wholebrain. In the case of FSL, the seed ROI is the selected region only. Waypoint ROIs are regions chosen to highlight a streamline population that has already been seeded. In TrackVis, any user-selected ROI is a waypoint (e.g. the olfactory bulb) because the seed ROI of the wholebrain is generated automatically (wholebrain tractogram). Secondary waypoints are used throughout the study to further delineate streamline populations. In TrackVis for example, we delineated the ipsilateral anterior commissure intrabulbar (secondary waypoint) for olfactory bulb (first waypoint) streamline populations, revealed by the wholebrain tractogram (seed ROI).

Optimization of Tractography Parameters

Differences in standard tensor modeling and HARDI/Qball tractography were observed by visually inspecting streamlines seeded from ROIs in the optic nerves rostral to optic chiasm using TrackVis.

Tractography parameters were optimized for the anterior commissure (AC) by waypointing (TrackVis) or seeding (MRtrix, FSL) an ROI manually at the midline. The AC was chosen because the tracts project in a rostral-caudal direction with midline crossing. The quality of the delineated tract was assessed visually according to the AC anatomy described by Sturrock (1977). All ROIs used in the present study appear in Supp. Fig. 1.

Parameters adjusted in TrackVis include the tractography algorithms (2^nd order Runge-Kutta versus FACT) and the turning angle threshold, which is enforced when a streamline enters a new voxel. The step size was left at the default value (0.1×voxel size). Diffusion Toolkit has two stages of masking. By using the b0 image, the first mask eliminates the surrounding noise from the calculation of the diffusion parametric images (FA, DWI, eigen vectors and values, and the apparent diffusion coefficient). The second mask filters the tracking using the DWI, which is the geometric mean of all the raw high b value images. This means that no streamlines are generated through voxels with a low (subthreshold) DWI value. Generally, subthreshold voxels are those in the noise surrounding the brain sample and in the cerebrospinal fluid. The maximum threshold for this second mask prevents streamlines passing through high DWI voxels. This second mask can be applied automatically or by user input. When automatic mode is selected, the high DWI threshold is generally the highest DWI voxel in the brain sample, so that tracking is possible throughout the entire brain. Obviously, by increasing the minimum and decreasing the maximum DWI value manually (constrained), the possibility to propagate streamlines is decreased. And vice versa (unconstrained), leading to streamlines appearing in the noise external to the brain.

For MRtrix, the step size and curvature parameters were independently optimized. Step sizes investigated were 0.005, 0.01, 0.025, 0.05 and 0.1 mm (i.e. ranging from 1/20 of the voxel size up to the size of the voxel) for both deterministic and probabilistic tractography. Curvature values ranged from 0.01 to 0.3 mm. The maximum turning angle α can be calculated as follows:

$$\mathrm{\alpha }=2^{*}\text{arcsin}(\text{step}/2^{*}\text{curvature})$$ (1)

Once the optimum combination of step size and curvature was established, the influence of the FOD amplitude cutoff value on the tracking results was examined.

A sufficiently high number of streamlines are required to generate a tract profile of high confidence. Although increasing the number of streamlines increases the number of false positives, these false positives will be widely distributed in space (i.e. low streamline density), while streamlines following the true pathway tend to group together (i.e. high streamline density). Streamlines constituting the high density population provide an indication of the confidence measure. When looking at 3D streamline images, the true pathway may not be visible because these streamlines may be obscured by the large number of false positives. This problem can be overcome by generating streamline density maps, in which the number of streamlines traversing each voxel is counted. These streamline density maps can be visualized as a 3D rendering with a low threshold applied (to remove pathways of low confidence, i.e. false positives), or by projecting the maximum intensity onto one plane (maximum intensity projection, MIP). For a high number of streamlines, we chose to visualize tracking results using MIPs.

FSL uses angular thresholds to prevent streamlines from tracking back onto themselves. Therefore, the default voxel-wise angle (80 degrees) was not changed, and only the dependence of the tractography results on the step size was assessed. Tractography was also performed with and without using the “anisotropy constraint” option for tracking for all step sizes. Streamline density maps were visualized as MIPs.

Tractography of pathways between the cortex and thalamus

Cerebral white matter is particularly suited to tractography because the fibers are highly orientated, thereby resulting in a large diffusion vector and high FA. However, these fibers originate from cell bodies present in the grey matter, which tends to have a low FA and high uncertainty in fibre orientation. Because of this, deterministic streamline propagation methods often terminate prematurely before reaching the grey matter, or low FA thresholds need to be applied. Probabilistic tractography includes a probability function of the true fiber orientation, thereby providing a measure of confidence (Behrens et al., 2003). Therefore, streamlines can be propagated through grey matter regions of high uncertainty. Therefore, when investigating grey matter to grey matter pathways (i.e. ROIs are drawn within grey matter), probabilistic tractography may be better suited than deterministic tractography. In turn, density maps can be used to illustrate probabilistic tractography targeting to grey matter regions from multiple grey matter seed regions. Projections between the cortex and thalamus are organized along the rostrocaudal and lateromedial axes of the mammalian cerebral cortex (reviewed in Vanderhaeghen and Polleux, 2004). This topography allows the anatomy of the thalamus to be parcellated based on streamlines generated from cortical regions (as demonstrated by Behrens et al., 2003 for the human thalamus). Unilateral cortical target ROIs were drawn for each of the following regions: rhinal and piriform cortices (ventrolateral cortex), auditory cortex, somatosensory cortex, motor cortex and visual cortex (Supp. Fig. 1). The drawing of ROIs was aided by using brain landmarks such as the external capsule, anterior commissure, hippocampal commissure and the corpus callosum, following the mouse brain atlas of Franklin and Paxinos (1997). A target region was drawn of the ipsilateral thalamus, excluding the fasciculus retroflexus and the mammillothalamic tract, but including the medial lemniscus and zona incerta. Wholebrain tractograms were generated at one seed per voxel or 50 seeds per voxel using MRtrix, and the thalamus and each cortical mask in turn was used as waypoint masks. For every voxel of the thalamic ROI, the number of streamlines connecting each cortical target was recorded, and the cortical target with the highest streamline density was then assigned to the voxel, thus producing a hard segmentation of the thalamus.

Within FSL, the built-in option for connectivity-based seed classification was used (Behrens et al, 2003). Briefly, each thalamic voxel was seeded 500 or 5000 times, and the number of streamlines projecting into each cortical target was recorded. As with MRtrix, the cortical target showing the strongest connectivity with the specific thalamic voxel was assigned.

Frontal cortex tracts and statistics

To determine the capability of the tractography approaches to quantify tract changes in the mouse brain we used Fgf17^−/− mice (Xu et al., 1999), which have reduced prefrontal cortex volume and which exhibit deficits in tracts arising from the frontal cortex, such as the cerebral peduncle (Cholfin and Rubenstein, 2007).

The left frontal cortex was manually outlined for each wild type and Fgf17^−/− brain. The frontal cortex was used as a waypoint ROI within TrackVis, and as a seed ROI within FSL (500 streamline seeding events per voxel) and MRtrix (seeding 50 streamlines per voxel or 1000 streamlines total). Additionally, a whole brain tractogram was generated using MRtrix (seeding 1 or 50 streamlines per voxel), with the frontal cortex as the waypoint ROI. Once the frontal cortex streamlines were extracted, further waypoint ROIs were applied to separate the frontal cortex streamlines into populations corresponding to the corticospinal tract (cst), the cingulum (cg), the ventrolateral cortex (including piriform cortex) and the forceps minor of the corpus callosum (fmi) (Supp. Figure 1).

The number of streamlines projecting into (wholebrain tractography) or emanating from (seed ROI approach) the frontal cortex was obtained. These data were compiled and analyzed using Two-way ANOVA and post-hoc Dunnet’s t-test in GraphPad Prism. Where indicated, streamline number was normalized against the total number of streamlines generated from the frontal cortex. Three animals were used for each experiment to generate a mean and standard error of the mean for statistical analysis.

For all wildtype and Fgf17−/− mice, we determined the mean and standard deviation of the FA values for the entire brain volume, the manually outlined frontal cortex ROI, and the pathways emerging from the frontal cortex. A low threshold level (5 streamlines / voxel; determined empirically) was applied to the pathways to remove regions of low confidence before calculating the average and standard deviation within the pathway. A t-test was performed using GraphPad Prism to test for significant differences (p < 0.05) between wildtype and Fgf17−/− mice.

Results

White matter tractography in the mouse brain

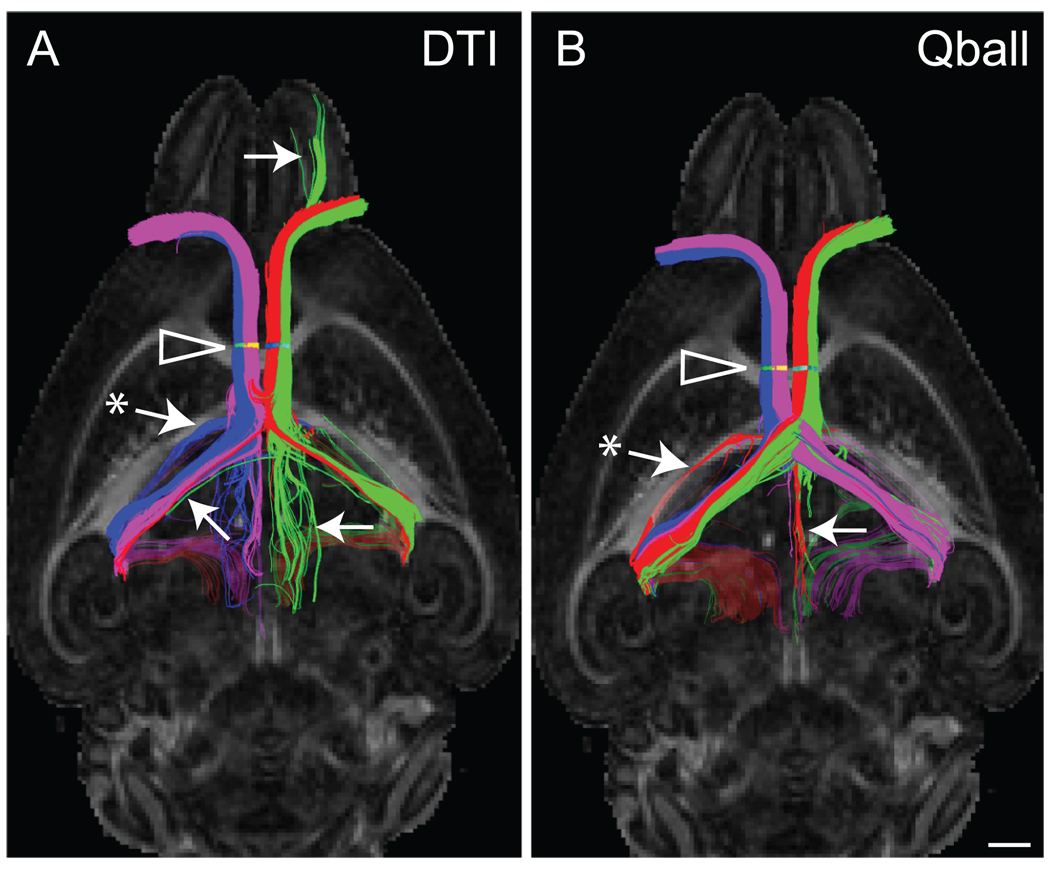
Standard tensor tractography has difficulty in resolving crossing fibers (reviewed in Jones, 2009, and Seunarine and Alexander, 2009). To illustrate this point in mouse brain, and to demonstrate the delineation of crossing fibers using HARDI/Qball, we performed tractography on the bilateral optic nerves using the FACT algorithm option in TrackVis (Fig. 1). The optic nerve provides an ideal example because each optic nerve consists of ipsilateral projecting fibers and contralaterally projecting fibers that cross at the optic chiasm. Tractography can be assessed by the ability to resolve these populations and propagate streamlines through the optic chiasm to the contralateral hemisphere. Using color-coded streamlines, the number of false-positive streamlines consisting of ipsilateral and contralateral pathways is greater in the standard tensor example than in the HARDI/Qball example (Fig. 1). Furthermore, we show that HARDI/Qball modeling of diffusion-weighted images acquired in 30 directions can achieve better results than standard tensor tractography with regard to crossing fibres.

Fig. 1.

An example of HARDI/Qball tractography demonstrates the difference in streamline profile compared to an example of standard tensor modeling (DTI). Streamlines of the optic nerves are viewed from the ventral surface of the brain and streamlines overlay FA horizontal planes at the level of the hippocampal commissure. ROIs (arrowheads) of the optic nerve were drawn as follows: left-lateral (green) and left-medial (red), and right medial (purple) and right-lateral (blue). These ROIs produced a greater delineation of ipsilateral and contralateral streamline populations following Qball modeling compared to DTI. Examples of false-positive streamlines include those indicated by arrows. The asterisk in both examples represents an example of streamlines failing to terminate and instead, crossing the caudal corpus callosum (this is dealt with elsewhere in the study). Scale bar = 1 mm.

With diffusion-weighted imaging acquired in sufficient directions to permit HARDI/Qball modeling, we next considered the streamline propagation strategy. Tractography using Second-order Runge-Kutta (Basser et al., 2000) and FACT (Mori et al., 2002) algorithms were directly compared using HARDI/Qball modeling in TrackVis. Using our ex vivo mouse data, second-order Runge-Kutta generated a prolificacy of streamlines that increased the likelihood of false positive errors compared to FACT (Supp. Fig. 2A). Using the AC as a waypoint ROI, failure of the second-order Runge-Kutta streamlines to terminate in the caudal cortex was observed around the hippocampus resulting in streamline continuation across the splenium. A streamline length limit can be assigned with TrackVis to avoid this continuation by removing streamlines longer than this limit.

Qball-FACT tractography was then employed to investigate the effect of streamline turning angle on the AC profile (Supp. Fig. 2B). Large angle turning thresholds (e.g. greater than 45 degrees) produced streamline prolificacy and increased the likelihood of false positives. Small angle turning thresholds (e.g. less than 35 degrees) resulted in a loss of the AC streamline profile. Based on these observations, a turning angle threshold of 40 degrees was employed for all further experiments. Finally, the tracking mask threshold, automated by Diffusion Toolkit, was tested to visualise the effect of further constraint or unconstraint on the streamline profile (Supp. Fig. 2C). Constraining the threshold window from automatic (approximately 2000–16000) to 5000–10,000 reduced the number of AC streamlines considerably, however, with a comparatively unconstrained window 500–20,000, little difference in streamline profile was observed. This is expected given that the mask distinguishes between the signals of sample and noise. When using the unconstrained window, short streamlines were produced in the space outside the brain volume – in the background noise (data not shown) – and were unsuitable for our purposes. Using these parameters, the FACT tractography method was applied to additional white matter regions of interest (Fig. 2).

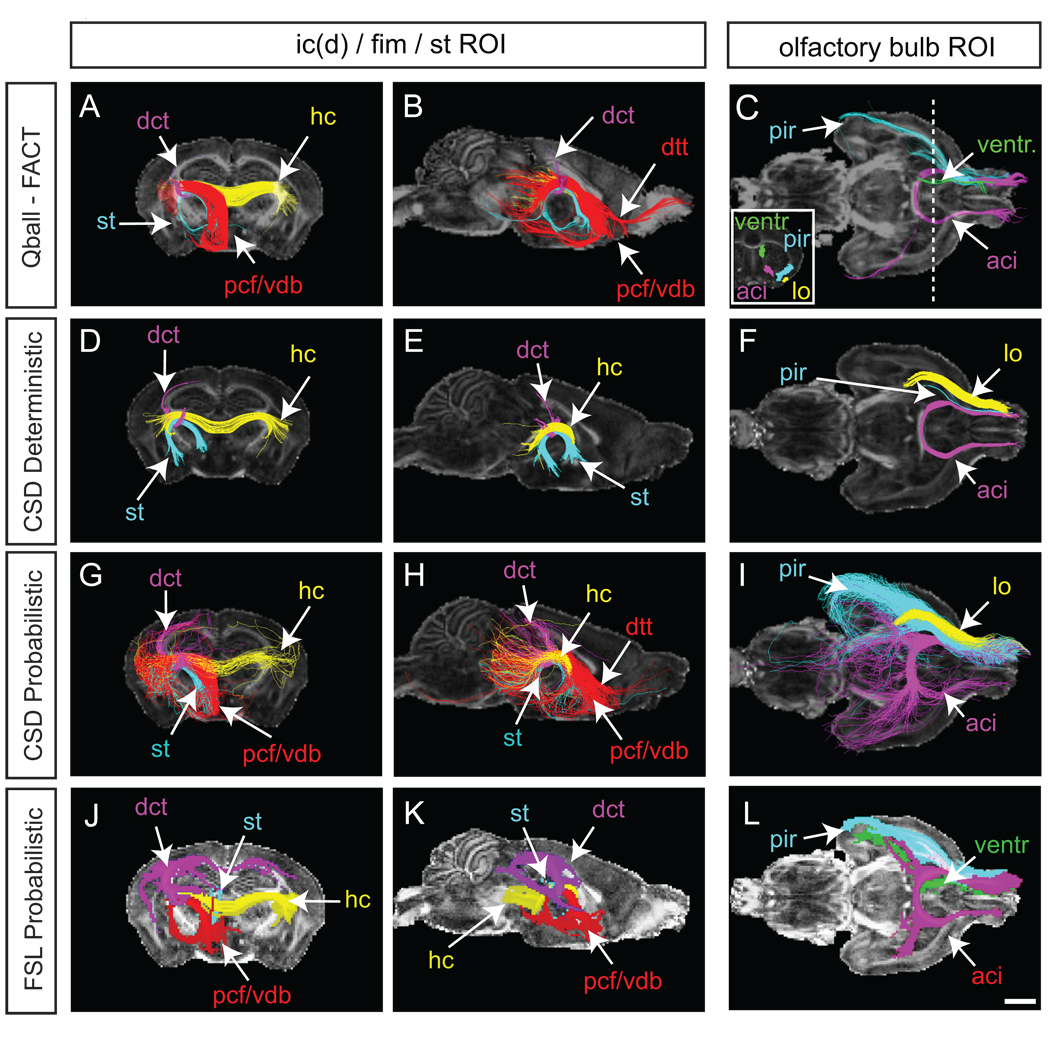
Fig. 2.

Tractography of white matter regions of interest using Qball-FACT (A–C), CSD deterministic (D–F), CSD probabilistic (G–I) and FSL probabilistic (J–L) methods. Streamlines are three-dimensional, while FA maps are shown at two-dimensional planes: coronal, −1.70 mm Bregma; sagittal, midline; horizontal, anterior crossing at the midline. Streamlines were generated from an ROI placed at the intersection of the fimbria, stria terminalis and dorsal internal capsule (left and middle columns), or from a unilateral olfactory bulb (right column). Streamlines shown are colored according to their waypoint ROIs (Supp. Fig. 1). For the ROI of the left and middle columns a number of streamline populations were identified which accord with known anatomical tracts: hippocampal commissure (hc; yellow), stria terminalis (st; light blue), precommissural fornix (pcf; red), ventral diagonal band (of Broca) (vdb; red), dorsal tenia tecta (dtt; red), dorsal corticothalamic tracts (dct; dark blue in A, B, J and K; purple in D, E, G and H). J, K and L are maximum intensity projection (MIP) maps for the ROIs as generated in FSL. C, F, and I, Streamlines from the olfactory bulb in colour-coded schemes (L is a MIP for the olfactory bulb generated by FSL). Insert in C shows the coronal waypoint ROIs used to delineate streamline populations. The dashed line shows the point along the anterioposterior axis from which the coronal waypoint ROIs were drawn. While the anterior commissure was consistently plotted, the lateral olfactory tract (lo) was more variable depending on the method used. The lateral olfactory tract was generated by Qball/FACT but streamlines did not reach the waypoint ROI, and hence is not delineated in C. The ventricle streamlines have been eliminated from I for clarity. Additional abbreviations: aci, anterior commissure intrabulbar; cor, coronal; CPu, caudate putamen; hc, hippocampal commissure; hor, horizontal (axial); pir, piriform cortex; sag, sagittal. Scale bars = 1 mm.

One point in the adult mouse brain that harbors multiple crossing fibers is around the hippocampal fimbria at the point of the dorsal aspect of the stria terminalis and lateromedial crossing of the corticothalamic projections belonging to the dorsal aspect of the internal capsule (Supp. Fig. 1). Seeded at this heterogeneous ROI, FACT streamlines delineated the hippocampal commissure, precommissural fornix, ventral diagonal band of Broca, dorsal tenia tecta, stria terminalis and dorsal corticothalamic tracts (Fig. 2A–B).

A separate waypoint ROI in the olfactory bulb revealed FACT streamlines through the dorsal entorhinal and piriform cortices, as well as contralateral anterior commissure streamlines (Fig. 2C). Interestingly, the olfactory bulb ROI generated streamlines following the rostral migratory stream/rostral extension of the subventricular zone into the dorsolateral wall of the lateral ventricle. Each of these streamlines could be isolated using waypoint ROIs as indicated in Fig. 2C. The lateral olfactory tract was represented by only a few FACT streamlines that did not reach the coronal plane for waypoint ROI selection.

For CSD tractography of the AC, the turning angle threshold was determined according to equation 1 for each combination of step size and curvature employed (Supp. Fig. 3). Increasing step size and maintaining small curvature resulted in streamline prolificacy (Supp. Fig. 3), while decreasing step size and maintaining high curvature resulted in streamline poverty. From these tests, anatomically accurate streamline profiles for deterministic tractography and probabilistic tractography, without excessive prolificacy, were used for further analysis. For deterministic tractography these parameters included a step size of 0.01 mm and curvature of 0.15 mm (α ~ 4°). For probabilistic tractography, these parameters included a step size of 0.01 mm and curvature of 0.07 mm (α ~ 8°) Until this point, the step size and curvature determination had been obtained with the default fiber orientation distribution (FOD) amplitude threshold of 0.1. The chosen parameters were then cross-checked against varying FOD thresholds (0 to 1). The extreme FOD thresholds affected streamline profile or prolificacy (Supp. Fig. 4), hence the choice was made to continue further analyses with the default FOD threshold of 0.1. Varying the number of streamlines generated from a seed ROI can impact on streamline profile also (Supp. Fig. 4), to the extent that the true tract can be obscured. MIP images can help to overcome this obstacle. MIPs of the AC were generated using 1000 and 100,000 streamlines, and despite a 100-fold increase in streamline number, the AC MIP was not markedly different (Supp. Fig. 4), indicating that a convergence and high confidence was achieved using 1000 streamlines. Additional white matter tracts were investigated using the above parameters for CSD deterministic and probabilistic tractography (Fig. 2). Using the heterogeneous ROI described above, CSD deterministic streamlines were generated for the stria terminalis, hippocampal commissure and corticothalamic tracts. In addition to these tracts, CSD probabilistic tractography also revealed streamlines corresponding to the ventral diagonal band, precommissural fornix and dorsal tenia tecta. Similarly, while CSD deterministic and Qball-FACT tractography inconsistently revealed the lateral olfactory tract, piriform and ventricle streamlines from the olfactory bulb ROI, CSD probabilistic tractography demonstrated no shortcomings in representing all three.

The representation of white matter tracts was also investigated using maximum intensity projections of tractograms generated by FSL. Here, step size was independently optimized (Supp. Fig. 5) and 500 streamlines seeded per voxel was chosen based on the convergence of anatomically accurate pathways at high intensity (data not shown). Between a step size of 0.005 and 0.01 mm there was a notable difference in the AC profile within the pathways of high confidence. For example, at the smaller step size, the lateral extent of the posterior AC was not as large. Beyond the step size of 0.01 mm, there was little difference in AC profile within the pathways of high confidence, but a noticeable enlargement in profile within low confidence regions. This increase in noise resembled that seen using CSD probabilistic tractography. Projection intensities were also mapped for ROIs that had been used for Qball-FACT and CSD tractography (Fig. 2). Overall, these intensity maps were in agreement with Qball-FACT and CSD tractography streamline results. A step size of 0.01 mm was used in further experiments.

Grey matter tractography in the mouse brain

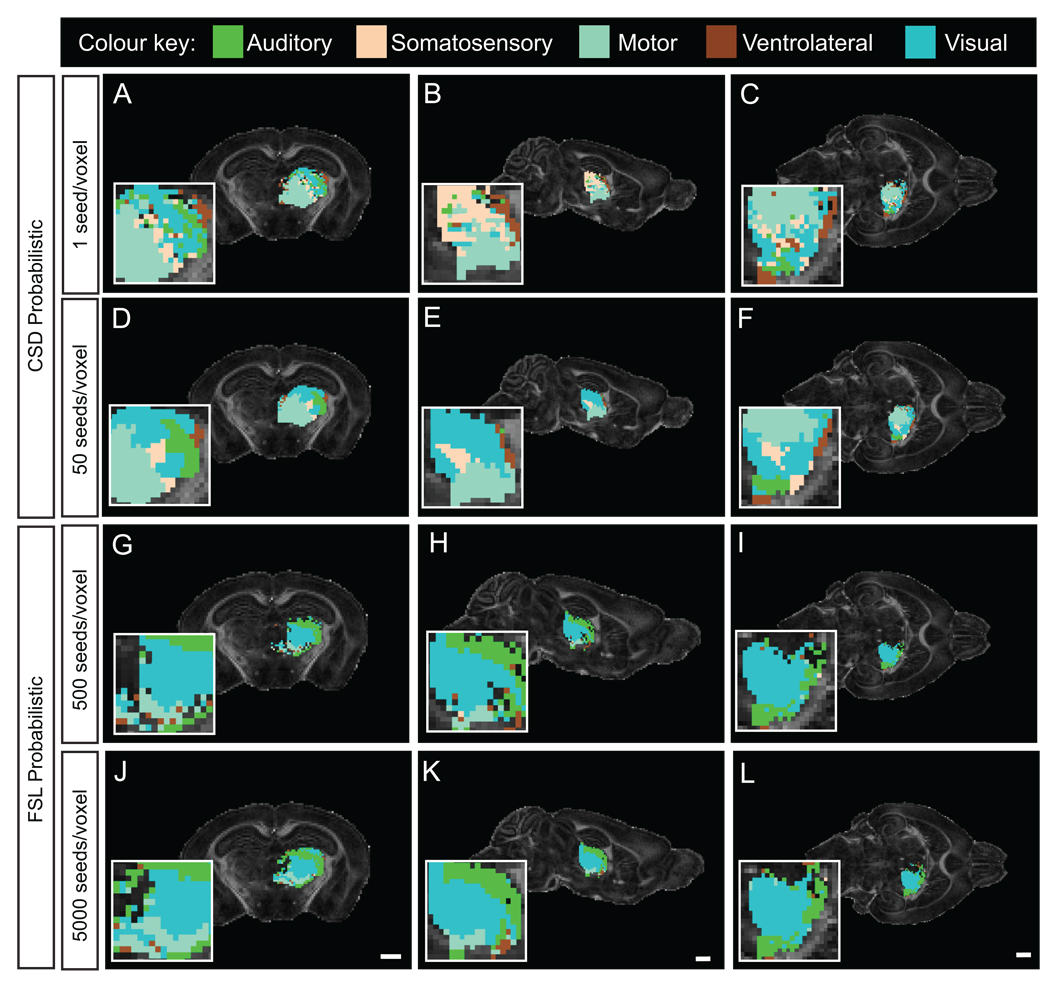
We tested the hypothesis that probabilistic tractography would generate pathway information from grey matter by performing a streamline-based parcellation of the thalamus. Streamline propagation errors are more likely through voxels with high uncertainty in diffusion direction, and hence probablilistic tractography, which considers local fiber uncertainty, would be suited to the task. Preliminary tests with deterministic streamline approaches such as FACT and 2^nd Order Runge-Kutta showed these to be inadequate (data not shown). CSD probabilistic tractography seeded at one streamline per voxel (seeding the entire brain) failed to parcellate the entire thalamus (Fig. 3A–C). By comparison to ventral or lateral regions, the mediodorsal thalamus (MD) was weakly mapped. In contrast, at 50 streamlines seeded per voxel, the entire thalamus was mapped (Fig. 3D–F). From the coronal plane shown in Fig. 3, we can identify that dorsal thalamic regions, which include the lateral geniculate nuclei and the lateral posterior nuclei, are mapped strongly by the caudal and visual cortex streamlines. Ventral regions, which include the zona incerta, ventral medial and ventral posterior nuclei, are largely segmented by streamlines waypointed by the somatosensory cortex. Laterally, the thalamus is dominated by streamlines from the lateral cortex, motor cortex and auditory cortex, whereas medially, the thalamus is comparatively heterogeneous with voxels dominated by streamlines waypointed via the visual, somatosensory and ventrolateral cortices. By comparison, FSL probabilistic tractography failed to map streamlines around the MD at 500 or 5000 seeds per voxel (seeded in the thalamus ROI; Fig. 3G–L). The ventral thalamus was dominated by somatosensory and visual cortex streamlines, while the dorsal thalamus was dominated by auditory cortex streamlines, with the exception of the region corresponding to the lateral geniculate nucleus, which was dominated by visual cortex streamlines. In contrast to CSD probabilistic tractography, very little thalamus was dominated by streamlines targeting the motor cortex. Considering that, typically, the rostral thalamus connects to the rostral cortex and the caudal thalamus connects to the caudal cortex, CSD probabilistic tractography is capable of delineating this topography, under the conditions employed.

Fig. 3.

Segmentation of the thalamus according to probabilistic tractography streamlines seeded in various cortical ROIs. Segmentation was made using unilateral ROIs in the somatosensory, visual, motor, auditory and the ventrolateral cortices (Supp. Fig. 1). A–C, Wholebrain CSD at 1 streamline seeded per voxel failed to map the entire thalamus, unlike 50 streamlines seeded per voxel (D–F). The same ROIs were employed for segmentation using the FSL ROI tractography approach seeded at 500 streamlines per voxel (G–I) or 5000 streamlines per voxel (J–L). Under the conditions employed, CSD probabilistic tractography produces a hard segmentation of the entire thalamic ROI, unlike FSL probabilistic tractography. Segmentation of the thalamic ROI by CSD probabilistic tractography follows the anatomical cortico-thalamic topography. The coronal plane shown correlates to Bregma - 2.06 mm, the sagittal plane corresponds to 2mm from the midline, and the horizontal plane corresponds to 2.5 mm from the interaural line from the mouse brain atlas (Franklin and Paxinos, 1997). The inserts are at 4× zoom. For similar planes, scale bars = 1 mm.

Quantitative analysis of frontal cortex tractography differences in a mouse deficient for Fgf17

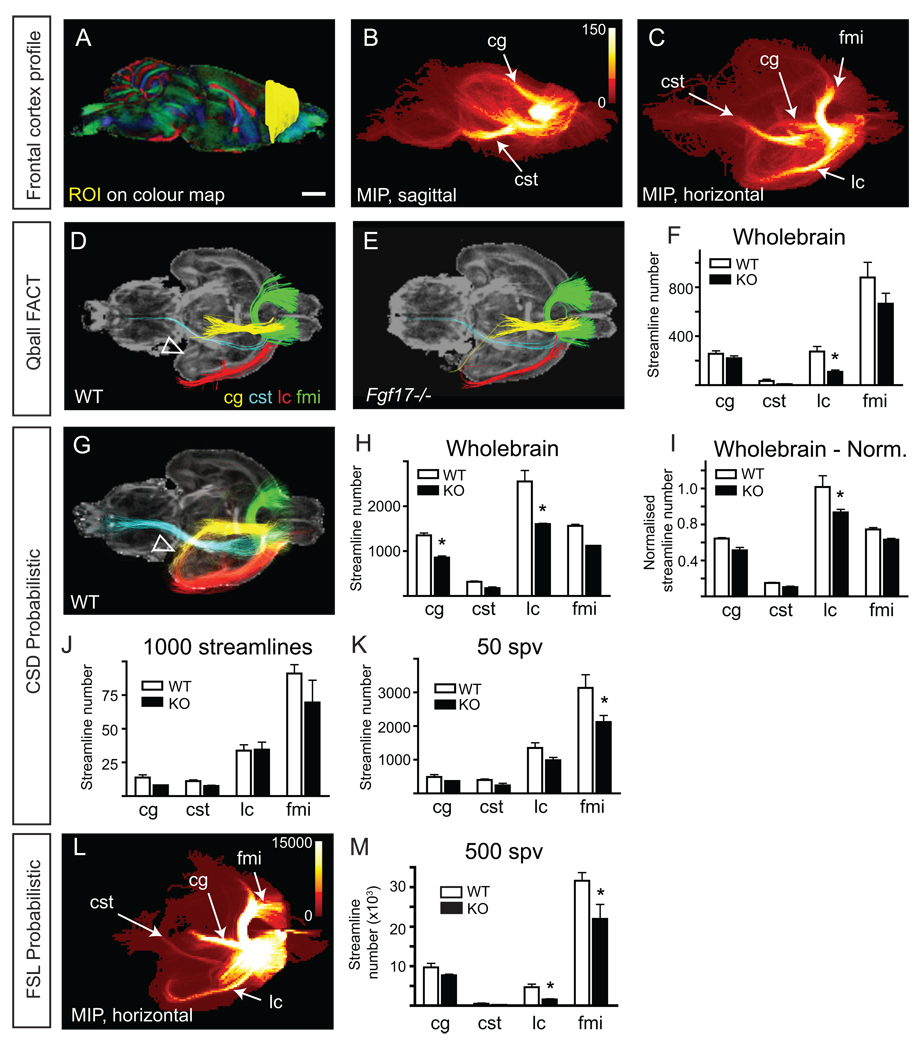
Having established the parameters necessary for white matter and grey matter tractography, we next set out to test these in a mouse brain with subtle neuroanatomical defects. For this we have used the Fgf17 null mutant mouse that has a hypoplastic frontal cortex, and accordingly reduced frontocortical efferent pathways, as demonstrated with tracer dyes and genetically encoded axon markers (Xu et al., 1999; Cholfin and Rubenstein, 2007). We began by establishing the tractography profile of the frontal cortex. A unilateral ROI was drawn of the frontal cortex extending from Bregma 2.10 mm (Franklin and Paxinos 1997) rostrally to the anterior cortical pole (Fig. 4A). By generating a large number of streamlines using CSD probabilistic tractography, a number of substantial streamline populations were identified in the MIP that passed through the cingulum, the corticospinal tract (via the cerebral peduncle), and the forceps minor of the corpus callosum (fmi; Fig. 4B and C). Additionally, frontal cortex streamlines passed laterally through a heterogeneous cortical area, which included the ectorhinal, perirhinal, lateral entorhinal, dorsal and ventral endopiriform (En) and piriform cortices. These were collectively named the lateral cortex (lc) streamline population for simplicity. MIP images of the frontal cortex were also generated using FSL and indicate the same streamline populations (Fig. 4L). Having identified the streamline populations from the frontal cortex we then set about quantifying these using the different tractography approaches. Waypoints were drawn in the heterogeneous lateral cortical region (as described above), the contralateral fmi, caudal cingulum, and the medial lemniscus and longitudinal fasciculus of the pons for the corticospinal tract (Supp. Fig 1).

Fig. 4.

Fgf17−/− (KO) mice have frontocortical tract deficits. An ROI was drawn in the frontal cortex of one hemisphere from each wildtype (WT) and KO mouse, using the colour-FA maps (A). From this ROI, four streamline populations were delineated (B–C): those passing laterally through the rhinal and piriform cortices (noted for simplicity as lateral cortex (lc), red); those following the cerebral peduncle and pyramidal tracts, noted as the corticospinal tract (cst, light blue); those crossing the midline via the forceps minor of the corpus callosum (fmi, green) into the contralateral frontal cortex; and, those following the cingulum (cg, yellow). From this, waypoints were created (Supp. Fig. 1). D and E, Representative tractography of WT and KO brains using Qball-FACT deterministic tractography in TrackVis. Streamlines were generated from the ROI in A, then waypoint ROIs were applied. Genotype differences in streamline number for each streamline population are quantified in F. Since TrackVis generates wholebrain tractograms prior to the selection of seed ROIs, this quantification is noted as Wholebrain. * p < 0.05, compared to WT within that streamline population. G, Representative streamline populations of WT brains using CSD probabilistic tractography. Here, the parahippocampal extent of the cingulum is seen (arrowhead), as opposed to its absence in Qball-FACT deterministic tractography in D. CSD streamline number for each population was quantified by three different means: using a wholebrain (WB) tractogram (H), arbitrarily at 1000 streamlines (J), or at 50 streamlines per voxel (50 spv) (K). * p < 0.05, compared to WT within that population. The wholebrain tractogram approach was used for normalization based on the volume of the frontal cortex (I). Using the normalized streamline approach, there remains a significant difference in streamlines belonging to the lateral cortex (I), but not for the cingulum. For comparison, FSL was also used to generate streamline statistics. A representative MIP of the WT frontal cortex streamlines is shown in L, which is not markedly different from that generated by MRtrix (C). Statistical analysis reveals that once normalized, the lateral cortex streamline population is significantly different in KO mice. Histograms represent the mean ± s.e.m from three animals. Scale bar = 1 mm.

While a small decrease in each streamline population was noted in the Fgf17^−/− mice compared to wildtype using Qball-FACT tractography, only the difference in the lateral cortical streamline population was statistically significant (Fig. 4F). Using CSD probabilistic tractography, more streamline information emerged (compare Fig. 4D and 4G). Under these conditions and according to known anatomy (Franklin and Paxinos, 1997), the cingulum is observed to project caudally, dorsal to the corpus callosum and then medially along a lateroventral path to the hippocampus (arrowhead in Fig. 4G). By generating a wholebrain tractogram (at 1 seed per voxel), quantification of the streamline number using CSD revealed statistically significant differences in the cingulum and the lateral cortical streamline populations (Fig. 4H). The Qball-FACT deterministic tractography approach may not have identified this difference because of the difference in cingulum streamline profile. That is, Qball-FACT deterministic tractography did not propagate streamlines along the ventrolateral course of the caudal cingulum, only within the mediodorsal aspect.

An alternative approach to generating wholebrain CSD probabilistic streamline information involves setting streamline number limits for seed ROIs. The effect of streamline number on streamline profile was demonstrated for the AC (Supp. Fig. 4C). In that case, a threshold of 1000 streamlines produced an accurate AC tract profile, whereas thresholds greater or less than this value produced increased false positives or poor AC profile, respectively. The anatomically accurate threshold amounted to approximately 50 streamlines seeded per voxel. To investigate the possibility that streamline number needs to be appropriated to the seed ROI volume we tested this threshold on the frontal cortex of the wildtype and Fgf17^−/− mice. Since the volume of the frontal cortex ROI was substantially larger than that of the AC ROI, we used two controls for streamline number, seeding 50 streamlines per voxel (equating to approximately 350,000 streamlines) or applying a 1000 streamline threshold (regardless of the number of seed ROI voxels). Both these methods revealed results that contrasted with the wholebrain tractogram approach (Fig. 4J, K). At 50 streamlines per voxel the fmi was significantly decreased in Fgf17^−/− mice compared to control, while at 1000 streamlines, no statistically significant result was observed.

FSL probabilistic tractography produced a MIP very similar to that using CSD probabilistic tractography for the frontal cortex ROI (Fig. 4L). A value of 500 streamlines per voxel was used for FSL probabilistic tractography based on earlier experiments (Supp. Fig. 5 and Fig. 2). Quantification of the streamline populations revealed a significant difference in the lateral cortical and fmi streamlines (Fig. 4M). Overall, the wholebrain tractogram approach (Qball-FACT or CSD probabilistic) best resembled the decreases in cst and lateral cortex tracts seen in tracing experiments performed previously (see Supp. Fig. 15 from Cholfin and Rubenstein, 2007).

Fgf17^−/− mice are reported to have an approximately 7% decrease in cortical surface area compared to wildtype controls (Cholfin and Rubenstein, 2007). This decrease was confirmed in the present study (data not shown). Therefore, to control for a decrease in frontocortical volume and hence, the total number of streamlines generated from this region, the number of streamlines for each population was normalized against the total number of streamlines generated from the frontal cortex. Using the CSD probabilistic wholebrain tractogram approach at 1 seed per voxel, a decrease of 18% was found in the total number of streamlines from the frontal cortex of Fgf17^−/− mice compared to control. Following this adjustment, a statistical difference in streamline number was seen in the lateral cortical population only (Fig. 4I). Similar normalization was performed for wholebrain Qball-FACT tractography, following which, no significant difference in the lateral cortical streamline population was observed (data not shown).

Finally, we determined if there were noticeable changes in mean FA values amongst the tracts investigated (Table 2). Despite a small decrease of FA in the frontal cortex ROI and the tracts, with the exception of the cst, no significant differences were observed (t-test of mean FA between genotypes, where n=3 and p<0.05).

Table 2.

Mean FA values (with mean SD) of selected ROIs in wildtype and Fgf17−/− mice.

ROI	Wildtype	Fgf17−/−
whole brain	0.23 (0.14)	0.23 (0.14)
frontal cortex	0.20 (0.07)	0.17 (0.06)
cg	0.24 (0.12)	0.22 (0.11)
cst	0.36 (0.16)	0.37 (0.16)
lc	0.24 (0.10)	0.21 (0.09)
fmi	0.28 (0.12)	0.26 (0.14)

Discussion

Tractography is becoming increasingly common in clinical settings for understanding pathological development and disease, and for assessing pre- and post-operative diagnosis. Apart from acquisition parameters (reviewed in Jones, 2009), post-acquisition and tractography parameters can impact on the results. In the present study we have drawn upon an existing wealth of knowledge in tractography and applied this to understanding the representation of white and grey matter pathways in the adult mouse brain through the use of accessible tractography programs. Of those employed here, TrackVis supports only deterministic tracking, MRtrix supports both deterministic and probabilistic tracking, and FSL supports only probabilistic tracking. Generally, probabilistic tractography is preferred because deterministic tractography ignores uncertainty in fiber orientation (i.e. only one “true” streamline per seed) (Behrens et al., 2003), while probabilistic tracking generates a number of streamlines per seed and can show the routes of greater confidence (such as a maximum intensity projection map) (Jones, 2008). The advantage of deterministic tractography is that, by comparison, it provides a conservative output and generally requires less computer processing.

As shown in the present study, both deterministic and probabilistic tractography generate streamlines with no known anatomical correlate (false positives). Some streamlines followed the anatomically accurate trajectory, but failed to stop at the correct anatomical point or target region. This type of continuation was particularly common around the hippocampus and/or when using high angle and low FA thresholds. As evidenced in the present study, optimization of these heuristics can eliminate the majority of these errors. Additionally, false positives can normally be eliminated by applying streamline length limits or placing a termination mask just behind the target region to stop streamlines according to a priori knowledge. Exclusion masks are set by applying additional ROIs and toggling them against the seed ROI, thereby eliminating the streamline (as occurs in TrackVis). MRtrix and FSL support the use of multiple ROIs as inclusion/waypoints or exclusion masks, and termination masks can also be applied. Huang et al. (2004) found that using multiple waypoints increases between-session reproducibility and reduces between-subject variability. Using multiple waypoints can also remove false positives. Regardless, there remains a genuine need for anatomically mapped seed ROIs and termination masks for the mouse brain.

The incidence of false positive errors is likely to increase with probabilistic tractography, which appropriates more than one streamline per voxel and has the potential to accumulate errors when propagating a streamline. To counter this increase in error, a different approach or appreciation of the streamlines is required. This approach requires generation of MIPs and density maps.

Grey matter to grey matter tractography has the potential to indicate connectivity changes within the brain. We have found that deterministic tractography fails to generate sufficient streamlines from the grey matter in the mouse brain, which precludes use of this approach. Instead, we investigated grey matter probabilistic tractography approaches that would generate a topographic read-out of streamline propagation between the cortex and thalamus. Both CSD and FSL probabilistic tractography approaches were sensitive to the number of user-designated streamlines. However, the two methods generated different streamline density maps.

The topographic organization of thalamocortical projections in the mouse brain has been reviewed by Vanderhaeghen and Polleux (2004) and Lopez-Bendito and Molnar (2003). Typically, axons originating from rostral thalamic nuclei project to rostromedial cortical areas such as the medial cingulate cortex and motor cortex, whereas caudal thalamic nuclei project caudolaterally in the cortex to the caudal cortical pole and visual cortex. Axons originating from lateral thalamic nuclei tend to project caudally in the cortex, whereas axons originating from medial nuclei project more rostrally. More specifically, the lateral geniculate nucleus projects to visual cortex, the ventrobasal nucleus projects to primary somatosensory cortex and the ventrolateral thalamic nucleus projects to primary motor cortex. Of the tractography approaches investigated, CSD probabilistic tractography most closely reproduced this topography.

There are two important differences in the way parcellation of the thalamus occurs between MRtrix and FSL that may contribute to these results. In this case, MRtrix generated a whole brain tractogram from which streamlines were waypointed by the thalamus and cortical region for selection. FSL seeded the thalamus, not the whole brain, and the generated streamlines were waypointed by the cortical region. Hence, despite seeding the mediodorsal thalamus in the present study using FSL, no streamlines from this thalamic region were found to reach the cortical waypoints. Whereas 500 and 5000 streamline seeds per voxel were selected (Behrens et al., 2003), it is possible that even more streamline seeds are required. This option would need to be investigated by other users, depending on their scientific question. Another important consideration when presenting streamline density maps is that only the cortical region (in this case) with the greatest number of streamlines passing through the voxel will be shown, and only the strongest connection is represented. It is possible that in the ventral thalamus, the visual and somatosensory cortices differ only slightly in their streamline number between the two tractography approaches, yet result in different streamline density maps because of this.

Determining the thalamic segments directly by voxel-by-voxel tensor properties of the thalamus itself without tractography is possible, but difficult without substantial prior knowledge of how the thalamic nuclei appear in dMRI. Other compounding factors include permeating white matter tracts and, ultimately, the resolution of the dMR image. Visually determining the various nuclei in the color map requires substantial effort by experienced anatomists and ultimately does not provide an objective means of establishing a projection map. A recent study investigated the histological fiber orientation in white matter regions of the rat brain and compared these to diffusion tensor modelled fiber orientations or a modified version of spherical deconvolution derived fiber orientations (Leergaard et al., 2010). From this comparison, the latter analysis best represented the histological fiber orientations. Accurate FOD measurements constitute only part of tractography analysis. As we have shown in the present study, despite both methods using constrained spherical deconvolution, incorporating a measure of uncertainty (probabilistic tractography) revealed more pathway information from white and grey matter than omitting this measure (deterministic tractography). In the present study we have demonstrated the utility of tractography for known white matter tracts and those emanating from the frontal cortical grey matter. In future, the approach employed here could be used to investigate smaller tracts such as the external capsule or the medial lemniscus.

Probabilistic tractography was used to inform us of the important streamline populations emanating from the frontal cortex. We then used these populations to investigate frontal cortical pathway differences between wildtype and Fgf17^−/− mice. CSD probabilistic tractography optimization earlier in this study indicated that, apart from step size, curvature and FOD, streamline number was an important determinant in anatomically accurate streamlines. In these earlier experiments, an arbitrary streamline number such as 1000, or a streamline per voxel number of 50, appeared to generate suitable streamlines for white matter tracts. While 50 streamlines per voxel may have generated adequate streamlines for the smaller ROIs such as the anterior commissure, it appears that this method is sensitive to ROI size and the complexity of the tract under investigation. Conversely, 1000 streamlines were apparently insufficient for the frontal cortex. Ultimately, both these methods may require user optimization and are dependent on the tract and ROI. As demonstrated, a comparatively unbiased approach, which remains sensitive to pathway changes, is to seed the entire brain volume and extract streamline information from the region of interest.

If tractography methods can detect differences between MRI data such as the example presented here, it is possible that there is a cluster of voxels that accounts for the difference along the generated path. However, mining a mouse brain FA map, where the neurophenotype is not known, in search of a population of voxels whose FA is lower than control can be time consuming. There are automated processes for investigating voxel-by-voxel FA differences such as Tract-based spatial statistics (TBSS; Smith et al., 2004, Smith et al., 2006). However, this program involves registration optimized for human dMRI data, not the mouse brain. Therefore, TBSS analysis was not performed in this study. Nevertheless, two obvious region types in which there might be FA changes are the seed (in this case, the frontal cortex) and tract ROIs, such as the cingulum and the corticospinal tract. Yet, in the present study, despite a slightly lower FA value in most regions of the Fgf17−/− mouse brain, we found no statistically significant differences. Following volumetric normalization, it is possible that the FA difference in the frontal cortex ROI could contribute to the slight decrease in streamline number across all tracts emerging from this region.

Tractography in the present study revealed statistically significant differences in frontal cortex tracts in a mouse with a decrease frontal cortical volume. When corrected for streamlines generated by the frontal cortex – a variable dependent on the voxel number and brain volume –a slight decrease was observed in streamlines passing through the lateral cortex. Therefore, unlike the cingulum, the decrease in the lateral cortical pathway cannot be explained by a decrease in frontocortical volume alone. Fgf17^−/− exhibit behavioral phenotypes (Scearce-Levie et al., 2008); however, caution must be taken when inferring that tractography differences are directly responsible for functional or behavioral differences.

Conclusion

Diffusion MR tractography is able to chart neurodevelopmental or neurodegenerative conditions in the pre-clinical small animal models of disease, and quantitative output is more readily accessible by tractography than tracer mapping. However, our results show how the tractography result can be influenced by the parameters of choice. While most approaches adequately chart white matter tracts, probabilistic tractography accounts for the uncertainty in the fiber orientation and is also more appropriate for measuring streamline propagation between grey matter regions of interest than deterministic tractography. Tractography parameter optimization is different for white and grey matter regions of interest, with grey matter tractography reliant on more streamline seeding, which results in more false positive streamlines, and hence necessitating the use of a measure of confidence.

Supplementary Material

01. Supplementary Figure 1.

Regions of interest studied in the present investigation. All ROIs were filled for tractography, although some are presented here showing their boundaries only, permitting appreciation of the colour-FA information within the ROI. Colour-FA map colour codes are explained in the methods. ROIs were drawn in one hemisphere only to allow the visualization of any midline crossing streamlines. The exception was the AC, which was at the midline. A, A heterogeneous ROI that included the fimbria (fim), stria terminalis (st) and the dorsal internal capsule (ic(d)). The fim/st/ic(d) ROI is two-dimensional, drawn at −1.70 mm Bregma. The fim/st/ic(d) waypoints are shown, including stria terminalis (Bregma −0.58 mm), precommissural fornix (pcf)/ventral diagonal band (vdb) (Bregma 0.14 mm) and dorsal corticothalamic tracts (dct; Bregma 0.14 mm). The hippocampal commissure waypoint is not shown, but was placed in the contralateral fimbria on the same coronal plane of the fim/st/ic(d) ROI (i.e. Bregma −1.70 mm). B, The olfactory bulb ROI was drawn from Bregma 2.46 mm until the rostral pole of the olfactory bulb. C, The AC ROI volume = 3×3×2 voxels, centered at Bregma 0.14 mm. D, Corticothalamic ROIs were drawn with the aid of the mouse brain atlas and included association cortices. Cortical regions excluded were the granular, angular insular, ectorhinal and perirhinal cortices. The ventrolateral cortex ROI comprised the endopiriform, lateral entorhinal and piriform cortices. E, The frontal cortex ROI began rostral to the forceps minor of the corpus callosum (fmi; Bregma 2.10 mm) and ended at the rostral cortical pole, following the rhinal fissure at the ventral aspect. The fmi waypoint was drawn at Bregma 2.10 mm in the contralateral cortex. The corticospinal tract (cst) waypoint was drawn at Bregma −4.36 mm surrounding the medial lemniscus and the longitudinal fasciculus pons. The cingulate (cg) and lateral cortex ROIs were drawn at Bregma −0.58. The cingulate ROI included cingulate cortex areas 1 and 2. The lateral cortex ROI included granular insular, angular insular posterior, piriform, claustrum, and dorsal and ventral endopiriform cortices. Scale bar = 2 mm.

02. Supplementary Figure 2.

Optimization of anterior commissure tractography with Qball-FACT deterministic tractography. The difference between the two deterministic algorithms available following HARDI/Qball modeling in Diffusion Toolkit can be appreciated in A. Compared to FACT, a prolificacy of streamlines is produced using 2nd order Runge-Kutta that fail to stop in the lateral cortex, and instead, continue to cross at the caudal or rostral corpus callosum midline (arrows). B, Prolificacy and false positive streamlines are common beyond turning angle thresholds of 40 degrees (e.g. arrows), while below 30 degrees the streamline profile is compromised. C, Mask thresholds impact on streamline output. For this sample, the automatic mask threshold was 2072 and 15976, minimum and maximum, respectively. Constraining this threshold window to 5000 and 10000 (constrained) resulted in fewer streamlines, while increasing this window (unconstrained) to 500 and 20000 had no noticeable effect. Abbreviations: T, turning angle. Scale bar = 1 mm.

03. Supplementary Figure 3.

The correct combination of step size (step) and curvature (curv) setting is required to produce suitable turning angles in deterministic and probabilistic tractography following CSD modeling. A, Increasing the step size and decreasing the curvature results in streamline prolificacy and likelihood of false positives (e.g. step size 0.1 mm, curvature 0.05 mm). The final voxel-wise turning angle is shown in the bottom right of the image. Final angles within 4 to 10 degrees produce suitable streamline profiles. In B, a step size of 0.01 mm and curvature of 0.15 mm produces a profile with a few streamlines projecting around the hippocampus and crossing the midline via the corpus callosum (arrowhead). These streamlines can be eliminated using post-processing streamline length limits. C, Increasing the step size and decreasing the curvature results in streamline prolificacy and false positives to the point of redundancy with probabilistic tractography (e.g. step size 0.025 mm, curvature 0.02 mm). The final voxel-wise turning angle is shown in the bottom right of the image. Final angles near 10 degrees produce suitable streamline profiles. Scale bars = 1 mm.

04. Supplementary Figure 4.

In combination with suitable step sizes and curvatures, the FOD impacts on both deterministic and probabilistic tractography following CSD modeling. A and B, Decreasing the FOD threshold (e.g. to zero) results in streamline prolificacy and the likelihood of an increase in false positives. Increasing the FOD threshold (e.g. to 1.0) results in few streamlines and the likelihood of an increase in false negatives. MRtrix uses a default FOD threshold of 0.1, which is suitable in the present case for representing AC tractography. FOD threshold values are indicated in the top right of each image. C, Streamline number impacts on tractography profile. Using parameters established in Supp. Fig. 3, MRtrix was instructed to select a certain number of streamlines from the AC ROI seed point (i.e. 100 to 100000). The AC ROI volume is 18 voxels; hence, from the streamline number selected (top of image) the equivalent streamline number per voxel can be calculated (bottom of image). Little difference is observed between 27.7 and 55.5 streamlines per voxel. D, The maximum intensity projection map is also affected by streamline number. However, at higher intensities or higher confidence (i.e. 20 or 2000) the AC streamline profile is almost identical. Scale bars = 1 mm.

05. Supplementary Figure 5.

Step size impacts on maximum intensity projection images by increasing background noise in FSL. Comparing step size parameters reveals that at the highest intensities (1000), the tractography profile of the AC does not grossly change using the default option. For comparison, the anisotropy constraint was selected in FSL. Scale bar = 1 mm.