Dynamic calibration of pharmacokinetic parameters in dose-finding studies

Abstract

We introduce a dose-finding algorithm to be used to identify a level of dose that corresponds to some given targeted response. Our motivation arises from problems where the response is a continuously measured quantity, typically some pharmacokinetic parameter. We consider the case where an agreed level of response has been determined from earlier studies on some population and the purpose of the current trial is to obtain the same, or a comparable, level of response in a new population. This relates to bridging studies. The example driving our interest comes from studies on drugs for HIV that have already been evaluated in adults and where the new studies are to be carried out in children. These drugs have the ability to produce some given mean pharmacokinetic response in the adult population, and the goal is to calibrate the dose in order to obtain a comparable response in the childhood population. In practice, it may turn out that the dose producing some desired mean response is also associated with an unacceptable rate of toxicity. In this case, we may need to reevaluate the target response and this is readily achieved. In simulations, the algorithm can be seen to work very well. In the most challenging situations for the method, those where the targeted response corresponds to a region of the dose–response curve that is relatively flat, the algorithm can still perform satisfactorily.

1. INTRODUCTION

An early phase clinical trial in children, aimed at establishing an effective dose and where we have information on effective doses for adults, calls for a particular kind of design. Bridging studies, in which we have knowledge of effective doses for 1 group and we would like to extend this knowledge to another distinct group, come under the same heading. The example of children is especially important in light of recent Food and Drug Administration and National Institutes of Health requirements that drugs be evaluated rapidly in children following studies in adults. It is not enough to extrapolate based on the adult data. In this case, a useful approach can be to establish a dose for children that results in comparable pharmacokinetic levels (without excessive toxicity) shown to be safe and effective in adults. For some diseases, instead of using pharmacokinetic measures, it may be possible to use direct measures of drug activity. For example, in HIV studies, it may be possible to use the extent of suppression of viral load or some other indicator of the antiviral effect of treatment. In some respects, the problem is similar to the problem of bioequivalence, although the aim is not that of establishing the comparable effectiveness of 2 different compounds in the same population but rather that of establishing the effective equivalence of potentially different doses of the same compound in 2 different populations. Our interest was motivated by the study P1013 undertaken by the Pediatric AIDS Clinical Trials Group. In this study, a cohort of 6 children was to receive a test dose of an antiretroviral drug, indinavir. A criterion in that study for deciding that the test dose was too low, and hence (provided the test dose did not raise safety concerns) that a higher dose should be tested in a subsequent cohort of 6 children, was that the average AUC among the 6 children was below a target value determined on the basis of a previous adult study.

A range of candidate doses are available for study, and we aim to identify a dose providing an equivalence in response to some dose that has already been established as being safe and effective in a different population. Equivalence in this context is taken to mean the providing of a comparable pharmacokinetic response. The dynamic updating is analogous to that of the so called CRM, the continual reassessment method (O'Quigley and others, 1990) applied to a continuous rather than a binary outcome. Our motivation comes from studies where a drug has been evaluated in adults and a dose is desired for pediatric use and where the dose selection is based upon a pharmacokinetic parameter. However, the methods are more general and address the issue of dynamic calibration, which is to say that of continuously updating an estimated inversion of a monotonic relationship between dose and some outcome.

It will often be the case that pharmacokinetic studies have already been undertaken in the existing population. From these, we might have established a dose level considered to be safe and effective. In our own experience, an initial dose for evaluation in children (typically expressed as the number of milligrams of a drug per kilogram of weight or per meter squared of body surface area of the child) would have been established by the pharmacologists. The pharmacologists believe, or estimate, that this dose will be approximately equivalent to the dose used in adults. The first included children in the study will receive this dose. However, it often turns out that some further fine-tuning of the dose level is required. Typically, the range of doses around this initial dose that need to be considered is relatively narrow.

The statistical objective will be determined by which measures we use in defining “equivalent.” Different choices will often be available to us. For example, we may focus interest on establishing equivalence with respect to the pth quantile (0 < p < 1), denoted by Y_p^*, of the distribution of a particular pharmacokinetic parameter which we label Y. The goal would then be to identify a level of dose that produces an effect p% greater than this target in the new population. A particular case of a percentile is the median, and, possibly following some symmetrizing transformation, we may often approximate this by the mean. There may be a small finite number k of fixed, ordered doses, d₁,…,d_k or it may be possible to refine the dosing such that d could be considered effectively continuous (e.g. where liquid formulations of a drug are available, as is common for children). The goal studied here is to identify a level of dose d such that, at that level, an average or median response corresponds to some predetermined target response.

Note that, in practice, apparently different objectives can effectively coincide. For instance, the level of dose d, which produces a percentage p of patients having pharmacokinetic response Y less than Y_p^* will also be the dose producing an “average” response of, say, 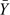(d). It may be simpler to construct a design whose purpose is to locate d such that 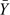(d) is close to some value rather than d producing a given percentage less than Y_p^*. If the form of the distribution of Y is known, for example, a transformed normal with variance independent of dose, the 2 objectives can be made to coincide exactly.

2. EFFICIENT CALIBRATION ALGORITHMS

There are 2 complementary components to any dose-finding algorithm. First, we use an allocation rule to assign sequentially the incoming patients to one of the possible doses, with the intent of assigning to doses ever closer to, and eventually recommending, a target dose. Second, we use a simple working linear model in which the intercept is held fixed in order to sequentially update information on mean response at each of the dose levels. The k doses, d₁,…,d_k, are now ordered in terms of their mean response, E{Y_j(d_i)}, at each of the levels. Here, Y_j(d_i) is the level of pharmacological response for patient j at dose level d_i, and, for given d_i, we take the Y_j(d_i), j = 1,…,n, to be i.i.d. The dose we aim to identify, the “target” dose, is that dose having an associated mean response across the patients as close as possible to some target response θ. We suppose some monotonic relation for E{Y_j(d_i)}. When k is large we can treat the dose as though it were continuous and denote it simply by d.

2.1. Calibrating a dichotomous outcome

Consider a clinical trial in which no more than n patients are to be entered. The dose level for the jth patient, X_j, is viewed as random taking values x_j, where x_j is either discrete, assuming some value from {d₁,…,d_k}, or continuous assuming the value d. Let Y_j be a random variable denoting some simple function of pharmacokinetic response for the jth patient. Among possible choices for this function would be the actual value of the pharmacokinetic parameter or an indicator variable taking the value 1 if some threshold is reached and 0 otherwise. We could then define P(Y_j > Y_p^*∥X_j = d_i) = R(d_i). The goal of the study is to find the smallest dose d_i such that R(d_i) is greater than some value p, typically of the order p = 0.9.

In this case, R(d_i) is the probability of a pharmacokinetic success at dose level d_i. In practice, the observations obtained in the course of any study present themselves as a dichotomy; success or failure to reach the pharmacokinetic threshold. In attempting to achieve the goal described above, we have also to keep in mind an ethical requirement indicating that we treat each patient at a level which is expected to be effective. Of course, the reason for the trial is that there is some uncertainty concerning which of the levels are effective, but each entered patient provides information reducing this uncertainty. The CRM, originally designed for use in the context of Phase I toxicity studies in cancer, can be readily adapted to this context. For our purposes, we modify the focus of the basic rationale from O'Quigley and others (1990) to a design in which (1) we use an allocation rule to assign sequentially the incoming patients to one of the possible doses, with the intent of assigning doses ever closer to, and eventually recommending, the minimally effective dose, and (2) we use a statistical procedure that updates the information on the probabilities of pharmacokinetic success in light of the results obtained for the patients already observed. We model R(x_j), the probability of obtaining a pharmacological success, at X_j = x_j; x_j∈{d₁,…,d_k} by

for some 1-parameter working model ψ(x_j,a). The working model ψ(x_j,a) is not anticipated to be able to reproduce R(d_i) at all doses d_i but will coincide with R(·) at the target dose. The precise restrictions needed to specify ψ(x,a) were described by Shen and O'Quigley (1996). The simple choice ψ(d_i,a) = α_i^exp(a), (i = 1,…,k), where 0 < α₁ < ⋯ < α_k < 1 and − ∞ < a < ∞, is widely used in practice. Once a model has been chosen and we have data in the form of the set Ω_j = {y₁,x₁,…,y_j,x_j}, the outcomes of the first j experiments, we obtain estimates 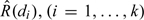of the true unknown probabilities R(d_i),(i = 1,…,k) at the k dose levels. After the inclusion of the first j patients, we can write down the log-likelihood or a posterior distribution and (1) obtain the estimates 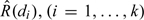and (2) select dose level x_{j + 1}∈{d₁,…,d_k} to be given to the (j + 1)th included patient so that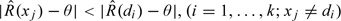

2.2. Calibrating a continuous outcome

For the observations (x₁,y₁), …, (x_n,y_n), we suppose for some unknown φ:

where the errors ϵ₁,…,ϵ_n are i.i.d. random samples with mean 0 and σ is an arbitrary scale parameter. The first derivative of φ(x) is assumed to exist and to be positive for all x so that a local linear approximation to φ(x) can be made.

The model assumes that the scale parameter σ, and thereby the error distribution, does not depend upon dose. Real situations may be more complex, and we consider the above model as only an approximation in any modeling context. The problem of robustness to these assumptions requires investigation. We do not pursue this here in depth although, for the illustrations of the method (below), the mechanism generating the data allowed for the error distribution to depend upon dose. Let θ be some target value for E(Y) and ξ₀ be the solution for φ(x) = θ. We are interested in sequential determination of the design values x₁,…,x_n, so that ξ₀ can be estimated consistently and efficiently from the corresponding observations y₁,…,y_n. Following Robbins and Monro (1951), stochastic approximation has been applied to this type of problem and has been studied by many authors. The idea of the Robbins–Monro procedure is to assume a linear approximation to φ(s), specifically M(x) = α + βx and to calculate the design values sequentially according to

(2.1)

where c is some constant. Lai and Robbins (1979) pointed out the connection between (2.1) and the following procedure based on the ordinary linear regression applied to (x₁,y₁), …, (x_n,y_n):

(2.2)

where 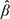_n is the least squared estimate of β. Wu (1985) indicated that (2.1) can be approximated by (2.2). Under certain circumstances, stochastic approximation can be considered as the fitting of an ordinary linear model to the existing data, treating the regression line as an approximation of M(·) and using it to calculate the next design point. However, the procedure can be unstable and slow to converge unless M(x) is rather steep. The approach taken here, inspired by the underparameterized models of the CRM, is to estimate ξ₀ by sequentially inverting an underparameterized working model. The model, in this case a 1-parameter linear model, needs only to be sufficiently flexible in order to be able to solve the regression equation at a single point, notably the solution of the equation itself. The only requirement on the true relationship between pharmacokinetic response Y and dose d is that it be monotonically increasing. Our specific proposal here is to estimate ξ₀ by fitting the data with a linear model without an intercept. Intuitively, a 1-parameter model would be sufficient for determining ξ₀ if most of the design values are around it. Furthermore, unlike the Robbins–Monro procedure, the estimate of the slope becomes relatively stable as a result of tying down the intercept parameter. The biggest concern is whether the estimate is consistent as the model becomes less flexible and is not able to reproduce the distribution of the data across the whole dose range. However, we will demonstrate that knowledge of the entire distribution is unnecessary for consistency.

Consider then the simple case where the data are generated according to the equation (M(x) = α + βx):

(2.3)

Then ξ₀ is the solution for equation α + βx = θ > 0. Suppose that we have collected data (x₁,y₁),…,(x_n,y_n). The usual way to proceed would be to write down the likelihood on the basis of the errors ϵ_i(i = 1,…,n). Suppose we fix the parameter α at some value which is, with probability 1, different from its true value, and, in particular, we decide to take α = 0. The variance of Y given X might be assumed known from studies in a reference population. This assumption can of course be relaxed in the context of a more sophisticated set up where we put some prior on σ and allow the data to update this prior information. An alternative approach, apparently less efficient and, at first glance, not even likely to be consistent, would be to calculate a least squares fit of a regression line constrained to pass through the origin. This avoids any consideration of σ and results in an estimate of the slope. We then use this estimate to obtain our next design point x_{n + 1} so that

(2.4)

After having made an observation on the outcome y_{n + 1} at the point x_{n + 1}, the whole process is then repeated. We iterate between the estimation process giving us the next design point and the new observation made at that design point. Note that the model employed by the procedure is different from that generating the data. Not only is it different but also it is simpler and could be considered underspecified in that a richer model, including an intercept term, would at least give an accurate linear approximation to the unknown function φ(x). Our poorer working model will not be rich enough to reproduce with any accuracy the function φ(x) over any range including x, but, at the point x itself, it will be rich enough for equality to hold.

Other related estimators can also be considered, in particular the simple ratio of the means. This arises from the observation that a straight line constrained to go through the origin and going through the point (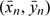), where 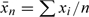and 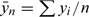, provides an estimate of the slope, leading to an estimator for β as 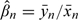. Again, setting x_n+1 = 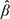⁻¹θ would yield the recommended design value for the next experiment. The design point x_n and the average 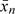can both serve as estimates of ξ₀. These estimates are “consistent” if they converge to ξ₀ almost surely when n goes to infinity. The definition of x_n implies that its consistency is equivalent to that of 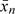. Below we shall establish consistency of x_n for 2 situations. The first is where x takes continuous values and the consistency result only essentially requires the monotonicity and continuity of φ. The second, where X takes only a finite number of values is more difficult and the conditions for consistency are more stringent. For the discrete case, there can be situations, where x_n fails to be consistent although it would still estimate a level providing a pharmacokinetic response Y which is close, if not the closest, to the target.

We may also want to take into consideration toxic side-effects which, in practice, would limit the level of dose which can be given. For this purpose, we would keep track of the number of toxicities in the neighborhood of the dose x. A binary variable z_j takes the value 1 for patient j in the presence of unacceptable toxicity and the value 0 otherwise. We denote the neighborhood itself by L(x). This could be a small interval centered about x although the restriction of being symmetrical about x is not a necessary one. A running estimate of the rate of unacceptable toxicity in the neighborhood of x is given by 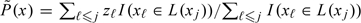. In the neighborhood of x, we wish to test the composite hypotheses H₀:0 < P(x) < p₀ against H₁:p₀ < P(x) ≤ 1. Associated with these intervals, we have a prior on P, denoted by g(p). Then, if we let C(H_m) denote the event that the trial concludes in favor of H_m, the type I and type II error rates are fixed by ϵ₁ = Pr{C(H₁)|H₀}, ϵ₂ = Pr{C(H₀)|H₁}. Obtaining a statistic for choosing between these 2 hypotheses is described in O'Quigley and others (2001).

3. EXAMPLE

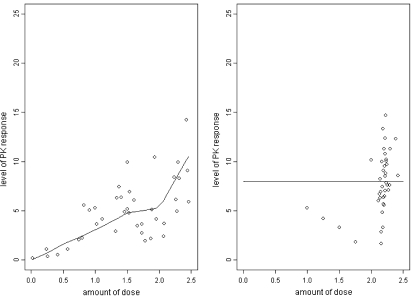
We illustrate our method with a simulated example, summarized in Table 1 and Figure 1. The first example is illustrated in a step-by-step way in both the table and the figure. Further examples are illustrated in the supplementary material available at Biostatistics online. For this example, the mean responses were driven by the underlying curve shown in the left-hand panel of the Figure 1. The variance was chosen to be large in order to mirror realistic situations. For the purposes of illustration, we constructed a piecewise nonlinear curve with varying amounts of curvature and for which, across the dose range, the probability of a very high or a very low response was small. The variability, which was allowed to depend on dose level, was taken to be as large as might realistically be encountered in practice. For smaller values of variance, the algorithm will perform better since its task becomes easier and conversely, for greater values of variance. A feature that experimenters will often want to include in these types of design is to limit the size of any increment or decrement in successive choices of dose. Here, we used a value of 0.25.

Table 1.

Step by step calculations of recommended doses

i	xi	yi	xi+1	i	xi	yi	xi+1
1	1.00	5.29	1.25	21	2.20	5.57	2.24
2	1.25	4.21	1.50	22	2.24	10.02	2.21
3	1.50	3.28	1.75	23	2.21	9.54	2.19
4	1.75	1.81	2.00	24	2.19	5.69	2.22
5	2.00	10.13	2.25	25	2.22	10.77	2.18
6	2.25	7.60	2.42	26	2.18	13.32	2.13
7	2.42	8.54	2.38	27	2.13	6.69	2.14
8	2.38	12.32	2.15	28	2.14	8.20	2.14
9	2.15	6.91	2.19	29	2.14	6.29	2.15
10	2.19	6.35	2.25	30	2.15	1.68	2.21
11	2.25	9.68	2.19	31	2.21	8.52	2.21
12	2.19	9.09	2.16	32	2.21	6.46	2.22
13	2.16	9.98	2.12	33	2.22	8.82	2.22
14	2.12	6.04	2.16	34	2.22	12.36	2.18
15	2.16	2.85	2.27	35	2.18	3.30	2.22
16	2.27	7.10	2.29	36	2.22	7.04	2.22
17	2.29	7.59	2.30	37	2.22	14.67	2.17
18	2.30	11.27	2.23	38	2.17	7.42	2.18
19	2.23	7.85	2.24	39	2.18	4.81	2.20
20	2.24	10.23	2.20	40	2.20	11.31

Fig. 1.

Left-hand figure shows the true dose–response curve and random sampling of size 40 about that curve. The right-hand figure illustrates dynamic calibration sampling of size 40 and where the target level is 8.0. The starting dose is 1.0 and step sizes constrained to be no greater than 0.25.1

For these illustrations, the targeted mean pharmacokinetic response was taken to be 8.00. The true log-dose that corresponds to a level producing 8.00 as an average response, can be read off from Figure 1 as 2.20. The initial log-dose given to the first patient was 1.00. The response of this patient, 5.29, is reasonably close to but still lower than the target. The algorithm indicated that the following patient ought then to be administered a dose of 1.25. At this dose, we obtained a weaker response, 4.21. Such values, quite far removed from the mean, are consistent with the relatively large value chosen for the variance. The recommended dose was again increased to 1.50 and the third patient responded once more with a weaker rather than a stronger response, 3.28. Note that had we simply fitted an unrestricted linear or higher-order regression, we would conclude that the dose–response curve is decreasing. Our underparameterized model forces the estimated dose–response relationship to be increasing despite being seemingly contradicted by the data.

At the dose given to patient 4, the response decreased yet further to 1.81, leading to another dose increment of 0.25 for patient 5. This time the response was higher than the target 8.00 (at 10.13) and yet the algorithm continues to indicate a further increment in the dose, as a result of the earlier rather lower responses. For the remaining patients, the increments quickly become smaller and patients 8–40 were treated at a log-dose within 0.10 of the target 2.20. The ability to concentrate such a large percentage of the patient observations at and around the target level is a central property of the design. This property is seen equally well in quite different settings where the relationship between dose and response can follow varying rules. It would be difficult not to do better than simple random sampling and this is only presented for the purposes of illustration.

The 4 pairs of figures illustrated in the supplementary material available at Biostatistics online show 4 different situations corresponding to 4 different and arbitrary choices of the association between pharmacokinetic response and dose.

A consistent feature, already observed in the more classical CRM setting (O'Quigley, 2001), is that the more incorrect the initial guess of dose turns out to be, the better the algorithm performs. At first this is puzzling, but it is easily explained. The method can detect very quickly that we are far below or far above the correct level. Once we are sampling in the vicinity of the correct dose level, then it is much more difficult to “fine-tune” the procedure since the natural variation that we are dealing with can often mask these smaller differences. Nonetheless, the sampling algorithm will quickly concentrate observations at and around the target level. The studies reported here and in the supplementary material available at Biostatistics online used a fixed sample size. For a fixed finite number of doses, we could use an early stopping rule such as the one described in O'Quigley and Reiner (1998). For a continuum of doses, it might be possible to derive analogous rules based on the construction of intervals within which the responses are deemed to be approximately equivalent. This has yet to be studied.

4. DISCUSSION

In the general approach to calibration described here, there are several design parameters that have to be fixed by the investigator. Simulation, recommended by several authors as a means to study operating characteristics, would also have its place in the implementation of dynamic calibration designs and in assessing robustness to departures from distributional assumptions.

Other design parameters are not chosen for their impact on efficiency or their ability to enhance performance in particular circumstances but more as a means to address clinical concerns arising in the context of the trial. For HIV studies, we would be careful not to allow any procedure which might permit large jumps to low levels of an antiviral agent because, at low levels, there is a high risk to the patient of developing resistance. For very toxic anticancer drugs, we might have a similar concern about too large steps in the period of escalation.

It is common practice in dose-finding studies to include patients in small groups so that, for example, a group of 3 would all have to be treated at the same level before recommending a different level. Such modifications raise no difficulties in practice but their impact on operating characteristics needs future study. In particular, it is likely that the effect of grouping would be similar to that of limiting the step size.

The clinical context, as much as statistical concerns, will provide guidance in setting certain design features. For HIV studies, the concern at “undertreating,” that is, giving doses which may be ineffective but still enough to produce resistance, would usually outweigh concerns of “overtreating” since toxicities are typically reversible. In cancer studies involving cytotoxic drugs, the opposite can be the case. Here, we often prefer to escalate cautiously, using groups of patients while disallowing the skipping of doses, but to de-escalate quickly, on the basis of information from a single patient, and quite possibly skipping dose levels. In the HIV setting, we might want to have more patients at a higher dose before applying any indicated decrease because a lower dose may not only reduce efficacy but also be associated with a higher risk of inducing viral resistance. In Phase II dose-finding studies for antibiotics, overdosing will typically correspond to unnecessary cost, whereas underdosing is likely to be not only ineffective but also to lead to resistance and, in the longer term, possibly greater cost. Such cost considerations, as reflected in any decision to escalate or de-escalate, are not symmetrical and this fact could be mirrored in the design if so desired.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

National Institute of Health grants (AI024643, AI068634 to M.D.H.; U01 AI068632-01 to T.F.).