Quantifying mRNA Synthesis and Decay Rates Using Small RNAs

Abstract

Regulation of mRNA decay is a critical component of global cellular adaptation to changing environments. The corresponding changes in mRNA lifetimes can be coordinated with changes in mRNA transcription rates to fine-tune gene expression. Current approaches for measuring mRNA lifetimes can give rise to secondary effects due to transcription inhibition and require separate experiments to estimate changes in mRNA transcription rates. Here, we propose an approach for simultaneous determination of changes in mRNA transcription rate and lifetime using regulatory small RNAs (sRNAs) to control mRNA decay. We analyze a stochastic model for coupled degradation of mRNAs and sRNAs and derive exact results connecting RNA lifetimes and transcription rates to mean abundances. The results obtained are then generalized to include nonstoichiometric coupled degradation of sRNAs. Our analysis suggests experimental protocols for determining parameters controlling the efficiency of stoichiometric regulation by small RNAs and for analyzing factors and processes regulating changes in mRNA transcription and decay.

Introduction

Cellular adaptation to changing conditions is critically dependent on processes that enable rapid responses to environmental fluctuations. Although considerable research has focused on changes in transcription, research over the past several years has demonstrated that control of mRNA decay plays an increasingly important role in cellular responses (1–3). Correspondingly, there is significant interest in understanding factors and processes that govern regulation of mRNA decay.

The traditional approach for measuring mRNA lifetimes involves quantification of mRNAs remaining at different times after inhibition of transcription, e.g., by the addition of rifampicin (2). This procedure requires multiple measurements during time intervals of the order of the mRNA lifetime; hence, high temporal resolution is required for short-lived mRNAs. More significantly, the procedure for inhibition of transcription can give rise to secondary effects that influence mRNA decay (2); this means that the estimates of mRNA lifetimes thus obtained may not be accurate.

In several experiments, the quantities of interest are the fold-changes in mRNA transcription and decay rates between different conditions. Recent research has shown that changes in mRNA transcription rates can be coordinated with changes in degradation rates to fine-tune gene expression (4). Current approaches for quantifying these changes require separate experiments to estimate mRNA transcription rates and mRNA decay rates and, as noted above, the estimates for mRNA lifetime can be influenced by secondary effects due to changes in cellular metabolism. Hence, it is of interest to consider alternative approaches to quantify changes in mRNA transcription and decay rates under different conditions.

A naturally occurring process that regulates turnover for many bacterial mRNAs involves interactions with regulatory small RNAs (sRNAs). Experiments have shown that posttranscriptional regulation of gene expression can occur via binding and subsequent coupled degradation of the mRNA and regulatory sRNA and that it occurs rapidly (5,6). The corresponding coarse-grained model of gene expression has been analyzed by several groups (7–11) and shown to be consistent with experimental observations (7). In this article, we show that the kinetic scheme for this mode of regulation leads to an exact result relating RNA lifetimes and abundances. The obtained result is valid for all parameters of the stochastic model, in particular even in the presence of large fluctuations that are typical for low abundance mRNAs. Furthermore, the result can be generalized to include nonstoichiometric degradation of small RNAs. The derived relationships can be used to propose novel experimental protocols and schemes for determining several quantities of interest such as quantifying the efficiency of stoichiometric degradation of small RNAs and determining fold-changes in mRNA transcription and decay rates.

Results

Our analysis considers a generalized stochastic model for regulation by sRNAs as illustrated in Fig. 1. The complexity of processes leading to transcription suggests that RNA synthesis in many instances is not adequately modeled as a Poisson process (12,13). Hence, we model mRNA and sRNA production by arbitrary stochastic processes with mean arrival rates k_m and k_s, respectively. Degradation of an mRNA and an sRNA can occur either independently (with constant probability per unit time $1/{\tau }_m$ and $1/{\tau }_s$, respectively) or through the coupled degradation process.

Figure 1.

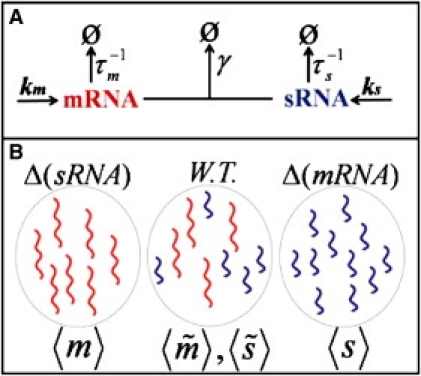
Unregulated steady-state mean levels of mRNAs and sRNAs along with regulated levels of these molecules are measured. The measured quantities allow determination of the average mRNA transcription rate k_m and decay rate τ_m relative to the sRNA production rate k_s. If k_s is held fixed, and the conditions are varied, the proposed scheme leads to simultaneous determination of fold-changes in the rate of transcription and the rate of mRNA decay. Note that the mRNA/sRNA interaction parameter can be arbitrary. (A) Kinetic scheme for mRNA and sRNA production and decay including coupled mutual degradation. (B) The proposed setup involves steady-state measurements for three strains: Δ(sRNA), WT, and Δ(mRNA).

We begin by considering the case of one sRNA species regulating one mRNA species. Consider three different strains as shown in Fig. 1 B: i.e., two unregulated strains (i.e., with either sRNA or mRNA deleted) and the wild-type (WT) strain. In the WT strain, both mRNA and sRNA are present and regulate each other. In steady state, we derive the following exact relations (Appendix) connecting mRNA/sRNA lifetimes and transcription rates to the mean abundances:

$$k_m{\tau }_m=\langle m\rangle ,$$

$$k_s{\tau }_s=\langle s\rangle ,$$ (1)

$$\frac{{\tau }_m}{{\tau }_s}=\frac{\langle m\rangle -\langle \tilde{m}\rangle }{\langle s\rangle -\langle \tilde{s}\rangle }.$$ (2)

Here 〈m〉 and 〈s〉 are the mean mRNA(sRNA) abundances in strains lacking the sRNA(mRNA), and $\langle \tilde{m}\rangle$ and $\langle \tilde{s}\rangle$ are the mean mRNA and sRNA levels in the WT strain where both are present.

The above relations can be extended to cover the possibility that sRNA decay, in general, need not be stoichiometric (14), i.e., the sRNA is not degraded every time the sRNA:mRNA complex is targeted for degradation. In previous work, this effect has been modeled using a parameter p (7,8) that denotes the probability that the sRNA is degraded whenever the sRNA:mRNA complex is targeted for degradation. Thus, p = 1 corresponds to the case of stoichiometric mutual degradation considered above, whereas p = 0 corresponds to the case that sRNA-based degradation is purely catalytic (14). For p > 0, the generalization of Eq. 2 is given by

$$\frac{{\tau }_m}{p{\tau }_s}=\frac{\langle m\rangle -\langle \tilde{m}\rangle }{\langle s\rangle -\langle \tilde{s}\rangle }.$$ (3)

Experimental Applications

The relations derived in the previous section suggest alternative approaches for quantifying changes in transcription and decay rates for mRNAs that have a naturally occurring small RNA regulator or for which an antisense RNA regulator can be designed. Consider first a regulatory network consisting of a single sRNA species regulating a single mRNA species. Because this network is based on current knowledge, it is possible that there are additional network elements (e.g., additional mRNA targets) yet to be discovered. The results derived suggest an experimental protocol that can indicate the presence of additional elements in the network, as detailed below.

We note that the following proposals will hold only for small RNAs whose mode of action is not purely catalytic, i.e., p must be finite. Consider an experimental setup expressing the sRNA from an inducible promoter such that its transcription rate is primarily controlled by inducer concentration. The basic parameters for the coupled system are k_m, k_s, τ_m, τ_s, and p. Now, as the inducer concentration is changed, the sRNA transcription rate k_s is altered. Correspondingly the mean mRNA ($\langle \tilde{m}\rangle$)and sRNA ($\langle \tilde{s}\rangle$) levels will change; however, the lifetimes τ_m and τ_s and the parameter p are unchanged. Thus Eq. 3 predicts that as k_s is changed, the mean mRNA and sRNA levels change in such a way that the ratio

$$R_{\text{ms}}=\frac{\langle m\rangle -\langle \tilde{m}\rangle }{\langle s\rangle -\langle \tilde{s}\rangle }$$

is unchanged, provided the network consists of a single sRNA species regulating a single mRNA species. On the other hand, if the ratio R_ms does change as k_s is changed, that implies that the network cannot be composed of just a single sRNA species regulating a single mRNA species, i.e., there must be additional elements in the network. Thus, by tuning small RNA production rates, we can determine whether there are additional elements in the sRNA:mRNA interaction network for a given set of conditions.

Alternatively, we can consider an experimental setup that changes k_m while keeping τ_m, τ_s, and p unchanged. This can be achieved, for example, by changing the promoter region upstream of the transcription start site for the regulated mRNA target. Although changes in the binding site regions upstream of the transcription start site can give rise to changes in mRNA transcription rate, they will not have any effect on the mRNA degradation rate or on sRNA-related parameters. If there are no additional elements in the network, the derived results predict that the ratio R_ms is invariant even as the mean sRNA and mRNA levels change, since the parameters τ_m, τ_s, and p are unchanged. Thus, the derived results lead to testable predictions for measurements of mean mRNA and sRNA levels as mRNA (or sRNA) transcription is varied. If the predictions are validated, it suggests that the interactions of the mRNA/sRNA with other sRNAs/mRNAs can be neglected, whereas if the predictions are not validated, that suggests the presence of additional network elements for the given set of conditions.

Given that we have a network composed of a single sRNA species regulating a single mRNA species (i.e., consistent with the predictions discussed above as mRNA/sRNA levels are changed), another quantity of interest is the parameter p, which quantifies the efficiency of stoichiometric degradation. The derived results suggest an experimental protocol for determining this parameter. Consider an experimental setup in which the sRNA is expressed from a promoter that is identical to the mRNA promoter, such that we have k_m = k_s. In this case, the ratio of mRNA/sRNA lifetimes (τ_m/τ_s) can be obtained by determining the ratio of mean mRNA/sRNA levels in the unregulated strains using Eq. 1. On the other hand, using Eq. 2 and measurements of mean mRNA and sRNA levels in the WT strain, we can determine τ_m/pτ_s. Upon combining the two results, we see that the effective parameter p can be determined by measuring mean mRNA and sRNA levels in the different strains.

For the single mRNA-single sRNA network, let us now consider how the derived relations can be used to determine changes in mRNA transcription and decay rates. Consider two different experimental conditions (for example, A and B) such that the mRNA transcription rate (k_m) and lifetime (τ_m) can change from A to B, whereas the sRNA transcription rate (k_s) and the stoichiometric efficiency parameter p can be maintained constant. The difference between A and B could be mutations in key sequence elements of the mRNA that could affect k_m and τ_m, without having any effect on τ_s, k_s, or p. Alternatively, the difference could correspond to deletion of factors that affect mRNA and sRNA natural degradation rates without affecting k_s and p. In such cases, quantities of interest (specifically fold-changes in mRNA transcription and decay rates) can be determined using experimental measurements of 〈m〉, 〈s〉, $\langle \tilde{m}\rangle$, and $\langle \tilde{s}\rangle$ in the two conditions in combination with the equations derived above. Specifically, if k_s is held fixed, then taking the ratio of unregulated sRNA levels 〈s〉 in the two conditions gives us the fold-change in sRNA lifetimes between the two conditions. Using this in combination with the ratio of R_ms values (measured experimentally) between the two conditions gives us the fold-change in mRNA lifetimes. Note that this is independent of the parameter p, assuming that it does not vary between the two conditions. Now, taking the ratio of the mean mRNA levels between the two conditions, we can determine the fold-change in the mRNA transcription rate k_m.

Finally, let us consider the case that the known network consists of a single sRNA species regulating multiple mRNA species. Deletion of all but one of the mRNA targets will lead to strains comprised of a single sRNA species regulating a single mRNA species. Thus, the experimental protocols indicated above for the 1 sRNA-1 mRNA network can be used to determine whether there are additional undiscovered elements in the network and, if not, to subsequently determine the parameters such as p and fold-changes in mRNA transcription and decay rates under changing conditions. Furthermore, the derived equations also determine the mRNA lifetime relative to the sRNA lifetime, and thus, can be used to obtain relative mRNA lifetimes for the different mRNAs in the network.

Discussion

In this article, we have derived exact relations for general stochastic models of regulation by small RNAs. The derived results relate mRNA and sRNA lifetimes to the corresponding steady-state abundances and are valid for all choices of parameters. It should be noted that mean-field analysis (e.g., using the law of mass action) does not lead to accurate values for mean sRNA and mRNA levels for a wide range of parameter values. Hence, while the derived results can be obtained using mean-field approaches, the validity of mean-field analysis is questionable for the range of parameters for which the true mean mRNA/sRNA levels differ significantly from the mean-field predictions. On the other hand, the current derivation shows that the results obtained are valid for all parameter values, and are also valid for arbitrary stochastic processes governing mRNA transcription rate. Given that the stochastic model cannot be solved analytically even for the specific case of Poisson processes governing mRNA transcription, it is of interest to note that some exact results can nevertheless be derived for more general models.

The derived results relate quantities of interest, such as mRNA/sRNA lifetimes and parameters quantifying the efficiency of stoichiometric degradation, to mean mRNA and sRNA abundances. Absolute RNA abundances, averaged over a population of cells, can be quantified using techniques such as qRT-PCR (15). In many cases, the quantities of interest are dimensionless, e.g., fold changes in mRNA lifetimes or relative lifetimes of mRNA and sRNA. Our results show that such quantities can be estimated using only relative mRNA/sRNA abundances (normalized to a standard gene say), and these are often easier to obtain than absolute abundances. Furthermore, we note that provided we can measure sRNA production rates, e.g., by using single molecule methods (15), then absolute mRNA lifetimes and transcription rates can be quantified using the derived results. We note that traditional approaches for measuring mRNA lifetimes (e.g., using rifampicin) typically give rise to secondary effects due to global inhibition of transcription that can lead to inaccurate estimates. The results derived suggest an alternative approach that avoids these difficulties and, hence, merits further investigation.

The proposed experimental approaches can be used to address several important questions of current interest, some of which are highlighted in the following. By targeted mutagenesis of specific mRNA sequence elements, the induced fold-change in mRNA lifetime (as well as the corresponding change in the transcription rate k_m) can be determined using the same experimental setup. This is an important feature, given that recent experiments have observed coordination between changes in transcription and changes in mRNA degradation (4). Quantifying the change in mRNA lifetimes induced by mutations to different components of cellular degradation pathways can address such issues as the role of polyadenylation in mRNA decay (16). More generally, given that the sRNA is to be expressed from a controlled (inducible) promoter, there will be a range of different environmental conditions for which the sRNA transcription rate can be taken to be constant, i.e., controlled by the inducer concentration, which is kept constant in the two conditions. In all such cases, our approach can be used to estimate fold-changes in transcription and decay rates. It would also be of interest to design high-throughput experiments for different mRNAs that are regulated by corresponding antisense RNAs, all of which are expressed from identical inducible promoters and thus have the same k_s. The proposed procedure can then be used for genome-wide determination of relative transcription rates and lifetimes of mRNAs. These effective parameters, in turn, serve as critical inputs to systems-level models of cellular processes (17).

In summary, we have proved exact relations for a nonlinear stochastic model of cellular posttranscriptional regulation. The derived results suggest novel procedures for determining quantities of interest such as simultaneous determination of changes in mRNA production rates and mRNA lifetimes. Although the focus was on bacterial mRNAs, the procedure outlined can also be applied to higher organisms and used to explore, systematically, the sequence determinants and processes involved in sRNA-based regulation of mRNA decay.

Appendix

For the network with a single sRNA species regulating a single mRNA species, the proposed experimental setup involves measurements of mRNA and sRNA abundances for three strains—the sRNA deleted (Δ(sRNA)) strain, mRNA deleted (Δ(mRNA)) strain, and the wild-type (WT) strain (both species are present and regulate each other). The regulation model (with constant creation rates for mRNA and sRNA) has been analyzed by several groups (7,9,11) and is summarized in the reaction scheme described in Fig. 1.

Recent experiments that provide evidence for transcriptional bursting (13) point toward the need to go beyond the Poisson process as a model for RNA synthesis. Accordingly, we take both mRNA and sRNA creation events as arbitrary stochastic processes. Degradation of RNA is assumed to be a Poisson process with rate τ_x⁻¹, where τ_x is the mean lifetime of xRNA, x = {m, s}. In the WT strain, mRNA and sRNA undergo a coupled degradation process. We first assume that this process is symmetric with respect to the number of mRNA and sRNA molecules involved, e.g., $M+S\to \varnothing$.

Let us choose a particular realization of the system evolution during time interval t = [0, T]. Correspondingly, we have

$$x\left(T\right)-x\left(0\right)=C_x\left(T\right)-Y\left(T\right)-Z_x\left(T\right),$$ (4)

where x(t) is the number of molecules of the species x = {m, s} at the time t.

In Eq. 4, C_x(t) is the total number of molecules of the species x created during system evolution until time T, and Y(T) is the total number of molecules of either species that is mutually degraded within the time interval [0, T]. Finally, the number of molecules degraded naturally in [0, T] is given by the last term in Eq. 4.

Dividing both sides of Eq. 4 by T and taking a limit T → ∞, we obtain

$$\underset{T\to \mathrm{\infty }}{\lim }\frac{x\left(T\right)-x\left(0\right)}{T}=k_x-\underset{T\to \mathrm{\infty }}{\lim }\frac{Y\left(T\right)}{T}-\underset{T\to \mathrm{\infty }}{\lim }\frac{Z_x\left(T\right)}{T},$$ (5)

where k_x is the mean arrival rate of the species x = {m, s}. The limit on the left-hand side of Eq. 5 vanishes in the case of finite degradation rates τ⁻¹_x (number of molecules at any time is finite.) Note that Y(T) is proportional to T (for large T) and the limit on the right-hand side of Eq. 5 is finite. Finally $Z_x\left(T\right)/T$ is the time average of the number of molecules that are naturally degraded. For large enough T, the time average over a single system evolution will be the same as the corresponding average over an ensemble of systems evolving at steady state. For the ensemble, the average number degraded in the time interval [t, t + dt] is ${\tau }_x^{-1}\langle \tilde{x}\rangle dt$ and correspondingly the time average $Z_x\left(T\right)/T$ is given by ${\tau }_x^{-1}\langle \tilde{x}\rangle$.

Hence, we derive

$$\begin{array}{c}{k}_m-{\tau }_m^{-1}\langle \tilde{m}\rangle -\underset{T\to \mathrm{\infty }}{\lim }\frac{Y\left(T\right)}{T}=0,\\ k_s-{\tau }_s^{-1}\langle \tilde{s}\rangle -\underset{T\to \mathrm{\infty }}{\lim }\frac{Y\left(T\right)}{T}=0,\end{array}$$ (6)

which immediately yields the expression

$$k_m-{\tau }_m^{-1}\langle \tilde{m}\rangle =k_s-{\tau }_s^{-1}\langle \tilde{s}\rangle .$$ (7)

In the unregulated case Y(T) ≡ 0 for any T, as one of the RNA species is deleted and there is no coupled degradation. In this situation one gets

$$k_m-{\tau }_m^{-1}\langle m\rangle =0,$$

$$k_s-{\tau }_s^{-1}\langle s\rangle =0,$$ (8)

where 〈x〉, x = {m, s} are the average number of molecules during unregulated system evolution. Combining the set of equations above with Eq. 7, we derive the results from Eqs. 1 and 2. We note that the derived results are valid even if the binding of mRNA and sRNA is taken to be reversible and the lifetime of the mRNA-sRNA complex is finite. Finally, the time average can be replaced by the ensemble average in the steady state.

We have validated the derived results using stochastic simulations based on the Gillespie algorithm (18). Production of RNA molecules was taken to occur in transcriptional bursts (13), i.e., each burst corresponds to the arrival of a random number of RNAs drawn from a geometric distribution, conditional on the production of at least one RNA molecule (19). The waiting-time between bursts was a random variable drawn from exponential or Gamma-distributions. As expected, the results from the simulations were in excellent agreement with the derived analytical results.

The extension of the above results for nonstoichiometric degradation of small RNAs is straightforward. If the probability of small RNA degradation (when the complex is degraded) is given by p, then if Y(T) is the number of mRNA degraded due to interaction with small RNAs, the corresponding number of sRNAs degraded is given by pY(T) (using the law of large numbers). Correspondingly, we obtain the equation

$$p\left(k_m-{\tau }_m^{-1}\langle \tilde{m}\rangle \right)=k_s-{\tau }_s^{-1}\langle \tilde{s}\rangle ,$$ (9)

from which the results in the main text are readily derived. The derived relations have been validated for different p values using stochastic simulations with the Gillespie algorithm, as described above.