Sensitivity of Prestin-Based Membrane Motor to Membrane Thickness

Abstract

Prestin is the membrane protein in outer hair cells that harnesses electrical energy by changing its membrane area in response to changes in the membrane potential. To examine the effect of membrane thickness on this protein, phosphatidylcholine (PC) with various acyl-chain lengths were incorporated into the plasma membrane by using γ-cyclodextrin. Incorporation of short chain PCs increased the linear capacitance and positively shifted the voltage dependence of prestin, up to 120 mV, in cultured cells. PCs with long acyl chains had the opposite effects. Because the linear capacitance is inversely related to the membrane thickness, these voltage shifts are attributable to membrane thickness. The corresponding voltage shifts of electromotility were observed in outer hair cells. These results demonstrate that electromotility is extremely sensitive to the thickness of the plasma membrane, presumably involving hydrophobic mismatch. These observations indicate that the extended state of the motor molecule, which is associated with the elongation of outer hair cells, has a conformation with a shorter hydrophobic height in the lipid bilayer.

Introduction

Outer hair cells (OHCs), a class of mechanoreceptor cells in the cochlea, are critical for the sensitivity and frequency-selectivity of the mammalian ear (1). This property must depend on active processes in OHCs, whether in hair bundles (2,3), in their cell bodies (4), or in both. Electromotility in the cell body is based on a membrane protein prestin (SLC26A5), which is a member of the SLC26 solute transporter family (5). The significance of prestin for ear function has been demonstrated by the hearing loss of transgenic mice with mutated prestin (6).

In an isolated OHC, electromotility changes the cylindrical cell's length. Hyperpolarization induces elongation and depolarization induces shortening. The amplitude can reach 4–5% of the total length (7). These mechanical changes are associated with charge transfer across the membrane, which gives rise to nonlinear membrane capacitance with bell-shaped voltage dependence (8). Mechanical changes and electric changes are coupled, satisfying the reciprocal relationship (9), similar to piezoelectricity. These observations can be successfully described by a membrane motor model (or area-motor model). These observations assume that electromotility is based on a piezoelectric membrane motor that undergoes conformational changes between two conformations which differ in membrane charge and in membrane area (10). The existence of conformational changes in which area change and charge transfer is coupled is confirmed by an observation that a membrane area constraint resulted in a drastic reduction in nonlinear capacitance (11).

Such conformational changes could include the thickness of the protein in the membrane. If we assume that protein volume is conserved, an area increase should be associated in a reduction in the thickness. Because prestin's putative structure, which is determined by its amino acid sequence, has very small extracellular domains (12,13), the height of its hydrophobic surface must be dominated by its putative 10 transmembrane helices. The thickness of the protein's conformation is, therefore, well correlated with the height of its hydrophobic domain, which affects hydrophobic mismatch with the lipid bilayer. Because hydrophobic mismatch can involve large energy, bilayer thickness should significantly affect prestin conformation.

To investigate the conformational changes in the membrane motor, here we examine the effect of membrane thickness on electromotility by incorporating electrical neutral phosphatidylcholines with various acyl-chain lengths. We use carboxyethyl-γ-cyclodextrin (CE-γ-CD) as the vehicle. Membrane thickness can be monitored by the regular (or linear) voltage-independent component of the membrane capacitance and its effect on the motor can be monitored by nonlinear capacitance (NLC).

Materials and Methods

Media

Our standard external medium contained 135 mM NaCl, 4 mM KCl, 2 mM MgCl₂, 1.5 mM CaCl₂, and 5 mM Na-HEPES with pH adjusted to 7.4. The osmolarity was adjusted to 300 mOsm/kg by glucose.

The external blocking medium that we used consisted of 145 mM NaCl, 5 mM CsCl, 2 mM MgCl₂, 1 mM CaCl₂, 2 mM CoCl₂, 10 mM Cs-HEPES, and ∼10 mM glucose, which was used to adjust the osmolarity to 300 mOsm/kg. pH was adjusted to 7.4.

The intracellular blocking medium was made of 140 mM CsCl, 2 mM CaCl₂, 2 mM MgCl₂, 5 mM EGTA, and 10 mM Cs-HEPES, pH 7.4.

Outer hair cells

Isolated outer hair cells were prepared in a manner described earlier (9). Briefly, bullas were harvested from guinea pigs in accordance with our animal protocol (1061-02 NINDS/NIDCD). The organ of Corti was dissociated from opened cochleas by teasing with a fine needle under a dissection microscope. OHCs were isolated by gently triturating these strips for three times with a plastic pipette. Isolated OHCs were placed in a chamber mounted on an inverted microscope. The length of the cells used for patch-clamp recoding ranged between 40 and 75 μm.

Cultured cells

Human embryonic kidney (HEK) 293T cells (ATCC, Manassas, VA) were cultured in Dulbecco's Modified Eagle Medium (Invitrogen, Grand Island, NY) with 10% fetal bovine serum (Atlanta Biologicals, Lawrenceville, GA), 100 units/mL penicillin, and 100 μg/mL streptomycin (Invitrogen).

When HEK cells were ∼80% confluent, these cells were transfected with prestin-encoding plasmid pcDNA3.1 and GFP (pEGFP-N1; Bioscience Clontech, San Jose, CA) using Fugene HD (Roche Applied Science, Indianapolis, IN). The plasmid was a gift of Dr. L. Madison of Northwestern University. The ratio of Fugene HD/prestin/GFP was 5:1:1. After transfection, HEK cells were incubated in Dulbecco's Modified Eagle Medium containing 10% fetal bovine serum. The experiments were performed on those cells between 36 and 48 h after transfection. Those cells were washed with phosphate-buffered saline briefly before introduced to the experimental medium.

Incorporation of phosphatidylcholines

Carboxyethyl-γ-cyclodextrin (CE-γ-CD) was purchased from Cyclodextrin Technologies Development (High Springs, FL). A stock solution of 30 mM CE-γ-CD was prepared by dissolving it in the external blocking medium and the pH was adjusted to 7.4. Phosphatidylcholines were purchased from Avanti Polar Lipids (Alabaster, AL). Before loading CE-γ-CD with PC, 0.1 μM of each PC was taken up in a vial and dissolved with 5 mL chloroform. The chloroform was then completely evaporated under a gentle N₂ stream. The resulting PC film in each vial was suspended with 1 mL solution of 5 mM CE-γ-CD diluted with the blocking external medium and then sonicated in a ultrasonic chamber (model 1510; Branson, Danbury, CT) with water bath until a clear solution was obtained. The temperature of the bath was ∼50°C for PC with longer chains (18–24) and room temperature for PC with shorter acyl chains (10–16). The duration was <10 min at room temperature with short-chain PCs and was up to 30 min for PCs with long chains.

These 5 mM CE-γ-CD solutions loaded with 0.1 mM PC were perfused from a perfusion pipette to either HEK cells or OHCs in the experimental chamber. Specifically for recording the time course of capacitance changes due to PC 12:0 incorporation in prestin-transfected cells, a perfusion medium with half of the normal one was also used.

Electrophysiological recording

Electrophysiological recording was performed using an inverted microscope (Diaphot 300; Nikon, Tokyo, Japan) in combination with a micromanipulator (model MP225; Sutter Instruments, Novato, CA), The patch pipette was mounted on the micromanipulator associated with the head stage of the patch amplifier (Axopatch 200B; Axon Instruments, Foster City, CA). Voltage waveforms were generated with an ITC-16 interface (Instrutech, Fort Washington, NY) in combination with a Macintosh computer running the IGOR program (WaveMetrics, Lake Oswego, OR) with Pulse Control XOPs, data acquisition modules from Instrutech. The patch pipettes were made from borosilicate capillaries (OD 1.5 mm, ID 0.86 mm; Sutter Instruments) with a pipette puller (Model P-97; Sutter Instruments) and used without fire-polishing.

To facilitate membrane capacitance measurement, the channel blocking media described earlier were used for experiments. The pipette resistance was between 2.5 and 4.5 MΩ in the bath. In the whole-cell configuration, the access resistance R_a was between 5 and 8 MΩ. The membrane resistance R_m was somewhat dependent on the membrane potential and was between 200 and 800 MΩ. The room temperature was 23°C.

Membrane capacitance and length changes

The membrane capacitance was determined in the whole-cell configuration from the capacitive current elicited by applying staircase waveforms with 5 mV steps (14). The waveforms used were either with a narrower voltage range between −100 mV and 50 mV or a wider range between −150 mV and +100 mV. For the narrower voltage range, the dependence of membrane capacitance C_m of outer hair cells on the membrane potential V is reasonably described by a two-component equation (8,10,15,16),

$$C_{\text{m}}\left(V\right)=C_{\text{lin}}+\frac{N{q}^2}{k_{\text{B}}T}\times \frac{B\left(V\right)}{{\left[1+B\left(V\right)\right]}^2},$$ (1)

with

$$B\left(V\right)=\exp \left[q\left(V-V_{\text{pk}}\right)/k_{\text{B}}T\right]\text{.}$$ (2)

This equation assumes that the cell has N motile units that have two conformational states, which differ in charge as well as in membrane area. Transitions between these states involve transfer of q electric charge across the membrane (10). Here C_lin is the linear capacitance, V_pk the voltage of the peak capacitance, k_B Boltzmann's constant, and T the temperature.

The image of the cell during the experiment was captured with a video camera, recorded on a DVD disk, and then converted to a movie file on a computer. The time course of cell length was determined from the image using the National Institutes of Health Image program with a macro. The equation for cell length that corresponds to Eq. 1 is (7,8,10)

$$L\left(V\right)=L_0+\frac{\Delta L}{1+B\left(V\right)},$$ (3)

where L₀ is the asymptote for large positive potential and ΔL is the amplitude.

Capacitance data taken from the wider voltage range show that the membrane capacitance is indeed asymmetric, with respect to the peak potential. The negative side of the peak is higher than the positive side of the potential (17). The membrane capacitance can be expressed by

$$C_{\text{m}}\left(V\right)=C_0+N\left[\frac{q^2}{k_{\text{B}}T}\times \frac{B_1\left(V\right)}{{\left(1+B_1\left(V\right)\right)}^2}+\frac{\delta c{B}_1\left(V\right)}{1+B_1\left(V\right)}\right],$$ (4)

where C₀ is the membrane capacitance at an infinitely negative potential, δc is a constant, which is the capacitance difference in the two conformational states of the motor, and B₁(V) = exp [q(V − V₁)/k_BT] with a constant V₁. The potential V₁ is related to the peak potential V_pk by

$$V_{\text{pk}}=V_1-\ln \frac{q^2-\delta c{k}_{\text{B}}T}{q^2+\delta c{k}_{\text{B}}T}\text{.}$$ (5)

Results

Voltage shifts in the motile response of OHCs

The bell-shaped voltage dependence of OHCs membrane capacitance showed voltage shifts on perfusion of CE-γ-CD loaded with phosphatidylcholines (PCs). If the PCs loaded have short acyl chains with <12 carbons, PC10:0 or PC11:0, the peak of NLC shifted in positive direction very rapidly. However, the shift was accompanied by a sharp decline in the membrane resistance, leading to membrane breakdown within 1 min of perfusion. With PC12:0, we could follow the time course of the voltage shift until saturation (Fig. 1 A). The saturating shift was ∼120 mV and the time constant was ∼80 s (Fig. 1 C). The peak height and the steepness of the voltage dependence were not significantly affected. The length changes had corresponding voltage shifts (Fig. 1 B) without a significant change in the amplitude.

Figure 1.

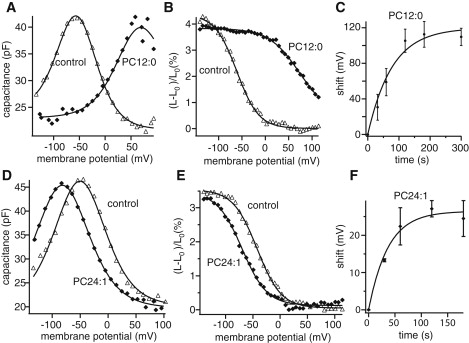
Effect of phosphatidylcholines on outer hair cells. PC12:0: (A) the membrane capacitance. Control (▵) and PC12:0 (♦). Equation 1 is used for curve fit. Parameter values are given in Table 1. (B) Length changes. Control (▵) and PC12:0 (♦). Equation 3 is used for curve fit. Parameter values for the fit are given in Table 1. (C) Time course of voltage shift with PC12:0. The time constant is (76.2 ± 16.9) s. The saturating shift by PC12:0 is (121.0 ± 10.1) mV. PC24:1: (D) Voltage-dependent capacitance. Control (▵) and PC24:1 (♦). Equation 1 is used for curve fit. Parameter values for the fit are given in Table 1. (E) Length changes. Control (▵) and 100 μM PC24:1 (♦). Equation 3 is used for curve fit. Parameter values for the fit are given in Table 1. (F) Time course of voltage shift with PC24:1. The time constant is (36.9 ± 7.1) s. The saturating shift is (26.5 ± 1.5) mV. Error bars show standard deviations (SDs). Holding potential is −75 mV.

The potency of PCs to induce positive shifts of NLC decreased with increasing hydrocarbon chain length. PCs with hydrocarbon chains longer than 22 induced positive shifts. Perfusion of PC24:1 induced a positive shift with a time constant of ∼40s. The saturating level of the shift was ∼27 mV (Fig. 1 F). Again, the peak height and the steepness of the voltage dependence were virtually unaffected (Fig. 1 D). The length changes had similar voltage shifts without accompanying amplitude changes (Fig. 1 E). See Table 1 for parameter values.

Table 1.

Parameter values (mean ± SD) for the fit in Fig. 1

	q (e)	Clin (pF)	Nq (pC)	Vpk (mV)
Control (A)	0.91 ± 0.03	20.7 ± 0.4	2.4 ± 0.1	−59.6 ± 0.8
PC12:0 (A)	0.97 ± 0.08	22.5 ± 0.8	2.0 ± 0.2	66.9 ± 2.9
Control (D)	0.84 ± 0.03	20.2 ± 0.5	3.2 ± 0.2	−50.4 ± 0.8
PC24:1 (D)	0.81 ± 0.01	19.8 ± 0.2	3.3 ± 0.1	−81.9 ± 0.5
	q (e)	(L − L0)/L0 (%)		Vpk (mV)
Control (B)	1.10 ± 0.04	4.3 ± 0.1		−60.9 ± 1.1
PC12:0 (B)	0.87 ± 0.04	3.9 ± 0.3		73.6 ± 4.3
Control (E)	1.18 ± 0.04	3.5 ± 0.04		−42.2 ± 0.8
PC24:1 (E)	1.13 ± 0.05	3.3 ± 0.07		−69.7 ± 1.4

The saturating voltage shifts showed correlation with the hydrocarbon chain length of phosphatidylcholines incorporated (see Fig. 3 B).

Figure 3.

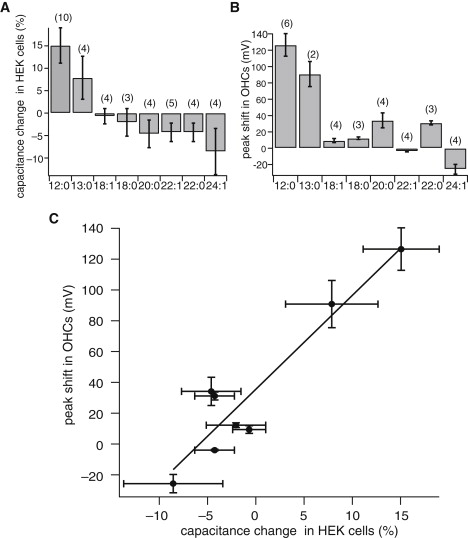
Changes in the membrane capacitance by the incorporation of phosphatidylcholines. (A) Changes in the membrane capacitance of HEK cells. (B) Peak shifts in the nonlinear capacitance of OHCs. In panels A and B, each phosphatidylcholine is identified with a set of two numbers: (Acyl chain length):(number of unsaturated bonds). The numbers in the parentheses indicate the number of the cells from which the data are collected. Error bars show SDs. The holding potential −75 mV. (C) Correlation between capacitance peak shifts of OHCs and changes in the capacitance in HEK cells. The best fit slope (solid line) is (6.1 ± 0.9) mV percent change of linear capacitance.

Linear capacitance of OHCs

Initially we assumed that the membrane capacitance of OHCs consists of two components—linear and nonlinear (Eq. 1)—and tried to determine the linear capacitance using the data points between −100 mV and 50 mV. Changes in the linear capacitance during PC12:0 incorporation determined with this method was up to ∼5 pF, and was proportional to the peak shift of NLC. Thus, a positive shift of NLC appeared to be correlated with an increase in the linear capacitance. This correlation, however, could be attributed to a systematic error resulting from asymmetry of the membrane capacitance around its peak because the negative potential asymptote is higher than the one on the positive side (17).

To address this issue, data points were obtained from a wider voltage range between −150 and 100 mV (Fig. 2), and analyzed with a three-component equation (Eq. 4), which has an additional asymmetric Boltzmann term. This equation fits the data well and revealed the asymmetry term of ∼4 pF, the major part of the ∼5 pF shift in the apparent linear capacitance obtained earlier. Changes in the true linear capacitance was <1 pF, barely exceeding the uncertainties of the curve fit (Fig. 2).

Figure 2.

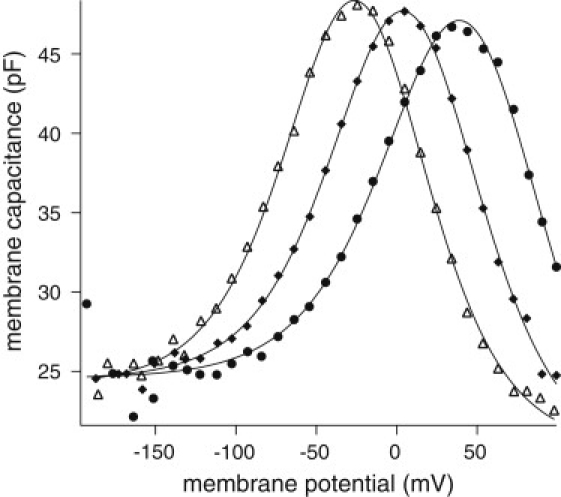
Peak shift and the linear capacitance of an OHC. Eq. 4 is used for curve fit. Parameter values (mean ± SD) for the fits. (▵) q = (0.86 ± 0.02)e, C₀ = (24.1 ± 0.4) pF, Nδc = (3.9 ± 0.4) pF, Nq = (3.13 ± 0.08) pC, and V₁ = (−24.1 ± 0.7) mV; (♦) q = (0.83 ± 0.02)e, C₀ = (24.5 ± 0.6) pF, Nδc = (5.3 ± 0.6) pF, Nq = (3.20 ± 0.08) pC, and V₁ = (5.3 ± 0.6) mV; and (•) q = (0.93 ± 0.06)e, C₀ = (24.6 ± 0.6) pF, Nδc = (9.2 ± 5.8) pF, Nq = (3.6 ± 0.6) pC, and V₁ = (44.5 ± 5.2) mV.

Capacitance of cultured cells

To test the effect that incorporating PCs into the plasma membrane has upon membrane thickness, human embryonic kidney (HEK) 293 cells were used. In contrast to OHCs, the membrane capacitance of HEK cells, which did not have a voltage-dependent component, showed significant changes in response to the perfusion of phosphatidylcholine-loaded CE-γ-CD. Those PCs with short acyl chains had the effect of increasing the linear capacitance and those with long chains decreased the capacitance. The time course of these changes are similar to voltage shifts in OHCs with time constants of ∼1 min. Saturating changes for PC12:0 are an increase of (15 ± 5)% and for PC24:1 a decrease of (10 ± 6)% (Fig. 3 A). These changes in the membrane capacitance were furthermore well correlated with voltage shifts in OHCs (Fig. 3 C).

Capacitance of prestin-transfected cells

To examine the relationship between the regular capacitance and the voltage shift of the prestin-based membrane motor, we examined HEK cells that were transfected with a plasmid that encoded gerbil prestin. On perfusion of CE-γ-CD loaded with PC, the membrane capacitance of these cells showed changes dependent on the acyl chain length of the PC. PCs with short acyl chains with 12 carbons (PC12:0) increased the linear capacitance as in nontransfected HEK cells, and significantly shifted nonlinear capacitance, as in OHCs (Fig. 4 A). See Table 2 for parameter values.

Figure 4.

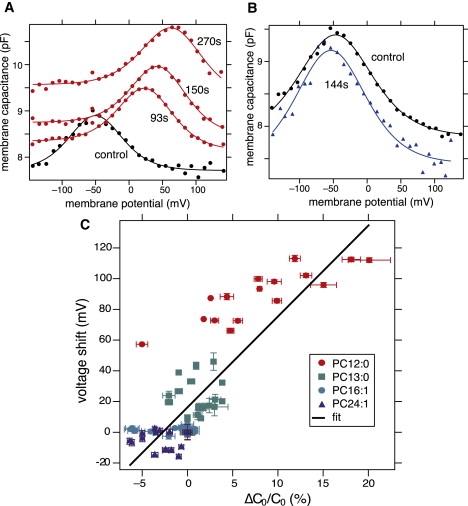
Membrane capacitance of prestin-transfected HEK cells. (A) An example of time course during PC12:0 perfusion. Control (black) and 93 s, 150 s, and 270 s from the onset of perfusion (red), from the bottom to the top. CE-γ-CD concentration 2.5 mM. Parameter values are given in Table 2. (B) PC24:1, Control (black), and 144 s from the onset of perfusion (red). Parameter values for two-component fit (Eq. 1) are given in Table 2. (C) Relationship between voltage shifts and change in the linear capacitance. Data points are taken while PCs were incorporated into the cell membrane. The best fit slope (solid line) is (5.9 ± 0.5) mV percent change of the linear capacitance.

Table 2.

Parameter values (mean ± SD) for the fit in Fig. 4, A and B

	q (e)	C0 (pF)	Nδc (pF)	Nq (fC)	V1 (mV)
Control (A)	0.93 ± 0.06	7.53 ± 0.09	0.09 ± 0.08	136 ± 12	−52.4 ± 2.4
93 s (A)	0.95 ± 0.03	8.14 ± 0.04	0.20 ± 0.04	136 ± 6	24.7 ± 1.2
150 s (A)	0.93 ± 0.04	8.46 ± 0.07	0.29 ± 0.06	151 ± 9	45.0 ± 1.5
270 s (A)	0.86 ± 0.06	9.26 ± 0.18	0.31 ± 0.02	167 ± 2	65.3 ± 3.4
	q (e)	C0 (pF)	Vpk (mV)	Nq (fC)
Control (B)	0.71 ± 0.02	7.85 ± 0.03	−46.9 ± 0.9	228 ± 10
144 s (B)	0.75 ± 0.05	7.42 ± 0.07	−53.6 ± 2.1	241 ± 23

The increase in the linear capacitance and the voltage shift of nonlinear capacitance during PC12:0 incorporation into the cell membrane were correlated (Fig. 3 C). PC13:0 is less potent in increasing the linear capacitance and voltage shifts (Fig. 4 C). PC24:1 with longer acyl chain had the opposite effects of PCs with short ones, although the effects were not as large (Fig. 4 B). PC16:1 did not induce significant voltage shifts. The correlation between changes in the capacitance and voltage shifts is (5.9 ± 0.5) mV (Fig. 4 C), consistent with the value (6.1 ± 0.9) mV for OHCs (Fig. 3 C).

Asymmetry of NLC, which was observed in OHC, was also present in prestin-transfected cells. The ratio of the magnitude Nδc of the asymmetry term to the total charge Nq (see Eq. 4) was (1.5 ± 0.2) F/C for transfected cells, similar to the value (1.6 ± 0.2) F/C for OHCs, despite the ∼10-fold difference in total charge Nq in these two preparations. The agreement of the ratio suggests that the asymmetry term stems from prestin, presumably reflecting the difference in prestin's intrinsic capacitance in its two states.

Discussion

Linear capacitance and membrane thickness

What happens to the plasma membrane when the cells are perfused with CE-γ-CD loaded with PCs?

Given the high affinity of CE-γ-CD to phospholipids, it is likely that phospholipids are exchanged between the plasma membrane and CE-γ-CD. Indeed, perfusion of unloaded CE-γ-CD results in breakage of the cells within 20 s. Our experimental data show that the changes in the linear capacitance of the cell depend systematically on the length of the acyl chains of the PC, which is loaded in CE-γ-CD (Fig. 3 A).

Remember that the linear membrane capacitance C_lin of a lipid bilayer is given by (18)

$$C_{\text{lin}}=\frac{\epsilon A}{d}$$ (6)

with the dielectric constant ɛ, the membrane area A, and the membrane thickness d. Equation 6 shows that our data are consistent with the interpretation that the plasma membrane becomes thinner when the cell is perfused with CE-γ-CD loaded with PCs with short acyl chains (PC12:0 and PC13:0) and thicker when the acyl chains in the PC are longer (PC20:0, PC22:1, PC22:0, and PC24:1).

It is highly unlikely that the perfusion changes the membrane area or the dielectric constant because the PCs with medium lengths acyl chains (PC18:0 and PC18:1) do not significantly affect the linear capacitance even though the incorporation of these PCs should incur the least mechanical stress and thus should be energetically favorable. If these factors were significant, the PCs with medium-length acyl chains would have increased the linear capacitance. If the membrane area or the dielectric constant were significant, we could have detected significant capacitance changes with PCs with this range of acyl chain lengths, the incorporation of which would be energetically most favorable.

For these reasons, we interpret that the changes in the linear capacitance reflects changes in the membrane thickness. Therefore, we associate the observed shifts in the voltage dependence of nonlinear capacitance of prestin in HEK cells to changes in the thickness of the plasma membrane.

It has been previously suspected that similarly large shifts up to ∼100 mV associated with addition or removal of cholesterol could be due to membrane thickness (19). However, the linear capacitance was not monitored in those experiments and significance of direct interaction between cholesterol and prestin could not be ruled out (19). In addition, the effect of cholesterol on bilayer thickness has not been shown for biological membranes (20).

Linear capacitance of OHCs

Changes in the linear capacitance of OHCs are relatively small compared with that of cultured cells. The likely reason for the difference is the high density of membrane proteins in their lateral plasma membrane, which dominates the membrane capacitance (20). An estimate based on electron microscopic study indicates one-third of the lateral membrane is made of membrane proteins (21). The density of the motor molecule in the plasma membrane of OHCs obtained from nonlinear capacitance is ∼10⁴/μm² (22) (Fig. 2, for example, gives a value 1.2 × 10⁴, based on the values 3.1 pC/(0.86e) for the number N of motor molecule in the cylindrical plasma membrane 60 μm long and 10 μm in diameter). Given the molecular mass of 80 kDa for prestin (5), the membrane area is ∼30 nm² if the molecule is ∼4 nm thick. Thus the area of the membrane occupied by the motor protein is ∼30%, similar to the value obtained by the electron microscopic study. This value suggest that changes in the linear capacitance must be relatively small because the thickness of the interfacial area between the proteins and the lipid bilayer could be affected by the motor protein (20).

Nonetheless, shifts in the voltage dependence of nonlinear capacitance in OHCs is as large as those in prestin-transfected cells. The relationship between the voltage dependence of electromotility in OHCs and changes in the linear membrane capacitance in HEK cells is ∼6 mV shift per 1% change in capacitance, virtually identical to the ratio of voltage shift to linear capacitance change for prestin-transfected HEK cells. This observation appears to be consistent with a report that large interaction between lipid bilayer and membrane proteins has a significant effect upon membrane thickness (20).

Implications on prestin's conformations

Because the changes in the linear capacitance can be explained by changes in bilayer thickness, the observed voltage shifts of nonlinear capacitance are associated with changes in membrane thickness. Perfusion of loaded CE-γ-CD could induce lipid asymmetry and possibly bend the membrane. However, the effect of bending is always positive and up to ∼20 mV (23), not compatible with the present data. Because changes in the thickness of lipid bilayer change hydrophobic mismatch in membrane proteins (24), our observations indicate that prestin's conformation with larger membrane area, which is dominant in the most negative range of the membrane potential, has a thinner hydrophobic domain than another conformation, which is dominant in the most positive range of the membrane potential. This observation would impose a constraint in molecular models of prestin (12,13).

Our observations on voltage shifts and changes in the linear capacitance can be related to asymmetry of the membrane capacitance determined with Eq. 4. Asymmetry of the membrane capacitance could be expected from electrostriction (25,26), unrelated to prestin. However, this effect has a quadratic dependence on the voltage. For HEK cells, its minimum is at ∼+80 mV, presumably because of its surface charge asymmetry (25), and it is higher at −150 mV than +100 mV by 0.5% (26). The expected value of this effect is thus 0.04 pF for a HEK cell with 8 pF capacitance, smaller than ∼0.2 pF of the observed asymmetry(Table 2). Indeed, we did not observe electrostriction effect in our nontransfected HEK cells with 0.05 pF of accuracy. The capacitance asymmetry in OHCs is much larger. For these reasons, our capacitance data are consistent with Eq. 4.

The asymmetry term Nδc (the last term in Eq. 4) is proportional to motor charge Nq. This indicates that the motor molecule in the conformation with a larger membrane area has a larger contribution to the membrane capacitance than another conformation with a smaller area. If we assume the standard value 1 μF/cm² for specific capacitance (27) and a membrane area of 30 nm² for the molecule, the membrane capacitance expected is 0.3 aF (or 0.3 × 10⁻¹⁸ F). Estimates for area changes of the motor molecule are between 2 and 4 nm² (11,28). If we use the 4 nm² value, the change is ∼13% of the molecule's surface area. The corresponding change in the thickness would be 13%, assuming constant volume. Thus, the expected capacitance change would be up to ∼0.1 aF. This value is somewhat less than previously reported values between 0.11 and 0.13 aF/motor (17). The present experiment provides the value of 1.5 F/C for δc/q. Together with q = 0.9 e, this value leads to a value 0.2 aF for the difference in the capacitance in the two states, approximately twice as large as the prediction. The difference could be attributed to larger membrane capacitance of the molecule, change in the dielectric constant associated with conformational changes, or both. The first possibility is based on an expectation that the dielectric constant of proteins is somewhat higher than the lipid bilayer (29). The rationale for the second is that large conformational changes in a membrane protein can accompany changes in the dielectric constant.

As a means of applying mechanical stress to prestin, PC incorporation appears to be very effective. The observed voltage shifts up to 120 mV compared very favorably to shifts up to 30 mV elicited by increasing membrane tension (28).

Comparison with other membrane proteins

Activities of various membrane proteins show membrane thickness dependence (30,31). While many of those proteins show biphasic dependence of their activities on bilayer thickness, some of them show monophasic dependence similar to prestin. Among those membrane proteins, the large mechanosensitive channel from Escherichia coli (MscL) and the BK channels are of particular interest because their free energy associated with bilayer thickness has been evaluated.

The threshold of MscL opening elevates with thickness of the lipid bilayer in which it is reconstituted (32). This observation is explained as the result of hydrophobic mismatch. Specifically, thicker lipid bilayer favors the closed state because the closed state has higher profile in the lipid bilayer than the open state, in which transmembrane helices are more tilted. The energy difference estimated is up to ∼20 k_BT (32), ∼5 times larger than the value up to ∼4 k_BT (or ∼110 meV, corresponding to the work of moving 0.9 electronic charge across an electric potential difference of 120 mV) for prestin. It is interesting to note that voltage shifts of prestin by membrane-bending chemicals is up to 20 mV (23), not as sensitive to thickness changes, unlike MscL (32,33). Presumably, conformation-dependent changes in the bending modulus in prestin may not be as significant as in this channel.

Shifts in the voltage dependence due to membrane thickness reported for the BK channel is biphasic unlike prestin and the magnitude is up to 30 mV (34,35). If we use the value for the gating charge of between 2.6 and 4.4 e (36,37), the energy involved is between 80 and 130 eV (or between 3 and 5 k_BT), similar to prestin. The monophasic voltage shifts of prestin is presumably based on simpler conformational transitions that prestin undergoes.

Conclusions

The membrane motor of outer hair cells based on prestin is sensitive to bilayer thickness. A reduction in bilayer thickness results in a positive shift in its membrane potential dependence up to 120 mV and an increase in membrane thickness results in a negative shift up to 10 mV. These observations indicate that the depth of prestin is associated with conformational changes in the membrane motor. Specifically the conformation with larger membrane area has a narrower band of hydrophobic surface that makes contact with lipid bilayer.