A Modeling Approach to the Self-Assembly of the Golgi Apparatus

Abstract

The dynamic compartmentalization of eukaryotic cells is a fascinating phenomenon that is not yet understood. A prominent example of this challenge is the Golgi apparatus, the central hub for protein sorting and lipid metabolism in the secretory pathway. Despite major advances in elucidating its molecular biology, the fundamental question of how the morphogenesis of this organelle is organized on a system level has remained elusive. Here, we have formulated a coarse-grained computational model that captures key features of the dynamic morphogenesis of a Golgi apparatus. In particular, our model relates the experimentally observed Golgi phenotypes, the typical turnover times, and the size and number of cisternae to three basic, experimentally accessible quantities: the rates for material influx from the endoplasmic reticulum, and the anterograde and retrograde transport rates. Based on these results, we propose which molecular factors should be mutated to alter the organelle's phenotype and dynamics.

Introduction

A hallmark of eukaryotic cells is their compartmentalization by membrane-engulfed organelles (1). Understanding how these organelles form, self-organize, and maintain their identity while rapidly exchanging most of their protein contents is a major challenge. The Golgi apparatus (GA), the major hub for protein sorting and lipid metabolism in the secretory pathway (1), is a prominent example for such a highly dynamic organelle. In interphase, the GA typically assumes the form of a stack of chemically distinct, flattened membrane cisternae that are laterally connected to form a larger, juxtanuclear Golgi ribbon (2). Before mitosis, the Golgi stack/ribbon disintegrates at least in part, and it reassembles with a remarkable precision after cytokinesis (2,3). Although the size and number of cisternae may vary between individual cells and cell types, the major feature of the GA, its stack structure, is widely conserved in eukaryotes. Prominent exceptions to this rule are the phenotypes found in the yeast Saccharomyces cerevisiae and in the fruit fly Drosophila melanogaster. While the former shows a distribution of individual cisternae dispersed in the cytoplasm (4), the latter shows (during certain stages of development) a collection of cisternae that are arranged like a bunch of grapes (5). Despite major advances in elucidating the molecular players that participate in the morphogenesis and biogenesis of the GA, the reason for the widely observed robust stack formation and alternative Golgi phenotypes has remained elusive.

The current view of how the GA is established and maintained is intimately intertwined with general transport phenomena in the secretory pathway (6). After clearing the quality control in the ER, nascent cargo proteins and glycosylation enzymes are packaged into COPII vesicles at distinct ER exit sites (ERES) (7). After pinch-off, these COPII vesicles uncoat and fuse to larger transport entities (vesicular tubular clusters, VTCs) that deliver their cargo to the cis face of the Golgi stack (8,9). Upon arrival, cargo proteins are sequentially modified by Golgi-resident glycosylation enzymes that adopt overlapping gradientlike distributions across the stack of cisternae (10). While intra-Golgi transport and retrograde shuttling of proteins to the ER is mediated by COPI proteins (6), properly modified cargo proteins leave the GA at the trans face via clathrin-coated vesicles (11). Fusion of any of these transport intermediates with an acceptor membrane is mediated by specialized triples of SNARE proteins (12). In addition, Golgi matrix proteins that tether adjacent cisternae to each other have been found (13,14), as well as channels and pumps that are responsible for the distinct intra-cisternal milieu (15). Blocking the anterograde delivery of membranes and proteins, e.g., by prohibiting the emergence of COPII vesicles, leads to a disassembly of the GA (16) by COPI-dependent and COPI-independent retrograde pathways (17). Hence, the GA can only exist if anterograde and retrograde transport are properly balanced.

Despite all of these detailed insights on the molecular level, it has remained unclear how proteins and lipids act in concert to achieve the highly dynamic formation of a GA with its different phenotypes. In particular, it has remained elusive so far why/how a GA forms de novo (e.g., after mitosis), and how the GA dynamically attains and maintains its stack structure or the alternative phenotypes in yeast and flies.

Zooming out from the molecular and biochemical details, we propose here a computational model for the morphogenesis of the GA that is capable of reproducing the experimentally observed Golgi phenotypes with physiological dynamics. Although previous modeling approaches have addressed generic aspects of protein sorting in a given stack of cisternae (18–20), we have focused here on the formation of the spatial structure itself. Our model for the morphogenesis of a Golgi apparatus considers aspects of protein sorting only in minor detail whereas we gain a fundamental understanding of the conditions under which a stack of cisternae can form de novo and remain stable under stationary flux. Major control parameters are the influx and outflux rates of membranes and proteins, and we highlight the parameter regimes in which, for example, a stack structure can form. Based on these data, we predict which process is responsible for the emergence of phenotypes, and we propose which changes in molecular players may be used to test our predictions experimentally.

Model Definition

Philosophy of the model

Before giving details of our model for the morphogenesis of a Golgi apparatus, we would briefly like to sketch its gross structure and main features. The length and timescales involved in Golgi morphogenesis (from molecular diffusion on the scale of 1 μs and 10 nm to shape changes on the scale of 15 min and 100 μm) clearly dictate that a detailed model, e.g., in the spirit of molecular dynamics, is computationally not feasible. Therefore, a coarse-graining has to be done that neglects detailed phenomena on fine scales while still allowing the simulation of the large-scale events. This also requires that molecular players like COPI proteins, lipids, and accessory regulators cannot be modeled explicitly but, instead, enter the model only in terms of effective rates for certain events. Similar approaches are used when formulating mean-field models for biological phenomena, e.g., in the context of timing cell division (21). Dealing with membranes, i.e., two-dimensional objects embedded in three-dimensional space, a mean-field approach can be very demanding because the local geometry of membranes (curvature, etc.) and topological changes (e.g., budding and fission) have to be considered. Simulations of discrete units, i.e., a particle-based approach, lends itself here as the more appropriate tool for modeling. By applying this rationale, we have based our model for Golgi morphogenesis on discrete particles that have roughly the size of larger transport intermediates, e.g., VTCs. These particles enter a cubic simulation box at a window that mimics an ER exit site (ERES). Thus, we concentrate on the formation of a small Golgi compartment that is driven by a diffusive transport of particles rather than a motion that is driven by molecular motors. Our simulation box hence resembles a scenario that occurs, for example, in the yeast Pichia pastoris or in mammalian cells with disrupted microtubules (16).

Particles are injected into the simulation box at the ERES region with rate J_in. Within the simulation box, particles can diffuse, reversibly tether to, and irreversibly fuse with each other to form larger structures. Tethering (via Hookean bonds) imitates the action of Golgi matrix proteins while fusion accounts for the action of SNAREs. After fusion, larger structures behave similar to a fluid drop with a high surface/volume ratio, i.e., particles are mobile within the drop, but try to assume a flat overall structure, hence assuming a pancakelike shape that is typical for cisternae.

To couple these mechanical degrees of freedom to some rudimentary implementation of the cisternal protein chemistry, each particle carries two protein pools A and B. Species A shall represent, for example, the pool of SNAREs that mediate fusion events in the early cis Golgi. Proteins of species A are lost from particles with rate r_A to model protein recycling. Protein species B (lost with rate r_B) may represent an anterograde cargo protein that leaves the Golgi apparatus after having been processed. Hence, both species measure the age (or degree of maturation) of particles and emerging cisternae. Whereas species A reflects the fusion competence to newly arriving transport intermediates from the ER, species B determines how far the glycosylation processes have advanced.

As a basic readout, we monitor the number, size, and orientation of particle structures, e.g., cisternae. As a result, the balances among tethering and fusion, cisternal maturation (aging), and material influx are the dominant determinants of the phase space area in which stable stack formation is observed. All parameters of the simulation are listed in Table 1.

Table 1.

Table of parameters used in the simulations

Parameter	Value
Δt	500 μs
r0	100 nm
rc	340 nm
D	0.1 μm2/s
krep	4.1 μN/m
ktet	2.5 μN/m
F0	17 μN/m
ron	10/s
roff	0.5/s
rfiss	1/s
α⊥	2.5 10−19 J
α‖	1.0 10−21 J

Setup of the model

To allow for an efficient computer simulation that captures the relevant length and timescales inherent to the self-assembly of a Golgi stack, we restricted ourselves to producing single Golgi stacks (rather than a full Golgi ribbon). Single stacks are naturally observed, for example, in the yeast Pichia pastoris or in mammalian cells after microtubules have been disrupted. As our basic building blocks for the simulations we chose spherical particles with radius r₀ = 100 nm. Structures of this size, so-called VTCs, have been observed as major transport intermediates between ER and the GA in living cells (8,9).

All simulation were performed using a cubic simulation box (4-μm edge length) with reflecting boundary conditions. New particles entered the volume from a square ERES region (500 × 500 nm²) on one of the faces of the cube according to a flux J_in. New particles were assigned a random position inside the ERES region, and could then explore the simulation box by diffusion.

Particle movement was implemented as Brownian dynamics, i.e., for each particle i the position vector was updated according to

$${\mathbf{x}}_i\left(t+\Delta t\right)={\mathbf{x}}_i\left(t\right)+\mathit{\xi }+\Delta t{\mathbf{F}}_i/\gamma \text{.}$$

The components of the random vector ξ are independent, and have zero mean and variance 2DΔt to allow for diffusion with a low diffusion coefficient D = 0.1 μm²/s in the dense cytoplasm. The time increment was chosen as Δt = 0.5 ms. The term F_i denotes the sum of all conservative forces acting on particle i while γ = k_BT/D is the friction associated with the diffusion coefficient.

To respect excluded-volume interactions, all particles were subject to a soft-repulsive potential that is commonly assumed in dissipative particle dynamics (22). Denoting by r_ij the center-to-center distance between two particles j and i, and by e_ij the unit vector pointing from j to i, the force on i is given by

$${\mathbf{F}}_{i,j}^{\text{rep}}=k_{\text{rep}}{\mathbf{e}}_{ij}\{\begin{array}{ll}1\hfill & r_{ij}\in \left[0,r_0\right]\hfill \\ 2-r_{ij}/r_0\hfill & r_{ij}\in \left(r_0,2r_0\right)\hfill \\ 0\hfill & r_{ij}>2r_0\hfill \end{array}\text{.}$$ (1)

Here, the repulsion parameter k_rep sets the maximum force.

Whenever two particles i and j were separated by a distance r_ij ≤ r_c = 340 nm, they were able to form a temporary bond, hence mimicking tethering via Golgi matrix proteins. Each particle was allowed to form up to three tether bonds, with the restriction of not pointing to the same aggregate. The forces of these bonds were chosen similar to Eq. 1 with a maximum force given by k_tet:

$${\mathbf{F}}_{ij}^{\text{tet}}=-k_{\text{tet}}{\mathbf{e}}_{ij}\{\begin{array}{ll}0\hfill & r_{ij}\in \left[0,2r_0\right]\hfill \\ r_{ij}/r_0-2\hfill & r_{ij}\in \left(2r_0,3r_0\right)\hfill \\ 1\hfill & r_{ij}\ge 3r_0\hfill \end{array}\text{.}$$ (2)

Formation and disruption of tethers occurred stochastically with rates r_on = 10/s and r_off = 0.5/s, i.e., the kinetics was assumed to be similar to the turnover time of COPI/II proteins on biomembranes (23,24). Tethers were also allowed to break instantly if the distance between tethered particles was larger than r_c = 340 nm.

Particles were also allowed to fuse to build larger aggregates. If two particles (not being part of a common aggregate already) were tethered and had a distance r_ij ≤ 2r₀, they were assumed to fuse to a larger aggregate with a probability that depended on their protein contents (see below for details). To allow for the fluidity of larger fusion aggregates, each particle i within an aggregate determined all companion particles j within a radius r_c. Each of these m_i companion particles contributed a density-dependent interaction force of the form

$${\mathbf{F}}_{ij}^{\text{fluid}}=\frac{2F_0}{M\left(r_{\text{c}}-2r_0\right)}\{\begin{array}{ll}2r_0-r_{ij}\hfill & r_{ij}\in \left[2r_0,r_0+r_{\text{c}}/2\right]\hfill \\ r_{\text{c}}-r_{ij}\hfill & r_{ij}\in \left(r_0+r_{\text{c}}/2,r_{\text{c}}\right)\hfill \\ 0\hfill & \text{else}\hfill \end{array}$$

to maintain the aggregate (M = min {m_i, m_j}, F₀ = 17 μN/m). Density-dependent forces deriving from a potential of the form Eq. 3 are commonly used to prevent a complete collapse of aggregating units (25).

Because Golgi cisternae are flat membrane structures that behave mechanically as a fluid drop, we introduced an additional force to flatten out aggregates. To this end, every particle was assigned an internal variable which we model as a spin s, so that any pair of particles i, j within r_c within an aggregate could interact via dipole-dipole potentials

$$U_i^{\perp }={\alpha }_{\perp }\sum _j\left({\left({\mathbf{e}}_{ij}{\mathbf{s}}_i\right)}^2+{\left({\mathbf{e}}_{ij}{\mathbf{s}}_j\right)}^2\right),$$ (3)

$$U_i^{\parallel }=-{\alpha }_{\parallel }\sum _j{\mathbf{s}}_i{\mathbf{s}}_j\text{.}$$ (4)

Here, α_⊥ and α_‖ represent bending stiffnesses. The forces acting on particle i and thus its displacement are derived from the gradient of the potential. In each timestep, all dipole moments were equilibrated via a Monte Carlo algorithm. To this end, each spin orientation was randomly varied and the step was accepted according to the Metropolis criterion using U^tot_i = U^⊥_i + U^‖_i. Hence, all spins aimed at being parallel in the same plane, yet thermally induced deformations such as bending modes were still allowed.

Because every particle in the system, whether it is part of an aggregate, may be viewed as a transport intermediate, each particle was assumed to carry two protein species (A and B) as molecular cargo. Species A may reflect, for example, cognate SNAREs that mediate fusion of VTCs with early Golgi cisternae, whereas species B may reflect secretory cargo that has been posttranslationally modified. Hence, both protein species determine the age of a particle or an aggregate of particles that may be identified with a cisterna of the GA. Upon entering the simulation box, new particles were assigned initial protein concentrations M_A(t = 0) = 100 and M_B(t = 0) = 0.

Each particle (being free or part of an aggregate) lost ΔM_A = 25 proteins of species A with probability P_A within each time step. These proteins were lost from the system, i.e., they were put back into the infinite pool of particles that equipped new particles before entering the system. The loss rate of an aggregate of size n was hence dependent upon the size of an aggregate as r_A = nP_A/Δt.

Within an aggregate of size n, all particles i = 1, …, n were assigned the same fraction of proteins, c_i(A) = N_A/n. This value determined the fusion probability for two particles i and j belonging to different aggregates as

$$P_{ij}^{\text{fuse}}=r_{\text{fuse}}\Delta t\frac{c_i\left(A\right)c_j\left(A\right)}{c_0^2},$$ (5)

where r_fuse denotes the optimal rate with which fusion events were allowed. All pairs of particles that fulfilled the necessary conditions of being tethered were allowed to fuse (see above) and were tested with the above probability within each time step.

Protein species B accumulated in each particle with rate r_B following a similar scheme to the loss of species A, i.e., each particle gained ΔM_B = 25 proteins of species B per time step according to the probability associated with rate r_B. Above a threshold c_max = 100, an aggregate of size n (i.e., a cisterna) was allowed to send off particles (i.e., transport vesicles) toward the plasma membrane with probability

$$P^{\text{fiss}}=n{r}_{\text{fiss}}\Delta t,$$ (6)

where r_fiss = 1/s denotes the maximum budding/fission frequency. The latter is necessary to ensure that a whole cisternae only gradually dissolves after reaching c_max.

Quantitative analysis of phenotypes

To avoid counting single particles as cisternae, we specified that all aggregates larger than 60% of the largest aggregate were counted as cisternae. The median of the number of cisternae was monitored starting after 20 min (or 2.4 10⁶ time steps), i.e., after the typical stack turnover time found in experiments (26), up to the end of the simulation. The monitored fluctuations in the median, i.e., the variance around the mean, were used to determine error bars. The same approach was used to determine the size of cisternae.

To obtain a quantitative measure for successful formation of a cisternal stack, we defined an order parameter S. To this end, for each aggregate a reference particle i with spin s_i was selected randomly and all remaining spins s_j (j ≠ i) of the aggregate for which the scalar product s_i·s_j was negative were inverted (reorientation). From this set of spins, the average spin s^c_k of each aggregate k was calculated. The set of average spins of all aggregates was then flipped as described for the individual spins within one aggregate.

Subsequently, for each pair of aggregates (i, j), all normalized connection vectors between the constituting particles of the aggregates were calculated. The orientation of these connection vectors was always from the younger (lower amount of protein species B) to the older aggregate (higher amount of protein species B). The mean of the connection vectors derived from this set were weighted with the inverse variance of the principal components (= e^c_{i, j}), hence highlighting the coplanarity of the two aggregates. The order parameter was then defined as

$$S=\frac{\left|\sum _{i,j}{n}_i{n}_j{\mathbf{e}}_{i,j}^{\text{c}}·{\mathbf{s}}_i^{\text{c}}\right|}{\sum _{i,j}{n}_i{n}_j},$$ (7)

with the aggregate sizes n_i, n_j. For proper stack formation, i.e., coplanar aggregates (compare to Fig. 2), we observed S → 1, whereas scattered aggregates yielded values for S near to zero.

Figure 2.

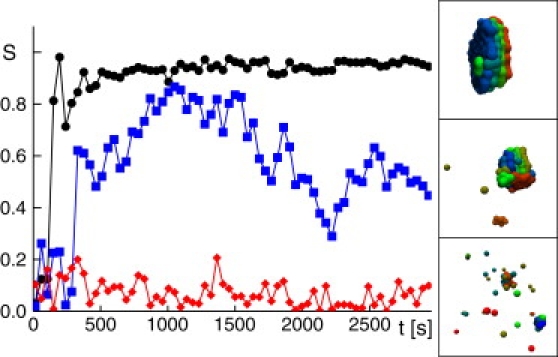
Temporal evolution of the order parameter S for three representative parameter settings, J_in = 0.8/s (•), 0.5/s (▪), and 0.1/s (♦); in all cases, r_A = 0.04/s and r_B = 0.005/s. Snapshots of the final configuration are shown on the right. Proper stacks were observed for S ≥ 0.75, whereas lower values indicated a more or less compromised stack structure.

Results

We first tested whether our simulation setup was capable of showing a de novo formation and dynamic maintenance of Golgi stacks without a preexisting template. Starting from an empty simulation box into which new particles (i.e., VTCs) were injected from an ERES-like area on one face of the simulation box, we frequently observed the formation of a dynamically maintained stack structure (Fig. 1). The first cisternal assemblies emerged within 2–3 min and a preliminary stack structure was formed within 10–15 min. This stack subsequently became stable as a dynamic steady-state structure while individual cisternae still underwent a maturation process, i.e., cisternae showed an aging process according to a change in protein contents (species A, B; cf. above).

Figure 1.

Representative snapshots of a time series showing the de novo formation of a Golgi stack (parameters: J_in = 0.6/s, r_A = 0.04/s, and r_B = 0.005/s). Starting from an initially empty simulation box, a steady-state stack developed after ∼700 s that was dynamically maintained until the end of the simulation (t = 3000 s). The maturation state of a cisterna, i.e., its age as measured by the amount of protein species A, is color-coded. Red and green color denote young (cis) and intermediate (medial) cisternae, while blue color represents old (trans) cisternae that are about to disassemble.

To avoid uncertainties as to whether an aggregate should be counted as a proper stack, we defined an order parameter S that yields an unbiased way to determine whether a stack has emerged (Eq. 8). Basically, S quantified whether adjacent clusters of particles (putative cisternae) did form parallel, concentric sheetlike structures that are ordered according to increasing age. The classification via the order parameter S agreed well with a classification by eye. For S ≥ 0.75, a proper stack structure was observed (Fig. 2), while smaller values were associated with a distorted or even lacking stack structure.

Having observed the possibility for a de novo generation of a stack structure, the important question arises: Within which parameter regime would a robust stack formation be observed? Before addressing this point, we will briefly examine which factors determine the amount and size of cisternae.

Owing to the maturation process, i.e., the loss of fusion SNAREs with rate r_A (compare to Model Definition), the youngest compartment (cis cisterna) loses its fusion competence for incoming particles within a time T_A ∼1/r_A. The number of particles that enter the simulation box during this period, and hence are able to join and build up the youngest cisterna, therefore scale as ∼T_AJ_in. Here, J_in is the number of new particles (i.e., VTCs) that enter the simulation box from the ERES region within 1 s. Using this simple scaling argument (a refined calculation is given in the Supporting Material), the total number of particles per cisterna should grow linearly with J_in/r_A. Indeed, our simulation results for varying J_in and r_A (relying only on simulations for which S ≥ 0.75) agree very well with our prediction (Fig. 3 a). Concerning the prefactor, our theoretical prediction in fact slightly overestimates the cisternal size because not all particles fuse to the same cisterna during the period T_A.

Figure 3.

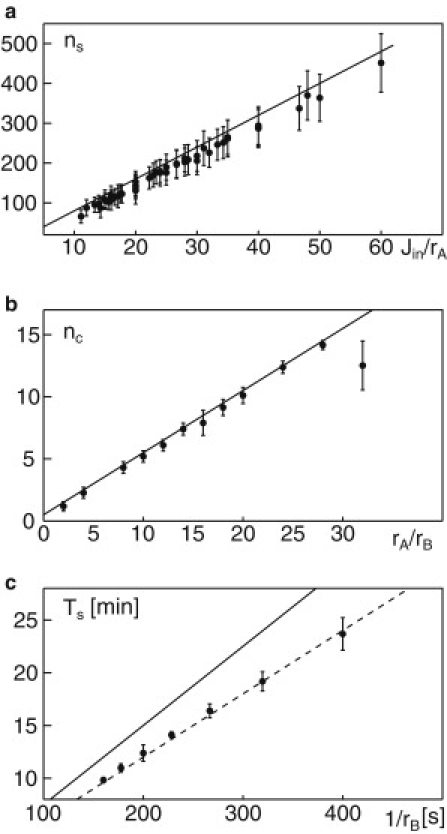
(a) The size of a cisterna (measured as the number n_s of participating particles) grows linearly with J_in/r_A as predicted. Numerical data are shown as symbols, with error bars being derived from the standard deviation of n_s within each simulation. The solid line corresponds to the theoretical prediction (see main text and Supporting Material). (b) The amount of cisternae n_c increases linearly with r_A/r_B as predicted theoretically. Numerical data (symbols) were determined in the time interval 20–50 min. Error bars denote the standard deviation of n_c within each simulation. The solid line corresponds to the theoretically predicted linear relationship (see main text and Supporting Material). (c) The turnover time T_s of the stack grows linearly with the inverse aging rate r_B (symbols and dashed line). Deviations from the theoretical prediction (solid line) most likely are due to the simplicity of the argument.

To estimate the number of cisternae, we recall that glycosylated cargo molecules are gained with rate r_B (compare to above). While T_A ∼1/r_A determines the period after which the youngest cisterna stops growing, T_B ∼1/r_B provides a timescale on which this youngest cisterna will eventually disassemble. Hence, the ratio of these times, i.e., r_A/r_B, provides a measure for how often a cisterna disassembles while a new one is being built up. Based on this consideration (a more rigorous calculation is given in the Supporting Material), we predict that the number of cisternae scales with r_A/r_B. To test this prediction, we plotted the median number of cisternae in several simulations with varying r_A and r_B (keeping S ≥ 0.75) as a function of r_A/r_B. In agreement with our prediction, we observed a linear growth of the number of cisternae with r_A/r_B (Fig. 3 b). Only for very large r_A/r_B is a significant deviation of the numerical data from the theoretical prediction observed, and this is due to an incomplete equilibration of the system during the simulation time.

By definition, the rate r_B with which glycosylated cargo proteins are gained also determines the turnover time of the stack, i.e., the period during which all material in the stack will be replaced by material coming from the ERES. Indeed, the numerically determined turnover time shows a linear dependence on 1/r_B (Fig. 3 c) in the physiologically relevant range (10–25 min has been estimated experimentally for a complete turnover of a Golgi stack (26)). Similar to our theoretical prediction for the cisternal size, the prefactor of the linear scaling deviates slightly from the numerically obtained data due to the simplicity of the argument.

In summary, the size of cisternae is determined by J_in/r_A while the number of cisternae is given by r_A/r_B; the stack turnover time is approximately given by 1/r_B. With these insights, it is now possible to explore the range of parameters in which stack formation is possible.

To explore the range of parameters in which stack formation is possible, we varied J_in, r_A, and r_B while keeping the ratio r_A/r_B fixed. With the chosen ratio, we expected on average 4–5 cisternae if a stack was able to form (as determined via the order parameter S). As a result, we found that the formation of regular stacks (defined via S ≥ 0.75) occurs for a wide range of parameters, i.e., it is a very robust phenomenon (Fig. 4). In particular, the key ingredient for stack formation at a given ratio r_A/r_B is the influx of new material from ERES, J_in. Reducing the rate r_B at which cargo is finished (the parameter that also determines the turnover time) at a given J_in stabilizes stack formation, because the period during which cisternae can build up and organize themselves is long enough that even a low material influx can sustain proper stack formation.

Figure 4.

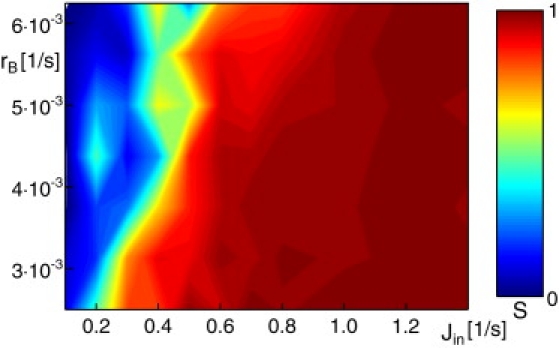
Map of the order parameter S as function of influx rate J_in and aging rates r_A and r_B. While the individual parameters were varied, the ratio r_A/r_B = 8 was kept constant to have, on average, 4–5 cisternae. Proper stacks, defined via S ≥ 0.75, were found for a broad set of parameters.

Based on our above results, we next asked how the number and spatial arrangement of ERES regions influences the formation of Golgi stacks. As a first step, we decreased the ERES region from a 500 × 500 nm² to a 250 × 250 nm² window and varied J_in while keeping r_A = 0.04/s and r_B = 0.005/s fixed. Again, stable stacks emerged, yet they formed already for J_in ≥ 0.4/s as compared to the slightly higher threshold J_in ≈ 0.6/s for a larger ERES (Fig. 5 a). This result highlights that the influx rate, i.e., the rate at which COPII vesicles are produced, is the dominant parameter while a smaller width of an ERES region may only help to focus the influx of material toward an emerging structure.

Figure 5.

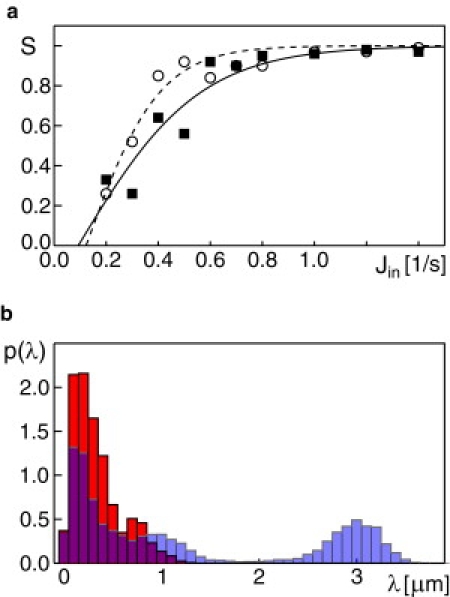
(a) The average order parameter S increased slightly more rapidly as a function of the flux J_in when the ERES area was decreased from 500 × 500 nm² (solid symbols, solid line) to 250 × 250 nm² (open symbols, dashed line). (b) Lateral distance distribution of VTC-clusters with two ERES regions per simulation box that are either 1.2 μm (red) or 3 μm (blue-transparent) separated.

Next, we asked: Under which conditions can two neighboring ERES give rise to two distinct stacks? To address this question, we performed simulations with r_A = 0.04/s, r_B = 0.005/s, J_in = 1.2/s and two ERES (each having an area of 500 × 500 nm²) at one face of the simulation box. The distance between ERES was varied in the physiological range of 1.2–3.5 μm. As a result, we observed that two distinct stacks could only emerge if the ERES separation was at least 2 μm. The emergence of two stacks (initially quantified by inspection of the simulation snapshots) can be visualized by the distance distribution of emerging cisternae, p(λ). When only a single stack formed, p(λ) showed a single peak at <0.5 μm as all cisternae are in close proximity (Fig. 5 b). When a second stack emerged, p(λ) showed a second peak, indicating the emergence of another length scale in the simulations that is associated with the center-to-center distance of the two stacks (Fig. 5 b). Indeed, the observation that ERES-dense regions give rise to a larger single stack, while well-separated ERES build up their individual stack, is supported by observation in nocodazole-treated cells that exhibit mini-Golgis near to ERES (16).

Discussion

Summarizing our results, we have shown that the de novo formation of Golgi stack structures can be understood in a minimal self-assembly model. This model relies on the balance of anterograde and retrograde flux, and on the rate with which the chemical identity of cisternae is altered (that is, experiences aging or maturation).

For the chosen parameters, the timescales for a de novo formation of a stack structure and its steady-state turnover compare favorably to experimentally accessible data: In steady state, the typical turnover of a Golgi stack takes 10–25 min (26) while the de novo formation of a GA takes ∼30 min (27). Provided that a sufficiently high anterograde flux of membrane carriers is given, i.e., if J_in is high, our model indeed confirms the formation/turnover of a stack structure within these physiological timescales. Reducing J_in, i.e., reducing the secretory flux, the size of cisternae is predicted to shrink and ultimately a disorganization of the stack is observed. This observation matches nicely the experimental reports that introducing a dominant negative mutant of the Sar1 GTPase, i.e., hampering cargo export at the level of the ERES, leads to a decrease of cisternae size with subsequent disassembly (28).

The model also highlighted that a change of the exit site area, which acts as the source for an anterograde flux, has only minor effects on the structure formation. Changing the proximity of ERES, however, had a significant effect, because the inter-ERES distance determined whether all anterograde material accumulated in a single stack structure or gave rise to more than one stack. Owing to the setup of our simulations, the entry window of new material (our ERES) may alternatively be interpreted as the terminal end of a bundle of microtubules. Our simulation box, hence, would represent a juxtanuclear volume element toward which VTC-like entities are transported along cytoskeletal tracks while, within the simulation box, motors and the cytoskeleton are neglected. In fact, including the intimate interactions of cisternae, motors, and microtubules would require a massive extension of model parameters. These aspects are beyond the scope of this study, but are the subject of ongoing and future work.

Because the loss rate of early SNAREs, r_A, and the rate of maturation r_B as well as the influx of membrane carriers J_in crucially determine the appearance of a stack structure, we would like to discuss these rates (and how to change them) in a more detailed biological context.

The anterograde secretory flux that is summarized in J_in lies at the very heart of any Golgi structure formation and a lack of material flux abolishes the formation or maintenance of any Golgi structure. The flux J_in essentially quantifies the amount and contents of vesicles that emerge at ERES. Hence, the value of J_in can be modulated by changing the cargo load (compare to (29) for an experimental realization). Indeed, poisoning export at ER exit sites by massively overexpressing a hydrolysis-incapable Sar1 mutant (Sar1T39N) leads to the disappearance of the Golgi apparatus (16,17,28). More differential effects, i.e., partial destruction or shape perturbation of the Golgi, may be obtained by tuning the degree of Sar1T39N expression, by (partially) downregulating COPII components via RNAi, and/or by inhibiting protein synthesis via cycloheximide (all of which decreases J_in). Time-lapse microscopy or fluorescence recovery after photobleaching on cells with disrupted microtubules (to ensure the local formation of Golgi structures) may be used to determine J_in, while electron microscopy and tomography may be used to determine the geometrical properties of a stack. Controlled overexpression of secretory cargo, on the other hand, may help to increase J_in. The latter approach also may be used to change the size and distance distribution of ERES (29), i.e., the model predictions concerning the influence of ERES distances on (local) stack formation can be tested.

Changing the rates r_A and r_B is somewhat less straightforward. Because r_A is associated with retrograde transport of SNAREs which is mediated by COPI proteins, the most direct approach to manipulate r_A is an interference with COPI proteins. Perhaps the most feasible way to modulate the parameter r_A experimentally is by modifying the action of ARFGAPs that stimulate GTP hydrolysis, as these are crucial for vesicle formation and protein sorting. Another possibility could be the overexpression of inhibitory SNAREs (30), which affect retrograde transport by interfering with the fusion machinery.

By construction, the maturation rate r_B describes the internal aging of cisternae and consequently the cisternal decomposition time during which carriers are exported, e.g., to the plasma membrane. Owing to this very definition, different molecular processes that progress in parallel are lumped into r_B, e.g., the sequential glycosylation of cargo proteins, the formation of clathrin-dependent carriers, or the change in pH and lipid thickness of individual cisternae. Given this multitude of contributing factors, the most straightforward way to alter the value of r_B may be an interference with clathrin-mediated transport, the dominant path for post-Golgi trafficking. Also, downregulating Golgi resident enzymes, i.e., slowing down the glycosylation processes, may be a way to reduce r_B.

A basic mechanism that we used in our simulations was the formation of temporary bonds (i.e., tethers) between different membrane aggregates. On the molecular level, tethering of cisternae during different stages of maturation may be provided by Golgi matrix proteins such as GRASP65/55 and/or GM130 (13,31). Tethering VTCs to cisternae, however, may invoke golgins instead (32). As a result of our simulations, we observed that modifying the formation of tethers dramatically alters the phenotype. Allowing tether formation before fusion (an event that most likely relies on SNAREs but does not have to involve Golgi matrix proteins), but disallowing tether formation after fusion, resulted in a phenotype that resembles that of the yeast S. cerevisiae (Fig. 6 a): Clusters of different age floated independently within the simulation box with a fair number of single VTCs in between. This observation suggests that the different yeast phenotypes observed in S. cerevisiae and P. Pastoris are due to differences in golgins and/or Golgi matrix proteins.

Figure 6.

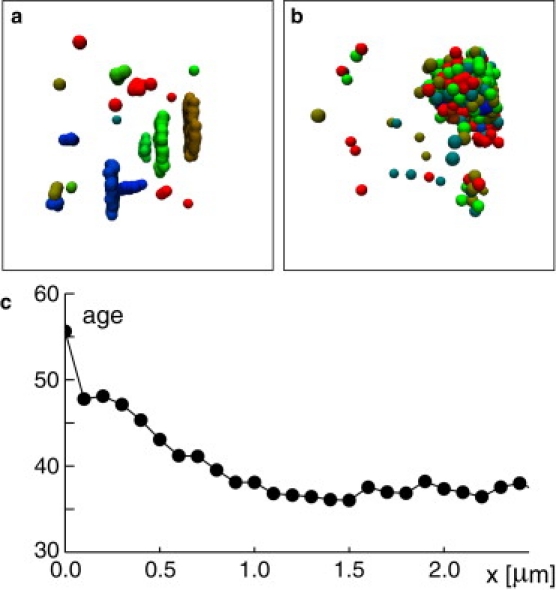
(a) Inhibiting tether formation resulted in a phenotype of single, free-floating cisternae reminiscent of observations in Saccharomyces cerevisiae. (b) An enhanced loss rate of SNAREs (r_A = 0.32/s) while keeping J_in = 0.6/s and r_B = 0.005/s fixed leads to grapelike structures of small VTC-clusters, reminiscent of observations in Drosophila melanogaster. (c) The maturation stage of the grapelike structure depends on the radial distance x from the center of mass of the structure. A maturation age of 100 corresponds to a unit that is marked for immediate disassembly, whereas a zero value indicates a newborn VTC.

A completely different structure emerged when the loss rate r_A was massively enhanced. This would mean, for example, that SNAREs are rapidly backtransported to the ER, hence abolishing the fusion competence of the Golgi cis compartment with new incoming VTCs. For this case, our simulations resulted in grapelike structures consisting of a large amount of very small stacks (Fig. 6 b). Still, the structure retained a maturation order as evidenced by the radial age distribution of the aggregate (Fig. 6 c). This phenotype is reminiscent of observations made for early stages in the embryogenesis of Drosophila melanogaster (5,34), hence suggesting that the rate r_A, at which new cisternae lose their fusion competence with newly arriving VTCs, is here much faster than in many other eukaryotes. Different molecular mechanisms could be responsible for this, e.g., an enhanced retrograde transport of fusion SNAREs or an increased expression of inhibitory SNAREs that might hamper fusion events.

In our model, we have tacitly assumed a scenario in which Golgi stacks are subject to maturation, as several lines of evidence support this view (35,36). The exact nature of intra-Golgi transport, however, is still under debate and a variety of mechanisms has been proposed (see, e.g., (37) for a recent review). Our model, by construction, does not allow one to test the validity of the maturation model directly. However, an experimental falsification of our above predictions on the emerging Golgi phenotypes when altering the fundamental rate constants (r_A, r_B, and J_in) could provide strong evidence that maturation may not be the dominant means of intra-Golgi transport.

Taken together, the large variety of different GA morphologies found in nature is captured by our self-assembly model (compare to Fig. 7). This model reduces the emergence of phenotypes to three basic, important parameters that summarize the action of individual classes of proteins. Clearly, future work will be needed to unify the morphology approach taken here with previously published, more explicit descriptions of protein sorting and selection (20). Such an elaborate model ultimately should be able to reproduce the steady-state distributions of Golgi residents across a self-assembling Golgi apparatus (10,38–40).

Figure 7.

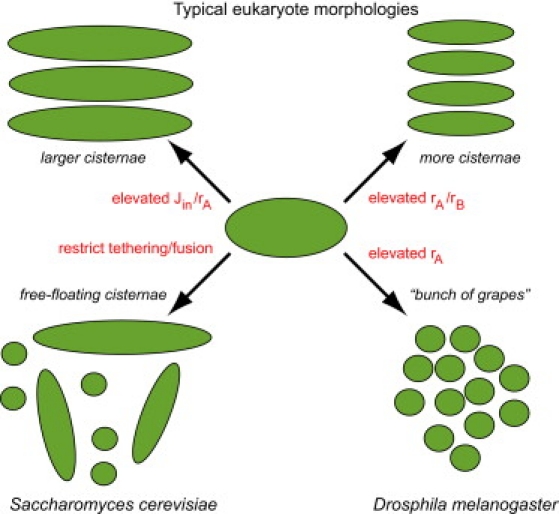
Morphology diagram showing the correspondence of the predicted structure of the self-assembled Golgi stacks with their biological phenotypes as a function of the model's key parameters. Parameter J_in is the export rate of transport intermediates from ERES regions; r_A is the retrograde loss rate of protein species A (e.g., representing SNAREs of the Golgi-ER interface); and r_B is the rate at which protein species B (e.g., cargo proteins that are modified in the Golgi) reaches its functional form. The tether rate determines the speed at which bonds form between VTCs and growing cisternae. See main text for details.

Supporting Material

Analytical results for the scaling in Fig. 3 are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00368-1.