An Electrostatic Model for DNA Surface Hybridization

Abstract

DNA hybridization at surfaces is a crucial process for biomolecular detection, genotyping, and gene expression analysis. However, hybridization density and kinetics can be strongly inhibited by electric fields from the negatively charged DNA as the reaction proceeds. Here, we develop an electrostatic model to optimize hybridization density and kinetics as a function of DNA surface density, salt concentrations, and applied voltages. The electrostatic repulsion from a DNA surface layer is calculated numerically and incorporated into a modified Langmuir scheme, allowing kinetic suppression of hybridization. At the low DNA probe densities typically used in assays (<10¹³/cm²), electrostatics effects are largely screened and hybridization is completed with fast kinetics. However, higher hybridization densities can be achieved at intermediate DNA surface densities, albeit with slower kinetics. The application of positive voltages circumvents issues resulting from the very high DNA probe density, allowing highly enhanced hybridization densities and accelerated kinetics, and validating recent experimental measurements.

Introduction

The physical mechanisms that govern the hybridization of a DNA target from solution with a complementary probe immobilized at a surface are highly relevant for optimizing the performance of nucleic acid biosensors and microarrays (1). However, it can be difficult to reconcile thermodynamic and kinetic measurements of DNA surface hybridization with corresponding measurements in dilute solution (2). An important distinction between these two scenarios is the electrostatic and steric crowding that occurs when DNA probes are immobilized at high grafting densities on a surface. Such interactions can dramatically affect polymer conformation and morphology. For instance, in the limit of low densities, isolated chains can assume largely unperturbed mushroom conformations. As the density increases and the interchain spacing decreases, polymers form a strongly stretched brush layer. In this regime, experimental measurements have revealed a strong suppression of DNA target hybridization (3–14). The situation is further complicated as hybridization proceeds and additional DNA chains are inserted into the layer, causing the steric and electrostatic conditions to vary dynamically. These crowding effects may contribute to issues with reliability and reproducibility in DNA microarrays, such as cross-hybridization (15).

An additional consequence of high probe densities is a significant slowdown in hybridization kinetics (4). In fact, at densities above 10¹³/cm² (one molecule per 10 nm²), the hybridization reaction may not reach completion on experimentally practical timescales, particularly at low target concentrations in solution (16,17). One compromise is to work at low surface probe densities, where electrostatic and steric effects are minimized so that complete hybridization and relatively fast kinetics can be achieved. However, this comes at the expense of the signal/noise ratio, since the absolute target number densities are limited by the surface probe density. Our group recently demonstrated that the use of applied voltages in the ideally polarizable voltage regime (i.e., no electrochemical current) reduces these electrostatic effects and greatly elevates hybridization densities relative to the case of zero voltage (18). This approach may circumvent issues resulting from the very high DNA probe density by enabling enhanced hybridization signals with accelerated kinetics even in the limit of high probe densities.

Investigators have examined DNA surface hybridization theoretically using a variety of approaches. Chan et al. (19) and Erickson et al. (20) considered the case in which DNA probes are immobilized at low density, permitting surface adsorption and lateral diffusion of DNA targets. Vainrub and Pettitt (21–23) treated electrostatic charging effects by using an analytical solution for a penetrable charged sphere of DNA interacting with an impenetrable surface, valid only in the linear Debye-Hückel limit of weak electrostatic potentials and not generally applicable over a wide range of electrostatic conditions. Halperin et al. (17,24,25) investigated the role of electrostatics and competitive hybridization on Langmuir isotherms using scaling arguments for a polyelectrolyte brush layer with finite thickness, without explicit numerical predictions for experimental comparison. Hagan and Chakraborty (26) explored the effect of steric crowding on initial hybridization rate constants using polymer brush models; however, they did not consider changes in these constants as hybridization proceeded and the physical properties of the polymer brush varied. To accurately model experimental results at high DNA densities, a model is needed that can account for the changing electrostatics within the layer, which rapidly become nonlinear as hybridization proceeds.

One difficulty in addressing these crowding effects is that electrostatics in aqueous solution are poorly understood at high charge densities. Historically, these systems have been modeled with the use of continuum theories that do not account for finite ion sizes. However, these theories diverge to unphysically high ion concentrations for electrostatic potentials exceeding the thermal voltage, where the discrete nature of ions becomes relevant (27). Since classical treatments of polyelectrolyte brushes are based on these approximations, their validity becomes suspect at high charge densities and ion concentrations (28,29). In particular, DNA is highly negatively charged, with a linear charge density of 1e⁻ per basepair (∼0.4 nm for single-stranded DNA (ssDNA)).

At sufficiently high probe grafting densities, DNA is expected to fall into the strongly charged regime of polyelectrolyte brushes. This regime is characterized by stretching of the polymers beyond the linear Gaussian regime into the rod-like limit, where the end-to-end distance becomes comparable to the contour length, as well as by a renormalization of backbone charge density due to Manning condensation effects (29,30). Recent experiments have demonstrated that short DNA oligos can be immobilized at relatively high grafting densities that approach the steric close-packed limit of ∼6 × 10¹³/cm² (31–33). This is significant because the DNA molecules, including hydration shells and condensed counterions, occupy an appreciable fraction of the available volume within the layer.

In this work, we investigate DNA surface hybridization using a numerical model to evaluate the electrostatics of a DNA layer over a wide range of probe densities, ion concentrations, and applied voltages. The negative electric fields from the DNA act as a kinetic activation barrier, limiting the insertion and subsequent hybridization of DNA targets from solution. This activation barrier varies continuously with DNA hybridization due to the increasing charge density of the layer. As a result, the dynamically changing rate constants drive a suppression of target hybridization density and kinetics. In the absence of applied voltage, these high charge densities cause a considerable slowdown in hybridization kinetics, but are nevertheless necessary to optimize DNA hybridization densities. However, the application of positive voltages can compensate for these charge densities, allowing strongly enhanced target hybridization densities as well as accelerated hybridization kinetics. This corroborates recent experimental work by our group and others (3,18,34).

We also find that the importance of electrostatics differs greatly depending on the initial DNA probe density. At low probe densities, where the ssDNA chains are relatively isolated and unperturbed, the layer charge density is strongly screened and electrostatics do not significantly influence hybridization. In this regime, the extent and kinetics of hybridization are largely unaffected by the particular model used to treat electrostatics or brush height. However, at high probe densities, the DNA chains behave more like fully extended, rigid rods. In this regime, the best agreement with experimental results was achieved by treating the DNA layer as a region of uniform charge density with constant height, reminiscent of two-component box theories for polyelectrolytes (Fig. 1). Moreover, mobile counterions appear to be largely excluded from this layer, although partial charge neutralization due to immobilized (Manning-condensed) counterions can occur. Outside the layer, mobile counterion screening is treated explicitly using a modified Poisson-Boltzmann equation that accounts for the strongly nonlinear electrostatic effects in this regime, including a discrete counterion size. Remarkably, these results imply that applied electric fields are less screened at high DNA densities, and thus may be more effective at regulating hybridization that at low probe density.

Figure 1.

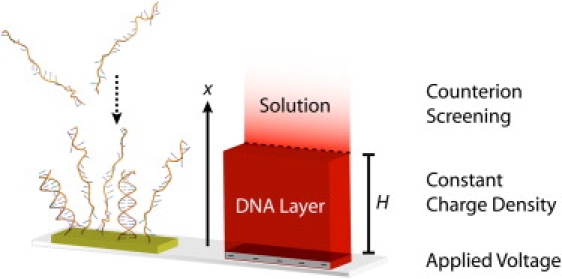
Schematic of the modified two-component box model used to evaluate the electrostatics of a DNA probe layer. The boundary condition at the surface is the applied voltage, the probe layer is approximated as a region of constant monomer/charge density, and counterion screening is allowed only outside the layer and modeled using a modified Poisson-Boltzmann equation.

Theory

Two-component box models for polyelectrolyte brushes

The scenario of strongly stretched polymer chains grafted on a surface at high density was first approximated by Alexander (35) and de Gennes (36) as a simple step function for the monomer density profile. This treatment was extended to polyelectrolyte brushes by Pincus (37), Wittmer and Joanny (38), and Borisov et al. (39). In this so-called two-component box model, the assumption of a step-function monomer profile allows the polyelectrolyte brush to be treated as a continuum region of uniform, smeared-out charge density. For polyelectrolyte chains, the charge (monomer) density as a function of distance x from the surface is given by:

$${\rho }_{Layer}\left(x\right)=\left(fN\sigma /H\right)\theta \left(H-x\right)$$ (1)

where f is the charging fraction, N is the number of monomer units, σ is the areal density of polymers, H is the layer height, and θ is the Heaviside step function.

The electrostatic potential and counterion concentrations can then be solved self-consistently using a Poisson-Boltzmann equation:

$${\nabla }^2\psi ={2l}_B^2\left[{\rho }_{Layer}\left(x\right)+C_0\sinh \left(\psi \right)\right]$$ (2)

where ψ = eV/kT is the dimensionless electrostatic potential, l_B = e²/4πɛkT is the Bjerrum length, and C₀ is the bulk salt concentration. The first term on the right-hand side corresponds to the charged polyelectrolyte brush layer defined in Eq. 1, and the second term corresponds to the counterion distribution.

One limitation of simply solving the unmodified Poisson-Boltzmann equation is that at large electrostatic potentials (or high surface charge densities), the local counterion concentration can be unphysically large. For example, in the context of the model just described, there is no limit to the quantity of counterions that can enter the layer to screen highly charged polyelectrolyte chains. Such an unphysical scenario is not likely to be an issue for polyelectrolytes in the dilute to semidilute phase. However, DNA probe arrays are somewhat unusual in this regard, since the DNA molecules, along with their associated hydration shells and immobilized (Manning-condensed) counterions can occupy a significant fraction of the available volume within the layer. For instance, DNA hybridization has been reported at probe densities up to σ ∼ 4 × 10¹³/cm², which is equivalent to one DNA strand per 2.5 nm² (8). In comparison, the maximum steric close-packed density of ssDNA is approximately σ ∼ 6 × 10¹³/cm², which is consistent with grafting densities achieved experimentally with the use of divalent cations (33). DNA probes can thus comprise roughly two-thirds of the available volume within the layer. In this crowded regime, the entropic cost of inserting additional counterions into the layer to screen the added charge of hybridized targets may be unfavorable. This effect may be particularly pronounced in the so-called osmotic-brush regime, where the (mobile) counterion concentration within the layer associated with the polyelectrolytes already exceeds the bulk ion concentration in solution (29,30).

The electrostatic conditions in this high-density limit were investigated using a modified Poisson-Boltzmann equation (40):

$$\rho \left(x\right)=\left(\frac{C_0\sinh \left(\psi \right)}{1+2\nu {\sinh }^2\left(\psi /2\right)}\right)$$ (3)

where ν = 2C₀a³ is a steric size parameter that corresponds to an effective counterion diameter. In solution, the maximum allowed counterion density was limited to a⁻³ ∼ 4.6 M (41). However, within the layer, the steric size parameter was weighted by the total DNA density to account for the volume occupied by the DNA: ν = 2C₀a[1+100(σ/σ_sat)], where σ_sat represents the saturating DNA density at which the volume is fully occupied and no additional mobile counterions can enter the layer. The fraction of available volume for mobile counterions can be estimated from 1 − σ/σ_sat.

Surprisingly, the best agreement with experimental data is found when mobile counterions are completely excluded from the DNA layer, as discussed in Results. Within this limit, the charge density remains constant throughout the layer due to the lack of further screening, which has some precedent in experiment (32). Therefore, the remaining calculations are implemented using this simpler assumption of no mobile counterions, so that the charge density within the layer is given exclusively by Eq. 1, where the charge density is renormalized by Manning condensation to f = b/l_B = 55%, and b = 4 Å is the linear charge spacing for ssDNA. Obviously, this lack of screening for mobile counterions is unphysical at low DNA densities. However, since the corresponding charge densities are also low, electrostatic effects are negligible in this regime and this assumption produces minimal error. Similarly, the electrostatic model also exhibits good agreement with experiment when we assume a constant brush height H ∼ 7.8 nm, corresponding to the contour length of a double-stranded DNA oligomer with N = 20 bp. Such a step-function monomer density profile is appropriate due to the strong stretching of DNA at higher densities, and is consistent with neutron scattering measurements (42). This model is largely indistinguishable from a modified model using a variable layer height, since again the variability is most pronounced at low DNA densities where electrostatics are relatively weak (see the Supporting Material).

The electrostatic potential and counterion concentration are then solved self-consistently using a modified Poisson equation of the form: ${\nabla }^2\psi ={2l}_B^2\left[{\rho }_{DNA}\left(x\right)+{\rho }_{Solution}\left(x\right)\right]$, where ρ_DNA is the sum of Eqs. 1 and 3 using the density-dependent steric size parameter ν, which applies only within the layer, and ρ_Solution uses ν = 2C₀a³, which applies only in solution outside the layer. This equation must be solved numerically due to the nonlinear nature of the modified Poisson-Boltzmann equation (Eq. 5), as well as the incorporation of a boundary condition ψ(x = 0) = ψ₀, which can be a voltage applied to the electrode surface.

Three representative examples of electrostatic potentials and charge densities are shown in Fig. S1 for DNA probe layers with varying grafting densities. Since this model does not allow mobile counterions within the layer, the charge density due to the DNA probes is not screened, and the electrostatic potential is nonzero and quadratic. This electrostatic potential is negligible at low grafting densities of σ = 10¹²/cm², but it becomes significant at higher grafting densities σ = 10¹³/cm² and 3 × 10¹³/cm², remaining appreciable at the outer edge of the DNA layer (x = H) and extending several nanometers out into solution. Screening these negative electrostatic potentials requires increasing quantities of positive counterions in solution outside the layer. The implications of these longer-ranged electrostatic effects on DNA hybridization density and kinetics are considered in the following section.

DNA hybridization kinetics

The kinetics of DNA surface hybridization are generally treated using a simple first-order Langmuir scheme. For a target density σ; initial probe density σ_P; association and dissociation constants k_on and k_off, respectively; and a bulk target concentration C_T, the target density at time t can be determined by integrating

$$\frac{d\sigma }{dt}=k_{on}{C}_T\left({\sigma }_P-\sigma \right)-k_{off}\sigma$$ (5)

If there is a large excess of targets in solution, and target transport to the surface occurs much faster than target hybridization (i.e., small Damköhler number), the system is reaction-limited and can be solved analytically:

$$\theta \left(t\right)=\frac{\sigma \left(t\right)}{{\sigma }_P}=\frac{C_T/K_D}{1+C_T/K_D}\left(1-e^{-\left(k_{on}{C}_B+k_{off}\right)t}\right)$$ (6)

where θ(t) is the fractional target hybridization and K_D = k_off/k_on is the equilibrium dissociation constant or binding affinity. This reaction has a characteristic timescale given by τ = (k_onC_T + k_off)⁻¹. Depending on the relative magnitudes of the association constant, dissociation constant, and bulk target concentration, the speed limits for this reaction are set so that it cannot occur faster than τ_fast ∼ (k_onC_B)⁻¹ or slower than τ_slow ∼ k_off⁻¹. In steady state at times longer than this critical timescale τ ≪ t, the fraction of probes hybridized to a target is given by θ_ss = (C_T/K_D)/(1+ C_T/K_D).

The idealized scenario represented by this first-order Langmuir scheme models DNA hybridization well in the limit of low DNA probe densities σ_P ≤ 10¹²/cm², characterized by ∼100% hybridization and single-exponential kinetics (5,15,43). However, the hybridization fraction becomes increasingly suppressed at higher probe densities and the kinetics must be fit to stretched exponentials (4––14). Previous approaches with theoretical models attempted to model this suppression of hybridization by modifying the (steady-state) Langmuir isotherm using an electrostatic correction factor that depends on hybridization density (21–23). In particular, the scaling approach presented by Halperin et al. (24) is a linearized analog of the numerical model presented here.

In this work, a modified Langmuir equation is solved numerically using a hybridization-dependent association constant k_on within a Kramers-type model for thermally activated diffusion over a harmonic potential:

$$k_{on}=k_{on,dilute}\sqrt{\frac{\Delta G_a\left({\sigma }_P+\sigma \left(t\right)\right)}{k_{B}T}}\exp \left[-\frac{\Delta G_a\left({\sigma }_P+\sigma \left(t\right)\right)}{k_{B}T}\right]$$ (7)

where k_on,dilute is the association constant in the dilute, low-density limit, where crowding effects are expected to be negligible. Bulk ion concentrations and applied voltages, rate constants, and bulk target concentration were held constant, with k_on,dilute ∼ 10⁴ M⁻¹s⁻¹, k_off ∼ 10⁻⁵ s⁻¹, and C_T ∼ 1 μM (43).

The activation barrier ΔG_a is determined by the energy of inserting the DNA target into the DNA probe layer against the electrostatic potential of the charge density. Since the hybridization of DNA oligos in dilute solution is rate-limited by the nucleation of ∼3 bp (44), the electrostatic energy barrier is computed by summing the discrete (Manning-condensed) backbone charges on a DNA target inserted three basepairs into the layer surface and extended linearly outward (Fig. S2). When the calculated activation barrier ΔG_a < 1, the association constant is set to the dilute association constant, i.e., k_on = k_on,dilute, so the hybridization kinetics cannot occur faster than the dilute low-density limit. In general, this calculation yields a nonlinear dependence of activation barrier on total DNA density, necessitating the numerical approach used here. However, in the limit of strong screening at high salt concentrations, the numerical model is reasonably consistent with the linearized model developed by Halperin et al. (24).

Results

Validation of the electrostatic model by comparison with experiment

We first examined how different assumptions for mobile ion screening in the DNA layer itself influenced the predicted hybridization as a function of density. We varied the amount of screening through the excluded volume of the DNA by changing the density at which DNA would occupy the entire free volume. These saturated DNA densities were set to σ_sat = 10¹³/cm², 3 × 10¹³/cm², and 10¹⁴/cm², as well as the limiting case in which mobile counterions are excluded from the layer. In each case, the charge on the DNA was assumed to be screened to 55% by Manning-condensed counterions, such that even in the no-mobile-counterion case there was still a significant fraction of ions within the DNA layer. In Fig. 2 A, the normalized target densities at steady state are compared for models that allow mobile counterion screening (dashed lines), the model with no mobile counterions (continuous lines), and experimental data (markers) from Gong and Levicky (3) over a range of initial probe densities. Unexpectedly, the electrostatic model with no mobile counterions shows the best agreement with experimental data. In comparison, the modified models that allow mobile counterions significantly overestimate the target density, and are progressively worse with increasing σ_sat (more screening). At lower probe densities (σ ∼ 10¹²/cm²), all of the models converge, because the charge densities are small and therefore the electrostatic effects are relatively weak.

Figure 2.

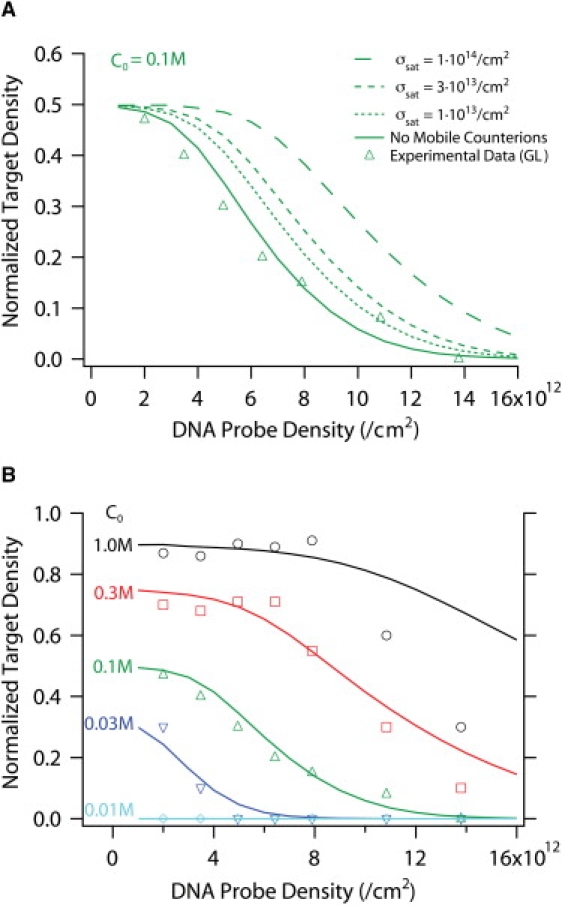
(A) Normalized target hybridization at varying probe densities and C₀ = 0.1 M from electrostatic models and experimental data. Dashed lines correspond to models allowing varying mobile counterions in the layer, continuous line corresponds to model with no mobile counterions, and markers are experimental data replotted from Gong and Levicky (4). As the threshold density σ_sat increases, the target hybridization is systematically overestimated because the electrostatic barriers are underestimated. (B) Normalized target density at varying probe densities, ion concentrations, and zero voltage. The continuous line corresponds to the electrostatic model with no mobile counterions, and markers are experimental data replotted from Gong and Levicky (4). The model has been empirically modified for better agreement with data, including a lower binding affinity and a numerical constraint at low densities (Supporting Material).

These results suggest that mobile counterions play a limited role in screening within the layer at high probe densities. Although this premise is counterintuitive, the magnitudes of the repulsive electric fields are not as large as one might imagine, especially given the 55% effective charge density after Manning condensation. Consider a high probe density of σ ∼ 3 × 10¹³/cm² and an ion concentration of C₀ = 0.3 M. The maximum electrostatic potential in the layer is ∼130 mV (Fig. S1), and thus the electrostatic driving energy to insert a positive counterion is only ∼5 k_BT at room temperature (130 meV). Given the relatively small magnitude of this energy, it is plausible that steric crowding effects could largely exclude mobile counterions. The reduction in hybridization at high DNA densities may also arise from increased steric hindrance to target insertion, which would require a large number of base pairings to nucleate hybridization. However, these models have very different responses to applied voltage compared to our previous experimental results (18). Thus, given the fits to the data and the reasonable electrostatic energies involved, we believe the most appropriate model is one in which mobile counterions are largely excluded from high density DNA layers. Additional validation through future experiments and molecular-scale simulations will help refine the model of DNA layers at high densities.

In Fig. 2 B, the normalized hybridization fraction obtained using an electrostatic model with no mobile counterions (lines) is compared with the complete experimental data (markers) over both varying probe densities and bulk ion concentrations. The implementation of this limiting case appears to correctly reproduce the experimental data over two decades in bulk ion concentration and one decade in DNA probe density, although there are some discrepancies at the highest salt concentration and probe densities. This may reflect nonspecific basepairing or other steric effects that are not treated in this electrostatic model.

Surprisingly, in the limit of low probe densities, the experimentally measured normalized hybridization densities appear to plateau at values well below unity. For example, θ_ss ∼ 0.9 at low probe densities for C₀ = 1.0 M, θ_ss ∼ 0.75 at C₀ = 0.3 M, etc. To our knowledge, this counterintuitive trend has not been observed elsewhere, and its physical origin remains unclear. We could not account for this result using any electrostatic model described here, since complete hybridization is expected at low DNA densities and relatively high ion concentrations. Instead, we implemented an empirical modification that constrained the maximum allowed hybridization at low probe densities (Supporting Material). Further experiments may be necessary to clarify this behavior.

DNA surface hybridization varies with probe density and salt concentration

In Fig. 3, the normalized target hybridization at steady-state θ_ss is shown as a function of initial DNA probe density and (bulk) ion concentration. This model reproduces the three hybridization regimes observed experimentally by Gong and Levicky (3), and the regimes are labeled using their terminology, i.e., psuedo-Langmuir (PL), suppressed hybridization (SH), and no hybridization (NH). For simplicity, the empirical modifications discussed in the previous section have not been incorporated into the following results.

Figure 3.

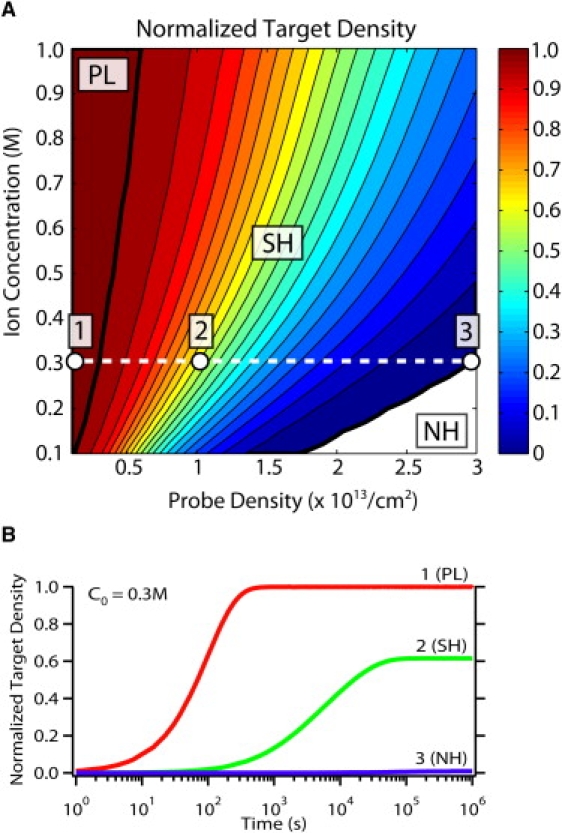
(A) Normalized target hybridization as a function of probe density and ion concentration. The PL regime has ∼100% hybridization at low probe density and high ion concentrations, the SH regime has <100% hybridization at intermediate probe densities and ion concentrations, and the NH regime has ∼0% hybridization at high probe densities and low ion concentrations. (B) Representative hybridization kinetics for these three regimes at a bulk ion concentration of C₀ = 0.3 M and probe densities of σ_P = 10¹²/cm², 10¹³/cm², and 3 × 10¹³/cm², corresponding to the labeled points labeled 1–3 in panel A.

At low probe densities and high ion concentrations, the PL regime is characterized by ∼100% hybridization. A representative hybridization kinetic curve is shown in Fig. 3 A for this regime at low probe density σ_P = 10¹²/cm² and bulk ion concentration C₀ = 0.3 M, corresponding to point 1 in Fig. 2 B. The hybridization kinetics observed in this regime are consistent with first-order Langmuir kinetics due to the low charge densities both before and after hybridization is completed. As a result, both the initial electrostatic barrier and the change in electrostatic barrier during hybridization are small, and the effective association constant is approximately the same as the dilute association constant throughout the reaction, i.e., k_on ∼ k_on,dilute. The hybridization kinetics are well approximated by a single exponential using the dilute association constant (Fig. S3), with a fast characteristic timescale τ ∼ (k_on,diluteC_T)⁻¹ ∼100 s, since k_off ≪ k_onC_T.

At increasing probe densities and decreasing ion concentrations, the SH regime is characterized by incomplete hybridization (<100%). Representative hybridization kinetics for this intermediate probe density regime (σ = 10¹³/cm²) are shown in Fig. 3 B, corresponding to point 2 in Fig. 3 A. In this instance, there is suppression of the steady-state hybridization fraction (θ_ss = 62%) and the characteristic timescale increases at least 60-fold (τ ∼ 6000 s). It should be noted that these hybridization kinetics are more complex than the simple Langmuir model because the initial electrostatic barrier is appreciable and increases significantly as hybridization proceeds. Since the association constant decreases exponentially with barrier energy (and target hybridization), the hybridization reaction reaches steady state when the reactive association flux becomes comparable to the reactive dissociation flux for some critical hybridization density.

Given the temporal distribution of binding affinities, it is not surprising that the hybridization kinetics are poorly fit by a single exponential. Hybridization kinetics in this regime are often described using a stretched exponential θ(t) ∼ 1 − exp[−(t/τ)^α], where smaller values of α (0 < α < 1) correspond to wider distributions (Fig. S3). This parameter is not used here, because the distribution of barrier energies can be directly determined from the model and is directly related to the hybridized target number density. For comparison purposes, we estimate an effective characteristic timescale in this regime where θ (τ)/θ_ss ∼ (1 − e⁻¹) ∼ 0.63, and find that it falls between the fast and slow limits of τ_fast ∼ (k_onC_T)⁻¹ = 10² s and τ_slow ∼ k_off⁻¹ = 10⁵ s. The distribution of characteristic timescales for these parameters is shown in Fig. S4.

In the limit of high probe densities and low ion concentrations, there is a regime where NH occurs. A representative hybridization kinetic curve is shown in Fig. 3 B for this regime at high probe density σ_P = 3 × 10¹³/cm², corresponding to point 3 in Fig. 3 A. Here the initial electrostatic barrier of the DNA probe layer is too high, and minimal hybridization occurs. These high barriers are associated with the slow limit of hybridization, i.e., τ_slow ∼ k_off⁻¹ = 10⁵ s.

The hybridization cutoff boundary between the SH and NH regimes occurs for high (initial) electrostatic barriers ΔG_a ≥ 13 k_BT (Fig. S5). This boundary scales as ∼σ_P/HC₀, the ratio of the charge density contained in the probe layer compared to the bulk ion concentration in solution. This is consistent with the cutoff observed experimentally by Gong and Levicky (3), as well as scaling arguments presented by Halperin et al. (24). A second boundary occurs between PL and SH regimes when electrostatic effects become significant enough to suppress DNA hybridization at ΔG_a ≥ 2.5 k_BT. This boundary scales as ∼2σ_P/HC₀^1/2, since the total charge density at 100% hybridization is twice the initial probe density, and the spatial extent of the electrostatic repulsion scales roughly with the Debye screening length λ_D ∼ C₀^−1/2.

Experimental measurements of DNA hybridization densities and kinetics are often performed at low probe densities in the PL regime so that they will exhibit simple Langmuir kinetics. However, the maximum target number density is never achieved in the PL regime, despite 100% hybridization. In Fig. 4 A, the hybridized target number density σ is shown as a function of initial DNA probe density and ion concentration. At fixed ion concentration (i.e., C₀ = 0.3 M), as the probe density increases initially in the PL regime (point 1 in Fig. 4 A), the target number density σ also increases linearly with probe density σ_P, since hybridization is limited primarily by the number of probes available. Further increases of probe density in the SH regime increase the number of available probes, but also increase the electrostatic potential outside the DNA probe layer that repels incoming DNA targets and leads to a kinetic suppression of hybridization. At some intermediate critical probe density (point 2 in Fig. 4 A), these two mechanisms are roughly comparable, allowing the maximum number of targets to hybridize. As the probe density is increased further, the electrostatic suppression begins to dominate, culminating in the NH regime (point 3 in Fig. 4 A). The corresponding hybridization kinetics for each of these three cases are plotted in Fig. 4 B, which shows that point 2 in the SH regime has the highest target number density σ, even though the fraction of hybridized probes is only θ_ss ∼ 60%.

Figure 4.

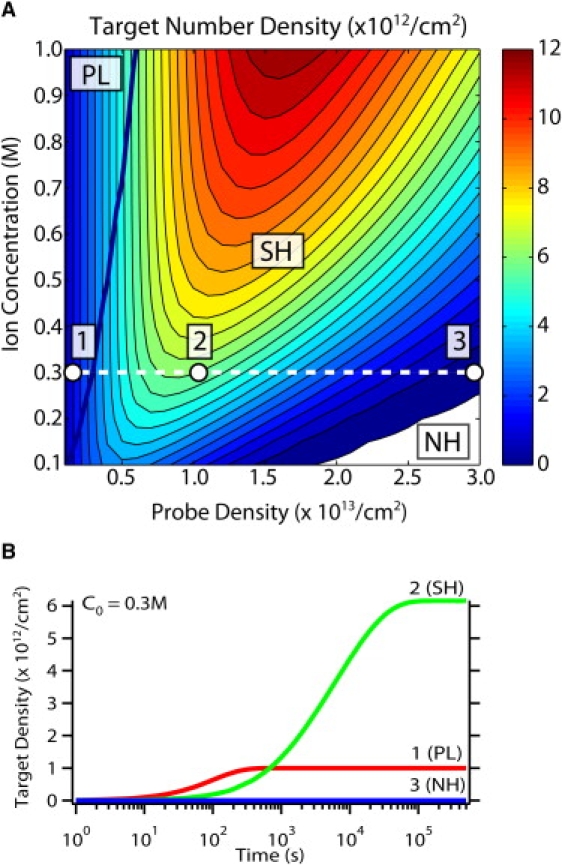
(A) Hybridized target number density as a function of probe density and ion concentration. The maximum target densities always occur in the SH regime, even though <100% of the probes are hybridized. (B) Representative unnormalized hybridization kinetics for these three regimes at an ion concentration of C₀ = 0.3 M and probe densities of σ_P = 10¹²/cm², 10¹³/cm², and 3 × 10¹³/cm², corresponding to the labeled points labeled 1–3 in panel A.

In general, increasing the ion concentration will increase the optimum probe density as well as the maximum target number density at this optimum. This model predicts that the optimum conditions yield a target density of σ = 1.2 × 10¹³/cm² at the highest ion concentration considered, C₀ = 1 M, and an intermediate probe density in the SH regime of approximately σ_P ∼ 1.6 × 10¹³/cm². It should be noted that the characteristic timescale here is ∼40 times slower than the PL regime. Although this timescale (τ ∼ 4000 s ∼ 1 h) is not experimentally prohibitive, driving the reaction to completion may require considerably longer timescales under more realistic experimental conditions, such as lower target concentrations. The use of applied voltages to compensate for this electrostatic kinetic barrier is considered in the next section.

DNA surface hybridization with applied voltage

The critical role played by electrostatics in suppressing DNA hybridization led our group (18) and the Georgiadis group (34) to experimentally examine the effects of applying a voltage to the (electrode) surface upon which the DNA probes are immobilized. In Fig. 5, the normalized target hybridization at steady-state θ_ss is shown as a function of the initial DNA probe density and applied voltage at ion concentration C₀ = 1 M.

Figure 5.

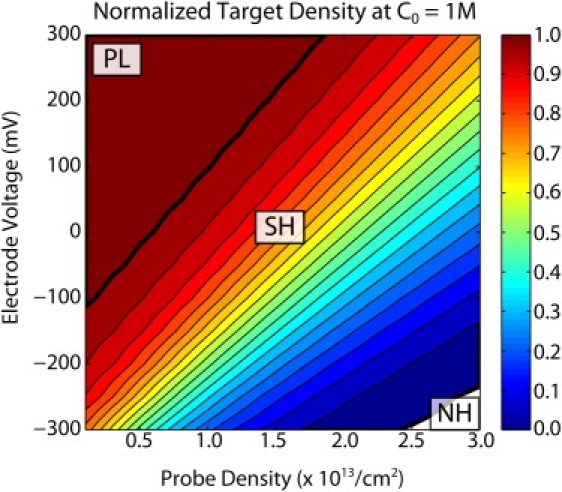
Normalized hybridization as a function of probe density and applied voltages. Three hybridization regimes exist that are analogous to the ones described previously at varying ion concentrations. The PL regime has ∼100% hybridization at low to medium probe densities and positive voltages, the SH regime has <100% hybridization at medium to high probe densities, and the NH regime has ∼0% hybridization at high probe densities and negative voltages.

The application of more positive voltages can be compared with increasing ion concentration, leading to three hybridization regimes analogous to the ones shown in Fig. 3. As the voltage is increased to more positive values, it compensates for the electrostatic barrier from the DNA, shifting the PL regime to higher probe densities. Similarly, as the voltage is decreased to more negative values, it augments the electrostatic barrier and shifts the NH regime to lower probe densities. The boundaries between regimes appear to have an approximately linear dependence on probe density σ_P and applied voltage V, scaling as ∼σ_P/V for the SH/NH boundary and ∼2σ_P/V for the PL/SH boundary, since the total DNA density cannot exceed twice the probe density (Fig. S6).

The effect of applied voltages becomes evident in Fig. 6 A, where the hybridization enhancement is plotted as the ratio of the hybridization densities at applied voltage and zero voltage. At low to intermediate probe densities in the PL regime, there is minimal enhancement of DNA hybridization at positive voltage, since nearly complete hybridization is already achieved at zero voltage. For example, at a probe density of σ_P ∼ 10¹³/cm², the hybridization densities at +300 mV and 0 mV are roughly comparable, whereas hybridization is strongly suppressed at −300 mV, consistent with measurements by the Georgiadis group (34).

Figure 6.

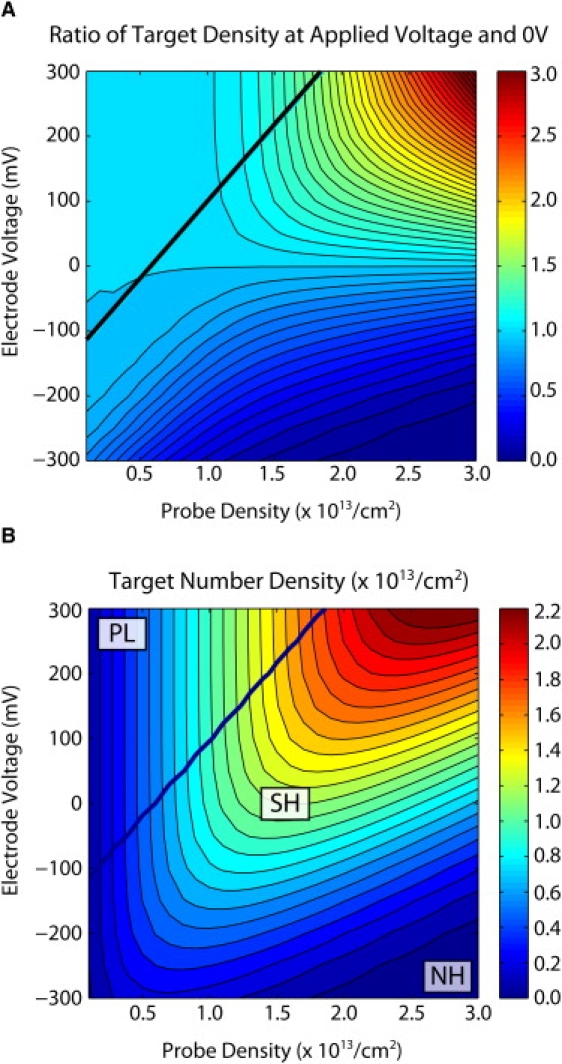
(A) Ratio of hybridization densities at applied voltage and zero voltage. Large enhancements of DNA hybridization can be achieved at high probe densities and positive voltages. (B) Hybridized target number density as a function of probe density and applied voltage at C₀ = 1 M. The maximum target densities increases approximately linearly with positive voltage and dominates over the electrostatic suppression of the probes.

In contrast, at high probe densities in the SH regime, the high electrostatic barriers to hybridization can be canceled out at positive voltages, allowing strong enhancement of hybridization densities. For example, the largest enhancement occurs at a probe density of σ_P = 3 × 10¹³/cm², where there is a threefold increase in hybridization density at +300 mV relative to 0 mV, in good agreement with measurements from our group (18). This corresponds to the global maximum for the hybridized target number density, i.e., σ ∼ 2.2 × 10¹³/cm² at +300 mV (point 3 in Fig. 6 B), using label-free measurements by Gong et al. (8) as a reference for σ ∼ 7 × 10¹² /cm² at 0 mV (point 2 on Fig. 6 B). This decrease in electrostatic barrier at positive voltages is also predicted to accelerate the hybridization kinetics by 20-fold (Fig. S7).

The optimum conditions for globally maximizing hybridized target number density thus occur under high voltages, high ion concentrations, and high probe densities. This last result is somewhat counterintuitive in comparison to the scenarios at zero voltage, where the maximum target number density occurs at some intermediate probe density. Indeed, at positive voltages greater than +300 mV (Fig. 6 B) and at lower salt concentrations with weaker screening (Fig. S8, Fig. S9, Fig. S10, and Fig. S11), suppression of hybridization due to the electrostatic barrier becomes more pronounced. Under these conditions, the optimum probe densities will again be at intermediate values, which will not permit such high target hybridization densities.

Experimentally, there exist physical limitations that prevent further optimization of these parameters. First, applied voltages > V = +300 mV lead to Faradaic currents on gold electrodes, which are well known to denature biomolecules due to pH changes and can also break gold-thiol bonds, although they can have advantageous effects such as the enhancement of mass transport (45). Second, σ_P ∼3 × 10¹³/cm² represents approximately the highest DNA probe density that can be achieved without the use of divalent cations (33).

Discussion

A key assumption of this model is that all probes can be hybridized and suppression arises purely from the electrostatic barrier. It is unclear whether this assumption is valid in the limit of high probe densities. For example, Hagan and Chakraborty (26) considered the random deposition of DNA probes using a Monte-Carlo simulation of two-dimensional hard disks, and predicted that a density-dependent fraction of these probes would be situated too close together to allow hybridization. This clustering effect would certainly present an additional limitation to the enhancement of target hybridization density even when positive voltages are applied. Recent work by Mirmomtaz et al. (13) suggested that nanografting techniques employing an atomic force microscope tip can be used to promote lateral ordering in DNA probe arrays, leading to an enhancement of DNA target hybridization.

Crowding effects at high probe densities may have additional unexpected consequences. The use of a Langmuir model implicitly assumes that targets hybridize uniquely to a single probe due to the molecular specificity imparted by the target sequence and length (16). However, recent work has suggested the possibility of targets hybridizing with two separate probes in close proximity (2,11). This scenario can be further complicated by the particular techniques used to prepare the probe layer. For instance, photolithographic synthesis can generate polydispersity in the probes, whereas the probe orientations are less controlled when they are spotted or physisorbed (1). Nevertheless, these scenarios should still result in the probes adopting some charge density profile that has a distribution of DNA probe ends near the outer edge, so the model described here should be useful for gaining qualitative insight. This model should be similarly applicable for treating DNA hybridization where local curvature is important, such as DNA-decorated gold nanoparticles (14) or cantilevers (7), although the electrostatic effects will be shorter-ranged in these geometries.

Finally, this model does not treat mass transport effects (17), which may further slow surface hybridization as the local concentration of targets becomes depleted in the diffusion-limited regime. The application of positive voltages to enhance hybridization density and kinetics, in combination with microfluidic technologies that allow convective mixing, represent a powerful route toward enhanced biosensor performance.

Conclusions

In this work, a numerical model is presented that explores the dependence of DNA surface hybridization on probe density, ion concentrations, and applied voltage. The model explicitly treats electrostatics using a fully nonlinear modified Poisson-Boltzmann scheme that accounts for variable conditions as hybridization proceeds. This model leads to predictions of suppressed DNA hybridization densities and kinetics that are in excellent quantitative agreement with previous experimental measurements.

Historically, DNA surface hybridization has been conducted in the limit of low probe densities, where complete hybridization occurs and kinetics are relatively fast. However, the density of available probes ultimately limits hybridization densities in this regime. Instead, in the absence of voltage, the optimum conditions are shown to occur at intermediate probe densities and high ionic salt concentrations, despite partial inhibition of hybridization density and kinetics.

The global conditions for maximizing the hybridized target number density are shown to occur with positive applied voltage, high probe densities, and high ion concentrations. Although ordinarily these high probe densities strongly suppress hybridization at zero voltage, electrostatic effects are dramatically reduced with applied voltage. As a result, a threefold enhancement in hybridization target density and accelerated kinetics can be achieved even at very high probe densities. An unexpected result of this work is that mobile counterions appear to be largely excluded from the DNA layer at high densities, suggesting that electric fields in this regime can be unusually effective for precisely tuning the energy landscape of hybridization to a particular binding affinity. These ideas may prove to be useful for tuning the applied voltage to reduce the hybridization of mismatched DNA targets, thereby enhancing selectivity (46).

Supporting Material

Eighteen figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00347-4.