Molecular Dynamics Free Energy Calculations to Assess the Possibility of Water Existence in Protein Nonpolar Cavities

Abstract

Are protein nonpolar cavities filled with water molecules? Although many experimental and theoretical investigations have been done, particularly for the nonpolar cavity of IL-1β, the results are still conflicting. To study this problem from the thermodynamic point of view, we calculated hydration free energies of four protein nonpolar cavities by means of the molecular dynamics thermodynamic integration method. In addition to the IL-1β cavity (69 ų), we selected the three largest nonpolar cavities of AvrPphB (81 ų), Trp repressor (87 ų), and hemoglobin (108 ų) from the structural database, in view of the simulation result from another study that showed larger nonpolar cavities are more likely to be hydrated. The calculations were performed with flexible and rigid protein models. The calculated free energy changes were all positive; hydration of the nonpolar cavities was energetically unfavorable for all four cases. Because hydration of smaller cavities should happen more rarely, we conclude that existing protein nonpolar cavities are not likely to be hydrated. Although a possibility remains for much larger nonpolar cavities, such cases are not found experimentally. We present a hypothesis to explain this: hydrated nonpolar cavities are quite unstable and the conformation could not be maintained.

Introduction

Interiors of proteins are not completely filled with protein atoms, but have several cavities (1). In some cases, protein cavities contain water molecules (1–3), and such internal water molecules can play important roles in many biological processes, e.g., in redox reaction (4), electron (5,6) and proton transfer (7,8) in proteins, and catalysis of substrates (9,10). Internal water molecules also affect the thermodynamic stability of proteins. A systematic mutation analysis of Ile to Ala (11) showed that inserting one water molecule into cavities created by mutation generally produces a free energy gain of 1–2 kcal/mol. There are many other experimental (12–14) and theoretical (12,15–24) studies on internal water molecules that indicate the biological importance of water.

Despite many characterization studies on protein cavities performed so far, little is known about the cases in which no polar sites (i.e., atoms serving as a hydrogen-bond donor or acceptor) appear on the cavity surface. Whether such particular cavities, referred to as nonpolar cavities, contain water molecules remains uncertain. An analysis of 121 protein structures that included high-resolution data indicated that no water molecules were found for any of the cavities that lacked surface polarity (3). However, the result has to be carefully understood that even if no water molecules are observed crystallographically, another possibility remains. Water molecules in nonpolar cavities may be in a dynamic, disordered state without any directional interactions such as hydrogen bonds (25,26). It will be difficult to detect such water molecules from conventional x-ray or neutron crystal analyses.

Interleukin 1β (IL-1β) is well known for the large nonpolar cavity ∼69 ų (note that all cavity volumes shown hereafter are based on the Connolly surface calculations that we performed; see Materials and Methods). Several experiments have been performed to measure the state of this cavity, but the results are not consistent with each other; different experiments led to different conclusions on the existence of water in the cavity. In 1995, Ernst et al. (26) reported that several signals were detected by water-selective two-dimensional nuclear magnetic resonance (NMR) spectroscopy, which implied the existence of water molecules. In 1999, Yu et al. (25) maintained (based on an electron density analysis of the cavity) that two water molecules reside there. However, Quillin et al. (27), in 2006, reached the opposite conclusion: independent analysis of the electron density showed that the nonpolar cavity of IL-1β was not hydrated. And in other x-ray (25,27–31) and NMR (32) structure data, no water molecules were observed in the cavity. Thus, it remains controversial whether the nonpolar cavity of IL-1β is hydrated.

Because it is currently difficult to draw a definite conclusion from experiments, a theoretical approach by molecular simulation will be useful. Thermodynamic stability of cavity hydration can be theoretically evaluated by molecular simulation techniques, which have been applied to various protein cavities, i.e., BPTI (22), Barnase (22), tetrabrachion (16), and T4-lysozyme (12). However, all of these cavities were polar. Nonpolar cavities have not been studied extensively so far. Somani et al. (33) and Zhang and Hermans (34) carried out molecular dynamics (MD) simulations on the nonpolar cavity of IL-1β. However, these studies cannot resolve the controversies about the nonpolar cavity either, because their results were different from each other. Somani et al. showed that four water molecules stably exist within the cavity, whereas Zhang and Hermans showed that the cavity is empty. Vaitheeswaran et al. (35) performed Monte Carlo simulations to calculate hydration free energies of an ideal nonpolar cavity of spherical shape and fullerenes C₁₄₀ and C₁₈₀. Their result showed that hydration of the nonpolar sphere becomes stable only when its diameter is >10 Å (we calculated the volume to be ∼137 ų; see Materials and Methods). These sufficiently large cavities are able to contain at least three-to-four water molecules, so the water molecules can stably exist within the cavity by forming a hydrogen-bonded cluster.

Size dependence of the hydration free energy reported by Vaitheeswaran et al. (35) has provided valuable insight into the possibility of hydration of nonpolar cavities. According to their result of size dependence, hydration of the IL-1β nonpolar cavity with the volume ∼69 ų is judged to be unstable. However, their calculation was performed using an ideal, solid spherical cavity, and such calculation did not consider the nature of protein cavities, i.e., their anisotropy and flexibility. Hydration of nonpolar cavities in real proteins should be carefully addressed, in order to permit consideration of these effects.

Here, to answer the question of whether hydrated nonpolar cavities exist in proteins, we calculated the hydration free energies of protein nonpolar cavities by using MD simulations that were themselves based on a model that took the structural anisotropy and flexibility of protein cavities into account. In addition to the cavity of IL-1β, the three largest protein nonpolar cavities were chosen from the structural database: Pseudomonas avirulence protein (AvrPphB), Trp repressor, and trematode hemoglobin. These cavities have the volumes 81, 87, and 108 ų, respectively, which belong to the largest class of existing protein nonpolar cavities. As shown by the result of Vaitheeswaran et al. (35), larger cavities are more likely to be hydrated, although even our largest cavity (108 ų) is insufficient for stable hydration.

In this study, we performed MD simulations using two protein models, namely, flexible and rigid. The flexible model allows protein atoms around the cavity to fluctuate and move, but the rigid one does not. From our results for free energies, we were able to clarify the effects of anisotropy and flexibility on the cavity, and found that these effects were not so large as to cause any essential change of the hydration thermodynamics. This means hydration of the four largest cavities studied here are energetically unfavorable. For smaller cavities, hydration is even less probable. For larger nonpolar cavities, a possibility remains; however, such hydration is not greatly expected, as discussed later. With this conclusion in mind, we again discuss the unsolved problem with the IL-1β nonpolar cavity.

Materials and Methods

Selection of proteins with a large nonpolar cavity

Four nonpolar cavities of IL-1β, AvrPphB, Trp repressor, and hemoglobin were chosen as follows. To begin, we prepared a data set of 1371 protein structures that included 100 structures selected by Word et al. (36) and a second data set of 1271 structures from the PISCES server (37) (results obtained July 21, 2007). The first data set was used because all the structures were measured at high resolution (<1.7 Å). The second data set of structures was selected to accord with the criteria of 20% sequence identity, 1.6 Å resolution, and R-factor 0.25. Because 12 structures were found to be in both data sets, a total of 1359 nonredundant structures were actually used.

Next, the 1359 structures were analyzed by the Molecular Surface Package (MSP) (38) to search for the cavities. Note that a “protein cavity” was defined as a space that is enclosed by the Connolly surface (39) and is separated from the protein exterior. The Connolly surface was calculated using a probe sphere of a radius 1.4 Å. Atomic radii 1.54, 1.45, and 1.57 Å were used for hydroxyl and carbonyl oxygen atoms, carboxyl oxygen atoms, and peptide nitrogen atoms, respectively. For other atoms, a default setting (38) was used. Before executing the MSP program, protein hydrogen atoms and any molecules other than proteins, such as crystallographic water, were removed.

From the MSP analysis, we found 5948 cavities; among them, 859 had no heavy atoms other than carbon on the surface. We defined them as “nonpolar cavities”. Volumes of these nonpolar cavities were 12–108 ų (Fig. 1). We chose the three largest cavities of AvrPphB (81 ų, 1UKF (40)), Trp repressor (87 ų, 2WRP (41)), and hemoglobin (108 ų, 1H97 (42)), considering that larger cavities are more expected to be hydrated (35). In addition, the large nonpolar cavity of IL-1β (69 ų) was selected because of many reports about this cavity (25–27). Several structural data of IL-1β are deposited in PDB. We used the structure of 9ILB (25) in accordance with the previous theoretical work (33). We carefully checked the neighbor regions of these cavities, and confirmed that all polar sites are at least 1.9 Å away from the cavity surface. Thus, internal water molecules cannot make a hydrogen bond unless the cavity changes structurally (shown later in Results).

Figure 1.

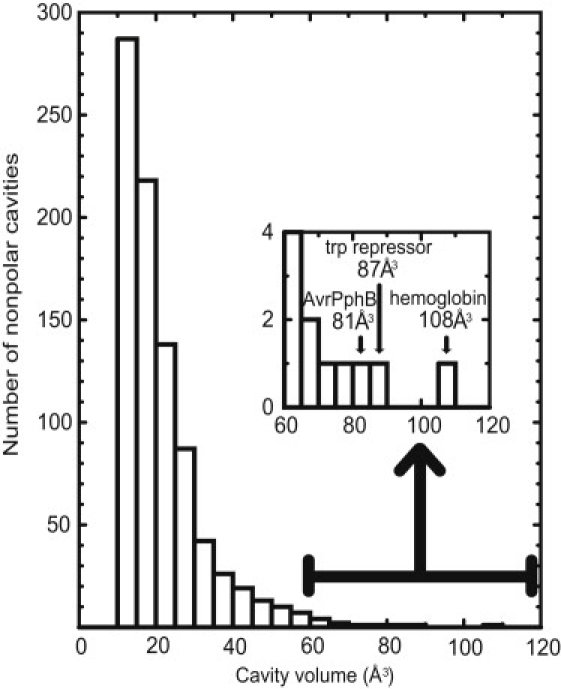
Distribution of volumes of 859 nonpolar cavities found using the MSP (38) (see Materials and Methods). (Inset) Enlarged view for the range from 60 to 120 ų.

Shapes and locations of the four selected nonpolar cavities are shown in Fig. 2. The nonpolar cavity of IL-1β is located at the center of the protein. The other cavities are located near the protein surface. The hemoglobin cavity has a dumbbell shape, while the others are nearly spherical. The cavity of the Trp repressor is located in the interface of the homodimer, so it has a twofold rotational symmetry.

Figure 2.

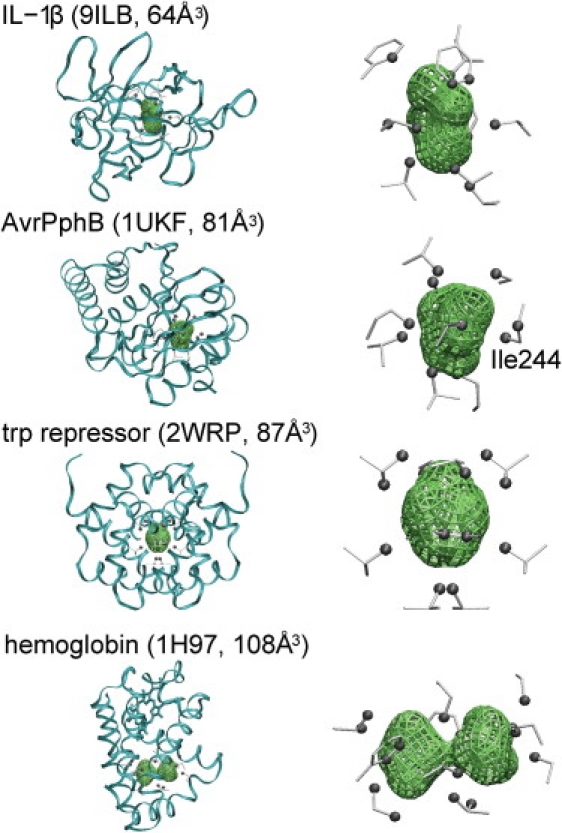
Cavity locations of the four selected proteins (left) and the shapes of nonpolar cavities (right). Cavity surfaces are shown by green mesh. Side chains of residues, which construct the cavities, are shown by gray sticks. Among them, atoms exposed to the cavity surface are shown by gray spheres. The figures were created by using VMD (62).

Method for the free energy calculation

Hydration free energy of protein cavities was evaluated by the statistical mechanics formulation proposed by Roux et al. (15). We assume a protein cavity that would be large enough to contain n water molecules. Using the Roux's formulation, we can calculate the free energy change of transferring n water molecules from a bulk region to the protein cavity, $\Delta G_{\text{hyd}}^{0\to n}$, as

$$\Delta G_{\text{hyd}}^{0\to n}=\Delta G_{\text{cavity}}^{0\to n}-n\Delta G_{\text{bulk}}^{0\to 1}-n{k}_{\text{B}}T\ln \left[{\rho }_{\text{bulk}}{\left(2\pi k_{\text{B}}T/k_{\text{harm}}\right)}^{3/2}\right]+k_{\text{B}}T\ln n!,$$ (1)

where k_B is the Boltzmann constant, T is the temperature, and ρ_bulk is the density of water in the bulk phase. The value $\Delta G_{\text{cavity}}^{0\to n}$ is the free energy difference between following two protein-water systems. One system is given by the potential

$$U_0+u^{\text{res}},$$

in which n water molecules have no interactions with the rest of the system, but are weakly restrained around an internal cavity site r^∗ with the harmonic potential acting on the position of water oxygen r_i, as

$$u^{\text{res}}={\sum }_{i=1}^n\left(1/2\right)k_{\text{harm}}{\left({\mathbf{r}}_{\text{i}}-{\mathbf{r}}^{\ast }\right)}^2\text{.}$$

Another system is given by a potential U₁, in which n water molecules interact with the rest of the system and reside within the cavity. Using these potentials, $\Delta G_{\text{cavity}}^{0\to n}$ is written by

$$\Delta G_{\text{cavity}}^{0\to n}=-k_{\text{B}}T\ln \frac{{\int }_{\text{cavity}}\text{d}{\mathbf{r}}_1\cdots {\int }_{\text{cavity}}\text{d}{\mathbf{r}}_n{\int }_{\text{bulk}}\text{d}{\mathbf{r}}_{n+1}\cdots {\int }_{\text{bulk}}\text{d}{\mathbf{r}}_{\text{N}}\int d\Gamma e^{-U_1/{\text{k}}_{\text{B}}\text{T}}}{\int \text{d}{\mathbf{r}}_1\cdots \int \text{d}{\mathbf{r}}_n{\int }_{\text{bulk}}\text{d}{\mathbf{r}}_{n+1}\cdots {\int }_{\text{bulk}}\text{d}{\mathbf{r}}_N\int d\Gamma e^{-\left[U_0+{\sum }_1^n(1/2)k_{\text{harm}}{\left({\mathbf{r}}_{\text{i}}-{\mathbf{r}}^{\ast }\right)}^2\right]/{\text{k}}_{\text{B}}\text{T}}},$$ (2)

where N is the total number of water molecules in the cavity and bulk regions, and $\int d\Gamma$ denotes the integral over the configurations of atoms other than water (i.e., protein and ions).

The value $\Delta G_{\text{cavity}}^{0\to n}$ was calculated by the thermodynamic integration passing through the intermediate systems between the systems U₁ and U₀+ u^res. In this study, we change a system from U₁ to U₀ + u^res by following three processes:

$$\left(U_1^{\text{ele}},U_1^{\text{vdW}},0\right)\to \left(U_1^{\text{ele}},U_1^{\text{vdW}},u^{\text{res}}\right)\to \left(U_0^{\text{ele}},U_1^{\text{vdW}},u^{\text{res}}\right)\to \left(U_0^{\text{ele}},U_0^{\text{vdW}},u^{\text{res}}\right)\text{.}$$ (3)

This is achieved by changing three coupling parameters (λ^ele, λ^vdW, and λ^res) for electrostatic, van der Waals, and restraining potentials to be

$$\left(0,0,0\right)\to \left(0,0,1\right)\to \left(1,0,1\right)\to \left(1,1,1\right)\text{.}$$ (4)

In the first and second processes, intermediate systems for

$${\lambda }^{\text{res}}=\left\{0,0.01,0.02,0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1\right\}$$

and

$${\lambda }^{\text{ele}}=\left\{0,0.25,0.5,0.75,1\right\}$$

were generated by linearly combining the two end-point systems. In the third process, the nonlinear combination with the soft-core potential (43) was used to avoid a singularity appearing near λ^vdW = 1 (44). Intermediate systems were generated for

$${\lambda }^{\text{vdW}}=\left\{0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1\right\}\text{.}$$

The value $\Delta G_{\text{bulk}}^{0\to 1}$ in Eq. 1 is the free energy difference between the two bulk water systems; one system requires that all water molecules interact with each other, and the other system requires that one water molecule, out of all of them, does not interact. The water molecule whose interaction changes between the two systems has a fixed center of mass. The value $\Delta G_{\text{bulk}}^{0\to 1}$ was evaluated using the thermodynamic integration as well, but in this case, the following two processes were employed:

$$\left(U_1^{\text{ele}},U_1^{\text{vdW}}\right)\to \left(U_0^{\text{ele}},U_1^{\text{vdW}}\right)\to \left(U_0^{\text{ele}},U_0^{\text{vdW}}\right)\text{.}$$ (5)

The coupling parameters (λ^ele, λ^vdW) change as follows:

$$\left(0,0\right)\to \left(1,0\right)\to \left(1,1\right)\text{.}$$ (6)

Intermediate systems for the $\Delta G_{\text{bulk}}^{0\to 1}$ calculation were set in the same way as in $\Delta G_{\text{cavity}}^{0\to n}$.

The third and last terms in the right-hand side of Eq. 1 are the correction terms. The former is the compensation for introducing the restraining potential (15). The latter considers the configuration overlap of n noninteracting water molecules.

In principle, the resultant free energy $\Delta G_{\text{hyd}}^{0\to n}$ (Eq. 1) does not depend on the restraining potentials (15). However, sampling efficiency for the configurations of restrained water (see Eq. 2) highly depends on the parameters r^∗ and k_harm. In this study, r^∗ was set to the center of the cavity. The k_harm values, 0.23, 0.28, 0.35, and 0.11 kcal/mol Ų, were used for IL-1β, AvrPphB, Trp repressor, and hemoglobin, respectively. These values were obtained from the relation (15)

$$V={\left(2\pi k_{\text{B}}T/k_{\text{harm}}\right)}^{\frac{3}{2}},$$

so that the whole space of the cavity could be sampled when interactions of internal water molecules were turned off and the restraining potential was applied. Here, V is the volume of a sphere that envelops the cavity.

System preparations and MD simulations

We carried out MD simulations for protein-water and bulk water systems to obtain the free energy changes, $\Delta G_{\text{cavity}}^{0\to n}$ and $\Delta G_{\text{bulk}}^{0\to 1}$ (Eq. 1).

Protein-water systems

For each of the IL-1β, AvrPphB, Trp repressor, and hemoglobin configurations, we prepared four systems that differed in the number of water molecules in the cavity (i.e., n = 1, 2, 3, and 4). Crystallographic water molecules were removed from the crystal structures, except in polar cavities. Hydrogen atoms were generated according to the protonation state at pH 7, and missing heavy atoms were modeled by the AMBER7 Leap module (45).

Because no water molecules were assigned for the nonpolar cavities considered here, we incorporated them into the cavities as follows. The first water molecule was placed at the center of the cavity. Further water molecules, ≤4, were sequentially inserted near the first one. Then, energy minimization was performed on each arrangement of water.

Sodium counterions, i.e., one for IL-1β, nine for AvrPphB, six for Trp repressor, and five for hemoglobin, were added for system neutralization. Approximately 6000–8000 water molecules were placed around the proteins to maintain at least 8 Å hydration layers, and then a three-dimensional periodic boundary condition was imposed.

The systems of IL-1β, AvrPphB, and Trp repressor were modeled with the OPLS-AA (46,47) and TIP3P parameters (48). The van der Waals interactions were calculated with cutoff of 9 Å, and the electrostatic interactions were calculated by the particle-mesh Ewald (49) with real-space cutoff of 9 Å. Only the hemoglobin was modeled with the GROMOS 53A6 parameters (50) because the heme parameters were not included in the OPLS-AA. This system was simulated in the GROMOS default setting (50), with simple point charge (SPC) water (51) and twin-range cutoff of 10 and 14 Å, for van der Waals force evaluation.

For each system, simulations using both rigid and flexible models were performed. All protein atoms were fixed in the rigid model, whereas in the flexible model they were allowed to move. However, even in the flexible case, weak harmonic potentials with a force constant of 2 kcal/mol Ų were applied to the protein backbone atoms (which are >15 Šapart from the center of the cavities) to enable us to avoid translational displacement of the proteins.

All MD and free energy calculations were performed using the GROMACS 3.3.1 package (52,53). MD simulations were started from the system where n internal water molecules have full interactions, i.e.,

$$\left({\lambda }^{\text{ele}},{\lambda }^{\text{vdW}},{\lambda }^{\text{res}}\right)=\left(0,0,0\right)\text{.}$$

After steepest-descent minimization of 2000 steps, 110-ps MD simulations were carried out at 300 K and 1 atm. Subsequently, the system was updated along the path of λ (see Eqs. 3 and 4) by gradually reducing the interactions of n water. At each stage of λ, 10-ps equilibration and 100-ps production runs were carried out. We confirmed the validity of this trajectory length by additionally performing the calculation with different settings, 5-ps equilibration + 50-ps production and 20-ps equilibration + 200-ps production (data not shown). At the final stage of (λ^ele, λ^vdW, λ^res) = (1,1,1), the interactions of n water were removed completely. In this way, $\Delta G_{\text{cavity}}^{0\to n}$ for any case of n = 1–4 was directly calculated by reducing the interactions of n water molecules simultaneously, rather than one by one.

Atomic trajectories were generated by numerically solving the equation of motion with the 2-fs time step. Temperature and pressure were controlled by the Langevin thermostat and the Berendsen barostat (54), respectively. However, it should be noted that in the GROMACS 3.3.1 package, options of fixed atoms and pressure control cannot be used at the same time. Thus, the rigid MD simulations were performed with the volume fixed at a value obtained from the corresponding flexible MD simulation in which the pressure was controlled at 1 atm.

Bulk water systems

$\Delta G_{\text{bulk}}^{0\to 1}$(Eq. 1) was evaluated for two cases of TIP3P and SPC. The setting for calculating intermolecular interactions was the same as in the protein-water systems. The TIP3P and SPC water systems were constructed using 512 and 1000 water molecules, respectively. A three-dimensional periodic boundary condition was imposed on each system. The larger number of SPC water molecules is due to the usage of the long distance twin-range cutoff. After the simulation at (λ^ele, λ^vdW) = (0, 0), the system was updated by changing λ (see Eq. 5). At each stage of λ, 1-ns equilibration and 10-ns production runs were performed at 300 K and 1 atm. Other MD settings such as those for force evaluation and temperature and pressure controls, were the same as in the protein-water simulations.

Results

Rigid-model calculation: comparison with the previous results with a spherical cavity

Cavity hydration free energies obtained from the rigid-model calculation are shown in Fig. 3 (see the legend for several missing points, e.g., Trp repressor). For comparison, previous results by Vaitheeswaran et al. (35) are also shown. The previous calculations were performed on an ideal, rigid nonpolar sphere, i.e., interaction sites are uniformly distributed on the sphere. Thus, the main difference between the present and previous models is the shape of the cavities. As shown in Fig. 3, any insertion of water molecules increases the free energy monotonically, showing that hydration of nonpolar cavities is not favorable. Results from both models qualitatively agree with each other; the previous sphere model (35) is enough to make rough estimates of cavity hydration thermodynamics despite the simplicity. Small differences remain between both of the results, which may be due, in part, to the difference in the force field used.

Figure 3.

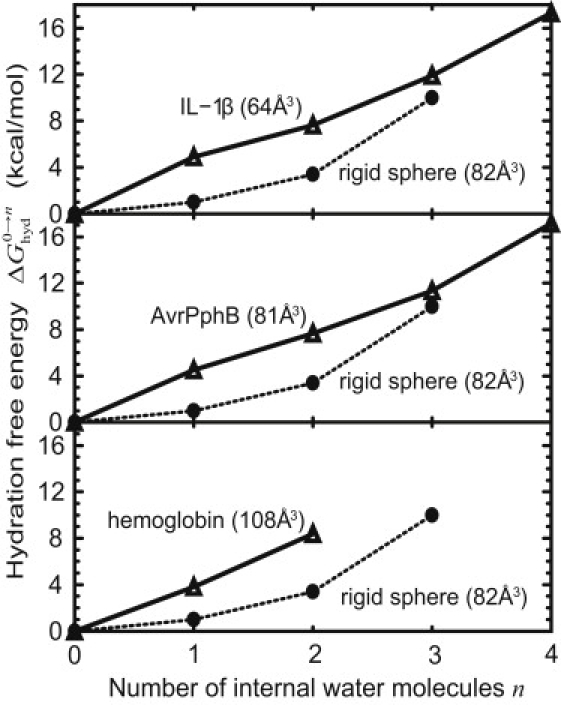
Cavity hydration free energies from the rigid-model calculations. For comparison, previous data from a spherical model (taken from Fig. 1 in (35)) are shown (solid circles). Results for Trp repressor are not shown, because water molecules got out of the cavity during the MD simulation. For the same reason, data for hemoglobin (n = 3 and 4) are missing from the figure. Details of the free energies are given in Table S1 in the Supporting Material.

Flexible-model calculation: comparison between the flexible and rigid models

Cavity hydration free energies from the flexible-model calculations are shown in Fig. 4 (some points of the data are not shown as in the rigid case; see Fig. 4 legend), together with the rigid-model results shown above (Fig. 3). The flexible model yielded lower free energies than the rigid model; however, they were all positive, which indicated that the hydration of the nonpolar cavities is unfavorable. The distinct feature from the rigid case is that the flexible model exhibits irregular changes (e.g., AvrPphB). The free energy does not monotonically increase as the number of water molecules increase. Note that these results were reproducible, so it is not due to calculation error. Independently performed simulations with different length of trajectories and different initial conditions provided almost the same results. (Protein conformational changes may occur on much longer nanosecond-to-millisecond timescales (55,56). Strictly speaking, the free energy should be obtained by averaging over all these conformations. We should mention, however, that our free energies in Fig. 4, which were calculated from only conformations near the starting x-ray structure, do not include contributions of this slow fluctuation.) We will mention the reason for the nonmonotonic increase in the last part of this section.

Figure 4.

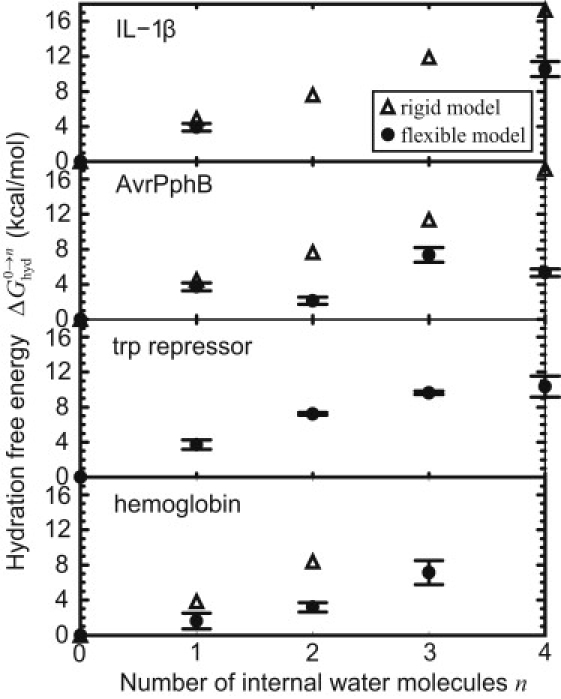
Cavity hydration free energies: comparison between the rigid- and flexible-model results. Data for IL-1β (n = 3 and 4) could not be evaluated because the water molecules got out of the cavity during the MD simulations. Errors of the free energies were estimated from three independent simulations performed with different random seed numbers for the Langevin thermostat. The errors were <0.3 kcal/mol in any case of the rigid-model results. Details of the free energies are given in Table S2 in the Supporting Material.

As expected, the flexible model induces some changes in interactions between water and cavity wall, leading to suppression of the increase in free energy. To check the free energy contribution of interactions between water and cavity, we calculated the potential energy difference ΔE^(flexible) – ΔE^(rigid) from 1-ns MD trajectories, where ΔE is the potential energy due to the interactions between internal water molecules and the surrounding residues. Residues were included in this analysis if any atom existed within 8 Å of the center of the cavity in x-ray crystal conformation. In Fig. 5, we show the ΔE^(flexible) – ΔE^(rigid) as well as ΔG^(flexible) – ΔG^(rigid) (here, ΔG^(flexible) and ΔG^(rigid) denote the flexible and rigid $\Delta G_{\text{hyd}}^{0\to n}$, respectively). We can see that both values are almost the same amount, e.g., for IL-1β (n = 4), ΔE^(flexible) – ΔE^(rigid) = −6.63 kcal/mol, while ΔG^(flexible) – ΔG^(rigid) = −6.75 kcal/mol. This component of potential energy substantially contributes to the free energy difference between the flexible and rigid models.

Figure 5.

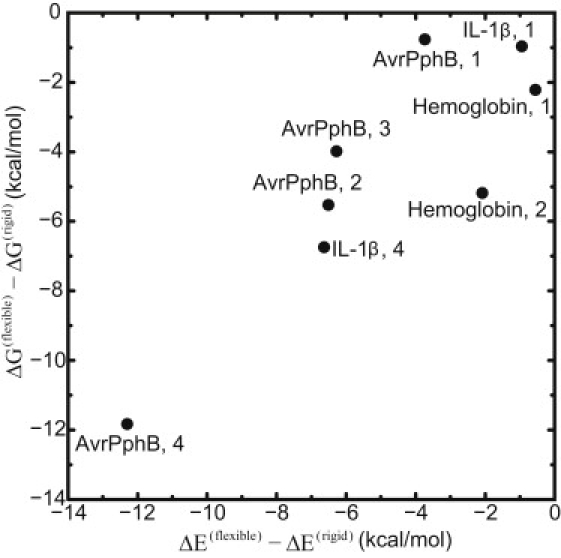
Energy differences between flexible and rigid models. ΔG is the cavity hydration free energy (Figs. 3 and 4) and ΔE is in the potential energy due to the water-cavity wall interactions. Each point has a label for the protein name and the number of internal water molecules n. Data for Trp repressor were not obtained (see the caption in Fig. 3).

We further found that the above observation comes from positional displacement of cavity-forming residues. Some parts of the cavity wall were replaced by polar atoms, and internal water molecules often made hydrogen bonds to the exposed atoms. This means that nonpolarity of the cavity cannot be maintained. We show the formation of the hydrogen bonds in Fig. 6 a, where the average numbers of protein-water and water-water hydrogen bonds calculated using 1-ns trajectories are given. No protein-water hydrogen bonds were found in rigid cases, whereas they were frequently formed in flexible cases. Thus, the flexible cavities had more hydrogen bonds than did the rigid cavities. We give a graphical example in Fig. 6 b. Only a water-water hydrogen bond was formed in the rigid cavity (Fig. 6 b, left). However, in the flexible cavity, not only the water-water hydrogen bond but also two hydrogen bonds were formed between the water and the cavity (Fig. 6 b, right). These additional hydrogen bonds are thought to help the reduction of free energy in the flexible model.

Figure 6.

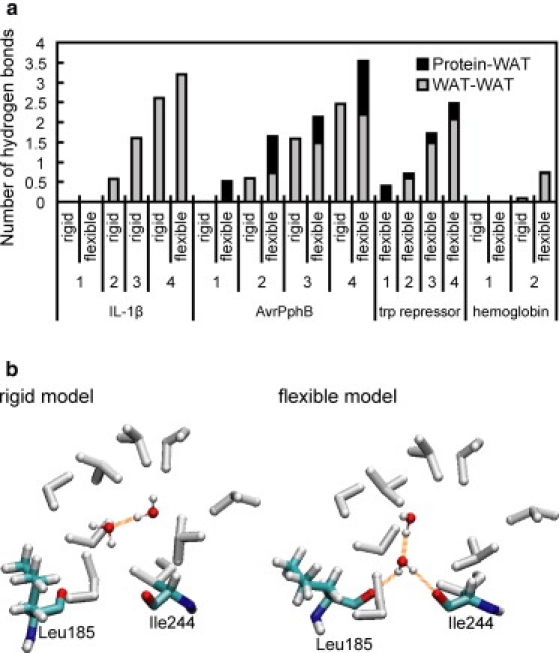
(a) Number of hydrogen bonds associated with the internal water molecules. Water-water and protein-water hydrogen bonds are shaded and solid, respectively. These were obtained by averaging over 1-ns trajectories. (b) Typical snapshots from the rigid (left) and flexible (right) simulations of AvrPphB (n = 2). Hydrogen bonds are represented by orange dashed lines. Protein atoms near the cavity surface are shown. Main-chain carbonyl oxygen atoms of Leu¹⁸⁵ and Ile²⁴⁴ form a hydrogen bond to the water molecule in the cavity (right). The figures were created by using VMD (62).

The nonmonotonic increase of free energy, which was prominently observed in the case of AvrPphB (Fig. 4), can be also explained in terms of the number of protein-water hydrogen bonds (Fig. 6 a). AvrPphB with n = 2 and 4 had approximately one more protein-water hydrogen bond than those with n = 1 and 3. It is probable that these additional hydrogen bonds reduce the free energy for n = 2 and 4, which results in the obtained unusual free energy change noted above.

Discussion

Hydration free energies for the nonpolar cavities of IL-1β (69 ų), AvrPphB (81 ų), Trp repressor (87 ų), and hemoglobin (108 ų) were evaluated to assess the possibility of hydration of nonpolar cavities. The rigid-model calculation showed that changes in free energy were positive for all the cavities examined, indicating that these nonpolar cavities are not hydrated stably. This result is essentially consistent with the previous result from an ideal, spherical cavity (35), as it is shown in the previous study that nonpolar cavities of these sizes (69–108 ų) are not expected. By the flexible model, positive values decreased, but the overall tendency did not change; the free energy changes were still positive. Therefore, the probability of water molecules residing in the protein nonpolar cavities is low, regardless of the cavity models. These four nonpolar cavities were the largest ones among existing protein nonpolar cavities. For smaller nonpolar cavities, hydration becomes less probable (35). Therefore, hydration of protein nonpolar cavities is unlikely in general.

Suppose there were still-larger nonpolar cavities than those studied here. Could hydration then occur? Vaitheeswaran et al. (35) predicted that very large nonpolar cavities (>∼137 ų) can be hydrated by the making of a hydrogen-bonded water cluster. However, according to our studies, nonpolar cavities of this size are not found experimentally (see Fig. 1). We suppose the reason is as follows. If the cavity was rigid, hydration could be achieved by making a water cluster, as suggested previously (35). However, hydrated protein nonpolar cavities will be quite unstable, as our MD simulations indicated; the nonpolar cavities often changed their shape and became polar. In other words, if hydrated nonpolar cavities were given, they could not be maintained owing to their flexibility. This scenario reasonably explains why water-clustering hydration is not found in nonpolar cavities of real proteins. Our hypothesis is strengthened by the fact that so many hydrated polar cavities, of such large size, are found (see Fig. 7 a). If our hypothesis is correct, such hydration will never be found even if the structural database is updated in the future.

Figure 7.

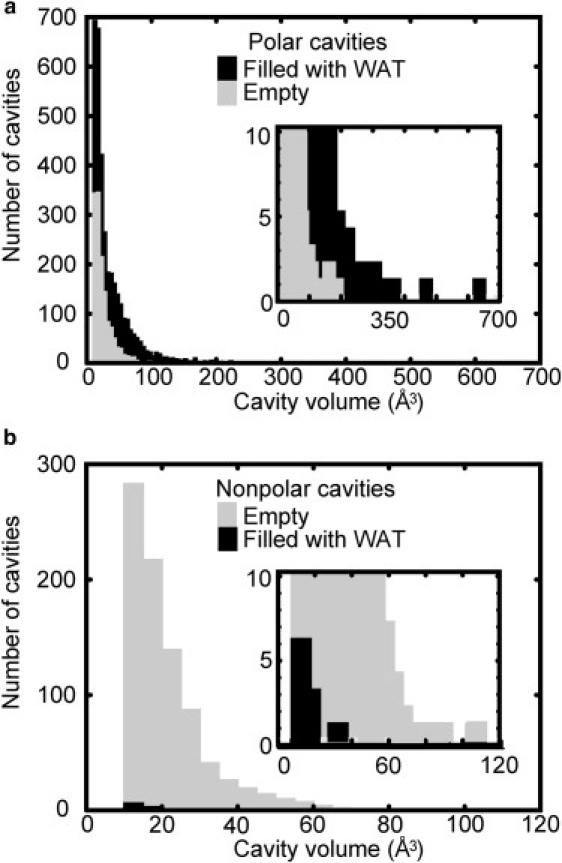
Distribution of the volume of 5948 protein cavities; (a) polar and (b) nonpolar cavities. Cavities with and without water molecules are solid and shaded, respectively. One-hundred-eighty-three polar cavities, which were found to be filled with molecules other than water, are not shown. In the insets, ordinates are enlarged.

Water molecules in cavities of crystal structures

In this study, we have shown that any water insertion to nonpolar cavities is thermodynamically unfavorable, which suggests a low probability of water residence in protein nonpolar cavities. This conclusion is consistent with our statistical analysis (Fig. 7), which shows the distribution of polar/nonpolar cavities with/without water molecules in 1359 proteins (see Materials and Methods). Water molecules are very often found in polar cavities, whereas they are scarcely observed in nonpolar cavities. Exceptionally, 10 nonpolar cavities had a single water molecule, but these did not turn out to be strictly nonpolar; by checking these cases in detail, we found that polar atoms exist in sites deeply buried below the cavity surface. The distances from the internal water were <∼3.8 Å, and thus, hydrogen bonding is possible. These 10 cases were found to be “nonpolar” under the present definition that is based only on the atoms on the cavity surface (see Materials and Methods); however, they actually did possess polarity.

Reconsideration about the nonpolar cavity of IL-1β: Is it hydrated or not?

The nonpolar cavity of IL-1β has been most frequently examined among the four cavities studied here; however, there is still controversy about the state within the cavity. Quillin et al. (27) analyzed electron density within the cavity and indicated that the nonpolar cavity is not hydrated. Indeed, in atomic coordinates solved by other x-ray (25,27–31) and NMR (32) experiments, no water molecules are assigned for the nonpolar cavity. Our calculations also lead to the same conclusion. Contrary to this, two results have been reported. By water-selective two-dimensional NMR spectroscopy, Ernst et al. (26) reported several signals that would imply that the cavity is hydrated. Yu et al. (25) also maintained that, by integrating electron density within the cavity, the cavity is hydrated. It is, however, pointed out by Quillin et al. (27) and Matthews et al. (57) that some problematic points are involved in these interpretations. In the analysis of Yu et al. (25), a spherical region of radius 6 Å was considered as the cavity, but the volume of 905 ų was too large compared to the actual cavity size of 69 ų. Thus, the number of electrons within the cavity may be overestimated (27). As for the NMR signals detected by Ernst et al. (26), we cannot deny the possibility that water molecules at other sites are attributed to the signals (57).

It may be important to note the following point. As shown by the results of free energies, stable hydration is not allowed energetically, but water molecules can visit the cavity at least transiently. Nevertheless, this consideration does not explain the current discrepancy about the water existence, as the probability of water residence is still very low. Our estimated free energy cost of hydrating the IL-1β cavity was >∼4 kcal/mol (Figs. 3 and 4), so the probability of water residence is <0.1% under physiological conditions, although the water existence supposed by Ernst et al. (26) and Yu et al. (25) was meant for a stable residence such as probability ∼70% (25).

The state of the IL-1β cavity has been studied theoretically as well. Somani et al. (33) calculated cavity hydration free energies by using an approximate representation based on the cumulant expansion. The free energy changes were 7.8, 5.4, 9.0, and −3.6 kcal/mol for 1–4 water molecules. From the negative value of −3.6 kcal/mol, Somani et al. insisted that the nonpolar cavity of IL-1β is filled with four water molecules. This finding may have an important implication for future studies of nonpolar hydration, but currently we must be careful about the interpretation, as, contrarily, the present calculations provided large positive values for this hydration. Somani et al. (33) estimated the contribution of the fourth water molecule to be −12.6 (= −3.6–9.0) kcal/mol. It seems, however, that this value is too large for the contribution of a single water molecule. According to the free energy data obtained by using a more rigorous method (17), free energy change of adding a single water molecule to a protein is, at most, −11.2 ± 0.5 kcal/mol. The approximation adopted by Somani et al., i.e., that potential energies of internal water molecules have Gaussian distribution, may be a reason for this discrepancy. However, such an assumption was not employed in our free energy calculations.

Another theoretical study on the nonpolar cavity of IL-1β was done by Zhang and Hermans (34). They calculated potential energy changes with water insertion, and suggested that the hydration is not favorable.

A remaining possibility of transient visit of water molecules in concert with protein motion

Proteins structurally fluctuate and sometimes experience a large conformational change. Water molecules in proteins are also dynamic; several experimental (55,56,58,59) and simulation studies (60) show that water molecules in a polar cavity sometimes escape from the cavity and again enter it, coupled with the protein motion. Therefore, our last concern is about a transient, metastable state that appears as the result of a protein conformational change. Suppose that a cavity was usually nonpolar, but transiently achieved some polarity with the conformational change. Could water molecules then visit the temporary space? Although such reversible switching between the stable and metastable states was not obtained in our simulations, we cannot make any clear assessment on this possibility. This is because even if there is a possibility, it is difficult to sample protein conformations structurally far from the starting one with MD simulations. Such an event might be obtained from a simulation with a much longer time. Another possible choice is the strategy of overcharging (8,61), which can drive slow events by introducing artificial changes to atomic charges of a residue. If we can generate a conformational change suitably by this method, energy contributions of associated electrostatic changes will be evaluated.

Conclusions

To investigate whether hydration happens in protein nonpolar cavities, we calculated hydration free energies of four protein cavities that are the largest among the existing protein nonpolar cavities. The resultant free energies showed that hydration of these nonpolar cavities is not plausible for any case of flexible or rigid models. Together with lower expectation for smaller nonpolar cavities (35), stable hydration is not expected for any existing protein nonpolar cavities. There remains a possibility that water molecules visit a nonpolar cavity transiently, particularly when conformational changes occur in the protein.

If there were still larger nonpolar cavities, does hydration occur? To our knowledge, such large nonpolar cavities have not been found experimentally. The possibility that very large nonpolar cavities are filled with clustered water molecules has been suggested from a simulation using an ideal, solid sphere (35). However, we speculate that as for protein cases, such hydration is not achieved. We observed that nonpolar cavities filled with water underwent deformation and finally became polar, i.e., conformations of the nonpolar cavities are quite unstable. This may be one reason why hydrated nonpolar cavities do not appear in protein interiors.

As for the nonpolar cavity of IL-1β, two opposite notions have been proposed. Our results revealed that, when viewed from the thermodynamic point of view, hydration of the nonpolar cavity is not favored.

Supporting Material

Two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00173-6.