Abstract
Many neurons exhibit postinhibitory rebound (PIR), in which neurons display enhanced excitability following inhibition. PIR can strongly influence the timing of spikes on rebound from an inhibitory input. We studied PIR in the lateral pyloric (LP) neuron of the stomatogastric ganglion of the crab Cancer borealis. The LP neuron is part of the pyloric network, a central pattern generator that normally oscillates with a period of ∼1 s. We used the dynamic clamp to create artificial rhythmic synaptic inputs of various periods and duty cycles in the LP neuron. Surprisingly, we found that the strength of PIR increased slowly over multiple cycles of synaptic input. Moreover, this increased excitability persisted for 10–20 s after the rhythmic inhibition was removed. These effects are considerably slower than the rhythmic activity typically observed in LP. Thus this slow postinhibitory rebound allows the neuron to adjust its level of excitability to the average level of inhibition over many cycles, and is another example of an intrinsic “short-term memory” mechanism.
Introduction
Postinhibitory rebound (PIR) is a common phenomenon that contributes to the firing patterns of neurons (Getting, 1989). It has long been understood that rebound firing after inhibition can provide important timing signals in motor systems (Selverston and Moulins, 1985), and is also important for the generation of oscillations in other brain systems (Llinás, 1988). In most cases, PIR elevates the spike rate compared to that observed before the inhibitory input (Perkel and Mulloney, 1974; Winograd et al., 2008). The amount of PIR can also influence the latency of the first spike after inhibition, which can be functionally important. Generally, the properties of PIR depend upon several of the neuron's intrinsic membrane currents (Hartline and Gassie, 1979; Harris-Warrick et al., 1995a,b).
In most experiments, PIR is evoked by a single hyperpolarizing input. Measured this way, PIR typically peaks tens or hundreds of milliseconds after inhibition (Harris-Warrick et al., 1995a,b; Bertrand and Cazalets, 1998; Angstadt et al., 2005). Previous studies have shown that the latency to firing after inhibition depends on both the amplitude and duration of the hyperpolarization, and this was used to suggest that rebound firing latency could be a sensitive pattern detector, as long as the time constants of the effects were relatively rapid in comparison to the duration and frequency of the signal to be detected (Hooper, 1998).
In contrast, in this study we measure PIR in response to long trains of rhythmic inhibition. We do this in the lateral pyloric (LP) neuron of the stomatogastric ganglion (STG) of the crab Cancer borealis. We find that PIR builds up over many cycles of rhythmic inhibition, and that enhanced excitability is extremely long lasting after rhythmic inhibition ends.
Spike frequency adaptation (SFA) has been extensively documented in numerous sensory systems, and it occurs on both short and long timescales (Nelken, 2004; Gardner et al., 2005; Höger and French, 2005; Gabbiani and Krapp, 2006). Just as there is a slow form of SFA, the phenomenon documented here is a slow form of PIR. Similar slow and long-lasting increases in intrinsic excitability have been previously seen in response to rhythmic depolarizations (Storm, 1988; Marder et al., 1996; Turrigiano et al., 1996). In principle, postinhibitory rebound that develops and decays over many seconds will serve as a “memory mechanism,” allowing a neuron to keep track of the history of inhibitory inputs over a significant period of time.
Materials and Methods
Adult Cancer borealis crabs were obtained from Yankee Lobster and maintained in artificial seawater until used. Crabs were cold-anesthetized for 30 min before dissection. The complete stomatogastric nervous system, consisting of the paired commissural ganglia, the esophageal ganglion, the STG, and several motor nerves, was dissected out of the animal and pinned out in an elastomer-coated dish containing chilled (9–13°C) saline. The physiological saline solution consisted of the following (in mm): NaCl, 440; KCl, 11; CaCl2, 13; MgCl2, 26; Trizma base, 11; and maleic acid, 5, pH 7.45.
Electrophysiological recordings.
The STG was desheathed, and petroleum jelly wells were placed on motor nerves. Stainless steel pin electrodes were placed in the wells for extracellular recordings. Signals were amplified and filtered using a differential AC amplifier (A-M Systems). Intracellular recordings from somata were made using 20–40 MΩ glass microelectrodes filled with 0.6 m K2SO4 + 20 mm KCl, using an Axoclamp 2A amplifier (Molecular Devices). The LP neuron was impaled with two electrodes, one for measuring voltage and one for passing current. During recordings, the preparations were continuously superfused with chilled saline (9–13°C). For dynamic- and voltage-clamp experiments, the LP neuron was isolated from inputs by building a petroleum jelly well around the desheathed stomatogastric nerve (stn) with 1 μm TTX in the well to block modulatory inputs, adding 10 μm picrotoxin to the bath to block glutamatergic synaptic inputs (Marder and Eisen, 1984), and hyperpolarizing the two pyloric dilator neurons to remove cholinergic inputs. Currents measured in voltage clamp were low-pass filtered using a four-pole RC filter (Krohn-Hite 3323) with a nominal 300 Hz cutoff before digitization.
Data acquisition and analysis.
Data were acquired with a Digidata 1200 data acquisition board (Molecular Devices) and subsequently analyzed in Spike2 (Cambridge Electronic Design) and SigmaStat (Systat Software). In most cases, we used one-way repeated-measures (RM) ANOVA with post hoc Holm–Sidak tests to establish statistical significance between the measurements of spike rate, delay, and the time constants of their changes. These data passed tests for normality and equal variance. In the case of Figure 4A, the data failed a Levene median test for equal variance, so we used Friedman's RM ANOVA on ranks followed by Tukey multiple-comparison tests. Additionally, we had data for the DC hyperpolarization group only in a subset of n = 5 preparations, so we performed an RM ANOVA on ranks comparing just the other three groups, with n = 10, and then performed a separate RM ANOVA on ranks with the n = 5 subset. For the data of Figure 2, E and F, we were compelled to use conventional (not repeated-measures) ANOVAs, because the sparsity of data did not allow for within-subjects comparisons. All measurements reported in the text are given as mean ± SEM.
Figure 4.
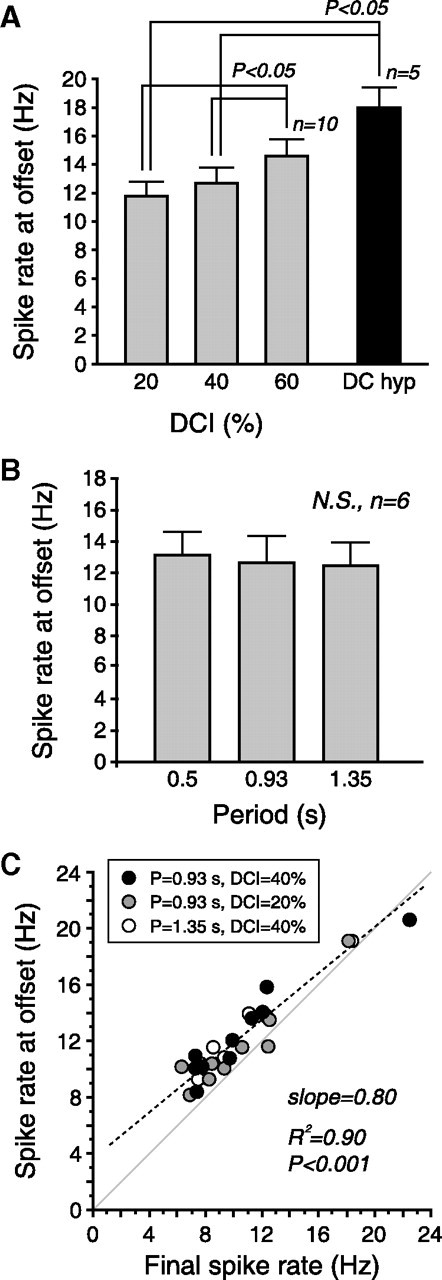
Spike rate at offset reflects DCI, independent of period. A, Effect of DCI on peak spike rate at offset. Period was held constant at 0.93 s, except for “DC hyp” data, which was DC hyperpolarization for the same duration as the rhythmic inhibition was applied (18.6 s). DC hyperpolarization was done on a subset (n = 5) of experiments (see Materials and Methods). B, Effect of period on peak spike rate at offset. DCI was held constant at 40%. Differences were not statistically significant (N.S.). C, Correlation between peak spike rate at offset and spike rate during the final burst (see Fig. 1D). Dashed line is a linear fit. Gray line is the identity line. Data were pooled for periods of 0.93 s (DCI of 20% and 40%) and 1.35 s (DCI of 40%). Error bars in all panels give SEM.
Figure 2.
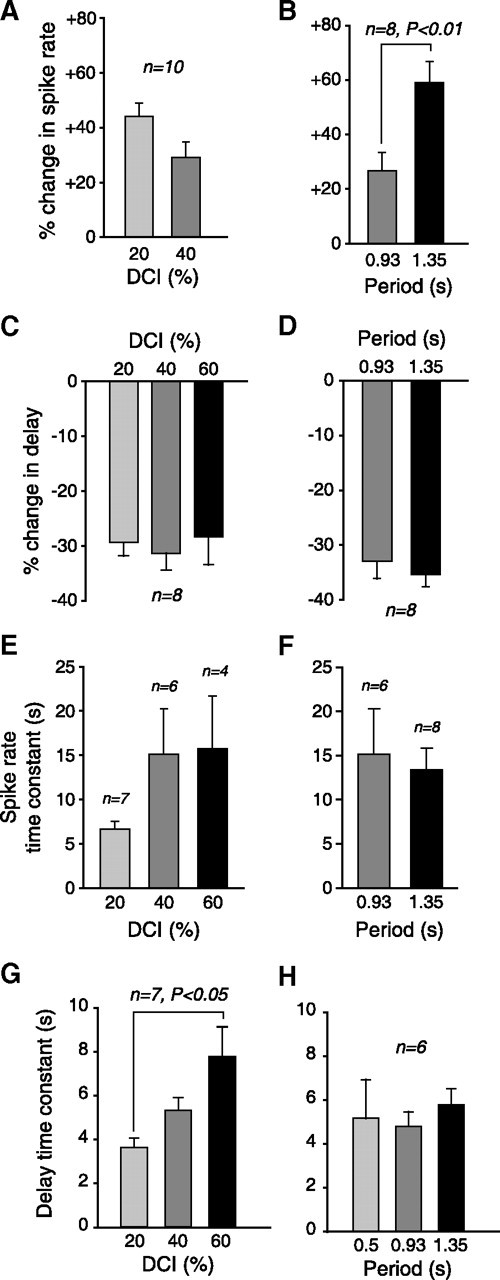
Summary data on slow postinhibitory rebound, showing effect of varying period and DCI. A, Mean change in spike rate, for different DCIs. Sixty percent DCI not shown because cells rarely spiked during early cycles in this condition. B, Mean change in spike rate, for different periods. Period of 0.5 s not shown here or in D and F because cells rarely spiked during early cycles in this condition. C, Mean change in delay to first spike, for different DCIs. D, Mean change in delay to first spike, for different periods. E, Mean time constant of change in spike rate, for different DCIs. F, Mean time constant of change in spike rate, for different periods. G, Mean time constant of the change in delay over the course of stimulation, for several different DCIs. H, Mean time constant of the change in delay over the course of stimulation, for several different periods. Panels A, C, E, and G all show data for a period of 0.93 s. B, D, F, and H all show data for a DCI of 40%. Error bars in all panels give SEM.
Dynamic clamp recordings.
The dynamic clamp (Sharp et al., 1993) was used to inject artificial synaptic inputs into the isolated LP cell using the Real-Time Linux Dynamic Clamp (Pinto et al., 2001) running on a 600 MHz Dell Pentium III computer at a sampling rate of 1 kHz. The artificial synapse delivered a current of the following form:
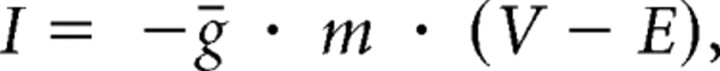 |
where I is the current, ḡ the maximal conductance of the synapse, m the fractional activation of the synapse, V the membrane potential of LP, and E the reversal potential of the synapse. The variable m was a low-pass filtered version of a square wave with a set period and duty cycle. It satisfied the following equation:
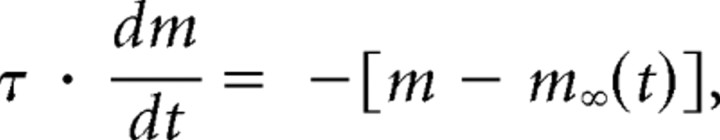 |
where m∞(t) is the square wave (with value either zero or one), and τ is the time constant of the low-pass filter. In the text, the duty cycle given is the fraction of the cycle for which the inhibitory synapse is on, and so is called the duty cycle of inhibition (DCI). For all experiments reported here, E was set to −90 mV, and τ was either 50 or 0 ms. In the latter case, there is no low-pass filtering and m = m∞(t). Because changing the time constant did not significantly affect the delay and spike frequency of the LP neuron (data not shown), experiments with different values of τ are pooled in the results. If necessary, the LP neuron was tonically depolarized so that it rebounded to a membrane potential of between −40 mV and −50 mV when not inhibited. The maximal conductance (ḡ) was then adjusted such that the most hyperpolarized voltage reached was between −70 mV and −80 mV. To achieve this, the maximal conductance was typically set in the 150–250 nS range.
Results
Slow PIR in response to rhythmic artificial synaptic input
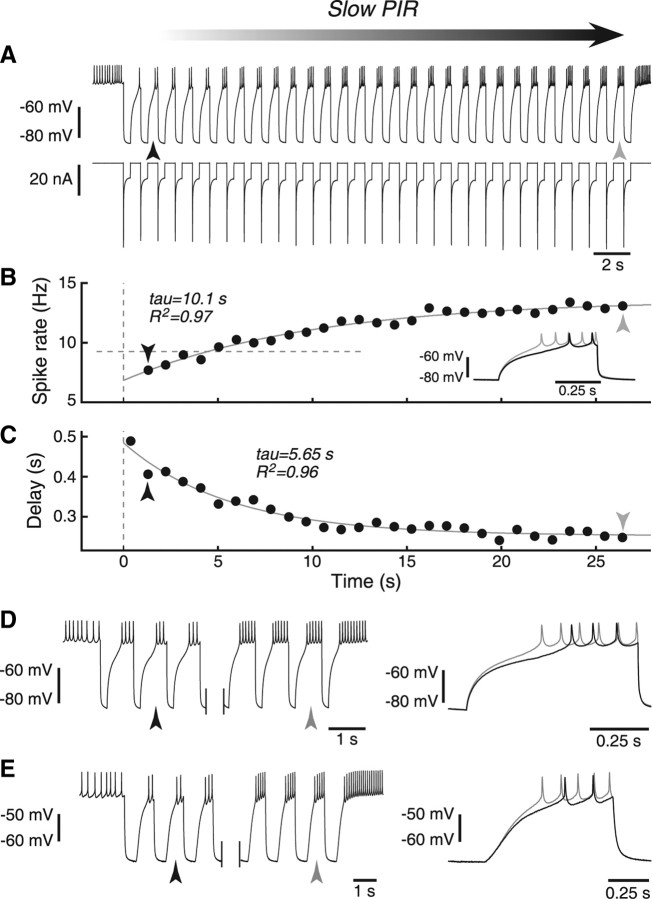
During an ongoing pyloric rhythm, the LP neuron receives rhythmic synaptic inhibition during each cycle. Therefore, we examined the LP neuron's response to an artificial synaptic input designed to mimic the kind of rhythmic inhibitory drive it receives during the pyloric network (Fig. 1A). LP generally spiked on release from inhibition during each cycle. The spike rate during rebound slowly increased over the course of this input (Fig. 1B), while the delay to first spike slowly decreased (Fig. 1C). We call this phenomenon slow PIR because it involves a buildup of excitability over the course of many inhibitory pulses.
Figure 1.
Examples of slow PIR. A, LP neuron rhythmically hyperpolarized by conductance pulses shows slow PIR in spike rate and delay. Shaded arrow indicates the buildup of slow PIR over the course of many cycles. Period of rhythmic inhibition was 0.93 s, DCI (the fraction of the cycle for which hyperpolarizing current was delivered) was 40%. Top trace shows membrane potential, bottom trace is injected current. Large current “transient” at the start of each inhibitory pulse is a result of the large driving force of the artificial synaptic conductance. This effect is particularly strong here because the time constant of the artificial synapse was zero in this case (see Materials and Methods). Black and gray arrows point to second and last cycles, respectively. B, Spike rate in the burst for each burst. Dashed horizontal line indicates spike rate before injection. Dashed vertical line indicates time origin (also in C). Inset shows an overlay of the second and last cycle, displaying the increase in spike rate and decrease in delay during stimulation. C, Delay to first spike for each burst. D, Early and late cycles of the same protocol, but with a period of 0.93 s and DCI of 20%. Right side shows overlay of cycles indicated with black and gray arrows. E, Like D, but for a period of 1.35 s and DCI of 40%.
We observed slow PIR over a range of input periods and duty cycles. The data shown in Figure 1A–C were for a period of 0.93 s and a DCI (the fraction of the cycle in which inhibition is applied) of 40%. An example trace with a DCI of 20% is shown in Figure 1D, and one with a period of 1.35 s is shown in Figure 1E. Both exhibit clear slow PIR, reflected both in the spike rate and the delay to first spike.
We quantified a number of properties of the slow PIR observed in the LP neuron, for a range of periods and DCIs. We used periods of 0.5, 0.93, and 1.35 s. The mean period of the pyloric rhythm in Cancer borealis is ∼0.93 s, and 0.5 and 1.35 s are approximately two SDs below and above the mean, respectively (Goaillard et al., 2009). The LP neuron is strongly inhibited by the pyloric rhythm pacemaker neurons for ∼40% of a pyloric cycle (Goaillard et al., 2009), so the DCIs chosen were centered on this value.
The observed slow increase in spike rate was a robust effect, seen in all preparations examined (Fig. 2A,B). This was measured by comparing the mean spike rate in the bursts from two cycles: (1) the first cycle in which the LP neuron fired two or more spikes and (2) the final cycle. The data shown are only for DCIs of 20% and 40% because duty cycles of 60% often caused fewer than two spikes to be fired over much of the stimulus duration. Varying the input period had a significant effect on the percentage increase in spike rate (Fig. 2B). The data are shown only for periods of 0.93 s and 1.35 s because a period of 0.5 s often caused fewer than two spikes to be fired over much of the stimulus duration (as for DCI = 60%).
The observed decrease in delay to first spike was also a robust effect, seen across a variety of DCIs (Fig. 2C) and periods (Fig. 2D). The time constant of the increase in spike frequency was difficult to estimate reliably, but was generally longer than 5 s (Fig. 2E,F). Because of the difficulties in estimating this time constant, we were able to determine it for multiple DCIs or multiple periods only in a small number of animals. Therefore we pooled data from preparations in which we were only able to estimate this time constant in a subset of conditions (note different n values for different conditions in Fig. 2E,F). No significant differences in the spike rate time constant were observed between conditions. The time constant of the decrease in delay to first spike was always several seconds, and increased as DCI increased (Fig. 2G). In contrast, the time constant showed no significant changes as period was varied (Fig. 2H).
Recovery after slow PIR
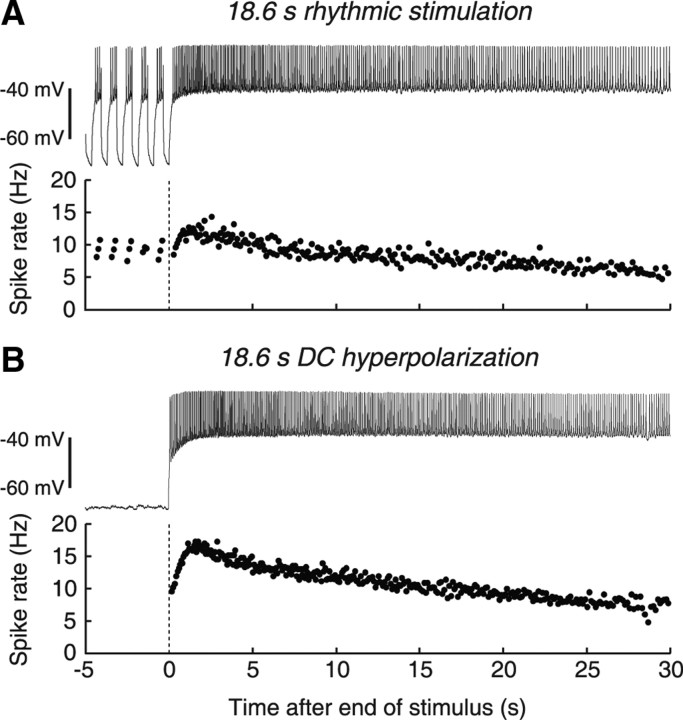
The LP neuron showed a long-lasting period of enhanced firing after artificial rhythmic synaptic input was terminated (Fig. 3A). Typically, the tonic spike rate peaked within a few seconds of stimulus offset and then slowly returned to steady-state in 20–30 s (Fig. 3A, bottom). A similarly slow recovery occurred in response to long hyperpolarizing DC current injection of equal total duration; therefore, this phenomenon was not a consequence of rhythmic stimulation (Fig. 3B). The response to long DC hyperpolarization also emphasizes that slow PIR is PIR in the fullest sense of the term, but occurring on a long timescale.
Figure 3.
Examples of offset firing after rhythmic stimulation and DC hyperpolarization. A, Increase in spike frequency after release from 18.6 s rhythmic hyperpolarization, at a period of 0.93 s and a DCI of 40%. Bottom trace shows instantaneous spike frequency. Vertical dashed line indicates stimulus offset. B, Increase in spike frequency after release from DC injection of hyperpolarizing current. Bottom trace shows instantaneous spike frequency. Vertical dashed line indicates stimulus offset.
Offset firing rate reflects “down time” during rhythmic inhibition
The peak offset firing rate was sensitive to the DCI of the synaptic input (i.e., “down time”) (Fig. 4A), but was not affected by the period of the rhythmic drive (Fig. 4B). (Fig. 4A is consistent with Fig. 2A because the former shows absolute spike rate vs DCI, and the later shows the change in spike rate vs DCI.) Consistent with this, the offset firing rate after 18.6 s (20 cycles × 0.93 s/cycle) of constant hyperpolarization peaked at a significantly higher frequency than that of the rebound spiking after rhythmic trains (Fig. 4A, black bar). This makes sense, since constant hyperpolarization is analogous to a DCI of 100%. The steady-state spike rate during rhythmic inhibition predicted the peak offset spike rate (Fig. 4C), even across different combinations of period and DCI. Thus, the higher the steady-state spike rate during rhythmic inhibition, the higher the spike rate after rhythmic inhibition ceased.
Period and DCI also affected the steady-state delay to firing. There was a significant effect of DCI on steady-state delay with period held constant at 0.93 s (p < 0.001, n = 9, one-way RM ANOVA, data not shown), and a significant effect of period on steady-state delay with DCI held constant at 40% (p < 0.001, n = 6, one-way RM ANOVA, data not shown). This indicates that steady-state delay depends on period, unlike the spike rate at offset.
Potential mechanisms underlying slow PIR
To determine whether slow PIR was associated with a large change in conductance, we measured the LP neuron's input resistance over the course of many inhibitory pulses by examining the current injected at the end of each inhibitory pulse and the resulting voltage deflection. We found no significant difference in input resistance between the first and last cycles of inhibition (mean difference was −4.8 ± 3.4%, p = 0.11, n = 10, paired t test, data not shown). Consistent with this, we found that blockade of Ih with 5 mm Cs+ (Golowasch and Marder, 1992) did not reliably modify slow PIR (n = 3, data not shown).
To determine whether slow PIR might be associated with a change in spike threshold, we measured the threshold of the first spike after each inhibitory pulse, and compared these thresholds between the first and last cycles. There was a small but significant decrease in spike threshold (mean difference was −0.9 ± 0.4 mV, p < 0.05, n = 10, paired t test, data not shown). The extent to which slow PIR is attributable to this rather small change is unclear.
Voltage-clamp experiments revealed a slowly decaying 100–400 pA net inward current evoked after a 20 s step from −45 mV to −75 mV (n = 6, data not shown). The magnitude and time course of this current are consistent with the rebound depolarizations observed following DC hyperpolarization in current clamp (Fig. 3B).
Discussion
PIR has long been recognized as an important mechanism of central pattern generation in motor systems (Perkel and Mulloney, 1974; Getting, 1989) and in the generation of oscillations in other brain circuits (Llinás, 1988). But PIR is usually thought of as operating in response to a single inhibitory input, or during a single cycle of an oscillation. Here we describe a form of PIR operating on longer timescales. In the case of the LP neuron, this slow PIR allows the cell to adjust its excitability to the average level of inhibition over ∼10 cycles. Thus, it constitutes a form of intrinsic short-term memory (Storm, 1988; Marom and Abbott, 1994; Marder et al., 1996; Turrigiano et al., 1996; Egorov et al., 2002; Pulver and Griffith, 2010).
Consistent with this description, the spike rate of the LP neuron at steady state (and at offset) varied as a function of the DCI, but was independent of period (Fig. 4A,B). This is expected of a process that depends upon the activity level averaged over a duration substantially longer than a single period.
Hooper (1998) found that both period and duty cycle of a rhythmic inhibitory input affected the steady-state delay to firing in the PY neurons of the pyloric network, but did not examine the effect of these parameters on spike rate. We found that both period and DCI had a significant effect on steady-state delay, but that offset spike rate was independent of period (Fig. 4). Hooper et al. (2009) found some of the same effects reported here, but did not examine changes in spike rate during long trains of inhibitory inputs, or look at the effects of changing DCI while holding period fixed. Thus our results are consistent with previous work, but reveal additional dimensions of the effects of rhythmic inhibition on excitability.
It is not clear what mechanisms underlie slow PIR in the LP neuron. The hyperpolarization-activated inward current (Ih) seemed a likely candidate, because it activates upon hyperpolarization, increases excitability, and has appropriate time constants (Golowasch and Marder, 1992; Pape, 1996; Hille, 2001). But experiments in which we blocked Ih with extracellular Cs+ did not reliably block slow PIR. Furthermore, we did not observe a significant decrease in input resistance over the course of multiple inhibitory pulses, as would be expected if Ih were slowly increasing. Another candidate is the slow deinactivation of the fast Na+ current (Rudy, 1978; Fleidervish et al., 1996), and this might account for the small change in spike threshold we observed. Additionally, there could be a low-threshold Ca2+ current that is strongly deinactivated by hyperpolarization, perhaps supplemented by a calcium-activated nonselective cation current (Golowasch and Marder, 1992; Zhang and Harris-Warrick, 1995; Zhang et al., 1995). Yet another candidate is a pump current, which could generate a slow activity-dependent current without changing membrane conductance (Baylor and Nicholls, 1969; Pulver and Griffith, 2010).
Another possibility is that the observed long time constants arise not from the slow kinetics of a single channel, but from an interaction of two or more channels with fast kinetics. For instance, fast inward and outward channels could both be deinactivated by hyperpolarization, in such a way that they nearly cancel each other. This could give rise to an observed time constant much longer than either of the individual time constants. The very long interspike intervals possible in the Connor-Stevens model of the crustacean walking leg axon are an example of this sort of phenomenon (Connor, 1975, 1978; Connor et al., 1977). This often happens when a nonlinear dynamical system (such as a neuron) has parameters close to those that would yield two equilibrium points (i.e., a constant steady state), one stable and one unstable. In the language of nonlinear dynamical systems, the absent equilibrium points leave behind a “ghost,” and the state of the system changes slowly in the vicinity of this ghost (Strogatz, 1994).
Winograd et al. (2008) recently described a hyperpolarization-activated increase in excitability in prefrontal cortex that decays with a time constant apparently much longer than 30 s, which was dependent on Ih. Thus, these two forms of PIR appear to be distinct.
Slow PIR can be viewed as a cellular short-term memory mechanism, like neuronal multistability or delayed excitation (Storm, 1988; Marder et al., 1996; Egorov et al., 2002; Pulver and Griffith, 2010). Such mechanisms may underlie some forms of working memory, either alone or in concert with reverberatory synaptic mechanisms (Goldman et al., 2003; Loewenstein and Sompolinsky, 2003; Major and Tank, 2004; Major et al., 2008).
Slow PIR can be viewed as the “flip side” of delayed excitation, in which prolonged depolarizing current injection causes slowly increasing excitability (Getting, 1989). Delayed excitation has been proposed as a mechanism for temporal integration of excitatory inputs on a timescale of tens of seconds (Storm, 1988; Marom and Abbott, 1994; Turrigiano et al., 1996). Slow PIR might be an analogous mechanism for inhibitory inputs.
Slow PIR is a form of cellular dynamics that enables a cell to tune its excitability in response to the overall level of recent inhibition received. It is a form of cellular memory that depends not on changes in synaptic strength, but on the intrinsic membrane processes of the neuron itself. Plasticity timescales of 10–20 s may be particularly well suited to circuit functions in which it is important for the animal to integrate information before making a decision.
Footnotes
Support for this work was contributed by National Institutes of Health (NIH) Grant NS50928 (A.L.T.), NIH Grant MH46742 (E.M.), and the McDonnell Foundation (E.M.).
References
- Angstadt JD, Grassmann JL, Theriault KM, Levasseur SM. Mechanisms of postinhibitory rebound and its modulation by serotonin in excitatory swim motor neurons of the medicinal leech. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2005;191:715–732. doi: 10.1007/s00359-005-0628-6. [DOI] [PubMed] [Google Scholar]
- Baylor DA, Nicholls JG. After-effects of nerve impulses on signalling in the central nervous system of the leech. J Physiol. 1969;203:571–589. doi: 10.1113/jphysiol.1969.sp008880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertrand S, Cazalets JR. Postinhibitory rebound during locomotor-like activity in neonatal rat motoneurons in vitro. J Neurophysiol. 1998;79:342–351. doi: 10.1152/jn.1998.79.1.342. [DOI] [PubMed] [Google Scholar]
- Connor JA. Neural repetitive firing: a comparative study of membrane properties of crustacean walking leg axons. J Neurophysiol. 1975;38:922–932. doi: 10.1152/jn.1975.38.4.922. [DOI] [PubMed] [Google Scholar]
- Connor JA. Slow repetitive activity from fast conductance changes in neurons. Fed Proc. 1978;37:2139–2145. [PubMed] [Google Scholar]
- Connor JA, Walter D, McKown R. Neural repetitive firing: modifications of the Hodgkin-Huxley axon suggested by experimental results from crustacean axons. Biophys J. 1977;18:81–102. doi: 10.1016/S0006-3495(77)85598-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egorov AV, Hamam BN, Fransén E, Hasselmo ME, Alonso AA. Graded persistent activity in entorhinal cortex neurons. Nature. 2002;420:173–178. doi: 10.1038/nature01171. [DOI] [PubMed] [Google Scholar]
- Fleidervish IA, Friedman A, Gutnick MJ. Slow inactivation of Na+ current and slow cumulative spike adaptation in mouse and guinea-pig neocortical neurones in slices. J Physiol. 1996;493:83–97. doi: 10.1113/jphysiol.1996.sp021366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabbiani F, Krapp HG. Spike-frequency adaptation and intrinsic properties of an identified, looming-sensitive neuron. J Neurophysiol. 2006;96:2951–2962. doi: 10.1152/jn.00075.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner JL, Sun P, Waggoner RA, Ueno K, Tanaka K, Cheng K. Contrast adaptation and representation in human early visual cortex. Neuron. 2005;47:607–620. doi: 10.1016/j.neuron.2005.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Getting PA. Emerging principles governing the operation of neural networks. Annu Rev Neurosci. 1989;12:185–204. doi: 10.1146/annurev.ne.12.030189.001153. [DOI] [PubMed] [Google Scholar]
- Goaillard JM, Taylor AL, Schulz DJ, Marder E. Functional consequences of animal-to-animal variation in circuit parameters. Nat Neurosci. 2009;12:1424–1430. doi: 10.1038/nn.2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman MS, Levine JH, Major G, Tank DW, Seung HS. Robust persistent neural activity in a model integrator with multiple hysteretic dendrites per neuron. Cereb Cortex. 2003;13:1185–1195. doi: 10.1093/cercor/bhg095. [DOI] [PubMed] [Google Scholar]
- Golowasch J, Marder E. Ionic currents of the lateral pyloric neuron of the stomatogastric ganglion of the crab. J Neurophysiol. 1992;67:318–331. doi: 10.1152/jn.1992.67.2.318. [DOI] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Barazangi N, Guckenheimer J, Gueron S. Dopamine modulation of transient potassium current evokes phase shifts in a central pattern generator network. J Neurosci. 1995a;15:342–358. doi: 10.1523/JNEUROSCI.15-01-00342.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Levini RM, Gueron S, Guckenheimer J. Dopamine modulation of two subthreshold currents produces phase shifts in activity of an identified motoneuron. J Neurophysiol. 1995b;74:1404–1420. doi: 10.1152/jn.1995.74.4.1404. [DOI] [PubMed] [Google Scholar]
- Hartline DK, Gassie DV., Jr Pattern generation in the lobster (Panulirus) stomatogastric ganglion. I. Pyloric neuron kinetics and synaptic interactions. Biol Cybern. 1979;33:209–222. doi: 10.1007/BF00337410. [DOI] [PubMed] [Google Scholar]
- Hille B. Ed 3. Sunderland, MA: Sinauer; 2001. Ion channels of excitable membranes. [Google Scholar]
- Höger U, French AS. Slow adaptation in spider mechanoreceptor neurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2005;191:403–411. doi: 10.1007/s00359-004-0597-1. [DOI] [PubMed] [Google Scholar]
- Hooper SL. Transduction of temporal patterns by single neurons. Nat Neurosci. 1998;1:720–726. doi: 10.1038/3721. [DOI] [PubMed] [Google Scholar]
- Hooper SL, Buchman E, Weaver AL, Thuma JB, Hobbs KH. Slow conductances could underlie intrinsic phase-maintaining properties of isolated lobster (Panulirus interruptus) pyloric neurons. J Neurosci. 2009;29:1834–1845. doi: 10.1523/JNEUROSCI.5392-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinás RR. The intrinsic electrophysiological properties of mammalian neurons: insights into central nervous system function. Science. 1988;242:1654–1664. doi: 10.1126/science.3059497. [DOI] [PubMed] [Google Scholar]
- Loewenstein Y, Sompolinsky H. Temporal integration by calcium dynamics in a model neuron. Nat Neurosci. 2003;6:961–967. doi: 10.1038/nn1109. [DOI] [PubMed] [Google Scholar]
- Major G, Tank D. Persistent neural activity: prevalence and mechanisms. Curr Opin Neurobiol. 2004;14:675–684. doi: 10.1016/j.conb.2004.10.017. [DOI] [PubMed] [Google Scholar]
- Major G, Polsky A, Denk W, Schiller J, Tank DW. Spatiotemporally graded NMDA spike/plateau potentials in basal dendrites of neocortical pyramidal neurons. J Neurophysiol. 2008;99:2584–2601. doi: 10.1152/jn.00011.2008. [DOI] [PubMed] [Google Scholar]
- Marder E, Eisen JS. Transmitter identification of pyloric neurons: electrically coupled neurons use different neurotransmitters. J Neurophysiol. 1984;51:1345–1361. doi: 10.1152/jn.1984.51.6.1345. [DOI] [PubMed] [Google Scholar]
- Marder E, Abbott LF, Turrigiano GG, Liu Z, Golowasch J. Memory from the dynamics of intrinsic membrane currents. Proc Natl Acad Sci U S A. 1996;93:13481–13486. doi: 10.1073/pnas.93.24.13481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marom S, Abbott LF. Modeling state-dependent inactivation membrane currents. Biophys J. 1994;67:515–520. doi: 10.1016/S0006-3495(94)80518-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelken I. Processing of complex stimuli and natural scenes in the auditory cortex. Curr Opin Neurobiol. 2004;14:474–480. doi: 10.1016/j.conb.2004.06.005. [DOI] [PubMed] [Google Scholar]
- Pape HC. Queer current and pacemaker: the hyperpolarization-activated cation current in neurons. Annu Rev Physiol. 1996;58:299–327. doi: 10.1146/annurev.ph.58.030196.001503. [DOI] [PubMed] [Google Scholar]
- Perkel DH, Mulloney B. Motor pattern production in reciprocally inhibitory neurons exhibiting postinhibitory rebound. Science. 1974;185:181–183. doi: 10.1126/science.185.4146.181. [DOI] [PubMed] [Google Scholar]
- Pinto RD, Elson RC, Szücs A, Rabinovich MI, Selverston AI, Abarbanel HD. Extended dynamic clamp: controlling up to four neurons using a single desktop computer and interface. J Neurosci Methods. 2001;108:39–48. doi: 10.1016/s0165-0270(01)00368-5. [DOI] [PubMed] [Google Scholar]
- Pulver SR, Griffith LC. Spike integration and cellular memory in a rhythmic network from Na+/K+ pump current dynamics. Nat Neurosci. 2010;13:53–59. doi: 10.1038/nn.2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudy B. Slow inactivation of the sodium conductance in squid giant axons. Pronase resistance. J Physiol. 1978;283:1–21. doi: 10.1113/jphysiol.1978.sp012485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selverston AI, Moulins M. Oscillatory neural networks. Annu Rev Physiol. 1985;47:29–48. doi: 10.1146/annurev.ph.47.030185.000333. [DOI] [PubMed] [Google Scholar]
- Sharp AA, O'Neil MB, Abbott LF, Marder E. Dynamic clamp: computer-generated conductances in real neurons. J Neurophysiol. 1993;69:992–995. doi: 10.1152/jn.1993.69.3.992. [DOI] [PubMed] [Google Scholar]
- Storm JF. Temporal integration by a slowly inactivating K+ current in hippocampal neurons. Nature. 1988;336:379–381. doi: 10.1038/336379a0. [DOI] [PubMed] [Google Scholar]
- Strogatz SH. Reading, MA: Addison-Wesley; 1994. Nonlinear dynamics and chaos. [Google Scholar]
- Turrigiano GG, Marder E, Abbott LF. Cellular short-term memory from a slow potassium conductance. J Neurophysiol. 1996;75:963–966. doi: 10.1152/jn.1996.75.2.963. [DOI] [PubMed] [Google Scholar]
- Winograd M, Destexhe A, Sanchez-Vives MV. Hyperpolarization-activated graded persistent activity in the prefrontal cortex. Proc Natl Acad Sci U S A. 2008;105:7298–7303. doi: 10.1073/pnas.0800360105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, Harris-Warrick RM. Calcium-dependent plateau potentials in a crab stomatogastric ganglion motor neuron. I. Calcium current and its modulation by serotonin. J Neurophysiol. 1995;74:1929–1937. doi: 10.1152/jn.1995.74.5.1929. [DOI] [PubMed] [Google Scholar]
- Zhang B, Wootton JF, Harris-Warrick RM. Calcium-dependent plateau potentials in a crab stomatogastric ganglion motor neuron. II. Calcium-activated slow inward current. J Neurophysiol. 1995;74:1938–1946. doi: 10.1152/jn.1995.74.5.1938. [DOI] [PubMed] [Google Scholar]