Relative Codon Adaptation: A Generic Codon Bias Index for Prediction of Gene Expression

Abstract

The development of codon bias indices (CBIs) remains an active field of research due to their myriad applications in computational biology. Recently, the relative codon usage bias (RCBS) was introduced as a novel CBI able to estimate codon bias without using a reference set. The results of this new index when applied to Escherichia coli and Saccharomyces cerevisiae led the authors of the original publications to conclude that natural selection favours higher expression and enhanced codon usage optimization in short genes. Here, we show that this conclusion was flawed and based on the systematic oversight of an intrinsic bias for short sequences in the RCBS index and of biases in the small data sets used for validation in E. coli. Furthermore, we reveal that how the RCBS can be corrected to produce useful results and how its underlying principle, which we here term relative codon adaptation (RCA), can be made into a powerful reference-set-based index that directly takes into account the genomic base composition. Finally, we show that RCA outperforms the codon adaptation index (CAI) as a predictor of gene expression when operating on the CAI reference set and that this improvement is significantly larger when analysing genomes with high mutational bias.

1. Introduction

Codon usage bias (CUB) is usually defined as a species-specific deviation from uniform codon usage in the coding regions of genomic sequences. This bias is possible due to the redundancy of the genetic code, which allows differential use of synonymous codons.¹ The particular pattern of bias observed in a given species is thought to be the product of drift and selection pressures acting on a number of parameters, but mainly on tRNA gene copy number and genomic %GC content.^2–5 CUB is therefore a strong species-specific statistic with numerous applications, such as gene prediction or the identification of laterally transferred genes.^6,7 It was observed early on that the CUB of individual genes correlates strongly with their expression level in many microbial organisms.^1,2,8 In these organisms, selective pressure to optimize translational efficiency during rapid growth can overcome drift and mutational bias, leading to highly skewed codon usage patterns within a genome. Genes that need to be highly expressed during rapid growth will resort preferentially to a small subset of codons recognized by the most abundant tRNA species. This deviation from the overall genomic CUB is known as the ‘major codon bias’¹ and its pattern appears to be highly uniform among fast-growing bacteria, despite significant differences in %GC content.⁴ A major codon bias has also been reported to some extent in multicellular eukaryotes, although it is absent in most mammals and in some bacteria.^9–11

Owing to the relationship between CUB and translational optimization, indices based on this bias can be applied to predict the expression of individual gene sequences and can thus play an important role in fields such as biotechnology, by assisting in the fine-tuning of heterologous gene expression.^12,13 Many different indices of CUB have been proposed to date.^14,15 Some indices, like the effective number of codons (N_c)¹⁶ or the χ² statistic,⁹ estimate deviation from true uniformity in codon usage. However, the vast majority of indices measures deviation from a subset of putative translationally optimal codons or genes. The codon bias index (CBI) and the frequency of optimal codons (F_op), for instance, calculate codon bias based on a set of ‘optimal’ codons derived, respectively, either from a subset of genes¹⁷ or from the tRNA concentration data.² Both the expression measure E(g) and the codon adaptation index (CAI) circumvent the necessity of categorizing codons as optimal or non-optimal by using directly the observed frequency of codons in a reference set in the calculation of their index.^18,19

CAI uses a subset of putative highly expressed genes in the organism of interest as its reference set, leading to

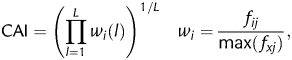1

where f_ij is the frequency of codon i encoding amino acid j as observed in the reference set, max(f_xj) the largest frequency among the codons encoding amino acid j and L the length, in codons, of the gene sequence of interest. The term w_i is called the relative adaptiveness of codon i and the CAI is computed as the geometric mean of the w_i values for all codons in the sequence.

In E(g),²⁰ three groups of genes are defined in the organism of interest: RP (ribosomal proteins), TF (transcription processing factors) and CH (chaperon-degradation genes). These gene classes are shown to present high codon biases due to their involvement in rapid division. The codon usage difference of gene g relative to gene class S is defined as:

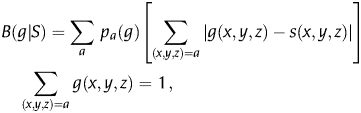2

where p_a(g) is the frequency of amino acid a in sequence g, and g(x,y,z) and s(x,y,z) are the frequencies of synonymous codons in g and S, normalized for each amino acid. Intuitively, it can be seen that a gene g sharing codon usage patterns with reference set S will generate low values for the |g(x,y,z) − s(x,y,z)| differences, leading to an overall low B(g|S) value. On the basis of the codon usage difference measure, Karlin et al. then derive the E(g) gene expression measure as:

3

where C represents the set of all protein-coding genes in the organism of interest. Predicted highly expressed genes can be defined based on E(g), noting that they should have high B(g|C) values (strong deviation from genomic average) and, conversely, low B(g|RP), B(g|CH) and B(g|TF) values. High E(g) values thus denote high predicted expression values.

Most CBIs have been shown to correlate relatively well with either mRNA or protein concentration levels in Saccharomyces cerevisiae and Escherichia coli.^{14,15,21–24} These results are relevant even though it is known that the correlation between mRNA and protein concentration cannot be perfect due to several factors, such as translational initiation/elongation rates and protein half-life.^14,22,25 This non-linear relationship, among other factors, puts an upper limit on the best correlations that can be obtained between CBIs and expression levels.²³ In most of these studies, CAI outperformed other methods in predicting gene expression¹⁴ or performed close to proposed improvements or variations.^21,23 Thus, CAI remains as the gold standard among CBIs. In spite of these successes, CBIs have several limitations. On the one hand, indices measuring deviation from uniform codon usage have been shown repeatedly to overestimate deviation for short sequences.^15,26,27 On the other hand, as defined originally, indices relying on a reference set are only applicable to species in which selection for translational efficiency has been established. Furthermore, these methods rely on a species-specific reference set that needs to be defined. Results are therefore not directly comparable between different species, although both CAI and E(g)²⁰ have been shown to be quite resilient to changes in their reference sets²¹ and iterative algorithms have been proposed to derive the CAI reference sets automatically.²⁸

In 2009, Roymondal et al.²⁹ proposed a novel CBI, termed relative CUB (RCBS), able to estimate CUB without a reference set. RCBS can be expressed as:

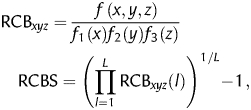4

where L is the length, in codons, of the gene, f(x,y,z) the observed frequency of codon xyz and f₁(x), f₂(y) and f₃(z) the observed frequencies of bases x, y and z at, respectively, codon positions 1, 2 and 3. In both cases, frequencies are computed relative to the sequence of interest. Therefore, for a particular codon, the method calculates the observed codon frequency and then computes its ratio to the expected codon frequency, which is derived as the product of the individual base frequencies at each codon position. The sequence index RCBS is computed as the geometric mean of codon bias over all sequence codons. Intuitively, it can be seen that codons deviating from what is expected based on the distribution of their individual base frequencies will contribute to larger RCBS values, whereas codons following the expected distribution will minimize the index.

Roymondal et al. showed that their method correlated significantly with CAI and E(g) in different E. coli data sets. They also showed that RCBS was a superior predictor of protein concentration and protein abundance than CAI and E(g), respectively, on these same data sets. On the basis of their observation that RCBS has a strong correlation with gene length, yielding larger values for shorter gene sequences and that it correlates well with protein abundance, the authors concluded that natural selection favours high expression levels in short genes, increasing their codon adaptation. In a second publication, the authors extended their analysis of RCBS to S. cerevisiae and arrived to the same conclusion (selection favours high expression levels in short genes) following the same logic.³⁰ Here, we show that the positive results reported by Roymondal et al.²⁹ in E. coli are based on built-in biases within the small data sets used for validation. Furthermore, we demonstrate that their conclusion that selection favours codon optimization in short genes is erroneous and stems from systematically ignoring an intrinsic bias in their method due to undersampling, which is implicit in short sequences. We proceed to show how RCBS can be corrected by different means and how its underlying principle, which we term relative codon adaptation (RCA), can be applied to different reference sets, leading to improved estimations of gene expression.

2. Materials and methods

2.1. Expression data

To validate the accuracy of different indices at predicting gene expression, expression data were collected from the Many Microbe Microarrays Database (M^3D). The M^3D is a compendium of single-channel gene expression experiments in E. coli, S. cerevisiae and Shewanella oneidensis, uniformly normalized using the log robust multiarray analysis (RMA) and encompassing over a thousand microarrays from a single platform (‘Affymetrix’).^31,32 Build 6 of the E. coli M^3D database was downloaded from the M^3D server. From this main data set, we selected only 18 experiments done on E. coli str. K-12 growing in log-phase. For these experiments, 31 different control sets were identified and used as a benchmark for E. coli K-12 expression in log-phase. Individual correlations among the 31 control sets were evaluated (average Pearson r = 0.779 ± 0.091) and found to be remarkably strong, suggesting that the use of a unified platform and resource for microarray data reduces significantly the amount of noise observed previously in microarray expression data.²⁴ Gene names, GenBank accession numbers and other identifiers for E. coli K-12, were downloaded from the EcoGene database³³ and cross-referenced on a Microsoft Excel spreadsheet with the 4149 protein-coding gene sequences for E. coli str. K-12 substr. MG1655 available on GenBank. The resulting annotated sequences were then correlated with the M^3D bulk download. This led to an annotated expression data set containing 31 independent log-phase expression values for 4029 E. coli protein-coding genes (Supplementary Table S1).

Protein abundance data for E. coli were obtained from the Supplementary material accompanying the E. coli cytosol profiling of Ishihama et al.²² This data set contains normalized exponentially modified protein abundance index (emPAI) values for 1103 E. coli cytosolic proteins. emPAI values for the 439 proteins for which CAI values were reported were cross-linked with EcoGene tags and GenBank sequence data sets as reported above, leading to a final data set of 359 E. coli proteins for which molecular weight/mass tags matched (±1) in both annotations (EcoGene and Ishihama et al.) and CAI values reported in Ishihama et al.²² could be reproduced (±0.05) based on GenBank gene sequence (Supplementary Table S2). Protein abundance data for Mycobacterium smegmatis were obtained from the Supplementary material accompanying the mass spectrometry analysis of the M. smegmatis proteome by Wang et al.³⁴ This data set contains a quantification of protein abundance as the number of observations for a particular protein in a sequence of experiments. Here, we used the number of observations in 15 exponential phase experiments as an indicator of protein concentration in exponential growth phase. The original data set contains data on 901 distinct proteins, with CAI and observation numbers provided for 892 proteins. Here, we cross-linked this data with M. smegmatis protein and protein-coding sequences downloaded from NCBI. After combining the data, we obtained a data set of 841 proteins and their corresponding protein-coding sequences (Supplementary Table S3).

All other protein and mRNA concentration data referenced by Roymondal et al.²⁹ were obtained from the Supplementary material accompanying their publication and verified using the references provided therein. To compute additional indices over these sets, the provided information was cross-linked with EcoGene tags and GenBank sequences as described above.

2.2. Computation of codon usage indices

Computation of CAI, RCA, RCBS and the correction proposed herein (RCBS^PC) was done integrally using custom Microsoft Excel functions, following the equations presented in this work. The functions are available at http://research.umbc.edu/~erill/, either as Visual Basic BAS modules or embedded in a macro-enabled Excel 2003 spreadsheet that illustrates their usage.

In E. coli, CAI was computed using the w values provided by Sharp and Li.¹⁹ For the calculation of RCA, codon and base frequencies were computed on the 27 highly expressed genes used by Sharp and Li¹⁹ and applying 0.0001 pseudo-counts for absent codons (AGG and TAG). For M. smegmatis, homologues for the 27 genes in the Sharp and Li data set were identified through reciprocal BLASTP,^35,36 enforcing a maximum e-value of 10⁻³ and a minimum coverage of 40% positives on all BLASTP searches. A total of 22 M. smegmatis homologues for the Sharp and Li gene set were identified in this manner and used for computation of the RCA codon and base frequencies in this organism. For the pseudo-count correction of RCBS (RCBS^PC), genomic frequencies were computed on the 4029 E. coli protein-coding gene set of the M^3D expression data set.

2.3. Generation of random sequences

Pseudo-random sequence was generated using two custom Microsoft Excel functions. A first routine was created to generate random sequence based on %GC content and length. This function ensures only that the generated sequence complies with the provided %GC content that the sequence is a congruent open reading frame (no nonsense mutations and terminating in a stop codon). The second routine uses a provided codon usage table (including stop codons) as a base distribution to generate congruent open reading frames. These functions are available at http://research.umbc.edu/~erill/, either as Visual Basic BAS modules or embedded in a macro-enabled Excel 2003 spreadsheet.

2.4. Statistical analysis

The Pearson and the Spearman rank correlation coefficients and their corresponding P-values were computed integrally using Microsoft Excel. The Pearson correlations were computed using built-in Excel functions. The Spearman rank correlations were computed using the statistical function set of Wim Gielis. Throughout the manuscript, the Pearson correlation coefficients are denoted by r and the Spearman rank correlation coefficients by ρ. The asterisk rating system is used for correlation P-values [single asterisk (*), P < 0.05–0.01; double asterisks (**), P < 0.01–0.001; triple asterisks (***), P < 0.001]. P-values are relative to a two-tailed Student's t-test on the null hypothesis (no correlation). For multiple correlations, we report the mean and standard deviation of the correlation coefficient and the largest P-value among the correlations.

3. Results and discussion

3.1. Dependence of RCBS on sequence length

A major result of Roymondal and colleagues' application of RCBS is the conclusion that natural selection favours higher expression and heightened codon optimization for short genes in both the E. coli²⁹ and the S. cerevisiae genomes.³⁰ This finding is based on two main observations. On the one hand, the authors observe that RCBS correlates negatively with gene length. On the other hand, they show that there is a positive correlation between RCBS and protein abundance data. This is a surprising result since a previous work had identified a positive, rather than a negative, correlation between CBIs and protein length after controlling for mRNA concentrations,^14,37 suggesting secondary selection on translational accuracy for long genes.^5,37,38 Moreover, even though some studies had reported some correlation between gene length and mRNA concentration in E. coli and S. cerevisiae,^14,24 the correlation turned out to be weak when controlling for codon bias.¹⁴ Moreover, and as stated above, many CBIs tend to overestimate deviation in short sequences.^15,26,27 Thus, it appeared that Roymondal et al. might have been too eager to identify causation in the correlations they reported, attributing to natural selection what could be the result of an intrinsic bias in their index.

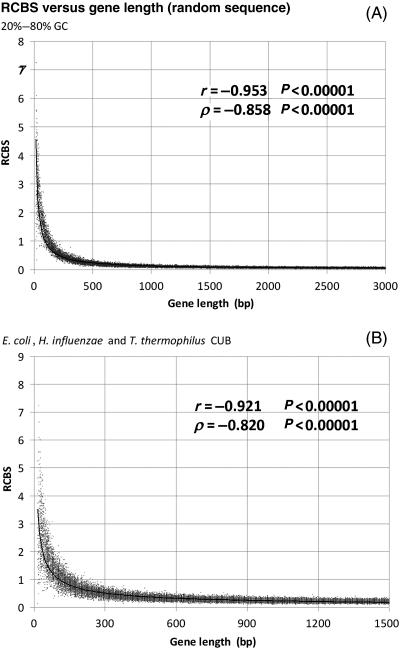
In their study, Roymondal et al. analyse and validate the length dependency of RCBS with randomization studies of E. coli sequences. Their randomization method is manifestly unclear and the E. coli genes to be randomized are ‘selected’ by the authors without proper justification. Nonetheless, the supporting material (Tables SIIA and SIIB in Roymondal et al.²⁹) seems to confirm that the strong (r = 0.812) inverse power-law-shaped correlation observed between RCBS and E. coli gene length still applies to randomized E. coli sequences (r = 0.999*** for both tables, Supplementary Fig. S1). In spite of this, the authors chose to ignore the length dependency of RCBS in their subsequent analysis, arguing that ‘smaller sequences have a greater probability of resulting in high value of RCBS (>0.5), but there is nothing to prevent longer sequences from having high RCBS’. To analyse whether the observed effect was limited to E. coli sequences or constituted a general property of the RCBS index, here we computed RCBS for randomly generated sequences using different %GC content values (Fig. 1A) and CUBs (Fig. 1B).

Figure 1.

Distribution of RCBS values versus length for 10 000 random-coding sequences generated using (A) random 20–80% GC content and length (1–3000 bp) or (B) E. coli, H. influenzae or T. thermophilus CUB and random length (1–1500 bp).

Our results on randomly generated sequence support the notion that RCBS has an inherent inverse power-law-shaped bias towards short sequences, regardless of %GC content (Pearson r = 0.953***, Spearman rank ρ = 0.858***) and particular CUBs (r = 0.921***, ρ = 0.820***). This length dependency is a consequence of undersampling effects in short sequences, which induce overestimation of both the f(xyz) and the f₁(x), f₂(y) and f₃(z) terms in Equation (2). Undersampling is more pronounced in the larger space of codon frequencies [f(xyz)], leading to consistent overestimation of f(xyz) over its expected value [f₁(x) · f₂(y) · f₃(z)]. This leads to extremely large RCBS values for short sequences and to the observed inverse power-law distribution. Our data thus confirm that the correlation between RCBS and gene length observed in E. coli can be reproduced in random sequences and is therefore intrinsic to the RCBS index. It is a mathematical artefact due to undersampling in short sequences and, as such, it cannot be attributed to natural selection or to any other evolutionary process.

3.2. Analysis of RCBS on E. coli microarray expression data

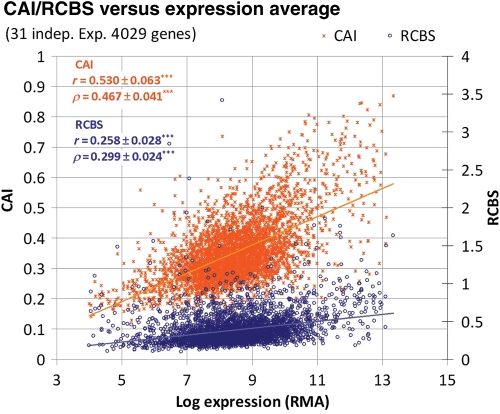
In the seminal RCBS paper, Roymondal et al. validate the RCBS index against different cDNA microarray data sets.^39,40 They report very weak correlations, which they attribute to the noisy nature of microarray data. However, the most probable cause of the weak correlations observed is their use of log expression ratios, rather than log expression values, as the basis for their correlations. Using log expression ratios to evaluate a CBI might arguably make sense for the data set of Tao et al.,³⁹ which compares log-phases on minimal and rich media, but it is clearly unjustified for the data set of Richmond et al.,⁴⁰ which analyses induction of heat-shock response genes. Even in the Tao et al.³⁹ data set, the use of log ratios can introduce undesired effects, such as a low ratio for ammonia assimilation genes, which are induced in minimal media to exploit ammonia as a nitrogen source. To correctly analyse the performance of the RCBS index on mRNA expression data, here we computed the RCBS and CAIs on the 4029 gene sequences derived from the M^3D data set, and we compared their values with mRNA log copy numbers in the 31 independent controls for experiments involving E. coli K-12 in log-phase growth.

The results in Fig. 2 reveal that RCBS correlates poorly with mRNA log expression values using both the Pearson (r = 0.258 ± 0.028***) and the Spearman rank (ρ = 0.299 ± 0.024***) correlation. RCBS also correlates moderately with CAI (r = 0.433***, ρ = 0.448***). In contrast, and in agreement with previous studies,^14,23,24 CAI correlates moderately well with log expression values (r = 0.530 ± 0.063***, ρ = 0.467 ± 0.041***). To determine whether the poor performance of RCBS was due to its strong built-in dependency on length, we re-computed these correlations for genes with sequence lengths above 1000 bp. This led to a subset of 1541 genes in our expression data set. In this gene set, the correlation of RCBS with sequence length is extremely weak (r = −0.086***, ρ = −0.080**). Controlling for sequence length in this way reduces vastly the difference in correlation with log expression values between RCBS (r = 0.489 ± 0.054***, ρ = 0.430 ± 0.045***) and CAI (r = 0.528 ± 0.053***, ρ = 0.474 ± 0.044***) and improves their mutual correlation significantly (r = 0.870***, ρ = 0.798***). As expected, this effect is mainly due to an increase in RCBS correlation with log expression, rather than a decrease in CAIs, since CAI shows very weak correlation with length (r = 0.114***, ρ = 0.143***) on the 4029 E. coli gene set (Supplementary Fig. S2).

Figure 2.

Distribution of CAI and RCBS values versus the average of normalized log expression values over 31 independent experiments for 4029 E. coli genes.

The fact that for sequences over 1000-bp long, RCBS correlates well with CAI and is able to predict expression levels with similar accuracy constitutes in itself a significant result, since both methods rely on a markedly different set of assumptions. CAI estimates the deviation from the major codon bias, as derived from a set of highly expressed genes,¹⁹ whereas RCBS estimates deviation from uniformity within the sequence. The strong correlation between both indices for sequences above 1000 bp indicates that at these lengths single-sequence information is enough to properly estimate codon bias. It should be noted that this estimation is independent of the bias source and even of the sequence genomic context. RCBS is thus by construction generic and, in principle, equally suited to detect bias from different sources without assuming the existence of a major codon bias.²⁸ In this respect, the strong correlation with CAI observed in E. coli supports the well-established notion that translational efficiency selection is the most important source for codon bias in this species.¹⁸

3.3. Pseudo-count correction for RCBS

Having established that the poor performance of RCBS as a predictor of gene expression is due to its length dependency, here we introduce a correction method for RCBS. Owing to its simultaneous estimation of sequence-based frequencies for both codons and codon positions, an analytical length-correction factor, such as the one implemented for the MILC-based expression level predictor,¹⁵ is impracticable for RCBS. Nonetheless, RCBS can be corrected generically by applying genome-derived pseudo-counts to prevent bias overestimation in short sequences.⁴¹ In this approach, both codon and codon position frequencies are estimated following:

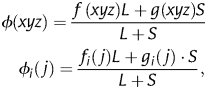5

where L is the length in codons of the sampled sequence, g(xyz) the observed frequency of codon xyz among genomic-coding regions, g_n(m) the observed frequency of base m at codon position n, also in genomic-coding regions, and S the weight on pseudo-counts (or priors), also measured in codons. The pseudo-count corrected version of RCBS (RCBS^PC) is then computed as in Equation (2), but substituting f(xyz) and f_n(m) by ϕ(xzy) and ϕ_n(m), respectively.

The pseudo-count weight can be adjusted by observing that the RCBS dependency on length (i.e. the observed inverse power-law distribution) starts to flatten out for sequences larger than 1000 bp and that this effect is independent on the nature of the sequences analysed (Fig. 1 and Supplementary Fig. S3). Following this observation, a pseudo-count weight (S) of 300 was used to compute RCBS^PC. For S = 300, genomic pseudo-counts dominate and dampen sequence-based frequencies up to lengths near 1000 bp. From this point onwards, sequence-derived frequencies start to dominate and are able to provide reasonable estimates of codon bias, as described in the previous section. When tested against the gene expression data set, RCBS^PC improved significantly the correlation with log expression values (r = 0.462 ± 0.047***, ρ = 0.415 ± 0.035***) and with CAI (r = 0.820***, ρ = 0.753***; Table 1, Supplementary Fig. S4A).

Table 1.

Summary of RCBS, CAI and RCBS^PC correlation with log expression values and with CAI

	Correlation with log expression		Correlation with CAI
	Pearson r	Spearman ρ	Pearson r	Spearman ρ
RCBS	0.258 ± 0.028***	0.299 ± 0.024***	0.434***	0.448***
CAI	0.530 ± 0.063***	0.467 ± 0.041***	1.000	1.000
RCBSPC	0.462 ± 0.047***	0.415 ± 0.035***	0.820***	0.753***

For each index, correlation values with log expression data reflect the mean and standard deviation of independent correlations with the 31 available experiments over 4149 genes.

3.4. Analysis of RCBS on E. coli protein abundance data

Roymondal et al. based their claim that selection favours codon optimization and the higher expression of smaller proteins on the good correlation observed both between RCBS and protein concentration data and between the RCBS and the CAI and E(g) indices. We have reported above that the correlation of CAI with RCBS improves significantly with the pseudo-count correction of RCBS, or when sequence length is controlled for. The same effect was observed for the correlation of RCBS with E(g) when the data from Karlin et al.¹⁸ were analysed. The correlation of RCBS with E(g) over the 96 genes analysed by Karlin et al. (r = 0.730***, ρ = 0.820***) is again improved by RCBS^PC (r = 0.844***, ρ = 0.894***; Supplementary Fig. S4B). Roymondal et al. also observed that RCBS correlates better (r = 0.453***) than E(g) (r = 0.262**) with the relative molecular abundance (RMB) of 96 E. coli proteins growing on glucose minimal medium.¹⁸ Here, we tested the correlation of RCBS, RCBS^PC and CAI with the log protein abundance for these same genes and for the data set of Eyre-Walker³⁸ (45 genes).

The results, summarized in Table 2, indicate that RCBS outperforms CAI and RCBS^PC in both data sets, although the difference is less noticeable in the larger data set of Karlin et al. The better performance of RCBS in the protein data sets thus contradicts the results on mRNA expression data reported above. Furthermore, it is also inconsistent with the improved correlation of RCBS^PC with both CAI and E(g) on both data sets. To explore the nature of this apparent discrepancy, here we tested the performance of RCBS, CAI and RCBS^PC against the more recent and larger protein concentration data set of Ishihama et al.²² The results, summarized in Table 3, are in broad agreement with those obtained in the former data sets. RCBS provides again the best correlation with protein concentration (r = 0.710***, ρ = 0.588***), followed by CAI and then RCBS^PC. To control for sequence length, we selected again sequences over 1000-bp long, leading to a subset of 170 genes. When controlling for sequence length in this way, the differences between RCBS and CAI become marginal. In agreement with this finding, the mutual correlation between RCBS and CAI goes up from moderate (r = 0.640***, ρ = 0.618***) in the original set to strong (r = 0.904***, ρ = 0.861***) in the >1000-bp data set. As before, the statistically significant increase in similarity between CAI and RCBS results for the >1000 data set does not stem from a worse performance of CAI (its correlation with relative protein abundance actually improves). Instead, they arise from a drop in RCBS performance, suggesting that its enhanced correlation on the whole-length data set could be due to an artefact in the protein data.

Table 2.

Correlation of RCBS, CAI and RCBS^PC indices with log RMB for the 96 gene set of Karlin et al.¹⁸ and with log protein concentration for the 45 gene set of Eyre-Walker³⁸

	Eyre-Walker, 45 genes		Karlin et al., 96 genes
	Pearson r	Spearman ρ	Pearson r	Spearman ρ
RCBS	0.708***	0.777***	0.453***	0.508***
CAI	0.616***	0.705***	0.405***	0.443***
RCBSPC	0.621***	0.652***	0.404***	0.451***

Table 3.

Correlation of RCBS, CAI and RCBS^PC indices with emPAI-estimated protein abundance²² for the original set of 359 genes and those with lengths larger than 1000 bp (170 genes)

	Ishihama et al. (full) 359 genes		Ishihama et al. (>1000 bp) 170 genes
	Pearson r	Spearman ρ	Pearson r	Spearman ρ
RCBS	0.710***	0.588***	0.616***	0.501***
CAI	0.590***	0.469***	0.611***	0.511***
RCBSPC	0.533***	0.432***	0.590***	0.487***

3.5. Analysis of E. coli protein abundance data

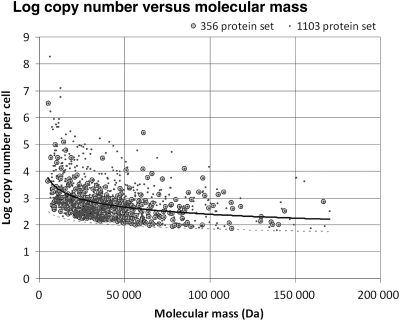
Having shown above that RCBS presents a strong built-in bias with sequence length, the results of Table 3 strongly suggest that the observed superiority of RCBS in the protein data sets might be the result of a similar bias in the protein concentration data. To test this hypothesis, we analysed the correlation between molecular mass and log protein abundance in the data set of Ishihama et al. As it can be seen in Fig. 3, log protein abundance and molecular mass correlate quite well under an inverse power-law distribution (r = −0.429***, ρ = −0.381***). Correlation coefficients are nearly identical for the 359 subset analysed above (r = −0.439***, ρ = −0.421***), but the strength of this correlation falls dramatically in the length-controlled (>1000 bp) data set (r = −0.120, ρ = −0.182*).

Figure 3.

Distribution of emPAI-estimated log protein abundance versus molecular mass for the 1103 proteins reported by Ishihama et al.²² and the subset used in this study (359 proteins, see Materials and methods). The overall shape of the distribution is in broad agreement with the log protein abundance versus length plot reported in Fig. S7 of Ishihama et al. The correlation coefficients under a power-law distribution are: r = −0.429***, ρ = −0.381*** for the 1103 protein set and r = −0.429***, ρ = −0.394*** for the 359 protein set. The Pearson correlation coefficients under a linear distribution are r = −0.318*** and r = −0.304***, respectively. For the 359 protein subset, the correlation between molecular mass and gene length is very strong (r = 0.999***, ρ = 0.999***). The dotted line underscores the length-dependent bias in the method's lower detection limit.

The results in Fig. 3 confirm that there is a strong correlation between protein molecular mass (or length) and the estimated protein concentration in the data set of Ishihama et al. Similar, albeit weaker, correlations can be observed in the Eyre-Walker (r = −0.319*, ρ = −0.492***) data set and in that of Karlin et al.¹⁸ (r = −0.214*, ρ = −0.254*). This result is significant in several ways. On the one hand, it establishes that there is a length-dependent bias in the estimation of protein concentration by three separate groups and methods.^22,38 Furthermore, it suggests that this bias follows an inverse power-law distribution, strongly overestimating the concentration of smaller proteins. The causes for this bias are not easy to discern, but there are several processes that might be concurrently contributing to the observed distribution. Having established that mRNA concentration does not appear to be length-dependent (r = 0.026 ± 0.015*, ρ = 0.026 ± 0.017 on the 4029 gene sequences derived from the M^3D data set; Supplementary Fig. S5), it seems likely that from a biological standpoint protein concentration can be affected by three main parameters: translation initiation and elongation rates and protein turnover.^14,22,25

An exponential negative correlation between protein turnover and length has been reported for yeast and higher eukaryotes,^42,43 suggesting that a similar trend might be also present in prokaryotes. In addition, and regardless of codon optimization, it makes sense to assume that the amount of misreadings and frame-shifts during translation must be proportional to length. If Boolean outcomes and conditional independence are assumed for these events, the amount of properly formed protein should follow a binomial distribution, yielding exponential decay with length. Finally, methodological factors may also come into play. Protein concentration in 2D gels is assessed by measuring the average intensity of spots.^25,44 Since smaller proteins diffuse more readily than larger ones, they become more difficult to detect and this introduces a systematic bias in the detection limit. Abundant small proteins are more likely to be detected than less abundant proteins of the same size. This bias is length-dependent and tends to disappear for large proteins (O'Farrell, 2009, Personal communication). The liquid chromatography-tandem mass spectrometry (LC-MS/MS) techniques used by Ishihama and colleagues are in principle less sensitive to biases in their lower detection limit.⁴⁵ However, it is apparent from Fig. 3 that the mass-dependent bias in protein concentration stems, at least partially, from a bias in the method's detection limit.⁴⁶

The identification of a negative correlation between protein concentration estimates and protein length accounts for the superior performance of RCBS in these data sets, but it also casts doubts on the validity of using protein concentration data for the evaluation of CBIs or, conversely, using these indices to estimate protein concentration. Historically, prediction of expression by CBIs has been assessed indistinctly with both mRNA²¹ and protein^18,22,34,38 concentration data. Here, we find that for large data sets, the most well-established index (CAI) yields similar correlations (r = 0.530*** for mRNA and r = 0.590*** for protein) in E. coli. This suggests that the practice of using either type of data indistinctly, although unfounded, might be justified. Selection for translational optimization is carried out at the gene level by assessment of essential protein concentrations during log-phase growth. This means that, even without methodological biases, the non-linearity in the coupling of transcription, translation and post-translation processes imposes an upper threshold on the performance of any bias index. For instance, high turnover rates for a log-phase-required protein will select for increased codon optimization, yielding to an overestimation of protein concentration based on bias indices. On the other hand, genomic location and promoter efficiency can increase mRNA concentrations for key log-phase proteins, leading to reduced codon optimization and incorrect estimates from indices.

3.6. The RCA index and its application to different reference sets

Owing to its reliance on the query sequence alone, the RCBS index has a strong bias towards short sequences. This length dependency prevents its application to sequences shorter than 1000 bp. With more than half of the E. coli gene set below 1000 bp (Supplementary Fig. S6), length dependency thus becomes a severe handicap for the application of RCBS. As shown above, the length dependency of RCBS can be corrected with genomic pseudo-counts, but this in turn limits its application to complete genomes, and its performance on short sequences is still noticeably weak. In spite of these pitfalls, the basic principle behind RCBS (computing codon deviation from expected codon frequencies as relative codon frequencies) remains sound. Relative codon frequencies provide a sensible estimate of deviation from expected codon usage if provided with large enough samples to infer frequencies from. This is illustrated by the reasonable predictions of gene expression obtained with RCBS when controlling for sequence length. In order to exploit the potential of relative codon frequencies as a CBI without requiring genomic corrections or limiting their usage to sequences larger than 1000 bp, here we extend the basic principle of relative codon frequencies, which we term RCA, by defining its generic application to any reference sequence set. Formally,

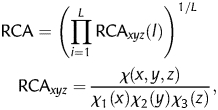6

where χ(xyz) is the observed frequency of codon xyz in any particular reference gene set, χ_n(m) the observed frequency of base m at codon position n in the same reference set, and L the length in codons of the query sequence. Like CAI and RCBS, RCA is computed as the geometric mean of the RCA_xyz term for each codon xyz in the sequence of interest.

As defined above, RCA makes use of a given reference set to compute observed and expected codon frequencies. In this sense, RCA is similar to other reference-set-based indices, but most notably to CAI, since it makes use of a single reference set that can be defined following the same principles applied to CAI.¹⁹ Like CAI, RCA is also amenable to iterative algorithms designed to identify the reference set without prior biological knowledge.^28,47 Since it is also defined on a reference set, RCA should not present significant length dependencies if its reference set is well-defined.^26,27 There is, however, an important difference between CAI and RCA. In CAI, the relative adaptiveness of a codon (w_i) is computed as the ratio between the frequency of that codon in the reference set and the largest frequency among its synonymous codons [Equation (1)]. This implicitly assumes that the background nucleotide distribution is uniform. The inability to take into account background nucleotide composition is a fundamental problem of many CBIs.²⁷ Assuming a uniform background nucleotide composition is a major drawback for those indices relying on a uniform null hypothesis, like N_c. However, it can also skew the results of indices based on reference sets, like CAI, leading them to attribute to translational selection the patterns of mutational bias observed in the reference set.

In contrast to CAI, for any given reference set, the RCA index first computes the expected frequency of a codon based on its positional base frequencies. It then measures codon adaptation as the deviation of the observed codon frequency from the expected codon frequency. Thus, RCA takes explicitly into account sequence composition in the calculation of each RCA_xyz term and should be able to provide more robust and accurate estimates of gene expression. This improvement in accuracy should be more apparent in cases of high mutational bias and/or lowered selection for translational efficiency, in which CAI may easily be mislead by mutational bias artefacts in the reference set.

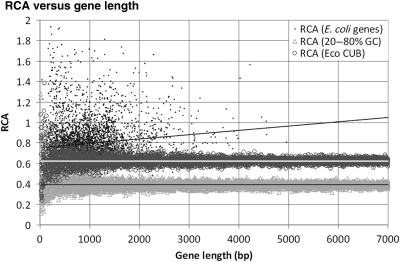
Here, we investigated the benefits of using RCA as a CBI by establishing first the absence of a systematic bias with length and by analysing then the performance of the RCA index at predicting expression data in E. coli and M. smegmatis. For E. coli, RCA frequency computations were carried out using the original reference set (27 genes) of Sharp and Li.¹⁹ For M. smegmatis, 22 orthologues of the Sharp and Li genes were identified through reciprocal BLASTP and used to compute the relative frequencies for RCA. The presence of an intrinsic length dependency in RCA was assessed by analysing the correlation of RCA values with gene length in both E. coli and randomly generated gene sequences. As before, random gene sequences were generated both for a broad range of %GC contents or following the CUB of E. coli. Fig. 4 shows that, as expected, RCA does not present any intrinsic bias with gene length. RCA shows a slight yet significant (r = 0.122***, ρ = 0.173***) linear positive correlation with gene length for E. coli genes, but none with randomly generated gene sequence. This indicates that the observed correlation is not due to an intrinsic mathematical artefact of the RCA index. Furthermore, the observed correlation for E. coli genes is in accordance with similar correlations reported previously for CAI in E. coli and S. cerevisiae.^14,37 The fact that no significant correlation with sequence length can be observed for RCA values on artificial gene sequences provides further support to the hypothesis of selection for translational efficiency in long gene sequences.³⁷

Figure 4.

Distribution of RCA values versus length for the 4029 E. coli genes in the M^3D-derived expression data set, 5000 randomly generated sequences of random length (6–6999 bp) with random %GC content in the 20 − 80% range and 5000 randomly generated sequences of random length (6–6999 bp) following the E. coli CUB. Correlation coefficients are as follows: E. coli genes (r = 0.122***, ρ = 0.173***), E. coli CUB random sequence (r = −0.0138, ρ = 0.005) and 20–80% GC random sequence (r = 0.012, ρ = 0.025).

To assess the validity of RCA as a predictor of gene expression, we used CAI as a benchmark for comparison. Apart from the remaining golden standard among CBIs, CAI is based on the same set of assumptions as RCA and uses identical reference sets, thereby allowing direct comparisons between the two methods. The results in Table 4 show that even in a genome with low mutational bias like E. coli, RCA is able to slightly outperform CAI on both mRNA and protein data sets. Furthermore, the difference between both methods becomes significantly more pronounced when analysing the M. smegmatis mass spectrometry proteomic data reported by Wang et al.³⁴ Mycobacteria present heavy mutational biases, with genomic %GC contents ranging from 57% (Mycobacterium leprae) to 67% (M. smegmatis) that have a strong effect on their CUB. However, it has been shown that translational selection can still play a significant role in the CUB of mycobacteria.⁴⁸ By integrating the background base composition into its computation, RCA takes directly into account the effects of mutational bias on codon usage, allowing it to provide considerably more accurate predictions of gene expression than CAI in genomes with strong mutational bias. As shown in Table 4, this allows RCA to significantly outperform CAI in M. smegmatis, yielding correlation coefficients with expression data (r = 0.525***, ρ = 0.464***) that are remarkably close to those reported by both CAI and RCA in E. coli. The improved reliability of RCA for estimating expression levels in different organisms and contexts thus makes this index a superior choice for undertaking and benchmarking predictions of gene expression.

Table 4.

Correlation of CAI and RCA indices with M^3D mRNA log expression values and emPAI-estimated protein abundance²² in E. coli and with protein abundance data in M. smegmatis³⁴

	M3D data set, 4149 genes		Ishihama et al. (full) 359 genes		Wang et al. (M. smegmatis) 841 genes
	Pearson r	Spearman ρ	Pearson r	Spearman ρ	Pearson r	Spearman ρ
RCA	0.540 ± 0.068***	0.478 ± 0.045***	0.603***	0.453***	0.525***	0.464***
CAI	0.530 ± 0.063***	0.467 ± 0.041***	0.590***	0.469***	0.346***	0.354***

Protein abundance data in M. smegmatis³⁴ are estimated from the number of observations of each protein in multiple experiments.

Supplementary material

Supplementary material is available at www.dnaresearch.oxfordjournals.org.

Funding

Funding was provided by the Department of Biological Sciences at the University of Maryland Baltimore County.