Principal Point Classification: Applications to Differentiating Drug and Placebo Responses in Longitudinal Studies

Abstract

Principal points are cluster means for theoretical distributions. A discriminant methodology based on principal points is introduced. The principal point classification method is useful in clinical trials where the goal is to distinguish and differentiate between different treatment effects. Particularly, in psychiatric studies where placebo response rates can be very high, the principal point classification is illustrated to distinguish specific drug responders from non-specific placebo responders.

1. Introduction

In typical applications of discriminant analysis, there is training data from two or more groups and the goal is to define a discriminant function to classify new observations to the correct groups. The goal of this paper is a bit different from the classical discriminant analysis problem. Consider a clinical trial with an active drug arm and a placebo arm. The problem of interest is to determine which subjects in the active drug arm are responding primarily to a non-specific (placebo) effect rather than the specific effect of the drug. Because we know which subjects receive the active drug or the placebo, there is no ambiguity as to which treatment group the subjects belong. However, if a drug-treated subject responds, we do not know to what degree the subject responded due to the specific (drug) effect and to non-specific (placebo) effects of the treatment. If a placebo treated subject responds, then we know it must be due to the non-specific effects of the treatment. Outside of clinical experiments in everyday treatment, patients typically receive the active drug for treatment, not a placebo. Interest lies in classifying drug treated patients who respond primarily due to specific (drug) effects or to non-specific (placebo) effects, or perhaps a combination of these two effects.

The problem of distinguishing a placebo response from a drug response in psychiatric illnesses has been of high interest for clinical research and practice for many years (e.g., see 1; 2). There is a need to apply modern statistical methods to address this important problem. One approach to the specific/non-specific treatment effects problem is to assume that the population consists of distinct latent subgroups of specific responders and non-specific responders. For longitudinal studies, a growth mixture model can be postulated (3; 4; 5). However, if subjects can experience both specific and non-specific effects ranging continuously from very weak to very strong, then modeling the outcomes as a growth mixture could erroneously lead investigators to believe real sub-populations exist. In this paper, an alternative strategy is implemented by determining an optimal partition of the underlying distribution. The partitioning method is based on determining optimal cluster centers, called principal points (6), for theoretical distributions.

In the classical normal theory discriminant analysis, observations are assigned to the different groups based on their proximity to the group means. In longitudinal studies, the outcomes of interest are curves over time. Focusing only on the mean curve ignores the fact that groups often contain a variety of distinct curve shapes. For instance, in longitudinal clinical studies, there may exist different types of outcome profile shapes over time corresponding to different types of response to treatment. The principal point classification method developed in this paper assigns observations based on proximity to principal points which can be regarded as a generalization of the mean from one to several points. In addition, if we know the outcome distributions differ for different groups (e.g., different treatment arms in a clinical trial), the principal point classification method developed below can identify prototypical outcome profiles that can distinguish these differences.

In Section 2 we define principal points and discuss methods of estimating principal points. The principal point classification method is described in Section 3. Results of a simulation experiment comparing principal point classification with normal theory discriminant analysis are provided in Section 4. Principal points for linear mixed effect models are described in Section 5. The principal point classification method is used to distinguish two drug therapies for depression (fluoxetine and imipramine) in Section 6. Additionally, outcome profiles from specific and non-specific effects are distinguished using the principal point classification methodology in this section as well. Finally, the paper is concluded in Section 7.

2. Principal Points

A classic statistical problem is to determine an optimal partition of a continuous distribution (7; 8; 9; 10). In signal processing, this problem is referred to vector quantization (e.g., ¹¹). In an optimal stratification of a distribution into k strata, the means of the k strata are called the k principal points of the distribution (6).

Let X denote a continuous random vector and consider k points ξ₁, … , ξ_k to be used to represent the distribution of X. We can define a k-point approximation Y to X as

$$\mathit{Y}={\mathit{\xi }}_j,\text{if}\Vert \mathit{X}-{\mathit{\xi }}_j\Vert <\Vert \mathit{X}-{\mathit{\xi }}_h\Vert ,\text{for}h\ne j.$$

Y is a self-consistent approximation to X if E[X|Y] = Y a.s. (12) in which case the points ξ₁, … , ξ_k are called k self-consistent points of X (13). Distributions, particularly multivariate distributions, may have more than one set of k self-consistent points (14). If E║X – Y ║² ≤ E║X – Y *║² for any other k-point approximation Y * to X, then the points ξ₁, … , ξ_k are called k-principal points of X. (13) showed that a set of k principal points of a distribution must be self-consistent points.

For k = 1, the single principal point corresponds to the mean of the distribution. For k > 1, the k principal points provide a k-point generalization of the mean from one to several points. For a N(μ, σ²) distribution, the k = 2 principal points are $\mu \pm \sqrt{\frac{2}{\pi }}\sigma$ (6); for k > 2 the principal points must be found numerically. Univariate distributions with log-concave densities have a unique set of k self-consistent points for each k and this unique self-consistent approximation must correspond to the k principal points (15; 16; 17).

2.1. Estimation of Principal Points

Given a set of observations from a distribution, nonparametric estimators of k principal points can be obtained by using the cluster means from running the k-means algorithm (e.g. ^{26; 27; 28}). Under general circumstances, the cluster means from the k-means algorithm are strongly consistent estimators of the principal points (29) and asymptotically normally distributed (30). More efficient methods of estimating principal points can be obtained by utilizing distributional assumptions (e.g., ^{13; 18}). For instance, maximum likelihood estimators of k = 2 principal points of a univariate normal distribution are $\overline{\mathit{x}}\pm \sqrt{\frac{2}{\pi }}s$.

For larger values of k and for multidimensional distributions, analytical formulas for principal points do not exist. (23) describes a parametric k-means algorithm that provides a computationally intensive but easy to utilize method of determining maximum likelihood estimators of k principal points, similar to the algorithm of (24) from the vector quantization literature using a known distribution. Suppose the data x₁, … , x_n comes from a distribution with density f(x; θ). For the parametric k-means algorithm, first obtain a maximum likelihood estimate θ̂ of θ. Next, run the k-means algorithm on a very large data set simulated from f(x;θ̂). (23) showed that the cluster means obtained by running the k-means algorithm on the large simulated data set are (approximately) maximum likelihood estimators of the k principal points of f(·; θ) distribution.

3. Principal Point Classification

In this section we describe a classification method based on principal points. Suppose a population consists of H sub-populations and the goal is to determine a discriminant function to classify observations to one of H sub-populations based on a measured outcome vector x. Let π_h denote a prior probability corresponding to the proportion of the population belonging to the hth sub-population. Then the classification regions associated with any optimal classification rule are defined as follows: classify an observation x to sub-population h if

$${\pi }_h{f}_h(\mathit{x};{\mathit{\theta }}_h)>{\pi }_l{f}_l(\mathit{x};{\mathit{\theta }}_l),\text{for}l\ne h,$$

where f_h and f_l are the densities for sub-populations h and l parameterized by vectors θ_h and θ_l respectively.

When the sub-populations are assumed to be normal, the optimal classification rule corresponds to the well-known quadratic discriminant function. For example, suppose the population consist of H normal sub-populations N(μ_h, Ψ_h), h = 1, … , H. Then a new observation x is classified to population h if

$${\pi }_h{\left|{\mathbf{\Psi }}_h\right|}^{-1/2}\text{exp}\{-(\mathit{x}-{\mathit{\mu }}_h)\prime {\mathbf{\Psi }}_h^{-1}(\mathit{x}-{\mathit{\mu }}_h)/2\}>{\pi }_l{\left|{\mathbf{\Psi }}_l\right|}^{-1/2}\text{exp}\{-(\mathit{x}-{\mathit{\mu }}_l)\prime {\mathbf{\Psi }}_l^{-1}(\mathit{x}-{\mathit{\mu }}_l)/2\}.$$ (1)

Thus, in the classic discriminant setup, an observation is classified according to which sub-population mean the point is closest in terms of a squared Mahalanobis distance $(\mathit{x}-{\mathit{\mu }}_h)\prime {\mathbf{\Psi }}_h^{-1}(\mathit{x}-{\mathit{\mu }}_h)$, scaled by the square-root of the determinant of the covariance matrix and the prior probability.

Recalling that the k principal points represent a generalization of the population mean from one to several points, the basic idea for the principal point classification is to classify an observation based on which principal point it is closest. The method is parametric in the sense that we assume we know the probability distribution for each sub-population. Let f_h(x; θ_h) denote the probability density for the hth sub-population and let π_h denote the prior probability for the hth sub-population. The density for the entire population is the finite mixture density given by

$${\displaystyle \sum _{h=1}^H{\pi }_h{f}_h(\mathit{x};{\mathit{\theta }}_h).}$$ (2)

Given training data x_h,1, … , x_h,nh, from the hth sub-population, h = 1, … , H, the following steps describe the principal point classification method:

Principal Point Classification

1. Using the training data, determine the maximum likelihood estimates θ̂_h for each sub-population.

2. Parametric k-means Algorithm. Simulate a very large sample size N >> (n₁ + ··· + n_H) from the finite mixture distribution

   $${\displaystyle \sum _{h=1}^H{\widehat{\pi }}_h{f}_h(\mathit{x};{\widehat{\mathit{\theta }}}_h)}$$

   as follows: set N_h to π_hN rounded to the closest integer and simulate sample of size N_h from f_h(·;θ̂_h), h = 1, … , H. Pool all the simulated data together and run the k-means algorithm on the simulated data using a value of k ≥ H. Let ξ̂_j, j = 1, …, k, denote the cluster means from the k-means algorithm. Then the ξ̂_j are (approximate) maximum likelihood estimators of the principal points of the mixture distribution (2). In the application in Section 6.2, we use a simulation sample size of N equal to 2 million. The prior probabilities π_h for the sub-populations may be known in which case they do not need to be estimated. In other cases when appropriate, the prior probabilities can be estimated using the proportion of the overall sample size that belongs to the hth sub-population: π^_h = n_h/(n₁ + ··· + n_H.
3. Principal Point Assignment. In this step we assign each of the k principal points from step (2) to one of the sub-populations. For the ith simulated data point from the hth sub-population in step 2, define an indicator variable d_hi(j) = 1 if this ith data point is closest to the jth estimated principal point ξ̂_j (in terms of a Euclidean distance) and set d_hi(j) = 0 otherwise. Let

   $$w{t}_h(j)={\displaystyle \sum _{i=1}^{N_h}{d}_{hi}}(j).$$ (3)

   Thus, wt_h(j) counts the number of simulated data points from sub-population h that are closest the the jth principal point. Now, the assignment rule is:

   $$\text{assign}{\widehat{\mathit{\xi }}}_j\to \text{sub-population}h\text{if}w{t}_h(j)>w{t}_l(j),l\ne h.$$ (4)

4. Classification Step. For an unclassified data point x, determine which estimated principal point x is closest, say ξ̂_j. Then classify x to sub-population h if ξ̂_j is assigned to sub-population h based on step 3.

Note that H denotes the number of distinct classes in the finite mixture defining the population (2) whereas k is the number of principal points used to approximate the finite mixture distribution. In order to obtain a good approximation to the underlying finite mixture distribution, we recommend using k > H.

4. A Simulation Illustration

This section reports on a small simulation study conducted to illustrate the classification method described in Section 3. Data sets were simulated from populations consisting of two (H = 2) bivariate normal sub-populations with equal prior probabilities π₁ =π₂ = 1/2. The mean of the first population was fixed at the origin. Successive means for the second sub-population of the form c(1, 1)′ for a sequence of values for c = 1, 1.25, 1.5, 2, 3. As c grows larger, the two sub-populations move apart. Sample sizes of n = 50, 100, and 200 were used in the simulation. Also, the number k of principal points used in the principal point classification were k = 2, 10 and 25. For each of these parameter settings, 100 data sets were simulated. The quadratic discriminant function was estimated as well as the principal point discriminant function for k = 2, 10 and 25. The parametric k-means algorithm was implemented by simulating 100,000 data points from each sub-population. Once the discriminant functions were estimated, 500 test data points were generated from each sub-population and then classified. Therefore, the discriminant functions were tested on data generated independently of the data used to estimate the classification functions.

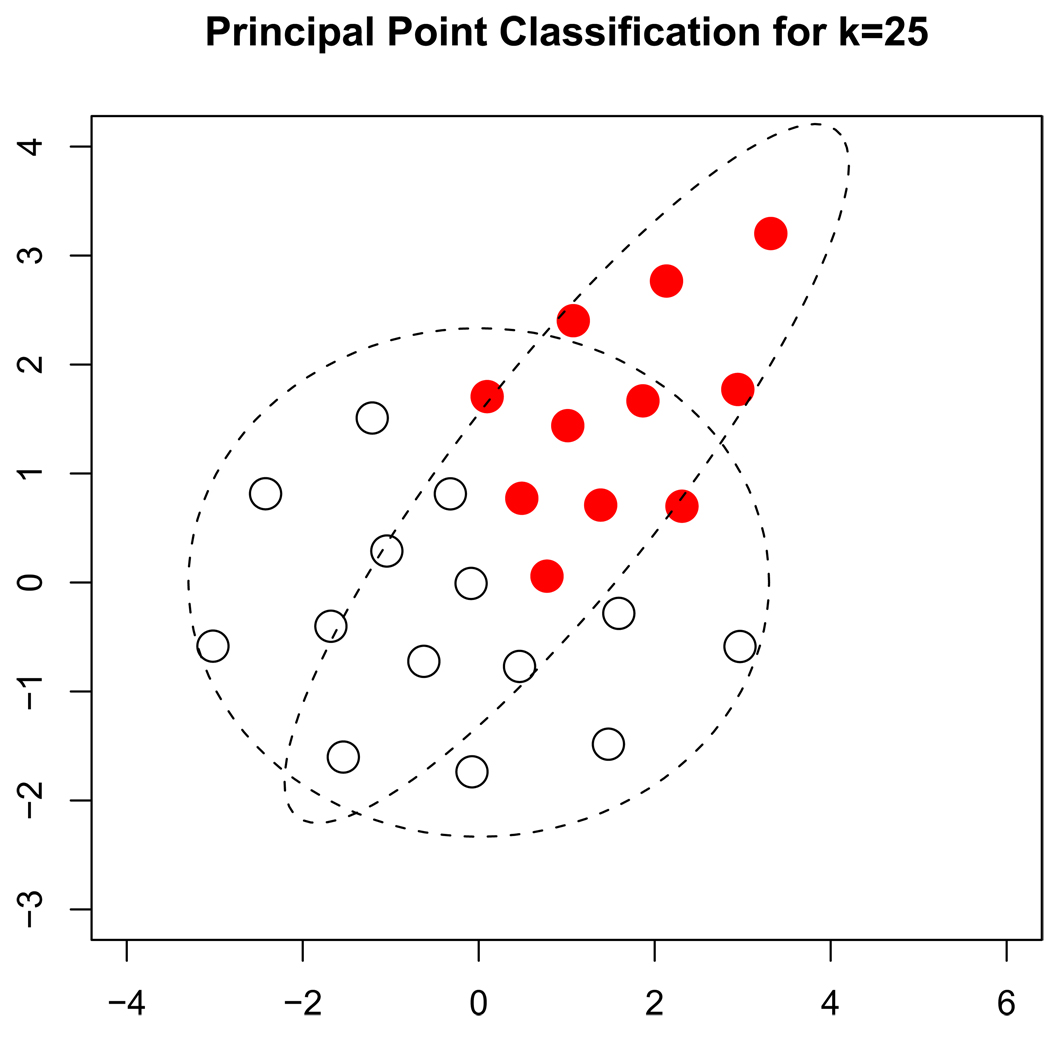
Figure 1 and Figure 2 show the results from one of the simulations. For this particular simulation, the covariance matrices for the sub-populations centered at the origin and the sub-population centered away from the origin are

$$\begin{array}{cc}{\mathbf{\Psi }}_1=\left(\begin{array}{cc}2\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right)\hfill & \text{and}{\mathbf{\Psi }}_2=\left(\begin{array}{cc}1.25\hfill & 0.75\hfill \\ 0.75\hfill & 1.25\hfill \end{array}\right).\hfill \end{array}$$

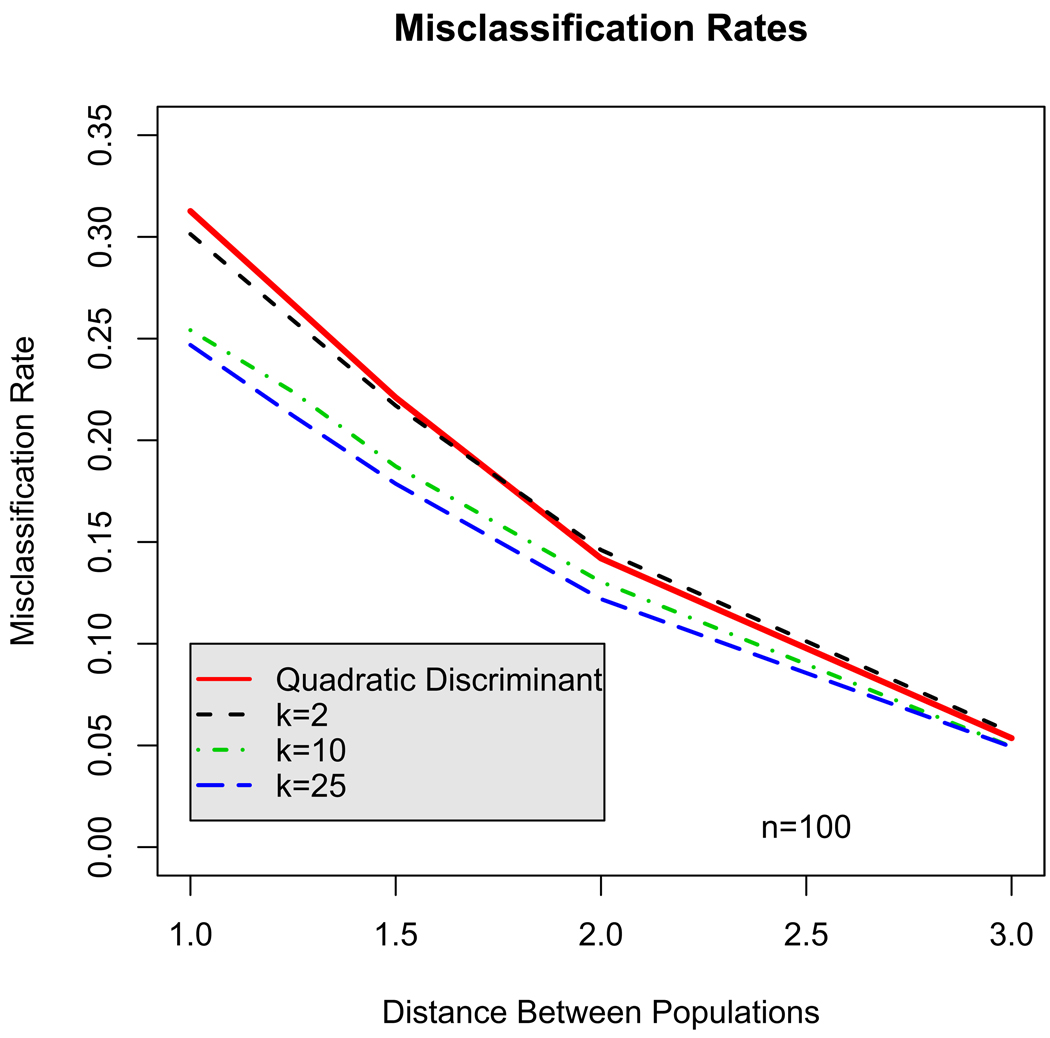
respectively. In this parameterization, the second sub-population represents a shift from the origin along with a 45° degree rotation. Figure 1 shows contours of equal density for the 2 sub-populations when the mean of the second sub-population is (1, 1)’. The k = 25 principal points estimated from the parametric k-means algorithm are also plotted. The rate of misclassification was computed for each discriminant procedure as the percentage of test points that were incorrectly classified. Figure 2 summarizes the misclassification rates for sample size n = 100. Similar plots are generated for sample sizes 50 and 200. The x-axis corresponds to c which controls the distance between the two sub-populations. As c grows larger, the two sub-populations move apart, overlap less and consequently, the misclassification rate drops. The solid line represents the misclassification rate for the quadratic discriminant function. For k = 2, the principal point classification approximates the quadratic classification if the sub-populations are spherical (i.e. the eigenvalues of the covariance matrices are all equal). Surprisingly, the misclassification rate for the k = 2 principal point classification performs about as well as the quadratic classification even though the two sub-populations are non-spherical. The k = 10 and 25 principal point discriminant functions perform similarly to each other. When the two populations overlap considerably, the k = 10 and 25 principal point discriminant functions have about a 5% lower misclassification rate than the quadratic discriminant function (25% versus 30%).

Figure 1.

Contours of equal density for the 2 sub-populations used in the simulation. The points correspond to the k = 25 estimated principal points. The open points are associated with sub-population 1 and the solid points are associated with sub-population 2

Figure 2.

Misclassification rates comparing the normal theory quadratic discriminant function to the principal point classification method using values of k = 2, 10, and 25 principal points for classification.

In the different simulation runs, the k = 25 principal point classification consistently performed about as well or better than the other classification rules. A simulation similar to that described above except that the prior probability in the first sub-population was increased to 2/3 from 1/2, was also run. In this case, the quadratic and principal point classifications methods all perform nearly the same except when the two sub-populations overlapped considerably in which case the k = 2 principal point classification had a higher misclassification rate. A simulation was run for spherical clusters in which case the k = 2 principal point discriminant function performed almost identically to the quadratic discriminant function and both of these performed marginally better than the k = 25 principal point discriminant function.

5. Principal Points Classification for Linear Mixed Effect Models

The primary motivation for this paper is to classify data from longitudinal studies where data points correspond to curves over time. Consider the standard linear mixed effects model for a longitudinal outcome y_i for the ith individual observed over a period of time:

$${\mathit{y}}_i={\mathit{S}}_i\mathit{\beta }+{\mathit{Z}}_i{\mathit{b}}_i+{\mathit{\epsilon }}_i,$$ (5)

where β ∈ ℜ^q is a vector of fixed effects, b_i is a vector of random effects assumed to have mean zero and covariance matrix G, ε_i is a mean zero vector of random errors with covariance matrix σ² I assumed to be independent of b_i. S_i and Z_i are design matrices. In this section, we shall assume the random effects and the random error are all normally distributed. We shall also constrain our attention to the case when there are no baseline covariates in which case we can assume S_i = Z_i. Details for incorporating covariates can found in (25).

Determining principal points for the linear mixed effect model fit to longitudinal data will identify prototypical outcome profile curves. However, this requires de-convolving the random effects from the error ε_i in the model (5). In the case of classifying longitudinal observations to one of H sub-populations, let π₁, … , π_H denote the prior probabilities as before and let

$${\mathit{y}}_i={\mathit{S}}_i({\mathit{\beta }}_h+{\mathit{b}}_i)+{\mathit{\epsilon }}_i,$$ (6)

denote the linear mixed effect model for the hth sub-population, where b_i ~ N(0, G_h) and ${\epsilon }_i~N(\mathbf{0},{\sigma }_h^2\mathit{I}),h=1,\dots ,H$ Because the longitudinal profiles are determined by their regression coefficients, the principal point classification method requires estimating the principal points of the finite mixture coefficient distribution

$${\displaystyle \sum _{h=1}^H{\pi }_{h}N(·;{\mathit{\beta }}_h,{\mathit{G}}_h)},$$ (7)

where N(·; β_h, G _h) denotes the multivariate normal density with mean β_h and covariance matrix G_h. After fitting a standard linear mixed effects model to the data for each sub-population and obtaining estimators β̂_h and Ĝ_h, h = 1, …, H, the parametric k-means algorithm can easily be applied as described in Section 3: we simulate a very large sample of size N from (7) using maximum likelihood estimates in place of the β_h and G_h and then run the k-means algorithm on the simulated data. This will yield approximate maximum likelihood estimators of the principal points of the joint linear mixed effect model for the H sub-populations (25).

The principal point classification rule for linear mixed effect models follows the first 3 steps in the principal point classification rule defined in Section 3. The only distinction arises from the fact that in the linear mixed effect models, the random effect regression coefficients are not directly observed and therefore the distance between a principal point ξ_j and the random regression coefficients of a new observation y_i can not be measured. Instead, for each sub-population h we have a conditional distribution of (β_h+b_i) given y_i that can be computed using well-known results for the multivariate normal distribution:

$$({\mathit{\beta }}_h+{\mathit{b}}_i)|{\mathit{y}}_i~N({\mathit{\beta }}_h+{({\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\sigma }_h^2{\mathit{G}}_i^{-1})}^{-1}{\mathit{S}}_i^{\prime }({\mathit{y}}_i-{\mathit{S}}_i{\mathit{\beta }}_h),{({\sigma }_h^{-2}{\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\mathit{G}}_h^{-1})}^{-1}).$$ (8)

For a set of k principal points for the q-dimensional coefficient distribution (7), let D_j denote the subset of ${\Re }^q$ closest to the jth principal point j = 1, … , k. Using (8), we define d_hi(j) as an indicator function that (β_h + b_i) is closest to the jth principal point and estimate it using:

$$\begin{array}{ccc}{\widehat{d}}_{hi}(j)\hfill & =\hfill & E[d_{hi}(j)|{\mathit{y}}_i]\hfill \\ \hfill & =\hfill & P[({\mathit{\beta }}_h+{\mathit{b}}_i)\in D_j|{\mathit{y}}_i]\hfill \\ \hfill & =\hfill & {\displaystyle {\int }_{D_j}N(\mathit{w};{\mathit{\beta }}_h+{({\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\sigma }^2{\mathit{G}}_h^{-1})}^{-1}{\mathit{S}}_i^{\prime }({\mathit{y}}_i-{\mathit{S}}_i{\mathit{\beta }}_h),{({\sigma }^{-2}{\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\mathit{G}}_h^{-1})}^{-1})d\mathit{w},}\hfill \end{array}$$ (9)

where w is the integration variable. Because d̂_hi(j) is the conditional expectation of a zero-one indicator variable, we will regard (9) as a posterior probability for y_i from the hth sub-population to be associated with the jth principal point. This probability can be computed for each sub-population h = 1, … , H, and each principal point j = 1, … ,k. The weights (3) are computed as before with d̂_hi(j) in place of d_hi(j). From the set {1,2, … ,k}, let P_h denote the set of principal points associated with sub-population h using (4). Then P1 ∪· ··∪ P_H = {1, 2, … , k}. A new observation y_i will then be classified to sub-population h if

$${\displaystyle \sum _{j\in P_h}{\widehat{d}}_{hi}(j)>}{\displaystyle \sum _{j\in P_l}{\widehat{d}}_{li}(j),}l\ne h.$$ (10)

6. Mixed Effects Classification Examples

In clinical practice, typically there will not be ambiguity about which treatment a subject is receiving. Hence, the motivation of using a principal point classification is not to classify subjects according to the treatment they received. Instead, the purpose here is to determine if there are outcome profiles that distinguish the different treatments. In a typical analysis of treatment efficacy from a longitudinal clinical trial, a formal test is performed to determine if the mean outcome profiles differ between the treatments. If a statistically significant difference is found between the mean outcome profiles for two or more treatments, the principal point classification can be used to identify the types of profiles that distinguish different treatments.

In this section, we use data from a 3-armed depression clinical trial. The three arms were placebo, imipramine, and fluoxetine (doses varying according to a schedule). Subjects were evaluated at baseline (time zero) and at six additional (approximately) weekly visits. The response of interest is the Hamilton Depression score (HAM-D) where lower scores correspond to lower levels of depression. A linear mixed effects model using quadratic polynomials on time was fit to each arm of the study separately. Before applying the principal point classification, the regression coefficient distribution was linearly transformed to an orthogonal polynomial basis. (22) provides the following reasons for using orthogonal polynomials when clustering curves: (a) The standard k-means algorithm assigns observations to clusters based on a minimal Euclidean distance; because the outcome profiles are curves, the L² distance between curves corresponds to the usual Euclidean distance between regression coefficients. (b) Differences in cluster results that occur due to the choice of basis functions used to estimate the curves are minimized when using orthogonal basis functions. (c) When fitting a quadratic model using orthogonal polynomials, the coefficient of the linear polynomial corresponds to the average quadratic slope of the parabola, which is an overall measure of improvement throughout the trial (19). We shall refer to the coefficient of the linear polynomial as the average slope (of the parabola) in this paper. The parametric k-means algorithm was then applied to the joint coefficient distribution (7) using a simulated data set of one million for each arm of the study. The posterior probabilities (9) were computing using 10,000 simulated data points. Equal prior probabilities were set for each arm of the trial. Variability in the intercepts of the parabolas mostly corresponds to baseline differences in HAM-D among subjects. The intercept terms from the quadratic models were not used in the parametric k-means algorithm for estimating the principal points for two reasons: (i) the shapes of the curves do not depend on the intercepts and (ii) after transforming to orthogonal polynomials, the variability in the intercept term greatly dominates variability in the linear and quadratic coefficient terms which prevents the k-means algorithm from discovering distinct and clinically meaningful curve shapes (20; 21). The next two subsections provide results comparing the imipramine vs. the fluoxetine arm and the fluoxetine vs. the placebo arm of the study.

The principal point classifications will be contrasted with responder/non-responder classifications made by clinicians. In this study, a clinicians global impression (CGI) was recorded for each subject. The CGI is a 1–7 scale where 1 = very much improved, 2 = much improved, 3 = minimally improved, 4 = not improved, 5 = minimally worse, 6 = much worse, 7 = very much worse. Subjects were classified as responders if their CGI at the end of the study is a 1 or a 2.

6.1. Imipramine versus Fluoxetine

In this section, we apply the principal point classification for linear mixed effects model to distinguish between the outcome profiles of imipramine (n = 185) and fluoxetine (n = 196) treated subjects. The results presented here are from applying the parametric k-means algorithm using k = 10 clusters.

The results of fitting a quadratic mixed effects model separately for the fluoxetine and imipramine arms yielded the following fixed effect parabolas:

$$\begin{array}{cc}\text{fluoxetine}\hfill & \widehat{y}=23.69-4.29t+0.37t^2\hfill \\ \text{imipramine}\hfill & \widehat{y}=24.27-5.13t+0.51t^2.\hfill \end{array}$$

The estimated random effect covariance matrices Ĝ for the fluoxetine and imipramine arms are:

$$\begin{array}{ccc}\left(\begin{array}{ccc}8.277\hfill & 0.313\hfill & -0.216\hfill \\ 0.313\hfill & 7.943\hfill & -1.058\hfill \\ -0.216\hfill & -1.058\hfill & 0.163\hfill \end{array}\right)\hfill & \text{and}\hfill & \left(\begin{array}{ccc}6.008\hfill & 2.185\hfill & -0.457\hfill \\ 2.185\hfill & 3.458\hfill & -0.435\hfill \\ -0.457\hfill & -0.435\hfill & 0.083\hfill \end{array}\right)\hfill \end{array}.$$

respectively. The error variances for the fluoxetine and imipramine arms were estimated to be σ̂ = 3.43² and 3.84² respectively. There is little difference between the estimated fixed effect coefficients and the error variance for the arms. However, the variances in the linear and quadratic random effect terms in the fluoxetine arm are about twice as big as the variances in the imipramine arms. A likelihood ratio test comparing the random effect covariance matrices and error variances was conducted: the chi-square test statistic for this test is χ² = 14.11 on 7 d.f., which yields a p-value of p = 0.0492. Thus, the fluoxetine and imipramine distributions overlap considerably with only a mild statistical significance of the difference between their random effect covariance matrices. Consequently, the misclassification rates are very high: 0.44 for the quadratic discriminant classification and 0.47 for the principal point classification using k = 10 (a similar rate is obtained using k = 25).

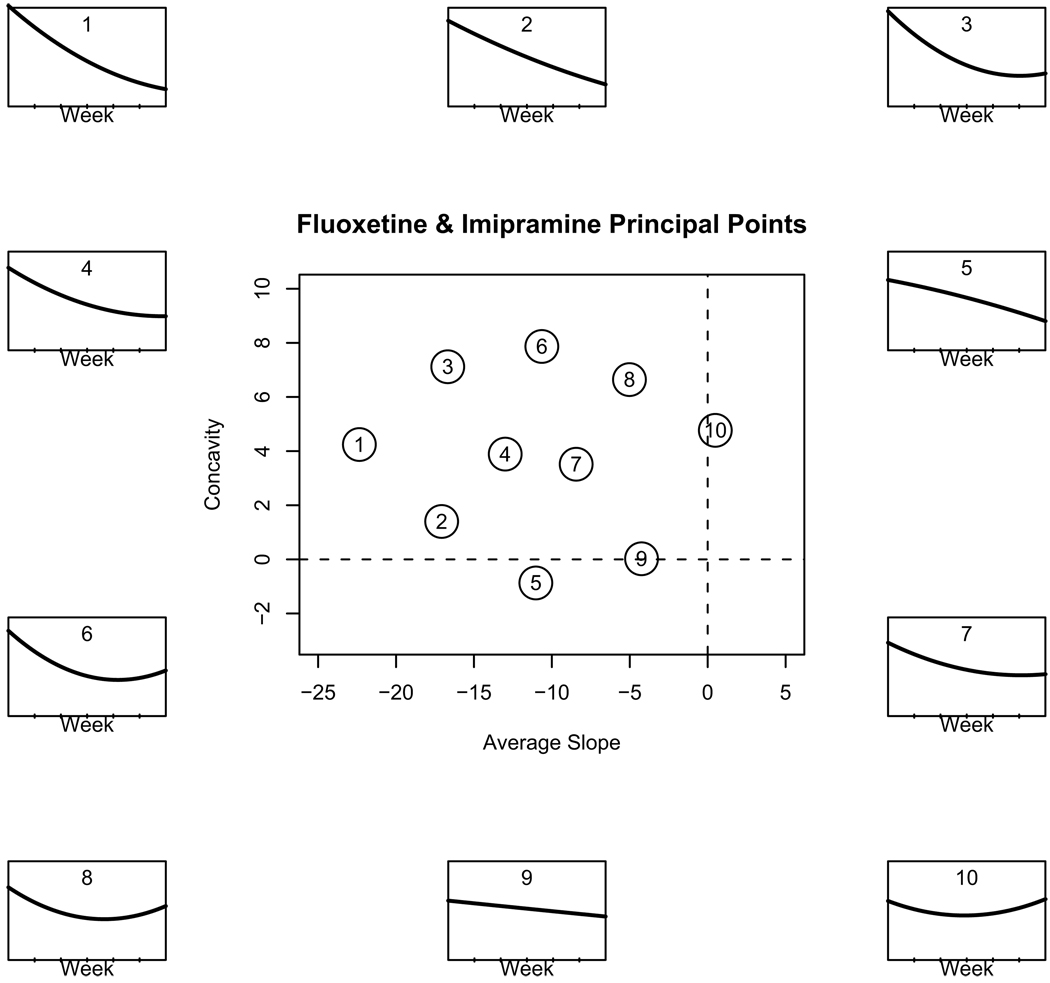
Although the two classification methods have very high misclassification rates, results from the principal point classification can be used to to identify differences in how the fluoxetine and imipramine treatments manifest themselves in the outcome profiles. The center panel in Figure 3 shows the estimated k = 10 principal points for the joint fluoxetine and imipramine arms in the coefficient subspace of the average slope and the concavity. The surrounding panels show the principal point profile curves corresponding to the points in the center panel. The 10 principal points induce a partition of the regression coefficient space. From the parametric k-means simulation, we can compute the proportion of the coefficient distribution associated with each principal point. These results are presented in Table 1 below:

Figure 3.

Center panel: k = 10 principal points for the combined fluoxetine and imipramine arms, plotted in the coefficient subspace of the linear (average slope) and quadratic polynomials. The surrounding panels show the corresponding principal point quadratic profile curves associated with each point in the center panel.

Table 1.

Proportions of the fluoxetine and imipramine random regression coefficient distributions associated with each of the k = 10 principal points shown in Figure 3.

PP	Fluoxetine	Imipramine
1	0.0504	0.0645
2	0.1018	0.0996
3	0.1063	0.0998
4	0.1400	0.1746
5	0.1297	0.0408
6	0.0994	0.1241
7	0.1417	0.1582
8	0.0734	0.1405
9	0.1181	0.0368
10	0.0391	0.0611

From Table 1 we see that of the one million coefficients simulated for the fluoxetine distribution, 5.04% of them are closest to the first principal point (labeled 1) in Figure 3. Similarly, 6.45% of the simulated imipramine coefficients were closest to the first principal point. Thus, the proportion of fluoxetine and imipramine treated subjects associated with principal point profile #1 are roughly equal. From Table 1, we can see large differences in proportions between fluoxetine and imipramine for principal point profile curves #5 and #8, and #9. Based on these proportions, principal point profiles #5 and #9 are associated with fluoxetine treated subjects. It is interesting to note that these two profiles are the only ones that are not concave up. Principal point #5 is the prototypical specific (“pure drug”) responder: very little initial improvement, followed by a steadily decrease of depression severity, presumably, due to the specific effect of the drug. Table 2 below shows a breakdown by responder/non-responder status (based on CGI).

Table 2.

CGI Responder/Non-responder counts for fluoxetine and imipramine treated subjects associated with each principal point category.

	Fluoxetine		Imipramine
PP	Responder	Non-Responder	Responder	Non-Responder
1	5	0	5	0
2	15	0	14	0
3	34	0	31	0
4	30	1	30	4
5	16	8	1	0
6	13	3	16	2
7	12	15	13	29
8	1	10	4	21
9	0	31	2	4
10	0	2	0	8

From Table 2 we see that the principal point classification clearly identifies principal point profiles #1, 2, 3, 4, and 6 as responder profiles that occur in roughly equal frequencies in both the fluoxetine and imipramine treatment arms. Principal point profile #9 is a non-responder fluoxetine treatment profile. Profiles #8 and #10 are also non-responder profiles with more imipramine treated subjects in them – these two profiles each show an immediate improvement at baseline followed by a deterioration in mood as the trial progresses that can be attributed to either an initial response to non-specific treatment effects and/or an immediate but short-lasting imipramine drug response. Unlike profiles #8 and #10, non-responder profile curve #9 does not show a strong initial improvement indicating that subjects associated with profile #9 do not experience a significant initial non-specific effect. Nonetheless, profile #9 has a negative average slope and an approximate zero concavity indicating an overall rate of steady improvement throughout the trial but the degree of improvement by the trial’s end was not strong enough to warrant a classification of responder. Subjects associated with profile #7 straddle the boundary between responder and non-responder status. From Table 2, we see that profile #5 is characteristic of a fluoxetine treated subject and is primarily associated with responders.

In longitudinal studies, standard testing procedures are typically used to test if there are differences between treatments with respect to their mean outcome profiles. Here we have used the principal point classification to focus on where and how outcome profiles differ between two treatments. In the next section we show how principal points classification can be used to identify outcome profiles corresponding to specific and non-specific antidepressant treatment effects.

6.2. Identifying Placebo Responders Among Drug Treated Subjects

In this subsection, we focus attention on the fluoxetine and placebo (n = 162) arms of the study in order to determine which fluoxetine treated subjects responded due to the specific effect of the drug and which responded due to nonspecific placebo effects. Principal points were estimated for the joint placebo/fluoxetine mixture distribution using the parametric k-means algorithm as described in Section 5. A set of k posterior probabilities using (9) were computed for each subject indicating how closely associated a subject is to the different principal points. In this section we use a large value of k = 50 for illustration.

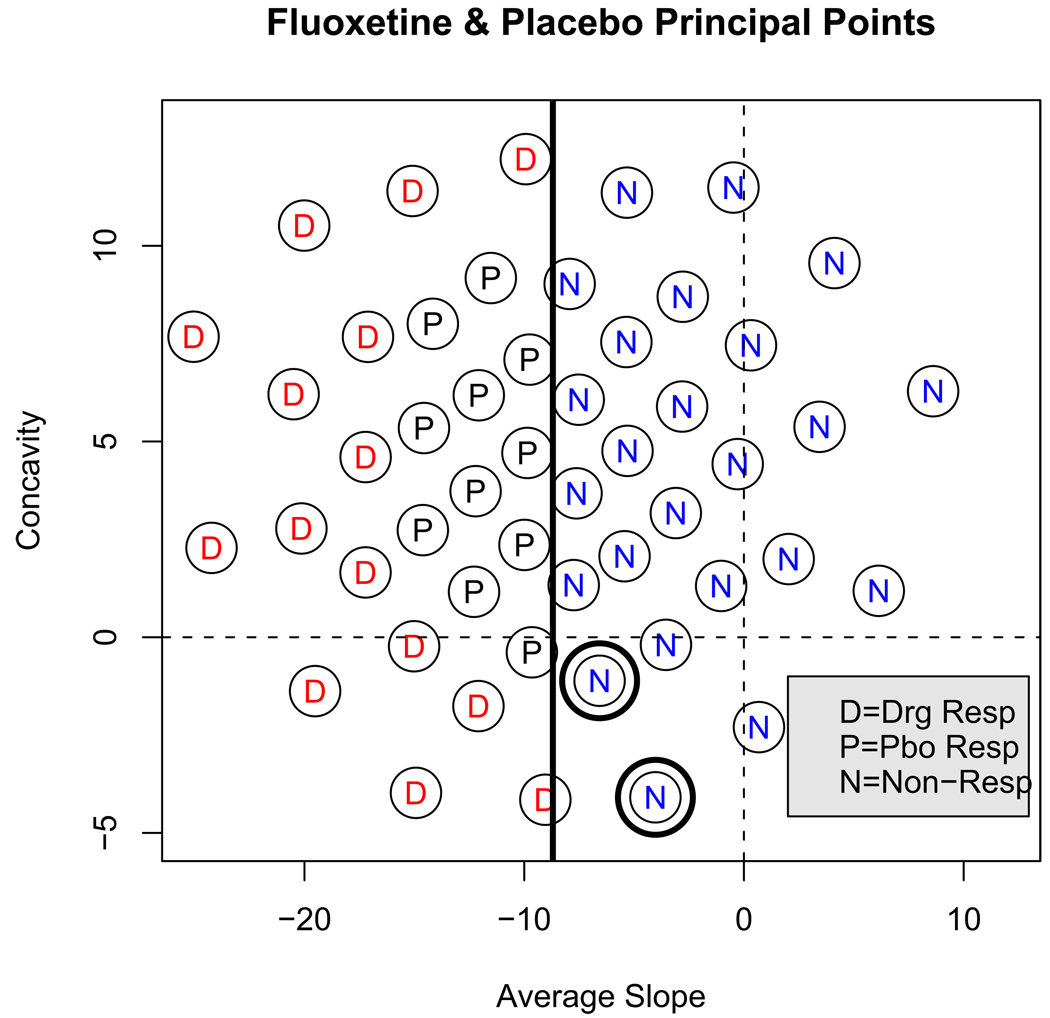
Next, a classification boundary between CGI rated responders and non-responders was determined using a logistic regression: the binary variable responder/non-responder was modeled as functions of the average slope, concavity (obtained using the best linear unbiased predicted (BLUP) values). The concavity coefficient was not statistically significant in any of the logistic regression models; the squared average slope coefficient was not significant either; and the interaction terms between the average slope and concavity in all models were also not significant. Therefore, only the average slope coefficient was used as a predictor which results in a vertical classification line in the coefficient space. This represents another advantage of using orthogonal polynomials to model the outcome profiles. The classification lines based on the fluoxetine only sample and on the placebo only sample differed very little, as was to be expected, since researchers were rating patients’ improvement based only on observed symptoms severity and were blind to treatment assignment. Therefore the data was pooled to estimate a single classification line between responders and non-responders (common for both treatment arms). Figure 4 shows a plot of the k = 50 estimated principal points for the joint fluoxetine and placebo arms of the study. The vertical line in the figure is the responder/non-responder classification boundary determined by the logistic regression. The principal points to the right of this line are labeled “N” for non-responder.

Figure 4.

k = 50 estimated principal points for the joint fluoxetine and placebo arms in the coefficient subspace of the average slope and concavity. The principal points have been labeled: D=Drug (specific) Responder, P= Placebo (non-specific) Responder, and N=Non-responder.

It is interesting to note that two of the non-responder principal points in Figure 4 correspond to fluoxetine treated subjects only – these are the two points indicated with a double-circle in Figure 4. 12 subjects were classified to these two points and all 12 of these subjects were fluoxetine treated non-responders. These two points illustrate that there are drug treated non-responders that are distinct from placebo treated non-responders. On close examination, all but one of the 12 subjects turned out to have dropped out of the study for reasons of side effects, or alternatively, because they started to feel better and stopped coming for treatment. Therefore, it is possible that these profiles are characteristic of subjects who respond to the specific drug effect, but discontinue treatment, likely, due to side effects.

The next problem is to determine which “responder” principal points (to the left of the classification line on Figure 4) correspond to response to specific (drug) effect and which correspond to non-specific (placebo) treatment effects. The idea is to identify the principal points that are most associated with placebo treated responders. In the placebo arm of the study, 38.9% (63/162) of the subjects were rated as responders based on CGI. This high placebo response rate is typical in antidepressant studies (e.g., see 31). Due to the randomization and the double-blind design of the study, it stands to reason that if the potential outcomes of drug treated subjects, had they been treated with a placebo, could be observed, then we would see a similar placebo response rate.

Consider only the k₁ principal points (k₁ < k = 50) that are associated with responders (i.e. on the left of the discrimination line on Figure 4). Order these principal points according the proportion of the placebo treatment arm that are classified to them – these proportions can be estimated using the large simulation sample from the parametric k-means algorithm used to estimate the principal points. Let j₁, j₂, … , j_k1 correspond to the principal points for this ordering from the largest to the smallest proportion. Let p_f (j) denote the proportion of the fluoxetine treated distribution classified to the jth principal point (which again can be estimated using the parametric k-means simulation sample). We then select l* ≤ k₁ such that the sum of the p_f (j) classified to the first l* of j₁, j₂, … , j_k1 principal points is equal to the proportion of responders in the placebo arm, here 38.9%. Formally, we choose l* such that

$${\displaystyle \sum _{i=1}^{l*}{p}_f(j_i)\le 0.389<{\displaystyle \sum _{i=1}^{l*+1}{p}_f(j_i).}}$$

The first l* of the “responder” principal points j₁, j₂, … , j_k1 are now associated with the outcome from a non-specific effect (i.e. placebo response), whereas the remaining principal points are associated with outcomes for subjects who experience at least some specific effect of the fluoxetine treatment (i.e. drug response).

The principal points labeled “P” in Figure 4 are the points identified as placebo responder points using this criterion. These eleven points represent 37.8% of the fluoxetine distribution which is very close to the placebo response rate of 38.9% seen in the placebo arm. Using such a large number of principal points (k = 50) allows close approximation the actual percentage of placebo treated responders. The points labeled “D” are the remaining responder principal points that correspond to subjects who respond and experience a specific drug effect not seen in the placebo arm of the study. That is, subjects classified to the “D” principal points are primarily responders that have very little overlap with the placebo treated distribution. These subjects may experience a beneficial placebo effect, but because they lay outside the placebo treated distribution, their response could not have been a result of placebo effect alone. This procedure then identifies the roughly 40% of drug treated subjects that resemble placebo treated responders.

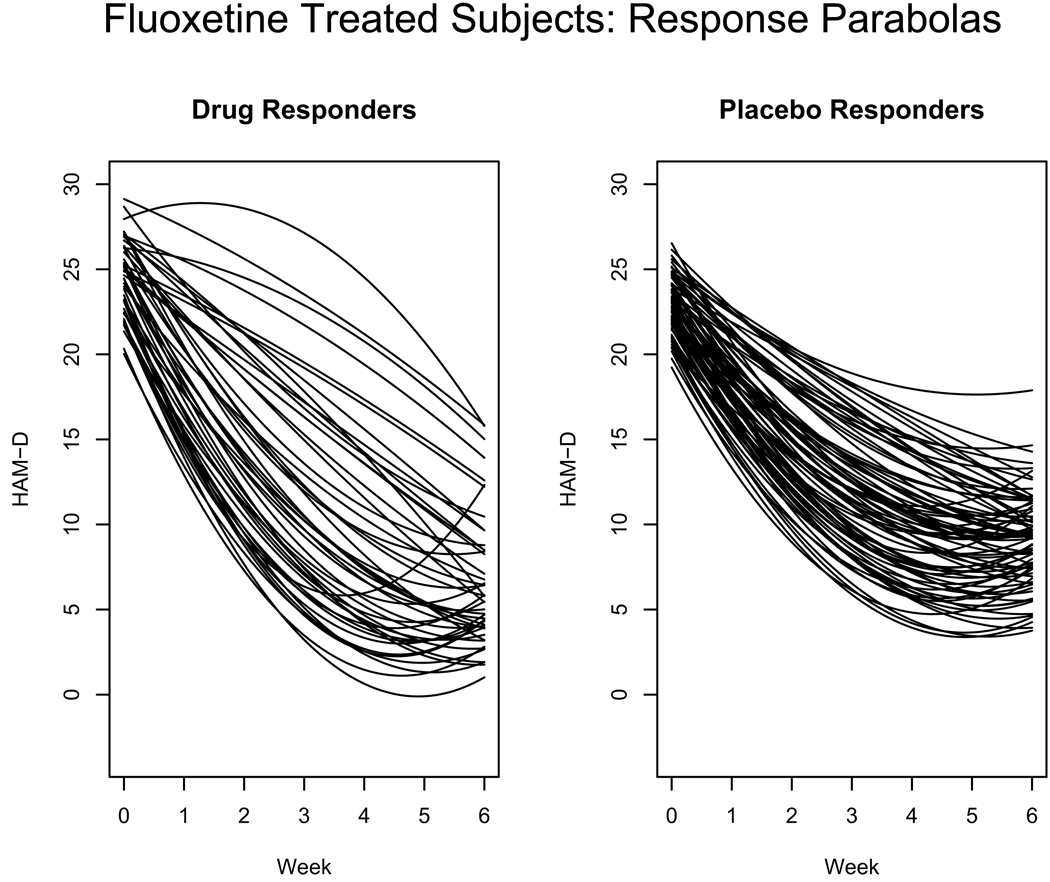
Figure 5 shows the estimated profiles for responders among fluoxetine treated subjects classified as responding to specific drug effects (left panel) and those responding to non-specific placebo effects (right panel) using the above classification. The drug responder profiles correspond to subjects associated to principal points labeled “D” in Figure 4 while the placebo responder parabolas in the right panel correspond to subjects associated to principal points labeled “P” in Figure 4. The placebo responder profiles in the right panel show an immediate improvement from baseline (week 0) followed by a steady consistent improvement that begins to level off around week 4. Most of the drug responder profiles in the left panel of Figure 5 also show an immediate improvement at baseline but the rate of improvement is stronger than for subjects classified as placebo responders as evidenced by the steeper decline in the parabolas. This is indicative of a strong drug effect or a combination drug/placebo effect. Some of the parabolas in the left panel of Figure 5 start off relatively flat and are concave down. These subjects do not experience an immediate improvement at baseline as to be expected with a placebo effect, but once the drug has a chance to take effect, a steady improvement is seen later in the trial.

Figure 5.

Response parabolas for fluoxetine treated responders. The parabolas in the left panel correspond to subjects classified as drug responders and the parabolas in the right panel correspond to subjects classified as placebo responders.

In the next section we look at the utility of the classification boundaries, defined based on the 3-arms depression study discussed so far (training data), for studying specific and non-specific treatment effects in a different study (test data).

6.3. Test Data

In this subsection, we treat the data in the previous subsection as training data and we use the estimated principal point classification to classify subjects from a test data set. The test data set is from a study with similar design, where subjects were randomized to either fluoxetine (20 mg fixed dose, in a contrast with the flexible dose used in the training data study) or a placebo for six weeks. The fixed effect average slope for the test data is β̂₁ = −7.913 which is considerably larger than the estimated average slope β̂₁ = −10.998 from the training data set. Additionally, only 46.0% of the fluoxetine treated subjects in the test data set were rated as responders based on the CGI compared to 64.3% in the training data set.

Subjects were classified as responders/non-responders based on the cutoff value of the average slope determined by the logistic regression from the training data. The agreement rate of responder/non-responder classifications using the logistic cutoff and the CGI criteria is 85.71%(compared to 88.78% in the training data).

The k = 50 principal point estimates shown in Figure 4 were also used to classify the fluoxetine treated subjects (n = 315) as either responders to specific effects of the treatment (drug responders), responders to non-specific effects (placebo responders) or non-responders. Based on the principal point classification, 14.9% of the fluoxetine treated subjects in the test data set were rated as drug responders and 27.0% were rated a placebo responders.

A question of interest in clinical practice is whether or not a subject can be classified as a drug or placebo responder early in treatment. To shed light on this question, we re-classified subjects in the test data set using the principal point classification, except that the random regression coefficient for use in the classification were estimated only from the outcomes at baseline and the first three weeks. 86% of subjects had the same classification (drug responder vs. not a drug responder) when the classifications used data from only the first 3 weeks and when using data from all 6 weeks of treatment.

The baseline HAM-D score is also predictive of being a drug responder. Defining a binary variable equal to 1 if a subject is classified as a drug responder and 0 if not a drug responder, a logistic regression was used to assess the effect of baseline depression severity (HAM-D) on the odds for response to specific drug effect. The logistic regression slope coefficient was estimated to be 0.1405 with standard error 0.0403 which is highly significant (p = 0.0005). Thus, there is almost a 6-fold increase in the odds of being a drug-responder for every 10 point increase in baseline depression severity as measured by the HAM-D. (Similar results are obtained using the training data.)

It is unclear why the test data set had so fewer responders than the training data set. One difference could be due to the fixed dose versus the varying dose. Another difference is in baseline HAM-D scores – the training data had a mean baseline score of 24.27 with standard deviation 4.165 versus a mean of 22.52 and standard deviation 3.844 for the test data set. Thus, subjects in the training data set had a significantly higher baseline depression severity (t = 4.764) than in the test data set, and yet there was a higher response rate in the training data set. According to the results presented above, subjects with higher baseline depression severity are more likely to respond to the specific effects of the drug.

7. Conclusion

In this paper, we have introduced a discriminant function defined in terms of principal points. However, the main purpose of the principal point classification illustrated here is to differentiate outcome profiles for different treatments in longitudinal studies. That is, the principal point classification can identify regions in the curve coefficient space where different treatments coincide and where they differ. This approach has allowed us to address the longstanding problem of differentiating a specific drug response from a non-specific placebo response which is endemic to studies of psychiatric illness.