Effective screening of the DNA charge in a nanopore

Abstract

Extensive all-atom molecular dynamics simulations were performed to characterize the microscopic origin of the force experienced by DNA in a bulk electrolyte and a solid-state nanopore when subject to an external electrostatic field E. The effective screening of the DNA charge was found to originate from the hydrodynamic drag of the electroosmotic flow that is driven by the motion of counterions along the surface of DNA. We show that the effective driving force F in a nanopore obeys the same law as in a bulk electrolyte: F = ξμE, where ξ and μ are the friction coefficient and electrophoretic mobility of DNA, respectively. Using this relationship, we suggest a method for determining the effective driving force on DNA in a nanopore that does not require a direct force measurement.

Electric field-driven transport of DNA molecules through nanopores holds promise for ultra low-cost whole-genome sequencing [1] and high-throughput single molecule force spectroscopy [2–4]. Quantitative characterization of the force experienced by DNA in a nanopore is critical to understanding the microscopic mechanics of the DNA transport. Such force was recently measured directly by trapping one end of the DNA molecule with optical tweezers while the other end of the molecule was subject to an electric field in a nanopore [5]. The measurements revealed scaling of the effective force F with the electrostatic field E, i.e., F = q_effE, where the scaling factor q_eff, also known as the DNA’s effective charge, was found to be about 25% of the DNA’s bare charge Q. However, the interpretation of these measurements was ambiguous. On the one hand, the measurements are in perfect agreement with the Manning condensation theory [6] that predicts a 76% reduction of the DNA charge arising from the electrostatic field of counterions that condense near the DNA surface. Such interpretation neglects solvent as a possible source of the effective screening and assumes that the fraction q* of the DNA charge that is not screened by the electrostatic field of the condensed counterions is the effective charge that determines the effective force. On the other hand, theoretical and experimental studies of DNA electrophoresis suggested that hydrodynamic drag is an important factor influencing DNA transport [7, 8]. The importance of hydrodynamic interactions between DNA and the solvent inside a solid-state nanopore was first pointed out by S. Ghosal [9, 10]. In this letter we demonstrate that the effective screening of the DNA charge is caused by the electroosmotic flow that develops near the DNA surface and is driven by the motion of counterions.

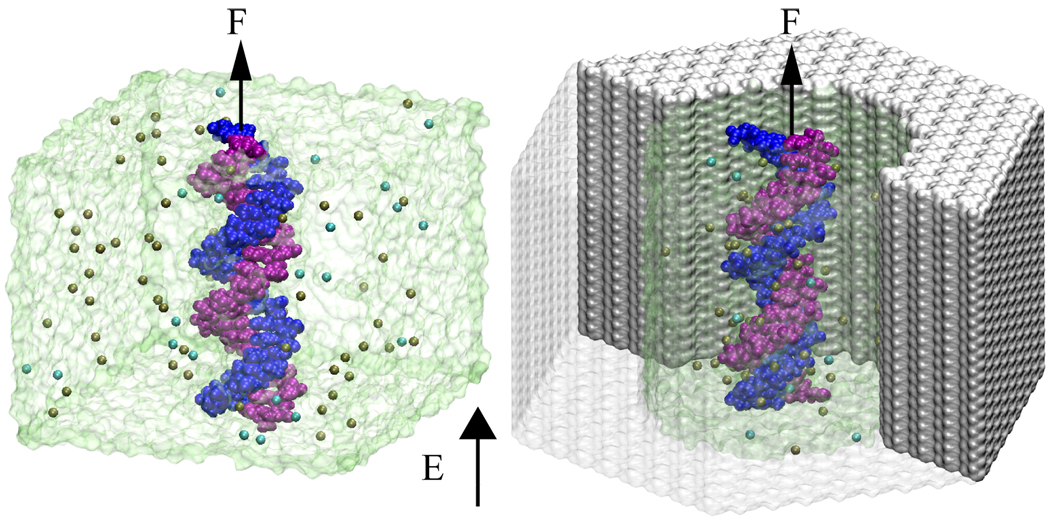
We consider the following two systems: a DNA fragment submerged in a bulk electrolyte [Fig. 1a], and a DNA fragment in a cylindrical channel [Fig 1b], that is used as a model of a solid-state nanopore. Using the all-atom molecular dynamics (MD) method, we simulate the response of the DNA and electrolyte to the applied electric field, and measure directly the stall force that is required to stop the DNA motion and balance the effective driving force.

FIG. 1.

Setup of MD simulations. (a) DNA helix in a water box. (b) DNA helix in a solid-state nanopore. In both systems, a uniform external electric field E is applied to all atoms, whereas a harmonic spring force F is applied to DNA only. The two strands of DNA are colored in blue and purple. Ions K⁺ (tan) and Cl⁻ (cyan) are shown as vdW spheres; water is shown as a transparent surface.

First, we investigate the microscopic origin of the stall force in a bulk electrolyte. A fragment of double-stranded DNA, two helical turns in length (poly(dA)₂₀·poly(dT)₂₀), was submerged in a rectangular volume of pre-equilibrated aqueous solution of 0.1 M KCl. The 5’ and 3’ ends of each strand were covalently linked over the periodic boundary of the system, producing an effectively infinite DNA molecule [Fig. 1a]. Using the MD package NAMD [11], this system was equilibrated in the NpT ensemble at 1 bar for 10 ns. Following that, the system was simulated in the NVT ensemble. The temperature was kept constant at 310 K by applying Langevin forces [12] to all oxygen atoms of water; the damping constant γ of the thermostat was set to 0.1 ps⁻¹ unless specified otherwise. To measure the stall force, the DNA motion was restrained using a weak harmonic spring with a spring constant of 1 pN/Å. One end of the spring was fixed in space, while the other end was attached to the center of mass of the DNA’s phosphorous atoms.

Subject to an external electric field, the DNA initially drifts opposite the field direction, increasing the force of the spring on the DNA. Eventually, the spring force balances the effective driving force and the DNA motion stops [Fig. 2a]. The stall force measured thereby depends on the magnitude of the external electric field [Fig. 2a]. The plot of the stall force versus the total force of the external electric field on bare DNA [Fig. 2b] reveals a linear dependence with a slope of 0.243. If the unscreened (by counterions) fraction q* of the DNA charge were to determine the stall force as F = q*E, that fraction would be 24.3% of the bare DNA charge. Below, we demonstrate that such interpretation is an oversimplification, as the effective screening of the DNA charge originates from the hydrodynamics drag of the electroosmotic flow.

FIG. 2.

Stall force in a bulk electrolyte. (a) Stall force F versus simulation time at various strengths of the external electric field E, from 0.125 to 1.0 V per 6.4 nm. Accordingly, the electric force QE on bare DNA varies from 125 to 1000 pN. The horizontal lines indicate the average values of the force computed for the last 20 ns of each trajectory. (b) Stall force versus total electric force on bare DNA. (c) Ion density versus distance from the DNA central axis. (d) Velocity of the electroosmotic flow versus distance from the DNA central axis.

Figure 2c demonstrates that the radial distribution of ions around DNA does not depend on the strength of the external electric field. The density of potassium ions has a maximum inside the major groove of the DNA helix and near the phosphate groups of the DNA backbone. The peak at r = 5 Å is caused by strong interaction between potassium ions and nitrogen atoms of the adenine bases. The peak around r = 12 Å arises from a cloud of potassium ions attracted to the negatively charged phosphate groups of the DNA backbone. The average residence time of potassium ions at the DNA surface was found to be just several picoseconds, close to the average residence time of water. This indicates that ions are not bound to DNA. The chloride ions in the same region are depleted.

Up to 30 Å away from the DNA central axis, the density of potassium ions is higher than that of chloride ions. Under the action of the external electric field, ions of both types move in opposite directions. Because the total charge of the electrolyte near the DNA surface is unbalanced, the electroosmotic effect is prominent. The velocity profile of water as a function of the radial distance from the center of the DNA helix is shown in Fig. 2d. The water velocity reaches a maximum at about 22 Å. The maximum velocity increases with the strength of the applied electric field. Clearly, the stall force depends on the electroosmotic flow and thus on the friction between DNA and the flow.

To further clarify the relationship between the stall force F and the electroosmotic flow, we measured F as a function of the electrolyte viscosity. In a molecular dynamics simulation, the solvent viscosity can be adjusted by tuning the damping rate γ of the Langevin thermostat [12]. As shown in Fig. 3a, increasing the electrolyte viscosity (increasing γ) requires a larger stall force in the same external electric field. If the stall force F is solely determined by the distribution of counterions, that distribution should depend on the electrolyte viscosity. However, Fig. 3b reveals that a cumulative net charge of the electrolyte q(r)=Σq_ion(r′ < r), where r′ is the distance between an ion and the DNA central axis, does not depend on the electrolyte viscosity. Therefore, F ≠ q*E, where q* is a factor solely derived from the distribution of counterions.

FIG. 3.

Dependence of stall force on electrolyte viscosity. (a) Spring force versus time in simulations performed at various values of the damping rate γ of the Langevin thermostat. Increasing γ effectively increases the electrolyte viscosity. All simulations were performed under the same external electric field E= 500 pN/Q. (b) The radial distribution (from the DNA central axis) of the cumulative net charge of the electrolyte, normalized by the bare charge Q of DNA. (c) The friction coefficients ξ (left ordinate) and electrophoretic mobility μ (right ordinate) determined independently from MD simulations. (d) The spring force from panel (a) normalized by ξμE.

The Manning condensation theory does not provide the distribution of counterions around DNA. Recent extension of the Manning theory to finite ion concentrations suggests [13] that a layer of condensed (around DNA) counterions has a finite thickness d ~ (aλ)^1/2, where a is the radius of a DNA helix and λ is the Debye length. At the ion concentration of 0.1 M, the Debye length λ is about 10 Å hence, the theoretically predicted d is about 11 Å. As q* = Q − q(R_M), where R_M ≡ a + λ, the unscreened by counterions charge of DNA is about 0.25Q, independent of the electrolyte viscosity [Fig. 3c]. Hence, the simulated ion distribution is consistent with the prediction of the extended Manning condensation theory [13]. Nevertheless, the dependence of the stall force on the solvent viscosity cannot be described by the ion distribution alone, as the distributions are essentially identical at different viscosities of the solvent [Fig. 3c].

To explain the dependence of the stall force on the electrolyte viscosity we consider the hydrodynamic interaction between DNA and electrolyte. It was previously suggested that, under the simultaneous action of a nonelectric and electric force, the motion of DNA can be described by a superposition of the motion driven by the nonelectric force F (υ = F/ξ) and the electrophoretic motion (υ = μE) [7]. The above description assumes a linear approximation of the underlying electrohydrodynamic equations. Hence, we performed independent measurements of the DNA’s friction coefficient ξ and electrophoretic mobility μ at different values of γ. To determine ξ, we measured the value of a nonelectric force F required to displace DNA through the electrolyte at a constant velocity υ = 50 Å/ns in the absence of the external electric field. To determine μ, the drift velocity of DNA was measured under an external electric field of E = 500 pN/Q; the spring force was not applied to DNA in these simulations. As shown in Fig. 3c, the friction coefficient increases with the electrolyte viscosity, whereas the DNA mobility decreases. Figure 3d demonstrates that the ratio of the simulated stall force to ξμE is 1 regardless of the electrolyte viscosity, which proves that F = ξμE in the bulk electrolyte.

Next, we performed MD simulations of DNA electrophoresis through Si₃N₄ nanopores using a method described elsewhere [14]. In these simulations, the Langevin thermostat was applied only to atoms of the Si₃N₄ membrane [14]. Harmonic restraints were used to prevent DNA from drifting in the direction perpendicular to the pore axis and ions from adhering to the surface of Si₃N₄. Three pores were considered: two atomically smooth, cylindrical pores of 22.5 and 30 Å radii, and one corrugated pore of a 30 Å mean radius. The radius of the corrugated pore varied along the pore axis as R(z) = 30+2 cos (3πz/16) Å. In a typical simulation, 5 ns was required to balance the effective driving force by the force of the spring. Each simulation was continued for an additional 15 ns to determine the radial distribution of ions, the velocity profile of water, and the average stall force F.

In a nanopore, the radial density of counterions depends on the pore radius, but not on the strength of the external electric field [Fig. 4a]. Compared to the ion distribution in a bulk electrolyte, the counterions in a nanopore are located, on average, closer to the DNA surface. Using the Manning criterion for the effective charge, the latter is found to be 0 for R = 22.5 Å, 0.13Q for R = 30 Å, and 0.2Q for the corrugated 30 Å-radius nanopore. Hence, we find that the surface roughness can significantly alter the distribution of ions in a pore. In our simulations, this effect is purely electrostatic, as the distribution of the surface charge in a corrugated pore differs from that in a smooth surface pore.

FIG. 4.

DNA electrophoresis through nanopores. (a) Radial distribution of the cumulative charge normalized by the charge of bare DNA, Q. The dashed line indicates the radius of 11 Å. The data obtained for the rough surface pore are labeled as “W”. (b) Water flow profile in three nanopores. Symbols used are defined in panel (a). Lines in (b) and (c) are to guide eyes. (c) Friction coefficients (left ordinate) and electrophoretic mobility (right ordinate) of DNA in three nanopores. (d) Stall force as a function of ξμE. The line is the theoretical prediction F = ξμE. The error bars for the stall force are smaller than the symbols.

In all systems studied, the total charge of the counterions within 11 Å from the DNA cental axis is about 0.28Q[Fig. 4a]. However, it is incorrect to consider the counterions near the DNA surface as being bound to the DNA and, hence, assume 0.28EQ to be the electrostatic screening force. In fact, the stall force can exceed 0.28QE in a high viscosity bulk electrolyte [Fig. 3a] or in a nanopore having a corrugated surface [Fig. 4d].

The electroosmotic flow in the three nanopores is described in Fig. 4b. The water velocity vanishes near the pore surface and near the DNA center; however, it is nonzero in the major groove of DNA. At the same strength of the electric field, the mean velocity of the flow decreases with the nanopore radius, as in the case of a laminar flow through a pipe. Another factor that may contribute to reduced flow is an increased effective viscosity of a thin water film [15]. For the two 30 Å-radius pores, the flow velocity is lower in the pore with a rough surface, caused by a higher interfacial friction. Accordingly, the friction coefficient for DNA permeation in a nanopore is bigger for a pore of smaller radius, whereas for the nanopores of the same mean radius, ξ is about 20% higher for the rough surface pore [Fig. 4c]. The electrophoretic mobility of DNA, plotted in Fig. 4c, depends both on the hydrodynamic friction and the ion distribution in the pore [Fig. 4a]. The simulated values of the DNA mobility are comparable to estimates (1.4 Åe/(pN ns)) obtained by analyzing the results of the nanopore experiments [16].

The simulated stall force depends linearly on the applied electric field and is about 25% of the total electrostatic force QE on bare DNA in the smooth surface pores. Hence, the simulated values of the stall force are in very close agreement with experiment [5]. However, our interpretation of the force is quite different. We note that the values of the stall force cannot be explained using the Manning criterion for the effective charge because the ion distribution depends on the pore radius whereas the stall force barely does [Fig. 4d]. At the same time, we find that the stall force depends on the surface properties of the pore: it is significantly higher in the rough surface pore. The friction force between the electrolyte and pore surface affects the velocity of the electroosmotic flow [Fig. 4b], and thereby the hydrodynamic drag force on DNA. Thus, we conclude that the reduction of the electric driving force QE in a nanopore arises from the hydrodynamic drag of the electroosmotic flow.

As in the case of DNA elecrophoresis through a bulk electrolyte, the stall force in a nanopore is accurately described as F = ξμE [Fig. 4d]. This relation allows the effective driving (stall) force in a nanopore to be determined without laborious direct force measurements [5]. The electrophoretic mobility of DNA can be determined from DNA translocation experiments [17–19]. The friction coefficient can be determined using the active control setup [20], which measures the DNA escape time from a nanopore in the absence of the external electrostatic field. Although it is not yet clear if this relation holds in the case of very narrow pores, using available estimates of the diffusion constant and electrophoretic mobility of DNA in α-hemolysin we estimate the effective charge of DNA in that system to be between 2 and 3 electron charges, which is consistent with the previous estimates [21–23].

In summary, we have demonstrated that the hydrodynamic drag of the electroosmotic flow determines the value of the effective driving force on DNA in a bulk electrolyte and in a nanopore. We have shown that the extended ion condensation theory [13] correctly describes the distribution of ions in a bulk electrolyte but is insufficient to predict the value of the effective driving force. Our study demonstrates that the effective charge defined as q_eff = ξμ accurately describes the effective driving force F = q_effE of the elecric field E in a nanopore.