Simulation of cell motility that reproduces the force–velocity relationship

Abstract

Many cells crawl by extending an actin-rich pseudopod. We have devised a simulation that describes how the polymerization kinetics of a branched actin filament network, coupled with excluded volume effects, powers the motility of crawling cells such as amoebae and fish keratocytes. Our stochastic simulation is based on the key fundamental properties of actin polymerization, namely growth, shrinkage, capping, branching, and nucleation, and also includes contributions from the creation and breaking of adhesive contacts with the substrate together with excluded volume effects related to filament packing. When reasonable values for appropriate constants were employed, this simulation generated a force–velocity relationship that resembled closely that observed experimentally. Our simulations indicated that excluded volume effects associated with actin filament branching lead to a decreased packing efficiency and resultant swelling of the cytoskeleton gel that contributes substantially to lamellipod protrusion.

The motility of crawling cells is important in a range of central biological functions including chemotaxis, cancer metastasis, and development. Although the precise mechanisms by which locomotion is generated remain somewhat controversial, there is a general consensus that this crawling is mediated by the dynamics of the actin cytoskeleton, which itself is regulated by a host of accessory proteins (reviewed in refs. 1 and 2). Crawling cells have a characteristic thin leading edge or lamellipod that is packed with actin filaments arranged in a dendritic meshwork (2, 3). Cells crawl by protruding this lamellipod while drawing the cell body forward. Direct observation of moving cells has indicated that actin polymerization is concentrated at their leading edge, after which the cytoskeleton flows rearward (retrograde motion) as the lamellipod advances. Within the lamellipod, actin filament density initially increases with distance from the leading edge, before reaching a plateau and then decreasing toward the rear of the lamellipod (3, 4). Although most of the central players in this process are thought to have been identified, the precise manner in which they interact to generate locomotion is less clear. For example, although there is a general consensus that actin polymerization makes a major contribution to lamellipod protrusion through an elastic Brownian ratchet mechanism (2, 5, 6), current models have not simulated closely the force–velocity behavior of motile cells observed experimentally. This force–velocity relation of crawling cells is somewhat counterintuitive, in that small restraining forces do not produce a significant reduction in the velocity, whereas when the force is increased above a threshold, velocity decreases dramatically (7).

The actin cytoskeleton is constructed from a dendritic array of F-actin filaments, the polymerization dynamics of which is orchestrated by a range of actin-binding proteins that can facilitate polymerization, sever filaments, or prevent polymerization by capping filament ends. Filament branching is generated by the Arp2/3 complex that binds to the sides of actin filaments and nucleates the formation of a new daughter filament angled at ∼68° to the original filament. At the leading edge of the lamellipod, recurrent branching generates a dendritic array of intermeshed filaments that can be observed directly by electron microscopy (3).

There have been a number of attempts to model the motility of crawling cells (reviewed in refs. 2 and 8). Models of a network of elongating noninteracting rod-like actin filaments have been produced (9, 10), from which the expansion speed of the resultant gel can be estimated. Theoretical attempts to describe actin-based motility using a mean field approach have also been made (11). However, these models describe the cytoskeleton only in terms of its bulk mechanical properties. The pioneering work of Mogilner and Oster (5, 6) identified the importance of a Brownian ratchet mechanism for the generation of a protrusive force in both crawling cells and Listeria. This model explains how protrusion can be generated by thermal motion and diffusion enabling actin subunits to be inserted between the ends of growing filaments and the cell’s leading edge. Thermal motion causes fluctuations in the position of the membrane and, when a gap opens up, actin subunits can be added to the end of the filament, preventing the membrane from returning to its original position. Thus, actin polymerization generates a forward motion of the leading edge of the cell by rectifying Brownian motion. A refined version of this model includes contributions from the elastic properties and fluctuations of the filaments to produce an elastic Brownian ratchet model that more closely reproduces observed behavior. However, this model treats the cytoskeleton as a rigid support for the growing filament network which contrasts with the retrograde flow observed experimentally. Recently, the actin cytoskeleton has been modeled as a two-dimensional network of growing noninteracting rods which move by an externally imposed retrograde velocity (12). Other workers (13) have studied two-dimensional models of lamellipod formation and have been able to reproduce the filament orientation observed experimentally. Three-dimensional Brownian dynamics simulations of branched networks have also been conducted, but in a geometry more relevant to Listeria propulsion than lamellipod protrusion (14).

We have extended this work and describe here a three-dimensional model of actin-based cell motility that includes the microscopic properties of actin (such as growth, shrinkage, branching, capping, nucleation, and formation of adhesions to the substrate) and, crucially, excluded volume effects. Excluded volume effects assume major importance in filament packing when the filaments are relatively rigid and when their aspect ratio (length/diameter) becomes large. In this context, it is important to realize that the structure of gels formed from actin filaments that are substantially shorter than their persistence length [10–15 μm (15, 16)] differs from that seen with flexible polymers in which the gel properties are dominated by polymer chain entropy (17, 18). A range of experimental and theoretical studies have shown that the volume fraction occupied by randomly oriented filaments varies approximately as the inverse of the aspect ratio (19–21), and so maximum packing density decreases dramatically as filaments lengthen. For example, the volume fraction occupied by filaments is only 0.1 for an aspect ratio of 50 (corresponding to 400-nm-long filaments, as is typical within the lamellipod). These excluded volume effects arise because two objects cannot occupy the same space and so filaments cannot intersect. As filaments lengthen, it becomes progressively more difficult to arrange them so they do not intersect. Although the random way in which growing rods pack is metastable relative to the liquid-crystal phase, entanglement effects (17) make diffusion so slow as to prevent the system reverting to the denser liquid-crystal packing. Excluded volume effects have been shown experimentally to make a substantial contribution to protrusion in the simple motile apparatus of nematode sperm that is based on polymerization dynamics of unbranched filaments of major sperm protein (22), but its importance in actin-based dendritic filament meshworks in lamellipods has not been investigated in detail. Although intuitively branched filaments would be anticipated to pack even less closely than unbranched filaments, it is unclear precisely how the restrictions on filament movement (both of rotation and translation) might contribute to these excluded volume effects. The simulations we have generated from our more comprehensive model indicate that these excluded volume effects are indeed important for actin-based motility and that, in addition to their contributing to lamellipodial protrusion, the mainly uniform retrograde flow of the actin cytoskeleton relative to the substrate can only be reproduced when these effects are incorporated. In addition, we find that filament–substrate interactions are important in simulating a force–velocity relation that matches closely that observed experimentally.

Overview and Biological Background of the Simulation

General Architecture of the Model.

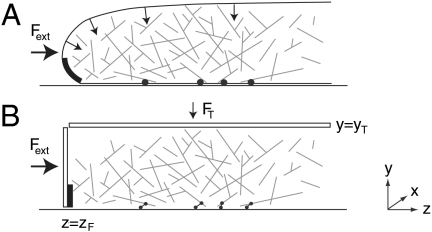
In our simulation, the lamellipod was modeled as a three-dimensional box of adjustable dimensions (see Fig. 1). A hard wall at the base (y = 0) corresponded to the substrate on which the cell moves. We modeled the cell membrane, within which the filament network is contained, by means of two movable hard walls: a “front” wall at z = z_F represented the leading edge of the lamellipod, and a “top” wall at y = y_T represented its upper surface. Because lamellipods have an approximately uniform thickness of 100–200 nm (23), this is likely to be a close approximation except at the very tip of the lamellipod where the membrane is curved. A vertical force, 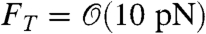, was applied to the top wall to model the containing effect of the cell membrane surface tension. This force was small compared to the external load F_ext applied to the front wall when evaluating the force–velocity behavior of the simulation. We incorporated periodic boundary conditions along the x axis so that the motion of F-actin was not limited parallel to the leading edge. No constraint was imposed in the positive z direction, toward the interior of the cell.

Fig. 1.

Model lamellipod. (A) Schematic drawing of a lamellipod, illustrating the basic physical assumptions of our model. The slight curvature of the membrane on the upper surface of the lamellipod generates forces (arrows) due to surface tension that constrain the actin gel. The Arp2/3 complex mediates filament branching when it is in the proximity of the highly curved section on membrane at the base of the leading edge, marked in black. Filaments close to the substrate can form transient adhesions (●). (B) Simplified geometry of the model. A small vertical force F_T mimics the forces due to membrane surface tension. Filament branching can occur in the cuboid region marked in black. An external force F_ext applied to the leading edge is balanced by the reactive force due to adhesions (which are represented as springs).

We treat F-actin as branched rigid rods that we call dendrals to distinguish them from unbranched filaments. Individual actin filaments have a persistence length l_p ≈ 10–15 μm (15, 16) and diameter b = 8 μm. Because filaments in both cells and our model have typical lengths ∼1 μm ≪ l_p, treating them as rigid rods is reasonable. We can therefore describe the system by a set of state variables: In our simulation, each filament i is described at time t by its center of mass rⁱ(t), a unit vector nⁱ(t) describing its orientation, its length l_i(t), the barbed and pointed end capping states, and the identity K of the dendral to which it belongs (defined below).

The state of the system was evolved iteratively with each step corresponding to a constant time interval, dt, during which each filament moves in space and could also undergo various kinetic processes. Throughout the simulation, a random number generator was employed to simulate stochastic events. If the average rate of occurrence for an event is k, the probability p of the event was taken as p = kdt. A random number r∈[0,1] was then generated to determine whether the event occurs: If r ≤ p, the event was allowed.

Actin Polymerization Kinetics.

Actin polymerization is controlled at several levels, most importantly by nucleation, branching, capping, and depolymerization. The barbed and pointed ends of actin filaments behave differently. Growth occurs predominantly at the barbed end by addition of actin monomers. We modeled uncapped barbed-end growth by incrementing the filament length l_i by l_mon = 2.7 nm, the size of an actin monomer, at a rate k₊(z_i) given by

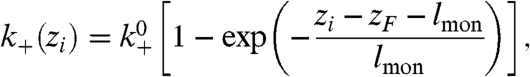[1]

where z_i is the z coordinate of the barbed end. This dependence ensured that a filament cannot grow beyond the wall corresponding to the leading edge. Assuming that the force experienced by filaments in a dendral is a function of distance from the leading edge, a distance-dependent growth speed corresponds to a force-dependent growth speed, as established by Mogilner and Oster (5, 6).

Actin filament depolymerization is dominated by proteins such as ADF/cofilin and depends on the age of the filament. Within seconds of their incorporation into a filament, actin monomers hydrolyze their bound ATP; after τ ≈ 3 min, phosphate is released generating actin-ADP (24–26), enhancing the probability that ADF/cofilin will bind, and so increasing depolymerization. We therefore used an age-dependent pointed-end depolymerization rate in our model, given by 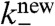if the pointed end is younger than τ, and 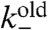otherwise. For depolymerization, the filament length l_i was decreased by l_mon and, if a branching point was passed, the branch was released to create two new dendrals from the original one. Filaments can also be severed at any point along their length at rate k_sever per subunit.

Both filament growth and shortening can be arrested by capping filament ends by, for example, proteins such as capZ that caps barbed ends. We modeled barbed-end capping as having a constant rate per end, k_cap. We considered capping irreversible because of the slow off-rate (27). Pointed-end capping was treated by assuming each branch of a dendral is capped at its pointed end. There is thus only one filament per dendral whose pointed end is uncapped (the “trunk” of the tree), and this filament may be used to identify the dendral K to which the trunk and all the branches belong.

New filaments are created predominantly by branching from existing filaments, which is mediated by the Arp2/3 complex (28–30). Arp2/3 is activated by Wiskott-Aldrich syndrome protein (WASp)/suppressor of camp receptor/WASP family verprolin homologous protein, which are themselves potentiated by interaction with proteins containing Bin/amphiphysin/Rvs (BAR) domains that bind to highly curved regions of the cell membrane (31). We propose, therefore, that nucleation of new branches occurs only in a very localized region at the base of the leading edge, where the cell curves up from the substrate. Thus in our simplified model, branching takes place within a volume of width Δ_z = 10 nm and height Δ_y = 50 nm (the typical radius of curvature recognized by BAR domains), although the results were not critically dependent on the precise way in which Arp2/3 activation was modeled (SI Text). New branches are created on any section of a dendral within this volume at rate k_br per actin subunit and make an angle of 68° with the existing filament (30). Filaments can also be nucleated de novo, although this is generally considered to be less important. However, to initiate our simulation in an empty box, we nucleated filaments stochastically at the front edge of the box at rate per unit area ρ_nuc. Their initial length was five actin subunits and their orientation was random.

Actin Motion.

Dendrals experience stochastic Brownian forces due to the cytosolic fluid and may also interact with other dendrals, adhesion complexes, and the boundaries of the lamellipod. In response, dendrals move as overdamped rigid bodies and their motion is described by a Langevin equation. In the SI Text, we describe in detail how the translational and rotational motion of each dendral was computed during each time step, from a knowledge of the forces acing on it.

Determining Forces.

For filament–filament interactions, we defined an effective hard-core interaction potential that forbade rods intersecting. Iterative steps in the simulation that generated an intersection were discarded. We also introduced an effective hard-rod potential between rods to enable them to exert force on one another. For any two rods i and j, the shortest possible vector r_ij linking the surfaces of the two rods was found. The total force f_ij has magnitude |f_ij| = f₀(δ - |r_ij|)/δ if |r_ij| < δ, 0 otherwise with a range δ = 1 nm. The force f₀ was chosen to avoid rejecting iterative steps due to intersections in more than 0.1% of the total steps. We found that a force in the piconewton range worked well. The direction of the force f_ij was along the vector r_ij with the sign chosen as to keep the rods away from each other.

Cells must exert a force on a substrate to move on it, which they do by forming adhesion complexes. Although the precise molecular details of adhesion complexes are unclear (32), their key feature is that they produce a retarding force that acts against the motion of the filament to which they are attached. They were therefore modeled as elastic springs, with one end attached to the substrate (the base of the box) and the other adhering to the filament. We permitted adhesions to form in the region y < Δ_adh, with Δ_adh = 10 nm (a typical protein size); for those sections of any dendral that protrudes into this region, there is a constant rate per actin subunit k_on of attaching to the substrate. The force exerted by the spring was modeled as f = -κx, with x being the vector linking the two ends of the adhesion. Detachment of an adhesion complex from a filament was modeled as strain-dependent using Bell’s equation (33),

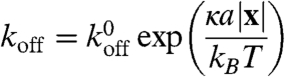[2]

with a molecular length scale a which describes the typical stretching of an adhesion before breaking. This equation has been found phenomenologically to describe adhesion and detachment well (33).

Finally, the force exerted by the leading edge of the lamellipod on the filaments was modeled using the same effective hard-wall potential employed for filament–filament interactions. We assume a rapid mechanical equilibration of the leading edge; thus at each time step, its location z_F is changed to ensure that the total force exerted by the filaments on the leading edge exactly balances a fixed external load F_ext on the lamellipod. By varying F_ext, the force–velocity relation of the model lamellipod can be investigated.

Choice of Parameters.

The choice of parameters is summarized in Table 1. The values of most of these parameters have been determined experimentally, with the notable exception of the parameters describing adhesion, k_on, 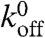and a; the choice of values of these adhesion parameters is described in the SI Text.

Table 1.

Default parameter values used in the simulations

Symbol	Description	Value	Ref.
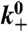	Polymerization rate	100/s	(34, 35)
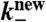	Depoly. rate (new)	1/s	(4)
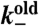	Depoly. rate (old)	30/s	(4)
kbr	Branching rate	1.4 × 10-3/(s.u. s)	(9)
kcap	Capping rate	0.2/s	est. in (36)
kon	Adhesion on-rate	0.07/(s.u. s)	est. from (37)
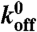	Adhesion off-rate	4 × 10-4/s	est. from (38)
ksever	Severing rate	0/(s.u. s)	N/A
κ	Adhesion spring const.	10-3 N/m	(38)
a	Molecular scale	3 nm	N/A (est.)
ρnuc	Nucleation rate density	20/(μm2 s)	N/A
Δz	Branching region	10 nm	N/A (est.)
Δy	Branching region	50 nm	N/A (est.)
Δadh	Adhesion region	10 nm	N/A (est.)
η	Viscosity	0.02 Pa s	(39)
dt	Simulation time step	10-5 s	N/A

Limitations of the Model.

As in all simulations of biological systems, it was necessary to make several simplifications of the extremely complex molecular detail involved. Thus, filaments were considered to be rigid rods, which is a reasonable approximation because 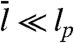. Moreover, even if filament bending was included, its influence on the overall density of the gel should be small. A contribution due to the strengthening of adhesions under strain observed experimentally (40) was also not included. Despite the current lack of detailed knowledge about the kinetics of adhesion formation and of their mechanics, our description of the adhesion complexes as springs seems a good starting point that captures the key points of adhesion formation and its mechanics. Finally (see SI Text), we did not include a contribution from hydrodynamics when obtaining the mobility matrix in the Langevin equation, because these effects would not be expected to be important due to screening by the actin network.

Results and Discussion

Simulating Cell Crawling.

Provided contributions from polymerization, branching, excluded volume effects, and adhesions were included, our model was able to replicate the basic features observed in crawling cells (see Movie S1). It was possible to simulate the characteristic force–velocity relation, a retrograde flow at a speed v_R, the concentration of the filaments with respect to the leading edge and a protrusion speed v_F that had the appropriate order of magnitude.

In total, 443 simulations were run, both to test the model and to explore the influence of key parameters such as 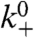, k_br, etc. The robust nature of the model was demonstrated by varying these parameters over a range of one-quarter of their default value to four times their default value to verify that the overall behavior, i.e., persistent motion of a crawling cell, was retained. We repeated these simulations in the presence of a significant external retarding force and found that the qualitative form of the force–velocity relation was also robust to parameter variation. Results that could not be shown in the main article are included in Robustness to choice of Arp2/3 activation model and Robustness to variation of parameters in SI Text. To explore the significance of the branched geometry of actin in lamellipods, we also conducted simulations with purely linear filaments (i.e., k_br = 0) and compared them with the simulations with dendrals.

Network Structure and Concentration Profiles.

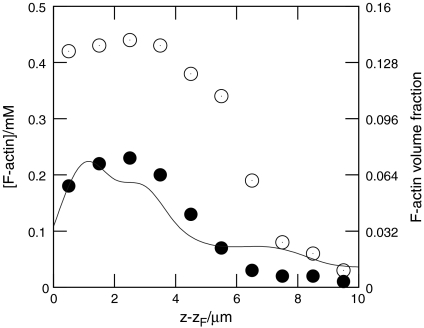
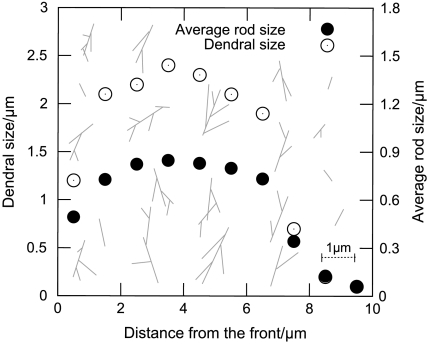
Fig. 2 shows snapshots from typical simulations, for both branched and unbranched networks, when motion of the model lamellipod was unopposed. Initially, filaments close to the leading edge are very short because they have just been created. The filaments then experience a period of growth after which they are capped. During this period of growth, excluded volume effects cause the network formed to expand considerably, because long rods pack less efficiently in a random assembly than short rods (19–21). Packing difficulties were exacerbated in the case of growing branched networks, and consequently these expanded more rapidly, compared to simulations in which unbranched filaments were employed. This difference is reflected in the concentration profiles of F-actin, shown in Fig. 3, where branched networks are clearly less dense. These profiles exhibited a broad peak 1.5–3 μm from the leading edge, as observed experimentally (3). It is within this region that the network becomes overcrowded, and so excluded volume effects cause the gel to expand. In the absence of an external opposing force, this expansion mostly pushes the leading edge forward relative to the substrate, while the filaments move rearward relative to the leading edge. Further from the leading edge (5–10 μm), the filaments are old enough for depolymerization to become significant and the F-actin concentration consequently drops toward zero, marking the rear boundary of the lamellipod. Fig. 4 illustrates how dendrals first grow, and are then dismantled, as they move rearward.

Fig. 2.

Typical networks obtained in the simulation, viewed from above the substrate: (Top) unbranched rods; (Middle) branched rods (two individual dendrals, which are also shown below, have been colored in dark gray to improve their visibility); and (Bottom) individual dendrals from the branched network.

Fig. 3.

Concentration profiles of F-actin as a function of distance z - z_F from the leading edge, for small external forces: ●, branched rods; ○, unbranched rods; —, rescaled experimental data from ref. 4 (courtesy of N. Watanabe).

Fig. 4.

Size of dendrals (○) and average length of rods within dendrals (●), as a function of distance z - z_F from the leading edge. Also illustrated are the forms of representative dendrals at various locations behind the leading edge.

Retrograde Flow.

The simulation indicates that protrusive force is generated throughout a region of the cell close to the leading edge—a consequence of increasing excluded volume effects as polymerization takes place. The resultant motion of the network in response to these protrusive forces depends on external forces, principally, the adhesive force exerted by the substrate and any external load that might be applied to the leading edge. Because these external forces oppose one another, it follows that, at higher loads, the adhesions must be more strained. Such stretching of the adhesions will occur if network expansion drives dendrals both away from the leading edge and also rearward relative to the substrate, i.e., if this expansion causes retrograde flow. To investigate this mechanism in more detail, we applied various opposing loads to the leading edge and measured both the retrograde flow speed v_R (defined as the mean velocity of individual actin filaments in the region 3–4 μm from the front) and the velocity of the leading edge v_F (Fig. S1). For branched networks at low values of the external load, there is an almost linear dependence of v_R on v_F, indicative of a constant expansion speed v_exp = v_R + v_F of the actin gel along the z axis. At high values of the external load, however, the retrograde flow approaches a limiting speed whose magnitude v_R ∼ 3 μm/ min is in broad agreement with that seen in moving keratocytes (41).

Lamellipod Height.

As well as swelling along the z axis, the gel of growing dendrals also expands in the vertical direction. Because expansion occurs only in the region close to the leading edge, the thickness of the remainder of the lamellipod stays essentially constant. Thus the extent of the expansion determines the height y_T of the lamellipod. As shown in Fig. S2, for small external loads and physiological values of the key parameters, y_T ∼ 200 nm, which agrees well with measurements made on crawling cells (23). At high values of the retarding force, a greater part of the gel expansion occurs in the vertical direction—a consequence of the compressive forces acting in the z direction that also limit the speed of the retrograde flow. As a result, the lamellipod becomes thicker, a prediction of our model that could be tested experimentally.

Force–Velocity Relation.

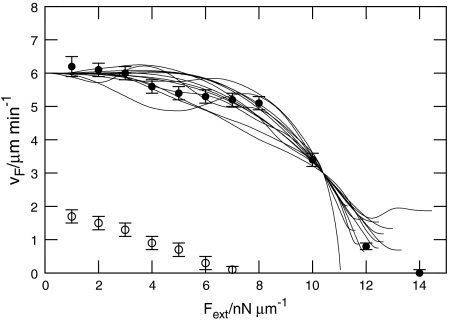
A major goal of our model was to simulate a relationship between the speed of locomotion and opposing load that agreed with experimental observations. Fig. 5 shows the simulated force–velocity curves for both branched and unbranched networks. For branched dendrals, the data display the characteristic feature observed experimentally that the speed of locomotion is little affected at modest loads, but then falls to zero fairly abruptly as the load is raised further. Motion of the leading edge is halted at a “stall force,” the value of which was found to be F_stall ≈ 14 nN/μm per unit length of perimeter of the lamellipod. For loads exceeding F_stall, the leading edge was pushed rearward.

Fig. 5.

Simulated force–velocity relationship: protrusion speed vs. external force per unit length along the perimeter of the model lamellipod: ●, branched rods; ○, unbranched rods; —, rescaled experimental data from ref. 7 (courtesy of M. Radmacher).

Overall, the agreement between the simulations of branched networks and experimental data (7), which is included in Fig. 5 for comparison, was remarkably close. Crucially, in our simulations, the velocity of a moving cell did indeed go to zero for some stall force F_stall, which contrasts with the purely Brownian ratchet model that predicts an asymptotic approach to zero velocity (5, 6). This difference probably derives from the models used to explore the ratchet mechanism treating the cytoskeleton as a rigid support against which the polymerizing filaments push the leading edge of the lamellipod forward. By contrast, our model incorporates a retrograde sliding of the cytoskeleton, which is slowed down by adhesions. Therefore, in models based solely on rectified Brownian motion, the contribution of the filaments pushing against the leading edge dominates the force–velocity relation. By contrast, the force–velocity relation in our model contains important contributions from excluded volume-related swelling and adhesion to the substrate. Although our simulations used only a very simplified model of the formation of adhesions and their mechanical properties, the assumptions made are robust and capture the principal features of the motility of crawling cells.

Influence of Varying the Parameters.

The values for the parameters in our model were chosen to be within the physiological range established experimentally and also to generate a physiological behavior in the model. Although overall the model appeared to be robust and retained all the key aspects of crawling cells over a range of different parameter values (see Figs. S3, S4, and S5), we observed that different parameters influenced the behavior of the different aspects of the system differentially. Thus, increasing the capping rate leads to a decreased protrusion speed (Fig. S6A), whereas increasing the branching rate leads to an increased protrusion speed (Fig. S6B). Increasing the rate of growth (Fig. S6C) leads, as expected, to an increased protrusion speed. Increasing the rate of attachment formation (Fig. S6D) initially increased the rate of protrusion, but above a certain value, its influence diminished, most likely because most filaments that can be fixed to the surface had already formed sufficient attachments to impede sliding, and so further adhesions would not be expected to change the adhesion behavior greatly for the forces employed in the model. Parameter variation that enhances protrusion speed also augments lamellipod height, as might be expected from consideration of the mechanism of propulsion through gel swelling.

Significance of Branching.

A key feature of actin networks is that they consist, in the presence of Arp2/3, of dendrals, i.e., branched actin filaments. Our simulations are consistent with filament branching playing an important role in actin-based cell motility. As is clear in Figs. 2–5, dendrals pack less efficiently than unbranched filaments. Thus, the speed at which the cytoskeletal gel expands when composed of growing branched dendrals is significantly greater than that seen with unbranched filaments. We speculate that a principal advantage of branching is that it greatly hinders the rotation of individual filaments within the network, thereby ensuring that the orientation of filaments remain disordered and that excluded volume interactions remain large, even in the presence of internal and external forces that could otherwise align filaments. Details of filament orientation in branched and unbranched networks are provided in Filament orientation in SI Text.

Importance of Excluded Volume Effects.

Excluded volume effects result from packing constraints that derive from not allowing the filaments to intersect with each other or to cross over one another. We assessed the importance of these effects by running simulations in which these constraints were not included. Although removing these constraints is somewhat artificial, it provided an easy means to assess the importance of excluded volume effects. Compared with simulations in which excluded volume effects were included, the protrusion speed at zero load was reduced to 60% of that seen when they were included, and the stall force was reduced by 78%. This significant diminution of motility occurs because only those dendrals that are attached to the substrate and in contact with the leading edge contribute to the generation of force and motion. Moreover, significant retrograde motion of the network could only be simulated by not allowing the filaments to intersect with each other or to cross, which is equivalent to taking into account excluded volume effects (Fig. S7).

Role of Adhesions.

The importance of adhesions in producing the force–velocity relation was confirmed using a simplified model of force generation by a swelling gel of growing dendrals that is described explicitly in the SI Text. The model assumed that (i) growing filaments pack together as tightly as possible while remaining orientated randomly; (ii) as the filaments in a region close to the leading edge elongate, that region of the network expands; (iii) the expansion leads to both forward propulsion of the leading edge and retrograde flow of the network; (iv) the total number of adhesions that the network makes with the substrate is independent of the external load opposing the advancement of the leading edge; (v) the external load is balanced by the elastic force of the adhesions, which get stretched as a result of the retrograde flow; and (vi) detachment of the adhesions is strain-dependent, following Bell’s law, Eq. 2. Quantitative predictions of this model shown in Fig. S8 provide a reasonable first approximation to the simulation data. In particular, the model points to the strain-dependent detachment of adhesions as the origin of the distinctive nonlinearity in the force–velocity relation of locomoting cells.

Concluding Remarks

We have developed a simulation to evaluate the influence of filament branching on the swelling of actin gels induced by molecular crowding and show that branching leads to an enhanced rate of swelling. In the context of actin-based motility, filament branching leads to a higher rate of protrusion. Furthermore, it was only possible to simulate cell motility closely by supplementing Brownian ratchet and other mechanisms related purely to filament growth with a model that also included excluded volume effects, consistent with both mechanisms contributing to locomotion. Such a model also accounts for the retrograde flow observed in lamellipodial motion and suggests a plausible physical mechanism that gives rise to the uniform height of a protruding lamellipod.