Calculating and controlling the error of discrete representations of Pareto surfaces in convex multi-criteria optimization

Abstract

A discrete set of points and their convex combinations can serve as a sparse representation of the Pareto surface in multiple objective convex optimization. We develop a method to evaluate the quality of such a representation, and show by example that in multiple objective radiotherapy planning, the number of Pareto optimal solutions needed to represent Pareto surfaces of up to five dimensions grows at most linearly with the number of objectives. The method described is also applicable to the representation of convex sets.

1 Introduction

In radiation therapy planning, there is always a tradeoff between achieving the desired dose to the target region and overdosing nearby healthy structures in the patient [5, 11]. This gives rise to a multi-criteria optimization problem: instead of finding one plan by solving a single optimization problem, a multi-criteria treatment planning system finds a set of Pareto optimal treatment plans, and the physician then selects the plan to use by smoothly navigating amongst these [9]. Considering computation time and storage, we would like to find a small number of treatment plans which closely approximate the true Pareto surface of plans. With this as the motivation, we consider the following mathematical setting, which is directly applicable to multi-criteria intensity modulated radiation therapy (IMRT) treatment planning [3, 7]. In brief, the IMRT treatment planning problem optimizes the beamlet intensity of hundreds of individual beamlets coming into the patient from given directions in order to deliver a prescribed uniform dose to the target region while sparing the nearby healthy organs. The mapping from beamlet intensities to dose, discretized as volume cubes (voxels) in the patient, is linear and known.

The method presented here is applicable to general convex multi-objective optimization, but in this work we focus on IMRT planning, which appears to be one of the only areas in which high dimensional Pareto surfaces are used for decision making.

2 Problem statement

Our main goal is to calculate the error of a discrete representation of a Pareto surface. By Pareto surface, we mean the set of all Pareto optimal (see below for definition) solutions in objective function space. Consider the following general multi-critieria optimization problem (MOP):

$$\begin{array}{cc}\hfill \text{minimize}\hfill & \hfill \left\{F_j\right(x\left)\right\},j=1\dots n\hfill \\ \hfill \hfill & \hfill x\in C_x,\hfill \end{array}$$ (1)

F_j is the jth objective function (assumed throughout to be convex), x is a vector of decision variables, and C_x is a convex constraint set in the decision variable space. Formulation 1 is shorthand for “find all Pareto optimal solutions with F_j as the objective functions”. For a solution x we let F(x) denote the vector of objective functions of that solution. A solution x is Pareto optimal if there is no other feasible solution $\tilde{x}$ where $F\left(\tilde{x}\right)\le F\left(x\right)$ with at least one strict inequality (in this paper, vector inequalities are always meant component-wise). Typically the set of all Pareto optimal solutions is not available in closed form. Therefore, one seeks a discrete set of points on the Pareto surface (PS) which approximates the surface well. (By Pareto surface, we mean the surface in objective function space, that is, the space with one coordinate axis for each objective function F_j. One could also speak of the surface of Pareto optimal points in the underlying decision variable space.) In our setting, we allow convex combinations of the discrete points representing the Pareto surface, thus, if in 2D the Pareto surface is a straight line, the two end points constitute an exact representation of the surface. This differs from the work of Sayin [12] which does no allow for convex combinations of the discrete points representing the surface, but otherwise has similar goals.

Let F(C_x) denote the mapping of the feasible points into the objective function space, i.e.:

$$F\left(C_x\right)=\{y\in \mathrm{I}{\mathrm{R}}^n\mid \exists x\in C_x\text{with}F(x)=y\}.$$ (2)

This set is not necessarily convex, but the following outward extension of F(C_x), which we call C_F, is:

$$C_F=\{y\in \mathrm{I}{\mathrm{R}}^n\mid \exists x\in C_x\text{with}F(x)\le y\}$$ (3)

The proof of the convexity of C_F is given in A.1. See Figure 1 for depictions of F(C_x) and C_F. For the remainder of this work we use the set C_F due to its convexity. Note that the lower boundary of C_F is exactly the Pareto surface (See Figure 1). Notation used appears in Table 1.

Figure 1.

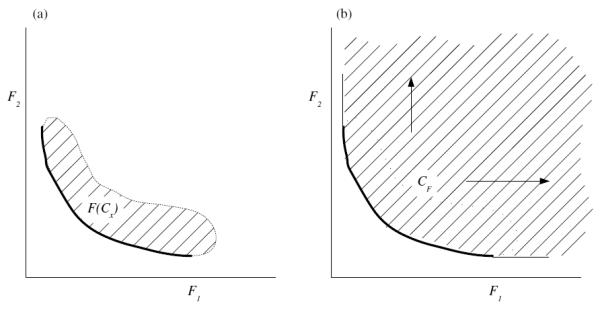
In (a) the hashed area is the set F(C_x) = {y | ∃ x ∈ C_x with F(x) = y}. The bold lower envelope is the Pareto surface. In (b) the hashed area is C_F = {y | ∃ x ∈ C_x with F(x) ≤ y}, i.e. the outward extension of the set F(C_x), which is a convex set if C_x is convex.

Table 1.

Notation used throughout the text.

symbol	meaning
x	vector of decision variables
Fj(x)	jth indicator function, j = 1 … n
F(x)	vector of all n indicator functions
Cx	constraint set for the decision variables
CF	convexified set of feasible indicator function vectors
v, y, z	used to denote points in indicator function space, $\mathrm{I}{\mathrm{R}}^n$
vi, i = 1 … m	m points in indicator function space representing the Pareto surface
CH(v1, v2, … , vm)	convex hull of the m representing points. Serves as approximation of CF
d(z → y)	distance (one sided maximum norm) from z to y
d(z → S)	distance from z to the set S

We next define a distance measure which is appropriate for measuring the difference between a discrete representation of the Pareto surface and the true Pareto surface. To begin, let d(z → y) be the distance from point z to point y, both of which lie in $\mathrm{I}{\mathrm{R}}^n$. We define d as:

$$d(z\to y)≔{\max }_j\left({(y_j-z_j)}^{+}\right)$$ (4)

where (a)⁺ = max(a, 0). Note this is a one sided maximum norm that takes a non-zero value only if some component of z is less than the same component of y. We extend this definition to the distance from a point z to a convex hull of a set of points, CH(v), as follows:

$$d(z\to \mathrm{CH}(v\left)\right)≔{\min }_{y\in \mathrm{CH}\left(v\right)}d(z\to y).$$ (5)

At this point we turn to evaluating a discrete representation of the Pareto surface. Let v¹, …, v^m be m points in the set C_F, and let CH(v) denote their convex hull. In general the points vⁱ can be anywhere within the set C_F but in this work they will be on the Pareto surface. Given this discrete representation v, the error e is defined as

$$e\left(v\right)={\max }_{z\in C_F}d(z\to \mathrm{CH}(v\left)\right).$$ (6)

This is the optimization problem we wish to solve, which gives a quality measure for a discrete representation v. However, this is a difficult optimization problem since it is the maximization of a convex function over a convex set (MCCS). (The proof that d is convex in z follows from the Theorem 5.1 in [2] once d(z → CH(v)) is written as the optimal solution to a linear program, formulation 7 below). Therefore, it is possible that there are local optima that are not global. On the other hand, it is easy to show that optimal solutions to the MCCS problem exist on the boundary of the convex set, e.g. [1]. If the convex set is polyhedral (e.g. linear programming) one might consider enumerating the vertices in an exhaustive search. However, for our case this is not feasible due to the dimension of the problem and hence the large number of vertices. Furthermore, many IMRT problems are modeled as nonlinear convex optimizations. General techniques for the MCCS problem exist [1], but here we develop a new method tailored to the specific form of the problem at hand. The idea is that the distance measure to maximize is a piecewise linear convex function (proved in [2]), and hence we can enumerate the gradients of the function d(z → CH(v)) and search in each of the gradient directions individually (proof of the validity of this strategy is in A.2). Next we turn to enumerating the gradients for a fixed discrete Pareto representation given by v.

We begin by writing the distance d in formulation (6), for a fixed z and a fixed set of points v on the Pareto surface, as the solution to a linear program:

$$\begin{array}{cc}\hfill \text{minimize}& \hfill d\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \hfill d\ge \sum _{i=1}^m{\lambda }_i{v}_j^i-z_j,j=1\dots n\hfill \\ \hfill & \hfill \sum _{i=1}^m{\lambda }_i=1\hfill \\ \hfill & \hfill d\ge 0\hfill \\ \hfill & \hfill {\lambda }_i\ge 0,i=1\dots m\hfill \end{array}$$ (7)

Note that ${\sum }_{i=1}^m{\lambda }_i{v}^i$ denotes a convex combination of the members of C_F, and as such is also a member of C_F. The dual values (also termed Lagrange multipliers or marginal values) of the constraints $d\ge {\sum }_{i=1}^m{\lambda }_i{v}_j^i-z_j$ (the dual values are optimal values of p_j in formulation 8 below) are equal to how the minimum of d (i.e. the distance) changes with a change in z_j. More specifically, p_j is, by linear programming duality theory, the partial derivative of the distance from z to C_F with respect to z_j, thus together giving the gradient of the distance with respect to z. Note that increasing z, i.e. bringing z closer to the Pareto surface, causes the distance to the Pareto surface to go down, and hence the relationship between the dual variables p and the gradient g of the distance with respect to z is off by the sign, i.e. g = −p. There is also a geometric visualization of the gradient (and hence the dual variables p) which is described in Figure 2 and the caption. The gradient points in the direction of maximal increase of the distance function, and thus the gradient of the distance function in the region of a face is perpindicular to that face (iso-distance lines are parallel to the face). For high dimensional faces which are not fully dimensional (e.g. lines in 3D, instead of fully dimensional triangles) the geometric interpretation is more difficult, which is why we choose to calculate the gradients by appealing to duality theory rather than geometry.

Figure 2.

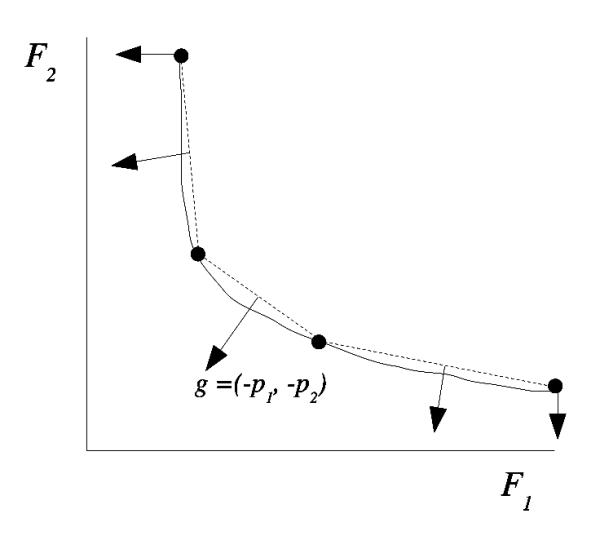
The arrows indicate the gradients g of the distance function, and are equal to the negative of the vector of dual variables p, as discussed in the text. The distance is the one-sided maximum norm distance of a point to the convex hull of the points which define the Pareto surface thus far, which are the dots in the figure. The gradients are associated with faces of the Pareto surface approximation and are normal to those faces (in this example, the vertical and horizontal gradients shown are associated with the degenerate faces, which are the anchor points). The true (unknown) Pareto surface is displayed as well as the convex hull approximation of it. By running each of the gradients through formulation 10, we can calculate the maximum error of the discrete representation.

The dual problem associated with the primal problem given in formulation (7) is:

$$\begin{array}{cc}\hfill \text{maximize}& \hfill -p^{\prime }z+q\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \hfill -p^{\prime }{v}^i+q\le 0,i=1\dots m\hfill \\ \hfill & \hfill \sum _{j=1}^n{p}_j\le 1\hfill \\ \hfill & \hfill p_j\ge 0,j=1\dots n\hfill \end{array}$$ (8)

The solutions p to this problem are the dual variables associated with the constraints $d\ge {\sum }_{i=1}^m{\lambda }_i{v}_j^i-z_j$ in the primal. We would like to enumerate all possible dual solutions p for all possible values of z. Since z is continuous we cannot do this simply by varying z and solving formulation (8). Instead we appeal to linear programming theory, which states that the optimal solution to a linear program lies on a vertex of the feasible set (which is a polytope for linear programs). Since there are finitely many vertices of a polytope, if the dimensions are small enough it is feasible to enumerate them. In our case n, the number of indicator functions (i.e. objectives) is usually under 6 and m, the number of solutions representing the Pareto surface, can also be kept small (on the order of 50) and still achieve a close approximation, as we will see.

The dual problem has n + 1 variables (p is a vector of length n and q is a scalar), thus from LP theory we know that vertex solutions have n + 1 tight constraints (a tight constraint is a constraint satisfied at equality). The LP theory of complementary slackness states that when you pair a constraint with its dual variable, or vice versa, for example the primal variable d ≥ 0 is paired with the dual constraint ${\sum }_{j=1}^n{p}_j\le 1$, at least one of the inequalities is tight. For all of the primal/dual pairings, see Table 2. Since we are only interested in gradients associated with non-zero distance values, we can consider only cases where d > 0. This tells us that we can enforce ${\sum }_{j=1}^n{p}_j=1$. Then we need to have n more of the n + m dual inequalities be tight (so that we have a total of n + 1 tight constraints), and there are $\left(\begin{array}{c}\hfill n+m\hfill \\ \hfill n\hfill \end{array}\right)=\frac{(n+m)!}{n!m!}$ possibilities for this. To get these, we solve the resulting set of equalities for each choice, and then retain only those solutions where p ≥ 0.

Table 2.

Primal dual pairings of primal problem (7) and its dual, (8). Pairings are on the same row.

Primal	Dual
variables	constraints
d	${\sum }_{j=1}^n{p}_j\le 1$
λi, i = 1 … m	−p’vi + q ≤ 0, i = 1 … m
constraints	variables
$d\ge {\sum }_{i=1}^m{\lambda }_i{v}_j^i-z_j$, j = 1 … n	pj, j = 1 … n
${\sum }_{i=1}^m{\lambda }_i=1$	q

At this point, with all of the gradients (i.e. the negative of the dual solutions, g = −p) enumerated, we can solve formulation 6 by solving

$$\begin{array}{cc}\hfill \text{maximize}& \hfill g^{\prime }z\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \hfill z\in C_F\hfill \end{array}$$ (9)

for all enumerated gradients g, and then, for each optimal solution z, computing the distance via formulation 7. Note that formulation 9 is equivalent to solving the following for all enumerated gradients g:

$$\begin{array}{cc}\hfill \text{maximize}& \hfill g^{\prime }z\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \hfill x\in C_x\hfill \\ \hfill & \hfill F\left(x\right)\le z\hfill \end{array}$$ (10)

by the definition of the set C_F. Also note that g ≤ 0, otherwise the problem is unbounded by letting the correct component of z go to infinity.

In order to solve the problem at hand – calculate the error of a given discrete Pareto surface representation – it is now sufficient to run all of the gradients through formulation 10. Note however that formulation 10 is the full IMRT problem, and hence is expensive, and there are a large number of gradients to check. Therefore, we next derive an upper bound formulation to avoid having to run all of them. Appealing again to LP duality theory, we know that if we could solve the primal (7) and dual (8) formulations simultaneously (with z as a variable, constrained by z ∈ C_F, along with the other variables d, λ, p, and q), while equating the two objectives, we would have an optimal solution to our problem. However, with z as a variable, this becomes a set of simultaneous nonlinear equations, since z multiplies p in the dual objective, and is therefore not straightforward to solve. But, if we fix a gradient by fixing p, we remove the nonlinearity. Let g^k, k = 1 … L, be a set of gradients we have already run through formulation 10, and let z^k be the corresponding Pareto surface points. By construction of these points, we know that g^k’z ≤ g^k’z^k for all feasible z and for all k = 1 … L (since g^k maximizes g^k’z for all feasible z). Therefore we can add these as valid constraints to the primal/dual constraint set, and we get the following optimization problem which yields an upper bound for the distance achievable for a given gradient g = −p:

$$\begin{array}{cc}\hfill \text{maximize}& \hfill d\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \hfill d\ge \sum _{i=1}^m{\lambda }_i{v}_j^i-z_j,j=1\dots n\hfill \\ \hfill & \hfill \sum _{i=1}^m{\lambda }_i=1\hfill \\ \hfill & \hfill d\ge 0\hfill \\ \hfill & \hfill {\lambda }_i\ge 0,i=1\dots m\hfill \\ \hfill & \hfill d=g^{\prime }z+q\hfill \\ \hfill & \hfill g^{\prime }{v}^i+q\le 0,i=1\dots m\hfill \\ \hfill & \hfill g^{k\prime }z\le g^{k\prime }{z}^k,k=1\dots L\hfill \end{array}$$ (11)

Decision variables are d, λ, z, and q. Fixed quantities are vⁱ, g, g^k, and z^k. Note this is an upper bound on the maximum distance to the convex hull because we are replacing the difficult constraint z ∈ C_F with a looser set of constraints on z, g^k’z ≤ g^k’z^k. This upper bound is helpful because if the upper bound for a particular gradient g yields a distance value which is less than an already calculated distance value, or yields a distance within our error tolerance, we do to need to run that gradient through formulation 10.

In order to run these ideas as an algorithm for generating a Pareto surface, it is left to decide 1) how to compute an initial set of Pareto surface points and then 2) when to add points to the Pareto surface and how often to re-convex hull. For the initial discrete points, we compute the n anchor points of the multi-objective problem, that is, we minimize each of the objectives individually. Then to add additional points, we enumerate the gradients of the current discrete point representation, and for each gradient, we run formulation 10. If a gradient yields a point with a distance > 0.05 (objective functions are normalized from 0 to 1, so this represents a 5% error), and we add the point to the discrete representation and re-convex hull.

3 Examples

We analyze three IMRT cases in this study: a pancreas, a prostate, and a brain. We consider the pure beamlet optimization problem, which is convex, and ignore the issue of deliverability of plans [14]. Note however that with a pencil beam algorithm designed with beamlet based IMRT planning in mind, the errors that enter when idealized fluence maps are sequenced are not overly large [6]. Problem sizes for the examples used are given in Table 3.

Table 3.

Sizes of each case in terms of voxels and beamlets.

Case	# voxels used in optimization	# beamlets	voxel size dx, dy, dz (cm)	beamlet size (cm)
Pancreas	18,093	633	0.27, 0.29, 0.25	1.0×1.0
Prostate	16,615	491	0.36, 0.36, 0.25	1.0×1.0
Brain	17,335	418	0.28, 0.29, 0.25	1.0×1.0

We are interested in how the number of plans needed to represent a Pareto surface to a specified accuracy (always 5% in this work) grows with the dimensionality of the tradeoff. For each case we compute a series of Pareto surfaces by successively adding objective functions. We use hard constraints to limit maximum doses to all voxels and minimum doses to the target voxels. The following function is used as a target dose objective function:

$$R(d,P)=1∕N\sum _{i\in \text{target}}\max \{0,P-d_i\}$$ (12)

where N is the number of voxels in the target, d_i is the dose to voxel i, and P is the prescription dose. Note when d_i < P then voxel i positively contributes to the function R, which stands for “ramp”. A symmetric version is used to penalize doses above a certain limit P:

$$\stackrel{‒}{R}(d,P)=1∕N\sum _{i\in \text{region of interest}}\max \{0,d_i-P\}$$ (13)

The upper ramp function $\stackrel{‒}{R}$ is used in these studies to control dose to the unclassified tissue, and P is always set to half of the target prescription dose.

For the pancreas case, with a prescription dose of 50.4 Gy, we begin by trading off combined kidney mean dose, liver mean dose, stomach mean dose, and the upper ramp $\stackrel{‒}{R}(d,25)$ on the unclassified tissue. We constrain the target coverage with a hard minimum dose of 45 Gy and R(d, 50.4) ≤ 0.1. This Pareto surface requires 25 plans to guarantee an error of less than 5%. When we add the next objective, minimize the planning target volume (PTV) underdose, we require 44 plans. Results for this case and other cases are shown in the Table 4 and graphically in Figure 4.

Table 4.

Multi-objective formulations and the number of plans required to represent the Pareto surfaces.

Pancreas optimization (prescription: 50.4 Gy)
Objectives	Pareto surface dimension	Number of plans needed on Pareto surface
Kidneys mean, stomach mean, liver mean, unclassified tissue ramp	4D	25
+ PTV ramp	5D	44

Prostate optimization (prescription: 79 Gy)
Objectives (tradeoff set 1)	Pareto surface dimension	Number of plans needed on Pareto surface
Rectum mean, bladder mean, PTV ramp	3D	10
+ femoral heads mean	4D	25
+ unclassified tissue ramp	5D	45
Objectives (tradeoff set 2: target dose fixed by constraints)	Pareto surface dimension	Number of plans needed on Pareto surface
Rectum mean, bladder mean	2D	3
+ femoral heads mean	3D	10
+ unclassified tissue ramp	4D	21

Brain optimization (prescription: 59.4 Gy)
Objectives	Pareto surface dimension	Number of plans needed on Pareto surface
CTV ramp, brain stem mean, chiasm mean	3D	8
+ CTV upper ramp (for hotspots)	4D	25
+ Left optic nerve mean	5D	33

Figure 4.

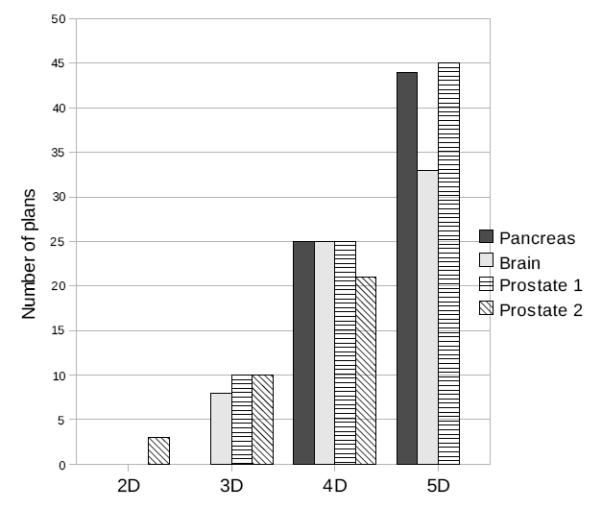
The number of plans required to represent each Pareto surface to an error tolerance of 5%.

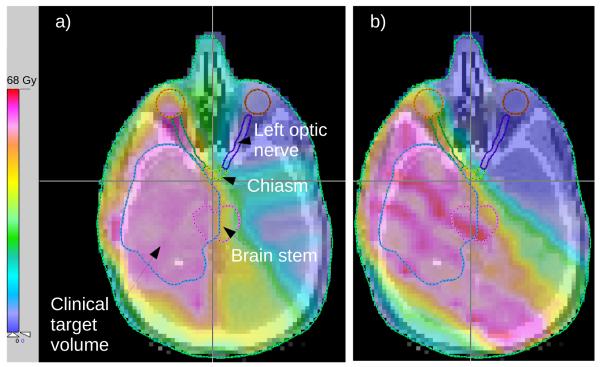
Two Pareto surface results are depicted for the brain case in Figure 3. This case requires fewer plans for the 5D case than the Pancreas case probably due to the fact that the tradeoff is relatively simple here: target coverage versus the sparing of every other organ [4].

Figure 3.

Two Pareto optimal solutions shown for the brain case. a) shows a balanced plan and b) shows the best plan regarding the left optic nerve (which is on the right due to the flipping of the image). The sparing of the left optic nerve causes the target dose homogeneity and the dose in the brain stem to noticeably worsen.

For the prostate case, we examine two different formulations, both given in Table 4. Tradeoff set 1 has the prostate coverage (planning target volume, PTV) as an objective, where as tradeoff set 2 merely constrains it. Due to this constraint, which restricts the size of the feasible set, the number of plans needed for the 3D and 4D Pareto surfaces is always less or equal for tradeoff set 2, as observed in Figure 4.

4 Discussion and conclusions

The Pareto surface approach for decision making is essential if the decision maker is not able to articulate all tradeoff possibilities and preferences before seeing the options. For high dimensional tradeoffs this should almost always be the case since even articulating preferences is overly ambitious. Furthermore, even in simple 2D cases it is likely that the shape of the tradeoff surface is important for making the final decision.

When faced with making a decision based on a Pareto surface, the decision maker would like to know that the Pareto surface he is observing is to some extent complete. We have defined a useful error measure for a Pareto surface using a one sided maximum norm, Equation 4. We then provide a technique to calculate the error which consists of enumerating gradients of the underlying distance function for a given PS representation. The most important distinction of our work compared to other works involving convex Pareto surface computations is the definition of the error. Our definition of error has been used instead of the more commonly used measures of cardinality, coverage, and uniformity, for the following reasons. When the underlying problem is convex, the convex combination of computed solutions is feasible and cheaply available computationally and therefore for all practical purposes is immediately available. If these convex combinations are very close to true Pareto plans (which they will be when the error, as defined in this paper, is small) then it is sufficient to have a small set of Pareto plans from which an approximation of the entire Pareto surface can be obtained by convex combinations of them. Therefore, the measure of coverage (distance of the worst represented Pareto surface point to its closest represented point) and uniformity (maximum distance between two represented points) are not useful in this setting. In a recent similar work [13], convex combinations of IMRT plans are not taken into account when evaluating the Pareto surface, and this results in a large number of plans to approximate the Pareto surface. Due to the resulting computational burden, the authors do not move beyond 3D tradeoff surfaces, and they devise an approximation scheme to further reduce the number of plans to calculate, but still do not take advantage of convex combinations of computed plans.

The approach we provide can be modified for representing a complete bounded convex set, as opposed to just the Pareto boundary, by using a two-sided distance measure d(z → y) := max_j (∣y_j − z_j∣), which is symmetric in z and y. This would apply to a decision making scenario where a decision maker would like to explore the region of all feasible points.

For up to 5 dimensional tradeoff surfaces, we have shown that the number of plans needed to represent an IMRT Pareto surface is less than 50. The values shown in Figure 4 are in fact upper bounds to the number of points required for a few reasons. Since we are using convex functions, the distance given by formulation 7 is an upper bound to the actual distance from a point to the Pareto surface. Also, it remains a possibility that there exists a smaller number of points with the same or smaller error. Finding algorithms which efficiently find a set of points which give minimum error representations is a topic for future research. Finally, the IMRT treatment cases we have studied here do not use dose constraints (other than target minimum and global maximum dose constraints). In an actual setting, one might include additional dose constraints (mean dose to some organ at risk less than some value, for example) which would further restrict the Pareto surface extent [5, 8, 10], which would therefore require fewer plans for representation. To calculate the largest possible tradeoff surface, we do not include such constraints.

The growth of number of plans required versus problem dimension appears to be linear for each individual problem. This may be surprising: simple dimensional arguments – like the number of points on a unit cube – point toward exponential growth. However, one reason for the linear growth observed is the order in which the objectives are added to the problem. In each case we have started with the most important and largest tradeoffs (known from experience in this problem domain) and successively added more minor objectives, which offer less of a tradeoff opportunity.

Future work includes extending this to higher dimensional problems. Already with n = 5 dimensions and m = 40 points on the surface, the number of enumerated gradients is on the order of $\left(\begin{array}{c}\hfill n+m\hfill \\ \hfill n\hfill \end{array}\right)\approx 1\times {10}^6$. However, most of these are not actual gradients, i.e. most have negative components. Negative components arise from, for example, the facet connecting the two extreme points in Figure 2. In high dimensions most of the facets of a convex hull of a set of points have normal vectors with some positive and some negative components. Still, even if one can discard mixed gradients, one must enumerate them anyhow if using the technique of this paper, and this becomes prohibitively expensive as n and m increase.

On the other hand, even 5 objective functions is already a large number of competing structures in radiotherapy and easily covers most clinical situations. Even if the number of planning structures is large, as it is for example in head-and-neck cases, many of the structures would be included as constraints rather than objectives in the MCO formulation, allowing the planning process to focus on the tradeoffs deemed most important by the physician. It has also been shown that for multicriteria IMRT instances with a large number of tradeoffs, the effective number of tradeoffs is usually much smaller, on the order of 3 or 4 [15], due to the correlation between objective functions (for example, trying to reduce the dose to the chiasm in the brain case of Figure 3 will tend to lower the dose to the left optic nerve as well). Finally, since treatment planning is not currently done with multi-objective optimization, even a system that computes Pareto surfaces up to 5 dimensions would be very useful.

A Appendix

A.1 Proof that set C_F is convex

$C_F=\{y\in \mathrm{I}{\mathrm{R}}^n\mid \exists x\in C_x\text{with}F(x)\le y\}$. Let y₁ and y₂ be two members of C_F. Need to show that any convex combination of them is also in C_F. Choose a λ ∈ (0, 1). Let x₁ and x₂ be two feasible solutions associated with y₁ and y₂, i.e. F(x₁) ≤ y₁ and F(x₂) ≤ y₂. Thus λF(x₁) + (1 − λ)F(x₂) ≤ λy₁ + (1 − λ)y₂. Let $\stackrel{‒}{x}=\lambda x_1+(1-\lambda )x_2$, which is feasible since C_x is convex. Since F_j are each convex, we have $F\left(\stackrel{‒}{x}\right)\le \lambda F\left(x_1\right)+(1-\lambda )F\left(x_2\right)$, and therefore $F\left(\stackrel{‒}{x}\right)\le \lambda y_1+(1-\lambda )y_2$, which shows that λy₁ + (1 − λ)y₂ ∈ C_F.

A.2 Proof that gradient enumeration solves the piecewise linear MCCS problem

Let d(z) be a piecewise linear convex function and let S be the convex feasible region for z. Let G denote the set of all gradients of d. Let z* be the optimal solution to the problem max_z∈Sd(z). Let g* be a subgradient of d at the optimal solution z*. Consider the problem: max_z∈Sg*’z. Let $\tilde{z}$ be an optimal solution to this problem. Since g* is a subgradient of d at the optimal solution z*, we have $d\left(z^{\ast }\right)+g^{\ast \prime }(\tilde{z}-z^{\ast })\le d\left(\tilde{z}\right)$. Also, $g^{\ast \prime }(\tilde{z}-z^{\ast })\ge 0$ by the definition of $\tilde{z}$. Thus we have $d\left(\tilde{z}\right)\ge d\left(z^{\ast }\right)$, and we thus prove that $\tilde{z}$ is optimal for the original problem max_z∈Sd(z).