Magnetic resonance imaging of oscillating electrical currents

Abstract

Functional MRI has become an important tool of researchers and clinicians who seek to understand patterns of neuronal activation that accompany sensory and cognitive processes. However, the interpretation of fMRI images rests on assumptions about the relationship between neuronal firing and hemodynamic response that are not firmly grounded in rigorous theory or experimental evidence. Further, the blood-oxygen-level-dependent effect, which correlates an MRI observable to neuronal firing, evolves over a period that is 2 orders of magnitude longer than the underlying processes that are thought to cause it. Here, we instead demonstrate experiments to directly image oscillating currents by MRI. The approach rests on a resonant interaction between an applied rf field and an oscillating magnetic field in the sample and, as such, permits quantitative, frequency-selective measurements of current density without spatial or temporal cancellation. We apply this method in a current loop phantom, mapping its magnetic field and achieving a detection sensitivity near the threshold required for the detection of neuronal currents. Because the contrast mechanism is under spectroscopic control, we are able to demonstrate how ramped and phase-modulated spin-lock radiation can enhance the sensitivity and robustness of the experiment. We further demonstrate the combination of these methods with remote detection, a technique in which the encoding and detection of an MRI experiment are separated by sample flow or translation. We illustrate that remotely detected MRI permits the measurement of currents in small volumes of flowing water with high sensitivity and spatial resolution.

In some cases, including living neural tissue, electric charges moving within the sample produce oscillating magnetic fields that can be visualized by MRI methods. The imaging of current distributions by MRI has developed significantly over the last 20 years, with early applications being directed toward the imaging of current density and conductivity in model systems (1, 2) and later in vivo (3–5). However, the primary focus in the development of current imaging is the possibility of directly imaging neuronal currents.

While the currents generated by a single neuron are far too small to measure, detectable magnetic field changes on the order of 0.1–1 nT (6) may result from synchronized postsynaptic currents in a large number of neurons. The frequency of oscillatory neural activity is also extremely significant. In addition to the previously demonstrated importance of alpha wave (∼10 Hz) processes (7), a body of recent work has identified the importance of brain activity in the gamma and high gamma frequency ranges (25–250 Hz) (8–10) to the synchronization of anatomically distant centers. To date, most successful approaches to the mapping of these frequencies have involved the implantation of electrodes in direct contact with the brain, usually during a surgical procedure. A noninvasive measurement of oscillating currents in the gamma frequency range is thus an important goal.

Unlike optical methods for neuronal current monitoring (11), magnetic resonance is noninvasive and can be applied deep within optically opaque tissue. The fMRI technique is a relaxometry measurement based upon the modulation of water relaxation by oxygenated hemoglobin in regions of neuronal activity [the blood-oxygen-level-dependent (BOLD) effect] (12). The fMRI experiment therefore provides the same level of spatial information as the underlying MR image from which it is derived. However, since the hemodynamic response to neuronal activity occurs over many seconds (13), its interpretation depends on assumptions about its correlation with neuronal activity, a connection that quite often cannot be justified (14). Indeed, recent evidence points to physiological mechanisms by which hemodynamic response is affected by mere anticipation of a stimulus, rather than by the stimulus itself (15).

Magnetoencephalography and EEG provide an alternate means to monitor changes in neuronal activity, but their advantages in temporal resolution are offset by poor spatial localization due to the difficulties in mathematical inversion of exterior field measurements to determine their source (16). Furthermore, as the methods involve measurement on the scalp, the strength of the detectable magnetic fields will be significantly weaker than if their effects are encoded into spins within millimeters of the source, as in MRI. Concurrent MRI and EEG measurements are possible with significant technical effort, although these yield images of neuronal processes with a resolution of only several millimeters per dimension (17). Because of these limitations, there has been a significant effort to develop a method to perform sensitive direct current imaging, with an emphasis on the detection of neuronal currents. These studies have primarily been proof-of-principle demonstrations using artificial systems (6, 18–20) and theoretical examinations of the feasibility of neuronal current detection (20–25). While work is being done to develop a viable and broadly applicable detection modality for in vivo experiments (26–29), a number of studies (30–33) have cast doubt as to the feasibility of a technique based on traditional current-imaging methods.

The most commonly used method for simulating these experiments in vitro relies upon application of a dc or slowly oscillating current during a conventional imaging sequence in a phantom. When the current-induced magnetic field is oriented parallel to the external field, it alters both the phase and the magnitude of nearby spins. Changes to the magnitude reflect a net spread in the phase of spins within an imaging voxel, while a phase change implies a coherent rotation of transverse magnetization. While some authors predict the phase effect to be stronger by up to 2 orders of magnitude (20, 34), it is highly susceptible to cancellation effects due to spatially disordered structures, oscillating signals with a mean phase change of zero, incoherent signals, and location of the current source within a given imaging voxel (18, 20). Other than a few specialized cases offering only a limited frequency range (35) or requiring careful synchronization of the pulse sequence to the current source (36, 37), present applications of this technique cannot easily image oscillating fields with frequencies above ∼10 Hz (38).

As has been shown previously (39), many issues related to cancellation of accumulated phase in phase contrast techniques can be resolved by using a rotating-frame resonant mechanism, termed stimulus-induced resonant saturation (SIRS), to generate current-induced contrast. SIRS builds upon earlier work (38), in which a prepolarized sample is simultaneously placed in an ultralow field (ω_H = 40–4,000 Hz) and an orthogonal magnetic field designed to mimic the oscillating fields of interest. When the current frequency is matched to the proton Larmor frequency, nearby spins undergo a detectable rotation around the orthogonal axis of the current-induced field. For higher sensitivity at low magnetic fields, the dynamics were observed using a superconducting quantum interference device (SQUID). While this method has several advantages, including applicability at low field and compatibility with oscillating zero-mean fields, it requires a SQUID for detection (along with additional prepolarization hardware) and suffers from the sensitivity challenges associated with low-field imaging (40, 41). The SIRS method, by contrast, exploits an analogous rotating-frame resonance condition by matching the power of an applied spin lock field to the frequency of oscillating currents. This method should be applicable at high field and is compatible with conventional clinical MRI hardware. However, in practice, experimental imperfections and nonidealities in biological current sources compromise its robustness.

Here, we demonstrate that, in addition to its advantages over phase and magnitude imaging, current imaging through a resonant mechanism permits spectroscopic control over the contrast mechanism. Spectroscopic control exercised through modulation of the spin-lock fields allows us to compensate for nonidealities in the experimental hardware or the current sources by producing inhomogeneity-compensated and band-selective variants of the experiment, essential for imaging biological sources with multiple constituent frequencies. Next, we introduce a Fourier imaging experiment in which the spatial variation of the magnetic field can be readily measured. Finally, after confirming the limit of detectable field strength to be on the level of synchronized neuronal activity, we perform a remotely detected analogue of the experiment (vide infra), in which we achieve high sensitivity and spatial resolution by using an optimized remote detector of magnetic resonance.

The imaging pulse sequence proceeds as follows (see SI Text for a graphical representation): An initial π/2_x pulse is applied, aligning the magnetization along 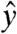, where it is then held via application of a spin lock modulated at the proton Larmor frequency with power B_sl and duration τ_sl. When viewed in the rotating frame, the spin-lock field remains aligned along 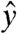, with magnitude B_sl (2.35 μT for ω_sl = -γB_sl = 100 Hz). Simultaneous application of an audio-frequency current will generate an oscillating magnetic field along 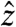. When ω_current ≈ ω_sl, the resonant component of the audio field induces a rotation of M_y around 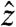. When viewed in a frame of reference rotating both around 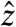at the Larmor frequency and around 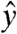at the spin-lock frequency, the situation is analogous to the application of a normal pulse (the current, in our case) to magnetization aligned with a static field (here, the spin lock). After τ_sl, a π/2_-x pulse is applied to store M_y along 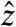, after which a conventional spin-echo imaging sequence is carried out. Resonant rotations of spin magnetization will be initiated by any components of the current-induced field that are orthogonal to the axis of the spin lock. The method will be nearly insensitive for components that are not orthogonal, complicating retrieval of the true field distribution in cases where this is of interest. For the example of a spin lock along 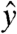, fields along both 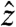and 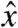will contribute to oscillations in M_y. In order to image the effects of field components along 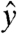, we can simply apply the spin lock along 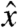. The effects of any remaining transverse magnetization at the start of the imaging sequence are canceled out via a two-step phase cycle of the π/2 and spin-lock pulses.

Results

Resonance Spectra and Images.

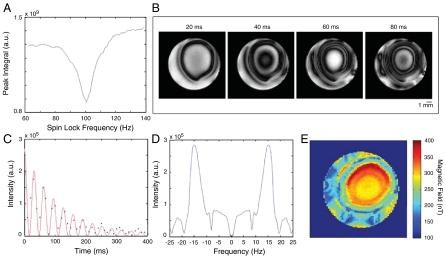
The resonant spin-lock power was determined by arraying the spin-lock power during excitation of the loop by current at a fixed frequency and acquiring a spectrum after the spin-lock period τ_sl. A plot of the integral of these peaks vs. the spin-lock power, shown in Fig. 1A, clearly indicates the point of maximum resonance at 100 Hz and displays ∼10 Hz width at half maximum. Because these spectra contain a signal from the entire sample, the degree of the observed resonant effect will be much weaker than for the voxels nearest to the current source.

Fig. 1.

Data from current-imaging experiments using a single loop phantom. (A) Integrated peak area during a sweep of the spin-lock power across resonance with an audio-frequency magnetic field (τ_sl = 100 ms, ν_current = 100 Hz, and V_current = 800 μV). (B) Two-dimensional images with ν_current = 100 Hz, and V_current = 1.5 mV, at τ_sl = 20, 40, 60, and 80 ms. (C–E) Data from a τ_sl-incremented series of images with ν_current = 100 Hz and V_current = 1.5 mV. The magnitude of a voxel in the center of the current loop is shown in C with an overlaid fit of a cos²-modulated exponential decay that would simulate the projection of the y component of an oscillating transverse magnetization. Fourier transformation of these data (after correcting for the relaxation decay) (D) reveals an average oscillation frequency of ∼12.8 Hz in the center of the loop, corresponding to a field strength of ∼300 nT at this voltage. Plotting the magnetic field given by the average frequency in each voxel yields a map of the field strength throughout the slice (E).

Two-dimensional axial images at 100 Hz were obtained using the modified spin-echo imaging sequence described above and are shown in Fig. 1B. The images exhibit patterns of rotary resonance with a characteristic oscillation frequency that varies spatially throughout the sample. Since only the magnitude of M_y is stored after the spin-lock period, the images shown rely on detection of changes in magnitude rather than phase. Phase-sensitive images can easily be reconstructed if a complementary experiment is performed to store the M_x component.

Next, we collected a series of rotary resonance images as a function of the spin-lock duration, illustrating the oscillatory behavior of the transverse magnetization within each imaging voxel, as shown in Fig. 1C. In Fig. 1D, we applied Fourier analysis to determine the average current frequency driving the oscillation, which allows for direct calculation of current-induced magnetic field strength throughout the sample. In this way, the evolution of M_y may be followed and used to map the audio-frequency magnetic field strength, as shown in Fig. 1E for a current with voltage 1.5 mV. The strength of the field at the center of the loop is calculated to be ∼300 nT (these data were collected well above the sensitivity threshold), and the field map is in good agreement with simulations of the magnetic field density from a current loop (see SI Text). The node-like features near the edge of the sample tube are caused by rf inhomogeneity, as verified by an image of the rf nutation frequencies within the sample. In situations where the current sources are not isotropically distributed, or where multiple frequencies are stimulated by the resonant spin lock, the oscillatory behavior becomes less distinct and the saturation effect manifests itself as a damped exponential decay with a rate constant shorter than the intrinsic T_1ρ.

Spectroscopic Control via Modulated Spin Lock Pulses.

Because the contrast mechanism is under spectroscopic control, several modifications to the spin lock might render the sequence able to selectively excite specific bands of the current spectrum and also make it more robust in the presence of experimental imperfections including rf inhomogeneity. As a test of this idea, we explored several variations on the elementary rotary saturation pulse sequence.

The frequency range over which the resonant mechanism operates to produce detectable changes in the image is a particularly important feature of this experiment, especially with respect to in vivo neuronal activity. The resonant saturation effect remains strong at lower frequencies: Experiments were performed at conditions down to one 200-ms cycle of current oscillating at 5 Hz. However, the very weak spin-lock fields required to meet the resonant condition contribute to increasingly noticeable artifacts due to imperfections in the spin-lock field (42). Fortunately, this effect can be easily corrected through the use of a phase-alternating spin-lock sequence designed to refocus the effects of inhomogeneities in the spin-lock pulse as well as rf inhomogeneities in the B₀ field (42). It is important to note that the simplest of these sequences (π/2_x-τ_sl/2_y-τ_sl/2_-y-π/2_-x) will refocus the accrued phase angle from the resonant rotation as well as the inhomogeneous effects. Insertion of a π_y rotation in the center of the sequence compensates for this effect and, with a 180° change in phase of the storage pulse, provides a spin lock that is insensitive to inhomogeneities in both B₀ and B_sl. Thus, with the use of phase-alternating spin-lock sequences, the resonant method provides consistently strong effects throughout the full range of neuronal activity.

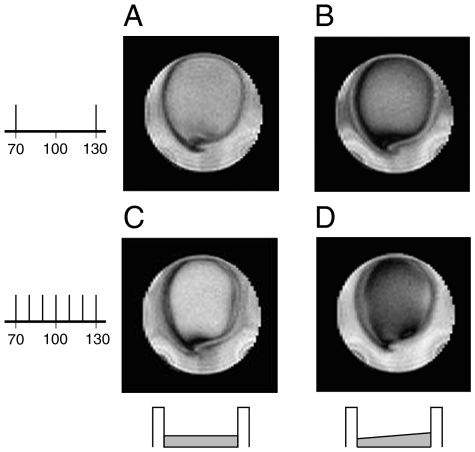
Images using a current excitation spectrum containing several frequencies were also explored in order to approximate the effect of incoherent neuronal currents. The current signal (a sum of sine functions with randomly assigned phase) was comprised of a series of frequencies spanning the resonance condition (but not necessarily containing the resonant frequency). In addition to the typical constant-amplitude spin lock, images were taken with a ramped spin lock in which B_sl is linearly increased from 70% to 130% of the resonant power. As shown in Fig. 2 for a signal containing 70- and 130-Hz frequencies, the addition of the ramped spin lock (Fig. 2B) shows a marked improvement over a spin lock with constant 100-Hz amplitude (Fig. 2A). Fig. 2 C and D show images taken with a signal containing frequencies from 70 to 130 Hz in 10-Hz increments. While the ramped version is dramatically enhanced, it should be noted that a constant resonant spin-lock power still produces substantial resonance effects when multiple frequencies are present within a signal.

Fig. 2.

Two-dimensional images taken with multitone current signals (V_current = 1.5 mV). Two illustrative situations are shown: the top row shows images taken with a current pulse containing 70- and 130-Hz frequencies, both with (A) the standard constant-amplitude spin lock at resonance and with (B) a ramped spin lock that increases from 70% to 130% of the resonant power (τ_sl = 100 ms). The bottom row shows images taken with a current pulse containing frequencies from 70 to 130 Hz, in 10-Hz increments, again (D) with and (C) without a ramped spin lock.

3D Images and Frequency Selectivity.

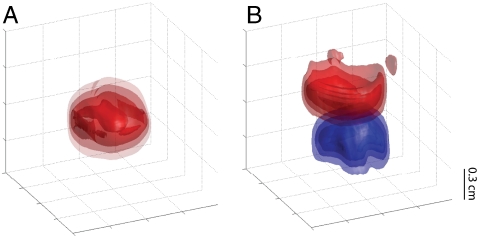
Fig. 3A shows a 3D image of the resonance effect with 500-μV current at 100 Hz in a single loop, with contours denoting the intensity of saturation. Images such as these are an extraordinarily easy way to visualize the full spatial extent of the magnetic field and could easily be combined in a τ_sl-incremented series to form a complete 3D map of the audio-frequency magnetic field strength throughout the sample. A related experiment, shown in Fig. 3B, demonstrates the application of this technique in frequency-selective current imaging. Two loops were axially aligned, each carrying simultaneous current pulses at different frequencies (but equal amplitudes) during the spin-lock interval. By simply adjusting the power of the spin lock to match one of the two frequencies, the rotary resonant effect in each loop may be imaged independently.

Fig. 3.

Three-dimensional images of the saturation effect at V_current = 500 μV. In A, the single-loop phantom is imaged with τ_sl = 50 ms and ν_current = 100 Hz. In the double-loop phantom of B, current (τ_sl = 160 ms) is applied simultaneously in each loop at different frequencies, while the spin-lock power is switched between resonance conditions to selectively image only one loop. The top loop (red) has ν_current = 100 Hz, while the bottom loop (blue) has ν_current = 250 Hz. Contours are shown at 30%, 50%, 70%, and 90% saturation with respect to controls.

Sensitivity.

The limits of detection are determined by the angle of rotation that the y magnetization is able to traverse during the spin-lock period, which is limited by the strength of the current-induced field and the duration of the current burst. Because the spin-lock module ends by projecting the y magnetization, the first point of maximum saturation will occur when the audio-frequency field rotates the spins through an angle of π/2. When very small magnetic fields are being imaged, the correspondingly slow rotation of the transverse magnetization means that relaxation will govern the sensitivity. Thus, samples with long relaxation constants will permit longer spin-lock times (and therefore larger angles of rotation) before the image degrades.

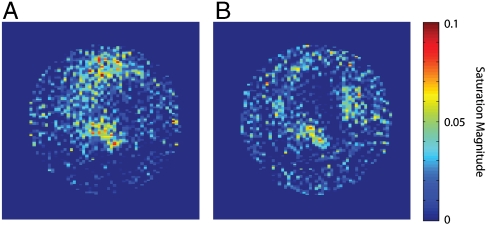
Fig. 4 shows two images with audio-frequency current voltages of (Fig. 4A) 4.74 μV and (Fig. 4B) 2.38 μV using a 160-ms spin lock in a sample of 20% H₂O and 80% D₂O doped with ∼0.5 mM GdCl₃ (T₁ = 463 ms, T_1ρ = 336 ms at 100-Hz spin lock). Comparisons of the average signal (in a region containing noticeable current effects) to the rms noise give signal-to-noise ratios of ∼2.5 and ∼2.0, respectively. The magnetic field generated at the center of the loop in Fig. 4B is calculated to be approximately 0.46 nT, based on the level of attenuation and the field map in Fig. 1E, which agrees well with previous sensitivity characterizations (39).

Fig. 4.

Images of a single loop at very low-driving voltages. The voltage of the audio-frequency currents are approximately (A) 4.74 μV and (B) 2.38 μV, with estimated field strengths at the center of the loop of (A) 0.92 nT and (B) 0.46 nT. Images were taken with ν_current = 100 Hz, τ_sl = 160 ms, and eight averages. Voxel magnitude is displayed as percentage saturation with respect to a control.

Remote Detection.

While we have already demonstrated that this method can detect current distributions of biologically relevant magnitudes, we recognize that the conditions of any in vivo current-imaging experiment would be far less ideal. There, the experiment will be principally limited by nonidealities and incoherence in the signal source as well as low-filling factors, compromising the sensitivity necessary to elucidate neuronal currents with physiologically informative spatial resolution. The former may be mitigated by appropriately compensated spin-lock sequences, as discussed earlier; in order to address the latter problem of detecting very small volumes of resonant spins, we have explored the use of remotely detected MRI (43).

In a remote detection sequence, the encoding and detection portions of the experiment are spatially separated and individually optimized. This approach has been applied to flows in microfluidic systems and porous materials and is now being applied to study biological microvasculature, including in the brain. In the case of a remote current detection experiment, the encoding region contains the oscillating currents of interest, and nuclei flowing through it are subjected to an analogue of the normal phase-encoded, resonant current detection sequence that has been adapted for flow. The magnetization is stored longitudinally and is detected elsewhere in a coil whose filling factor is matched to the voxel size of interest. When the detector is an optimized microsolenoid or surface coil, and the encoding coil is a volume coil or large surface coil, the approach yields a sensitivity enhancement of several orders of magnitude over conventional detection (see ref.–44 for a detailed discussion and examples of the sensitivity enhancement, which we do not treat here).

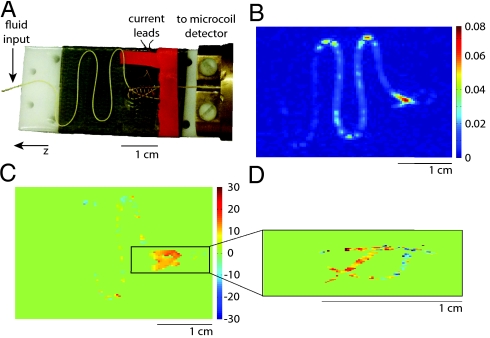
Fig. 5A shows the flow phantom constructed for this experiment. Water flows (at ∼160 μL/ min) through a length of 150-μm i.d. polyether ether ketone (PEEK) tubing fashioned into a planar serpentine structure and secured to a flat support by means of double-sided adhesive film. It then enters a solenoid (∼0.5-cm diameter) used for current encoding, is looped to increase the transit time in the current excitation region and finally travels to a microsolenoid detector of ∼150-nL volume (approximately matched to voxel size). The remote detection sequence consists of excitation into the transverse plane (with optional slice selection), current encoding via a synchronous current burst and resonant spin-lock pulse sequence, velocity-compensated phase encoding along two spatial axes, and, finally, a pulse to store all encoded magnetization along the z axis for transport to the detection coil. Data are acquired from the flowing system by stroboscopic acquisition in the detector microcoil, yielding all encoded information together with a correlated time-of-flight parameter that reflects transit to the coil. Fig. 5B shows a 2D time-of-flight image from a control experiment with no application of current. In Fig. 5C, we show the phase difference (in degrees) between a control and a current-encoding experiment with 1.6-mV current at 400 Hz and τ_sl = 20 ms, which clearly shows detection of resonant phase effects localized to the region of the solenoid (some residual phase remains in the serpentine region due to minor deviations in data between experiments). Furthermore, because the remote detection experiment is optimized when the voxel volume is matched to the detector volume, the image field of view can be narrowed (or alternatively, a smaller slice can be selected) without the dramatic loss in sensitivity associated with the comparable set of directly acquired experiments. Fig. 5D shows a phase contrast experiment in which the coil region has been isolated and “zoomed in” by applying a slice selective pulse and narrowing the field of view. The features of the coil are resolved with far greater clarity at no cost to experiment duration or sensitivity.

Fig. 5.

Remotely detected current-imaging experiments in (A) a serpentine flow phantom. Water flows in 150-μm PEEK tubing laid out in s-shaped curves, travels through a solenoid in which audio-frequency current encoding takes place and then flows into an optimized microsolenoid NMR detector. (B) A single time-of-flight image from a control experiment without current excitation. Images illustrating the phase accrued during current excitation and due to a resonant mechanism, relative to a control, are shown for (C) a nonselective experiment with FOV_y = 2.41 cm and FOV_z = 3.62 cm and for (D) a zoomed-in experiment that isolates a slice containing the coil, giving FOV_y = 0.48 cm and FOV_z = 1.45 cm. Images were taken with ν_current = 400 Hz, τ_sl = 20 ms, and V_current = 1.6 mV. All images have resolution 90 × 90 after zero filling by a factor of 2 and have comparable signal to noise.

Discussion

Our experiments demonstrate the substantial benefits of resonant current imaging as compared to nonresonant alternatives. The difficulties associated with using phase contrast MRI to image oscillating currents at higher frequencies significantly limit the utility of conventional techniques, especially given the likely importance of high gamma activity (60–250 Hz) in brain function. Using the resonant method, low-intensity currents can be detected at any chosen frequency, allowing for frequency-selective imaging across the full spectrum of neuronal activity. In the case of neuronal current imaging, this technique could be applied to independently localize different types of brain activity in a set of experiments. In addition, the resonant method is unaffected by other factors that may diminish or eliminate the conventional phase contrast MRI signal, including the position of the current source within an imaging voxel, and the degree of coherence of the exciting waveform.

Sensitivity has been a primary focus in the development of current-imaging techniques, largely due to the emphasis on pushing the method toward the regime of neuronal currents. Estimates of the magnetic field from synchronized neuronal activity range from the pT scale (25) to 0.1–1 nT (6). While the authors of the former estimate acknowledge that the corresponding simulations were performed at a neuronal density several factors less than is realistic, it is certainly clear that sub-nT sensitivity is necessary for direct neuronal current imaging to become viable. To assess whether or not our method is a realistic candidate, we note that the T₁ of water in gray matter ranges from approximately 1–1.8 s (depending on the external field) (45), while the T_1ρ for gray matter at 1.5 T is approximately 100 ms with a 500-Hz spin-lock field (46). Thus, it is the latter factor that provides the primary limitation on the angle of rotation that may be accrued in the transverse plane without allowing unacceptable signal degradation. The experiments described above demonstrate sub-nT sensitivity for a current burst of 160 ms, although additional images taken with τ_sl comparable to T_1ρ yield very acceptable images. While a slight reduction in sensitivity would be expected with a decrease in τ_sl, it could be more than compensated by additional averaging or further optimization of the instrumentation. However, to fully investigate the bounds of sensitivity, further care with instrumentation and coil design would need to be taken in order to generate a clean signal at extremely low voltages and also to eliminate the effects of rf inhomogeneity throughout the sample.

The resonant mechanism proved to be very effective even when using one current cycle at 5 Hz, provided that a phase-alternating spin lock is implemented to compensate for rf inhomogeneities in B₀ and B_sl. Frequencies below 5 Hz may begin to pose some difficulty, as they require increasingly long spin-lock durations for meaningful oscillatory behavior to take place. However, with regard to biological applications, the entire frequency range of neuronal activity fits comfortably inside the range of our method and may easily be probed via resonant current imaging. Furthermore, currents with multiple constituent frequencies do not preclude application of the technique, allowing robust current imaging suited to a wide range of possible signals.

In addition to the obvious applications in the development of neuronal current imaging, the resonant technique could easily be applied to selectively map other current distributions with high resolution in vivo. Current-imaging techniques would be invaluable in the calibration of imprecise medical procedures such as defibrillation, electroconvulsive shock therapy, and deep brain stimulation, and the flexibility, sensitivity, and control of the resonant spin-lock technique would add a great deal to the existing work in this area (3–5, 47), especially with regard to rapidly oscillating fields and samples containing multiple or incoherent frequencies.

Finally, we demonstrate the application of our technique to a remote detection experiment, in which we are able to detect significant phase contrast within very small volumes of flowing liquid. By separating the encoding and detection steps of the MRI experiment, remote detection allows the separate optimization of each. We are thus able to overcome filling factor, magnetic susceptibility, and other limitations to achieve high spatial and temporal resolution without sacrificing sensitivity. In this way, we can easily acquire high-resolution images that display features of the phase distribution that may otherwise be compromised by spatial averaging when viewed at lower resolutions.

We are presently adapting remote detection to the imaging of microvasculature in vivo, an idea that is also well suited to neuronal current detection. In this case, functionally relevant volumes of current-encoded blood must reach the detector before spin relaxation erases the encoding. Assuming that the encoded volume is the brain and that the detected volume is a segment of the jugular, typical physiological parameters and blood flow rates suggest that a remote experiment is within reach. As with any experiment involving flow, the resolution will be limited by the incoherent motion of the spins during the encoding time, arising from effects such as diffusion during the spin-lock period. Spin motion during the image encoding is more easily ameliorated: Rapid imaging sequences such as echo-planar imaging can dramatically shorten acquisition times, and a number of techniques including breath hold, cardiac synchronization, and motion compensation are routinely applied under similar circumstances.

Materials and Methods

Detailed methods appear in SI Text.

Apparatus.

All spectra were acquired on commercial 300-MHz imaging spectrometers produced by Varian or Bruker. Current-imaging phantoms consisted of 28-gauge insulated wire immersed in a solution of deionized water (diluted to 20% in D₂O and paramagnetically doped to decrease relaxation times) within a 10-mm glass NMR tube. The wire loops in both single- and double-loop phantoms had ∼6.5-mm diameter and were oriented perpendicular to B₀ in order to create magnetization along 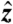. In the double-loop phantom, the two loops were positioned coaxially along 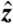with ∼6.5-mm vertical spacing. Current was generated by isolated and calibrated current sources.

Imaging.

Two-dimensional images in the plane of the loops and 3D images were obtained in ∼1–1.5 min and ∼40 min per experiment, respectively, and used a spin-echo imaging sequence with resolutions of 128 × 64 and 128 × 64 × 32 and a field of view (FOV) of 12 mm in each dimension. The spin-echo imaging sequence was chosen to minimize artifacts from the copper loop, although a gradient echo version also generates satisfactory images at resonance and would be a suitable choice in biological samples and when factors such as experiment duration or power deposition are a matter of concern.

Remote Detection.

Water flowed through a microcapillary phantom driven by a regulated constant pressure source (see SI Text). Excitation, spin lock, and storage pulses were performed with a 40-mm Varian volume imaging probe, while gradients were applied using a Varian triple-axis gradient system producing up to 100 G/cm on all three axes. The detection probe was a custom-built microcoil probe connected to the capillary tubing via commercially available connectors.