Body temperatures of modern and extinct vertebrates from ¹³C-¹⁸O bond abundances in bioapatite

Abstract

The stable isotope compositions of biologically precipitated apatite in bone, teeth, and scales are widely used to obtain information on the diet, behavior, and physiology of extinct organisms and to reconstruct past climate. Here we report the application of a new type of geochemical measurement to bioapatite, a “clumped-isotope” paleothermometer, based on the thermodynamically driven preference for ¹³C and ¹⁸O to bond with each other within carbonate ions in the bioapatite crystal lattice. This effect is dependent on temperature but, unlike conventional stable isotope paleothermometers, is independent from the isotopic composition of water from which the mineral formed. We show that the abundance of ¹³C-¹⁸O bonds in the carbonate component of tooth bioapatite from modern specimens decreases with increasing body temperature of the animal, following a relationship between isotope “clumping” and temperature that is statistically indistinguishable from inorganic calcite. This result is in agreement with a theoretical model of isotopic ordering in carbonate ion groups in apatite and calcite. This thermometer constrains body temperatures of bioapatite-producing organisms with an accuracy of 1–2 °C. Analyses of fossilized tooth enamel of both Pleistocene and Miocene age yielded temperatures within error of those derived from similar modern taxa. Clumped-isotope analysis of bioapatite represents a new approach in the study of the thermophysiology of extinct species, allowing the first direct measurement of their body temperatures. It will also open new avenues in the study of paleoclimate, as the measurement of clumped isotopes in phosphorites and fossils has the potential to reconstruct environmental temperatures.

The mechanisms by which animals regulate their body temperatures are among the most fundamental aspects of their biology. The acquisition of endothermy, the ability to maintain high and stable body temperatures through internal heat production, is a major physiological change that occurred at an unknown stage during the evolutionary transition to mammals and birds from their ancestors among the nonmammalian therapsids and nonavian dinosaurs, respectively (1). Approaches to understanding the physiology of extinct animals and the evolution of endothermy have largely focused on biophysical modeling, anatomical observations, growth rate analysis from bone histology, and behavioral studies such as estimating predator/prey ratios (1–7). The validity of each of these approaches is uncertain (for contrasting viewpoints on approaches to dinosaur thermoregulation see refs. 4 and 5).

Modern endothermic mammals and ectotherms, such as alligators and crocodiles, generally have significant differences in average body temperatures. With rare exceptions, mammals have high and stable body temperatures around 36–38 °C regardless of their environment, whereas the body temperatures of ectotherms are generally lower on average and often fluctuate depending on environmental temperatures (1). While not a completely unambiguous indicator of physiology, the ability to measure the body temperature of extinct vertebrates would provide crucial information in tracing the evolution of thermoregulation. However it has been widely assumed that it would not be possible to make a direct measurement of the body temperatures of extinct organisms (2, 8).

An indirect geochemical approach to reconstructing temperature is based on the oxygen isotope composition (δ¹⁸O) of minerals such as calcite, aragonite, and apatite (9–12). However, the δ¹⁸O values of these minerals depend on both growth temperature and the δ¹⁸O of the water from which the mineral formed. Because waters are rarely preserved in the geologic record, it is generally necessary to assume a value for the δ¹⁸O of water in order to draw conclusions regarding biomineral growth temperatures.

The oxygen isotope composition (δ¹⁸O) of the phosphate and carbonate component of bioapatite in bone, teeth, and scales reflects both the body temperature of the animal and the oxygen isotope composition of its body fluids (13–19). The δ¹⁸O of body waters, and hence bioapatite, can be influenced by local meteoric water compositions (14, 15, 19, 20), humidity (20–23), diet (24, 25), and physiology of the animal (19, 20, 24, 25). The complex factors influencing body water δ¹⁸O mean that it is difficult to make robust assumptions regarding the body water δ¹⁸O of an extinct species. Attempts have been made to address thermoregulation in extinct species with the oxygen isotope thermometer. However, these studies are to some extent ambiguous due to the requirement for assumptions regarding body water δ¹⁸O (26–28) and the preservation of primary oxygen isotope compositions when fossil bone was analyzed (29, 30).

Here we describe the application of a previously undescribed approach to bioapatite—the carbonate “clumped-isotope” thermometer—that holds promise for overcoming some of the drawbacks of oxygen isotope paleothermometry and providing a relatively assumption-free measurement of body temperatures of extinct species. Clumped-isotope thermometry relies on the propensity of ¹³C and ¹⁸O to form bonds, or “clump,” with each other in a carbonate molecule. This effect is independent of bulk isotopic compositions but is dependent on temperature (31–33). The abundance of ¹³C-¹⁸O bonds in carbonate can be determined from the abundance of mass 47 CO₂ produced on phosphoric acid digestion of carbonate-containing minerals. The relationship between temperature and ¹³C-¹⁸O bond abundance is defined by the deviation of the measured abundance of mass 47 CO₂ compared to the abundance of mass 47 CO₂ expected for a random distribution of isotopes and is given the notation Δ₄₇ (34). As δ¹³C and δ¹⁸O are simultaneously determined, this approach also allows an assumption-free calculation of the δ¹⁸O of the water from which the mineral formed. Carbonate clumped-isotope thermometry has been applied to a number of materials and questions, including using soil carbonates to examine the uplift history of the Altiplano (35), brachiopods to examine Phanerozoic marine temperatures (36), and speleothems to examine glacial-interglacial terrestrial climate change (37)

Results and Discussion

Clumped-Isotope Analysis of Modern Bioapatite.

Ghosh et al. (31) derived the following relationship between the Δ₄₇ value of CO₂ extracted from inorganic calcite grown at temperatures ranging from 0–50 °C, on reaction with phosphoric acid at 25 °C:

[1]

In order to assess the relationship between growth temperature and the Δ₄₇ value of CO₂ extracted from bioapatite, we made measurements on a range of modern vertebrate species whose physiologies are well constrained (Table 1).

Table 1.

Δ₄₇ measurements from tooth bioapatite of modern species

Species	n *	Δ47	Estimated Body Temperature (°C) †	Δ47 Temperature (°C) ‡
White Rhinoceros (Ceratotherium simum)	6	0.597 ± 0.006	37	36.6 ± 1.4
Indian Elephant (Elephas maximus indicus)	4	0.596 ± 0.008	37	36.9 ± 2.0
Nile Crocodile (Crocodylus niloticus)	7	0.638 ± 0.006	28 ± 3	26.9 ± 1.4
American Alligator (Alligator mississippiensis)	3	0.639 ± 0.011	28 ± 3	26.7 ± 2.5
Sand Tiger Shark (Carcharias taurus)	5	0.641 ± 0.013	25.3	26.2 ± 3.0
Sand Tiger Shark (Carcharias taurus)	3	0.654 ± 0.010	23.6	23.1 ± 2.3

± Uncertainty in Δ₄₇ values represent the external precision of the measurement (one standard error). Uncertainty in Δ₄₇ body temperature values represent the error in body temperatures in °C propagated from the external precision of the Δ₄₇ measurement (one standard error).

^*Number of distinct extractions of CO₂ from bioapatite analyzed for each species. Between 1–5 teeth for each species were analyzed. Data for individual extractions is shown in Table S1.

^†Estimated from published body temperature measurements (see main text for details). In the case of sand tiger sharks the two samples were from two different aquariums with different ambient water temperatures.

^‡Calculated assuming Δ₄₇ values in bioapatite exhibit the same temperature dependency as inorganic calcite, given in Eq. 1.

Samples of tooth enamel from a single tooth from a modern Indian elephant (Elephas maximus indicus) and a single tooth from a modern white rhinoceros (Ceratotherium simum) were analyzed from six and four separate CO₂ extractions, respectively. The published calibration of the carbonate clumped-isotope thermometer for inorganic calcite predicts a Δ₄₇ value of 0.596‰ for calcite grown at 37 °C (31), which is the average body temperature of almost all placental mammals (31, 38). Analysis of rhinoceros and elephant tooth enamel bioapatite yielded Δ₄₇ values of 0.597 ± 0.006‰ (1 s.e.) and 0.596 ± 0.008‰, respectively (Table 1). Therefore Δ₄₇ measurements from mammal bioapatite are indistinguishable from values of inorganic calcite grown at equilibrium at the same temperature. See Methods for more details on error estimation.

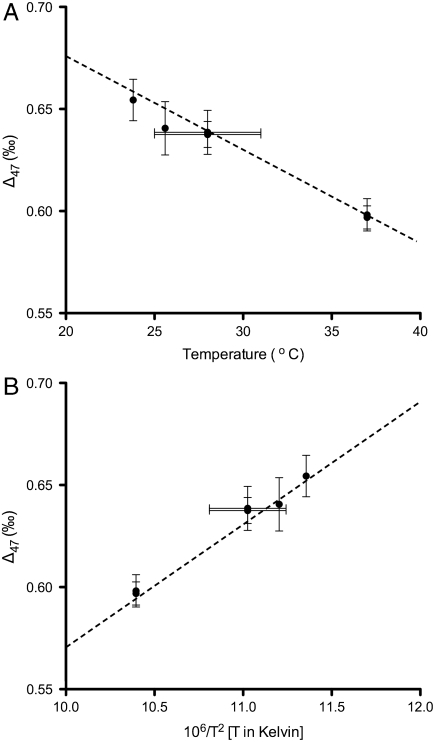
In order to evaluate the temperature sensitivity of the carbonate clumped-isotope thermometer in bioapatite we also analyzed specimens from “cold-blooded” (ectothermic) vertebrates (Table 1 and Fig. 1), specifically teeth from modern Nile crocodiles (Crocodylus niloticus) from Egypt and modern American alligators (Alligator mississippiensis) from a farm in Colorado. Enamel/dentin mixtures from ectotherm teeth were analyzed because their enamel is very thin. The body temperatures of these species are known to fluctuate daily by 8–12 °C, and by as much as 20 °C during the course of a year (6, 39, 40). Therefore there is some uncertainty over exactly what body temperatures biomineralization occurs at in these species. Both Nile crocodiles and American alligators have been observed to reduce growth (i.e., to grow at low rates or not grow at all) in the cold season months, which has been attributed to a reduction in food intake and in some instances, hibernation (41, 42). Based on published studies on alligator and crocodile thermoregulation we estimated an average spring-to-autumn body temperature of 28 °C for a medium sized adult, with an uncertainty of ± 3 °C (6, 39, 40). The low temperature points on our calibration were from the analysis of enamel/dentin mixtures from Sand Tiger shark (Carcharias taurus) teeth that were kept at distinct and stable water temperatures of 25.3 °C and 23.6 °C in two separate aquariums. Shark body temperatures were assumed to reflect ambient water temperatures (43). Individual stable isotope measurements used to calculate the average results presented in Table 1 and Fig. 1 are given in SI Text.

Fig. 1.

The relationship between measured Δ₄₇ values from bioapatite and the body temperature of the organism. The Y-value for each data point represents the mean Δ₄₇ value derived from 3–7 measurements of distinct extractions of CO₂ from tooth bioapatite. Y-axis error bars represent the external precision of the measurement, to one standard error. The X-axis scale shows the predicted body temperature of each species, based on previous studies on their thermoregulation, as described in detail in the main text. X-axis error bars represent uncertainties in body temperatures. (A) Δ₄₇ data plotted against temperature, reported in °C. (B) The same data plotted as 10⁶/T² [T in Kelvin]. The inorganic calcite calibration derived by Ghosh et al. is plotted as a dotted line (31). Δ₄₇ measurements of CO₂ extracted from bioapatite all fall within one standard error of the inorganic calcite line.

All bioapatite data are within one standard error of the inorganic calcite calibration line (Fig. 1 and Eq. 1) of Ghosh et al. (31). Eq. 1 represents a line of best fit through the Δ₄₇ values for inorganic calcite and uses arithmetic means calculated from data for multiple extractions (31). Huntington et al. (44) performed a weighted least squares linear regression on inorganic calcite calibration data from Ghosh et al. (31) to take into account both the error in each measurement and the uncertainty in the absolute growth temperature of each synthetic calcite. This regression was carried out using the weighted mean Δ₄₇ value for each sample. The algorithm of York was used for this analysis (45). This analysis yielded the following relationship:

[2]

We carried out the same regression analysis for the inorganic calcite data from Ghosh et al. (31) using arithmetic means, which results in:

[3]

We also applied this regression model to arithmetic mean values for the bioapatite data using taxon mean Δ₄₇ values (Fig. 1 and Table 1) and get the following result:

[4]

A Student’s T-test shows that the slope and intercept of the calcite and apatite calibrations (Eqs 3 and 4) are statistically indistinguishable from each other (for the slope, p = 0.8962; for the intercept, p = 0.8886). For the population of modern apatite samples (n = 6), the root mean square error (RMSE) of the residuals (between Δ₄₇ values predicted from the inorganic calcite calibration and measured Δ₄₇ of CO₂ extracted from apatite) is 0.004‰. The RSME is a standard measure of how close a fitted line is to data points (i.e., the goodness of fit) and reports the average distance (measured along a vertical line) between each data point from the regression. It is interpretable in measurement units; in this case, the RMSE is less than the external precision of Δ₄₇ measurements in the bioapatite calibration (1 s.e.; see Methods for a more detailed description of the treatment of errors).

In theoretical models, it has been shown that in a variety of carbonate minerals (calcite, aragonite, dolomite, magnesite, witherite, and nahcolite) the crystal structure and the identity of the cation has only a modest influence of the abundance of ¹³C-¹⁸O bonds (32). Shark tooth enameloid mainly consists of fluorapatite, rather than hydroxyapatite that predominates in mammalian teeth (46). Because measurements on both types of apatite are within one standard error of the inorganic calcite calibration lines (Fig. 1), this further reinforces the conclusion that mineral structure and composition only have a minor influence on the abundance of ¹³C-¹⁸O bonds in the carbonate component. It also suggests that the isotopic fractionation associated with phosphoric acid digestion of apatite must be similar to that of calcite (47).

These data are consistent with the hypothesis that the ordering of ¹³C-¹⁸O bonds in carbonate minerals records the state of ordering of bonds in the dissolved inorganic carbon (DIC) pool (i.e., 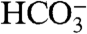and 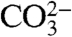ions) from which bioapatite grows, which are in isotopic equilibrium with body water (48–50). Studies of other calcifying organisms also support this hypothesis; for example, it has been shown that Δ₄₇ measurements of both calcitic and aragonitic foraminifera and corals are at equilibrium, whereas both are well known to show nonequilibrium δ¹⁸O and δ¹³C values (31, 49, 50).

Thermodynamic Model of Clumped-Isotope Equilibrium in Apatite.

We further investigated the relationship between growth temperature and the Δ₄₇ values of CO₂ extracted from bioapatite by creating a theoretical thermodynamic model describing the equilibrium constant for isotopic order–disorder reactions in carbonate ion units in crystalline apatite. This model is based on “B-type” carbonate substitution into apatite—where a 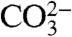group replaces one 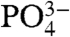group in each unit cell. B-type substitution is thought to be the dominant mechanism for incorporating carbonate into the apatite structure (51). This model is based on first-principles descriptions of force constants on bonds within carbonate-apatite and a statistical-thermodynamic treatment of equilibrium constants for relevant isotope exchange reactions. Fluorapatite is chosen because it has a simpler unit cell than hydroxylapatite, facilitating density-functional theory calculations. Further details of the model are given in SI Text.

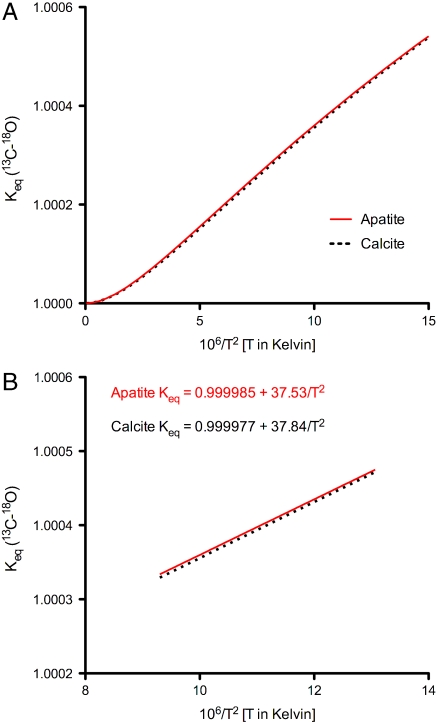
Calculated ¹³C-¹⁸O clumping equilibria (K_eq) are shown in Fig. 2. Results for a calcite model constructed with the same pseudopotentials and energy cutoff parameters are also given. See Schauble et al. (32) for a more general treatment of such models in solid carbonates. The positionally averaged K_eq of B-type carbonate-substituted fluorapatite is remarkably similar to the analogous calcite model as well as to a previously described calcite model created with different software and pseudopotentials (29). Differences among the three models are equivalent to 1–2 °C at a given Δ₄₇ value of CO₂. Thus, barring systematic differences in Δ₄₇ arising from variations in the acid-digestion fractionation (47), these models predict that the carbonate clumped-isotope thermometer for carbonate apatite should be nearly indistinguishable from that for calcite. We consider this to be a relatively simplified and preliminary theoretical calculation because it will be necessary to construct models that permit various alternative substitutions in both fluorapatite and hydroxylapatite. Nevertheless, this model result provides a context for understanding our empirical observation that the calcite and apatite calibrations are indistinguishable.

Fig. 2.

A shows the results of first-principles theoretical calculations of the equilibrium constant for the ¹³C-¹⁸O “clumping” equilibria, plotted versus temperature, for carbonate-bearing apatite (solid red line), and calcite (dotted black line). In B the X-axis is 10⁶/T² [T in Kelvin] over the relevant biological temperature range (276–328 K). The modeled K_eq of apatite and calcite are almost identical.

Considering both the empirical and theoretical results, we can draw two inferences. Firstly, as both the model and data show that K_eq and measured Δ₄₇ values in apatite and calcite are indistinguishable, this suggests that the acid-digestion fractionation factors for apatite and calcite (α_CO2-apatite and (α_CO2-calcite) are also indistinguishable within the error of our Δ₄₇ measurements. Secondly, as the theoretical values of K_eq for the reactions governing ¹³C-¹⁸O bond abundance in calcite and apatite are almost identical, our data cannot prove the hypothesis that clumping is set in the DIC pool, although it is consistent with it.

Measuring the Body Temperatures of Extinct Species.

In order the test the ability of clumped-isotope thermometry to measure the body temperature of an extinct organism from fossilized bioapatite, we made measurements from woolly mammoth (Mammuthus primigenius) teeth from the Late Pleistocene. The teeth examined were derived from two sites (SI Text): the upper Rhine River valley, where specimens were recovered by dredging gravel pits proximal to the Rhine River (52, 53); and the southern North Sea, where specimens were obtained by dredging with ground reaching fishing nets (54, 55). One specimen from each site was selected for analysis because they were exposed to different burial environments and diagenetic fluids (freshwater and seawater). These samples are described in more detail in a previous study (56), where the oxygen isotope composition of phosphate (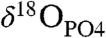), the nitrogen content, and rare earth element (REE) composition were examined. Both 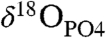and REE content suggested a degree of diagenic alteration in the dentin component of the teeth but not in the enamel component (56).

Measurements of Δ₄₇ in enamel from both localities were within one standard error of the measured value for a modern Indian elephant and also within error of the predicted Δ₄₇ of inorganic calcite grown at 37 °C (Table 2). Combining the measurements on mammoth enamel from both sites yielded a Δ₄₇ value of 0.590 ± 0.007‰ (1 s.e; Table 2). Solving Eq. 1 with this value yields a body temperature of 38.4 ± 1.8 °C for Mammuthus primigenius, an expected number based on their similarity to modern large mammals such as elephants (38).

Table 2.

Δ₄₇ measurements from fossil mammoth tooth bioapatite

Sample	Locality	n *	Δ47	Δ47 Temperature (°C)
Enamel	Rhine River	4	0.587 ± 0.011	39.1 ± 2.8
Dentin	Rhine River	3	0.643 ± 0.027	25.6 ± 6.3
Enamel	North Sea	2	0.596 ± 0.006	36.8 ± 1.3
Dentin	North Sea	2	0.620 ± 0.001	30.9 ± 0.3
Enamel	Average from both sites	6	0.590 ± 0.007	38.4 ± 1.8

± Uncertainty in Δ₄₇ values represent the external precision of the measurement (one standard error if more than two analyses were made; if fewer were made, then the standard deviation is shown). Uncertainty in Δ₄₇ body temperature values represent the error in body temperatures in °C propagated from the external precision of the Δ₄₇ measurement (one standard error).

^*Number of distinct extractions of CO₂ made from bioapatite of each species. Data for individual extractions is shown in Table S2.

In contrast, the dentin component of teeth from both sites yielded lower temperatures of 25.6 °C and 30.9 °C from the Rhine River and North Sea specimens respectively. These temperatures are unlikely to equal the temperatures of the diagenetic fluids that each specimen was exposed to but is consistent with partial recrystallization at lower temperatures. These data are consistent with widespread evidence that organic-rich dentin, which contains smaller apatite crystals, is more susceptible to diagenetic alteration than the large and closely packed apatite crystals found in (relatively organic-poor) enamel (17, 56, 57). None of the fossil material analyzed here showed significant alteration in X-ray diffraction peak shape, which is sometimes used as an indicator of recrystalization (58; Fig. S2).

To assess the utility of clumped-isotope thermometry in accurate determination of body temperatures for much older fossil material, we analyzed enamel from extinct Miocene rhinocerotid and alligator species. Specimens are from the Agricola Road Site in Polk County, Florida. The age of the deposit is late middle Miocene, ca. 12 Ma, based on a biochronologic assessment of the diverse assemblage of equids (59, 60). Measurements from Miocene rhinoceroses and alligators were within error of modern mammals and alligators, respectively (Table 3). A 6 °C difference between endotherm and ectotherm body temperature was resolved. Therefore clumped-isotope thermometry has the potential to accurately reconstruct body temperatures and resolve different thermophysiologies from fossil teeth of at least Miocene age.

Table 3.

Δ₄₇ measurements from Miocene mammal and ectotherm tooth bioapatite

Species	N *	Δ47	Δ47 Body Temperature (°C) †
Rhinocerotidae Acquisitions from 2 teeth	6	0.597 ± 0.005	36.6 ± 1.3
Alligator sp. Acquisitions from 5 teeth	2	0.623 ± 0.017	30.4 ± 3.9

± Δ₄₇, ± values represent the external precision of the measurement (one standard error if more than two analyses were made; if fewer were made, then the standard deviation is shown). Body temperature ± values represent the error in body temperatures in °C calculated by propagating the uncertainty in Δ₄₇.

^*Number of distinct extractions of CO₂ made on bioapatite of each taxon. In the case of the rhinocerotid specimens, three extractions were made of each tooth. In the case of the Alligator sp. one extraction was made on powder from two teeth, and a second extraction on three teeth. Material from multiple alligator teeth was pooled as a necessity to gain enough enamel for analysis. Data for individual extractions is given in Table S3.

^†Calculated assuming Δ₄₇ values in bioapatite show the same temperature dependency as inorganic calcite, given in Eq. 1

Conclusions

Previous attempts to address the body temperatures of extinct species using stable isotope geochemistry have been limited by the assumptions necessary to apply the traditional oxygen isotope thermometer (23, 25). Here we have shown that by analyzing ¹³C-¹⁸O bonds in the carbonate component of bioapatite it is possible to make robust and relatively assumption-free measurements of the body temperatures of extinct species using enamel from teeth that are millions of years old. An external precision of 0.005–0.010‰ was routinely achievable in this study, showing that it should be possible to reconstruct body temperatures from fossil teeth with an error of 1–2 °C. Application of this technique to well-preserved bioapatite from more ancient extinct species (e.g., nonavian dinosaurs) offers a previously undescribed approach to study the evolution of thermoregulation. The clumped-isotope analysis of the carbonate component of phosphate minerals also has considerable potential in other areas. Oxygen isotope analysis of calcium-phosphate biomineralizing organisms such as conodonts, fish, and brachiopods are widely used in paleoclimate studies, particularly in the study of pre-Cenozoic environments. Even in materials that are subject to rapid alteration, such as bone, the isotopic composition of bioapatite may yield information on climate change by recording an early diagenetic environmental signal (61). In addition, phosphorite (carbonate fluorapatite) is found both in modern sediments and sedimentary rocks dating back to the Pre-Cambrian, and phosphorite geochemistry is widely used to obtain information on ancient marine environments (62). Therefore this study also provides a basis for the application of clumped-isotope thermometry on carbonate-containing apatite to paleoclimate questions.

Methods

Sample Preparation.

Bioapatite is commonly intimately intergrown with organic matter that is a potential source of contamination to mass-47 CO₂ measurements. In order to probe the necessity of oxidative cleaning to remove organic material from apatites, a series of tests were run on samples of rhinoceros enamel. Powdered samples were either untreated or treated with aqueous solutions of 3% H₂O₂ for 15 min, 4 h, or 24 h. All treatments yielded Δ₄₇ measurements that were within two standard errors of the expected value for inorganic calcite grown at 37 °C (the body temperature of a rhinoceros), except for the untreated sample (SI Text). Because we anticipated many samples could contain higher levels of organic matter than the enamel samples used as a test, we utilized a midrange cleaning condition in all further analyses (4 h in 3% H₂O₂). It is also common to treat fossil bioapatite samples with an acid wash to achieve selective dissolution of labile and diagenetic carbonates but not carbonate ion that is a structural component of bioapatite (58). We subjected modern elephant and Rhine River mammoth enamel and dentin to a second treatment step of 0.1 M acetic acid, buffered to pH 2.8 or pH 4.6 (SI Text). The Δ₄₇ of mammoth dentin was much more susceptible to acid treatment than other materials, a probable indication of the presence of diagenetic carbonates (SI Text). Because treatments of 4 h and 24 h in pH 4.6 buffered 0.1 M acetic acid gave values within one standard error of each other, these treatments were compiled together in the construction of Table 2 (SI Text). The modern bioapatite calibration samples were treated for 4 h in 3% H₂O₂ but not subjected to an acid wash.

Phosphoric Acid Digestion and Mass Spectrometry.

CO₂ analyte was obtained by reacting bioapatite samples in H₃PO₄ on a custom-built automated online vacuum system that is described elsewhere (Passey et al., manuscript in preparation) adapted with a large reaction vessel to allow complete acid digestion of large bioapatite samples. Because carbonate is a minor (2–10%) component of bioapatite it was necessary to react 100–200 mg of each sample to liberate enough CO₂ for analysis. Reactions were carried out at 90 °C for 20 min, and CO₂ was immediately trapped on liquid nitrogen as it evolved. Each sample was then subjected to cryogenic purification in dry ice/ethanol and liquid nitrogen traps and purification on a gas chromatograph to remove hydrocarbon contaminants according to the scheme outlined in Ghosh et al. (31). CO₂ was also passed through an Ag adsorbent to remove any sulfur gas contamination. Sample gases were analyzed for masses 44–49 on a Thermo-Finnigan MAT 253 gas source isotope ratio mass spectrometer for 8 acquisitions of 10 cycles, each with an integration time of 8 s and a total analysis time of approximately 3 h. Measurements were made with a stable 16-volt signal at mass 44, with peak centering, background measurement, and pressure-balancing before each acquisition. Detailed descriptions on the methods involved in making precise and accurate clumped-isotope measurements are given elsewhere (44).

Standardization.

The majority of data for this study was collected between December 2008 and May 2009. Analyses of Miocene samples were conducted from January 3 to 7, 2010. Each day, gases that had been heated to 1,000 °C and quenched were analyzed to define the stochastic distribution of isotopologues (34). Carbonate standards were run every 4–6 analyses. Seven distinct extractions of NBS-19 reference standard during this period yielded a mean Δ₄₇ value of 0.361 ± 0.008‰, δ¹³C of 1.94 ± 0.04‰ (PDB), and a δ¹⁸O of -2.2 ± 0.05‰ (PDB). Seven separate extractions of a vein calcite, termed 102-GC-AZ01, yielded a Δ₄₇ of 0.646 ± 0.009‰, δ¹³C of 0.62 ± 0.06‰ (PDB), and δ¹⁸O of -13.76 ± 0.05‰ (PDB). Accepted Δ₄₇ values for these standards from > 40 analyses by multiple analysts in our laboratory are 0.352‰ and 0.657‰ for NBS-19 and 102-GC-AZ01 respectively.

Treatment of Errors.

The error in Δ₄₇ of CO₂ extracted once (‘n = 1’) from a bioapatite sample ranged from 0.006 to 0.017‰ and averaged 0.010‰. This uncertainty is calculated as one standard error of the mean Δ₄₇ value determined from eight acquisitions of the same gas. The external precision for modern bioapatite samples that were analyzed multiple times (n > 1) ranged from 0.006 to 0.013‰ and averaged 0.009 ‰. For n≥3, this uncertainty is calculated as one standard error of the mean Δ₄₇ value determined from multiple CO₂ samples extracted from separate aliquots of the same material, with each extraction analyzed for eight acquisitions. For n = 2, the standard deviation is reported. Huntington et al., (2009) present a more detailed description of methods and limitations of clumped-isotope thermometry (44).

For the results presented in this section, the external precision of the data is reported. The internal precision of individual stable isotope measurements is presented in SI tables. In some cases, measurements were excluded due to known or suspected errors in sample preparation and analysis. For example, in some cases incomplete acid digestions of apatite samples was observed, or too little CO₂ was derived from acid digestion to allow for stable gas pressures (i.e., 8 acquisitions at a mass 44 signal of 16 V).