Abstract
We study the calcium-induced vesicle release into the synaptic cleft using a deterministic algorithm and MCell, a Monte Carlo algorithm that tracks individual molecules. We compare the average vesicle release probability obtained using both algorithms and investigate the effect of the three main sources of noise: diffusion, sensor kinetics and fluctuations from the voltage-dependent calcium channels (VDCCs). We find that the stochastic opening kinetics of the VDCCs are the main contributors to differences in the release probability. Our results show that the deterministic calculations lead to reliable results, with an error of less than 20%, when the sensor is located at least 50 nm from the VDCCs, corresponding to microdomain signaling. For smaller distances, i.e. nanodomain signaling, the error becomes larger and a stochastic algorithm is necessary.
1. Introduction
The role of stochasticity in biological processes has been the subject of increasing interest. In particular, fluctuations arising due to a limited number of signaling molecules in subcellular pathways have been recognized as important sources of noise [1–8]. These fluctuations can have a profound effect on the dynamics of the pathway and can determine the final outcome of the signaling cascade. Importantly, these fluctuations prohibit the use of deterministic, mean-field approaches to model these pathways. Instead, fluctuations arising from the small number of signaling molecules and the stochasticity of binding and reaction kinetics need to be taken into account.
A number of algorithms have been developed to deal with stochastic pathways. Some of these subdivide the computational space into small regions within which the concentration is assumed to be well mixed [9] while others model the Brownian motion of individual molecules [10]. An example of the latter, MCell, incorporates complex geometries, channel kinetics and molecule–molecule interactions [11] and has been used to study a number of biophysical problems including the characterization of fluctuations in receptor–ligand binding [7, 8, 12], the signaling in neurons [13, 14] and the Min pathway in bacterial division [15].
Even though these programs have been optimized, it is clear that for most problems a deterministic approach is computationally more efficient and easier to implement. Thus, it is worthwhile to determine in which cases a deterministic analysis is not sufficient and a stochastic study is needed. Such an analysis has been carried out recently for the calcium-induced calcium release in the dyadic cleft of cardiac cells using a custom-made random walk algorithm [16]. This study, however, described the ryanodine receptor as having a single binding site with linear kinetics. This is, of course, not the case in all signaling pathways and in this paper we will compare the results of stochastic and deterministic simulations in a system where the receptor contains multiple binding sites, exhibiting nonlinear binding kinetics. Our goal is to determine under which conditions a deterministic approach is valid and for what parameter values a stochastic analysis is required. We should note that we only compare averaged quantities and that determining the variance of the biophysical quantities necessitates a stochastic approach.
The system we investigate is the calcium-induced vesicle release into the synaptic cleft. Calcium controls a number of important biological processes and the role of noise in the dynamics of intracellular calcium has been widely studied in recent years [17]. In neurons, the release of vesicles, critical for neuronal information processing, is controlled largely through the local calcium concentration. Calcium ions bind to a calcium sensor which leads to the release of a nearby vesicle. Our goal here is not to construct a detailed calcium model for this release, as this has been the subject of a number of recent studies. Rather, we set out to question the role of stochasticity in the release process using two representative models [18]. In particular, we ask the question under what conditions stochastic simulations that incorporate fluctuations give rise to release probabilities that are markedly different from the results of deterministic simulations in which these fluctuations are ignored. Note that we will not address the neuroscience of the vesicle release problem, the subject of a recent study [14].
2. Model
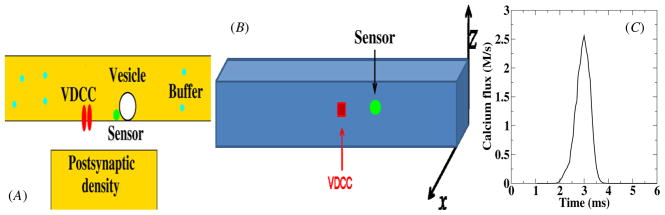
A full description of our model synapse is given in the supplementary data available at stacks.iop.org/PhysBio/7/026008/mmedia and is further detailed, along with the relevant neurophysical details, in [14]. Briefly, we modeled the sequence of events at a pre-synaptic terminal synapse beginning with the arrival of an action potential, the opening of voltage-dependent calcium channels (VDCCs), diffusion of calcium from the VDCCs to a calcium sensor and the triggering of vesicle fusion and release. A schematic overview of the synapse, along with the relevant components, is shown in figure 1(A). More specifically, we considered a cluster of VDCCs located at the center of one of the faces of our computational box (see figure 1(B)). Each channel is described by a five-state process with time-dependent transition rates detailed in the supplementary data. The number of VDCCs in the cluster can be varied and the average flux through a single channel is shown in figure 1(C).
Figure 1.
(A) The geometry considered in this paper. A cluster of VDCCs emits calcium molecules into the pre-synaptic space where they can bind to mobile buffers. A calcium sensor, indicated in green, controls the release of vesicles and is located at a variable distance from the VDCC cluster. (B) The computational geometry, representing the synaptic space in the simulations, has a dimension of 4 μm × 0.5 μm × 0.5 μm. The faces of the space are covered uniformly by PCMA pumps. (C) Average time-dependent calcium concentration of a single voltage-gated channel. The concentration was measured in a 25 nm3 voxel adjacent to the channel.
The computational domain contains a fixed concentration of mobile buffers and the boundaries of the domain are covered by plasma membrane calcium (PMCA) pumps that keep the resting calcium concentration at a constant value of 100 nM. The kinetic schemes of the buffers and the pumps are given in the supplementary data. A calcium sensor is located at a variable distance from the VDCC cluster and at the same face as this cluster. This sensor has multiple binding sites for calcium ions and the kinetics of these bindings determine the probability of vesicle release.
The resting calcium concentration of 100 nM corresponds to roughly 60 ions in our computational domain with a volume of 1 μm3. Furthermore, as we will see below, the peak concentration of calcium at the sensor following the opening of a small number of VDCCs is of the order of 5 μM. These small numbers make it likely that calcium concentration fluctuations can become significant. It is important, however, to realize that these fluctuations arise from different sources. First, the opening kinetics of the VDCCs is a stochastic process, resulting in a fluctuating number of calcium ions introduced into the synapse. Second, the PMCA pump kinetics is also described stochastically. Third, the binding of calcium ions to the buffer molecules is a stochastic process. Fourth, the diffusion of calcium ions and buffering molecules will lead to fluctuations. Fifth, the binding of calcium ions to the vesicle release sensor is controlled through stochastic reactions.
A full evaluation of all five noise sources is computationally challenging. Fortunately, two of the five can be safely neglected and we will focus here on the three noise sources which are likely to be the largest: the VDCC opening kinetics, the diffusion process and the sensing process. The fluctuations arising from the pumps can be neglected since the faces of our computational domains are covered uniformly with a density of 180 μm−2. This high density will render the calcium fluctuations far from the VDCC cluster, and thus at the location of the sensor, independent of the pump kinetics. We have verified this through direct numerical simulations in which we compared the fluctuations at different distances from the VDCC cluster with and without PCMA pumps. For the physiological concentration of 100 nM, we found that the signal-to-noise ratio (SNR), defined as the mean calcium concentration divided by the standard deviation of the calcium concentration, in the presence of pumps and in the absence of pumps were virtually indistinguishable (data not shown). We can also neglect the fluctuation caused by the buffer-calcium kinetics since the off-rates for the unbinding of calcium ions from the buffer molecules are such that multiple-binding events during the time course of a vesicle release event are unlikely.
In the rest of the paper, we systematically investigate the effect of the three remaining noise sources on the average vesicle release probability using MCell as our computational tool. Throughout this paper, the release probabilities are computed as the average of 1000 independent simulations. We compare these probabilities to the results from a deterministic finite-difference implementation of the model synapse. Details of this implementation are given in the supplementary data.
3. Results
3.1. Global Ca2+ dynamics
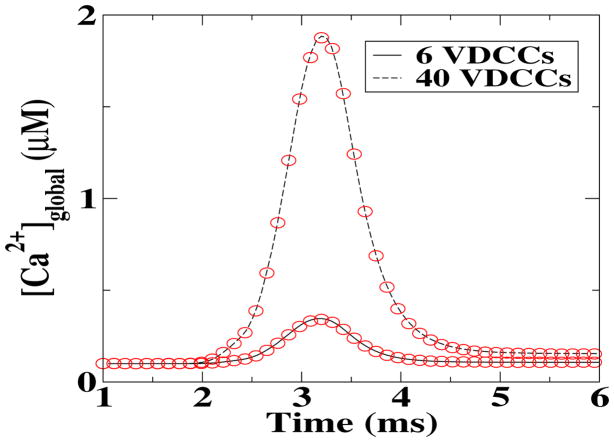
As a first comparison between the deterministic and stochastic simulations, we calculated the global Ca2+ concentrations, [Ca2+]global, as a function of time following the opening of two different numbers of VDCCs. This result is a global measurement and, as such, should be least susceptible to fluctuations. Indeed, as shown in figure 2, the time course of [Ca2+]global for the deterministic model (symbols) is virtually indistinguishable from the one of the MCell simulations (solid and dashed lines). In reference to what follows, we should note that the deterministic results were obtained using a deterministic description for all involved processes while the stochastic results were obtained using MCell in which each step is modeled stochastically.
Figure 2.
Comparison between the deterministic (solid and dashed lines) and stochastic (symbols) global Ca2+ concentration, following an influx through the VDCCs.
3.2. Local Ca2+ dynamics
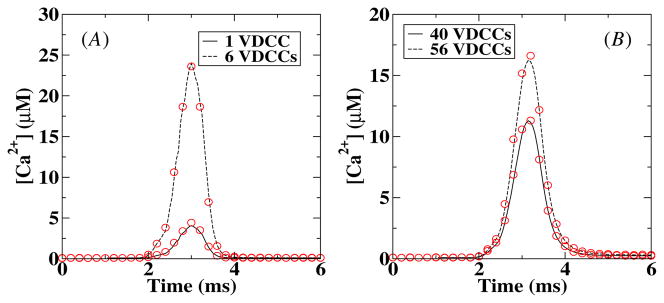
Next we measured the local Ca2+ profiles following channel openings in the VDCC cluster. This measurement is straightforward in the deterministic simulation while for the stochastic simulations we used a built-in MCell algorithm. In this algorithm, the concentration is determined by computing the number of molecules that pass through a ‘counting’ plane and converted this into a concentration. We placed this 50 × 50 nm2 counting plane parallel to and 10 nm away from the membrane while the distance between the center of the VDCC cluster and the center of the counting plane was varied. The results are shown in figure 3 where we have plotted the Ca2+ concentration as a function of time for two different number of VDCCs at 50 nm (A) and 250 nm (B) from the VDCC cluster. The agreement between the deterministic and stochastic results is very good for both curves although a small difference can be observed at the peak value of the calcium concentration. This difference is most likely due to the larger spatial extent of the counting plane in MCell than the box size of the deterministic model. To avoid the possibility that this small error affects our further analysis, we will take from now on the averaged calcium profile measured using MCell as our ‘deterministic’ signal. The computed amplitudes of the calcium signal are consistent with experimental data [18, 19].
Figure 3.
Comparison between deterministic and stochastic local Ca2+ concentration at 50 nm (A) and 250 nm (B) from the center of the VDCC cluster and 10 nm from the membrane. The solid and dashed lines correspond to deterministic results while the symbols are the results of the stochastic (MCell) simulations. The stochastic [Ca2+] was obtained by averaging over 1000 runs.
3.3. Release model
Since it is currently unclear how the calcium sensor is coupled to the vesicle release machinery in the synapse, we have considered two models to calculate the vesicle release probability. In the first one, which we will call model A, one sensor controls only one vesicle. As a result, once the vesicle is released the sensor is unable to release additional vesicles. In the second model, termed model B and used in a recent study [18], sensor and vesicles are not coupled in a one-to-one fashion and a single sensor can release more than one vesicle. For both models, we consider a sensor–VDCC distance between 10 nm and 250 nm, consistent with experimental observations [20–22].
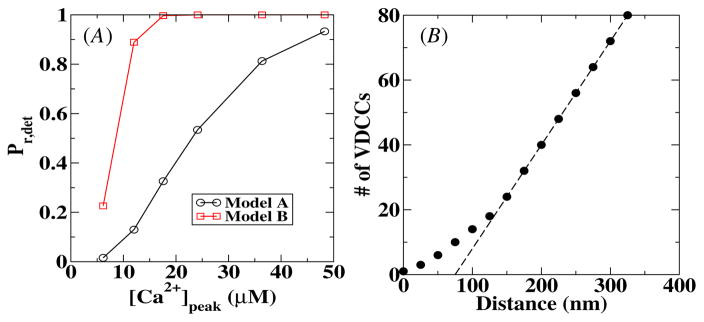
To investigate the difference between the two release models, we have calculated for both models the release probability as a function of the peak calcium concentration, [Ca2+]peak. The results are shown in figure 4(A) for a sensor–VDCC cluster distance of 10 nm. These curves were obtained using the deterministic model and show clearly that, for the same peak [Ca2+], the release probability in model B is higher than the release probability in model A. In other words, model B is more sensitive than model A. For the remainder of this paper, we will compare the results from the stochastic simulations with this deterministic release probability Pr,det.
Figure 4.
(A) The deterministic release probability as a function of the peak calcium concentration for both release models used in this paper. The distance between the VDCC cluster and the calcium sensor is 10 nm. (B) The minimum number of VDCCs required to have a release probability of 0.2 as a function of the distance between the VDCC cluster and the calcium sensor. The dashed line is a straight line with slope 0.32.
The release probability Pr,det for larger VDCC–sensor distances increases slightly for the same peak calcium concentration. For example, for a distance of 250 nm, Pr,det is approximately 5% larger at [Ca2+]peak = 20 μM than for a distance of 10 nm. This can be understood by realizing that to obtain Pr,det, one integrates over the entire calcium profile. For larger distances, this profile become broader for the same peak calcium concentration, leading to a slightly large Pr,det. Of course, to obtain the same release probability at a larger distance requires a larger influx of calcium. This is shown in figure 4(B) where we plot the required number of channels in the VDCC cluster to obtain Pr,det = 0.2 as a function of the distance between the VDCC cluster and the sensor for model A. For distances larger than 150 nm, the required number of channels scales linearly with the distance, as shown by the dashed straight line.
3.4. Fluctuations from the diffusion process
To study the effect of [Ca2+] fluctuations from the diffusion process, we eliminated the fluctuations in the calcium concentration caused by the stochasticity of the VDCCs by modeling the VDCC cluster in MCell deterministically. This is accomplished by using an identical flux pattern of calcium ions for each simulation in MCell. The resulting calcium profiles within our presynaptic terminal will then contain fluctuations that are due purely to diffusive noise. These calcium profiles were used as an input for a deterministic description of the release kinetics of our two models. The deterministic sensor is placed at different distances from the VDCC cluster and the release probability Pr,diff is obtained. This release probability differs from the deterministic release probability Pr,det only because of the calcium concentration fluctuations and we can define a diffusion error as Δdiff = |Pr,diff − Pr,det|/Pr,det.
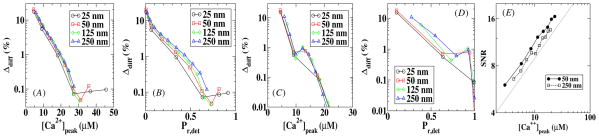
In figures 5(A) and (B), we plot Δdiff as a function of the peak value of the calcium concentration at the sensor location and as a function of Pr,det for model A while in (C) and (D) we do the same for model B. Figure 5 shows that for large values of [Ca2+]peak, and thus high values of Pr,det, the error approaches a small value and only for low [Ca2+]peak and small Pr,det does the error become appreciable. We can also see from figure 5 that the error is largely independent of distances between the VDCC cluster and the sensor and that the error in model B is slightly smaller than the error in model A.
Figure 5.
The error in the release probability due to diffusion as a function of the peak calcium concentration and the release probability for model A (A and B) and model B (C and D). The signal-to-noise of the local calcium concentration is plotted as a function of the peak calcium concentration for two different sensor locations in (E). This SNR scales as , which is the scaling of the solid line.
These errors are caused by the fluctuations in the calcium concentration which can be quantified by computing the signal-to-noise ratio (SNR). For this, we have calculated the variance σ 2 of the calcium profiles in a 1 ms time window containing [Ca2+]peak. This time scale is representative of the fast experimental time scale of vesicle release [23]. The resulting signal-to-noise ratio is plotted in figure 5(E) as a function of [Ca2+]peak. Not surprisingly, the SNR decreases as the peak calcium concentration decreases, leading to a larger error between the release probability obtained using a deterministic calcium profile and obtained using a stochastic profile. Furthermore, fluctuations are roughly independent of the distance between the VDCC cluster and the sensor. The solid line in the figure has approximately the same slope as the experimental data and represents a scaling. We have verified that this scaling is largely unchanged when choosing a time window which is ten times smaller or two times larger.
3.5. Fluctuations from the VDCCs
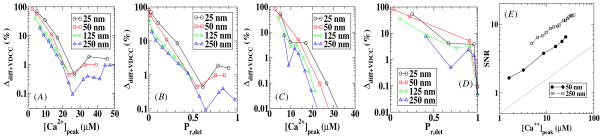
Next, we considered the release probability Pr,diff+VDCC using stochastic calcium profiles obtained with stochastically modeled VDCCs. Thus, in addition to diffusion fluctuations there are fluctuations caused by the non-synchronous opening and non-identical flux profiles of the VDCCs. The results of these calculations are shown in figure 6 where we have again defined an error as Δdiff+VDCC = |Pr,diff+VDCC − Pr,det|/Pr,det and have plotted this error for two values of the VDCC–sensor distance. Now, the relative error is strongly dependent on the distance between the VDCC cluster and the sensor and is much larger if the sensor is close to the VDCC cluster. Furthermore, we can see that for the same value of Pr,det the error is significantly higher than that for the case where only the diffusion was treated stochastically (compare with figure 5). In figure 6(E) we plot the corresponding SNR which now depends on the position of the sensor and is much smaller for a small value of the VDCC cluster–sensor distance. Furthermore, a comparison with figure 5(E) reveals that the SNR for stochastic VDCCs becomes comparable to the SNR for deterministic VDCCs only for large distances.
Figure 6.
The diffusive and VDCC error introduced in the release probability as a function of the peak calcium concentration and the release probability for model A (A and B) and model B (C and D). The signal-to-noise ratio of the local calcium concentration is plotted as a function of the peak calcium concentration for two different sensor locations in (E), along with a solid line representing a dependence.
3.6. Comparison between fully stochastic and fully deterministic simulations
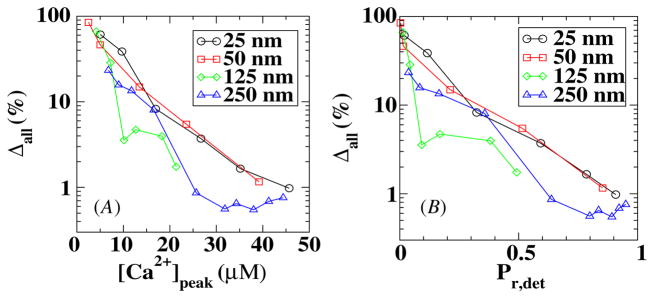
Finally, we considered the results of simulations in which the calcium profiles are generated from stochastic VDCCs using MCell and are used as input into a stochastic description of model A for the sensor. In figure 7 we plot Δall = |Pr,stoch − Pr,det|/Pr,det as a function of the peak value of the calcium concentration at the sensor location and as a function of Pr,det. Again the maximum error occurs when the number of VDCCs is small, corresponding to a small distance between the sensor and the VDCC cluster. However, by comparing figures 6 and 7 we can conclude that the stochastic kinetics of the sensors do not add significantly to the release probability error.
Figure 7.
The error in a fully stochastic simulation in model A as a function of the peak calcium concentration (A) and release probability (B).
4. Discussion
The release of a synaptic vesicle is a stochastic process, controlled largely by the local calcium concentration. This concentration exhibits considerable fluctuations coming from several different sources. To investigate the relative contribution of these different sources, we compared the outcome from deterministic simulations to the results from stochastic calculations in which the concentration profiles were obtained using MCell, a numerical algorithm that describes individual molecules.
We find that the fluctuations arising from the diffusion process only play a significant role when the concentration at the sensor is small (figure 5). Equivalently, the diffusive fluctuations only play a role when the release probability is very small (<0.1). This result is not surprising since for large concentrations the fluctuations become less important. After all, for a purely diffusive process, the fluctuations in a small volume lead to a SNR that is proportional to (see figure 5(E)). Thus, these fluctuations become less and less important as the concentration becomes higher. This also explains why the error is roughly independent of the distance between the sensor and the VDCC cluster. The release probability is determined in large part by the peak [Ca2+]. Thus, no matter how far the sensor is removed from the VDCC cluster, it will experience approximately the same fluctuations for the same [Ca2+], resulting in the same error in release probability.
We also find that the inclusion of fluctuations due to the stochastic openings of the VDCCs increases the error in release probability significantly. Indeed, as can be seen from figure 6, we find that the error at the same peak value of calcium increases roughly 3- to 5-fold when the fluctuations from the VDCCs are taken into account. Furthermore, we find that the inclusion of VDCC fluctuations renders the error dependent on the location of the sensor: a sensor close to the VDCC cluster will exhibit a larger error than a sensor further away for the same calcium peak concentration or release probability (figures 6(A)–(D)). Consistent with this observation is the spatial dependence on the SNR with a larger SNR further away from the VDCC cluster (figure 6(E)). This result can be explained by noting that the stochastic openings of the VDCC channels within the cluster will have a large effect close to the cluster while diffusion will ‘smear out’ these fluctuations further away from the cluster. We also conclude from figure 7 that the stochasticity of the sensor kinetics changes the error only slightly. Finally, we should note that a description of stochastic VDCCs can be easily included into a model that treats the diffusion deterministically.
Taken together, we can conclude that the major source of difference between the deterministic and stochastic simulations is coming from the stochastic opening kinetics of the VDCC channels. To determine when a stochastic treatment of these channels is necessary, we can examine the error of a physiologically relevant probability release of Pr = 0.2 [24]. Taking 20% as the maximum allowable error, we conclude that fully deterministic simulations are viable for sensor–VDCC distances larger than 50 nm and that a stochastic treatment of the VDCCs is needed for sensor–VDCC distances smaller than this critical value. Interestingly, this critical distance is identical to the value used in the literature to distinguish nanodomains from microdomains in neuronal calcium signaling [25]. We should note that the error caused by diffusive noise is always smaller than 20%. Using again a 20% error as our cut-off criterion, we can conclude that it is sufficient to implement a stochastic treatment of the calcium flux through the VDCC cluster while solving the diffusion and release problem deterministically.
Finally, our calculations did not investigate the effect of local depletion on the release probability. This depletion is caused by the binding of calcium ions to the sensor, which changes the local calcium concentration. To understand when this effect is important we have carried out an analysis of a simplified single sensor model of size R0 that binds ligands at a rate kon. In the supplementary data, we show that for this model one can analytically obtain the steady-state solution. This solution shows that the depletion effect can be neglected as long as kon/(2π DR0) ≪ 1, where D is the diffusion constant of the ligands. A similar condition was found numerically in [16]. This analysis shows that for small diffusion constants, small sensor sizes or large on rates, removing a ligand molecule can have a significant effect on the number of binding events to the sensor. However, the removal of ligands upon binding is not a process that requires a stochastic simulation algorithm as it can be incorporated into a deterministic approach through the inclusion of appropriate boundary conditions (see the supplementary information). For our time-dependent problem we have verified that depletion in the deterministic calculation changes the release probability at most 7% for the smallest values of Pr,det considered. Furthermore, we also compared the release probability in an MCell calculation using fixed VDCC fluxes to the release probability of a deterministic calculation that incorporated calcium removal. We found that the results differed by less than 15% for all release probabilities considered here (data not shown). Since this difference is of the same order as the diffusive error (see figure 5) we do not expect that local removal of ions contributes to a significant difference between deterministic and stochastic calculations.
In summary, our main conclusion is that stochastic effects can be important in calcium signaling within nanodomains while signaling in microdomains can be safely simulated by deterministic algorithms. Of course, this conclusion is reached using two release models with specific parameter values. However, these models, along with their parameter values, are based on multiple experimental studies and should be representative for vesicle release. Finally, we should reiterate that we only examined averaged quantities and that knowledge about the variance of the release probability requires a stochastic approach.
Supplementary Material
Acknowledgments
CM would like to thank the Office of the Higher Education Commission, Thailand, for support by a grant fund under the program Strategic Scholarships for Frontier Research Network for the Joint PhD Program Thai Doctoral degree for this research. WT is supported by the Thailand Research Fund, the Commission on Higher Education, and the National Center for Genetic Engineering and Biotechnology. SN, HL and W-JR acknowledge support from the Center for Theoretical Biological Physics (NSF PHY-0822283).
Footnotes
Online supplementary data available from stacks.iop.org/PhysBio/7/026008/mmedia
References
- 1.Swain PS, Elowitz MB, Siggia ED. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc Natl Acad Sci USA. 2002;99:12795–800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Steuer R, Zhou C, Kurths J. Constructive effects of fluctuations in genetic and biochemical regulatory systems. Biosystems. 2003;72:241–51. doi: 10.1016/j.biosystems.2003.07.001. [DOI] [PubMed] [Google Scholar]
- 3.Paulsson J. Summing up the noise in gene networks. Nature. 2004;427:415–8. doi: 10.1038/nature02257. [DOI] [PubMed] [Google Scholar]
- 4.Samoilov MS, Price G, Arkin AP. From fluctuations to phenotypes: the physiology of noise. Sci STKE. 2006;2006:re17. doi: 10.1126/stke.3662006re17. [DOI] [PubMed] [Google Scholar]
- 5.Tǎnase-Nicola S, Warren PB, ten Wolde PR. Signal detection, modularity, and the correlation between extrinsic and intrinsic noise in biochemical networks. Phys Rev Lett. 2006;97:068102. doi: 10.1103/PhysRevLett.97.068102. [DOI] [PubMed] [Google Scholar]
- 6.Erban R, Chapman SJ. Reactive boundary conditions for stochastic simulations of reaction-diffusion processes. Phys Biol. 2007;4:16–28. doi: 10.1088/1478-3975/4/1/003. [DOI] [PubMed] [Google Scholar]
- 7.Rappel WJ, Levine H. Receptor noise limitations on chemotactic sensing. Proc Natl Acad Sci USA. 2008;105:19270–5. doi: 10.1073/pnas.0804702105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rappel WJ, Levine H. Receptor noise and directional sensing in eukaryotic chemotaxis. Phys Rev Lett. 2008;100:228101. doi: 10.1103/PhysRevLett.100.228101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hattne J, Fange D, Elf J. Stochastic reaction-diffusion simulation with MesoRD. Bioinformatics. 2005;21:2923–19. doi: 10.1093/bioinformatics/bti431. [DOI] [PubMed] [Google Scholar]
- 10.Andrews SS, Bray D. Stochastic simulation of chemical reactions with spatial resolution and single molecule detail. Phys Biol. 2004;1:137–51. doi: 10.1088/1478-3967/1/3/001. [DOI] [PubMed] [Google Scholar]
- 11.Kerr RA, et al. Fast Monte Carlo simulation methods for biological reaction-diffusion systems in solution and on surfaces. SIAM J Sci Comput. 2008;30:3126. doi: 10.1137/070692017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang K, Rappel WJ, Kerr R, Levine H. Quantifying noise levels of intercellular signals. Phys Rev E. 2007;75:061905. doi: 10.1103/PhysRevE.75.061905. [DOI] [PubMed] [Google Scholar]
- 13.Coggan JS, et al. Evidence for ectopic neurotransmission at a neuronal synapse. Science. 2005;309:446–51. doi: 10.1126/science.1108239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nadkarni S, Bartol TM, Sejnowski T, Levine H. Spatial and temporal correlates of vesicular release at hippocampal synapse arXiv:1004.2009v1 [q-bio.NC] 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kerr RA, Levine H, Sejnowski TJ, Rappel WJ. Division accuracy in a stochastic model of min oscillations in escherichia coli. Proc Natl Acad Sci USA. 2006;103:347–52. doi: 10.1073/pnas.0505825102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hake J, Lines GT. Stochastic binding of Ca2+ ions in the dyadic cleft; continuous versus random walk description of diffusion. Biophys J. 2008;94:4184–201. doi: 10.1529/biophysj.106.103523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Falcke M. Introduction to focus issue: Intracellular Ca2+ dynamics—a change of modeling paradigm? Chaos. 2009;19:037101. doi: 10.1063/1.3234259. [DOI] [PubMed] [Google Scholar]
- 18.Bollmann JH, Sakmann B, Borst JG. Calcium sensitivity of glutamate release in a calyx-type terminal. Science. 2000;289:953–7. doi: 10.1126/science.289.5481.953. [DOI] [PubMed] [Google Scholar]
- 19.Schneggenburger R, Neher E. Intracellular calcium dependence of transmitter release rates at a fast central synapse. Nature. 2000;406:889–93. doi: 10.1038/35022702. [DOI] [PubMed] [Google Scholar]
- 20.Meinrenken CJ, Borst JG, Sakmann B. Calcium secretion coupling at calyx of held governed by nonuniform channel-vesicle topography. J Neurosci. 2002;22:1648–67. doi: 10.1523/JNEUROSCI.22-05-01648.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shahrezaei V, Cao A, Delaney KR. Ca2+ from one or two channels controls fusion of a single vesicle at the frog neuromuscular junction. J Neurosci. 2006;26:13240–9. doi: 10.1523/JNEUROSCI.1418-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bucurenciu I, Kulik A, Schwaller B, Frotscher M, Jonas P. Nanodomain coupling between Ca2+ channels and Ca2+ sensors promotes fast and efficient transmitter release at a cortical gabaergic synapse. Neuron. 2008;57:536–45. doi: 10.1016/j.neuron.2007.12.026. [DOI] [PubMed] [Google Scholar]
- 23.Scheuss V, Taschenberger H, Neher E. Kinetics of both synchronous and asynchronous quantal release during trains of action potential-evoked EPSCs at the rat calyx of Held. J Physiol. 2007;585:361–81. doi: 10.1113/jphysiol.2007.140988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Murthy VN, Sejnowski TJ, Stevens CF. Heterogeneous release properties of visualized individual hippocampal synapses. Neuron. 1997;18:599–612. doi: 10.1016/s0896-6273(00)80301-3. [DOI] [PubMed] [Google Scholar]
- 25.Augustine GJ, Santamaria F, Tanaka K. Local calcium signaling in neurons. Neuron. 2003;40:331–46. doi: 10.1016/s0896-6273(03)00639-1. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.