Probing DNA Binding, DNA Opening and Assembly of a Downstream Clamp/Jaw in E. coli RNA Polymerase – λP_R Promoter Complexes Using Salt and the Physiological Anion Glutamate

Abstract

Transcription by all RNA polymerases (RNAP) requires a series of large-scale conformational changes to form the transcriptionally-competent open complex RP_o. At the λP_R promoter, E. coli σ⁷⁰ RNAP first forms a wrapped, closed 100 bp complex I₁. The subsequent step opens the entire 13 base DNA bubble, creating the relatively unstable (open) complex I₂. Additional conformational changes convert I₂ to the stable RP_o. Here we probe these events by dissecting the effects of Na⁺ salts of Glu⁻, F⁻ and Cl⁻ on each step in this critical process. Rapid mixing and nitrocellulose filter binding reveal that the binding constant for I₁ at 25 °C is ~30-fold larger in Glu⁻ than in Cl⁻ at the same [Na⁺], with the same log-log [salt] dependence for both anions. In contrast, both the rate constant and equilibrium constant for DNA opening (I₁ to I₂) are only weakly [salt]-dependent, and the opening rate constant is insensitive to replacement of Cl⁻ by Glu⁻. These very small effects of [salt] on a process (DNA opening) which is strongly [salt]-dependent in solution may indicate that the backbones of both DNA strands interact with polymerase throughout the process, and/or that compensation is present between ion uptake and release.

Replacement of Cl⁻ by Glu⁻ or F⁻ at 25 °C greatly increases the lifetime of RP_o and greatly reduces its [salt]-dependence. By analogy to Hofmeister salt effects on protein folding, we propose that the excluded anions Glu⁻ and F⁻ drive the folding and assembly of the RNAP clamp/jaw domains in the conversion of I₂ to RP_o, while Cl⁻ does not. Because the Hofmeister effect of these anions largely compensates for the destabilizing coulombic effect of any salt on the binding of this assembly to downstream promoter DNA, RP_o remains long-lived even at 0.5 M Na⁺ in Glu⁻ or F⁻ salts. The observation that Eσ⁷⁰ RP_o are exceedingly long-lived in moderate to high [Glu⁻] argues that Eσ⁷⁰ RNAP do not dissociate from strong promoters in vivo when the cytoplamsic increases during osmotic stress.

E. coli cells have the remarkable ability to grow over a very wide range of environmental conditions, including osmotic conditions ranging from very dilute (0.02 osmolal) to concentrated, high [salt] media (> 3 osmolal) (3-5). In vivo, increases in external osmolarity, which increase cytoplasmic [K⁺] and [Glu⁻], reduce bulk transcription (6) while transcription from genes involved in the osmotic stress response selectively increases (7-9). In the absence of any known osmosensing (e.g. glutamate binding) transcription factor, the simplest hypothesis is that changes in cytoplasmic [K⁺] and [Glu⁻] alone alter transcription (10) during the initial response to osmotic upshift. What features of RNA polymerase and promoter sequence allow the cell to achieve a dramatic reprogramming to maintain homeostasis?

Understanding how cells regulate their gene expression requires kinetic-mechanistic studies. Although transcription by E. coli RNAP has been studied in vivo and in vitro for four decades, we are only beginning to understand the workings of this machine at a molecular level. Key questions are how is DNA opened by RNAP and what significant conformational changes occur during the steps that precede and follow this central DNA opening step? How do variables like the identity of the sigma specificity subunit, the promoter DNA sequence, supercoiling, concentrations of solutes, small ligands, or regulatory proteins affect the rate of formation and lifetime of the transcriptionally-competent open complex, and thereby alter the frequency of productive versus abortive initiation from the promoter?

Because the RNAP machinery and promoter organization are conserved, it likely that the sequence of conformational changes that form the bacterial RP_o is largely invariant (promoter DNA recognition, DNA opening, stabilization of RP_o), but that the rates of interconversion and populations of initiation intermediates differ as a function of the variables noted above. Here we investigate how the substitution of the physiological anion Glu⁻ for the laboratory anion Cl⁻ affects each step in the process of open complex formation at the λP_R promoter by the housekeeping form of E. coli RNA polymerase (RNAP, subunit composition σ⁷⁰α₂ββ′ω). While our research focuses on this promoter, we expect that these results reflect the salient functional characteristics of many Eσ⁷⁰ RNAP promoter interactions.

In vitro, changes in salt concentration profoundly affect both the composite second order association rate constant (k_a) and composite dissociation rate constant (k_d) for the formation and dissociation of RP_o at the σP_R promoter, respectively (11, 12). One contributor to these salt effects is coulombic: positively charged residues in the promoter-RNAP interface reduce the high negative phosphate charge density of DNA, releasing locally accumulated salt ions (e.g. K⁺ or Na⁺ from DNA). In addition, the identity of the anion has large effects on the magnitude of k_a: for the σP_R promoter k_a was found to be at least 30-fold larger in glutamate (Glu⁻) than in chloride (Cl⁻) at 0.20 M K⁺ (13). Here we dissect this large salt anion effect. Large effects of substituting another anion for Cl⁻ are also observed for many other nucleic acid DNA binding proteins, including transcription factors (14-16), helicases (15), T7 RNAP (17) and DNA polymerases. Large Hofmeister effects of salt anions like Glu⁻ and F⁻, relative to Cl⁻, are expected on steps in which interface formation or coupled folding buries large amounts of nonpolar (hydrocarbon) surface (18, 19).

At the strong λP_R promoter (P), the mechanism of open complex formation consists of a minimum of three steps, proceeding through two kinetically significant intermediates (11, 20-22)

$$\mathrm{R}+\mathrm{P}\underset{{\mathrm{k}}_{-1}}{\overset{{\mathrm{k}}_1}{\rightleftarrows }}{\mathrm{I}}_1\underset{{\mathrm{k}}_{-2}}{\overset{{\mathrm{k}}_2}{\rightleftarrows }}{\mathrm{I}}_2\underset{{\mathrm{k}}_{-3}}{\overset{{\mathrm{k}}_3}{\rightleftarrows }}{\mathrm{RP}}_{\mathrm{o}}$$ (Mechanism I)

where R represents RNA polymerase Eσ⁷⁰, P is promoter, and I₁ and I₂ are the first and second kinetically significant intermediates, respectively. Opening of the entire DNA bubble (−11 to +2) occurs in the conversion of I₁ to I₂ ((23); Gries et al., unpublished). No other early intermediates are kinetically significant at the λP_R promoter. Solute upshift studies designed to study the late steps in RP_o formation reveal the existence of an intermediate (I₃) forming after I₂ and directly preceding the formation of RP_o (24). I₃ rapidly equilibrates with I₂ and RP_o under the conditions of this study, and thus can neglected in the analysis of k_d presented here. Because the kinetics of open complex formation (association) and dissociation are single exponential for almost all conditions examined, we deduce that: i. in association I₁ rapidly equilibrates with free RNAP and promoter DNA on the time scale required for I₁ to convert to I₂ in the forward direction (k₋₁>>k₂); and ii. I₂ rapidly equilibrates with RP_o on the time scale required for I₂ to convert to I₁ in the reverse direction (k₃>>k₋₂). The interconversions of I₁ and I₂ are the bottleneck steps in both the association and dissociation directions.

Using rapid mixing we recently dissected the composite association and dissociation rate constants for RNAP- λP_R interactions into their individual contributions from K₁ (=k₁/k₋₁), k₂, k₋₂ and K₃ (=k₃/k₋₃), respectively (22, 24). We discovered that destabilizing RP_o by a rapid upshift in salt or urea concentration creates a transient burst of I₂ (24). Coupling rapid mixing with filter binding, we determined the kinetics of forming this unstable open complex (I₂) from the stable open complex RP_o, and converting I₂ to the closed complex I₁ over a wide range of salt concentrations at 10 °C and 37 °C. These studies dissected the effect of [salt] on the dissociation kinetics for the first time. The rate constant k₋₂ is independent of salt concentration, while the equilibrium constant for the conversion of I₂ to RP_o decreases strongly with increasing [salt] (24). Permanganate footprinting of I₂ reveals that all reactive thymines in RP_o are also reactive in I₂, demonstrating that the entire transcription bubble is opened in the rate-determining, single step I₁ → I₂ (Gries et al., unpublished). Measurements of the time dependence of the decay of permanganate reactivity in conversion of I₂ to I₁ corroborate the rate constant k₋₂ obtained by rapid mixing and filter binding.

The unexpected result that the rate constant k₋₂ characterizing the conversion of I₂ to the transition state (I₁-I₂)^† is independent of salt concentration motivates the work here to dissect the effects of salt concentration on the steps on the first half of the mechanism, namely the formation of I₁ and the transition between I₁ and (I₁-I₂)^†. Melting of DNA in solution is strongly salt concentration dependent (25). How does melting DNA to form the initiation bubble in the isomerization of I₁ to I₂ compare?

To address this question we examine whether the rate constant k₂ characterizing the conversion of I₁ to (I₁-I₂)^† is [salt]-dependent. Using rapid mixing and filter binding, we dissect for the first time the overall second order association rate constant k_a into K₁ and k₂ over a range of NaCl and NaGlu concentrations. In addition, we obtain stringent tests of the single exponential character of both the association kinetic data (in [RNAP] excess) and dissociation kinetic data. These findings demonstrate that the initial steps of association (forming I₁) and of dissociation (forming I₂) do indeed rapidly equilibrate on the time scale of the subsequent slower conformational change (DNA opening or closing). We use manual mixing filter binding to examine the effects of salt concentration (NaX) and choice of anion (X = Cl⁻, Glu⁻, or F⁻) on the dissociation of RP_o at 25 °C.

We find that each step exhibits a uniquely different dependence on changes in [Na⁺] and choice of anion. While the formation of I₁ and conversion of I₂ to RP_o exhibit large dependences on both [Na⁺] and anion, the bottleneck DNA opening step (I₁ → I₂) is relatively insensitive to either solution variable. Formation of I₁ and especially RP_o are greatly favored in Glu⁻ relative to Cl⁻. Together these results shed additional light on the conformational changes occurring in each step, allowing us to refine our current structural-mechanistic hypotheses regarding open complex formation by E. coli RNAP. In particular, we propose that the very large effects of replacing Cl⁻ with Glu⁻ on the steps after DNA opening result from burial of hydrocarbon surface of RNAP in coupled folding transitions in late steps (24, 26, 27). Glu⁻ and F⁻ are more highly excluded from nonpolar surface than is Cl⁻ (18, 19). We deduce that these late remodeling events assemble a RNAP clamp/jaw on downstream DNA and contribute significantly to the entropic driving force that stabilizes the open DNA state in RP_o.

MATERIALS AND METHODS

Buffers

Storage Buffer (SB) for RNA polymerase holoenzyme contained 50% glycerol (v/v), 10 mM Tris-HCl (pH 7.5 at 4 °C), 100 mM NaCl, 0.1 mM dithiothreitol (DTT), and 0.1 mM Na₂EDTA. Binding Buffer for the study of the kinetics of RNAP-promoter binding as a function of univalent salt concentration in the absence of Mg²⁺ (BB) contained 10 mM Na₂HPO₄ buffer (pH 7.4), 6.5% (v/v) glycerol, 1 mM DTT, 100 μmg/mL BSA, 1.3 mM Tris (pH 7.5 at 4 °C; contributed by the Storage Buffer), and variable [NaCl] , [NaGlu] or [NaF] to bring [Na⁺] to the desired value. Wash Buffer (WB) contained 0.1 M NaCl, 10 mM Tris-HCl (pH 8.0 at room temperature), and 0.1 mM Na₂EDTA. Addition of NaGlu did not significantly affect the pH of the Tris-HCl buffer.

Wild-type Eσ⁷⁰ RNA polymerase holoenzyme

E. coli K12 wild type RNA polymerase holoenzyme was purified as described in (28) and stored in SB at −70 °C. All [RNAP] reported here are concentrations of active holoenzyme (capable of RP_o formation). Activities were determined at the time of use, either by analysis of forward titrations of promoter DNA with RNAP performed in the ‘complete binding of limiting reagent’ regime at 37 °C as described (11) or by comparison of association rate constant for different samples determined at the same total [RNAP]. Typically activities were ~70%. Systematic comparisons of the different preparations showed that no difference in promoter association kinetics between individual tubes or preps, when compared at the same active [RNAP].

λP_R promoter DNA

A ³²P-DNA fragment containing the λP_R promoter was obtained from the plasmid pBR81 as described in (29). BssH II and Sma I cleavage of pBR81 centrally positions the λP_R wild-type sequence (−60 to +20) in a fragment which extends from −115 to +76 relative to the transcription start site (+1) of the promoter. The specific activity of the fragment was generally ~10⁸ cpm/mole.

Association Kinetics

For conditions where the kinetics are sufficiently slow (e.g. RNAP concentrations below 10 nM at mid-range salt concentrations; high (<0.3M) salt concentrations), manual mixing and filter binding were used to determine the kinetics of formation of long-lived (open) complexes, resistant to a 10 - 30 s heparin challenge. For conditions where the kinetics are too fast (first order rate constant k_obs > 0.01 s⁻1) to determine by manual mixing (e.g. low salt and higher RNAP concentrations), rapid mixing (2 ms mixing time; RQF-3, Kintek Corp., Austin TX) followed by filter binding on quenched solutions was used (22). Rapid mixing and manual mixing experiments were performed as described in (22). Concentrations of active RNAP were always in at least 6-fold excess over that of promoter to ensure that the initial bimolecular binding step is pseudo-first order within experimental uncertainty.

Dissociation Kinetics

i. Irreversible dissociation initiated by adding heparin to pre-formed RP_o

Effects of [Na⁺] in Cl⁻ buffer on the dissociation of preformed λP_R DNA (0.08-0.09 nM) and RNAP (10 – 40 nM) open complexes at 25 °C were performed as described in (27).

ii. Decay to equilibrium assay to determine k_d

The irreversible dissociation of RP_o complexes initiated by the addition of excess heparin is exceedingly slow in Glu⁻ at 25 °C, yielding poorly determined values of k_d. Thus to determine k_d as a function of Na⁺ in Glu⁻ buffer, we used a decay to equilibrium assay at a low [RNAP] held constant by an excess of the competitor heparin. In this assay, 7 nM RNAP was initially mixed with a vast excess of heparin (0.1 – 1 mg/mL) at the salt concentration of the experiment. After 60 min of incubation, ³²P λP_R DNA (12.5 pM) was added, initiating promoter binding which proceeds to equilibrium at the low [RNAP] of the experiment. The amount of λP_R - RNAP open complexes was monitored using nitrocellulose filter binding. Typically >10⁵ s was required to approach promoter binding equilibrium. At longer times, a very slow decay of the plateau was noted, probably the result of inactivation of RNAP.

Nitrocellulose filter binding assays

The amount of open complexes as a function of time and solution condition was determined using nitrocellulose filter binding as described in (22). Studies in Glu⁻ and F⁻ cannot be performed above 0.70 M Na⁺ because filter efficiency becomes too low.

DATA ANALYSIS

Data were analyzed using either SigmaPlot 6.0 or 2000 (SPSS, Inc. Chicago, IL) on a Dell Optiplex GX270 workstation running Windows XP Professional v. 2002 (Microsoft, Seattle, WA), or using Igor 5.0.3.0 (WaveMetrics, Inc., Lake Oswego, OR)) on Dell Inspiron 8100.

Determination of k_obs, k_a, K₁ and k₂ from the kinetics of formation of open complexes

In excess RNAP, the kinetics of irreversible association of RNAP with λP_R promoter DNA to form open complexes (I₂, RP_o) are single exponential (see Results) with observed rate constant k_obs, determined by fitting the fraction of promoter DNA bound in open complexes at time $t\left({\theta }_t^{\mathit{open}}\right)$ (calculated as described in (22)) versus time to eq 1:

$${\theta }_t^{\mathit{open}}=1-e^{k_{\mathit{obs}}t}$$ (1)

The rate constant k_obs (previously called α_CR) is a hyperbolic function of RNAP concentration (22):

$$k_{\mathit{obs}}=\frac{K_1{k}_2\left[\mathit{RNAP}\right]}{1+K_1\left[\mathit{RNAP}\right]}=\frac{k_a\left[\mathit{RNAP}\right]}{1+K_1\left[\mathit{RNAP}\right]}$$ (2)

where K₁ (= k₁/k₋₁) is the equilibrium constant for formation of I₁, k₂ is the microscopic rate constant for the subsequent (rate-determining) conversion of I₁ to I₂ in Mechanism I, and k_a = K₁k₂ is the composite overall second-order association rate constant. The data for k_obs as a function of [RNAP] in Figs 3 and 4 were weighted by 1/σ², where σ is the standard deviation of k_obs, and fit to eq 2 to determine values of k_a, K₁ and k₂ at each salt concentration investigated. K₁ (= k₁/k₋₁) is the equilibrium constant for formation of the first kinetically-significant intermediate (I₁, in rapid equilibrium with free RNAP and DNA), k₂ (= k_i) is the microscopic rate constant for the subsequent (rate-determining; k₂ < k₋₁) conversion of I₁ to I₂ in Mechanism I, and k_a (= K₁k₂) is the composite overall second-order association rate constant. Values of k_obs (weighted by 1/σ², where σ is the standard deviation of k_obs) were plotted versus [RNAP] and fit to eq 2 to determine k_a, K₁ and k₂.

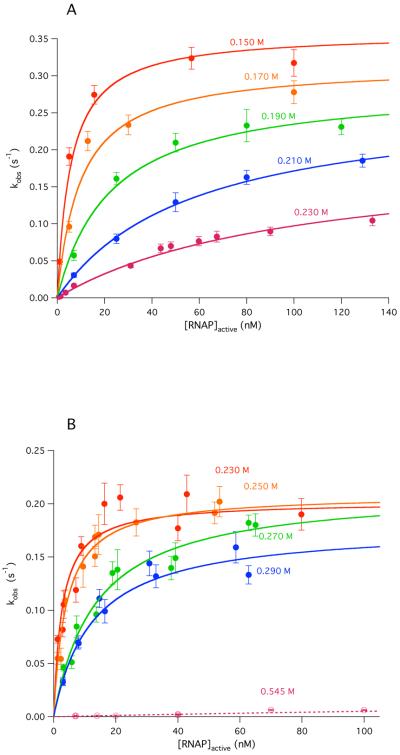
Figure 3.

Irreversible forward rate constant k_obs plotted as a function of the total, active RNAP concentration at five different [Na⁺] in Cl⁻ buffer (cf. Fig 1) (A) and in Glu⁻ buffer (cf. Fig 2) (B). With the exception of data obtained by manual mixing at 0.55 M Na⁺ in Glu⁻, data were obtained by rapid mixing and nonlinearly fit to eq 2, yielding values of K₁, k₂ and k_a (see Table 1) for each [Na⁺] investigated.

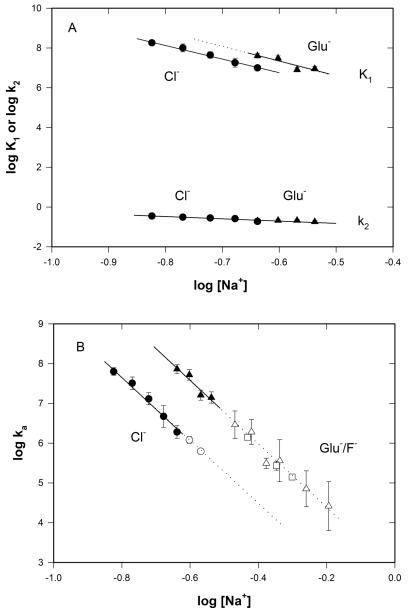
Figure 4.

Log-log [Na⁺]-dependence of K₁, k₂ and k_a as a function of anion. (A) Data from rapid mixing experiments (cf. Fig 3) fit to eq 2 allow a dissection of k_a (=K₁k₂) into individual values of K₁and k₂ in NaCl (circle) and NaGlu (triangle) buffers. (B) Values of logk_a as a function of log[Na⁺] in NaCl (circle), NaGlu (triangle), and NaF (square) buffers. Closed and open symbols represent values of k_a obtained using rapid and manual mixing, respectively. Dashed lines represent linear extrapolations of the log-log fits to the individual data sets, drawn for purposes of comparing the slopes for the different anions. Values of the log-log slopes Sk_a, SK₁ and Sk₂ are given in Table 1 (see Methods for details of the fitting).

Above 0.23 M Na⁺ in NaCl buffer and 0.29 M Na⁺ in NaGlu buffer k_obs increases linearly with [RNAP] up to the highest accessible concentration (~120 nM), indicating (eq 2) that K₁[RNAP] << 1. In this limit, the overall association rate constant was determined using the following equation:

$${\mathrm{k}}_{\mathrm{a}}={\mathrm{k}}_{\mathrm{obs}}∕\left[\mathrm{RNAP}\right](1+{\mathrm{K}}_1\left[\mathrm{RNAP}\right])\approx {\mathrm{k}}_{\mathrm{obs}}∕\left[\mathrm{RNAP}\right]$$ (3)

The quality of the approximation was estimated by linear extrapolation of the log-log plots of K₁ vs. [RNAP] (Fig 4A below) and found to be appropriate.

Determination of the Composite Dissociation Rate Constant k_d

1. The observed rate constant k_d for the irreversible dissociation of open complexes was determined by fitting ${\theta }_t^{\mathit{open}}$ versus time at a given [Na⁺] to a single-exponential decay equation

   $${\theta }_t^{\mathit{open}}={\theta }_{t=0}^{\mathit{open}}{e}^{-k_{d}t}$$ (4)

   where ${\theta }_{t=0}^{\mathit{open}}$ is the value of ${\theta }_t^{\mathit{open}}$ at time t = 0.
2. The promoter dissociation rate constant (k_d) and the RNAP-heparin binding constant (K_heparin) at 25 °C in Glu⁻ and F⁻ buffers were determined from the observed decay to equilibrium (relaxation) rate constant k_r (see below) and the RNAP-promoter association rate constant k_a (Table1). The data were modeled using the following mechanism:

   $$\begin{array}{cc}\hfill & {\mathrm{K}}_{\text{heparin}}\hfill \\ \hfill \mathrm{R}+& \mathrm{H}\rightleftarrows \mathrm{HR}\text{Rapid equilibrium}\hfill \\ \hfill \mathrm{R}+& \mathrm{P}\underset{{\mathrm{k}}_{\mathrm{d}}}{\overset{{\mathrm{k}}_{\mathrm{a}}}{\rightleftarrows }}{\mathrm{RP}}_{\mathrm{o}}\text{Slow to equilibrate}\hfill \end{array}$$ Mechanism II

   In mechanism II, H is heparin, P is promoter DNA, R is free RNAP and RP_o is the final open complex (concentrations of intermediates are negligible). K_heparin is the equilibrium constant for the formation of a heparin-RNAP complex; this equilibrates rapidly on the time scale of association of RNAP with promoter DNA. The composite rate constants for formation (k_a) and dissociation (k_d) of RP_o are defined by eqs 2 and 4, respectively. Our analysis of Mechanism II assumes one heparin binding site on RNAP and applies to conditions where [H]_total >> [R]_total >> [P]_total. For this situation, the experimentally determined approach-to-equilibrium rate constant ${\mathrm{k}}_{\mathrm{r}}=(\mathrm{dln}({\theta }_{t=\infty }^{\mathit{open}}-{\theta }_t^{\mathit{open}})∕\mathrm{dt})={\mathrm{k}}_{\mathrm{a}}\left[\mathrm{R}\right]+{\mathrm{k}}_{\mathrm{d}}$, where [R] is the free RNAP concentration. [R] is constant in these assays (though not in excess over promoter) because the heparin-binding equilibrium buffers its free concentration. The integrated form of this equation is used to determine k_d:

   $${\theta }_t^{\mathit{open}}=\frac{k_a\left[R\right](1-e^{-(k_a\left[R\right]+k_d)t})}{k_a\left[R\right]+k_d}$$ (5)

   where [R] is determined from eq 6:

   $$\left[R\right]=\frac{{\left[R\right]}_{\mathit{total}}}{(1+K_{\mathit{heparin}}{\left[H\right]}_{\mathit{total}})}$$ (6)

   For the set of relaxation data collected as a function of [H]_total at a given Na⁺ in Glu⁻ or F⁻ buffer, data at each [heparin] were fit to eqs 5-6, using the value of k_a determined from the independent kinetics of association experiments (Table 1). Reported values of K_heparin and k_d for each salt condition represent the average and standard deviation from these individual fits.

Table 1.

Values of k_a, K₁ and k₂ as a function of Na⁺ and anion (Cl⁻, Glu⁻ or F⁻) for RP_o formation at the λP_R promoter at 25 °C^a

	Na+ (M)	ka (M−1 s−1)			K1 (M−1)		k2 (s−1)
		Cl−	Glu−	F−	Cl−	Glu−	Cl−	Glu−
A	0.15	(6.3±0.6) × 107			(1.8±0.2) × 108		(3.5±0.1) × 10−1
	0.17	(3.2±0.5) × 107			(1.0±0.2) × 108		(3.1±0.1) × 10−1
	0.19	(1.3±0.2) × 107			(4.4±0.7) × 107		(2.8±0.2) × 10−1
	0.21	(4.7±1.3) × 106			(1.8±0.4) × 107		(2.6±0.3) × 10−1
	0.23	(1.9±0.3) × 106	(7.3±0.8) × 107		(9.9±1.2) × 106	(3.6±0.4) × 108	(1.9±0.2) × 10−1	(2.0±0.1) × 10−1
	0.25		(5.2±0.7) × 107			(2.5±0.3) × 108		(2.1±0.1) × 10−1
	0.27		(1.6±0.2) × 107			(7.3±0.8) × 107		(2.1±0.1) × 10−1
	0.29		(1.4±0.2) × 107			(8.0±0.9) × 107		(1.8±0.1) × 10−1
	SKb	−8.0±0.6	−8.0±1.7		−6.8±0.3	−7.5±2.3	−1.1±0.2	−0.9±0.3
B	0.25	(1.2±0.1) × 106
	0.27	(6.2±0.3) × 105
	0.34		(2.9±1.0) × 106
	0.37			(1.4±0.1) × 106
	0.38		(1.9±0.6) × 106
	0.42		(3.1±0.4) × 105
	0.45			(2.7±0.3) × 105
	0.46		(3.6±1.9) × 105
	0.50			(1.4±0.1) × 105
	0.55		(7.1±3.2) × 104
	0.64		(2.6±1.6) × 104
	SKc	−8.0±0.2	−8.3±0.2

^aFor 0.15-0.23 M Na⁺ in NaCl buffer and 0.23-0.29 M Na⁺ in NaGlu buffer (part A of the table), values of k_a, K₁and k₂ determined from fits of rapid quench mixing data to eq 2. For 0.34 – 0.64 M Na⁺ (part B of the table), the value of k_a was determined from fits of manual mixing data to eq 3; values of k_obs as a function of [RNAP] in this [salt] range do not determine K₁and k₂ (see text).

^bSK = −dlogX/dlog[Na⁺] where X = k_a, K₁ or k₂; each SK value determined from fits of the data in section A of the table.

^cValues of SK determined from fitting data from section A and B.

Results

Single Exponential Kinetics of Formation of E. coli RNA Polymerase – λP_R Promoter Complexes: Effects of Glutamate and Chloride Salts

To compare the effects of the laboratory anion chloride (Cl⁻) and the physiological anion glutamate (Glu⁻) on the binding of E. coli RNAP to the λP_R promoter to form a closed complex and on the subsequent DNA opening step, we determined the kinetics of association over wide ranges of RNAP concentration (1 nM – 100 nM) and concentrations of chloride and glutamate salts (0.13 M to 0.27 M Na⁺ in Cl⁻ buffer; 0.23 M to 0.64 M Na⁺ in Glu⁻ buffer) at 25 °C. A limited number of association experiments were performed in F⁻ buffer at low [RNAP] to compare to the results in Glu⁻ buffer. Sodium salts were used because complexation of potassium by heparin interferes with the heparin challenge (see Methods) at high concentrations of potassium salts (12); Mg²⁺ was omitted because it is complexed by glutamate (30). In most cases the full accessible range of RNAP and of salt concentration were investigated.

Following either manual or rapid mixing, nitrocellulose filter binding was used to determine the kinetics of formation of long-lived, competitor-resistant complexes (RP_o). Representative kinetic data for selected low and high RNAP concentrations over the range of NaCl and NaGlu concentrations are plotted as the fraction of promoter DNA in open complexes (θ_t^open) as a function of time in Figures 1 and 2, respectively. The plateau at θ_t^open = 1 observed at long times for all salt concentrations investigated demonstrates that open complex formation is irreversible and therefore directly interpretable in terms of the forward rate constant k_obs (see eq 1 in Methods), without the need for a decay-to-equilibrium analysis. Irreversibility of the forward kinetics is confirmed by direct measurement of the dissociation rate constant (see below).

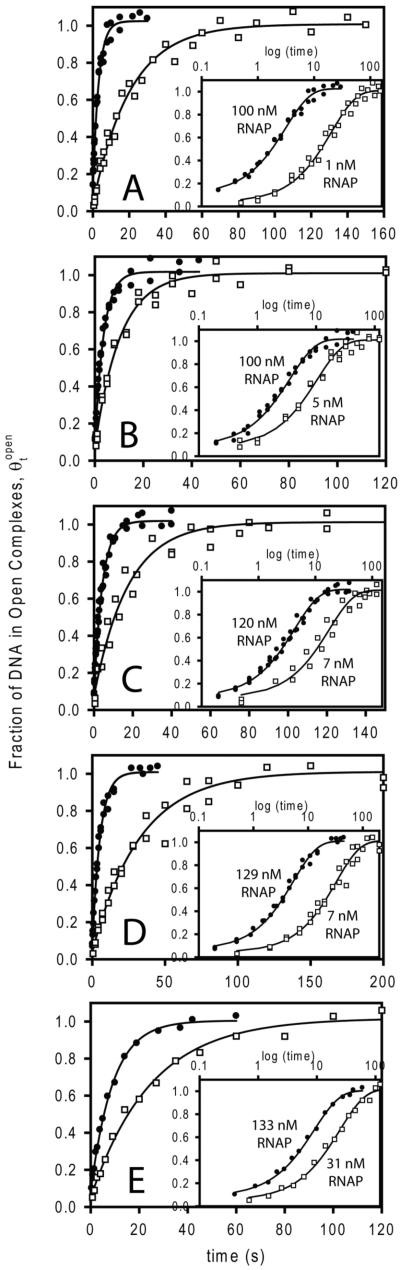
Figure 1.

Representative kinetic data for formation of open complexes at the λP_R promoter at high (closed circles) and low (open squares) concentrations of active RNAP (where RNAP is in excess over promoter DNA) at five different [Na⁺] at 25 °C in NaCl buffer. All data shown here were obtained using rapid quench mixing; the fraction of promoter DNA in the form of open complexes ${\theta }_t^{\mathit{open}}$ as a function of time (t) was determined using nitrocellulose filter binding after association reactions were quenched with the competitor heparin. Theoretical curves through the data are the best fits to eq 1; corresponding first order irreversible rate constants k_obs for each [RNAP] are given in Supplemental Table 1. Insets replot the data as a function of logt, demonstrating the single exponential character of the kinetics over the entire time range. (A) 0.15 M Na⁺. (B) 0.17 M Na⁺. (C) 0.19 M Na⁺. (D) 0.21 M Na⁺. (E) 0.23 Na⁺.

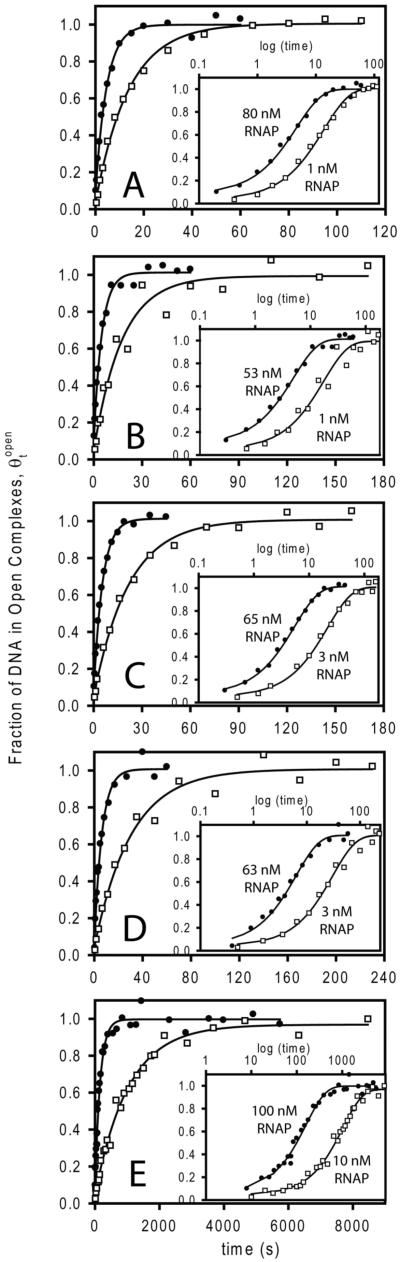
Figure 2.

Representative kinetic data for formation of open complexes at the λP_R promoter at representative high (closed circles) and low (open squares) concentrations of active RNAP at five different [Na⁺] at 25 °C in NaGlu buffer. (Details and insets as in Fig 1; values of k_obs for each [RNAP] are given in Supplemental Table 2.) With the exception of (E), all data were obtained using rapid quench mixing. (A) 0.23 M Na⁺. (B) 0.25 M Na⁺. (C) 0.27 M Na⁺. (D) 0.29 M Na⁺. (E) 0.55 M Na⁺.

Single exponential fits of these data to the irreversible first order rate eq 1 (Methods) are shown in Figs 1 and 2. Values of k_obs determined from these fits are given in Supplemental Tables 1 and 2, respectively. To expand the initial (ms) time regime and examine whether the short time data provide any indication of a second (faster) decay, the insets to the panels of Figs 1 and 2 plot the same data as θ_t^open vs. logt (cf. (1, 2)). For the λP_R promoter and the conditions investigated previously (cf. (11, 12, 20, 22)) and in the present study, all association kinetic data are well-described as single exponential decays. Single exponential kinetics of open complex formation indicate that the step forming the first kinetically significant intermediate (I₁) rapidly equilibrates with free promoter DNA on the time scale of the conversion of I₁ to I₂ (21).

The Observed Forward Rate Constant k_obs is a Hyperbolic Function of [RNAP] over the Accessible Range (1 nM to 100 nM)

Values of the overall rate constant k_obs are plotted versus RNAP concentration in Fig 3A (Cl⁻) and B (Glu⁻) for the salt concentrations investigated. In most cases these data cover a 100-fold range of RNAP concentrations (~1 nM to 100 nM). At all salt concentrations investigated, except the highest [Glu⁻], values of k_obs exhibit the expected hyperbolic dependence on [RNAP] (eq 2). Except at the highest salt concentrations, a well-defined plateau is obtained in the accessible range of [RNAP]. There is no evidence of sigmoidicity in any these plots at low [RNAP], as would be predicted if dissociation of holoenzyme into sigma subunit and core polymerase were significant at these concentrations of RNAP and salt (31). The observations of single-exponential association kinetics (Figs 1 & 2) and hyperbolic dependences of k_obs on [RNAP] (Fig 3) validate the use of eq 2 (Methods) to analyze the dependence of k_obs on [RNAP] and obtain k₂, the DNA opening rate constant and K₁, the equilibrium constant for forming I₁ (see Methods).

DNA Opening by RNAP is Relatively Slow and Only Weakly [Salt]-Dependent; Replacing Cl⁻ by Glu⁻ Has No Significant Effect on k₂ or on its log-log derivative Sk₂

Rate constants k₂ of the DNA opening step are plotted on a log-log scale as a function of [Na⁺] for experiments in Cl⁻ and Glu⁻ buffer in Fig 4. Values of k₂ decrease very modestly with increasing salt concentration, from 0.35 s⁻¹ at 0.15 M Na⁺ in Cl⁻ buffer to 0.18 at 0.29 M Na⁺ in Glu⁻ buffer, corresponding to time constants of 3-5 s for opening. Neither k₂ at 0.23 M salt (the overlap concentration in our experiments) nor Sk₂ is affected by replacement of Cl⁻ by Glu⁻ (Fig 4B); individual fits of these data yield Sk₂ values of −1.1 ± 0.1 and −0.9 ± 0.3 in Cl⁻ and Glu⁻ buffers, respectively. As shown in Fig 4A, the combined data fall on a common line with a log-log slope of Sk₂ = −1.1 ± 0.1. Previously we found from [KCl]-upshift experiments at 10 and 37 °C in transcription buffer (10 mM MgCl₂) that the rate constant k₋₂ for the reverse direction of this step (I₂ to I₁) is independent of [KCl] (Sk₋₂ = 0; (24)). Interpolation between values yields k₋₂ ≈1.7 s⁻¹ at 25 °C. Assuming this value of k₋₂ applies to the [salt] conditions investigated here, we obtain equilibrium constants K₂ for DNA opening by RNAP (i.e. I₁ ⇄ I₂) that decrease from 0.2 at 0.15 M salt to 0.1 at 0.29 M salt. I₂ is therefore unstable with respect to I₁ at all salt concentrations, and the [salt]-dependence of the DNA opening step I₁ ⇄ I₂ on the protein is small (SK₂ = Sk₂ − Sk₋₂ = −1.1 ± 0.1).

Formation of Wrapped I₁ Is Strongly [Salt]-Dependent (SK₁ = −6.9 ± 0.3); Replacing Cl⁻ by Glu⁻ Increases K₁ ~30-fold Without Significantly Affecting SK₁

The proposed RNAP-DNA interface in I₁ spans 100 bp; the net positive charge on RNAP in this interface is at least +37 (see Discussion). How [salt]-dependent is this binding interaction? In Cl⁻ buffer the binding constant K₁ for formation of I₁ decreases from 1.8 × 10⁸ M⁻¹ at 0.15 M Na⁺ to 9.9 × 10⁶ M⁻¹ at 0.23 M Na⁺. In Glu⁻ buffer at 0.23 M Na⁺, K₁ is 3.6 × 10⁸ M⁻1 and decreases to 8 × 10⁷ M⁻¹ at 0.29 M Na⁺. In both Cl⁻ and Glu⁻, logK₁ decreases linearly with log[Na⁺] with slopes SK₁ = dlogK₁/dlog[salt] which are the same within uncertainty (SK₁ = −6.8 ± 0.3 in Cl⁻, SK₁ = −7.5 ± 2.3 in Glu⁻; see Fig 4A and Table 1). Fitting both data sets together yields SK₁ = −6.9 ± 0.3. These are large [salt]-dependences, but not nearly as large as expected from consideration of the interface (see Discussion).

At 0.23 M Na⁺, the only salt concentration where the data sets overlap, the value of K₁ in Glu⁻ buffer exceeds that in Cl⁻ by a factor of ~30. This is the same factor by which the log-log plots of k_a vs. [Na⁺] in Fig 4B are displaced. Such a large effect of replacing Cl⁻ with Glu⁻ on K₁ is likely a Hofmeister salt effect, based on the observation that fluoride and glutamate have very similar effects on k_a = K₁k₂, as well as on k_d (see below).

Replacement of Cl⁻ by Glu⁻ Increases the Second-Order Association Rate Constant k_a by ~30-fold at All [Salt]

Above 0.23 M Na⁺ in Cl⁻ buffer and 0.29 M Na⁺ in Glu⁻ buffer, the equilibrium constant K₁ for I₁ formation becomes too small to allow us to dissect k_obs into K₁ and k₂. At higher [salt], we find that k_obs increases linearly with [RNAP], as shown in Fig 3B in Glu⁻ buffer at 0.55 M Na⁺. Linearity indicates that K₁[RNAP] << 1 over the accessible range of [RNAP]. In this limit, the second order association rate constant k_a = k_obs /[RNAP](1 + K₁[RNAP]) ≈ k_obs/[RNAP], where the quality of the last approximation can be estimated by extrapolation of the log-log plots of K₁ vs. [RNAP] (Fig 4A). Although individual values of K₁ and k₂ cannot be determine in this higher [salt] range, measurements of k_obs at low [RNAP] (typically 7 nM) were performed in Cl⁻, Glu⁻ and F⁻ buffers up to the highest [Na⁺] accessible in each to test for curvature of the log-log plots arising from Hofmeister effects (32). All determinations of k_a are listed in Table 1, and plotted in Fig 4B as a log-log plot together with those obtained from the data of Fig 3. A much wider range of high [Na⁺] can be investigated in Glu⁻ and F⁻ buffers because k_d is much smaller in Glu⁻ and F⁻ buffers than in Cl⁻. Over the full range of [Glu⁻ (or F⁻)] investigated, k_a decreases by more than three orders of magnitude (from 7.3 × 10⁷ M⁻¹ s⁻¹ at 0.23 M Na⁺ to 2.6 × 10⁴ M⁻¹ s⁻¹ at 0.64 M Na⁺). These log-log plots are linear and parallel within the uncertainty over the entire accessible salt range in both Cl⁻ (Sk_a = −8.0 ± 0.2) and Glu⁻/F⁻ (Sk_a = −8.3 ± 0.2). The offset corresponds to ~30-fold faster association in Glu⁻ than in Cl⁻. This difference is entirely the result of the difference in K₁.

Disassembly of the RNAP Clamp/Jaw in Dissociation of RP_o Complexes in Glu⁻ is Remarkably Slower and Much Less [Salt] Dependent than in Cl⁻

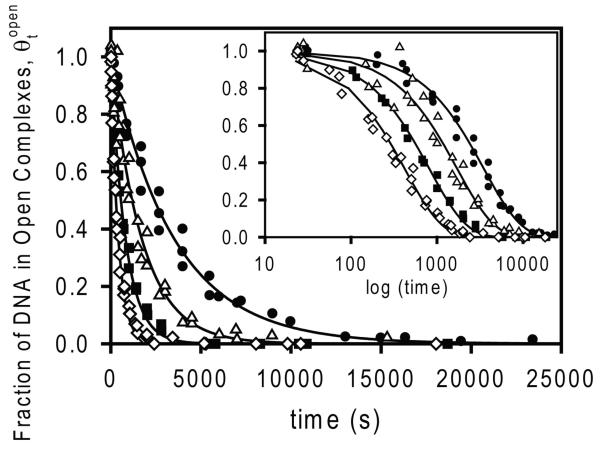
Dissociation kinetic studies probe the steps of disassembly of the clamp/jaw (conversion of RP_o to I₂) and DNA closing (conversion of I₂ to (I₁-I₂)^†). Irreversible dissociation data at 25 °C in 0.23 M – 0.29 M Na⁺ in Cl⁻ buffer are plotted in Fig 5 as θ_t^open vs. time, and fit to a single exponential decay equation (eq 4). To show the quality of these single exponential fits, the inset in Fig 5 plots θ_t^open vs logt; essentially 100% of the decay is described by the fit with dissociation rate constant k_d. This indicates that the steps that convert the final open complex RP_o to the kinetically significant, open intermediate I₂ rapidly equilibrate on the time scale of the dissociation-rate-determining conversion of I₂ to the closed intermediate I₁. (I₁ is not filter-retainable in the presence of heparin.) Values of k_d increase by an order of magnitude with this 25% increase in salt concentration (from 2.9 × 10⁻⁴ s⁻¹ at 0.23 M Na⁺ to 2.4 × 10⁻³ s⁻¹ at 0.29 M Na⁺); these are plotted on a log-log scale vs [Na⁺] in Fig 7 below. The plot is linear with slope Sk_d = 9.2 ± 0.1, consistent with a previous determination for this promoter in its natural context (12).

Figure 5.

Kinetics of the irreversible dissociation of open complexes at the λP_R promoter in NaCl buffer at 25 °C. Representative values of ${\theta }_t^{\mathit{open}}$ as a function of time (t) determined using nitrocellulose filter binding at four different [Na⁺]: 0.23 M (filled circles), 0.25 M (open triangles), 0.27 M (filled squares) and 0.29 M Na⁺ (open diamonds). Theoretical curves through the data are the best fits to eq 4; corresponding first order dissociation rate constants k_d for each [RNAP] are given in Table 2. Insets replot ${\theta }_t^{\mathit{open}}$ as a function of logt, demonstrating the single exponential character of the kinetics over the entire time range.

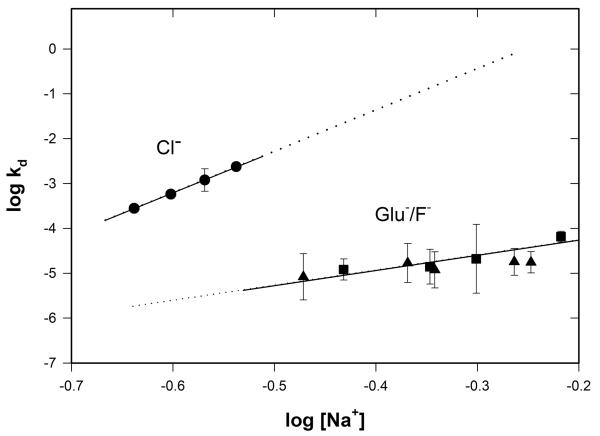
Figure 7.

Log-log plot of dissociation rate constants k_d of RNAP-λσ_R promoter open complexes as a function of [Na⁺] in Cl⁻ and in Glu⁻ or F⁻ buffers at 25 °C. Values of k_d in Cl⁻ are from irreversible dissociation experiments of Fig 5; values of k_d in Glu⁻ and F⁻ are from reversible dissociation experiments like those in Fig 6. Values of k_d are reported in Table 2.

By contrast, dissociation in Glu⁻ is extraordinarily slow at 25 °C and much less dependent on salt concentration. Attempts to directly determine k_d at 0.33 M and 0.6 M Na⁺ in Glu⁻ buffer, using a very high competitor concentration (2.5 mg/mL heparin) in an attempt to ensure irreversibility, exhibited very slow dissociation with rate constants in the range10⁻⁵ to 10⁻⁶ s⁻¹, orders of magnitude slower than in Cl⁻ at lower [salt] (Fig 7). Permanganate footprinting of these 25 °C promoter complexes as a function of [Na⁺] in Glu⁻ buffer shows them to be open in the vicinity of the transcription start site over the range 0.13 M to 0.6 M Na⁺ (TG, unpublished).

As an alternative, faster and more robust method to determine k_d at 25 °C as a function of [Na⁺] in Glu⁻ buffer, we observed the kinetics of approach to promoter binding equilibrium in experiments performed at very low, constant [RNAP], maintained by using heparin as an RNAP buffer. In these experiments, RNAP was initially equilibrated with excess heparin, and subsequently mixed with promoter DNA to initiate open complex formation, which is reversible in excess heparin because the free [RNAP] is so low.

Representative results at 0.46 M Na⁺ in Glu⁻ buffer are shown in Fig 6 as plots of θ_t^open as a function of time for different heparin concentrations. In these experiments, [heparin]_total >> [RNAP]_total >> [promoter]_total. The free [RNAP] is very small (generally [RNAP]_free < [promoter DNA]_total see supplemental Table 3) because almost all RNAP is bound to heparin under the conditions of these experiments. Though not in excess, the free [RNAP] is constant throughout the time course of reversible association because it is buffered by the heparin-binding equilibrium. The heparin binding equilibrium is found to be established rapidly on the time scale of the promoter binding equilibrium, which takes many hours, so the observed kinetics are entirely the approach to equilibrium of promoter binding. The first order rate constants obtained from single exponential fits to these data (see Methods) are relaxation rate constants k_r, which are the sum of the pseudo-first order (constant RNAP concentration) association rate constant (k_a[R]_free) and the dissociation rate constant k_d (see Supplemental Table 3). Hence these decay-to equilibrium experiments are less time-consuming than direct dissociation experiments. To obtain an accurate value for k_d from k_r, independently-determined values of k_a at each of these [Na⁺] in Glu⁻ and F⁻ buffers (Table 1) were used. Consequently k_d is well-determined, especially for conditions where k_d ≥ k_a[R]_free.

Figure 6.

Decay to equilibrium kinetics of promoter association-dissociation at high glutamate (25 °C, 0.46 M Glu⁻) and low, constant RNAP concentrations buffered by heparin. The fraction of promoter DNA in open complexes ${\theta }_t^{\mathit{open}}$ is plotted as a function of logt, where t is the time after addition of promoter DNA (12.5 pM final) to a solution of RNAP (10 nM total concentration) and heparin at total concentrations of 100 μg/mL, 200 μg/mL, 300 μg/mL, 600 μg/mL and 1000 μg/mL. Data points are from two independent experiments at each heparin concentration are plotted, except for 200 μg/mL which was done once. Fits shown are to the single-exponential decay to equilibrium kinetic equations derived for this situation (eqs 5-6 in Methods). From the observed first order rate constant, analyzed using the best fit value of the association rate constant k_a for these conditions (Fig 4B), the dissociation rate constant k_d, the free RNA polymerase concentration, and the equilibrium binding constant K_heparin for binding RNAP to heparin are determined (see Table 3 and supplemental Table 3).

Values of k_d obtained from the analyses of the data of Fig 6 and comparable series of reversible polymerase-promoter binding experiments performed over a range of [Na⁺] in Glu⁻ and F⁻ buffers are tabulated in Table 2 and plotted in Fig 7 as a log-log plot vs. [Na⁺] to compare with the behavior of k_d in Cl⁻ buffer. Values of k_d in Glu⁻ and F⁻ buffers fall on a common line on this log-log plot, greatly offset from k_d values in Cl⁻ buffer, and with a much shallower slope (Sk_d = 3.2 ± 0.8 for Glu⁻/F⁻ vs. Sk_d = 9.2 ± 0.1 for Cl⁻).

Table 2.

Values of k_d as a function of Na⁺ and anion (Cl⁻, Glu⁻ or F⁻) for the dissociation of RP_o at the λP_R promoter at 25 °C

Na+ (M)	kd (s−1)
	Cl−	Glu−	F−
0.23	(2.8±0.1) × 10−4
0.25	(5.8±0.4) × 10−4
0.27	(1.2±0.3) × 10−3
0.29	(2.37±0.09) × 10−3
0.34		(8±4) × 10−6
0.37			(1.2±0.3) × 10−5
0.43		(1.7±0.7) × 10−6
0.45			(1.4±0.5) × 10−5
0.46		(1.2±0.5) × 10−5
0.50			(2.1±0.2) × 10−5
0.55		(1.8±0.5) × 10−5
0.57		(1.8±0.4) × 10−5
0.61			(6.5±0.8) × 10−5
Skd	9.2±0.1	3.2±0.8

Values of k_d in Cl⁻ buffer determined by direct measure of the irreversible rate of dissociation of RP_o initiated by the addition of heparin. Values of k_d in Glu⁻ and F⁻ buffer determined using a decay to equilibrim experiment (eqs 5-6, see Methods) at 25 °C. Sk_d ≡ (∂logk_d /∂log[Na⁺]). Values of k_d in Glu⁻ do not differ from those in F⁻ outside of experimental uncertainty and were fit together to determine Sk_d.

At 0.31 M Na⁺, the salt concentration requiring the least extrapolation of the data sets in Fig 7, k_d is ~10³-fold larger in Cl⁻ than in Glu⁻ or F⁻ buffers. This ratio is predicted to increase with increasing salt concentration if the log-log plot remains linear in Cl⁻ buffer. These differences in magnitude and log-log salt derivative of k_d between Cl⁻ and F⁻ or Glu⁻ are very large, exceeding those previously observed for equilibrium/rate constants of other protein processes, and also contrast with the behaviors seen in Fig 4 for K₁, k₂, and k_a (see Discussion), indicating that very different conformational changes and interfaces are involved in these different steps.

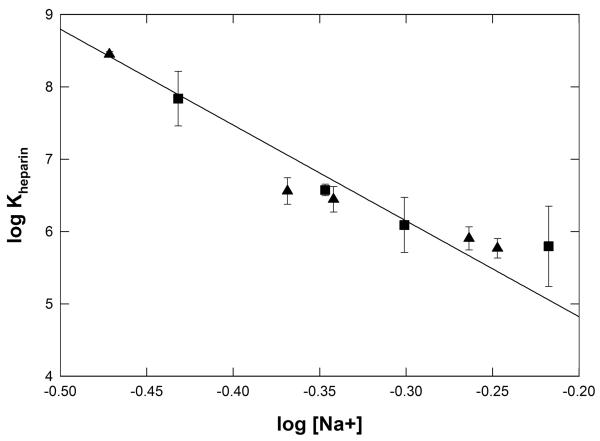
For all determinations of k_d from k_r, the constant free [RNAP] at each [heparin] investigated is also obtained. Values of the free [RNAP] range from ~10⁻¹² M at low [Na⁺] and high [heparin] to ~10⁻¹⁰ M at high [Na⁺] and low [heparin]. Analysis of these decay to equilibrium experiments as a function of heparin concentration at constant salt concentration provides no evidence for subunit dissociation of RNAP holoenzyme at any condition investigated. From these free [RNAP], values of the heparin binding constant K_heparin are obtained at each [Na⁺] investigated in Glu⁻ and F⁻ buffers. Values of K_heparin are plotted as a log-log plot vs. [Na⁺] in Fig 8. In Glu⁻ and F⁻ buffers, the [salt] dependence of K_heparin (SK_heparin = −13 ± 0.2) is similar to that of the RNAP-promoter binding constant (SK_obs = Sk_a − Sk_d = − (8.3 ± 0.2) + (3.2 ± 0.8) = 11.5 ± 1.0).

Figure 8.

Log-log plot of the heparin binding constant K_heparin as a function of [Na⁺] for experiments in Glu⁻ and F⁻ buffers at 25 °C. A linear fit of these data yields SK_heparin = (dlogK_heparin/dlog[Na⁺]) = −13.2 ± 0.8 and an extrapolated 1 M Na⁺ intercept of 2.2 ± 0.3.

DISCUSSION

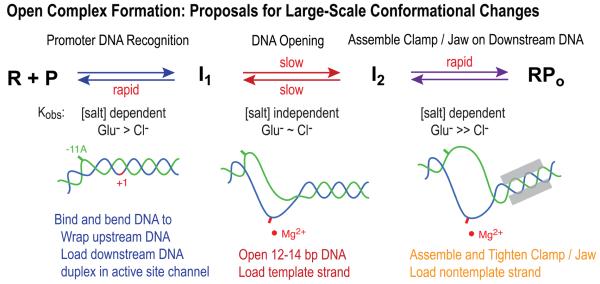
Here we propose interpretations of the effects of [salt] and the difference between effects of Glu⁻ and F⁻ versus Cl⁻ on the steps of open complex formation in terms of extant structural and thermodynamic characterizations of each step. Qualitative comparisons are also made with the effects of these salts on other protein-DNA interactions, on protein folding and DNA melting, and on model processes. Both the similarity of the effects of Glu⁻ and F⁻ and the large differences between effects of these anions and of Cl⁻ on the early and late steps of open complex formation indicate that these are Hofmeister effects and that they arise from greater exclusion of Glu⁻ and F⁻ than of Cl⁻ from nonpolar hydrocarbon surface, as proposed for protein folding (19) and for IHF-H'DNA binding (32). Fig 9 presents an overview of the steps, proposed conformational changes and the effects of [salt] and anion on each. We discuss how the Glu⁻ results here are predicted to affect σ⁷⁰ holoenzyme interactions at strong promoters in vivo during the adaptation to an osmotic upshift.

Figure 9.

Overview of the steps of RP_o formation, proposed conformational changes and the effects of [salt] and anion on each. Schematic based on results in (23, 24, 27, 33, Gries et al., unpublished).

Opening of the Initiation Bubble (−11 to +2) in the Active Site Cleft is Surprisingly Insensitive to [Salt] and Anion: Implications for Regulation of RP_o Formation

In many biochemical processes, including enzyme catalysis and active transport, rapidly reversible initial and final steps bracket a bottleneck step that performs the key biological function (e.g. catalysis/transport). In these cases, regulation is largely achieved by effects of ligands or solutes on the rapidly reversible initial and final steps, but not on the key central catalytic/transport step of the mechanism. In RP_o formation, the first and last steps rapidly equilibrate on the time scale of the cooperative DNA opening step (24). Here and in our previous work, we find large effects of [salt], anion and solutes on the initial and final steps, but not on the central bottleneck step that converts the closed complex I₁ to the unstable open complex I₂. An exception is the action of far upstream DNA as an effector ligand. Truncation of DNA upstream of −47 greatly reduces the opening rate because it reduces the extent of insertion of downstream duplex DNA in the active site cleft in I₁, thereby changing the nature of this intermediate (33).

Such a regulatory strategy would appear to be well-suited to organisms like E. coli that grow over a wide range of solution conditions, or in general to any cell responding to changes in environment. Clearly in order to reprogram genetic expression, DNA opening is required irregardless of solution conditions in the cell. The response to changes in growth conditions utilizes differences in promoter sequence, and/or shifts in the concentrations of sigma factors, “feedback” solutes (KGlu), and stress factors (ppGpp). It will be important to determine whether these factors act to increase or decrease levels of I₁ or I₂, leaving the opening step unaffected, or whether they affect structural features of I₁ or I₂ which are central for DNA opening.

The small magnitude of the [salt] dependences of both rate constants of the DNA opening step (Sk₂ = −1, Sk₋₂ = 0, SK₂ = −1) contrast with the situation for DNA melting in solution, which is significantly more strongly [salt] dependent (25). Indeed this small [salt] dependence of DNA opening by RNAP appears inconsistent with proposed mechanisms based on structural data in which DNA opening occurs outside (above) the active site channel (34-36). To explain the small salt dependence of opening in the active site cleft, we propose that these very small effects of [salt] on a process (DNA opening) which is strongly [salt]-dependent in solution may indicate that the backbones of both DNA strands interact with polymerase throughout the process, and/or that compensation is present between ion uptake and release. Possibly loading DNA as a duplex in the highly positively charged cleft in I₁ (see above) neutralizes the charge in the region (−11 to +2) opened in forming I₂. The subsequent movement of the template strand into the active site might then involve an exchange for basic contacts at the top of the cleft to those at the bottom, thereby buffering it from changes in [salt]. Compensations in the exchange between region 1.1 and the single strands in the channel (as well as unwrapping upstream DNA) may lead to small net changes in ASA, which in turn result in a small net change in binding free energy for the formation of I₂ from I₁. In addition, opening occurs in a deep cleft that is bounded by highly conserved structural features on the large subunits (37), which may in some way isolate the process from the bulk solution.

For the λP_R promoter at typical [salt], the initial open complex I₂ is unstable relative to I₁ at low temperatures (<15 °C), highly unstable relative to RP_o at higher temperatures (24), and therefore is only transiently populated at any temperature. Binding free energy (specifically a favorable entropy change, since the net enthalpy change for conversion of I₁ to I₂ is +25; (22, 24)) drives the opening of the DNA in the channel. However, the small magnitude of SK₂ indicates that ion release is not the origin of the favorable entropy change for this step.

While the thermodynamic origins of this driving force remain unclear, we propose the following series of structural events drive opening in the conversion of I₁ to I₂. Repositioning of σ region 1.1 in response to loading duplex DNA in the cleft in I₁ allows the strands to descend further the channel in (I₁-I₂)^‡, increasing the bending distortion at −12/−11. This change likely exposes bases in the −10 hexamer on the NT strand (38) which are “captured” by the conserved aromatic side chains on region 2 of sigma (39-42). Additionally, a gradient of positive charge may exist in the channel, increasing from the top to the bottom. Such a distribution of lysines and arginines could help bring the template strand down to the base of the cleft once region 1.1 has moved.

For the entire bubble to open, we propose that a highly conserved region on the downstream lobe of β known as fork loop 2 (T. thermophilus (T. th.) 413-430, E. coli 533-550; (37)) may insert in the minor groove of the DNA duplex, as the DNA descends, prying apart the strands and helping to stabilize the open bubble surrounding +1. By analogy with base flipping enzymes, this insertion would further unwind the helix and create an additional ~90° bend near −2/−1. In the crystal structure of the T. th. transcription elongation complex, fork loop 2 is positioned between the nontemplate strand and the backbone of the RNA product (43).

Conversion of the Unstable Open Complex I₂ to the Stable Open Complex RP_o: Evidence for Large-Scale Folding and Assembly of a Clamp/Jaw on Downstream DNA

The finding here that replacement of Cl⁻ by Glu⁻ (or F⁻) greatly increases the lifetime of RP_o at 25 °C, especially at higher [Na⁺] is most consistent with a large-scale burial of hydrocarbon surface in the late steps (from which F⁻ and Glu⁻ are more completely excluded than is Cl⁻ (19)). This work along with our previous studies of k_d as a function of temperature, KCl, urea, and glycine betaine all indicate that large-scale rearrangements occur in the late steps of forming RP_o (24, 27). These steps exhibit a large negative heat capacity change (−1 kcal/K), comparable to that for folding a 75-100 residue globular protein; the effect of urea is consistent with folding at least 100 residues, while the effects of [salt] and GB are consistent with formation of a significant new RNAP-DNA interface involving 10-15 DNA phosphates. The most plausible scenario is that >100 residues in RNAP fold and bind to the downstream DNA backbone in the conversion of I₂ to RP_o (24, 27).

From an analysis which predicts natively disordered regions in E. coli RNAP, we deduced that the regions that fold are parts of the downstream clamp and jaw of β′ (27). Highly conserved in bacterial RNAP (37), the following are positioned near the downstream DNA (+5 to +20) in the FRET model of RP_o (44) and the TEC structure (43): (i) a highly positively charged helix-hairpin-helix (T. th. 470-507, E. coli 194-232), (ii) a C-terminal region (T. th. 1378-1424, E. coli 1263-1310) adjacent to (i) and switch 5 (37); and (iii) the mobile downstream jaw (T. th. 1270-1329, E. coli 1142-1214). Regions (i) and (ii) form part of the ‘clamp’ of RNAP. Strong biochemical evidence exists for interactions between the clamp and jaw and downstream DNA in RP_o. Internal deletions in the jaw (45) as well as binding of the negatively charged phage protein Gp2 (46) to the jaw strongly destablize RP_o at various promoters including λP_R. The helix-hairpin-helix binds near the major groove at +10 in the TEC; deletion of E. coli 210-215 also strongly destabilizes RP_o (47). The lineage-specific sequence insertion 3 (SI3) in E. coli β′ (48) likely also plays a part in the assembly of the stabilizing clamp/jaw. Comprised of a repeated sandwich-barrel-hybrid motif, β′SI3 connects to the “trigger loop” by a flexible 13 amino acid linker (49). Deletion of β′SI3 increases k_d at λP_R by ~4 fold (27). In a model of the TEC, β′SI3 is positioned near the jaw, the downstream lobe of beta and the downstream DNA from +13 to +18 (49).

We proposed that the clamp and jaw domains are mobile and partially disordered in I₂ and assemble on the downstream DNA in the conversion of I₂ to RP_o (27). Because the regions in the clamp/jaw contain runs of positive residues, their interactions with duplex DNA are predicted to release cations. Importantly, our data indicate that the RNAP machinery clamps onto the downstream DNA during I₂ → RP_o, after the entire transcription bubble has been untwisted and opened in the active site channel (I₁ → I₂; Gries et al., unpublished).

Predicting the Salt Concentration Dependence of Forming the 100 bp Wrapped DNA Interface in the Closed Intermediate I₁

The first steps of RP_o formation discriminate promoter from nonpromoter DNA by establishing interactions between sigma regions 4 and 2 and conserved six bp sequences at −35 and −10, respectively (41). However, formation of I₁ at the λP_R promoter creates an extensive interface with DNA that extends well beyond the −10 and −35 regions: protection from hydroxyl radical (•OH) or DNase I cleavage of the DNA backbone in I₁ extends to at least +20 at λP_R (23, 50) (and at the λP_{RM up1} promoter (51)); upstream protection from •OH cleavage at λP_R extends to ~−85 (23) (also apparently at the T7A1 promoter (2)). These data, interpreted using structures of the free RNAP (35, 52) and a complex with a fork junction DNA (from −7 to −41; (34)), are most simply consistent with a model (23) where upstream DNA is wrapped around RNAP and downstream DNA is bound in the active site channel created by the opposition of the β and β′ subunits (footnote 1). What is the relationship between this model of I₁ and SK₁?

In our model of I₁, approximately sixty-two positive (arginine (R), lysine (K), histidine (H)) and twenty-five negative (aspartate (D), glutamate (E)) side chains lie near the DNA phosphate backbone, yielding a net charge of ~+37. With the exception of the C-terminal domain (CTD) of α (modeled using the crystal structure of the E. coli subunits (53)), this charge count is based on the T. th. RNAP subunits (αNTD, β, β′, ω, σ^A). However, the charged residues involved in forming the interface from −55 to +20 are highly conserved in bacterial RNAP. With the exception of three (R, K, H) and three (D, E) on β predicted to contact DNA from −11 to +5 in the model of I₁, the remainder from the count above (R, K, H, E, D) are present in E. coli. While the one-to-one correspondence for charged residues in the region upstream of −55 is more variable between T. th. and E. coli, the overall charge distribution near the upstream wrapping track (−70 to −85) appears relatively conserved. This approximate structural estimate provides a reasonable basis for predicting the contribution from neutralization of DNA phosphate charge to the observed [salt] dependence of I₁ formation. For binding of an oligocation ligand with a charge of +37 to DNA, the predicted low-[salt] value of SK_obs is approximately −32 (or more negative if ion release from the ligand contributes to SK_obs).

Interpretation of the Much Smaller than Expected Effect of [Salt] on I₁ Formation

While interactions with the −35 and −10 hexamers involve base specific interactions with σ⁷⁰ regions 4 and 2, respectively, the interface in I₁ is composed of predominantly nonspecific DNA backbone interactions with the other RNAP subunits (e.g. αCTDs, β and β′). Our estimate of SK₁ (~−30 (above)) is much larger in magnitude than the observed log-log dependence of K₁ on [Na⁺] (SK₁ ~ −7 in both Cl⁻ and Glu⁻ buffers). This difference suggests that some process involving extensive salt ion uptake by RNAP has evolved to largely compensate for this predicted cation release from the promoter DNA in forming I₁ from free RNAP and promoter DNA. We propose two scenarios involving cation uptake that may occur in I₁ formation: disruption of surface salt bridges on RNAP coupled to forming the interface (32, 54, 55), and the placement of duplex DNA next to negatively charged region 1.1 in the channel.

Given the juxtaposition of negative and positive charges in the upstream half of the I₁ interface, we propose that coupled salt bridge disruption acts to reduce the binding constant K₁ and the magnitude of its log-log salt derivative |SK₁|, and likely explains the large negative ΔC_P of this step (−1.4 kcal M⁻1 K⁻1; (22)). However, the walls and floor DNA active site channel of RNAP are highly basic. Given this charge distribution, it seems unlikely that salt bridge disruption could offset the salt ion release from binding >20 bp of downstream duplex in the channel. What does?

In free σ⁷⁰ RNAP, the highly negatively charged region 1.1 lies in the active site channel (44). Where is it in I₁? Solute probes of changes in anionic (GB) and amide (urea) surface area do not detect any signature of release of sigma region 1.1 in forming I₁ (27). Instead, our estimates of the burial of anionic and amide surface in the I₁ protein-DNA interface based on structural data are completely consistent with the magnitude of effects of glycine betaine and urea on K₁. As a result, we proposed that it was most likely that region 1.1 is not expelled during the formation of I₁, remaining bound and masking the active site (27). It seems likely that any cation release from loading of duplex DNA in the channel must be offset by cation uptake as a result of placing the two highly negatively charged regions next to each other.

In the model of I₁, DNA downstream of +1 lies above region 1.1 (23, 27). Region 1.1 has a net charge of −19 and can be modeled as a negatively charged alpha-helical “plug” at the N-terminus (56) followed by an unstructured, negatively charged coil. We speculate that positioning downstream duplex DNA next to this negatively charged single stranded (ss) DNA mimic may be somewhat analogous to DNA triplex formation. Theoretically the limiting law per charge ion association is 0.76 for ss DNA, 0.88 for double stranded (ds) DNA, increasing to 0.92 in a triplex (ts). If this model is appropriate for placing 20 bp of duplex DNA near sigma region 1.1, then we predict approximately five cations are taken up.

Implications of Effects of Glu⁻ on the Steps of Initiation for Adaptation to Osmotic Stress in vivo

In vitro, Gralla observed that transcription from open complexes at the strong σ⁷⁰ promoter lacUV5 decreases greatly as the KGlu concentration is increased from 0.1 to 0.4 M (9). If Cl⁻ were the cytoplasmic anionic osmolyte, such increases in K⁺ concentrations would cause dissociation of RNAP and many other proteins from nucleic acids. However, in Glu⁻, open complexes at the strong λP_R promoter are unexpectedly long-lived over the entire range of [salt] investigated here, (k_d < 10⁻⁵ s⁻¹ at 25 °C even at 0.5 M Glu⁻, corresponding to a lifetime (1/k_d) of open complexes exceeding one day). These data suggest that open complexes at strong σ⁷⁰ promoters in vivo (where negative supercoiling should also favor RP_o formation) do not dissociate after an osmotic upshift, but may have difficulty escaping the promoter to transcribe.

While transcription from many σ⁷⁰ holoenzyme-promoter is reduced at high Glu⁻, transcription of osmotically-regulated promoters by σ ^S holoenzyme increases (7, 8). Intriguingly, in vitro DNase I footprints of σ^S RNAP-osmY promoter complexes reveal that contacts upstream of −30 are lost as [KGlu] increases, allowing escape from the promoter (9). Gralla and coworkers deduced from these data that high concentrations of K⁺ and Glu⁻ are able to release σ^S RNAP that are poised at lower salt ion concentrations, allowing both transcription and reinitiation (9, 57, 58). By contrast, σ⁷⁰ RNAP appears to remain bound an open promoter complex as [salt] increases in Glu⁻ buffer (this work), but its ability to transcribe is progressively reduced (9). Hence in vivo salt ion concentrations themselves appear capable both of switching transcription from one set of genes to another, and of poising RNAP to rapidly start at another set when conditions change (9, 58, 59).

Gralla and coworkers observe that the ability of an anion to increase σ^S transcription at osmotic genes is correlated with its position in the Hofmeister series (10). Since the exclusion of the Hofmeister anion Glu⁻ from hydrocarbon surfaces causes it to favor processes that reduce the exposure of nonpolar surface to the solution (e.g. folding, assembly, binding) (18), differences in the amounts and types of surface area changes in biological processes will in turn give rise to differential effects of Glu⁻.

Abbreviations

ASA

water-accessible surface area

GB

glycine betaine

PNAI

protein nucleic acid interactions

RNAP

RNA polymerase

σ^S

stationary phase sigma factor