Abstract
Rapid developments in geographical information systems (GIS) continue to generate interest in analyzing complex spatial datasets. One area of activity is in creating smoothed disease maps to describe the geographic variation of disease and generate hypotheses for apparent differences in risk. With multiple diseases, a multivariate conditionally autoregressive (MCAR) model is often used to smooth across space while accounting for associations between the diseases. The MCAR, however, imposes complex covariance structures that are difficult to interpret and estimate. This article develops a much simpler alternative approach building upon the techniques of smoothed ANOVA (SANOVA). Instead of simply shrinking effects without any structure, here we use SANOVA to smooth spatial random effects by taking advantage of the spatial structure. We extend SANOVA to cases in which one factor is a spatial lattice, which is smoothed using a CAR model, and a second factor is, for example, type of cancer. Datasets routinely lack enough information to identify the additional structure of MCAR. SANOVA offers a simpler and more intelligible structure than the MCAR while performing as well. We demonstrate our approach with simulation studies designed to compare SANOVA with different design matrices versus MCAR with different priors. Subsequently a cancer-surveillance dataset, describing incidence of 3-cancers in Minnesota’s 87 counties, is analyzed using both approaches, showing the competitiveness of the SANOVA approach.
Key words and and phrases: Analysis of variance, Bayesian inference, conditionally autoregressive model, hierarchical model, smoothing
1. Introduction
Statistical modeling and analysis of spatially referenced data receive considerable interest due to the increasing availability of geographical information systems (GIS) and spatial databases. For data aggregated over geographic regions such as counties, census tracts or ZIP codes (often called areal data), with individual identifiers and precise locations removed, inferential objectives focus on models for spatial clustering and variation. Such models are often used in epidemiology and public health to understand geographical patterns in disease incidence and morbidity. Recent reviews of methods for such data include Lawson et al. (1999), Elliott et al. (2000), Waller and Gotway (2004) and Rue and Held (2005). Traditionally such data have been modeled using conditionally specified probability models that shrink or smooth spatial effects by borrowing strength from neighboring regions. Perhaps the most pervasive model is the conditionally autoregressive (CAR) family pioneered by Besag (1974), which has been widely investigated and applied to spatial epidemiological data [Wakefield (2007) gives an excellent review]. Recently the CAR has been extended to multivariate responses, building on multivariate conditional autoregressive (MCAR) models described by Mardia (1988). Gelfand and Vonatsou (2003) and Carlin and Banerjee (2003) discussed their use in hierarchical models, while Kim, Sun and Tsutakawa (2001) presented a different “twofold CAR” model for counts of two diseases in each areal unit. Other extensions allowing flexible modeling of cross-correlations include Sain and Cressie (2002), Jin, Carlin and Banerjee (2005) and Jin, Banerjee and Carlin (2007). The MCAR can be viewed as a conditionally specified probability model for interactions between space and an attribute of interest. For instance, in disease mapping interest often lies in modeling geographical patterns in disease rates or counts of several diseases. The MCAR acknowledges dependence between the diseases as well as dependence across space. However, practical difficulties arise from MCAR’s elaborate dependence structure: most interaction effects will be weakly identified by the data, so the dependence structure is poorly identified. In hierarchical models [e.g., Gelfand and Vonatsou (2003), Jin, Carlin and Banerjee (2005 Jin, Carlin and Banerjee (2007)], strong prior distributions may improve identifiability, but this is not uncontroversial, as inferences are sensitive to the prior and perhaps unreliable without genuine prior information. This article proposes a much simpler and more interpretable alternative to the MCAR, modeling multivariate spatial effects using smoothed analysis of variance (SANOVA) as developed by Hodges, Carlin and Fan (2007), henceforth HCSC. Unlike an ANOVA that is used to identify some interaction effects to retain and others to remove, SANOVA mostly retains effects that are large, mostly removes those that are small, and partially retains middling effects. (Loosely speaking, “large,” “middling” and “small” describe the size of the unsmoothed effects compared to their standard errors.) To accommodate rich dependence structures, MCAR introduces weakly identifiable parameters that complicate estimation. SANOVA, on the other hand, focuses instead on smoothing interactions to yield more stable and reliable results. Our intended contribution is to show how SANOVA can solve the multiple disease mapping problem while avoiding the dauntingly complex covariance structures imposed by MCAR and its generalizations. We demonstrate that SANOVA produces inference that is largely indistinguishable from MCAR, yet SANOVA is simpler, more explicit, easier to put priors on and easier to estimate. The rest of the article is as follows. Section 2 reviews SANOVA and MCAR, identifying SANOVA as a special case of MCAR. Section 3 is a “tournament” of simulation experiments comparing SANOVA with MCAR for normal and Poisson data, while Section 4 analyzes data describing the number of deaths from lung, larynx and esophagus cancer in Minnesota between 1990 and 2000. A summary and discussion of future research in Section 5 concludes the paper. Zhang, Hodges and Banerjee (2009) (Appendices) gives computational and technical details.
2. The competitors
2.1. Smoothing spatial effects using SANOVA
2.1.1. SANOVA for balanced, single-error-term models [HCSC (2007)]
Consider a balanced, single-error-term analysis of variance, with M1 degrees of freedom for main effects and M2 degrees of freedom for interactions. Specify this ANOVA as a linear model: let A1 denote columns in the design matrix for main effects, and A2 denote columns in the design matrix for interactions. Assume the design has c cells and n observations per cell, giving cn observations in total. To simplify later calculations, normalize the columns of A1 and A2 so and . (Note: HCSC normalized columns differently, fixing and .) Then write the ANOVA as
| (1) |
where with η0 being a precision, y is cn × A1 is cn × M1, A2 is cn × M2, Θ1 is M1 × 1, Θ2 is M2 × 1, and ε is cn × 1. This ANOVA is smoothed by further modeling Θ. HCSC emphasized smoothing interactions, although main effects can be smoothed by exactly the same means. Following HCSC, we add constraints (or a prior) on Θ2 as θM1+j ~ N(0, 1/ηj) for j = 1, …, M2, written as
| (2) |
where , in the manner of Lee and Nelder (1996) and Hodges (1998). Combining (1) and (2), express this hierarchical model as a linear model:
| (3) |
More compactly, write
| (4) |
where Y has dimension (cn + M2) × 1 and e’s covariance Γ is block diagonal with blocks for the data cases (rows of X corresponding to the observation y) and Γ2 = diag(1/η1, …, 1/ηM2) for the constraint cases (rows of X with error term δ). For convenience, define the matrix XD = [A1|A2], the data-case part of X. This development can be done using the mixed linear model (MLM) formulation traditionally written as y = Xβ + Zu + ε;, where our (1) supplies this equation and u = Θ2 ~ N(0, Γ2). The development to follow can also be done using the MLM formulation at the price of slightly greater complexity, so we omit it. HCSC developed SANOVA for exchangeable priors on groups formed from components of Θ2. The next section develops the extension to spatial smoothing.
2.1.2. What is CAR?
Suppose a map has N regions, each with an unknown quantity of interest φi, i = 1, …, N. A conditionally autoregressive (CAR) model specifies the full conditional distribution of each φi as
| (5) |
where i ~ j denotes that region j is a neighbor of region i (typically defined as spatially adjacent), and mi is the number of region i’s neighbors. Equation (5) reduces to the well-known intrinsic conditionally autoregressive (ICAR) model [Besag, York and Mollié (1991)] if α = 1 or an independence model if α = 0. The ICAR model induces “local” smoothing by borrowing strength from neighbors, while the independence model assumes spatial independence and induces “global” smoothing. The CAR prior’s smoothing parameter α also controls the strength of spatial dependence among regions, though it has long been appreciated that a fairly large α may be required to induce large spatial correlation; see Wall (2004) for recent discussion and examples. It is well known [e.g., Besag (1974)] that the conditional specifications in (5) lead to a valid joint distribution for φ = (φ1, …, φN)′ expressed in terms of the map’s neighborhood structure. If Q is an N × N matrix such that Qii = mi, Qij = − α whenever i ~ j and Qij = 0 otherwise, then the intrinsic CAR model [Besag, York and Mollié (1991)] has density
| (6) |
In (6) τ is the spatial precision parameter, τQ is the precision matrix in this multivariate normal distribution and G is the number of “islands” (disconnected parts) in the spatial map [Hodges, Carlin and Fan (2003)]. When α ∈ (0, 1), (6) is a proper multivariate normal distribution. When α = 1, Q is singular with Q1 = 0; Q has rank N − G in a map with G islands, therefore, the exponent on τ becomes (N − G)/2. In hierarchical models, the CAR model is usually used as a prior on spatial random effects. For instance, let Yi be the observed number of cases of a disease in region i, i = 1, …, N, and Ei be the expected number of cases in region i. Here the Yi are treated as random variables, while the Ei are treated as fixed and known, often simply proportional to the number of persons at risk in region i. For rare diseases, a Poisson approximation to a binomial sampling distribution for disease counts is often used, so a commonly used likelihood for mapping a single disease is
| (7) |
where . The xi are explanatory, region-specific regressors with coefficients β and the parameter μi is the log-relative risk describing departures of observed from expected counts, that is, from Ei. The hierarchy’s next level is specified by assigning the CAR distribution to φ and a hyper-prior to the spatial precision parameter τ. In the hierarchical setup, the improper ICAR with α = 1 gives proper posterior distributions for spatial effects. In practice, Markov chain Monte Carlo (MCMC) algorithms are designed for estimating posteriors from such models and the appropriate number of linear constraints on the φ suffices to ensure sampling from proper posterior distributions [Banerjee, Carlin and Gelfand (2004), pages 163–164, give details].
2.1.3. How does CAR fit into SANOVA?
To use CAR in SANOVA, the key is re-expressing the improper CAR, that is, (6) with α = 1. Let Q have spectral decomposition Q = VDV′, where V is an orthogonal matrix with columns containing Q’s eigenvectors and D is diagonal with nonnegative diagonal entries. D has G zero diagonal entries, one of which corresponds to the eigenvector , by convention the N th (right-most) column in V. Define a new parameter Θ = V′φ, so Θ has dimension N and precision matrix τD. Giving an N -vector Θ a normal prior with mean zero and precision τD is equivalent to giving φ = VΘ a CAR prior with precision τQ. Θ consists of , the scaled average of the φi, along with N − 1 contrasts in φ, which are orthogonal to by construction. Thus, the CAR prior is informative (has positive precision) only for contrasts in φ, while putting zero precision on , the overall level, and on G − 1 orthogonal contrasts in the levels of the G islands. In other words, the CAR model can be thought of as a prior distribution on the contrasts rather than individual effects (hence the need for the sum-to-zero constraint). A related result, discussed in Besag, York and Mollié (1995), shows the CAR to be a member of a family of “pairwise difference” priors. This reparameterization allows the CAR model to fit into the ANOVA framework, with ΘGM corresponding to the ANOVA’s grand mean and the rest of Θ, ΘReg, corresponding to V(−)′φ, where V(−) is V excluding the column , consisting of N − 1 orthogonal contrasts among the N regions and giving the N − 1 degrees of freedom in the usual ANOVA:
Giving φ a CAR prior is equivalent to giving Θ a N(0, τD) prior; the latter are the “constraint cases” in HCSC’s SANOVA structure. The precision DNN = 0 for the overall level is equivalent to a flat prior on ΘGM, though ΘGM could alternatively have a normal prior with mean zero and finite variance. If G > 1, the CAR prior also puts zero precision on G − 1 contrasts in φ, which are contrasts in the levels of the G islands [Hodges, Carlin and Fan (2003)].
2.2. SANOVA as a competitor to MCAR
2.2.1. Multivariate conditionally autoregressive (MCAR) models
With multiple diseases, we have unknown φij corresponding to region i and disease j, where i = 1, …, N and j = 1, …, n. Letting Ω be a common precision matrix (i.e., inverse of the covariance matrix) representing correlations between the diseases in a given region, MCAR distributions arise through conditional specifications for φ = (φi1, …, φin)′:
| (8) |
These conditional distributions yield a joint distribution for :
| (9) |
where Q is defined as in Section 2.1.2 and again (9) is an improper density when α = 1. However, as for the univariate CAR, this yields proper posteriors in conjunction with a proper likelihood. The specification above is a “separable” dispersion structure, that is, the covariances between the diseases are invariant across regions. This may seem restrictive, but relaxing this restriction gives even more complex dispersion structures [see Jin, Banerjee and Carlin (2007) and references therein]. As mentioned earlier, our focus is to retain the model’s simplicity without compromising the primary inferential goals. We propose to do this using SANOVA and will compare it with the separable MCAR only.
2.2.2. SANOVA with Minnesota counties as one factor
We now describe the SANOVA model using the Minnesota 3-cancer dataset. Consider the Minnesota map with N = 87 counties, and suppose each county has counts for n = 3 cancers. County i has an n-vector of parameters describing the n cancers, φi = (φi1, φi2, …, φin)′; define the Nn vector φ as . For now, we are vague about the specific interpretation of φij; the following description applies to any kind of data. Assume the N × N matrix Q describes neighbor pairs among counties as before. The SANOVA model for this problem is a 2-way ANOVA with factors cancer (“CA,” n levels) and county (“CO,” N levels) and no replication. As in Section 2.1.1, we model φ with a saturated linear model and put the grand mean and the main effects in their traditional positions as in ANOVA (matrix dimensions and definitions appear below the equation):
| (10) |
where HCA is an n × (n − 1) matrix whose columns are contrasts among cancers, so , and is the j th column of HCA; and V (−) is V without its N th column , so it has N − 1 columns, each a contrast among counties, that is, , and V(−)′V(−) = IN−1. The column labeled “Grand mean” corresponds to the ANOVA’s grand mean and has parameter ΘGM; the other blocks of columns labeled as main effects and interactions correspond to the analogous ANOVA effects and to their respective parameters ΘCA, ΘCO, ΘCO×CA. Defining prior distributions on Θ completes the SANOVA specification. We put independent flat priors (normal with large variance) on ΘGM and ΘCA, which are, therefore, not smoothed. This is equivalent to putting a flat prior on each of the n cancer-specific means. To specify the smoothing priors, define . Let the county main effect parameter ΘCO have prior ΘCO ~ NN−1(0, τ0D(−)), where D(−) corresponds to V(−), that is, D without its N th row and column, τ0 > 0 is unknown and τ0D(−) is a precision matrix. Similarly, let the j th group of columns in the cancer-by-county interaction, , have prior , for τj > 0 unknown. Each of the priors on ΘCO and the is a CAR prior; the overall level of each CAR, with prior precision zero, has been included in the grand mean and cancer main effects.
To compare this to the MCAR model, use SANOVA’s priors on Θ to produce a marginal prior for φ comparable to the MCAR’s prior on φ (Section 2.2.1); in other words, integrate ΘCO and ΘCO×CA out of the foregoing setup. A priori,
| (11) |
has precision , where K is the columns of the design matrix for the county main effects and cancer-by-county interactions—the right-most n(N − 1) columns in equation (10)’s design matrix—and is an orthogonal matrix. Appendix A in Zhang, Hodges and Banerjee (2009) gives a proof.
2.2.3. Comparing SANOVA vs MCAR
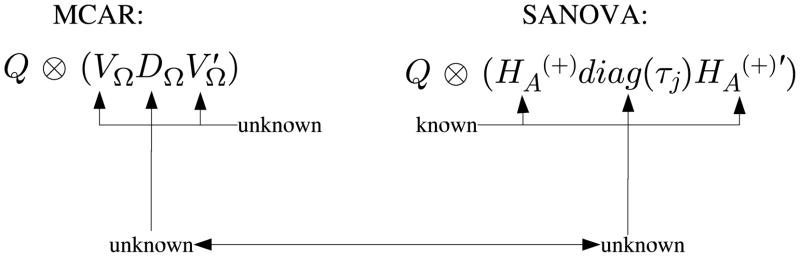
Defining φ as in Sections 2.2.1 and 2.2.2, consider the MCAR prior for φ, with within-county precision matrix Ω. Let Ω have spectral decomposition , where DΩ is n × n diagonal and VΩ is n × n orthogonal. Then the prior precision of φ is , where Q is the known neighbor relations matrix and VΩ and DΩ are unknown. Comparing MCAR to SANOVA, the prior precision matrices for the vector φ are as in Figure 1. SANOVA is clearly a special case of MCAR in which is known. Also, as described so far, has one column proportional to 1n with the other columns being contrasts, while MCAR avoids this restriction. MCAR is thus more flexible, while SANOVA is simpler, presumably making it better identified and easier to set priors for. MCAR should have its biggest advantage over SANOVA when the “true” VΩ is not like for any specification of the smoothing precisions τj. However, because data sets often have modest information about higher-level variances, it may be that using the wrong usually has little effect on the analysis. In other words, SANOVA’s performance may be relatively stable despite having to specify , while MCAR may be more sensitive to Ω’s prior.
Fig. 1.
Comparing prior precision matrices for φ in MCAR and SANOVA.
2.3. Setting priors in MCAR and SANOVA
2.3.1. Priors in SANOVA
For the case of normal errors, based on equations (1) and (10), setting priors for Θ, τj, η0 completes a Bayesian specification. Since τ and η0 are precision parameters, one possible prior is Gamma; this paper uses a Gamma with mean 1 and variance 10. As mentioned, the grand mean and cancer main effects θ1, θ2, θ3 have flat priors with π(θ) ∝ 1, though they could have proper informative priors. The priors for θ4, … are set according to the SANOVA structure as in Section 2.2.2. We ran chains drawing in the order θ, τ and η0 [Appendix B in Zhang, Hodges and Banerjee (2009) gives details]. Hodges, Carlin and Fan (2007) also considered priors on the degrees of freedom in the fitted model, some conditioned so the degrees of freedom in the model’s fit were fixed at a certain degree of smoothness. The present paper emphasizes comparing MCAR and SANOVA, so we do not consider such priors. For the case of Poisson errors, we use a normal prior with mean 0 and variance 106 for the grand mean and cancer main effects θ1, θ2, θ3. The other θi s are given normal CAR priors as discussed in Section 2.2.2. For the prior on the smoothing precisions τj, we use Gamma with mean 1 and variance 10. To reduce high posterior correlations among the θs, we used a transformation during MCMC; Appendix C in Zhang, Hodges and Banerjee (2009) gives details.
2.3.2. Priors in MCAR
MCAR models were fitted in WinBUGS. For the normal-error case, we used this model and parameterization:
| (12) |
i = 1, …, N; j = 1, …, n, where η0 has a gamma prior with mean 1 and variance 10 as for SANOVA. To satisfy WinBUGS’s constraint that Σi Sij = 0, we add cancer-specific intercepts βj. We give βj a flat prior and for S, the spatial random effects, we use an intrinsic multivariate CAR prior. Similarly, in the Poisson case
| (13) |
where Eij is an offset. Prior settings for βj and Sij are as in the normal case. For MCAR priors, the within-county precision matrix Ω needs a prior; a Wishart distribution is an obvious choice. If Ω ~ Wishart(R, ν), then E(Ω) = νR−1. We want a “vague” Wishart prior; usually ν = n is used but little is known about how to specify R. Thus, we considered three different Rs, each proportional to the identity matrix. One of these priors sets R’s diagonal entries to Rii = 0.002, close to the setting used in an example in the GeoBUGS manual (oral cavity cancer and lung cancer in West Yorkshire). The other two Rs are the identity matrix and 200 times the identity. For the special case n = 1, where the Wishart reduces to a Gamma, these Wisharts are Γ(0.5, 0.001), Γ(0.5, 0.5) and Γ(0.5, 100), respectively.
3. Simulation experiment
For this simulation experiment, artificial data were simulated from the model used in SANOVA with a spatial factor, as described in Section 2.2.2. Three different types of Bayesian analysis were applied to the simulated data: SANOVA with the same used to generate the simulated data (called “SANOVA correct”); SANOVA with incorrect ; and MCAR. SANOVA correct is a theoretical best possible analysis in that it takes as known things that MCAR estimates, that is, it uses additional correct information. SANOVA correct cannot be used in practice, of course, because the true is not known. MCAR vs SANOVA with incorrect is the comparison relevant to practice, and comparing them to SANOVA correct shows how much each method pays for its “deficiency” relative to SANOVA correct. Obviously it is not enough to test the SANOVA model using only data generated from a similar SANOVA model. To avoid needless computing and facilitate comparisons, instead of generating data from an MCAR model and fitting a SANOVA model as specified above, we use a trick that is equivalent to this. Section 3.1.2 gives the details.
3.1. Design of the simulation experiment
We simulated both normally-distributed and Poisson-distributed data. For both types of data, we considered two different true sets of smoothing parameters r = τ/η0 or τ (Table 1). For the normal data, we considered τ/η0, since this ratio determines smoothing in normal models, and we also considered two error precisions η0 (Table 1).
Table 1.
Experimental conditions in the simulation experiments
| Error distribution | η0 | (τ0/η0, τ1/η0, τ2/η0)|(τ0,τ1, τ2) | Data name |
|---|---|---|---|
| Normal | 1 | (100, 100, 0.1) | Data1 |
| 1 | (0.1, 100, 0.1) | Data2 | |
| 10 | (100, 100, 0.1) | Data3 | |
| 10 | (0.1, 100, 0.1) | Data4 | |
| Poisson | NA | (100, 100, 0.1) | Data5 |
| NA | (0.1, 100, 0.1) | Data6 |
3.1.1. Generating the simulated data sets
To generate data from the SANOVA model, we need to define the true . Let
We used HA1 as the correct ; its columns are scaled to have length 1. Given V(−) and with known, one draw of Θ and ε produces a draw of XDΘ +ε, therefore a draw of y. In the simulation, we let the grand mean and main effects, which are not smoothed, have true value 5. Each observation is simulated from a 3 × 20 factorial design, where 3 is the number of cancers and 20 is the number of counties. We used the 20 counties in the right lower corner of Minnesota’s map, with their actual neighbor relations. Thus, the dimension of each artificial data set is 60. The simulation experiment is a repeated-measures design, in which a “subject” s in the design is a draw of (δ(s), γ (s)), referring to equation (3), where and specify Θ and γ(s) ~ N60(0, I60) gives ε. For the normal-errors case, 100 such “subjects” were generated. Given a design cell in the simulation experiment with τ = (a, b, c) and η0 = d, the artificial data set for subject s is . All factors of the simulation experiment were applied to each of the 100 “subjects.” For the normally-distributed data, the simulation experiment had these factors: (a) the true (τ0/η0, τ1/η0, τ2/η0): (100, 100, 0.1) or (0.1, 100, 0.1); (b) the true error precision η0: 1 or 10; and (c) six statistical methods, described below in Section 3.1.2. Each design cell described in Table 1 thus had 100 simulated data sets. Similarly, for the Poisson-data experiment, another 100 “subjects” were generated, but now there is no γ(s). Thus, each “subject” s is a vector δ(s), where δ(s) is as described above. For the design cell with τ = (100, 100, 0.1), the artificial data for subject s is y(s) ~ Poisson(μ(s)), where . In the simulation experiment, we use “internal standardization” of the Minnesota 3-cancer data to supply the expected numbers of cancers Eij. Among the 20 extracted counties, Hennepin county has the largest average population over 11 years, about 1.1 million; its cancer counts are 5294, 119 and 439 for lung, larynx and esophagus respectively. Faribault county has the smallest average population, 16,501, with cancer counts 110, 7 and 13 respectively. The Eij have ranges 80 to 5275, 2 to 113 and 7 to 449 for lung, larynx and esophagus cancer respectively. For the Poisson data, the simulation experiment had these factors: (a) the true τ0, τ1, τ2: (100, 100, 0.1) or (0.1, 100, 0.1); and (b) six statistical methods described below in Section 3.1.2. Again, each of the two design cells in Table 1 had 100 simulated data sets.
3.1.2. The six methods (procedures)
For each simulated data set, we did a Bayesian analysis for each of six different models described in Table 2. The six models are: SANOVA with the correct , HA1; SANOVA with a somewhat incorrect , HA2 given below; a variant SANOVA with a very incorrect , HAM given below; MCAR with Rii = 0.002; MCAR with Rii = 1; and MCAR with Rii = 200 (see Section 2.3.2). HA2 and HAM are
Table 2.
The six statistical methods used in the simulation experiment
| Procedure | Prior |
|---|---|
| SANOVA with correct | η0, τj ~ Γ(0.1, 0.1) for j = 0, 1, 2 |
| SANOVA with incorrect | η0, τj ~ Γ(0.1, 0.1) for j = 0, 1, 2 |
| Variant SANOVA with HAM | η0, τj ~ Γ(0.1, 0.1) for j = 0, 1, 2 |
| MCAR | Ω~ Wishart(R, 3), R = 0.002I3 |
| MCAR | Ω~ Wishart(R, 3), R = I3 |
| MCAR | Ω~ Wishart(R, 3), R = 200I3 |
The incorrect HA2 has the same first column (grand mean) as the correct HA1, so it differs from the correct HA1, though less than it might. As noted above, we need to see how the SANOVA model performs for data generated from an MCAR model in which VΩ from Figure 1 does not have a column proportional to 1n. To do this without needless computing, we used a trick: we used the data generated from a SANOVA model with HA1 and fit the variant SANOVA mentioned above, in which is replaced by the orthogonal matrix HAM with no column proportional to 1n, chosen to be very different from HA1. For normal errors (Data1 through Data4), this is precisely equivalent to fitting a SANOVA with to data generated from an MCAR model with VΩ = BHA1, for , that is,
| (14) |
(to 2 decimal places). For Poisson errors (Data5, Data6), the equivalence is no longer precise but the divergence of fitted SANOVA [using ] and
generated data [using ] is quite similar. Finally, we considered three priors for MCAR because little is known about how to set this prior and we did not want to hobble MCAR with an ill-chosen prior. For the SANOVA and variant SANOVA analyses, we gave τj a Γ (0.1, 0.1) prior with mean 1 and variance 10 for both the normal data and the Poisson data.
3.2. Outcome measures
To compare the six different methods for normal and Poisson data, we consider three criteria. The first is average mean squared error (AMSE). For each of the 60 (XDΘ)ij, the mean squared error is defined as the average squared error over the 100 simulated data sets. AMSE for each design cell in the simulation experiment is defined as the average of mean squared error over the 60 (XDΘ)ij. Thus, for the design cell labeled DataK in Table 1, define
| (15) |
where L = 100, N = 20, n = 3, K = 1, …, 4 for Normal, K = 5, 6 for Poisson, Θ is the true value and Θ̂is the posterior median of Θ. For each design cell (K), the Monte Carlo standard error for AMSE is (100)−0.5 times the standard deviation, across DataK’s 100 simulated data sets, of . The second criterion is the bias of XDΘ. For each of DataK’s 100 simulated data sets, first compute posterior medians of (XDΘ)1,1, …, (XDΘ)20,3, then average each of those posterior medians across the 100 simulated data sets. From this average, subtract the true (XDΘ)ij s to give the estimated bias for each of the 60 (XDΘ)ij s. MBIAS is defined as the 2.5th, 50th and 97.5th percentiles of the 60 estimated biases. More explicitly, for design cell DataK, MBIAS is
| (16) |
Finally, the coverage rate of Bayesian 95% equal-tailed posterior intervals, “PI rate,” is the average coverage rate for the 60 individual (XDΘ)ij s.
3.3. Markov chain Monte Carlo specifics
While the MCAR models were implemented in WinBUGS, our SANOVA implementations were coded in R and run on Unix. The different architectures do not permit a fair comparison between the run times of SANOVA and MCAR. However, the SANOVA models have lower computational complexity than the MCAR models: MCAR demands a spectral decomposition in every iteration, while SANOVA does not. For each of our models, we ran three parallel MCMC chains for 10,000 iterations. The CODA package in R (www.r-project.org) was used to diagnose convergence by monitoring mixing using Gelman–Rubin diagnostics and autocorrelations [e.g., Gelman et al. (2004), Section 11.6]. Sufficient mixing was seen within 500 iterations for the SANOVA models, while 200 iterations typically revealed the same for the MCAR models; we retained 8000 × 3 samples for the posterior analysis.
3.4. Results
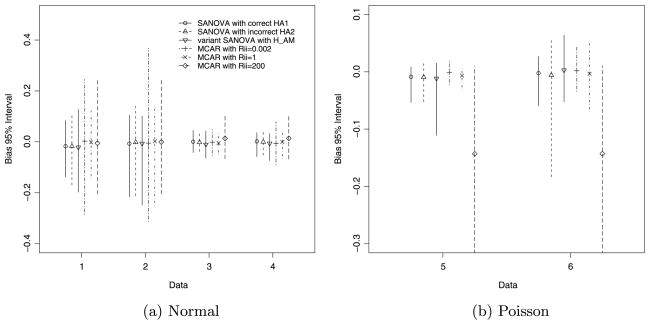
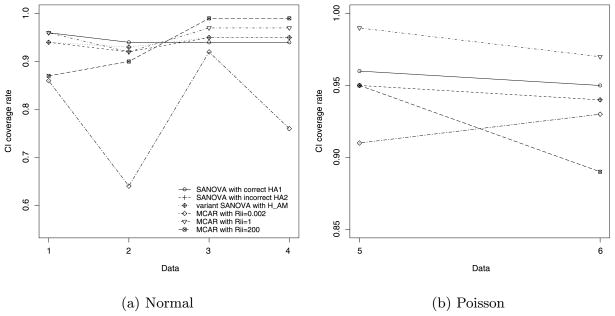
Table 3 and Figures 2 and 3 show the simulation experiment’s results. Table 3 shows AMSE; for all methods and design cells, the standard Monte Carlo errors of AMSE are small, less than 0.07, 0.005 and 0.025 for Data1/Data2, Data3/Data4 and Data5/Data6 respectively. Figure 2 shows MBIAS, where the middle symbols represent the median bias and the line segments represent the 2.5th and 97.5th percentiles. Figure 3 shows coverage of the 95% posterior intervals. Denote SANOVA with the correct (HA1) as “SANOVA correct,” SANOVA with HA2 as “SANOVA incorrect,” the variant SANOVA with HAM as “SANOVA variant,” MCAR with Rii = 0.002 as “MCAR0.002” and so on.
Table 3.
AMSE for simulated normal and Poisson data
| Model | Normal-error model |
Poission-error model |
||||
|---|---|---|---|---|---|---|
| Data1 | Data2 | Data3 | Data4 | Data5 | Data6 | |
| SANOVA with HA1 | 0.34 | 0.60 | 0.04 | 0.06 | 0.02 | 0.04 |
| SANOVA with HA2 | 0.47 | 0.84 | 0.05 | 0.07 | 0.02 | 0.14 |
| SANOVA with HAAM | 0.48 | 0.74 | 0.05 | 0.06 | 0.03 | 0.11 |
| MCAR with Rii = 0.002 | 0.66 | 1.88 | 0.04 | 0.13 | 0.02 | 0.04 |
| MCAR with Rii = 1 | 0.36 | 0.84 | 0.04 | 0.06 | 0.02 | 0.06 |
| MCAR with Rii = 200 | 0.93 | 0.92 | 0.09 | 0.09 | 0.24 | 0.36 |
Fig. 2.
MBIAS for simulated normal and Poisson data.
Fig. 3.
PI rate for simulated normal and Poisson data.
3.4.1. As expected, SANOVA with correct performs best
For normal data, SANOVA correct has the smallest AMSE for all true η0 and τ (Table 3). The advantage is larger in Data1 and Data2 where the error precision η0 is 1 than in Data3 and Data4 where η0 is 10 (i.e., error variation is smaller). For Poisson data, SANOVA correct also has the smallest AMSE. Considering MBIAS (Figure 2), SANOVA correct has the narrowest MBIAS intervals for all cases. In Figure 3, the posterior coverage for SANOVA correct is nearly nominal. As expected, then, SANOVA correct performs best among the six methods.
3.4.2. SANOVA with incorrect HA2 and HAM perform very well
Table 3 shows that, for normal data, both SANOVA incorrect and SANOVA variant have smaller AMSEs than MCAR200 and MCAR0.002, and AMSEs at worst close to MCAR1’s. For Poisson data, Table 3 shows that MCAR0.002 and MCAR1 do somewhat better than SANOVA incorrect and variant SANOVA. Considering MBIAS in normal data [Figure 2(a)], the width of the 95% MBIAS intervals for SANOVA incorrect are the same as or smaller than for all three MCAR procedures. Similarly, SANOVA variant has MBIAS intervals better than MCAR0.002 and MCAR200 and almost as good as MCAR1. Figure 2(b) for Poisson data shows SANOVA correct, MCAR0.002 and MCAR1 have similar MBIAS intervals. SANOVA variant in Data5 and SANOVA incorrect in Data6 show the worst performance for MBIAS apart from MCAR200, whose MBIAS interval is much the widest. Figure 3(a) shows that, for normal data, interval coverage for SANOVA incorrect and SANOVA variant is very close to nominal. It appears that the specific value of has little effect on PI coverage rate for the cases considered here. Apart from MCAR200 for Data1/Data2 and MCAR0.002 for Data1 through Data4, which show low coverage, all the other methods have coverage rates greater than 90% for normal data, most close to 95%. For Data3 and Data4, PI rates for MCAR200 reach above 99%. For Poisson data, the PI rates for SANOVA incorrect and SANOVA variant are close to nominal and better than MCAR0.002 and MCAR200. In particular, all SANOVAs have the closest to nominal coverage rates for both normal and Poisson data, which again shows the stability of SANOVA under different settings.
3.4.3. MCAR is sensitive to the prior on Ω
To fairly compare SANOVA and MCAR, we considered MCAR under three different prior settings. For normal data, MCAR1 has the smallest AMSEs and narrowest MBIAS intervals among the MCARs considered, while MCAR0.002 has the largest and widest, respectively. For Poisson data, however, MCAR0.002 has the best AMSE and MBIAS among the MCARs. MCAR200 performs poorly for both Normal and Poisson. The coverage rates in Figure 3 show similar comparisons. These results imply that the prior matters for MCAR: no single prior was always best. By comparison, SANOVA seems more robust, at least for the cases considered.
3.5. Summary
As expected, SANOVA correct had the best performance because it uses more correct information. For normal data, SANOVA incorrect and SANOVA variant had similar AMSEs, better than two of the three MCARs for the data sets considered. For Poisson data, SANOVA incorrect and SANOVA variant had AMSEs as good as those of MCAR0.002 and MCAR1 for Data5 and somewhat worse for Data6, while showing nearly nominal coverage rates in all cases and less tendency to bias than MCAR in most cases. Replacing the Γ (0.1, 0.1) prior for τ with Γ (0.001, 0.001) left AMSE and MBIAS almost unchanged and coverage rates a bit worse (data not shown). MCAR, on the other hand, seems more sensitive to the prior on Ω. MCAR0.002 tends to smooth more than MCAR1, more so in normal models where the prior is more influential than in Poisson models. (The latter is true because data give more information about means than variances, and the Poisson model’s error variance is the same as its mean, while the normal model’s is not.) For the normal data, MCAR0.002’s tendency to extra shrinkage appears to make it oversmooth and perform poorly for Data2 and Data4, where the truth is least smooth. For the Poisson data, MCAR0.002 and MCAR1 give results similar to each other and somewhat better than the SANOVAs except for interval coverage. Therefore, SANOVA, with stable results under different and with parameters that are easier to understand and interpret, may be a good competitor to MCAR in multivariate spatial smoothing.
4. Example: Minnesota 3-cancer data
Researchers in different fields have illustrated that accounting for spatial correlation could provide insights that would have been overlooked otherwise, while failure to account for spatial association could potentially lead to spurious and sometimes misleading results [see, e.g., Turechek and Madden (2002), Ramsay, Burnett and Krewski (2003), Lichstein et al. (2002)]. Among the widely investigated diseases are the different types of cancers. We applied SANOVA and MCAR to a cancer-surveillance data set describing total incidence counts of 3 cancers (lung, larynx, esophagus) in Minnesota’s 87 counties for the years 1990 to 2000 inclusive. Minnesota’s geography and history make it plausible that disease incidence would show spatial association. Three major North American land forms meet in Minnesota: the Canadian Shield to the north, the Great Plains to the west, and the eastern mixed forest to the southeast. Each of these regions is distinctive in both its terrain and its predominant economic activity: mining and outdoors tourism in the mountainous north, highly mechanized crop cultivation in the west, and dairy farming in the southeast. The different regions were also settled by somewhat different groups of in-migrants, for example, disproportionately many Scandinavians in the north. These factors imply spatial association in occupational hazards as well as culture, weather, and access to health care especially in the thinly-populated north, which might be expected to produce spatial association in diseases. With multiple cancers one obvious option is to fit a separate univariate model for each cancer. But diseases may share the same spatially distributed risk factors, or the presence of one disease might encourage or inhibit the presence of another in a region, for example, larynx and esophagus cancer have been shown to be closely related spatially [Baron et al. (1993)]. Thus, we may need to account for dependence among the different cancers while maintaining spatial dependence between sites. Although the data set has counts broken out by age groups, for the present purpose we ignore age standardization and just consider total counts for each cancer. Age standardization would affect only the expected cancer counts Eij, while other covariates could be added to either SANOVA or MCAR as unsmoothed fixed effects (i.e., in the A1 design matrix). Given the population and disease count of each county, we estimated the expected disease count for each cancer in each county using the Poisson model. Denote the 87 × 3 counts as y1,1, …, y87,3; then the model is
| (17) |
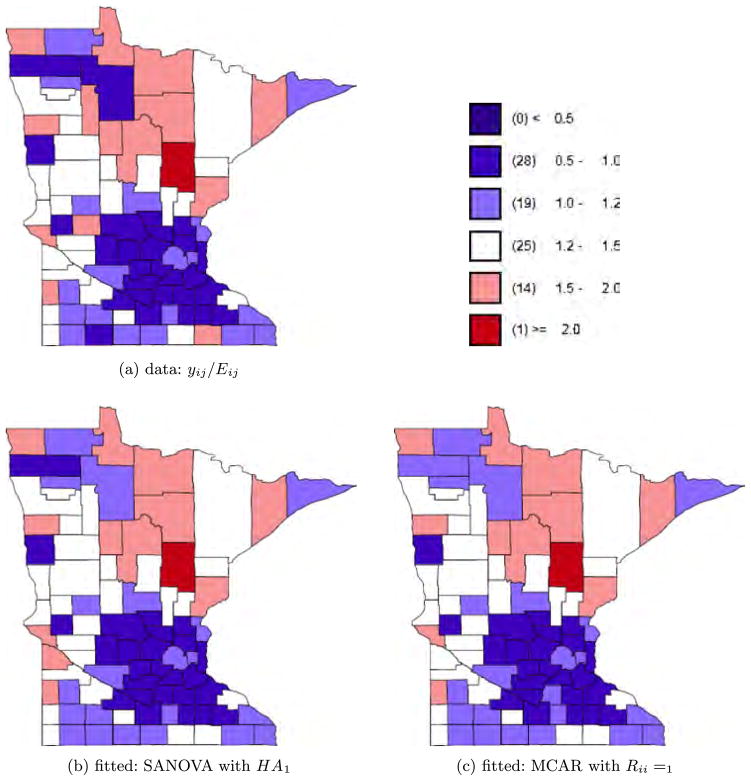
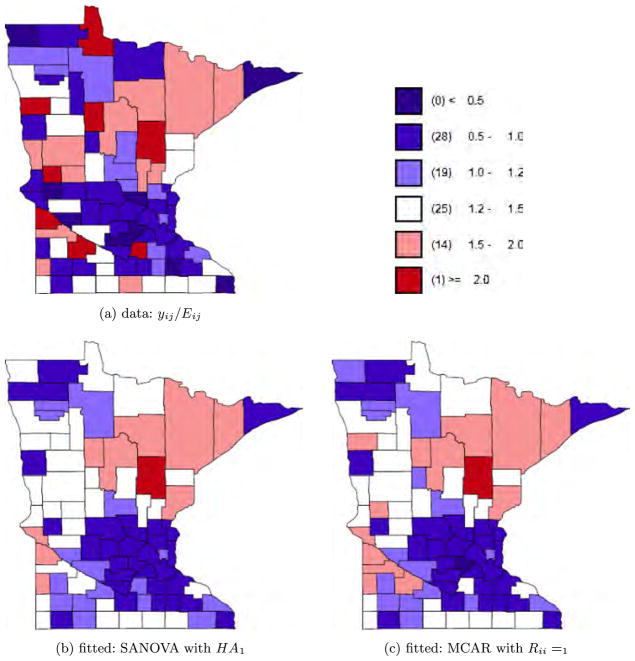
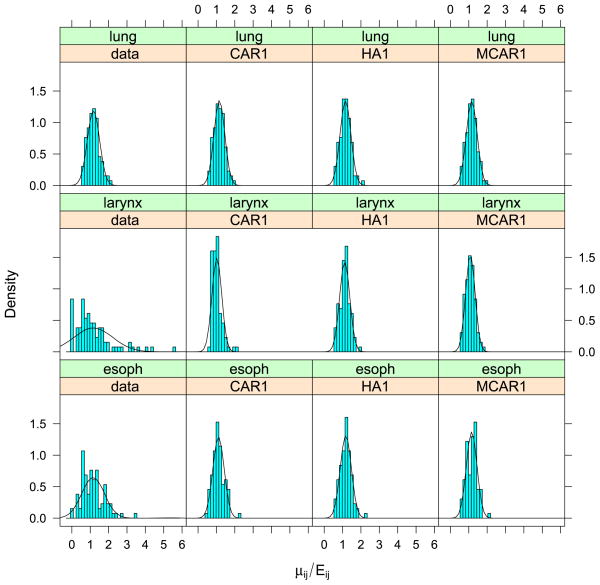
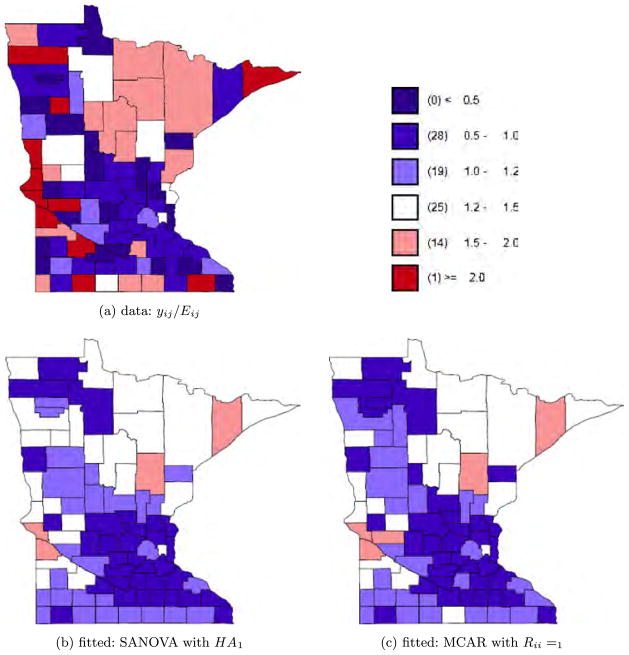
where XDΘ is the SANOVA structure and Θ has priors as in Section 2.2.2. For disease j in county i, , where Oij is the disease count for county i and disease j and Pi is county i’s population. For the SANOVA design matrix, we consider HA1 and HA2 from the simulation experiment, though now neither is known to be correct. We also consider a variant SANOVA analysis using estimated from the MCAR1 model, to test the stability of the SANOVA results. Appendix D in Zhang, Hodges and Banerjee (2009) describes the latter analysis. Figures 4 to 6 show the data and results for MCAR1 and SANOVA with HA1. In each figure, the upper left plot shows the observed yij/Eij; the two lower plots show the posterior median of μij/Eij for MCAR1 and SANOVA with HA1. Lung cancer counts tended to be high and thus were not smoothed much by any method, while counts of the other cancers were much lower and thus smoothed considerably more (see also Figure 7). Since SANOVA with HA1, HA2 and estimated gave very similar results, only those for HA1 are shown. Results for MCAR0.002 are similar to those for MCAR1, so they are omitted. As expected, MCAR200 shows the least shrinkage among the three MCARs and gives some odd μij/Eij. To compare models, we calculated the Deviance Information Criterion [DIC; Spiegelhalter et al. (2002)]. To define DIC, define the deviance D(θ) = −2 log f (y|θ) + 2 log h(y), where θ is the parameter vector in the likelihood and h(y) is a function of the data. Since h does not affect model comparison, we set log h(y) to 0. Let θ̄ be the posterior mean of θ and D̄ the posterior expectation of D(θ). Then define to be a measure of model complexity and define DIC = D̄+ pD. Table 4 shows D̄, pD and DIC for nine analyses, SANOVA with 3 different , MCAR with 3 different priors for Ω, and 3 fits of univariate CAR models to the individual diseases, discussed below. Considering D̄, the three SANOVAs and MCAR1 are similar; Figures 4 to 6 show the fits are indeed similar. Figure 7 reinforces this point, showing that MCAR1 and SANOVA with HA1 induce similar smoothing for the three cancers. SANOVA with estimated from MCAR has the smallest D̄ (1458), though its model complexity penalty (pD = 103) is higher than MCAR0.002’s (pD = 79). Despite having the second worst fit (D̄), MCAR0.002 has the best DIC, and the three SANOVAs have DICs much closer to MCAR0.002’s than to the other MCARs. Generally, all SANOVA models have similar D̄(≈1460) and DIC (≈1562), while MCAR results are sensitive to Ω’s prior, consistent with the simulation experiment. For comparison, we fit separate univariate CAR models to the three diseases considering three different priors for the smoothing precision, τ ~ Gamma(a, a) for a = 0.001, 1 and 1000. For each prior, we added up D̄, pD and DIC for three diseases (see Table 4). With a = 0.001 and 1, we obtained D̄’s (1461 and 1453 respectively) competitive with SANOVA, MCAR0.002 and MCAR1 but with considerably greater complexity penalties (141 and 149 respectively) and thus DICs slightly larger than 1600. For a = 1000, we obtained an even lower D̄ (1432), but an increased penalty (180) resulted in a poorer DIC score. Figure 7 shows fitted values for CAR1, which were smoothed like MCAR1 and SANOVA for lung and esophagus cancers but smoothed rather more for larynx cancer. Overall, these results reflect some gain in performance from accounting for the space-cancer interactions/associations.
Fig. 4.
Lung cancer data and fitted values.
Fig. 6.
Esophagus cancer data and fitted values.
Fig. 7.
Comparing data and fitted values for each cancer. The “Data” panel shows the density for yij/Eij, while the other three panels show the posterior median of μij/Eij for univariate CAR, SANOVA and MCAR.
Table 4.
Model comparison using DIC
| Model | D̄ | pD | DIC |
|---|---|---|---|
| SANOVA with HA1 | 1461 | 103 | 1564 |
| SANOVA with HA2 | 1463 | 102 | 1565 |
| SANOVA with HA estimated from MCAR1 | 1458 | 103 | 1561 |
| MCAR0.002 | 1476 | 79 | 1555 |
| MCAR1 | 1459 | 132 | 1591 |
| MCAR200 | 1559 | 356 | 1915 |
| CAR0.001 | 1461 | 141 | 1602 |
| CAR1 | 1453 | 149 | 1602 |
| CAR1000 | 1432 | 180 | 1612 |
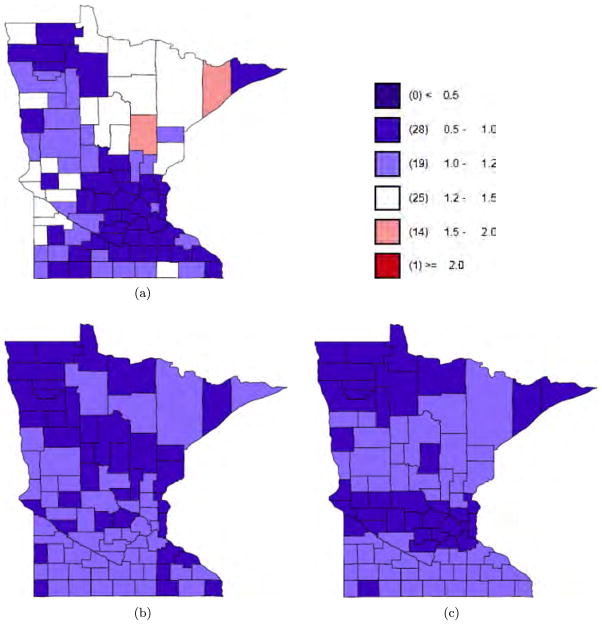
To further examine the smoothing under SANOVA, Figure 8 shows separate maps for the county main effect and interactions from the SANOVA fit with HA1. The upper left plot is the cancer main effect, the mean of the three cancers; the lower left plot is the comparison of lung versus average of larynx and esophagus; the lower right plot is the comparison of larynx versus esophagus. All values are on the same scale as yij/Eij in Figures 4 to 6 and use the same legend. The two interaction contrasts are smoothed much more than the county main effect, agreeing with previous research that larynx and esophagus cancer are closely related spatially [Baron et al. (1993)]. To see whether the interactions are necessary, we fit a SANOVA model (using HA1) without the interactions. As expected, model complexity decreased (pD = 77), while D̄ increased slightly, so DIC became 1558, a bit better than SANOVA with interactions. Now consider the posterior of the MCAR’s precision matrix Ω. The posterior mean of Ω is much larger for MCAR0.002 than MCAR200; the diagonal elements are larger by 4 to 5 orders of magnitude. This may explain the poor coverage for MCAR0.002 in the simulation. Further, consider the correlation matrix arising from the inverse of Ω’s posterior mean. As the diagonals of R change from 0.002 to 200, the correlation between any two cancers decreases and the complexity penalty pD increases. By comparison, the three SANOVAs have similar model fits and complexity penalties, leading to similar DICs. So again, in this sense SANOVA shows greater stability.
Fig. 8.
SANOVA with HA1: (a) county main effect; (b) cancer × county interaction 1 for larynx; (c) cancer × county interaction 2 for esophagus.
5. Discussion and future work
We used SANOVA to do spatial smoothing and compared it with the much more complex MCAR model. For the cases considered here, we found SANOVA with spatial smoothing to be an excellent competitor to MCAR. It yielded essentially indistinguishable inference, while being easier to fit and interpret. In the SANOVA model, is assumed known. For most of the SANOVA models considered, ‘s first column was fixed to represent the average over diseases, while other columns were orthogonal to the first column. Alternatively, could be treated as unknown and estimated as part of the analysis. With this extension, SANOVA with spatial effects is a reparameterization of the MCAR model and gains the MCAR model’s flexibility at the price of increased complexity. This extension would be nontrivial, involving sampling from the space of orthogonal matrices while avoiding identification problems arising from, for example, permuting columns of . Other covariates can be added to a spatial SANOVA. Although (10) is a saturated model, spatial smoothing “leaves room” for other covariates. Such models would suffer from collinearity of the CAR random effects and the fixed effects, as discussed by Reich, Hodges and Zadnik (2006), who gave a variant analysis that avoids the collinearity. For data sets with spatial and temporal aspects, for example, the 11 years in the Minnesota 3-cancer data, interest may lie in the counts’ spatial pattern and in their changes over time. By adding a time effect, SANOVA can be extended to a spatiotemporal model. Besides spatial and temporal main effects, their interactions can also be included and smoothed. There are many modeling choices; the simplest model is an additive model without space-time interactions, where the spatial effect has a CAR model and the time effect a random walk, which is a simple CAR. But many other choices are possible. We have examined intrinsic CAR models, where Qij = −1 if region i and region j are connected. SANOVA with spatial smoothing could be extended to more general CAR models. Banerjee, Carlin and Gelfand (2004) replaced Q with the matrix Dw − ρW, where Dw is diagonal with the same diagonal as Q and Wij = 1 if region i is connected with region j, otherwise Wij = 0. Setting ρ = 1 gives the intrinsic CAR model considered in this paper. For known ρ, the SANOVA model described here is easily extended by replacing Q in Section 2 with Dw − ρW. However, for unknown ρ, our method cannot be adjusted so easily, because updating ρ in the MCMC would force V and the design matrix to be updated as well, but this would change the definition of the parameter Θ. Therefore, a different approach is needed for unknown ρ. A different extension of SANOVA would be to survival models for areal spatial data [e.g., Li and Ryan (2002), Banerjee, Wall and Carlin (2003), Diva, Dey and Banerjee (2008)]. If the regions are considered strata, then random effects corresponding to nearby regions might be similar. In other words, we can embed the SANOVA structure in a spatial frailty model. For example, the Cox model with SANOVA structure for subject j in stratum i is
| (18) |
where X is the design matrix, which may include a spatial effect, a temporal effect, their interactions and other covariates. Banerjee, Carlin and Gelfand (2004) noted that in the CAR model, considering both spatial and nonspatial frailties, the frailties are identified only because of the prior, so the choice of priors for precisions is very important. Besides the above extensions, HCSC introduced tools for normal SANOVA models that can be extended to nonnormal SANOVA models. For example, HCSC defined the degrees of freedom in a fitted model as a function of the smoothing precisions. This can be used as a measure of the fit’s complexity, or a prior can be placed on the degrees of freedom as a way of inducing a prior on the unknowns in the variance structure. The latter is under development and will be presented soon.
Supplementary Material
Fig. 5.
Larynx cancer data and fitted values.
Acknowledgments
The authors thank the referees, the Associate Editor and the Editor for valuable comments and suggestions.
Contributor Information
Yufen Zhang, Novartis Pharmaceuticals, East Hanover, New Jersey 07936, USA.
James S. Hodges, Division of Biostatistics, School of Public Health, University of Minnesota, Minneapolis, Minnesota 55455, USA
Sudipto Banerjee, Email: sudiptop@biostat.umn.edu, Division of Biostatistics, School of Public Health, University of Minnesota, Minneapolis, Minnesota 55455, USA.
References
- Banerjee S, Carlin BP, Gelfand AE. Hierarchical Modeling and Analysis for Spatial Data. Chapman & Hall/CRC Press; Boca Raton, FL: 2004. [Google Scholar]
- Banerjee S, Wall MM, Carlin BP. Frailty modeling for spatially correlated survival data, with application to infant mortality in Minnesota. Biostatistics. 2003;4:123–142. doi: 10.1093/biostatistics/4.1.123. [DOI] [PubMed] [Google Scholar]
- Baron AE, Franceschi S, Barra S, Talamini R, La Vecchia C. Comparison of the joint effect of alcohol and smoking on the risk of cancer across sites in the upper aerodigestive tract. Cancer Epidemiol Biomarkers Prev. 1993;2:519–523. [PubMed] [Google Scholar]
- Besag J. Spatial interaction and the statistical analysis of lattice systems (with discussion) J Roy Statist Soc Ser B. 1974;36:192–236. MR0373208. [Google Scholar]
- Besag J, Green P, Higdon D, Mengersen K. Bayesian computation and stochastic systems (with discussion) Statist Science. 1995;10:3–66. MR1349818. [Google Scholar]
- Besag J, York JC, Mollié A. Bayesian image restoration, with two applications in spatial statistics (with discussion) Ann Inst of Statist Math. 1991;43:1–59. MR1105822. [Google Scholar]
- Carlin BP, Banerjee S. Hierarchical multivariate CAR models for spatiotemporally correlated survival data. In: Bernardo JM, et al., editors. Bayesian Statistics. Vol. 7. Oxford Univ. Press; Oxford: 2003. pp. 45–64. MR2003166. [Google Scholar]
- Elliott P, Wakefield JC, Best NG, Briggs DJ. Spatial Epidemiology: Methods and Applications. Oxford Univ. Press; Oxford: 2000. [Google Scholar]
- Gelfand AE, Vounatsou P. Proper multivariate conditional autoregressive models for spatial data analysis. Biostatistics. 2003;4:11–25. doi: 10.1093/biostatistics/4.1.11. [DOI] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. 2. Chapman and Hall/CRC Press; Boca Raton, FL: 2004. [Google Scholar]
- Hodges JS. Some algebra and geometry for hierarchical models. J Roy Statist Soc Ser B. 1998;60:497–536. MR1625954. [Google Scholar]
- Hodges JS, Carlin BP, Fan Q. On the precision of the conditionally autoregressive prior in spatial models. Biometrics. 2003;59:317–322. doi: 10.1111/1541-0420.00038. MR1987398. [DOI] [PubMed] [Google Scholar]
- Hodges JS, Cui Y, Sargent DJ, Carlin BP. Smoothing balanced single-error-term analysis of variance. Technometrics. 2007;49:12–25. MR2345448. [Google Scholar]
- Jin X, Banerjee S, Carlin BP. Order-free coregionalized lattice models with application to multiple disease mapping. J Roy Statist Soc Ser B. 2007;69:817–838. doi: 10.1111/j.1467-9868.2007.00612.x. MR2368572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin X, Carlin BP, Banerjee S. Generalized hierarchical multivariate CAR models for areal data. Biometrics. 2005;61:950–961. doi: 10.1111/j.1541-0420.2005.00359.x. MR2216188. [DOI] [PubMed] [Google Scholar]
- Kim H, Sun D, Tsutakawa RK. A bivariate Bayes method for improving the estimates of mortality rates with a twofold conditional autoregressive model. J Amer Statist Assoc. 2001;96:1506–1521. MR1946594. [Google Scholar]
- Lawson AB, Biggeri AB, Bohning D, Lesaffre E, Viel JF, Bertollini R. Disease Mapping and Risk Assessment for Public Health. Wiley; New York: 1999. [Google Scholar]
- Lee Y, Nelder JA. Hierarchical generalized linear models (with discussion) J Roy Statist Soc Ser B. 1996;58:619–673. MR1410182. [Google Scholar]
- Li Y, Ryan L. Modeling spatial survival data using semi-parametric frailty models. Biometrics. 2002;58:287–297. doi: 10.1111/j.0006-341x.2002.00287.x. MR1908168. [DOI] [PubMed] [Google Scholar]
- Lichstein JW, Simons TR, Shriner SA, Franzreb KE. Spatial autocorrelation and autoregressive models in ecology. Ecological Monographs. 2002;72:445–463. [Google Scholar]
- Mardia KV. Multi-dimensional multivariate Gaussian Markov random fields with application to image processing. J Multivar Anal. 1988;24:265–284. MR0926357. [Google Scholar]
- Ramsay T, Burnett R, Krewski D. Exploring bias in a generalized additive model for spatial air pollution data. Environ Health Perspect. 2003;111:1283–1288. doi: 10.1289/ehp.6047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich BJ, Hodges JS, Zadnik V. Effects of residual smoothing on the posterior of the fixed effects in disease-mapping models. Biometrics. 2006;62:1197–1206. doi: 10.1111/j.1541-0420.2006.00617.x. MR2307445. [DOI] [PubMed] [Google Scholar]
- Rue H, Held L. Gaussian Markov Random Fields: Theory and Applications. Chapman & Hall/CRC; Boca Raton: 2005. MR2130347. [Google Scholar]
- Sain SR, Cressie N. Proceedings of ASA Section on Statistics and the Environment. Amer. Statist. Assoc; Alexandria, VA: 2002. Multivariate lattice models for spatial environmental data; pp. 2820–2825. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit (with discussion) J Roy Statist Soc Ser B. 2002;64:583–639. [Google Scholar]
- Turechek WW, Madden LV. A generalized linear modeling approach for characterizing disease incidence in spatial hierarchy. Phytopathology. 2002;93:458–466. doi: 10.1094/PHYTO.2003.93.4.458. [DOI] [PubMed] [Google Scholar]
- Wakefield J. Disease mapping and spatial regression with count data. Biostatistics. 2007;8:158–183. doi: 10.1093/biostatistics/kxl008. [DOI] [PubMed] [Google Scholar]
- Wall MM. A close look at the spatial structure implied by the CAR and SAR models. J Statist Plann Inference. 2004;121:311–324. MR2038824. [Google Scholar]
- Waller LA, Gotway CA. Applied Spatial Statistics for Public Health Data. Wiley; New York: 2004. MR2075123. [Google Scholar]
- Zhang Y, Hodges JS, Banerjee S. Supplement to “Smoothed ANOVA with spatial effects as a competitor to MCAR in multivariate spatial smoothing”. 2009 doi: 10.1214/09-AOAS267SUPP. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.