Abstract
To provide utility in understanding the molecular evolution of ion-selective biomembrane channels/transporters, globular proteins, and ionophoric compounds, as well as in guiding their modification and design, we present a statistical mechanical basis for deconstructing the impact of the coordination structure and chemistry of selective multidentate ionic complexes. The deconstruction augments familiar ideas in liquid structure theory to realize the ionic complex as an open ion-ligated system acting under the influence of an “external field” provided by the host (or surrounding medium). Using considerations derived from this basis, we show that selective complexation arises from exploitation of a particular ion's coordination preferences. These preferences derive from a balance of interactions much like that which dictates the Hofmeister effect. By analyzing the coordination-state space of small family IA and VIIA ions in simulated fluid media, we derive domains of coordinated states that confer selectivity for a given ion upon isolating and constraining particular attributes (order parameters) of a complex comprised of a given type of ligand. We demonstrate that such domains may be used to rationalize the ion-coordinated environments provided by selective ionophores and biological ion channels/transporters of known structure, and that they can serve as a means toward deriving rational design principles for ion-selective hosts.
Introduction
The specific interactions between ions and macromolecules affect a plethora of important biological processes. In addition to the well known (for over 100 years (1)) fact that water-mediated ionic interactions with macromolecules affect their solubility (2–5) (the so-called Hofmeister effect), bound ions can play a crucial role in the catalytic processes of enzymes and in maintaining overall protein structure (6,7). Specific ion binding can affect the conformation and activity of nucleic acids (8) and various drugs (9,10), modulate the physical and electrostatic properties of the biomembrane/aqueous-solution interface (11,12), affect the binding and insertion of proteins into the cell membrane (13), and influence macromolecular aggregation processes such as domain formation in biological membranes (14–17), lipid vesicle fusion (18,19), and viral assembly (20). Ions also interact in a specific manner with dipolar or charged moieties lining the transport pathway through biomembrane-spanning channels and transporters. Such specific interactions allow these “ion transport” proteins to selectively allow the permeation of particular ions (21). This special property of “selectivity” is what imparts to ion transport proteins the capability of generating transmembrane electromotive and chemical forces necessary to carry out cellular functions.
The subject of ionic selectivity has received a great deal of attention recently (22–28) due to the determination, by diffraction methods, of several channel and transporter protein structures (29). With structural knowledge of exemplary selective binding sites for Na+, K+, Ca2+, and Cl− in hand (29), it is clear that the most selective membrane transport proteins use coordinating moieties in their ionic binding sites (“selectivity filters”) to compensate for the thermodynamic cost of dehydration upon ion binding. From this perspective, sites within the selectivity filters of such proteins have been compared to “multidentate” ionophoric ligands (29,30). One may note that the macroscopic selective permeability of an ion transport protein is not due solely to the specificity of a single site within its pore, and is sensitive to a plethora of interactions, such as correlative effects between multiple permeating ions and the protein and the wide range of conditions biologically available to the inner and outer solutions of a biological membrane. However, it appears that preferential ionic complexation by moieties available to a protein plays an important part in selective ion transport.
The synthesis of selective ionophores is part of the mature field of organic host-guest chemistry, which has produced a large number of compounds selective for many types of ions (31,32). The design of such compounds strives for control over certain variables that impart to the ionophoric system the capability of “molecular recognition” (where the “molecule” is a particular ion). As such, the design of a molecule that displays selective ionic complexation is viewed as a storage of information in the ionophore (or ligand), L, which is realized by the ion, M±, upon complexation, . The equilibrium constant in this reaction is often called the “stability constant” (31), , and the selectivity for a particular ion, A, over some other ion, B, is expressed as a “relative stability” or ratio of equilibrium constants, . Binding complementarity for a particular ion is said to be achieved when the maximum amount of information is stored in the ionophore (32). The types of information (physical/chemical properties) chemists use in the design of an ionophore, namely the selected ion's radius, average hydration number, hard/soft character (33–36) and polarizability, surface charge density, and hydration free energy (32) appear to be the same types of information that the process of molecular evolution has used to build the selectivity filters of ion transport proteins (29).
Many of the above physical properties that synthetic organic chemists account for when designing a compound to bind a specific ion are derived from the context of a hydrated ion. Knowledge of ionic radii is derived from coordination radii in aqueous solution (i.e., the first maximum in ion-water oxygen pair correlation functions) (37), and the average hydration number, by definition, is the number of water molecules coordinating the ion in bulk water. An ion's hard/soft character describes the extent to which the aqueous ion “shares” electrons with neighboring bulk water molecules. As such, it characterizes the strength with which the ion interacts with its surrounding water and gives it an acidlike (in the case of a cation) or baselike (in the case of an anion) character (36). Finally, it should be self-explanatory that the hydration free energy of an ion is derived from the ion's interactions with pure water. Strictly speaking, none of the properties described above have anything to do with the organic compounds to which a particular ion binds. Nonetheless, these concepts are found to be useful in designing the attributes that give rise to selective binding.
As pointed out in the earliest of commentaries on the subject (38), complementarity between a bioorganic host and its substrate “amounts to a sort of generalized ‘lock and key’ relationship not limited to steric fit …, but extending over other molecular features” (32). However, in practice, it can be difficult to know the importance of one particular molecular feature with respect to another, or whether specific features might be correlated. In what follows, we expound, in pedantic detail, on concepts introduced previously (24) to provide a generalized framework for understanding the determinants of selective ionic complexation in organic hosts (proteinaceous or otherwise), liquids, and gases. With a statistical mechanical treatment of the complexation event in hand, the physical elements outlined above (chemical identity of the coordinating ligands, structure of the complex, constraints placed on the complex by the host, etc.), which give rise to preferential ionic complexation, may be thought of in a more unified manner. We then move on to illustrate the concepts behind these physical elements by analyzing the coordinated states available to different ions in fluid environments. Finally, we show the utility of this framework in delineating domains of “coordination-state space” that are selective for a given ion in different fluid media, and its potential as a tool to provide guidelines for selective ion transport protein or ionophore design.
One will note that although much of our discussion is directed toward ions complexed by transport proteins, the general concepts we outline, although with some simplifications, should be useful in the consideration of any ion and any host, provided that no covalent bond making or breaking is involved in the complexation event. The treatment logically follows from principles previously applied to molecular liquids (39–43) and fluids or fluid droplets under the influence of an external field (44,45), so we expect it to be useful in the understanding of water structure around ions (i.e., the Hofmeister effect (1,2,4,5,46,47)) and also of the determinants of neat liquid structure. For example, the self-complexation of liquid water molecules has been found lately to be useful in explaining the multifaceted structural and phase properties of amorphous water (48).
Methods
To illustrate elements of the framework that follows, we utilize molecular dynamics (MD) simulations of ions in fluid media. All simulations were of “free” bulk liquid, and employed no biasing potentials. Each of the ions Li+, Na+, K+, F−, Cl−, and Br− were simulated in a box of 213 water molecules at a temperature of 298 K and a pressure of 1 atm using the polarizable AMOEBA force field (49,50) and the TINKER simulation package (51) as described in previous work (24). The production trajectory for each hydrated ion system was 4.0 ns long. For comparison, using the GROMACS simulation package (54,55), in the same manner as described in previous work (24), we also performed a 10-ns simulation of each of the ions Li+, Na+, K+, and Rb+, utilizing the models of Åqvist (52), in a periodic box of 2179 simple point charge (SPC) water molecules (53) at a temperature of 298 K and pressure of 1 atm. Finally, again using the GROMACS package and the ion models of Åqvist (52), we performed 4-ns simulations of Na+, K+, and Rb+ in a hypothetical/fictitious carbonyl fluid at a temperature of 298 K and zero pressure, and in exactly the same manner as described previously (24). Each ion-fluid system was comprised of a single ion and 396 carbonyl-like groups whose parameters were stripped from the OPLS force field (56) for proteins. We refer the reader to the Supporting Material for a brief digression on the molecular models used in this work.
The production portion of the trajectories was subjected to standard population and probability density (histogram) analyses to glean ion coordination properties (e.g., the probability density and its first and second moments as a function of prescribed order parameters such as coordination number or average ion-oxygen coordination radius), as described previously (24,57). These statistical analyses made use of the standard definition of the boundary of the first coordination shell, which coincides with the first minimum of the ion-oxygen pair correlation function for a given “solvent” medium. Standard statistics pertaining to the structure of the first coordination shell of each ion in the various simulated media are reported in Table 1, and are in agreement with observations by others (49,52,58).
Table 1.
Structural properties of various ions in simulated model fluid media
| Fluid medium | Ion | First maximum (Ropt (Å)) | First minimum (rc (Å)) | 〈n〉 | σn |
|---|---|---|---|---|---|
| Li+ | 1.97 | 2.83 | 4.2 | 0.5 | |
| Na+ | 2.39 | 3.09 | 5.6 | 0.6 | |
| H2O | K+ | 2.75 | 3.54 | 6.8 | 1.0 |
| (AMOEBA) | F- | 2.79 | 3.39 | 5.8 | 0.6 |
| Cl- | 3.23 | 3.96 | 7.6 | 1.3 | |
| Br- | 3.41 | 4.23 | 8.9 | 1.6 | |
| Li+ | 2.03 | 2.81 | 4.6 | 0.6 | |
| H2O | Na+ | 2.41 | 3.19 | 5.8 | 0.5 |
| (SPC/Åqvist) | K+ | 2.73 | 3.59 | 6.7 | 0.9 |
| Rb+ | 2.85 | 3.67 | 7.0 | 1.0 | |
| Na+ | 2.39 | 3.50 | 6.2 | 0.4 | |
| C=O (OPLS) | K+ | 2.70 | 4.09 | 7.1 | 0.7 |
| Rb+ | 2.85 | 4.10 | 7.3 | 0.7 | |
Properties included are the first maximum (Ropt) and minimum (rc) of the ion-oxygen pair correlation function, g(r), and the mean and standard deviation in the number of ion-coordinating oxygen atoms (〈n〉 and σn, respectively).
The collected probability density data were used with Eqs. 15 and 16 to produce one-dimensional (1D) and two-dimensional (2D) selective free-energy domain maps. We were able, because of significant overlap in the obtained coordination number distributions (see Figs. 5, A and C, and Fig. S1 A in Supporting Material), to derive 1D selectivity mappings over a substantial range of coordination numbers for several ion pairs using solely raw probability data (see Figs. 5, B and D, and S1 B). For 2D mappings (see Figs. 7–9) and 1D mappings involving average coordination radius (see Figs. 6 and S2), Gaussian probability models (see Figs. 5, 6, S1, S2, and S4–S6) were employed, as in our previous work (24), to facilitate smooth selective free energy surfaces (see Figs. 6–9 and S2). The Gaussian models allowed us to extend the bounds of our selectivity maps to regions of order-parameter space rarely sampled in unbiased MD simulations. In low-probability regions (corresponding to the tails of the probability density functions), selective free energies derived from Gaussian models were seen to deviate slightly from those obtained using raw probability data. Comparing Gaussian models and raw probability results in the most remote regions where raw probability data were available, we found quantitative deviations in selective free energy that were dependent on the particular fluid (water or fictitious carbonyl) model (for example, compare the raw selectivity of Fig. 5 B to the corresponding Gaussian-based selectivity of Fig. 8 at large values of coordination number). Such discrepancies in free energy for regions of low raw probability are entirely expected despite very good agreement between raw probability data and the employed probability models. This is because the proportionality, , between free energy, J, and probability, P, associated with observing events along an order parameter in an uncoupled fluid implies that the error in J propagates as , where δP is the error in the raw probability measurement (59). Thus, the relation underlying our mappings (Eqs. 15 and 16) implies that the error in selective free energy calculated from raw probability measurements will be large in low-probability regions of order-parameter space. In such circumstances, it is beneficial to use biased sampling methods (60) or, when possible, probability models. In this work, the latter approach will serve our illustrative purposes given the reasonable fit obtained with Gaussian models (see Figs. 5, 6, S1, S2, and S4–S6).
Figure 5.
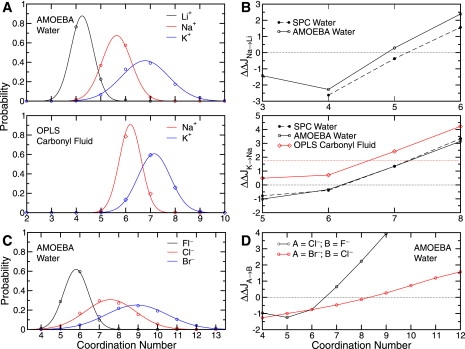
Population analysis and resulting selective free energy (kcal/mol) as a function of coordination number (irrespective of the complex configuration) for various ions in the simulated media. (A) Quasicomponent distribution functions for small monovalent Family IA cations in water (upper) and in a carbonyl HCF (lower). (B) Free energy of selectivity for Na+ over Li+ (upper) and K+ over Na+ (lower) as a function of coordination number. The horizontal dotted lines indicate , the contribution to the selective free energy arising from uncoupled ligands. By definition, this quantity has a value of zero for ions in water and in an OPLS carbonyl HCF (lower), kcal/mol as calculated by thermodynamic integration (24). (C) Quasicomponent distribution functions in water for small monovalent Family VIIA anions in water. (D) Free energy of selectivity for Cl− over F− and Br− over Cl−. The horizontal dotted line indicates .
Figure 7.
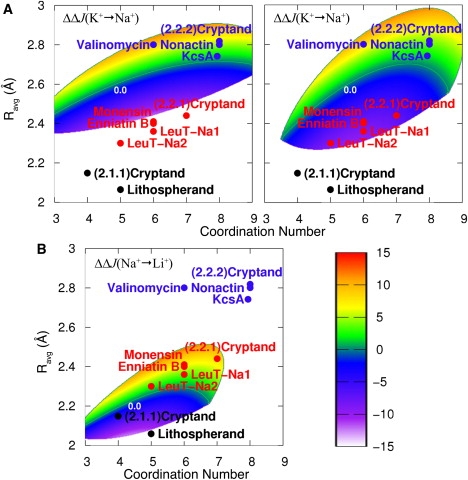
Selective free-energy, (kcal/mol), for monovalent cations in a hypothetical host that serves solely to organize a site to form a fixed coordination number and average coordination radius irrespective of other degrees of freedom available to a coordinator in an HCF. Positions corresponding to structures of exemplary K+-selective (blue dots), Na+-selective (red dots), and Li+-selective (black dots) ionophores/transporters bound to their selected ions are also shown. The locations of the exemplary sites on the map were determined from x-ray structures from the Protein Data Bank in the case of transport proteins (LeuT-Na1/Na2, 2a65, KcsA, and 1k4c) or from the Cambridge Structural Database in the case of ionophores ((2.1.1) Cryptand, SOCYIS; Lithospherand, CAWREX; (2.2.1) Cryptand, WOKTIZ; Monensin, BELDAX; Enniatin B, ENNBKI; (2.2.2) Cryptand, EWOCUO; and Nonactin, NONKCS), except for that of valinomycin, which was gleaned from a recent ab initio study (68). Note that placement of the exemplary sites on the above free-energy maps is intended to show structural agreement between naturally evolved selective sites and our free-energy analysis, and is not intended to imply knowledge of the behavior (i.e., changes in the variables n and Ravg) of the sites upon complexing different ions. (A) Selectivity for K+ over Na+ in AMOEBA liquid water (left) and in an OPLS carbonyl HCF (right). A green line in each map (0.0) denotes the contour for zero selectivity, which separates the K+-selective (positive) and Na+-selective (negative) domains. Notice that although there are differences between the shapes of the selective domains in these two fluids, both are qualitatively similar and are able to distinguish between the Na+- and K+-selective compounds. (B) Selectivity for Na+ over Li+ in AMOEBA liquid water. The 0.0 kcal/mol contour (green line) separates the Na+-selective (positive) and Li+-selective (negative) domains.
Figure 8.
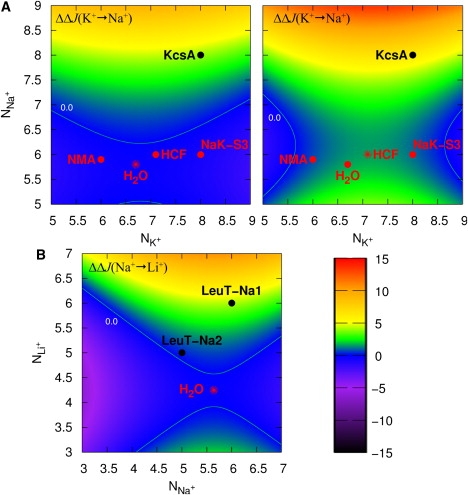
Selective free-energy, (kcal/mol), for monovalent cations in a hypothetical host that serves solely to organize a site such that nA ligands coordinate an ion of type A and nB ligands an ion of type B (irrespective of the complex configuration). (A) Selectivity for K+ over Na+ in AMOEBA liquid water (left) and in an OPLS carbonyl HCF (right). The 0.0 kcal/mol contour (green line) separates the K+-selective (positive) and Na+-selective (negative) domains. Also shown are average structural environments provided by exemplary low-selective media, which are known not to enforce a particular coordination radius for the selected ion (red star/dots, NMA (liquid N-methylacetamide (OPLS)); H2O, liquid water (AMOEBA); HCF, carbonyl fluid (OPLS); and NaK-S3, site 3 of the NaK channel as determined by simulation studies (72)) and the K+ selective environment exhibited by a canonical site in a K+ channel (black dot, KcsA, site 2 from the x-ray structure of PDB 1k4c or from calculations (23,26,72)). We refer the reader to Fig. 6 of Fowler et al. (76) for a similar, but more exhaustive, characterization of selectivity and coordination number in the binding sites of KcsA and NaK. (B) Selectivity for Na+ over Li+ in AMOEBA liquid water. The 0.0 kcal/mol contour (green line) separates the Na+-selective (positive) and Li+-selective (negative) domains. The nonselective environment of liquid water (red star), and the Na+-selective environments provided by the LeuT transporter sites Na1 and Na2 are shown (black dots, from the x-ray structure of PDB 2a65 or from calculations (73)).
Figure 9.
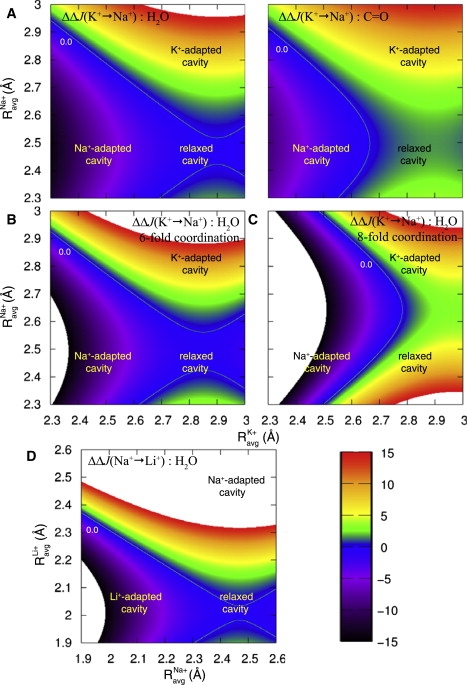
Selective free energy, (kcal/mol), in hypothetical hosts that serve to organize a site such that an average coordination radius is enforced for a cation of type A and an average coordination radius of for a cation of type B. (A) Selectivity for K+ over Na+ in AMOEBA water (left) and OPLS carbonyl HCF (right), irrespective of the coordination number as sampled in an uncoupled fluid. The 0.0 kcal/mol contour (green line) in each plot separates the K+-selective (positive) and Na+-selective (negative) domains. Both carbonyl and water yield qualitatively similar selective free-energy profiles. Environments consistent with enforcement of a Na+-adapted cavity, K+-adapted cavity, and a host that allows cavity relaxation are marked. (B and C) Selectivity for K+ over Na+ in AMOEBA liquid water given that (B) sixfold or (C) eightfold coordination is enforced. The 0.0 kcal/mol contour (green line) separates the K+-selective (positive) and Na+-selective (negative) domains. K+/Na+-adapted and relaxed cavity environments are marked. At eightfold coordination, K+ selectivity is enforced regardless of whether the host enforces a radially K+-adapted cavity or allows the cavity to radially relax in response to the ion type. (D) Selectivity for Na+ over Li+ in AMOEBA water irrespective of the coordination number sampled in a liquid. The 0.0 kcal/mol contour (green line) separates the Na+-selective (positive) and Li+-selective (negative) domains. Environments consistent with enforcement of a radially Li+-adapted cavity, Na+-adapted cavity, and a host that allows cavity relaxation are marked.
Figure 6.
Population analysis and resulting selective free energy (kcal/mol) as a function of average ion-oxygen coordination radius (irrespective of the complex coordination number) for various ions in water. (A) Probability of attaining a particular average coordination radius for small monovalent Family IA cations in water. The distributions are reasonably approximated with Gaussian probability models, except for that of Li+, which displays multimodality due to the high correlation between the average coordination radius and the coordination number (see Fig. 3A). Thus, for Li+, we show how the net distribution (open circles) is largely accounted for by the four- and fivefold coordinated states taken together. (B) Free energy of selectivity for Na+ over Li+ (black curves) and K+ over Na+ (red curve) as a function of the average coordination radius. The horizontal dotted line indicates , the contribution to the selective free energy arising from uncoupled ligands, which has a value of zero for ions in water. (C) Probability of attaining a particular average coordination radius for small monovalent Family VIIA anions in water. (D) Free energy of selectivity for Cl− over F− and Br− over Cl− as a function of the average coordination radius. The horizontal dotted line indicates .
Theoretical framework
Consider the potential energy function, , which contains all interactions within an ionophoric system. For example, in the case of an ion channel, would include the bathing intra- and extracellular electrolyte, membrane, protein, and any solvent or ions within the channel. Here, we explicitly represent the position x0 of a single ion within the system. The remaining degrees of freedom of the system are lumped into the set, S (Fig. 1, upper).
Figure 1.
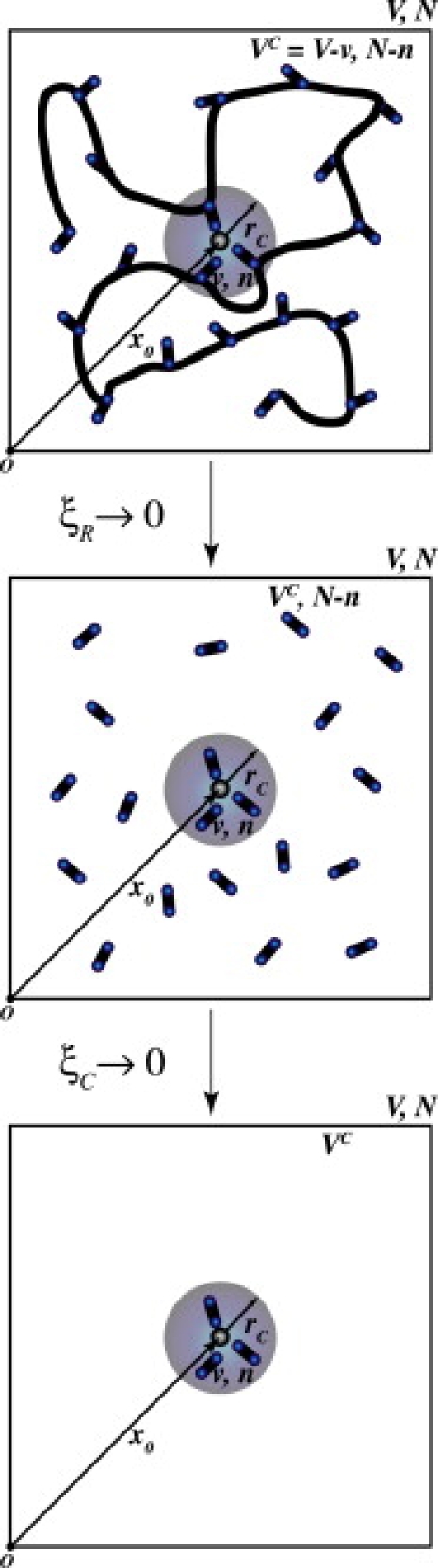
Sketch of the external environments “felt” by a complex encapsulated in a coordination subvolume, v, at different levels of uncoupling to the system remainder. The entire system (upper) has a macroscopic volume V, and consists of a solvated host complexing a central ion at x0 with n, out of a total of N, coordinators. Upon uncoupling the coordinators from the host (middle), the complex is under the field of an external hypothetical fluid of coordinators (HCF). When the complex is uncoupled from the external fluid (lower), it is under the influence of a hypothetical gas of coordinators (HCG) and interacts with nothing in the complementary volume, VC.
At constant total volume, V, and temperature, T, we may write a configuration integral for the system given a particular position, x0, of the candidate ion,
| (1) |
where (kB is Boltzmann's constant). This configuration integral is proportional to the canonical partition function (61) of the system, S, subjected to an “external field” due to the ion placed at x0. Thus, the Helmholtz free energetic cost to bring the ion of type “j” from the external bulk aqueous solution to a single site within the channel is
| (2) |
This free energy is the quantity to consider when determining the thermodynamic favorability of binding. Under constant pressure (rather than volume) an equivalence can be drawn with the canonical ensemble, as long as the system density is well defined (62), and we may obtain a similar expression for the Gibbs free energy of ion binding, .
In determining the selectivity of a site for an ion of type A over an ion of type B, the relative free energy,
| (3) |
is the relevant discriminant. One will note that , as the selectivity, , is defined in the introduction. When is positive, the site prefers to complex with ion A over ion B. However, since the free energy of Eq. 2 (and, consequently, of Eq. 3) requires integration over all degrees of freedom, it is difficult to see whether particular structural characteristics give rise to favorable complexation of a given ion.
The traditional emphasis on ion coordination and the environment provided by the protein architecture as contributors to selective ion complexation leads us to represent, more explicitly, certain degrees of freedom within the system. Thus, we consider the protein as a set of N “coordinators” or “ligands” (generally, polyatomic or monatomic moieties that can coordinate an ion) covalently bonded to their protein (as depicted in Fig. 1, upper). Examples of coordinators might include carbonyl, amide, or hydroxyl groups. For brevity, we rewrite all degrees of freedom in terms of the position of the ion, effectively placing the ion at the origin. We will explicitly state the position, x0 (e.g., whether the ion is in the bulk or at a particular site), when it is of consequence. We note that in the bulk, all positions of the ion are definitively equivalent. Further, we consider the potential of mean force, , where coordinator orientations are integrated (see Supporting Material). The set represents the positions of the coordinators (with respect to the position of the ion), and R represents the remaining degrees of freedom (all degrees of freedom that do not qualify as ion or coordinator).
Although a protein-ion complex may generally involve many different chemical moieties (6), it will serve our illustrative purposes to consider a simplification where these moieties are identical. Thus, our discussion will cover only structural determinants of selective ionic complexation by a given type of coordinator, and not the implications of “hybrid” complexation by moieties of varying chemical type. We note that it would be possible to generalize our development to include various types of moieties if desired. It is also worth noting that the implicit treatment of coordinator orientation implied by is a matter of choice. There are cases that would necessitate explicit treatment of coordinator orientation. For example, a site in a protein might enforce the orientation of coordinators possessing a significant dipole moment to determine whether a positive or negative ion will bind favorably. However, an implicit treatment will suffice to address selectivity among ions of like sign in valence.
Our choice to represent a set of coordinators explicitly does not necessarily imply that the particular site under scrutiny must utilize coordination to bind an ion (implying dehydration). This is an important consideration, because many channels that are selective for harder (33–36) or more kosmotropic (2,4) ions, such as Na+ or Ca2+, can have large pore sizes (compared to the size of their selected ions) and display promiscuity in the species they allow to permeate (21,63), but still maintain selective permeability for their ions. The ions for which these channels are selective may (or may not) pass through as partially hydrated species. As such, a “selective permeability” refers to a competitive preference for a particular species to permeate, and not absolute exclusion of all other species.
“Binding” events mediated largely by direct coordination of the ion by the protein can be considered a competition between the “process” of ion hydration, and the “process” of ion binding by interacting closely with the coordinators of the protein. We refer to this competition as between “processes” rather than between the water molecules and the site coordinators themselves, because the free energy of complexation at a site (Eq. 2) and the free energy associated with preferential complexation (Eq. 3) are both affected not only by the “chemical composition” of the binding-site coordinators versus that of the bulk phase (usually water molecules), but also by any type of structural constraints/allowances offered by the binding site versus the bulk. We point out that although of Eq. 3 encodes a relative ion binding preference, it hides information pertaining to absolute ion affinity (Eq. 2) for a given site. Given this, one should note that when considering different binding sites possessing similar selectivity and equivalent structural constraints/allowances, ligand chemical composition can play a key role in the absolute affinity, (Eq. 2), for ions A and B and their subsequent binding kinetics.
A small-system grand canonical description of ion complexation in a host
In the following text, and in the Appendix, using the above as a starting point, we define the distribution of coordinated states (i.e., coordination number and structure) for an ion at a site in a host. The procedure we use has been outlined previously (39) for defining a discrete quasicomponent distribution function in liquids. This distribution function is equivalent to the probability distribution function derivable from the so-called “small-system” grand canonical ensemble defined by Reiss and Merry (41), Soto-Campos et al. (42), and, earlier, in the work of Hill (64,65). The development also bears analogy with more recent theoretical (so-called quasichemical) approaches to the treatment of molecular association (i.e., clustering) in fluids (66,67). With this development, we arrive at a paradigm in which the free-energy functional of the ionic complex may be viewed as that for an ion-centered open system of coordinators (the size of the complexed ion's coordination shell) under the influence of the external field of the host (or system remainder). This perspective draws from ideas presented previously (44,45) for a fluid under the influence of an external field. In the case of an ionic complex formed by a host, the “external field” arising from elements of the host (or system remainder) serve as “topological control” over the free energy of complexation and, therefore, over the selective preference of the host for the complexed ion (24,26,28,68). Finally, we evaluate the role of the various system degrees of freedom in complexing the ion centered at x0 (or, rather, the origin of interest).
Consider a radius, rc, which traces out a spherical subvolume, v, around the ion (Fig. 1) open to the complementary external volume, , such that particles may enter or leave. Although any length may be chosen, for an appropriate choice of rc, a ligand can be said to coordinate the ion if it falls within the subvolume. To explore the ways in which a protein interacts with its bound ion, we begin by supposing that n (out of the total N) ligands occupy the subvolume, v, as shown in Fig. 1, upper.
We may write the probability density for observing a specific configuration, as (see Supporting Material)
| (4) |
where ρn, ρN−n, and ρR are the probability densities for observing the configurations in v, in VC, and R in V, respectively, if we consider them as independent systems. The function Cn is a correlation function that encodes their mutual dependence. We have also introduced the coupling parameters, ξC and ξR, within the correlation function, which may take on values from zero (completely uncoupled) to unity (completely coupled). The parameter ξC couples the interaction of the N − n coordinators in the complementary volume, VC, to the ion and the n coordinators inside v. The parameter ξR couples the interaction of the remaining degrees of freedom (corresponding to configuration R) with the coordinator degrees of freedom (corresponding to configuration rN) and the ion inside v.
In the Appendix, we show that Eq. 4 implies the probability density that the small open system within the subvolume, v, contains exactly n coordinators with configuration rn is
| (5) |
where is the potential describing interactions between all species in the subvolume, (defined by Eq. A25) is an external mean field (due to the influence of the coordinators outside of v and the system remainder) arising from the correlation function , and z (defined in Eq. A22) is the activity of a single coordinator. The normalization constant, (Eq. A23), is the grand canonical partition function. Integrating over configurational degrees of freedom, rn, produces the probability of observing exactly n coordinators inside v, otherwise known as a “discrete quasicomponent” distribution (39),
| (6) |
where is the n-fold configuration integral (discussed in relation with Eqs. A22 and A23 in the Appendix) for the subsystem under the influence of the external field, . This integral may be written as the product, , where is due to the n-fold complex taken independently (see Eq. A9), and is an “interfacial free energy” (41) of interaction between the n-fold complex inside v with the coordinators outside v and the remaining degrees of freedom in the system (see Eq. A13). Reiss and Merry (41) define the equality , in which has the interpretation of an angularly averaged surface tension (surface free-energy density; see Appendix). As discussed in our previous work (24), this equality dictates that no surface tension (tangential strain) at the interface of the complex can arise without influence from species exterior to v.
Analogous density functions (to Eqs. 5 and 6) may be derived (see Theoretical framework, Part III, in Supporting Material) for the case of an open complex in the environment of a hypothetical coordinator fluid (HCF) (Fig. 1, middle): (the superscript “C”, as compared with “CR”, is meant to imply ). Such functions may also be derived for the case of an open complex in the environment of a hypothetical coordinator gas (HCG) (Fig. 1, lower): . These descriptions of the “open” complex, under the influence of a given host, a fluid (HCF) under prescribed macroscopic conditions, or an ideal gas (HCG), provide a starting point for understanding the contribution of the external field provided by a particular host to the selective complexation of a given ion with a given type of coordinator.
“Topological control” and the “uncoupled” ionic complex
If we recall that the grand partition function in Eqs. 5 and 6 is dependent upon the position of the ion, x0, then the grand thermodynamic potential is . (We refer the reader to prior work (64,65,69) outlining the thermodynamic relations pertaining to a small-system grand ensemble). Thus, the free energy to move an ion of type “j” from bulk water to a site in the protein is
| (7) |
which amounts to choosing the ion solvated in bulk aqueous solution as a reference state. We may evaluate the contribution to the site (binding) free energy that is due to the protein and/or system remainder as (24)
| (8) |
where the subscript “top” refers to what we will call the “topological” contribution to the site free energy. Note that actually depicts a fictitious state () where the ion is solvated in a hypothetical coordinator fluid (HCF), and does not depend on the ion's position. Since we are dealing with states pertaining to the same ion, “j”, the bulk aqueous reference state does not come into play, and we may write (24)
| (9) |
where is the free energy of the ionic complex solvated in a fluid of coordinators, with the influence of the external field of the system remainder (host) “turned off” .
In previous treatments, would be termed the “intrinsic” free energy of the ion in the HCF (44,45). It follows, from the definition of free energy, that any field applied to the complex outside of an uncoupled HCF will uniquely determine the free energy of the complex by modulating (28,44,45). As such, the configurational distribution of ion-coordinated states observed in the HCF is a result of the ability of the field of an ion of type j to assemble/organize the surrounding fluid of coordinators. In this sense, the distribution of coordinated states in an uncoupled environment is the consequence of a generalized Hofmeister effect (1,2,4,5,46,47) for any type of coordinator fluid.
Given Eq. 9, the free energy of selectivity for ion A over ion B is
| (10) |
where is the selectivity at the site encoded in the “host” or system remainder, and is the selectivity of HCF for ion A over ion B (24). The latter term represents the ability of a particular type of moiety, in an uncoupled state, to select ion A over ion B with reference to a bulk water medium, and is independent of the position of the ion. If the HCF is taken to be bulk aqueous solution, then .
We must note that the definition of the topological contribution to the site free energy is dependent upon the choice of definition for the “uncoupled” system. This choice, in turn, depends upon what moieties one chooses to consider “coordinators”. For example, in Eq. 8, the uncoupled system chosen is the case in which there is correlation between the binding complex within v and the fluid of coordinators in the complementary volume, VC (i.e., (see Fig. 1, middle)), but no correlation between the complex and the system remainder (for example, the backbone of the host). This choice implies that the uncoupled contribution to the free energy of complexation is free of influence from the host (system remainder), but not free of influence from the HCF external to the complex. We could also have chosen the uncoupled system to be the case in which the binding complex interacts with nothing in the complementary volume (i.e., (Fig. 1, lower)). One could say that such a case corresponds to interaction of the complex with an external HCG instead of a fluid.
Both of these choices for the uncoupled system yield a different definition of the topological contribution of the host (or system remainder) to binding, but each affords a way to describe the effects of the protein's contribution to the free energy of complexation. Choosing that the external system be an HCG offers convenience in theory, because such an uncoupled system attributes the topological contribution of binding to all elements of the system falling outside the coordination subvolume, v. However, in practice, choosing an HCF for the uncoupled system is convenient and useful, because it corresponds to the familiar idea of a coordinated ion in a fluid, and results from “turning off” () all elements of the system that do not qualify as coordinator or ion. As is usual when defining correlation functions (43), there is no requirement that an uncoupled (uncorrelated) system represent a realistic system. So long as one's interpretation of the information encoded in is consistent, one may prescribe the macroscopic conditions (e.g., density or pressure) of an uncoupled state (HCG or HCF), and is defined.
Regardless of the choice for the uncoupled system, when an ion is complexed by coordinators at a site, its interactions will generally include both topological contributions and contributions from the coordinators within the complex itself. Thus, given any ion binding scenario, the correlation function, , will rarely be unity. The only case where interactions are entirely due to system topology is at a site where there is no coordination (i.e., ). In this case, , such that the “0-fold” interfacial free energy, , becomes the excess free energy of the ion fixed at x0.
Application to hypothetical models of selective sites
The discussion above illustrates the ways in which the formalism derived here covers the range of possibilities by which a protein/host might control the thermodynamics of an ion binding event. The relative affinity of different ions for a given medium or host (as in Eq. 3) may be approximately determined using computational and, in some cases, experimental techniques, and the distribution of coordinated states (as in Eq. 5) provided to an ion by a host can sometimes be modeled using computational techniques such as MD simulation. However, simulating all possible media and hosts for all possible ions is not necessarily the wisest way to go about drawing generalizations pertaining to selective complexation. To more generally understand the structural and/or chemical determinants of selectivity, it can be instructive to consider simplified models of the environment provided to an ion by a site within a hypothetical host. The framework above allows one to objectively identify assumption(s) made by common simplifications.
Perhaps the most pedagogical case pertaining to the determinants of selective complexation in the area of ion transport proteins is the rationale for the observed preference for K+ over Na+ displayed by the eightfold coordinated construct we have come to know as a “canonical” K+ channel cation binding site. In the spirit of host-guest chemistry's “hydration surrogate” rationale, one simplified model considers that the site consists of a tight-fitting cage of backbone carbonyl oxygen atoms that matches the hydration shell geometry of K+, but is too large to interact as favorably with Na+ (70) (schematically shown in Fig. 2 A). If, for the sake of discussion, we take this simplified model to its extreme (even though such an extreme interpretation may not have been intended), then the model explains selective complexation of K+ by assuming something about the functional form of the distribution of coordinated states provided for K+ and Na+ in both bulk water (i.e., , as in Eq. S10) and the channel protein (i.e., , as in Eq. 5). More specifically, the model assumes that in bulk water, K+ is coordinated by a cage of water oxygen atoms preferring the configuration , and that Na+ coordination is different in water by virtue of a smaller coordination radius provided by the configuration (Fig. 2). Thus, the simplification illustrated in Fig. 2 A assumes that the K+ channel protein serves to enforce the coordinated state (coordination number and configurational density) of bulk-solvated K+ regardless of whether K+ or Na+ is bound. In terms of probability density:
| (11) |
Above, δ is the Dirac delta function for the configurational degrees of freedom or the Kronecker delta function (with modified notation) for the discrete variable n. The set of vectors represents the expected positions of the “cage” of eight water molecules that coordinate K+ in water or in the canonical binding-site construct.
Figure 2.
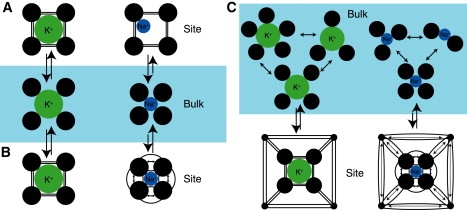
Sketches of different simplified models rationalizing selective complexation of K+ in the canonical eightfold construct of a K+ channel binding site. Large black circles represent oxygen atoms (carbonyl oxygen atoms in the channel “site” environment, and water oxygen atoms in the “bulk” aqueous environment). Straight lines between oxygen atoms represent relatively “unstrained” interactions and bowed lines (with arrows) represent relatively “strained” interactions. (A) A model in which the cavity size of the site is rigidly enforced (see Eq. 11). (B) A model in which the ensemble of coordinated states sampled by K+ or Na+ is considered to be generically “liquid-like” in both the channel and bulk water environments (see Eq. 12). The cavity size of the site is not enforced, but collapse of the site to cradle Na+ is unfavorable due to the high “field strength” of carbonyl moieties versus water molecules. (C) A model where the cavity size of the site is not explicitly enforced, but where enhancement/modulation of the coordination number of the complex by correlation (Eqs. 4 and 5) with the host (represented by the square object interacting with the oxygen atoms) causes a thermodynamic cost upon unfavorable collapse of the site to cradle Na+ (see Eqs. 13 and 14).
Another simplified model offers an alternative explanation (23,71,72) for K+ selectivity in which the carbonyl moieties of the selectivity filter are described as “liquid-like” and “dynamic”, resulting in an ablility to radially adapt to (or collapse around) the bound cation, whether it is Na+ or K+. In this model, since bulk aqueous solution and the filter both represent dynamic and liquid-like environments, selective complexation of K+ over Na+ is attributed to the high field strength (large dipole moment) of carbonyl moieties (comprising the K+-selective binding site) with respect to water molecules (comprising the nonselective bulk solution). The model asserts that upon replacement of water by carbonyl coordinators, selectivity arises from the strong electrostatic repulsion between the carbonyl ligands of the coordination sphere comprising the Na+-bound complex (72) (Fig. 2 B). If we interpret this illustrative model in terms of configurational probability density, the protein channel provides the same generic liquid-like ensemble for the coordinated ion as that provided by liquid water or an HCF of carbonyl ligands, i.e., for an ion of type j (K+ or Na+):
| (12) |
where is the configurational probability density given eightfold coordination in an HCF environment (see Eqs. A26 and A27). As such, the ion complex adapts fluidly to either K+ or Na+. The key of this model is the generic liquid-like configurational density, which has the same form for a given ion whether the medium is a liquid (such as carbonyl HCF or liquid water) or the protein. Only with this assumption of zero topological contribution ( from Eq. 9) can selective complexation of K+ be due to the electrostatic/chemical differences between water molecules and carbonyl groups, and not the external field provided to the complex. This is because the absence of topological control over the complex necessarily implies that there is no correlation between the complex and the host (system remainder): (Eqs. 4, 5, and S10). Without the assumption, it may be shown that, for a given type of coordinator (e.g., water or carbonyl), the free energy and the probability density of the system enclosed in the subvolume, v (i.e., the complex), is uniquely determined by the external field (44,45) provided by the protein/host or system remainder (Eq. 5) (24,28).
A third simplified model (Fig. 2 C) considers that although the site can conform and adapt to either K+ or Na+, it is the external field of the protein/host that is primarily responsible for the canonical binding site's K+ selectivity. Such a model might minimally assume that the K+ channel protein serves only to organize an eightfold cationic complex around an ion of type j (K+ or Na+):
| (13) |
This minimalistic model makes use of the knowledge that without an external field (topological control) from the protein, eightfold coordination is preferred by neither K+ nor Na+, whether the coordinator is taken to be a water molecule or a carbonyl moiety (24,26,28,68), in an “uncoupled” environment (i.e., there is no generic liquid behavior in the protein binding site). With this knowledge, the notion that the site maintains eightfold coordination and simultaneously behaves like a regular liquid is untenable. The model does not prevent the “collapse” of the ligands to accommodate K+ or Na+, nor does it assume that the configuration of the complex is uncorrelated with the host (system remainder).
One may express the topological contribution to the free energy of binding at this hypothetical site as (24)
| (14) |
(the free energy to assemble the site in an uncoupled HCF (see Eq. S10 and also Eq. 15)). And even though the selectivity of this simplified model has been shown to be quantitatively different upon taking the HCF of the uncoupled system to be composed of either water or carbonyl moieties, computational studies suggest that both types of coordinator display a value for (of Eq. 10) that is in line with or exceeds what can be expected from experimental measurements on K+ channels (24,26–28). Thus, imposing a coordination shell of eight water molecules or carbonyl ligands around K+ and Na+ irrespective of their positions, in an isotropic field produced by surrounding HCF, is a sufficient (though not a necessary) constraint on a complex to cause K+ selectivity (24,26–28). It will be shown that such a constraint on coordination number, in the absence of other explicit constraints, actually carries an implicit control over the other configurational degrees of freedom of the complex (e.g., as manifested by the preferred average coordination radius of a complex).
Results
Correlated observables in ionic complexes
By virtue of the exact treatment of the structural and chemical determinants of ionic complexation within a given host, liquid, or gas environment, the standard observables traditionally linked to ionic selectivity—configurational order parameters such as the cavity size of the complex or the coordination number, and the chemical identity of the coordinators—are generally correlated. Thus, although the pedagogical examples given, in the previous section, of simplified explanations for K+ selectivity exhibited by K+ channels might at first appear to treat these observable aspects separately, their seemingly pointed assumptions can have broader implications.
It has been shown previously, using combinatorially optimized spatial distribution functions for water around cations, that a constraint on the coordination number of an ion in liquid water also implies a particular coordination geometry (24,26). As a further illustration of the correlation between the number of coordinating ligands and the configurational degrees of freedom for a given ion in either water or (for cations) a carbonyl HCF, we show the average ion-oxygen coordination radius (a common observable in coordination chemistry (31,32,37)) observed as a function of the complex coordination number in Fig. 3. We note here that the average coordination radius within a complex is not equivalent to the optimal coordination radius, normally defined as the first maximum in the ion-oxygen pair correlation function (see Supporting Material). The optimal hydration radius (coordination radius in liquid water) of an ion can be related to the ion's size or to its physical radius, which is normally very close to the ion's Pauling radius as derived from crystallographic data (37). For the simulated media, we observe in Fig. 3 that the average coordination radius of each cation or anion increases with the coordination number, and that the optimal coordination radius agrees more closely with the average coordination radius at lower (usually four- to fivefold) coordination numbers. For cations, we note that the correlation between coordination number and average coordination radius is similar in water and a carbonyl HCF.
Figure 3.
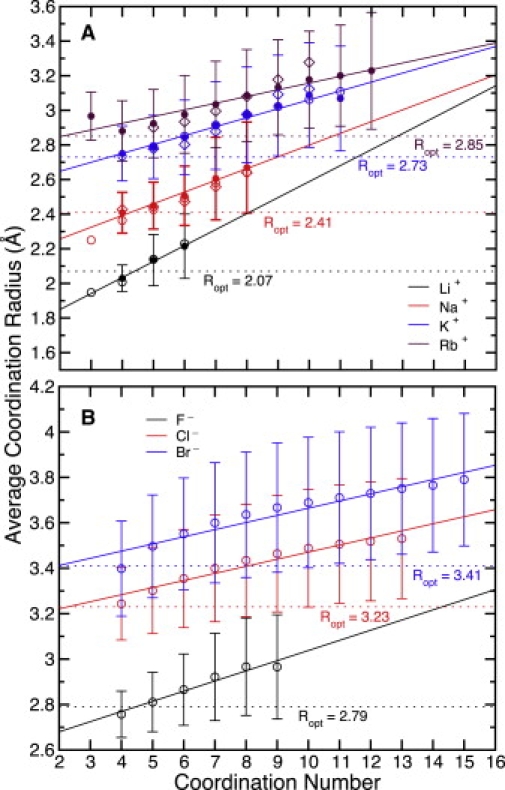
Correlation between the average ion-coordinator oxygen distance and the number of ion coordinating ligands in SPC (52,53) water (solid circles), AMOEBA (49,50) water (open circles), and an OPLS carbonyl (56,102) model HCF (open diamonds) for different monovalent cations (A) and for different monovalent anions in AMOEBA water (B). (A) Vertical bars centered around the SPC water values designate the standard deviation of the sample. Regression lines are also plotted for the SPC water data sets to serve as a guide for the eyes. Horizontal dotted lines indicate the optimal coordination radius, Ropt, for each ion as derived from the first maximum in the ion-oxygen pair correlation function in SPC water. (B) Vertical bars centered around each value designate the standard deviation of the sample. Regression lines are plotted for each data set to serve as a guide for the eyes. Horizontal dotted lines indicate the optimal coordination radius, Ropt, for each ion as derived from the first maximum in each ion-oxygen pair correlation function.
Further analysis of ions in these media suggests that a correlation exists between average coordination number and optimal ion coordination radius (related to effective ion size) (Fig. 4 A). Generally, smaller ions prefer fewer coordinating ligands and display less variability in the range of coordination numbers sampled (Table 1). This leads to a less compressible (more stiff) coordination shell for smaller/harder ions compared to larger ones (Fig. 4 B). These correlative trends imply complexation preferences that a host might exploit to elicit selective ion binding at a site. As will be seen in the discussion to follow, this implication is in no way a statement that a host must serve as a structural fluid/hydration surrogate for a particular ion to enforce selectivity for that ion.
Figure 4.
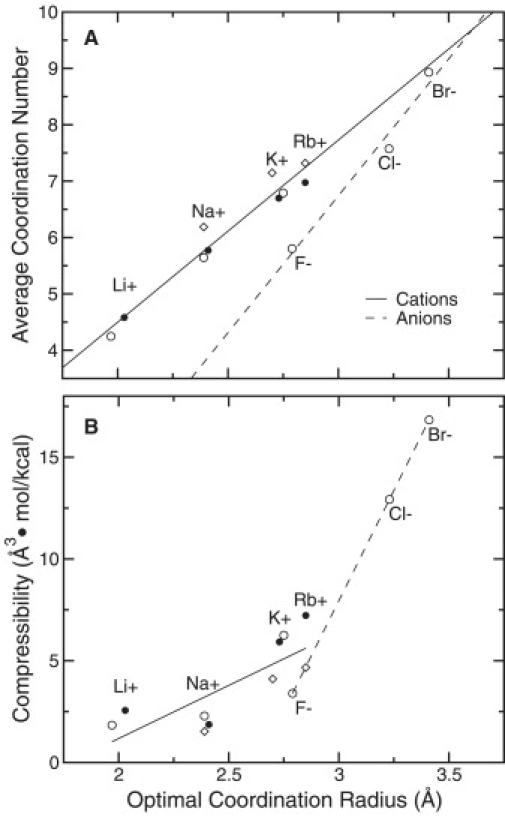
Examples of coordination preferences for various ions in SPC water (solid circles), AMOEBA water (open circles), and an OPLS carbonyl model HCF (open diamonds). (A) Correlation between the average coordination number of a given ion and its optimal coordination radius, Ropt. Regression lines are also plotted for cations and anions to serve as a guide for the eyes. (B) Correlation between the compressibility of the first coordination shell of a given ion, χT (see Theoretical framework in Supporting Material, Part V), and its optimal coordination radius, Ropt. Regression lines serve as a guide for the eyes.
In fluid media (as in Figs. 3 and 4), a wide range of coordination numbers may be sampled for a given ion, and the correlation between coordination number and configurational degrees of freedom indicate ionic preferences. In contrast, for a very “stiff” host (or system remainder), there can be a much larger thermodynamic penalty for removing a ligand from the imposed ionic complex because of resultant changes in the host's topology. Such alterations can generally propagate configurational changes in the complex. Obviously, the correlation between an ion's coordination number and average coordination radius will be dependent upon the host (system remainder), as stated in Eq. 5. Thus, one cannot know a priori, without explicitly considering the host (or system remainder), the exact dependence of the optimal complex configuration, (as determined by (see Eq. A26)), on n. However, structural evidence combined with statistical analysis of fluids supports the notion that in the interest of minimizing strain internal to a complex, the design or molecular evolution of a host that favors a particular coordination number, n, for its selected ion will also favor a particular optimal configuration, , for the selected ion that coincides with that derived from a suitably chosen uncoupled medium (24,26,68).
Such observed agreement in optimal coordination structure does not imply that the configurational distribution (Eq. 5) for any given host may be derived from an uncoupled medium (HCF (Eq. S10) or HCG (Eq. S12)) without any further information about the host, itself. The correlation between coordination number and the average coordination radius seen in Fig. 3 is a direct result of the internal stress field of the complex acting against an uncoupled HCF (24), and suggests that one way a host might favor a larger cavity size for a complexed ion is to increase the number of ligands forced to coordinate the ion. Obviously, this is not the only way to favor a particular cavity radius for an ionic binding site, but serves as an example of how the number of coordinating ligands and the configurational degrees of freedom of an uncoupled complex are intimately related.
Modeling structural determinants of selective ionic complexation
The identity of a given host will predetermine the distribution of coordinated states available to an ion (Eq. 5). Thus, it is impossible to invent a construct that predicts the mode of operation of any given host based on analysis of a host-uncoupled environment. However, for a given type of coordinator, we may explore the role of the host (or system remainder) as solely controlling identifiable parameters within the coordinated state of an ion. As such, we formulate “platonic” models from fluids (i.e., HCF) based on standard structural order parameters used by host-guest chemists that might serve as a basis for defining the bounds of preferential complexation for a given ion under a given set of structural constraints.
If we define a generalized structural order parameter for a complex, , an arbitrary function of the configurational degrees of freedom, then, in a manner analogous to that for the model described previously (Fig. 2 C and Eqs. 13 and 14), we may consider a platonic or minimalistic model of a host whose design only serves to “organize” or “assemble” a particular type of coordinator (from an uncoupled HCF) to form a complex around an ion of type j such that is constrained to a particular state, . The topological contribution for such a site upon complexing with an ion of type j may be formulated from Eqs. 5 and S10 as
| (15) |
Thus, such a model makes the important distinction between a “liquid-like” environment for the ion (of type j) solvated in an HCF (with free energy, ) and a topologically constrained environment (to state ) provided by a model host (or system remainder) represented by an external field acting on the complex.
Just as in Eq. 10, which treats an actual (indeterminate) host, we may use Eq. 15 along with the definition of the selective free energy (Eqs. 3 or 10) to obtain topological and uncoupled components of selectivity for an ion of type A over an ion of type B
| (16) |
where is the portion of selectivity at the site encoded in the hypothetical host; serving to constrain the coordinated states of ions A and B at states and , respectively. The above expression (and Eq. 10) is also easily derivable from simple reaction diagrams (24,57) and thermodynamic considerations. It is important to note the assumptions in this model: if the host provides the constraint corresponding to the free-energy cross section, , the topological contribution to the selectivity is simply the difference in free energy to assemble state λ around either ion, and if the model host provides for a condition where , then no more free energetic cost in the transformation is incurred than would be provided by the uncoupled HCF. Finally, we emphasize that the “topological contribution” to ionic complexation, and therefore to ionic selectivity, according to the definition outlined previously (24,28,57,68) and in this work (as in Eqs. 8 and 15), is a thermodynamic quantity due to the coupling between an abstracted complex and the host (system remainder). As such, in general, topological control over the selectivity of a complex is defined independently of the structural order parameters (such as the complex's coordination number, average coordination radius, coordinator orientation, etc.) that may be used to describe it.
We now consider examples of this sort of model put to use to facilitate understanding of different structural determinants that give rise to selectivity for exemplary biologically relevant monovalent ions. First, we explore model hosts/environments that provide a fixed constraint on the ion-coordinated state independent of the ion type (i.e., ), but are otherwise allowed to sample the configurational space of an HCF. We then move on to consider model variants that provide an ion-dependent constraint on a given order parameter of a complex (i.e., that allow complexation where ), but are otherwise allowed to sample the configurational space of an HCF. The order parameters we explore here are limited to the common choices—coordination number and average coordination radius. However in principle, one may concoct an infinite range of order parameters over which to explore the selectivity imparted by constraints placed on ionic complexation.
Environments that hold only coordination number fixed
Consider a model host similar to that depicted in Fig. 2 C and Eqs. 13 and 14, which constrains only the coordination number to nj for an ion of type j (i.e., , and the delta function in Eq. 15 is taken as a Kronecker delta function), irrespective of the configurational space available to the complex in the HCF. Fig. 5 shows 1D selective free-energy cross-sections ( such that for ions of type A and B) derived from fluids for different ions in such a model host.
Viewing the quasicomponent distributions (24,39,40) from which these profiles were derived (Fig. 5, A and C) makes the correlation between an ion's size and the compressibility of its first coordination shell (Table 1 and Fig. 4 B) more tangible. The implication of this trend is that larger (chemically softer) ions, preferring larger coordination numbers (Fig. 4 A), are better able to find a larger range of coordination numbers favorable (compared to smaller (chemically harder) ions). This result, and the general ion-dependent shape of the quasicomponent distributions, is qualitatively independent of the specific fluid medium sampled in this work (AMOEBA water, OPLS carbonyl fluid, and SPC water; see Figs. 5 A and S1 A).
The associated selective free-energy mappings suggest that in the absence of other constraints, approximately fivefold coordination provides minimal selectivity for Na+ over Li+ (or vice versa, Fig. 5 B, upper). Increasing the coordination number, n, to 6 creates an environment that is selective for Na+ over Li+ by more than 10-fold ( ≳ 1.5 kcal/mol). Decreasing n to 3 or 4 causes selectivity for Li+ over Na+ by anywhere from ∼10-fold to >100-fold ( in the range of ∼−1.5–2.5 kcal/mol).
The profile in Fig. 5 B, lower, was derived from liquid water and an OPLS carbonyl fluid in the same way as in previous work (24), and provides the same implication, namely, that a site providing solely five- or sixfold coordination, in the absence of other constraints, provides minimal selectivity for K+ over Na+ (or vice versa). Increasing n to 7 creates an environment that is selective for K+ over Na+ by anywhere from 10-fold to 100-fold (∼1.5–2.5 kcal/mol), depending on the type of coordinator. Increasing n further, to 8 or larger, provides >100- to 1000-fold selectivity. This n dependence of K+ selectivity over Na+ is the same for the two tested coordinator types (water molecules and carbonyl moieties) due to the similar shape of these ions' quasicomponent distribution in the two different media (Fig. 5 A, upper and lower), and Fig. S1 A). We note also, however, that the model carbonyl moieties shift the selectivity slightly in favor of K+ (by ∼10-fold) with respect to Na+, overall, as shown previously (24), due to a contribution from (though this shift may be model-dependent (see Supporting Material)).
A similar profile showing (Fig. S1 B) suggests that <10-fold selectivity for Rb+ over K+ (or vice versa) can be achieved by a host that enforces solely the coordination number (within the range of coordination numbers accessible to this study). It is also seen that the model carbonyl ligands used here, overall, have a very slight uncoupled selectivity for the larger Rb+ ion over K+.
The effect of constraining n on selectivity among small monovalent Family VIIA anions is shown in Fig. 5 D. An environment providing four to seven donors, in the absence of other constraints, is seen to be ≲10-fold selective or nonselective for Cl− over Fl− (or vice versa), whereas an environment that enforces coordination by eight or more donors is selective for Cl− over F− by ≳100-fold. The profile takes a value of zero kcal/mol between six- and sevenfold coordination. Between these coordination numbers, the hypothetical host shifts its preference from F− to Cl−. Selectivity for Br− over Cl− is less sensitive to a constraint on the coordination number. Approximately 10-fold or less selectivity is achieved for Br− over Cl−, or vice versa, in a host that constrains solely the coordination number to values within the range 4–12. The profile takes a value of zero kcal/mol between eight- and ninefold coordination. Between these coordination numbers, the hypothetical host shifts its preference from Cl− to Br−.
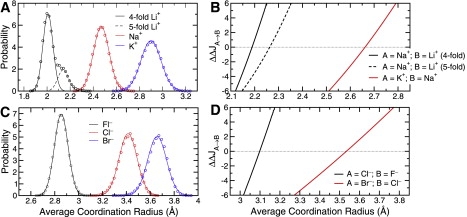
Environments that hold only average coordination radius fixed
Now, let us consider a hypothetical host that, instead, constrains solely the average coordination radius of a complex (not to be confused with the coordination radius itself; see Theoretical framework, Part V, and Fig. S3 in Supporting Material), irrespective of the coordination number sampled in an uncoupled HCF. This model differs from that of Fig. 2 A in that although there is a type of constraint on the cavity size provided to the ion, there is no constraint on the number of coordinators in the complex or the particular way in which they yield the average ion-oxygen radial distance. Thus, the delta function in Eq. 15, for an ion of type j, may be represented as , where
| (17) |
and represents the radial distance between the ion and the lth ligand of an n-complex.
The probability distributions, for small Family IA and VIIA ions in AMOEBA water are shown in Fig. 6, A and C. Distributions for cations obtained with the AMOEBA water model (Fig. 6 A) are very similar to those obtained with the SPC water model (Fig. S2 A) or an OPLS carbonyl HCF (Fig. S2 B). In nearly all cases, the distributions are modeled well by Gaussians. The exceptions are the distributions for Li+ in water, which display multimodality (Figs. 6 A and S2 A) due to the high correlation between the average coordination radius and coordination number (Fig. 3 A), and Na+ in the case of the carbonyl HCF (Fig. S2 B), which displays significant skewness. The multimodality in the Li+ distributions is largely accounted for by four- and fivefold quasicomponents. Although the Na+ distribution in carbonyl HCF may also possess multimodality, we did not pursue this issue.
The associated (cross-sectional) selective free-energy mappings, ( such that for ions of type A and B; see Figs. 6, B and D, and S2 C), were seen to be qualitatively independent of the fluid media from which they were derived and show a steep and nearly linear dependence on Ravg (over the range of Ravg investigated). Each curve takes on a value of zero somewhere in between the most probable value of Ravg for ions A and B (Fig. 6).
The free-energy profile, , suggests that for a host that enforces fourfold (Fig. 6 B, solid black curve) or fivefold (Fig. 6 B, dotted black curve) coordination around Li+ and no particular coordination number for Na+, imposing Å yields ∼10,000-fold selectivity or more (∼−6 kcal/mol) for Li+ over Na+. A host that provides four- or fivefold Li+ coordination can be ≳10,000-fold (∼+6 kcal/mol) selective for Na+ (enforcing no particular coordination number for Na+) over Li+ if it provides a constraint of Å or Å, respectively.
A profile for K+ selectivity over Na+, (Fig. 6 B, red curve), irrespective of the coordination number, suggests that a host enforcing Å provides minimal selectivity for either ion. Enforcing the condition Å, in the absence of other constraints, provides >10,000-fold selectivity for Na+ over K+, and enforcing the condition Å, in the absence of other constraints, provides >10,000-fold selectivity for K+ over Na+.
Although a host may weakly control selectivity for Rb+ over K+ by tuning n (Fig. S1 B), a more effective control arises from controlling Ravg (Fig. S2 C). A host enforcing Å provides minimal selectivity for either ion (Fig. S2 C). Increasing Ravg to ∼3.25 Å or greater provides ≳100-fold selectivity for Rb+ over K+, and decreasing Ravg to ∼2.75 Å or less provides ∼100-fold or more selectivity for K+ over Rb+.
Fig. 6 D shows analogous selective free-energy profiles for monovalent anions. The data for suggest that a host constraining Ravg to ∼3.09 Å is minimally selective for Cl− over F−. Increasing Ravg to ∼3.17 Å or higher yields ∼10,000-fold selectivity for Cl− over F−, and decreasing Ravg to ∼3.02 Å or lower yields a similar selectivity for F− over Cl−. A profile suggests that constraining Ravg to ∼3.53 Å is minimally selective for Br− over Cl−. Increasing Ravg to ∼3.77 Å or higher yields ∼10,000-fold selectivity for Br− over Cl−, and decreasing Ravg to ∼3.27 Å or lower yields similar selectivity for Cl− over Br−.
Environments that hold both coordination number and average coordination radius fixed
Examples of selectivity displayed by a hypothetical host that constrains both the average coordination radius and the coordination number regardless of the type of ion bound (represented by the following substitution in Eq. 15: , such that the host provides a constraint corresponding to the free-energy cross section, for ions of type A and B), are shown in Fig. 7. These free-energy mappings for K+, Na+, and Li+, derived from Gaussian probability models of data from simulations in fluid environments (Figs. S4–S6), delineate domains/phases in -space that are selective for one ion over another. Given that it can be difficult to “encode” or “build in” the physical response of a host's coordination structure upon binding different ion types, this sort of domain/phase mapping is, conceivably, the most useful construct for selective ion binding site design in proteins and ionophores. This is because (unlike the 1D mappings in Figs. 5 and 6) it provides a target for tuning both the coordination number and structure of a host's binding site. With this, the strategy for selecting a given ion would be to reinforce a prescribed structure within the appropriate domain.
Fig. 7 A, left and right, shows cross-sectional selective mappings in -space delineating domains of coordination states that are selective for K+ over Na+ when the coordinating ligand is taken to be a water molecule or a carbonyl ligand, respectively. Again, we see (just as in Figs. 5 B and S2, and mappings of previous work (24)) that although there are differences between the water- and carbonyl-based maps, both ligands provide similar selective domains for either cation. A mapping for Na+ selectivity over Li+ derived from population analysis in liquid water is also shown in Fig. 7 B.
Fig. 7, A and B, also shows -states provided by the binding sites of several exemplary K+-, Na+-, and Li+-selective compounds and transport protein structures (bound to their selected ions) as determined from diffraction and theoretical studies. In all cases, the selective-state space mappings display the capability of distinguishing which host should be naturally selective for a given ion. However, we must note that placement of a given ionophore's position on an -map does not constitute a statement that the ionophore strictly enforces the represented structure regardless of the type of ion bound (K+ or Na+ for Fig. 7 A and Na+ or Li+ for Fig. 7 B). Rather, it should be understood that the coordinated states shown in Fig. 7 in principle correspond to states of minimum strain within their respective crystal/simulated environments, since they represent hosts bound to the ions they are designed, whether artificially or by molecular evolution, to select. Thus, the fact that these states of minimum strain (for the represented hosts) show correspondence with the cation selective domain mappings of Fig. 7 demonstrates the underlying principle behind their design, namely, that molecular evolution (and artificial design) of a host exploits a generalized Hofmeister effect, and strives to enforce an ensemble of coordinated states that falls within the appropriate selective domain or phase.
Environments that allow ion-dependent constraints on coordination number
Let us now consider a model host/environment (system remainder) that constrains only the coordination number to nj for an ion of type j, irrespective of the configurational space sampled in an HCF, but does not enforce the condition for ions of types A and B. Recall, however, that if the model host provides for a condition where , then no more free-energetic cost in the transformation is incurred than would be provided by the uncoupled HCF. Fig. 8 shows 2D selective free-energy cross sections, for the small monovalent cations: K+, Na+, and Li+ corresponding to such a host.
The left and right panels of Fig. 8 A show a (cross-sectional) selective mapping in -space delineating the domain of coordinated states that are selective for K+ over Na+ when the coordinating ligand is taken to be a water molecule or a carbonyl ligand, respectively. These mappings are recapitulative of previous work (24), and again, we see (just as in Figs. 5 B, 7, and S2) that although there are differences between the water- and carbonyl-based maps (fictitious carbonyl groups exhibiting slightly higher overall selectivity by ∼1–1.5 kcal/mol; see also Fig. 5 B), both model ligands provide qualitatively similar selective domains for either cation. A mapping for Na+ selectivity over Li+ derived from population analysis in liquid water is also shown in Fig. 8 B.
Fig. 8, A and B, also shows the ion-dependent (average) coordination numbers provided by several different (fluid and transport protein) environments as determined from diffraction and theoretical/simulation studies (23,24,26,72–76). Placement of these positions on the map does not constitute a statement that the labeled medium does or does not provide stiff enforcement over other degrees of freedom within the provided complex (for example, stiff enforcement of average coordination radius). Rather, it should be understood that each coordinated state demarked in Fig. 8 represents the selectivity that the labeled medium would display in the absence of constraints on the complex beyond enforcement of the condition for A and B with a given type of coordinator (for example, in the absence of constraints on the average coordination radius).
In Fig. 8 A, we see that environments allowing for approximately sixfold coordination of Na+ (regardless of the coordination number, nK, provided for K+ within the plotted range), in the absence of other constraints, provide minimal selectivity for K+ over Na+ or vice versa (Fig. 8 A, red demarcations, and (24,27,28,68,76)). In contrast, enforcing eightfold coordination for Na+, as depicted by the construct of a canonical site in the K+-selective channel, KcsA (regardless of the coordination number, nK, provided for K+ within the plotted range), provides selectivity for K+ in the range of ∼3–6 kcal/mol (∼100-fold to ∼10,000-fold) in the absence of constraints on other degrees of freedom. Upon constraining the coordination number for Na+ to 9 or greater (and five- to ninefold coordination for K+), K+ selectivity over Na+ exceeds 10,000-fold.
Note, in the cross-sectional plot of Fig. 8 B, that there is a stronger dependence of Na+ selectivity over Li+ on coordination number. The contours successfully place the Na+-selective binding sites of the LeuT transporter in the Na+ selective region. Strict enforcement of fivefold coordination for both Na+ and Li+, such as that provided by site Na2 of LeuT, in the absence of other constraints on the complex, is sufficient to provide minimal (∼0.5 kcal/mol) selectivity for Na+ over Li+. Recent calculations employing an atomistic model of LeuT reported slightly higher Na+ selectivity for site Na2 (∼0.7–1.5 kcal/mol), which indicates that the protein likely exerts topological control over the stiffness of the site that favors the larger coordination radius of Na+ (73). According to Fig. 6 B (also Fig. 9 D), such control over the average coordination radius, irrespective of the coordination number, can indeed yield larger selectivity for Na+ over Li+. Strict enforcement of sixfold coordination for both Na+ and Li+, such as that provided by site Na1 of LeuT, in the absence of other constraints, is seen to provide ∼2.4–4 kcal/mol of selectivity in favor of Na+. This is substantially higher than calculations utilizing an atomistic LeuT model, which report an upper bound of ∼0.8 kcal/mol for site Na1 (73). One possible explanation for the discrepancy is that the models in Figs. 5 B and 8 B utilize neutral ligands, whereas one of the ligands in the actual Na1 binding site is a charged carboxylate of a bound Leu substrate. According to trends suggested by the Hofmeister effect (4) or by consideration of binding-site “field strength” (77–79), the presence of a charged ligand can be expected to shift the selectivity of the site in favor of the smaller, (electronically) harder, and more kosmotropic (referring to the ion's propensity to strongly bind (or organize) its first coordination shell) Li+ ion, which could result in a more neutral Na+/Li+ affinity (offsetting the larger Na+ affinity shown in Fig. 8 B).
Environments that allow ion-dependent constraints on average coordination radius
Finally, we consider a model host (system remainder) that constrains only the average coordination radius to Ravg,j for an ion of type j, irrespective of the coordination number sampled in an uncoupled HCF, but does not necessarily enforce the condition for ions of type A and B. Recall, however, that if the model host provides for a condition where , then no more free-energetic cost in the transformation is incurred than would be provided by the uncoupled HCF. Fig. 9, A and D, shows 2D selectivity cross sections, , for the small monovalent cations K+, Na+, and Li+ corresponding to such a host.
In Fig. 8 A, we demonstrated how enforcement by a host of a coordination number of 7 or more for Na+ is sufficient, in the absence of other constraints, to cause selectivity for K+ (over Na+). We see, from Fig. 9 A (and Fig. 6 B), that this constraint, though it is sufficient, is not necessary for K+ selectivity. The cross-sectional plots of in the Fig. 9 A, right and left, show that whether the coordinator is chosen to be a water molecule or a carbonyl moiety, a selectivity of >5 kcal/mol (>1000-fold) for K+ over Na+ is achieved by a host that constrains only the average coordination radius (around both ions) to a K+-adapted size (∼2.75–2.9 Å; see Fig. 6 A), but allows the site to sample coordination number space in the same manner as in a HCF. The domain mappings of Fig. 9 A also show that if a host were to enforce a size consistent with an Na+-adapted cavity (Ravg ≈ 2.4–2.55 Å; see Fig. 6 A) for both ions (in the absence of other constraints), then selectivity would be shifted in favor of Na+ by ∼5 kcal/mol or more (>1000-fold). An environment or host that allows the average coordination radius to relax to accommodate either ion's (uncoupled) preferred value (see Fig. 6 A) is seen to provide minimal selectivity for either ion.
To probe more intimately the implications of constraining n and Ravg together, it can be useful to consider the 2D cross sections, , which yield the selective free energy for a hypothetical host that constrains the coordination number to and the average coordination radius to and for K+ and Na+, respectively. Fig. 9, B and C, shows such cross sections, derived from analysis of K+ and Na+ in liquid water, for the constraints and , respectively.
The map of in Fig. 9 B is seen to be very similar to the map of in Fig. 9 A. This demonstrates that topological enforcement of either a K+- or Na+-adapted cavity while simultaneously enforcing sixfold coordination will yield selectivity for these respective ions. On one hand, in agreement with the maps of Fig. 8 A (and of previous work (24,26,27)), a host that allows cavity relaxation (to the extent seen in a HCF) while topologically enforcing sixfold coordination yields minimal selectivity for either ion. On the other hand, the map of in Fig. 9 C is different from those of Fig. 9, A and B, in an important way. This map shows also that a host fostering eightfold coordination while also enforcing either a K+- or Na+-adapted cavity will yield selectivity for these respective ions. However, in agreement with the map of Fig. 8 A (and with previous work (24,26,27)), if such a host were to allow cavity relaxation (to the extent seen in a HCF) while enforcing eightfold coordination, it would retain K+ selectivity over Na+. This type of control over selectivity exploits the correlation between the preferred average coordination radius and coordination number (Fig. 3 A).
Fig. 9 D shows the cross-sectional map derived from analysis of Na+ and Li+ in liquid water. This map demonstrates that in the absence of constraints on coordination number, a host that enforces either a Na+- or Li+-adapted cavity (Ravg ≈ 2.0–2.15 Å; Fig. 6 A) will yield selectivity for these respective ions. However, a hypothetical host that allows relaxation in either n or Ravg provides the same amount of selectivity as the uncoupled HCF medium (i.e., in the case of water, this implies nonselectivity). Thus, it is clear that one way a fivefold site, such as site Na2 of LeuT (as depicted in Fig. 8 B), can supply substantial Na+ selectivity over Li+ is to place control on the cavity radius allowed to either of these ions. Obviously, the extent of such control, by virtue of Eq. 5, depends upon the host.
Discussion
The theoretical framework we present here and elsewhere (24,57), by simpler means, provides a statistical thermodynamic basis for deconstructing the selective free energy of ionic complexation (of ion A over ion B, ) within a host into a contribution from the uncoupled properties of a given ligand type and a contribution from imposing the host's topology (system remainder, ; see Eqs. 10 and 16). This framework has been applied toward the analysis of “uncoupled” fluid-solvated ions (by means of Eq. 16) to develop platonic model binding sites in which the effects of particular structural elements, in the form of well-defined order parameters on the selective free energy, may be isolated and probed.
Without considering this coupling between complex and system remainder, it can be difficult to discern the physical and chemical elements leading to the ionic selectivity displayed by a given host. For example, it has been asserted recently (73) that the terminology we label “topological control” over selectivity refers solely to a constraint on coordination number, and that the formulations of Eqs. 10 and 16, derived previously by simpler means (24,57), cannot account for so-called “snug-fit” selectivity mechanisms—i.e., stiff enforcement of coordination radius by a host. The selective mappings of Figs. 6, 7, 9, and S2 provide tangible counterexamples to such assertions. Moreover, considering the logic leading to Eqs. 10 and 16 will lead one to understand that , resulting from coupling the host (system remainder) to an ionic complex considered as an open system described by the probability density of Eq. 5, is due to forces applied to the complex by the host or system remainder (regardless of what structural features such forces imply—stiff enforcement of cavity radius, modulation of coordination number, ligand orientation, etc.). Imposing (coupling) this external field enforces a preference (or lack thereof) for a given ion (24,28). To avoid confusion, one should be wary that “topological control” over the selectivity of a complex not be confused with the structural order parameters that may be used to describe it.
The platonic models probed in this work were constructed from analysis of liquid water and a hypothetical fluid of carbonyl coordinators. By virtue of Eqs. 10 or 16, it is obvious that the selective phase mappings provided by these models will be dependent upon such choices in the uncoupled state (i.e., on the chemical identity of the coordinating ligands). Although the framework we have presented can, in theory, be used to account for any type of ligand, and can be generalized to account for the diverse “hybrid” coordinative environments seen in nature's evolved ionic binding sites (29) (i.e., binding sites comprised of ligands of varying chemical type—charged, dipolar, etc.), practical extensions of our platonic selective domain analyses to address such diversity are outside the scope of this work. Despite the demonstrative nature of the selective domain/phase mappings for neutral ligands provided here, with discretion, one may apply the findings derived from them (Figs. 5–9, S1, and S2) to shed light on the physical determinants of selectivity in ion transport proteins and ionophoric compounds.
A survey of natural selective environments
For pedagogical purposes, we begin the discussion of the implications of our results for K+ channel selectivity or, rather, the construct we have come to know as a canonical K+ channel binding site. As outlined in Fig. 2 and the related discussion, explanations for the selective mechanism of such a site have fallen into two categories, the first (70) assuming a rigid binding site adapted to the size of K+ that does not “collapse” to cradle Na+ (as in Fig. 2 A), and the second (23–27,29,72,80) assuming that the binding site is nonrigid, but “conform(s) more favorably to an ion of a particular size” (i.e., conforms more favorably to K+ than Na+, as in Fig. 2, B and C) (29). The selective free energy mappings of this work suggest that a model host providing a topological constraint on the coordination radius such that the binding site is rigidly adapted to the size of K+ is sufficient, but not necessary, to provide K+ selectivity over Na+. This is seen to be the case whether the model host allows the binding site to sample coordination number space (n space) in a manner consistent with an uncoupled fluid (see Figs. 6 B, 9 A (K+-adapted region), or S2), or, additionally, constrains the coordination number to 8 (Figs. 7 A or the K+-adapted region of Fig. 9 C). The selective free energies yielded by these models are consistent with or exceed values expected from electrophysiological measurements on “maxi-” type K+ channels or KcsA (81–84). Thus, the mechanism depicted by Fig. 2 A (or Eq. 11) is a viable way in which a host might selectively bind K+ over Na+. However, modeling studies (23,26,72,76,80) have provided data suggesting that the canonical K+ channel binding site, although it can maintain eightfold coordination of the bound ion, does not prevent radial accommodation of Na+.
The mechanisms depicted in Figs. 2, B (Eq. 12) and C (Eq. 13), provide two different possible explanations for both K+ selectivity (over Na+) of the canonical K+ channel binding site and the notion that the site's cavity relaxes in response to the binding of either K+ or Na+. The selective domain mappings of Figs. 5 B, lower, and 8 A demonstrate, as in previous work (24,26–28), that constraining the coordination number, n, of a complex to values >6, in the absence of other constraints, is sufficient, but not necessary, to cause K+ selectivity over Na+ that is in line with values inferred from electrophysiological measurements in a variety of K+ channels (81–84). Further, constraining n to a value of 8 in the same manner as a canonical K+ channel binding site (23,72,75) or larger is sufficient, but not necessary, to cause K+ selectivity of >100- to 1000-fold. This result is seen to hold whether the coordinator is taken to be a carbonyl ligand (Figs. 5 B, lower, red curve, and 8 A, right)) or a water molecule (Figs. 5 B, lower, black curve, and 8 A, left)).
Thus, although the fictitious carbonyl moieties used here are shown to slightly favor K+ over Na+, the positive selectivity of an eightfold K+ channel binding is not a unique property of generically liquid carbonyl ligands as depicted by the “field-strength/carbonyl-repulsion” mechanism of Fig. 2 B. Numerous analyses (24,26–28,80) have demonstrated that the canonical K+ channel binding site does not behave like a liquid, and that when constraints enforcing eightfold coordination are removed, lower coordination numbers result, and selectivity for K+ is minimal (24,26–28). Such control over the coordination number derives from the protein channel, which provides “complementarity” (80) for K+, and has been labeled a type of “topological control” (24) called “phase” activation (26,68). This form of control (Fig. 2 C) exploits correlation between coordination number and preferred coordination radius (Figs. 3 and 4) to provide thermodynamic cost upon coordinating the smaller Na+ ion. Fig. 9 summarizes this idea. In the absence of any constraint on the coordination number (Fig. 9 A), a host providing minimal thermodynamic cost upon cavity relaxation to suit the coordination radius of either K+ or Na+ (as in a fluid) provides minimal K+ selectivity. A host enforcing sixfold coordination (Fig. 9 B), and allowing cavity relaxation without thermodynamic penalty, again provides minimal selectivity. However, a constrained eightfold coordinated complex (Fig. 9 C) provides a different selective map than that of a complex that allows the coordination number to fluctuate in a “liquidlike” manner (Fig. 9 A). A host that enforces such an eightfold constraint is seen to be selective for K+ regardless of whether or not the cavity relaxes to suit K+/Na+.
Contrariwise, the recently characterized Na+- and K+-conducting NaK channel (85) is an example of a channel that has been suggested to lack explicit enforcement of a cavity radius and to allow substantial hydration of a bound Na+ or K+ ion (72,76). Allowance of excess hydration within a site of this channel has been seen to result in approximately eightfold coordination of K+, and relaxation to approximately sixfold coordination of Na+. This and previous (24,26,28,68,76) analyses suggest that, whether the coordinators are purely water molecules or carbonyl moieties, such an environment will be minimally selective for K+/Na+ (Fig. 8 A).
One should not construe the mechanism of Fig. 2 C as implying that the chemical nature of a binding site's coordinating ligands is of no consequence. By virtue of Eqs. 10 and 16, such inferences would be analytically incorrect. Also, although it is clear that the K+ channel's molecular evolution has exploited the coordination preferences of K+ to provide its selectivity, one should not construe the mechanism of Fig. 2 C as equivalent to hydration “mimicry” as a generalized selectivity mechanism. Such an extrapolation was presented in a recent work (73), where it was asserted that the notion of “topological control” would dictate that if enforcement of eightfold coordination (a coordination number putatively close to the average hydration number of K+) is selective for K+, then inversely, enforcement of fivefold coordination (a coordination number putatively close to the average hydration number of Na+) should be selective for Na+. First, the statistical thermodynamic definition of “topological control” presented here and elsewhere (24,26–28,68) does not necessarily have anything to do with the notion of “hydration mimicry”. Second, our analysis (Figs. 5 B and 8 A) and those of others (24,26–28,68) show that sole enforcement of five- to sixfold coordination is minimally K+/Na+ selective.
We may, in addition (see(Figs. 6 B, 7 A, or 9, A or B), a reflection of the basis of K+ selectivity in hosts such as valinomycin (68,77) or of Na+ selectivity in recently characterized Na+-driven secondary transporters (73,86,87). These species are known to provide stiff cavity enforcement adapted to their selected ions in cases that override the effect of sole control over coordination number. For example, (K+-selective) valinomycin, which provides a coordination number of 6 for either K+ or Na+, would be nonselective for K+ (based on sole control over n; Fig. 5 B) were it not for a stiff control over coordination radius (Figs. 6 B or 9 B). Likewise, (Na+-selective) monensin, enniatin B, or sites Na1 and Na2 of LeuT (Fig. 7) provide five- to sixfold coordination of K+ or Na+, and would be minimally or nonselective for Na+ were it not for an analogous stiff control over cavity size (Figs. 6 B or 9 B). In addition, the structurally characterized Na+-driven secondary transporters are known to carry mild selectivity at their sites for Na+ over Li+ (73,86,87). One may glean from our selective domain mappings that by virtue of coordination number alone, the five- and sixfold ion binding sites of LeuT would be able to select Na+ over Li+ (Figs. 5 B and 8 B). Further constraints on the cavity size by the host can enhance such selectivity (Figs. 6 B, 7 B, and 9 D). Although our model may predict an excessive selectivity for Na+ over Li+ in the sixfold site, Na1 of LeuT, this may be due to the fact that the mappings we provide here were constructed for neutral ligands. The actual site, Na1, contains a charged leucine amino acid that, according to trends suggested by field strength considerations or the Hofmeister effect (4,77–79), could shift the Na+ selectivity seen here (e.g., Fig. 7 B) to milder values.
Finally, we discuss the implications of our selective mappings for the family of ClC transport proteins. Structural knowledge is available for this set of proteins via x-ray diffraction studies on prokaryotic Cl−/H+ exchange transporters (88,89). Although prokaryotic homologs of these transporters may manifest themselves as either diffusive Cl− channels or Cl−/H+ exchange transporters, it seems apparent that their conduction mechanisms are related (90–92). Such a relationship provides some difficulty in clearly identifying the source of Cl− selectivity, because of its very tight coupling with protonation of negatively charged residues in these transporters' selectivity filters. And even though selective flow of particular anions is not as much of a physiological necessity as selective flow of particular cations, the subset of ClC channels does show definite permeability sequences (93). MD simulations of the structurally characterized prokaryotic antiporters have suggested that Cl− in the selectivity filter accepts hydrogen bonds from neutral moieties (O-H and N-H groups) of the protein and water molecules (90,94,95). The coordination number for bound Cl− at the most central site in the ClC selectivity filter (so-called site Scen) appears to be controlled at ∼6–7 in total, which, according to Fig. 5 D, would allow for minimal selectivity in favor of Cl− over Br−, but renders selectivity for Cl− over the smaller F− unclear. Thus, to enforce Cl− selectivity over other anions to the mild extent observed in the ClC family (93), the protein will need to provide some level of radial stiffness at its selective anion binding site, according to Fig. 6 D, to favor a Cl− adapted cavity.
In the future, extensions of this type of analysis, in combination with its underlying concepts, may help us to understand more complicated selectivity mechanisms. For example, Na+/K+-ATPase and Ca2+-ATPase, according to recent structural data (96,97), illustrate of how chemically very similar binding pockets can display selectivity for a variety of mono- and divalent cations (i.e., Na+, K+, and Ca2+), depending on the structure of the topologically enforced coordination environment. Such dependence implies that selective mappings analogous to those we present here might provide insight into the underlying elements of alternating access mechanisms (98) that utilize conformational changes within a single binding pocket to enforce binding or dissociation of a given ion type.
Active and passive transport proteins will likely have evolved to use different strategies for enforcing selective environments, since they must operate in different ways. To allow fast permeation, a passive channel must not bind its selected ion too tightly, but the selectivity filter must still provide an environment where the selected ion can compete successfully with the “wrong” ion. The selectivity mechanism in a canonical K+ channel binding site, for example, satisfies this need. However, transporters such as pumps or secondary transporters can require significant conformational changes to make use of alternating access mechanisms. Thus, they may make use of very strict control over the conformation of their ionic binding sites to cause maximum selectivity for the desired ion, regardless of binding affinity, upon its recruitment from one side of the membrane, and to cause minimal affinity for the same ion upon changing conformation to allow its release to the other side of the membrane. As the availability of structural information increases for ion transport proteins, it will be necessary to augment the treatment developed here. For example, the mechanisms of selectivity for Ca2+- and Mg2+-specific transport proteins, for which there is growing structural information (29,63,99,100), will require special attention due to the hardness or kosmotropic nature of small divalent ions. Recent development of sophisticated models for treating such ions (49,101) may be of use in such an endeavor.
Conclusion
A unified conception of the ionic complexation event can provide broad utility in understanding the molecular evolution of selective channels/transporters as well as in guiding their modification and design. In our aim to provide a framework for understanding the statistical determinants of ionic complexation in a host, we have recast a very old idea in liquid structure theory known as the “mixture model” approach (39,40) in terms of a so-called “small-system” grand canonical ensemble (41,42,64,65). What results is a picture of the ionic complex conceived as an ion-centered system of coordinators the size of the central ion's first coordination shell and acting under the influence of an external potential provided by the host or system remainder. The system is open, allowing the exchange of coordinators with the exterior and the first coordination shell under its own influence and the influence of the external potential. As such, the properties of the system are determined not only by the chemical properties of the central ion and surrounding coordinators, but also, in a unique way, by the external potential provided by the system's surrounding environment.
The construct of a fluid under the influence of an external field is not a new one. It has been used extensively in the treatment of the stress field and interfacial properties of simple fluids (44,45). From such developments, one is able to draw a distinction between the free energy of a fluid, uncoupled from the external field that would be imposed by a host, and the free energy that is due to imposition of the external field. In terms of the development we provide here, the external field represents correlation of the host, or system remainder, with the ligands that are available to coordinate the central ion. This correlation serves to control the ensemble of coordination numbers and the other configurational degrees of freedom available to the complex.
With the distinction between the uncoupled contribution, , of a chemical type of coordinator and the topological contribution, , to the free energy of forming a complex around an ion (see Eq. 9 or Bostick and Brooks (24)), one may break the host's selective free energy for binding one ion (ion A) over another (ion B) into two contributions (see Eq. 10 or Bostick and Brooks (24))—one uncoupled, , and another topological, (Eq. 10). Whether by artificial or evolutionary means, a selective ion transport protein or ionophoric ligand possesses a molecular design such that a particular ion is favored. Given this, it may be established that the molecular evolution of a host must serve to optimize the external field (see Eq. 5) or correlation (see Eq. 4) that results in the topological contribution, , such that one ion (say, ion A) is favored over another (say, ion B). The discrepancy in favorability must provide a free-energy difference at the host's site such that the relative free energy between the two ions in the surrounding solvent medium (usually bulk water) is offset (Eqs. 3, 10, or 16). This simple idea of exploitation, by the host, of the local environmental preferences of ions to effect selectivity for a particular ion may be considered exploitation of a generalized Hofmeister effect (1–5,46,47). Thus, it may be said that the molecular evolution of ion-selective proteins serves as a learning process whereby the coordinative preferences of the candidate ions (ions that are either selected for or discriminated against) serve as the ultimate principle of molecular design.
No theoretical framework or model can provide a “silver bullet”, whereby the selectivity of any given ion in any given host may be predicted, because such a notion would require a priori knowledge of the topological control (“external field”) exerted by the host. However, using the framework presented here, one may derive platonic binding site models from systems comprised of ions in uncoupled media that make it possible to probe the selective effect of isolating and constraining plausibly relevant order parameters of an ionic complex (e.g., coordinator orientation, coordination radius, coordination number, radius of gyration of the complex, etc.) in a particular way. These platonic models lead to selective domain maps (or phase diagrams) that aid in understanding the determinants of selectivity in naturally occurring and synthetic hosts of known structure. The domain maps and framework presented in this work might be augmented to treat a broader range of ligand types and “hybrid” coordinative environments employing ligands of varying chemical identity. Such an extension would allow for a general and more explicit formulation of current knowledge pertaining to the relationship between the Hofmeister effect and charge-density-dependent ion-ligand pairing preferences (4). Nonetheless, as they stand, the developments of this work provide the constructs and methodology for systematically understanding the chemical and structural determinants of selective ionic complexation. Within this systematization lies an incisive means toward understanding how to modify and/or design the coordinative environments provided by proteins (whether globular or involved in membrane transport) and ionophoric compounds to yield selectivity for a desired ion.
Acknowledgments
This material is based upon work supported by the National Science Foundation under grant number 0434578. Additional National Science Foundation support (PHYS0216576 and MCB-0413858) and support from the National Institutes of Health (RR06009) are also acknowledged.
Appendix A: Small-System Grand Ensemble: Ion Complexation in a Host
It will be useful to define the canonical partition function for an ion-host system (Fig. 1, upper) in terms of the configuration integral defined in Eq. 1:
| (A1) |
The quantity qC is the partition function of a single coordinator, and is the analogous term for the remainder of the system. The tilde indicates division by the system volume raised to the “appropriate” power.
The implication of Eq. 4 is that the system configurational density function, , may be recast as
| (A2) |
where we have written (no assumption of pairwise additivity is required (41,42)),
| (A3) |
The energy, , encodes the interactions among the ion and n coordinators, those among the N − n remaining ligands, and those among the remainder of the system; is termed an “interfacial” energy (41). The superscript “CR” is meant to imply . Since is directly related to the correlation function, Cn, in Eq. 4, it represents an external field that couples the interactions between the ion and n coordinators within v to rest of the system. Note that is the only component of the energy that depends upon the coupling parameters, ξR and ξC, defined in Eq. 4. Henceforth, when ξR and ξC are not explicitly written as arguments, the reader may assume . Any discussion where a coupling parameter takes on a value other than unity will explicitly state so.
Now, we may write the probability that exactly n coordinators bind the ion as
| (A4) |
where is the Kronecker delta function, which takes on a value of unity if , and zero otherwise. The superscript “CR” is meant to imply . The coordination number, c, for a particular coordinator configuration, rN, is given by
| (A5) |
where H is the unit step function,
| (A6) |
The combinatorial factor comes about to account for the number of ways we might choose n out of N indistinguishable coordinator molecules to occupy the subvolume, v. It is arguable that one coordinator on a protein might be distinguishable from another by virtue of the fact that it is covalently bonded to a particular residue in the sequence. Note, however, that upon the exchange of, for example, a carbonyl group (coordinator) on the backbone of residue A with a carbonyl group (coordinator) on the backbone of residue B, the chemical identity of the protein will remain the same. Thus, the combinatorial factor is necessary. The delta function in the integrand of Eq. A4 implies that
| (A7) |
since the integrand, , takes on a value of zero when (or where ) for all values of i from 1 to n and when (or where ) for all values of i from n + 1 to N.
When and , we have (equivalently, the correlation function ), and
| (A8) |
where
| (A9) |
The superscript “0” on the configuration integrals , is redundant notation to emphasize the fact that they represent uncoupled, independent systems. Thus,
| (A10) |
Note that we have simply multiplied the exponential, , of Eq. A2 by a “judicious” 1. If we substitute the probability density of Eq. A10 into Eq. A7, we have
| (A11) |
The above integrand represents the weighted average,
| (A12) |
Reiss and Merry (41) define an “interfacial free energy” or surface free energy,
| (A13) |
where γn is a surface tension or surface free energy density. This quantity is the free energy of interaction between the n-fold coordination complex (ion plus coordinators) inside v and the coordinators outside the subvolume plus the remaining degrees of freedom in the system.
If we substitute the definition of (Eq. A1) and the identities
| (A14) |
into the prefactor of the integral in Eq. A11, we obtain
| (A15) |
Above, the product is the partition function for the uncoupled system (when and ). The quantity, is the partition function for the n coordinators interacting with the ion in v, is the partition function for the coordinators in , and is the partition function for the remainder of the system in V.
If the subvolume, v, is small in comparison to the macroscopic volume, V, then , and upon inserting the definition of the Helmholtz free energy for the ratio, , we obtain
| (A16) |
Again, the “0” superscript indicates a fully “uncoupled” state. are the free energies of N − n uncoupled coordinators in the complementary volume, VC, and of the uncoupled system remainder, respectively. Note that does not depend on v or on n. is the free energy of the entire, fully coupled system.
To understand the free-energy component (let us call it “ω”) in the brackets “[…]” of the exponential in Eq. A16, we may begin by adding a “judicious” zero to :
| (A17) |
where μ0 is the chemical potential, or free energy, to insert a single free coordinator “molecule” (uncoupled from the entire system except the other coordinators within VC) into a fluid of free coordinator molecules occupying the complementary volume . Thus, the free energy in the exponential of Eq. A16 becomes
| (A18) |
Adding another “judicious” zero, we obtain
| (A19) |
where we have associated specific terms (in braces “ ”) with particular elements of the process of “assembling” the ion binding site. For clarity, allow us to reexpress these elements of free energy more completely, and in a logical order within the context of Eq. A16.
-
1.
is due to opening a cavity around the ion of volume v against the external influence of the fully coupled system while constraining all N coordinators (coupled to the protein) to remain exterior to v.
-
2.
is due to uncoupling the protein from its coordinators and “switching off” their interactions with all degrees of freedom (including the ion) except those of other coordinators.
-
3.
is due to uncoupling n free coordinators from one another and from the remaining N-n free coordinators, removing them from , and placing them in the subvolume, v. Recall, in the macroscopic limit, .
Note that once we place a coordinator inside the subvolume in step 3, it “feels” the external field of the ion, because only uncouples the interaction of the N − n coordinators outside the subvolume from the ion. The n coordinators within the subvolume are still allowed to interact with the ion at full uncoupling . The interaction of the n coordinators with each other and the ion is not encoded in μ0, but in of Eq. A16. Thus, steps 1–3, above, account for the excess free energy built into the protein for bringing n coordinators together to complex the ion; the surface free energy, , of Eq. A13 represents the excess free energy due to the interaction of the ion-bound complex (ion plus n coordinators) with the rest of the system, and (in Eq. A16) is the free energy due to the internal interactions within the uncoupled binding complex, itself.
Combining Eqs. A16 and A19, the normalization of implies
| (A20) |
where we have defined (see step 3, above). Given that the term has no dependence on n, we have
| (A21) |
With the definitions, and , the expression for yields
| (A22) |
where is the activity of a single coordinator. The normalization constant, , may be recognized as the grand canonical partition function,
| (A23) |
In the spirit of the so-called “mixture-model” approach of Ben-Naim (39,40), we may identify the distribution, , as the discrete quasicomponent distribution. From this point of view, when a protein binds an ion via coordination, it can be said that the protein actually “binds” the entire ion-coordinated quasicomponent complex. As such, the “interfacial energy” function, , is the so-called “binding energy” (62) of the n-coordinate quasicomponent, and the surface energy, , of Eq. A13 can be considered to be related to the excess portion of the quasicomponent's “effective” chemical potential.
We may now express the probability density that the system within the subvolume, v, contains n coordinators with the configuration, rn, as
| (A24) |
where is an external potential of mean force derived from the influence of the coordinators outside of v and the system remainder,
| (A25) |
As usual, we may express the probability density that particles 1…m out of the n coordinators within the subvolume attain a particular configuration, , irrespective of the positions of the remaining n − m coordinators, , as
| (A26) |
such that may be expressed as a product,
| (A27) |
Supporting Material
References
- 1.Hofmeister F. Zur Lehr von der Wirkung der Salze. Arch. Exp. Pathol. Pharmakol. 1888;24:247–260. [Google Scholar]
- 2.Zhang Y., Cremer P.S. Interactions between macromolecules and ions: the Hofmeister series. Curr. Opin. Chem. Biol. 2006;10:658–663. doi: 10.1016/j.cbpa.2006.09.020. [DOI] [PubMed] [Google Scholar]
- 3.Boström M., Williams D.R.M., Ninham B.W. Specific ion effects: why the properties of lysozyme in salt solutions follow a Hoffmeister series. Biophys. J. 2003;85:686–694. doi: 10.1016/S0006-3495(03)74512-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Collins K.D. Charge density-dependent strength of hydration and biological structure. Biophys. J. 1997;72:65–76. doi: 10.1016/S0006-3495(97)78647-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Collins K.D. Ion hydration: implications for cellular function, polyelectrolytes, and protein crystallization. Biophys. Chem. 2006;119:271–281. doi: 10.1016/j.bpc.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 6.Harding M.M. The architecture of metal coordination groups in proteins. Acta Crystallogr. 2004;D60:849–859. doi: 10.1107/S0907444904004081. [DOI] [PubMed] [Google Scholar]
- 7.Dill K.A. Dominant forces in protein folding. Biochemistry. 1990;29:7133–7155. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- 8.Chalikian T.V., Völker J., Plum G.E., Breslauer K.J. A more unified picture for the thermodynamics of nucleic acid melting: a characterization by calorimetric and volumetric techniques. Biochemistry. 1999;96:7853–7858. doi: 10.1073/pnas.96.14.7853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Eisenman G., Dani J.A. An introduction to molecular architecture and permeability of ion channels. Annu. Rev. Biophys. Biophys. Chem. 1987;16:205–226. doi: 10.1146/annurev.bb.16.060187.001225. [DOI] [PubMed] [Google Scholar]
- 10.McLaughlin S., Eisenberg M. Antibiotics and membrane biology. Annu. Rev. Biophys. Bioeng. 1975;4:335–366. doi: 10.1146/annurev.bb.04.060175.002003. [DOI] [PubMed] [Google Scholar]
- 11.Berkowitz M.L., Bostick D., Pandit S. Aqueous solutions next to phospholipid membrane surfaces: insights from simulations. Chem. Rev. 2006;106:1527–1539. doi: 10.1021/cr0403638. [DOI] [PubMed] [Google Scholar]
- 12.McLaughlin S. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 1989;18:113–136. doi: 10.1146/annurev.bb.18.060189.000553. [DOI] [PubMed] [Google Scholar]
- 13.Ermakov Y.A., Averbakh A.Z., Yusipovich A.I., Sukharev S. Dipole potential indicates restructuring of the membrane interface induced by gadolinium and beryllium ions. Biophys. J. 2001;80:1851–1862. doi: 10.1016/S0006-3495(01)76155-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Groves J.T., Boxer S.G., McConnell H.M. Lateral reorganization of fluid lipid membranes in response to the electric field produced by a buried charge. J. Phys. Chem. 2000;104:11409–11415. [Google Scholar]
- 15.Huang J., Swanson J.E., Dibble A.R.G., Hinderliter A.K., Feigenson G.W. Nonideal mixing of phosphatidylserine and phosphatidylcholine in fluid lamellar phase. Biophys. J. 1993;64:413–425. doi: 10.1016/S0006-3495(93)81382-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ross M., Steinem C., Galla H.-J., Janshoff A. Visualization of chemical and physical properties of calcium-induced domains in DPPC/DPPS Langmuir-Blodgett layers. Langmuir. 2001;17:2437–2445. [Google Scholar]
- 17.van Dijck P.W.M., Kruijff B.D., Verkleij A.J., van Deenan L.L.M. Comparative studies on the effects of pH and Ca2+ on bilayers of various negatively charged phospholipids and their mixtures with phosphatidylcholine. Biochim. Biophys. Acta. 1978;512:84–96. doi: 10.1016/0005-2736(78)90219-5. [DOI] [PubMed] [Google Scholar]
- 18.Ohki S., Arnold D. A mechanism for ion-induced lipid vesicle fusion. Colloid Surf. B. 2000;18:83–97. [Google Scholar]
- 19.Ohki S., Düzgünes N., Leonards K. Phospholipid vesicle aggregation: effect of monovalent and divalent ions. Biochemistry. 1982;21:2127–2133. doi: 10.1021/bi00538a022. [DOI] [PubMed] [Google Scholar]
- 20.Speir J.A., Munshi S., Wang G., Baker T.S., Johnson J.E. Structures of the native and swollen forms of cowpea chlorotic mottle virus determined by x-ray crystallography and cryo-electron microscopy. Structure. 1994;3:1–16. doi: 10.1016/s0969-2126(01)00135-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hille B. Sinauer Associates; Sunderland, MA: 1992. Ionic Channels of Excitable Membranes. [Google Scholar]
- 22.Corry B., Chung S.-H. Mechanisms of valence selectivity in biological ion channels. Cell. Mol. Life Sci. 2005;63:301–315. doi: 10.1007/s00018-005-5405-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Noskov S.Y., Bernèche S., Roux B. Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands. Nature. 2004;431:830–834. doi: 10.1038/nature02943. [DOI] [PubMed] [Google Scholar]
- 24.Bostick D.L., Brooks C.L., III Selectivity in K+ channels is due to topological control of the permeant ion's coordinated state. Proc. Natl. Acad. Sci. USA. 2007;104:9260–9265. doi: 10.1073/pnas.0700554104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lockless S.W., Zhou M., MacKinnon R. Structural and thermodynamic properties of selective ion binding in a K+ channel. PLoS Biol. 2007;5 doi: 10.1371/journal.pbio.0050121. e121/1079–1088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Varma S., Rempe S.B. Tuning ion coordination architectures to enable selective partitioning. Biophys. J. 2007;93:1093–1099. doi: 10.1529/biophysj.107.107482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Thomas M., Jayatilaka D., Corry B. The predominant role of coordination number in potassium channel selectivity. Biophys. J. 2007;93:2635–2643. doi: 10.1529/biophysj.107.108167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bostick D., Arora K., Brooks C.L., III K+/Na+ selectivity in toy cation binding site models is determined by the “host”. Biophys. J. 2008 doi: 10.1016/j.bpj.2008.12.3963. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gouaux E., MacKinnon R. Principles of selective ion transport in channels and pumps. Science. 2005;310:1461–1465. doi: 10.1126/science.1113666. [DOI] [PubMed] [Google Scholar]
- 30.Morais-Cabral J.H., Zhou Y., MacKinnon R. Energetic optimization of ion conduction rate by the K+ selectivity filter. Nature. 2001;414:37–42. doi: 10.1038/35102000. [DOI] [PubMed] [Google Scholar]
- 31.Dietrich B. Coordination chemistry of alkali and alkaline-earth cations with macrocyclic ligands. J. Chem. Educ. 1985;62:954–964. [Google Scholar]
- 32.Lehn J.-M. Springer; Berlin: 1973. Structure and Bonding. [Google Scholar]
- 33.Drago R.S., Vogel G.C., Needham T.E. A four-parameter equation for predicting enthalpies of adduct formation. J. Am. Chem. Soc. 1971;93:6014–6026. [Google Scholar]
- 34.Klopman G. Chemical reactivity and the concept of charge- and frontier-controlled reactioins. J. Am. Chem. Soc. 1968;90:223–234. [Google Scholar]
- 35.Pearson R.G. Hard and soft acids and bases. J. Am. Chem. Soc. 1963;85:3533–3539. [Google Scholar]
- 36.Pearson R.G. Acids and bases. Science. 1966;151:172–177. doi: 10.1126/science.151.3707.172. [DOI] [PubMed] [Google Scholar]
- 37.Marcus Y. Ionic radii in aqueous solutions. Chem. Rev. 1988;88:1475–1498. [Google Scholar]
- 38.Pauling L. Nature of forces between large molecules of biological interest. Nature. 1948;161:707–709. doi: 10.1038/161707a0. [DOI] [PubMed] [Google Scholar]
- 39.Ben-Naim A. Mixture-model approach to the theory of classical fluids. J. Chem. Phys. 1972;56:2864–2869. [Google Scholar]
- 40.Ben-Naim A. Mixture-model approach to the theory of classical fluids. II. Application to liquid water. J. Chem. Phys. 1972;57:3605–3612. [Google Scholar]
- 41.Reiss H., Merry G.A. Upper and lower bounds on the chemical potential of a hard-sphere fluid and other inequalities from scaled particle theory. J. Phys. Chem. 1981;85:3313–3322. [Google Scholar]
- 42.Soto-Campos G., Corti D.S., Reiss H. A small system grand canonical ensemble method for the study of hard-particle systems. J. Chem. Phys. 1998;108:2563–2570. [Google Scholar]
- 43.Hill T.L. Dover Publications; New York: 1956. Statistical Mechanics: Principles and Selected Applications. [Google Scholar]
- 44.Henderson J.R., Schofield P. Statistical mechanics of a fluid drop. Proc. R. Soc. Lond. A. 1982;380:211–227. [Google Scholar]
- 45.Evans R. The nature of the liquid-vapor interface and other topics in the statistical mechanics of non-uniform, classical fluids. Adv. Phys. 1979;28:143–200. [Google Scholar]
- 46.Dill K.A., Truskett T.M., Vlachy V., Hribar-Lee B. Modeling water, the hydrophobic effect, and ion solvation. Annu. Rev. Biophys. Biomol. Struct. 2005;34:173–199. doi: 10.1146/annurev.biophys.34.040204.144517. [DOI] [PubMed] [Google Scholar]
- 47.Hribar B., Southall N.T., Vlachy V., Dill K.A. How ions affect the structure of water. J. Am. Chem. Soc. 2002;124:12302–12311. doi: 10.1021/ja026014h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Brovchenko I., Oleinikova A. Four phases of amorphous water: simulations versus experiment. J. Chem. Phys. 2006;124:164505. doi: 10.1063/1.2194906. [DOI] [PubMed] [Google Scholar]
- 49.Grossfield A., Ren P., Ponder J.W. Ion solvation thermodynamics from simulation with p polarizable force field. J. Am. Chem. Soc. 2003;125:15671–15682. doi: 10.1021/ja037005r. [DOI] [PubMed] [Google Scholar]
- 50.Ren P., Ponder J.W. Polarizable atomic multipole water model for molecular mechanics simulation. J. Phys. Chem. B. 2003;107:5933–5947. [Google Scholar]
- 51.Ponder J.W. Washington University; Saint Louis, MO: 2004. TINKER: Software Tools for Molecular Design. Version 4.2. [Google Scholar]
- 52.Åqvist J. Ion-water interaction potentials derived from free energy perturbation simulations. J. Phys. Chem. 1990;94:8021–8024. [Google Scholar]
- 53.Hermans J., Berendsen H.J.C., van Gunsteren W.F., Postma J.P.M. A consistent empirical potential for water-protein interactions. Biopolymers. 1984;23:1513–1518. [Google Scholar]
- 54.Berendsen H.J.C., van der Spoel D., van Drunen R. GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995;91:43–56. [Google Scholar]
- 55.van der Spoel D., Lindahl E., Hess B., Groenhof G., Mark A.E. GROMACS: fast, flexible and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 56.Jorgensen W.L., Maxwell D.S., Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- 57.Bostick D.L., Brooks C.L., III On the equivalence point for ammonium (de)protonation during its transport through the AmtB channel. Biophys. J. 2007;92:L103–L105. doi: 10.1529/biophysj.107.109165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Grossfield A. Dependence of ion hydration on the sign of the ion's charge. J. Chem. Phys. 2005;122:024506. doi: 10.1063/1.1829036. [DOI] [PubMed] [Google Scholar]
- 59.Taylor J.R. University Science Books; Mill Valley, CA: 1982. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. [Google Scholar]
- 60.Sprik M. Coordination numbers as reaction coordinates in constrained molecular dynamics. Faraday Discuss. 1998;110:437–445. [Google Scholar]
- 61.Hansen J.P., McDonald I.R. Academic Press; San Diego, CA: 1986. Theory of Simple Liquids. [Google Scholar]
- 62.Ben-Naim A. Plenum Press; New York: 1987. Solvation Thermodynamics. [Google Scholar]
- 63.Tinker A., Williams A.J. Probing the structure of the conduction pathway of the sheep cardiac sarcoplasmic reticulum calcium-release channel with permeant and impermeant organic cations. J. Gen. Physiol. 1993;102:1107–1129. doi: 10.1085/jgp.102.6.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hill T.L. Thermodynamics of small systems. J. Chem. Phys. 1962;36:3182–3197. [Google Scholar]
- 65.Hill T.L. Dover Publications; New York: 1963. Thermodynamics of Small Systems (Part I) [Google Scholar]
- 66.Beck T.L., Paulaitis M.E., Pratt L.R. Cambridge University Press; New York: 2006. The Potential Distribution Theorem and Models of Molecular Solutions. [Google Scholar]
- 67.Pratt L.R., LaViolette R.A. Quasi-chemical theories of associated liquids. Mol. Phys. 1998;94:909–915. [Google Scholar]
- 68.Varma S., Sabo D., Rempe S.B. K+/Na+ selectivity in K channels and valinomycin: over-coordination versus cavity-size constraints. J. Mol. Biol. 2008;376:13–22. doi: 10.1016/j.jmb.2007.11.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hill T.L. Dover Publications; New York: 1963. Thermodynamics of Small Systems (Part II) [Google Scholar]
- 70.Bezanilla F., Armstrong C.M. Negative conductance caused by entry of sodium and cesium ions into the potassium channels of squid axons. J. Gen. Physiol. 1972;60:588–608. doi: 10.1085/jgp.60.5.588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Noskov S.Y., Roux B. Ion selectivity in potassium channels. Biophys. Chem. 2006;124:279–291. doi: 10.1016/j.bpc.2006.05.033. [DOI] [PubMed] [Google Scholar]
- 72.Noskov S.Y., Roux B. Importance of hydration and dynamics on the selectivity of the KcsA and NaK channels. J. Gen. Physiol. 2007;129:135–143. doi: 10.1085/jgp.200609633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Noskov S.Y., Roux B. Control of ion selectivity in LeuT: two Na+ binding sites with two different mechanisms. J. Mol. Biol. 2008;377:804–818. doi: 10.1016/j.jmb.2008.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Zhou Y., MacKinnon R. The occupancy of ions in the K+ selectivity filter: charge balance and coupling of ion binding to a protein conformational change underlie high conduction rates. J. Mol. Biol. 2003;333:965–975. doi: 10.1016/j.jmb.2003.09.022. [DOI] [PubMed] [Google Scholar]
- 75.Zhou Y., Morais-Cabral J.H., Kaufman A., MacKinnon R. Chemistry of ion coordination and hydration revealed by a K+ channel-fab complex at 2.0 Å resolution. Nature. 2001;414:43–48. doi: 10.1038/35102009. [DOI] [PubMed] [Google Scholar]
- 76.Fowler P.W., Tai K., Sansom M.S.P. The selectivity of K+ ion channels: testing the hypotheses. Biophys. J. 2008;95:5062–5072. doi: 10.1529/biophysj.108.132035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Åqvist J., Alvarez O., Eisenman G. Ion-selective properties of a small ionophore in methanol studied by free energy perturbation simulations. J. Phys. Chem. 1992;96:10019–10025. [Google Scholar]
- 78.Eisenman G. Cation selective electrodes and their mode of operation. Biophys. J. 1962;2:259–323. doi: 10.1016/s0006-3495(62)86959-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Eisenman G., Horn R. Ionic selectivity revisited: the role of kinetic and equilibrium processes in ion permeation through channels. J. Membr. Biol. 1983;76:197–225. doi: 10.1007/BF01870364. [DOI] [PubMed] [Google Scholar]
- 80.Asthagiri D., Pratt L.R. Role of fluctuations in a snug-fit mechanism of KcsA channel selectivity. J. Chem. Phys. 2006;125:024701. doi: 10.1063/1.2205853. [DOI] [PubMed] [Google Scholar]
- 81.Latorre R., Miller C. Conduction and selectivity in potassium channels. J. Membr. Biol. 1983;71:11–30. doi: 10.1007/BF01870671. [DOI] [PubMed] [Google Scholar]
- 82.LeMasurier M., Heginbotham L., Miller C. KcsA: it's a potassium channel. J. Gen. Physiol. 2001;118:303–313. doi: 10.1085/jgp.118.3.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Neyton J., Miller C. Potassium blocks barium permeation through a calcium-activated potassium channel. J. Gen. Physiol. 1988;92:549–567. doi: 10.1085/jgp.92.5.549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Yellen G. Ionic permeation and blockade in Ca2+-activated K+ channels of bovine chromaffin cells. J. Gen. Physiol. 1984;84:157–186. doi: 10.1085/jgp.84.2.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Shi N., Ye S., Alam A., Chen L., Jiang Y. Atomic structure of a Na+- and K+-conducting channel. Nature. 2006;440:570–574. doi: 10.1038/nature04508. [DOI] [PubMed] [Google Scholar]
- 86.Boudker O., Ryan R.M., Yernool D., Shimamoto K., Gouaux E. Coupling substrate and ion binding to extracellular gate of a sodium-dependent aspartate transporter. Nature. 2007;445:387–393. doi: 10.1038/nature05455. [DOI] [PubMed] [Google Scholar]
- 87.Yamashita A., Singh S.K., Kawate T., Jin Y., Gouaux E. Crystal structure of a bacterial homologue of Na+/Cl−-dependent neurotransmitter transporters. Nature. 2005;437:215–223. doi: 10.1038/nature03978. [DOI] [PubMed] [Google Scholar]
- 88.Dutzler R., Campbell E.B., Cadene M., Chalt B.T., MacKinnon R. X-ray structure of a ClC chloride channel at 3.0 Å reveals the molecular basis of anion selectivity. Nature. 2002;415:287–294. doi: 10.1038/415287a. [DOI] [PubMed] [Google Scholar]
- 89.Dutzler R., Campbell E.B., MacKinnon R. Gating the selectivity filter in ClC chloride channels. Science. 2003;300:108–112. doi: 10.1126/science.1082708. [DOI] [PubMed] [Google Scholar]
- 90.Bostick D.L., Berkowitz M.L. Exterior site occupancy infers chloride-induced proton gating in a prokaryotic homolog of the ClC chloride channel. Biophys. J. 2004;87:1686–1696. doi: 10.1529/biophysj.104.042465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Dutzler R. The ClC family of chloride channels and transporters. Curr. Opin. Struct. Biol. 2006;16:439–446. doi: 10.1016/j.sbi.2006.06.002. [DOI] [PubMed] [Google Scholar]
- 92.Miller C. ClC chloride channels viewed through a transporter lens. Nature. 2006;440:484–488. doi: 10.1038/nature04713. [DOI] [PubMed] [Google Scholar]
- 93.Fahlke C. Ion permeation and selectivity in ClC-type chloride channels. Am. J. Physiol. Renal Physiol. 2001;280:F748–F757. doi: 10.1152/ajprenal.2001.280.5.F748. [DOI] [PubMed] [Google Scholar]
- 94.Cohen J., Schulten K. Mechanism of anionic conduction across ClC. Biophys. J. 2004;86:836–845. doi: 10.1016/S0006-3495(04)74159-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Gervasio F.L., Parrinello M., Ceccarelli M., Klein M.L. Exploring the gating mechanism in the ClC chloride channel via metadynamics. J. Mol. Biol. 2006;361:390–398. doi: 10.1016/j.jmb.2006.06.034. [DOI] [PubMed] [Google Scholar]
- 96.Morth J.P., Pedersen B.P., Toustrup-Jensen M.S., Sørensen T.L.-M., Petersen J. Crystal structure of the sodium-potassium pump. Nature. 2007;450:1043–1049. doi: 10.1038/nature06419. [DOI] [PubMed] [Google Scholar]
- 97.Olesen C., Picard M., Winther A.-M.L., Gyrup C., Morth J.P. The structural basis of calcium transport by the calcium pump. Nature. 2007;450:1036–1042. doi: 10.1038/nature06418. [DOI] [PubMed] [Google Scholar]
- 98.Jardetzky O. Simple allosteric model for membrane pumps. Nature. 1966;211:969–970. doi: 10.1038/211969a0. [DOI] [PubMed] [Google Scholar]
- 99.White, S. M. Membrane Proteins of Known Structure. http://blanco.biomol.uci.edu/Membrane_Proteins_xtal.html.
- 100.Xu L., Wang Y., Gillespie D., Meissner G. Two fings of negative charges in the cytosolic vestibule of type-1 ryanodine receptor modulated ion fluxes. Biophys. J. 2006;90:443–453. doi: 10.1529/biophysj.105.072538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Jiao D., King C., Grossfield A., Darden T.A., Ren P. Simulation of Ca2+ and Mg2+ solvation using polarizable atomic multipole potential. J. Phys. Chem. B. 2006;110:18553–18559. doi: 10.1021/jp062230r. [DOI] [PubMed] [Google Scholar]
- 102.Kaminski G.A., Friesner R.A., Tirado-Rives J., Jorgensen W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B. 2001;105:6474–6487. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


