Impact of Synaptic Depression on Spike Timing at the Endbulb of Held

Abstract

Many synapses show short-term depression, but it is not well understood what functional purpose depression serves and whether its effects are beneficial or detrimental to information processing. We study this issue at the synapse made by auditory-nerve (AN) fibers onto bushy cells (BCs) of the cochlear nucleus, called the “endbulb of Held.” AN fibers carry timing information about sounds and converge on BCs, which relay timing information to brain areas responsible for sound localization. Dynamic-clamp recordings of BCs in mouse brain slices indicated that nonphase-locked inputs influenced the contribution of phase-locked inputs when all inputs had equal strength. We evaluated whether this situation depended on activity-dependent synaptic plasticity. Voltage-clamp recordings indicated that the amount of depression varied over the population of endbulbs, but sibling endbulbs terminating on the same BC had similar plasticity. We tested the effects of endbulb depression on BC spiking using dynamic clamp. Under most conditions, increasing depression led to lower probability of BC spiking. However, the effects on spike timing were highly context dependent. When all inputs carried uniform timing information, depression indirectly affected BC spike precision, by determining how many inputs were required to cross threshold. Earlier work has indicated that this interacts with the temporal distribution of inputs to determine BC spike precision. When inputs carried different timing information, depression greatly improved BC precision by suppressing highly active inputs carrying little phase-locked information. These data suggest that endbulbs with different depression characteristics could produce BCs that enhance response probability or timing under different stimulus conditions.

INTRODUCTION

Activity-dependent changes in synaptic strength can lead to large changes in the efficacy of synaptic inputs at driving postsynaptic spikes. However, it is not clear how this influences neuronal computation. To answer this question, it is useful to examine a system in which the information carried by spikes is well understood, such as in the early stages of the auditory system. In the auditory nerve (AN), spike timing is used to encode salient features of sounds (Carr 1993; Kiang 1965). The precision of timing is typically quantified as either the degree of phase-locking or the SD of the spikes (“jitter”). Phase-locking by AN fibers is influenced by a number of factors, including not only the intensity of the sound relative to the fiber's threshold, but also its spontaneous firing rate. For amplitude-modulated (AM) sounds, phase-locking in AN fibers initially increases with intensity (Frisina et al. 1996; Joris and Yin 1992). However, as intensity increases past some optimal value, the spike rate continues to increase, but phase-locking decreases.

The cells postsynaptic to AN fibers, bushy cells (BCs) in the anteroventral cochlear nucleus (AVCN), integrate temporal information from multiple AN fibers (Liberman 1991; Oertel 1985; Sento and Ryugo 1989; Spirou et al. 2005) and relay that information on to brain areas associated with sound localization (Joris et al. 1994a; Smith et al. 1993). The timing of BC spikes could be more precise if the influence of inputs carrying less-precise timing information could be lessened.

One potential solution to this problem could be through activity-dependent changes in synaptic strength. AN fibers can fire at rates of ≤300 Hz in response to sounds (Joris et al. 1994a; Sachs and Abbas 1974; Taberner and Liberman 2005). At normal firing rates, the synapse made by AN fibers onto BCs (the “endbulb of Held”) (Lorente de Nó 1981; Limb and Ryugo 2000) shows short-term depression, which probably results from a combination of desensitization of postsynaptic receptors (Isaacson and Walmsley 1996; Oleskevich et al. 2000; Yang and Xu-Friedman 2008) and presynaptic vesicle depletion (Wang and Manis 2008; Yang and Xu-Friedman 2008), and other forms of depression have been proposed (Bellingham and Walmsley 1999). Synaptic plasticity has been implicated in changing the information relayed by synapses (Abbott and Regehr 2004; Blitz and Regehr 2003; Fortune and Rose 2001). Modeling approaches have suggested that depression can prevent highly active inputs from dominating the postsynaptic response (Abbott et al. 1997; Cook et al. 2003). In addition, changes in synaptic strength have been shown to affect the timing of postsynaptic responses to multiple converging inputs (Kuba et al. 2002; Xu-Friedman and Regehr 2005a).

However, depression can have other important consequences. If an input is highly active, depression could cause it to fail to trigger a postsynaptic spike, even if it was perfectly timed. For the endbulb synapse, which is often considered a relay, the failure to pass along this information could be detrimental to sound analysis and localization. Thus under some conditions, depression may be useful, whereas under other conditions it would be less favorable.

To understand how depression could influence firing under different conditions, we used dynamic clamp, applying inputs with different depression kinetics, and measured their effects on BC firing. We found that low depression increased the probability and shortened the latency of BC responses. In addition, under some stimulus conditions, low depression led to lower jitter. However, high depression played a particularly large role at improving the precision of spike timing when there were nonphase-locked inputs.

METHODS

All procedures were approved by the University at Buffalo's Institutional Animal Care and Use Committee (Protocol BIO05084N). Slices were cut from postnatal day 15 (P15) to P21 CBA/CaJ mice as described previously (Yang and Xu-Friedman 2008). Briefly, animals were anesthetized and decapitated and the brains placed into low-sodium, ice-cold cutting solution containing (in mM): 76 NaCl, 26 NaHCO₃, 75 sucrose, 1.25 NaH₂PO₄, 2.5 KCl, 25 glucose, 7 MgCl₂, and 0.5 CaCl₂, bubbled with 95% O₂-5% CO₂ (pH 7.8, 305 mOsm). Slices were cut through the cochlear nucleus at an angle close to parasagittal, to best preserve incoming AN fibers. Slices were cut using an Integraslice 7500 MM (Campden Instruments, Loughborough, UK) at 200-μm thickness and incubated at 30°C for 20 min in low-sodium solution and then for 40 min in standard recording solution containing (in mM): 125 NaCl, 26 NaHCO₃, 1.25 NaH₂PO₄, 2.5 KCl, 20 glucose, 1 MgCl₂, 1.5 CaCl₂, 4 Na l-lactate, 2 Na-pyruvate, and 0.4 Na l-ascorbate bubbled with 95% O₂-5% CO₂ (pH 7.4, 310 mOsm). Slices were then maintained at room temperature until recording. Patch-clamp recordings were carried out using an Axopatch 700B amplifier (Molecular Devices, Sunnyvale, CA) at 34°C in the presence of 10 μM strychnine to block glycine receptors. Voltage-clamp recordings were made with 1- to 2-MΩ pipettes containing (in mM): 35 CsF, 100 CsCl, 10 EGTA, 10 HEPES, and 1 QX-314 (pH 7.2, 302 mOsm). Cells were held at −70 mV, with access resistance 3–12 MΩ compensated to 70%. AN fibers were stimulated using one or two pipettes 30−50 μm away. Single or paired pulses were applied every 10 s. Train stimuli were applied every 30 s. BCs were identified by excitatory postsynaptic currents (EPSCs) showing paired-pulse depression and having rapid decay kinetics (τ <0.2 ms). There are no known physiological properties for distinguishing between spherical and globular BCs in brain slices (Ferragamo and Oertel 2001), so all recordings are grouped together. For dynamic clamp, BCs were patched with two 3- to 5-MΩ pipettes containing (in mM): 130 KMeSO₃, 10 NaCl, 2 MgCl₂, 0.16 CaCl₂, 0.5 EGTA, 10 HEPES, 4 Na₂ATP, 0.4 NaGTP, and 14 Tris-CrPhos (pH 7.2, 302 mOsm). One electrode measured cell voltage, while the other was used to pass current. Resting potential was maintained at −60 mV between trials by passing between +300 and −300 pA. BCs were identified by their response to strong depolarizing current pulses with single, undershooting spikes (Oertel 1983). Stimulation and data collection were done using an ITC-18 (Instrutech, Port Washington, NY) controlled using custom-written software (mafPC) running in Igor (WaveMetrics, Lake Oswego, OR). The ITC-18 system performs dynamic clamp at 50 kHz, implementing the relationship I_DC(t) = g(t)[V_m(t) − V_rev], where g is a user-specified conductance waveform (for examples, see Figs. 1, 7, and 8), V_rev is the α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptor reversal potential (i.e., 0 mV), and I_DC is the current to be injected by the amplifier. To allow better comparison between cells, we based the amplitude of synaptic conductances for dynamic-clamp experiments on the spike threshold for each cell. We defined threshold as the peak amplitude of an AMPA conductance that triggered a BC spike in dynamic clamp. On average, threshold was 21.4 ± 1.5 nS (n = 21). Voltage-clamp recordings indicated that EPSCs had peak conductance of 132.1 ± 7.3 nS (n = 26), which was a sixfold difference. To approximate this situation, we set the starting conductance of each input in dynamic clamp to 5 times threshold, which then decreased according to the depression model. The total conductance thus depended on the cell's threshold, the number of inputs applied, and the amount of depression. Peak conductances were somewhat less than this total when jitter in input timing was introduced. Spikes were discriminated in dynamic-clamp recordings using the derivative of the membrane potential, after subtracting the predicted passive response of a simple RC model cell. Average results are reported throughout as means ± SE.

In the experiments described in Fig. 6, we used two stimulus isolators to stimulate two separate AN fibers that converged on a single BC, which we refer to as “siblings.” To compare the properties of endbulbs, we developed a distance metric based on our measurements of resting EPSC amplitude (normalized to the population average), paired-pulse ratio (PPR; 10 time intervals), and trains of stimulation (three frequencies, 20 stimuli each, normalized to the first EPSC in the train), for a total of 68 measures. The distance D_i,j between endbulb i and endbulb j was calculated as

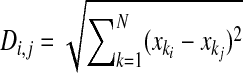(1)

where each x_k is a single measure and N is the number of measures used in the distance measurement: when calculating distances between PPR data, N was 10; for each set of trains data, N was 19 (leaving out the first pulse, which was normalized to 1); and for the entire set of measures, N was 68. The distances were measured between 10 sibling endbulbs and compared against the population of distances between all 20 endbulbs in that data set. Significance was tested using the Kolmogorov–Smirnov (KS) test.

RESULTS

Influence of nonphase-locked inputs

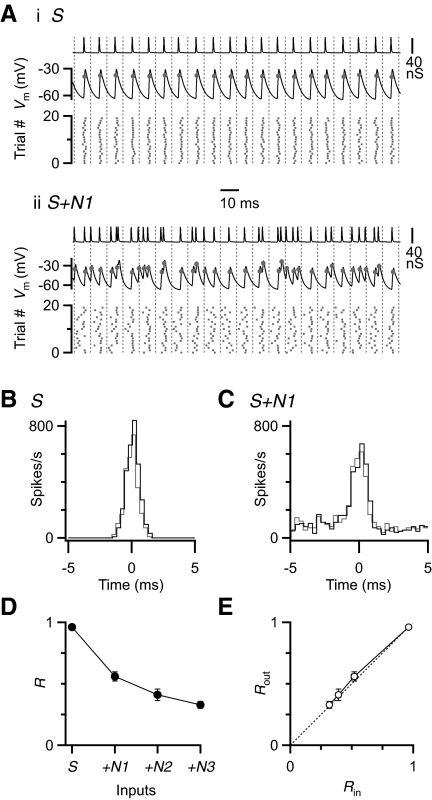
To understand how BC firing is influenced by convergence of multiple inputs carrying different amounts of temporal information, we conducted experiments in dynamic clamp (Robinson and Kawai 1993; Sharp et al. 1993). This technique allows us to completely control the number and timing of synaptic inputs. In this experiment, a single input carried timing information—i.e., phase-locked spikes with a jitter of 0.5 ms. We added up to three inputs that fired nonphase-locked spikes, where the timing of spikes followed a Poisson distribution. All inputs had the same firing rate (100 Hz) and the same unitary conductance based on the steady-state EPSC amplitude during 100-Hz trains recorded in voltage clamp (Fig. 1A). During the initial parts of trains, BCs undergo significant changes in intrinsic properties, which were not our focus. Therefore we applied these stimuli in dynamic clamp for trains of 40 cycles and restricted our attention to the last 20 cycles. In the example dynamic clamp recording in Fig. 1Ai (“S”), when we applied a single, phase-locked input, the BC fired a spike on every cycle with some jitter, reflecting the input jitter. When we added a single nonphase-locked input, BC firing became much more irregular (Fig. 1Aii, “S + N”).

FIG. 1.

The effect of nonphase-locked inputs on bushy cell (BC) spike timing. A: example responses in dynamic-clamp experiments to a single phase-locked input (i, “S”) and with a single additional nonphase-locked input (ii, “S+N1”). Top traces: representative conductances applied in dynamic clamp. Middle traces: example response of a BC. Markers on traces indicate BC spikes. [Note that BC spikes are normally undershooting (Oertel 1983).] Bottom rasters: spike times recorded over 20 trials. B and C: the timing of inputs (gray) and BC spikes (black) in response to S (B) and S+N1 (C) are plotted within one period. D: average BC synchronization (R) calculated from 4 cells similar to the one depicted in B and C, as the number of nonphase-locked inputs increases. E: the effect of input synchrony on BC synchrony. The dashed line is y = x, i.e., where synchrony is unchanged.

To quantify how phase-locking was affected, we constructed cycle histograms. For both S and S + N conditions, spike timing in the BC was nearly identical to the inputs (Fig. 1, B and C). However, as nonphase-locked inputs were added, the degree of phase-locking decreased. We quantified phase-locking by calculating the R-value, which ranges from 0 for no phase-locking to 1 for perfect phase-locking. With no nonphase-locked inputs, R for BC firing was close to 1, but it decreased substantially as nonphase-locked inputs were added (Fig. 1D). These values closely tracked the R-value for the inputs (Fig. 1E).

These results highlight the fidelity of the endbulb synapse. With phase-locked inputs, this fidelity means that timing information in AN inputs is preserved in BCs. However, if there are any nonphase-locked inputs, fidelity causes timing information in the BC to degrade, which could cause problems for downstream computations.

To address how this problem might be resolved, we considered how normal synaptic conductances differ from these conditions. First, when AN fibers are exposed to AM sounds louder than some optimal level, phase-locking decreases as firing rate increases, where the extra spikes appear to carry less precise timing information. In the preceding experiment, these extra spikes are indistinguishable for the postsynaptic cell. However, under normal conditions, a more highly active input will show more depression, which could reduce the impact of less precise spikes. Thus the second way the preceding experiment differs from normal conditions is that the effects of synaptic plasticity on different inputs were not included.

Short-term depression in voltage clamp

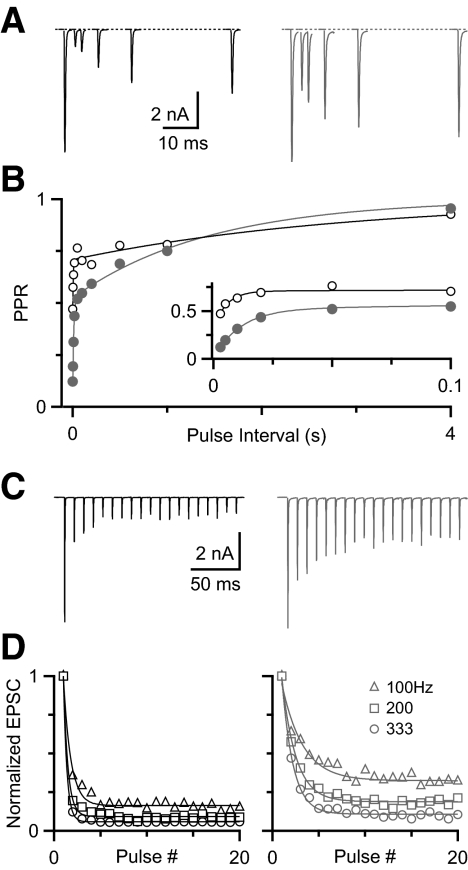
To test how depression could affect the situation presented in Fig. 1, we quantified levels of depression in endbulbs using voltage clamp. We found that the extent of depression varied for different synapses, when we assessed depression using pairs of pulses or trains of activity. Two representative experiments are illustrated in Fig. 2, with high depression (left) and low depression (right). For these two endbulbs at an interval (Δt) of 3 ms, the paired-pulse ratio (PPR) differed by a factor of 3.7 (Fig. 2, A and B). The time course of recovery of both cells could be fit with a double-exponential function: PPR(Δt) = 1 − A_f exp(−Δt/τ_f) − A_s exp(−Δt/τ_s). For the highly depressing cell, A_f = 0.40, τ_f = 12 ms, A_s = 0.48, τ_s = 1.4 s; for the less depressing cell, A_f = 0.22, τ_f = 5 ms, A_s = 0.29, τ_s = 3.0 s. Our previous work suggested that the fast component likely results from postsynaptic receptor desensitization and the slow component from a presynaptic form of depression, such as vesicle depletion (Yang and Xu-Friedman 2008).

FIG. 2.

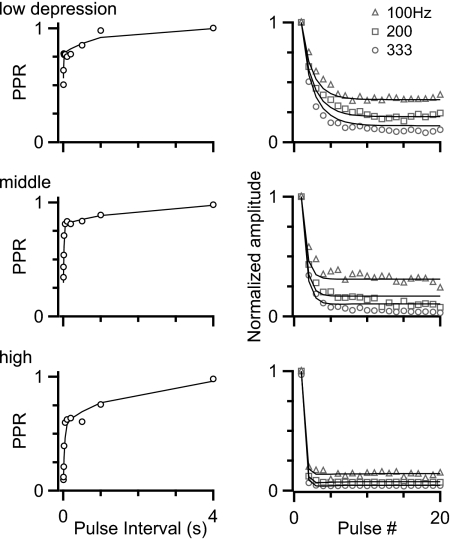
Variability of depression at the mouse endbulb of Held. A: example voltage-clamp recordings showing high (left) and low (right) depression in response to pairs of pulses of different intervals. B: the paired-pulse ratio (PPR) recovers according to a double-exponential function (see results for equation and parameters). Inset: magnified view of the fast component. C: excitatory postsynaptic currents (EPSCs) in response to 20 stimuli at 100 Hz. D: high (left) and low (right) depression during trains, normalized to the first peak for 100, 200, and 333 Hz. Data (open markers) were fitted (solid line) with a single-exponential function (see results for equation and parameters).

The amount of depression seen in paired-pulse experiments was also reflected in trains of activity (Fig. 2C). We examined the responses to trains of 100, 200, and 333 Hz, which are similar to firing rates observed in vivo. We quantified the steady-state level of depression using the average of the relative amplitude of the last three pulses in the train. For the two cells in Fig. 2C, steady-state depression differed by a factor of 2.2 at the end of 100-Hz trains. Similar results were found for trains of 200 and 333 Hz (Fig. 2D). Depression during trains was fit by a single-exponential function: EPSC(t) = 1 − A exp(−t/τ). For the highly depressing cell (left), the parameters were A₁₀₀ = 0.83, τ₁₀₀ = 8.0 ms, A₂₀₀ = 0.91, τ₂₀₀ = 2.4 ms; A₃₃₃ = 0.94, τ₃₃₃ = 1.1 ms. For the less depressing cell (right) the parameters were A₁₀₀ = 0.63, τ₁₀₀ = 22 ms, A₂₀₀ = 0.8, τ₂₀₀ = 7.6 ms; A₃₃₃ = 0.88, τ₃₃₃ = 3.6 ms.

Variability of depression

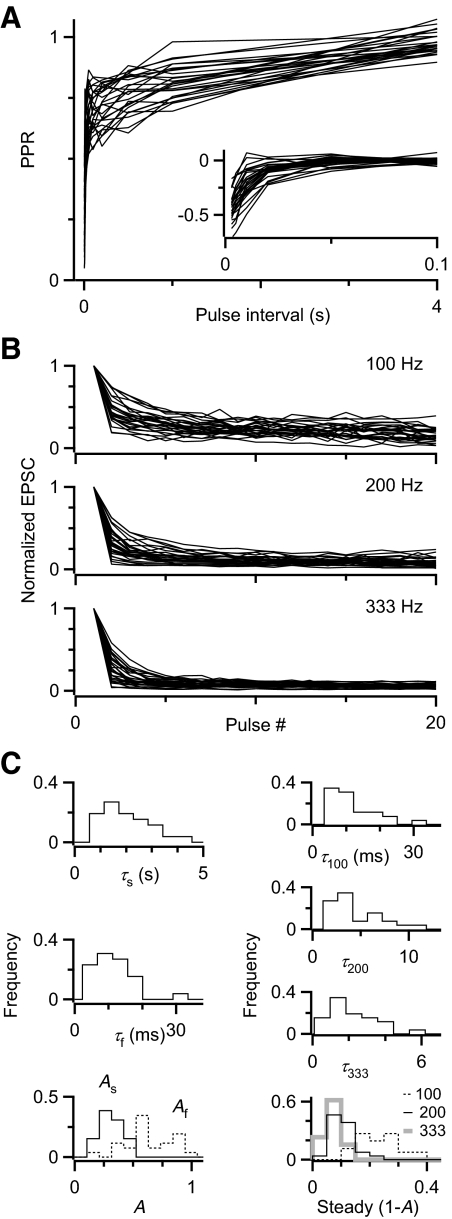
The slow component of paired-pulse recovery was quite variable over 26 cells examined (Fig. 3 A). We fit all the recovery curves with double-exponential functions. When we subtracted the slow component using the fit parameters, it revealed considerable variability in the fast component (Fig. 3A, inset). Different cells showed a wide range of parameter values (Fig. 3C, left). The average values were A_f = 0.64 ± 0.20 (mean ± SD, coefficient of variation [CV] = σ/μ = 0.3), τ_f = 10.9 ± 6.0 ms (CV = 0.6), A_s = 0.32 ± 0.09 (CV = 0.3), τ_s = 1.99 ± 0.94 s (CV = 0.5), similar to values we obtained before in fits to the population average response (Yang and Xu-Friedman 2008). We also quantified the responses during trains (Fig. 3B) and fit those to single-exponential functions (Fig. 3C, right). The average parameters were SS₁₀₀ = 0.23 ± 0.07 (CV = 0.3), τ₁₀₀ = 11.6 ± 6.7 ms (CV = 0.6), SS₂₀₀ = 0.11 ± 0.04 (CV = 0.4), τ₂₀₀ = 4.4 ± 2.5 ms (CV = 0.6), SS₃₃₃ = 0.07 ± 0.03 (CV = 0.4), τ₃₃₃ = 2.1 ± 1.2 ms (CV = 0.6). The large CVs indicate that each of these parameters varies considerably over the population of endbulbs.

FIG. 3.

Summary of depression parameters. A: PPR recovery curves for 26 cells, highlighting differences in the slow component. Inset: slow component subtracted from each cell to reveal differences in the fast component. B: depression during trains at different frequencies. C: distribution of parameters for fits to paired-pulse and trains data in A and B.

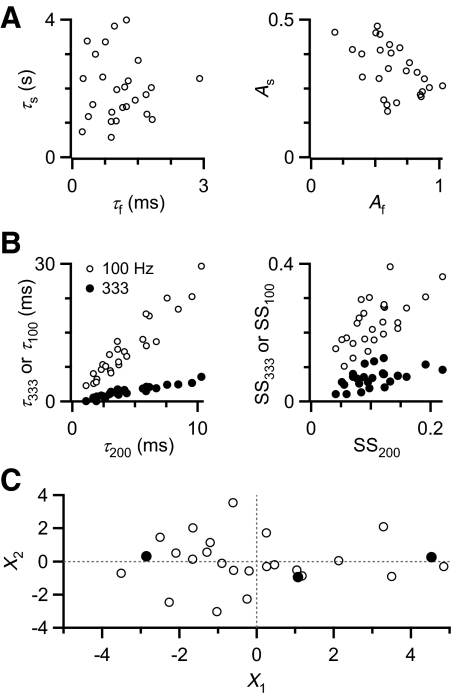
To study the effects of depression, we wanted to select endbulbs with representative kinetics and amplitude of depression. To do this, we aimed to use principal components analysis (PCA). PCA is used to describe a multivariate data set using the minimal number of variables and is particularly appropriate when different parameters are highly correlated. We compared the two paired-pulse recovery time constants τ_f and τ_s and found that they were uncorrelated (Fig. 4 A, left; R = −0.02), consistent with the two processes being independent that give rise to these two components. The amplitudes of the two recovery components are negatively correlated (Fig. 4A, right; R = −0.51). The parameters measured from trains also showed significant correlations. The time constants of decay were highly correlated (Fig. 4B, left), as were the steady-state depression levels (Fig. 4B, right). Correlations between all parameters are summarized in Supplemental Table S1.1

FIG. 4.

Depression parameters transformed by principal components analysis (PCA). A: correlations between parameters from PPR recovery curves. The time constants (left) are poorly correlated (0.02), but the amplitudes are highly correlated (−0.51). B: correlations between train parameters. Correlation coefficients between decay time constants are >0.9 (left) and between steady-state amplitudes are >0.5 (right). C: PCA. Shown are the results for the first 2 PCs, which capture 70% of the original variance. Each open circle represents the transformed data from one cell. Filled circles indicate 3 cells that differ mainly in the first PC and were selected to represent different extents of depression.

This high degree of correlation signaled that PCA was appropriate to simplify our view of the depression in different endbulbs. We found that the first two PCs (X₁ and X₂) could account for 70% of the original variance (Fig. 4C, Supplemental Table S2). From the transformed data set, we chose three endbulbs that had very different values for the X₁ component to represent different kinds of depression (Fig. 4C, filled circles). Upon further examination of these representative endbulbs (Fig. 5), they appeared to represent (roughly) low, middle, and high amounts of depression.

FIG. 5.

Three cells with different levels of depression, selected based on PCA (Fig. 4C). Markers represent data from paired-pulse (left) and train (right) stimulation; lines represent fits to the data using a simplified model of synaptic plasticity.

To test how these levels of depression influence firing, we aimed to use dynamic-clamp experiments. Because we wanted to test more complex activity patterns, it was not practical to use pulse amplitudes measured in voltage clamp. Instead, we used a simple model of synaptic plasticity, which tracks vesicle depletion, receptor desensitization, and activity-dependent forms of recovery (Yang and Xu-Friedman 2008) (see Supplemental methods). We fit parameters to the data from the three different endbulbs of Fig. 5 using a least-squares approach (lines in Fig. 5; Supplemental Table S3). This simple model was able to replicate the plasticity for each cell under the conditions of pairs of pulses and regular trains and we observed that, once fit to these, it follows other activity patterns reasonably well.

Similarity of converging endbulbs

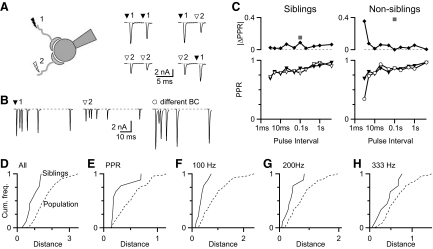
We wanted to examine how multiple endbulbs interact to drive BC firing. However, it is not known how similar the multiple endbulbs are that converge on a single BC. To address this, we used two stimulating electrodes to isolate two endbulbs onto a given BC (“siblings”; Fig. 6 A, left). We confirmed that the two pathways were distinct endbulbs by doing cross-depression experiments. When one stimulator was activated twice, the second EPSC was depressed compared with the first (Fig. 6A, middle traces). However, when alternate stimulators were activated, the second pathway stimulated was not depressed (Fig. 6A, right traces). Once two endbulbs were isolated, we quantified resting EPSC amplitude and relative EPSC amplitudes for 10 paired-pulse intervals, as well as trains of 20 pulses at three frequencies, yielding a total of 68 measures.

FIG. 6.

Similarity between the plasticity of endbulbs that converge onto the same BC (“siblings”). A: isolation of sibling endbulbs. Left: cartoon of the experimental setup. Middle: sample responses to paired activation of each stimulator, showing depression. Right: sample responses to activation of both stimulators, showing no depression. This indicates the 2 stimulators activate distinct endbulbs. B: responses to paired-pulse stimulation of sibling endbulbs (left and middle), as well as a randomly selected endbulb onto a different BC recorded separately (right). C: comparison of PPRs between the endbulbs shown in B. Bottom: quantification of PPR. Top: absolute difference in PPR between representative sibling endbulbs (left) and endbulbs onto different BCs (right). Differences across all time intervals were compiled into a single distance metric (gray square, Eq. 1). D: cumulative histogram of distances between sibling endbulbs (solid line, n = 10 pairs) and between randomly chosen endbulbs (dashed line, n = 190 comparisons). The distance is calculated according to Eq. 1 using PPR, responses during trains, and the resting EPSC. The difference in the 2 data sets is significant (Kolmogorov–Smirnov [KS] test, P = 0.008). E–H: analysis of the similarity between sibling endbulbs using distance measures based only on PPR (E, P = 0.015), 100-Hz trains (F, P = 0.007), 200-Hz trains (G, P = 0.029), and 333-Hz trains (H, P = 0.29). All comparisons suggested that sibling endbulbs were highly similar, except trains of 333 Hz.

Next we compared the plasticity of sibling endbulbs against the properties of randomly chosen endbulbs. To illustrate with a reduced example, we show the paired-pulse responses for sibling inputs in Fig. 6B. We quantified the PPR for these siblings in Fig. 6C (bottom left). To quantify their similarity, we calculated the absolute value of the difference between the PPR at each time interval, which was very close to 0 at all intervals (Fig. 6C, top left). These were grouped into a single distance measure by taking the square root of the sum of squares (Eq. 1; gray square in Fig. 6C, top left). We also measured the similarity between endbulbs onto different BCs (Fig. 6B, right). In the example shown, the two endbulbs had similar PPRs, except at the shortest interval (Fig. 6C, bottom right), leading to a greater distance between these endbulbs (Fig. 6C, top right).

We calculated distances like those illustrated in Fig. 6C for 10 pairs of siblings, using all 68 measures (Fig. 6D, “siblings”). We compared the sibling distances against the population by calculating the distances between all possible pairs of 20 endbulbs, for a total of 190 distances, which represents the random distribution (Fig. 6D, “population”). The distances between siblings were significantly shorter than those between randomly chosen endbulbs. This means that sibling endbulbs are more similar to each other than to randomly chosen endbulbs.

We wanted to determine whether particular aspects of plasticity were similar between siblings. We constructed plots similar to Fig. 6D for each individual measure. These plots suggested that most measures tended to be more similar for siblings than for randomly chosen endbulbs. No individual measure was smaller for randomly chosen inputs, but this rose to a level of significance for only half the measures, presumably because our data set was small (see Supplemental Table S5). To strengthen our statistical analysis, we grouped measures related to PPR, 100-Hz trains, or 200-Hz trains. When we did this, sibling endbulbs were significantly similar to each other (Fig. 6, E–G). The measures related to 333-Hz trains were not significantly different, but the trend was in the direction of similarity of siblings. Thus it appears that most features contributed to the similarity between sibling inputs.

Interactions of multiple inputs

PARADIGM 1: REGULAR INPUTS.

We next turned to dynamic clamp experiments to evaluate how multiple inputs interact to affect BC spike timing. We first examined how BC firing was affected when multiple inputs carried identical timing information. Earlier work has indicated that this depends critically on the amplitude and number of individual inputs (Xu-Friedman and Regehr 2005a,b). We used the model for the three representative levels of depression to determine amplitude. The number of AN inputs depends on the species and the subtype of BC. In mice, the number of inputs is 2–5 for BCs (Oertel 1985; Xu-Friedman and Regehr 2005b) and in cats it ranges from 1–4 for spherical BCs to 50–60 for globular BCs (Liberman 1991; Spirou et al. 2005). In addition, the number of endbulbs that are active at any given time depends on the response properties of the converging AN fibers to the specific sounds being presented. Important factors are not well understood, such as whether all the inputs to a BC have uniform response properties.

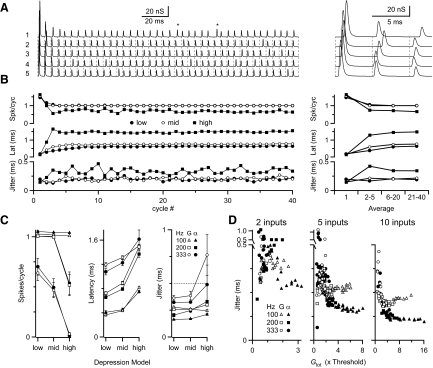
To take the simplest situation, we examined how multiple inputs affect BC spike timing. The number of inputs was set to 5 or 10 and each input was assigned activity responding to a periodic signal with phase-locked spikes. which were subject to jitter. We modeled jitter after the cycle histograms of AN fibers in response to sounds, which resemble Gaussian or alpha distributions (Johnson 1980; Joris et al. 1994a). We set the jitter to SD = 0.5 ms. An example experiment is shown in Fig. 7 A, with five inputs firing at 200 Hz with Gaussian-distributed jitter. The synaptic conductances were fairly uniform in size after the third cycle, except for cycles in which jitter caused a spike to arrive later than usual. In such cases the conductances showed noticeable recovery (examples marked with asterisks in Fig. 7A).

FIG. 7.

Effect of depression with multiple synaptic inputs on BC spike timing. A: example dynamic-clamp stimulation paradigm for 5 synaptic inputs firing at 200 Hz, with Gaussian distributed jitter (SD = 0.5 ms), using the middle depression model. Asterisks mark conductances that were somewhat larger, as a result of particularly long recovery times. B: BC responses during train of stimulation as in A, showing the number of spikes per cycle (top), latency (middle), and jitter (bottom). Averages over different periods of the train are shown at right. Pulses 21–40 are the focus for the remainder of this study. C: average results from 5 experiments for spikes per cycle (left), latency (middle), and jitter (right) at different stimulation rates and with input jitter following Gaussian or alpha distributions. The input jitter of 0.5 ms is indicated on the right. D: jitter as a function of the total synaptic conductance relative to threshold (G_tot) for 2 (left), 5 (middle), or 10 (right) inputs. Data are summaries of 5 or 6 experiments for the different conditions.

We applied these inputs using dynamic clamp and measured BC responses. For the example cell in Fig. 7B, multiple spikes were triggered on the first cycle, but as depression set in over the next two cycles, these disappeared. After the fifth cycle, the probability of response reached a steady state of 100% for low and middle models of depression and about 67% for high depression (Fig. 7B, top). In addition, once the cell reached steady state, the latency was shortest for the low depression model and was nearly 1 ms further delayed for the high depression model (Fig. 7B, middle). The low and middle depression models have higher response probability and shorter latency, probably because of the greater total conductance being applied. BC jitter was greatest for the high depression model and was significantly lower for less depression (Fig. 7B, bottom). Although BC jitter depended on the depression model used, it was always less than the jitter of 0.5 ms in the inputs.

To simplify our analysis, we restricted our attention to the second half of the stimulus train. Over this period, the number of spikes per cycle was highest for low input frequency and for models with low or middle depression (Fig. 7C, left). The latency increased with higher input frequency and for greater depression models (Fig. 7C, middle). Jitter also largely increased with increasing depression (Fig. 7C, right), but this relationship was not as simple as that for spike probability and latency. In addition, the specific distribution of input jitter (alpha or Gaussian) made little difference for BC spike probability and latency, but had a large effect on BC jitter.

Earlier studies have indicated that the amount of jitter depends not only on the total synaptic conductance (G_tot) but also on the input distribution (Xu-Friedman and Regehr 2005a,b). To test whether the data of Fig. 7C can be explained in the same way, we plotted jitter against G_tot for each BC under all the conditions tested (Fig. 7D). Because of depression, G_tot varied from cycle to cycle, so we used a simplified estimate for G_tot based on the steady-state depressed EPSC for the appropriate input frequency and depression model and normalized this value by our measurement of conductance threshold for each cell. [The conductance threshold was also corrected for shifts in threshold during trains of activity (Supplemental Table S4) (see Xu-Friedman and Regehr 2005a). The threshold conductance changes during activity because of low-threshold potassium channel activation (Manis and Marx 1991; Rothman and Manis 2003)]. When we examined how G_tot affected spike timing, we found that the jitter data over all the conditions (i.e., different cells, depression models, and input frequency) simplified to just two curves, one for alpha- and one for Gaussian-distributed inputs (closed vs. open markers; Fig. 7D). At low values of G_tot (i.e., at high rates of activity or high levels of depression), jitter was similar for both input distributions. Jitter reached a minimum when G_tot was 2 to 3 times threshold with Gaussian-distributed inputs, above which the jitter increased. For alpha-distributed inputs, jitter continued to decrease as G_tot increased, which is similar to previous findings (Xu-Friedman and Regehr 2005a,b). The relationship was qualitatively similar for 2, 5, and 10 inputs, but the overall jitter decreased with more inputs (Fig. 7D). These data indicate that BC spike timing depends on three factors: total synaptic conductance, the number of inputs, and the temporal distribution of inputs. The degree of depression and the input firing rate act indirectly on BC spike timing by setting the total synaptic conductance.

PARADIGM 2: IRREGULAR INPUTS.

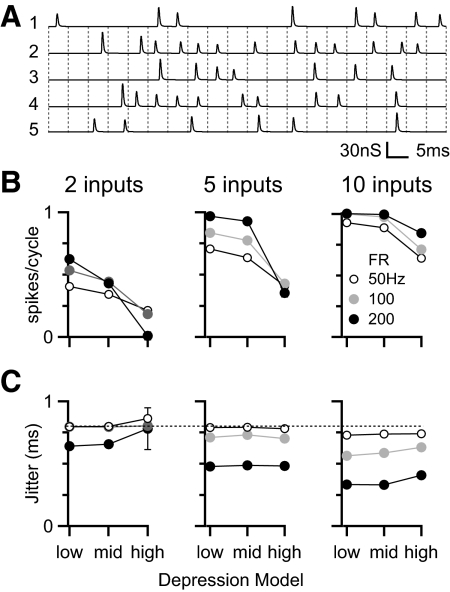
In the previous section we tested how depression affects multiple converging inputs that are active on every cycle of a periodic stimulus, such as a tone or AM sound. However, under normal conditions, the stimulus period and the AN firing rate are not identical. That means each input may not contribute timing information for all cycles of a periodic stimulus. To determine whether depression has an effect under those conditions, we considered a periodic stimulus with AN inputs firing at lower frequencies. Figure 8 A shows an example of five inputs, each firing at 100 Hz, in response to a 200-Hz periodic stimulus. The firing on a given cycle was dictated by a binomial process and could lead to an input being silent over a number of cycles. On active cycles, spike timing was phase-locked. For this experiment we based the input jitter on AN responses to AM tones, which reach a maximal synchrony (R) of close to 0.6 under similar conditions in cats (Joris and Yin 1992). For 200 Hz, this is equivalent to jitter of 0.8 ms (Goldberg and Brown 1969).

FIG. 8.

Effects of different depression models on BC spiking for irregularly firing inputs. A: example stimulus paradigm. The “stimulus” has a period of 200 Hz and the conductances of 5 inputs with firing rate of 100 Hz are illustrated below. B: average BC spiking probability in response to 2, 5, or 10 inputs with individual firing rates of 50, 100, or 200 Hz. C: BC jitter under the same conditions as in B. The jitter for individual inputs (0.8 ms, equivalent to R = 0.6) is marked by the dotted line. Results in B and C are averages of 11 experiments.

We tested how BC spiking was affected by the amount of depression for a range of different input firing rates, with the same underlying 200-Hz periodic signal. The number of BC spikes (Fig. 8B) was lower than that in the previous experiments (Fig. 7), especially with higher levels of depression. At higher input firing rates, response probability was higher despite the fact that this would have led to greater depression. This suggests that the number of inputs per cycle dominates the response probability and is sufficient to offset the increased depression at higher firing rates, except with few inputs and high depression. Under most conditions tested, the jitter of the BC spike was less than that for the individual inputs (Fig. 8C). The greatest reduction in jitter occurred with more inputs at the highest frequency of firing, which is equivalent to conditions with the most inputs per cycle, indicating that, under this paradigm, a larger number of inputs is the dominant factor in reducing jitter. The impact of the depression model was minor.

PARADIGM 3: NONIDENTICAL INPUTS.

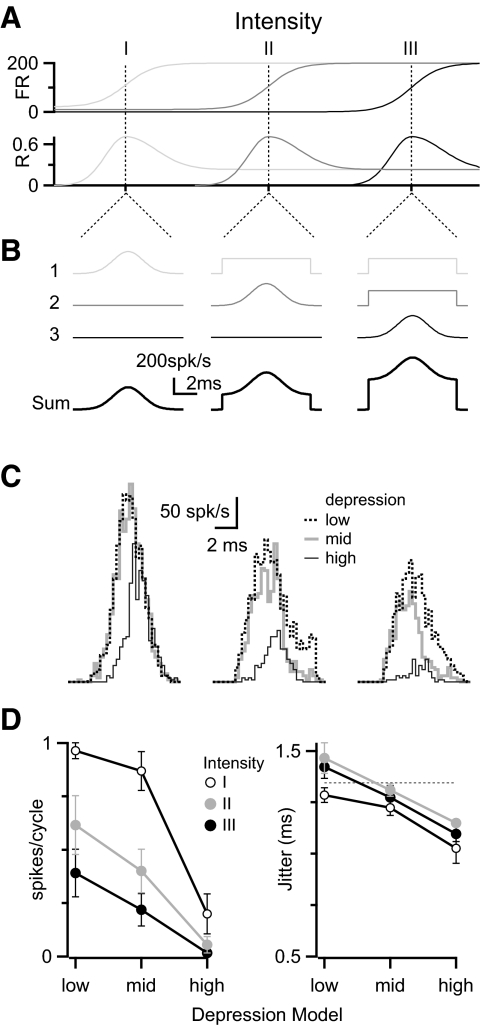
In the previous sections we examined multiple inputs that each contributed similar timing information to the BC. However, it is possible that multiple AN inputs may carry different timing information. As a population, AN fibers with the same characteristic frequency can have a range of thresholds (cat: Joris et al. 1994a; Liberman 1978; Sachs and Abbas 1974; mouse: Taberner and Liberman 2005). Therefore in response to a given sound, a population of identically tuned AN fibers will fire at different rates. Some may be maximally stimulated, whereas others may be still below threshold. A further issue is that AN fibers at their maximal firing rate may have reduced phase-locking. For example, for AM sounds, AN fibers show optimal phase-locking at intermediate sound levels, but as the sound level increases, phase-locking decreases to nearly tonic levels (Joris and Yin 1992). Thus different AN inputs to a BC might carry different timing information depending on their thresholds and the stimulus amplitude.

We tested how depression might influence the convergence of multiple inputs carrying different timing information. We based this paradigm on the responses of AN fibers to AM sounds (Joris and Yin 1992), but it also applies to other periodic stimuli. Using dynamic clamp we mimicked the situation of three inputs with different thresholds responding to different intensities of a 100-Hz AM sound (Fig. 9 A). We drew the spike times for these inputs randomly, based on the cycle histograms illustrated in Fig. 9B, and with a refractory period of 1 ms. The jitter for an input in its dynamic range had SD = 1.3 ms, which is equivalent to R = 0.7 over a 10-ms interval (Joris and Yin 1992), whereas a saturated input had SD = 2.7 ms (R = 0.24). To mimic a “low threshold,” one input fired phase-locked spikes at 100 Hz in the low-intensity condition (intensity I), but with poorly phase-locked spikes at 200 Hz to greater intensities (Fig. 9B, input 1). The “middle-threshold” input fired spontaneously (3 Hz) in the low-intensity condition, with phase-locked spikes for the medium-intensity condition (intensity II), and with poorly phase-locked spikes for the high-intensity condition (intensity III) (Fig. 9B, input 2). The “high-threshold” input fired at a very low rate (0.2 Hz) for both low- and medium-intensity conditions and with phase-locked spikes for the high-intensity condition (Fig. 9B, input 3). Thus with higher intensities, the BC mostly receives poorly phase-locked inputs (Fig. 9B, sum), similar to the conditions we examined in Fig. 1. This could reduce the precision of timing information relayed by the BC under high-intensity conditions.

FIG. 9.

The influence of depression on BC responses to multiple inputs with different response properties. A and B: stimulus paradigm, illustrating the response properties (firing rate and phase-locking) for 3 different synaptic inputs to sounds of increasing intensity (A) and their cycle histograms (B). When an input is in its dynamic range, its cycle histogram is a Gaussian of SD = 1.3 ms (equivalent to R = 0.7). C: BC responses in a representative experiment showing how depression affects the response at each sound intensity. D: average results for response probability (left) and jitter (right) over 5 experiments similar to that in C.

We applied these inputs using dynamic clamp and measured the effect of the different depression models on BC spiking. A sample experiment is shown in Fig. 9C. For the lowest-intensity condition (Fig. 9C, left), there was a high response probability and reliable phase-locking, essentially following the single active input. For the medium-intensity condition (Fig. 9C, middle), the response probability was slightly lower and the variability in timing appeared close to that shown by the input in its dynamic range (input 2). This happened despite the low-threshold input (i.e. input 1) contributing twice as many excitatory postsynaptic potentials (EPSPs) with poor phase-locking. For the high-intensity condition (Fig. 9C, right), the BC response probability was somewhat lower, but the spikes that were elicited were well phase-locked.

We saw similar effects in five cells tested. As the intensity increases, the number of impinging EPSPs increases, although BC spiking decreases (Fig. 9D, left). This likely happens because the higher spike rate in the saturated inputs leads to high levels of synaptic depression. So, even though there were more active inputs, the activity-dependent depression dominated. The lowest response was consistently found when inputs followed the high depression model. Importantly, BC jitter never rose much above the jitter for the single phase-locked input (Fig. 9D, right). Thus despite the fact that there could be as many as two more inputs providing little temporal information, they did not obscure the one input that did carry temporal information. Furthermore, the greatest jitter reduction was found using the high depression model over all intensities examined (Fig. 9D, right). The likely reason for this is that EPSPs from highly active inputs are depressed such that they do not greatly influence BC firing. This improvement in temporal precision evidently comes at the expense of a lower response probability.

DISCUSSION

Here, we examined how synaptic processing of timing information is affected by short-term depression in the cochlear nucleus. Spike timing in BCs plays an important role in the auditory system because it contributes to sound localization and analysis, which require high temporal acuity. We showed that one of the key features of endbulb EPSPs (i.e., their very large amplitude) can obscure precise temporal information. This can happen when spontaneously active synaptic inputs trigger spikes as well as phase-locked inputs. However, BCs are not merely relay units and synaptic depression does affect BC spiking under realistic conditions. Depression was particularly important in suppressing highly active inputs that may carry less precise temporal information. We also examined how the range of depression shown by different endbulbs influenced BC firing. Different amounts of depression appeared to confer different advantages under different conditions. When there were few active inputs firing at high rates, low amounts of depression permitted BCs to show some responses to presynaptic activity. High depression was particularly effective at screening out inputs carrying less information about stimulus timing. This may suggest that different degrees of depression could play a functional role in tuning different endbulbs for optimal responses under different stimulus conditions.

Variability of depression

We found considerable variability at different endbulbs in the kinetics of depression, for both fast- and slow-recovering components. The fast component likely results from desensitization (Isaacson and Walmsley 1996; Yang and Xu-Friedman 2008), which would be affected by factors such as the degree of glutamate pooling and AMPA receptor kinetics (Trussell et al. 1993; Xu-Friedman and Regehr 2003). The slow component likely results from vesicle depletion (Wang and Manis 2008; Yang and Xu-Friedman 2008), which would be affected by variations in vesicle release probability or recycling mechanisms.

We found no systematic changes in the kinetics of depression across the AVCN. The AVCN is organized tonotopically, but we did not find that cells recorded in similar parts of the AVCN had similar depression. This implies that AN fibers carrying information from similar cochlear regions probably show a range of depression amplitudes, although our initial examination suggested that AN fibers with similar plasticity converge on the same BC. Consistent with this finding, we considered the interaction of inputs with uniform depression characteristics.

Similarity between converging endbulbs

We found that two endbulbs that terminate on the same BC are particularly similar to each other in the characteristics of their plasticity. This was true both for PPR and for responses during trains of activity. Similarity in short-term plasticity has been well documented to depend on the general cell type (Toth and McBain 2000). To our knowledge, our results are the first that suggest short-term plasticity also depends on the individual target cell within a cell type. The mechanisms underlying this similarity are not yet clear. Depression at the endbulb appears to result from both pre- and postsynaptic processes (Wang and Manis 2008; Yang and Xu-Friedman 2008). There is no a priori reason that presynaptic forms of depression should be particularly similar for two endbulbs terminating on the same BC. Even postsynaptic forms of depression need not be the same, since the pools of receptors triggered by different endbulbs can function independently (Fig. 6; also see Otis et al. 1996) and need not have the same susceptibility to desensitization.

There are a number of possibilities as to how this similarity is established developmentally. First, it may be that AN fibers from a certain region of the cochlea have similar plasticities. We consider this possibility unlikely because we have not detected a particular tonotopic organization to plasticity in the AVCN. Second, it may be that AN fibers with similar plasticity are preferentially stabilized at or recruited by certain BCs. This would suggest that BCs play a role in selecting their inputs based on properties that relate to their plasticity. Third, it may be that the properties of endbulbs become similar after they form synapses on a BC. This could happen not just through postsynaptic forms of depression, but could also result from signaling from BCs back to their presynaptic endbulbs through such retrograde messengers as endocannabinoids (Kano et al. 2009). Further work will be necessary to evaluate the contribution of variability between preparations and to look at how similarity between sibling endbulbs changes over development.

Depression and response probability

We found context-dependent effects resulting from different, physiologically relevant levels of depression that were expressed by different endbulbs. BCs with highly depressing inputs were more likely to respond under conditions that activated AN fibers at low rates than at high rates (Figs. 7 and 8). Thus highly depressing endbulbs would be expected to drive the BC best under low-intensity conditions. Response amplitude has been observed to decrease with increasing sound intensity for some BCs recorded in vivo (Joris et al. 1994a,b; Kopp-Scheinpflug et al. 2002; Taberner and Liberman 2005; Winter and Palmer 1990a). At least part of this effect seems to result from the recruitment of inhibitory inputs at high intensities (Kopp-Scheinpflug et al. 2002; Winter and Palmer 1990b). However, our data suggest that synaptic depression could also contribute to this phenomenon. For cells with monotonically increasing responses, it seems likely that other synaptic features exist either to limit or to compensate for endbulb depression. These features could include recruitment at higher sound intensities of AN fibers that show less depression or feedback providing presynaptic inhibition.

The probability of BC response was generally greater with low-depressing inputs. This could be behaviorally significant under two rather different contexts. One would be when the number of active inputs is low, such as for spherical BCs that receive few total inputs (Nicol and Walmsley 2002; Ryugo and Sento 1991). A spherical BC with low-depressing inputs would be more likely to show at least some response to sounds, even if only one is active. For mouse BCs, it is not clear how many inputs a given BC receives, but we estimate it is around two to three inputs (Xu-Friedman and Regehr 2005b), so the effective loss of even one input through significant depression could appreciably influence firing and downstream computations. A similar situation could also be found with BCs that receive many inputs, such as globular BCs (Liberman 1991; Ostapoff and Morest 1991; Spirou et al. 2005). It is still not known whether those multiple inputs have uniform response characteristics to sounds (e.g., sound threshold, dynamic range, peak firing rate). If there is significant variability, then there are likely to be conditions under which only a few inputs are stimulated, so low depression could help ensure that the BC remains responsive. These situations are most likely to arise for low-intensity sound stimuli.

Another context in which low-depressing inputs increased BC responses over high-depressing inputs was when the firing rate of inputs was high. In this context, high depression can lead to a significantly low probability of response (Fig. 7). Our results suggest that this effect of depression is offset by having multiple active inputs (Fig. 8), except at the very highest rates of activity. These high rates of AN spiking are likely to arise during high-intensity sound stimuli, which are also likely to recruit more active inputs to a BC. The additional recruitment is likely to mitigate the effects of depression.

Depression and timing

Our primary focus was to understand how depression could influence the processing of timing information. The very presence of depression alone enhanced the temporal information passed on by BCs. When there was no depression at all, nonphase-locked inputs obscured the timing information carried by phase-locked inputs (Fig. 1). However, when depression was added, the influence of nonphase-locked inputs was greatly reduced (Fig. 9). Furthermore, the greater the degree of depression, the lower the jitter in BC response. These effects mainly resulted from the suppression of inputs carrying little timing information. However, this increase in precision appeared to come at a cost of reduced response probability. This suggests that different degrees of depression could confer different computational benefits. For optimally reducing jitter, it may be better to have high depression, whereas for optimizing response probability, it may be better to have low depression. By having synapses with different degrees of depression, that could potentially allow BCs to emphasize one or the other, which provides greater computational flexibility.

However, under conditions where multiple inputs all carried similar timing information, the effects of different amounts of depression were more subtle. In particular, the effect of depression depended on the temporal distribution of the inputs. Cycle histograms recorded in vivo depend on sound intensity and frequency, with rapid onsets at low frequencies and slower onsets at high frequencies. The shapes of the cycle histograms interact with the amplitudes of synaptic inputs to determine postsynaptic jitter (Xu-Friedman and Regehr 2005a,b). When the inputs carry timing information with jitter that is alpha-distributed, postsynaptic spike jitter decreases with larger (less depressed) conductances. Under these conditions, less depression enhanced the precision of BC spike timing (Fig. 7D). However, when the inputs have Gaussian-distributed jitter, postsynaptic jitter is most reduced over a restricted range of conductance amplitude. Thus an increase in depression can contribute to jitter reduction for Gaussian-distributed inputs (Fig. 7D). This could happen if such inputs were to increase their firing rate, thereby depressing more and entering the optimal range for reducing jitter. However, if the firing rate were to increase further, then the total conductance could move lower and out of the optimal range. This could permit the auditory system to optimize jitter reduction by having cells with different depression.

In vivo relevance of depression

Some in vivo experiments have examined the effectiveness of AN inputs in driving BC firing. In one study, the correlation between AN input and BC firing was strong only near AN threshold; as the intensity increased, the correlation between input and output decreased (Young and Sachs 2008). Although the experimental conditions are different enough to preclude a direct comparison, our results suggest that depression could contribute to this effect, such that as AN firing rates increase, the relative contribution of a given AN input to BC firing would be likely to decrease. However, a more direct examination of depression found only weak effects of preceding AN spike interval on BC firing (Young and Sachs 2008). A similar conclusion was reached in studies of the calyx of Held in the medial nucleus of the trapezoid body, where the spontaneous firing rate of synaptic inputs appears to maintain the synapse in a consistently depressed state, so that the reliability of firing is reduced and EPSC amplitudes do not vary greatly (Hermann et al. 2007).

Other lines of evidence suggest that synaptic depression does play an important role in vivo. AN fibers show monotonically increasing rate–intensity functions, but a significant proportion of BCs will show nonmonotonic responses (Kopp-Scheinpflug et al. 2002; Winter and Palmer 1990b). Recruitment of inhibitory inputs at high intensity only partially accounts for this because some cells retain nonmonotonic responses even in the presence of blockers of inhibitory receptors. The remaining effects could be explained by synaptic depression. Nonmonotonic responses would be predicted if the firing rate of AN fibers increases at high sound intensity levels, causing significant depression. It is likely that depression influences other aspects of responses to sounds.

Jitter reduction with one input

In our experiment of Fig. 9, we noticed that with the high depression model there was even a significant reduction in jitter when there was only a single active input (Fig. 9, C and D, intensity I). This is somewhat unexpected, given that the mechanisms of jitter reduction are usually thought to rely on convergence of multiple inputs, although in this case, there were effectively no other inputs. To understand how jitter is decreasing here, it is useful to examine which spikes are being eliminated. In Fig. 9C (left) the high depression case appears to specifically lack spikes in the early part of the cycle, which leads to a decrease in the overall SD. The early spikes in the cycle histogram result from EPSPs that follow soonest after EPSPs in the previous cycle, which are the most subject to depression. Thus depression is suppressing particularly early spikes and causes the BC to spike only after longer intervals.

This jitter reduction appears to reflect a form of resonance between the timing characteristics of the input signal and a tuning property of the detector. In this case, the response of the BC is tuned by the rate of recovery of the endbulb synapse from depression, which interacts with the spike train properties. The fact that we observed it here is probably somewhat fortuitous because it is likely to play a role only when the average firing rate is close to the recovery rate. It is a question whether this could be important under physiological conditions.