Abstract
Calcium binding in proteins exhibits a wide range of polygonal geometries that relate directly to an equally diverse set of biological functions. The binding process stabilizes protein structures and typically results in local conformational change and/or global restructuring of the backbone. Previously, we established the MUG program, which utilized multiple geometries in the Ca2+-binding pockets of holoproteins to identify such pockets, ignoring possible Ca2+-induced conformational change. In this article, we first report our progress in the analysis of Ca2+-induced conformational changes followed by improved prediction of Ca2+-binding sites in the large group of Ca2+-binding proteins that exhibit only localized conformational changes. The MUGSR algorithm was devised to incorporate side chain torsional rotation as a predictor. The output from MUGSR presents groups of residues where each group, typically containing two to five residues, is a potential binding pocket. MUGSR was applied to both X-ray apo structures and NMR holo structures, which did not use calcium distance constraints in structure calculations. Predicted pockets were validated by comparison with homologous holo structures. Defining a “correct hit” as a group of residues containing at least two true ligand residues, the sensitivity was at least 90%; whereas for a “correct hit” defined as a group of residues containing at least three true ligand residues, the sensitivity was at least 78%. These data suggest that Ca2+-binding pockets are at least partially prepositioned to chelate the ion in the apo form of the protein.
Keywords: rotamer, graph theory, side chain, clique, NMR, CaBP
Introduction
Ca2+-binding regulates the diverse functions of calcium binding proteins (CaBPs) and subsequent downstream protein–protein interactions.1–3 It is frequently accompanied with global or local conformational changes of the host protein [Fig. 1(A)]. Trigger proteins such as calmodulin (CaM) and calcium sensing receptor (CaSR) fulfill their functional roles in intracellular and extracellular signaling through Ca2+-induced local and global conformational changes.4–6 On the other hand, buffer proteins such as parvalbumin and calbindin D9K, exhibit predominantly local conformational changes and play important roles in maintaining calcium homeostasis. In addition, CaBPs often exhibit increased stability on calcium binding without concomitant large conformational changes.7 Further, CaBPs exhibiting Ca2+-induced local conformational changes have been designed to monitor calcium responses in cells and to probe the molecular bases of diseases associated with mishandling of calcium signaling.8,9
Figure 1.
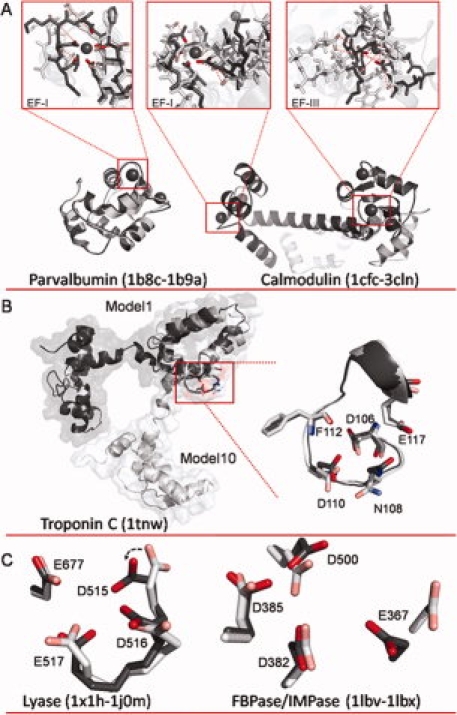
A: Overlays of apo and holo structures of parvalbumin and calmodulin (CaM). For parvalbumin (apo 1B8C.pdb and holo 1B9A.pdb), alignment indicates little change in the backbone conformation, but more significant restructuring in the EF-I binding site where side chains rotate inward to form the binding pocket. Conversely, for CaM (apo 1CFC.pdb and holo 3CLN.pdb), significant restructuring is observed both globally and within the binding sites. CaM sites EF-1 and EF-III were modeled individually by aligning only along the binding site residues in each loop for the apo and holo structures. Dashed red lines indicate distance between key binding ligands between the two structures. B: Model 1 (dark gray) and Model 10 (light gray) of NMR structure of troponin C (1TNW.pdb) aligned along residues 106–117. C: Overlay of calcium binding pocket of lyase (left) in apo (1X1H.pdb, light gray) and holo (1J0M.pdb, dark gray) structures, and overlay of calcium binding pocket of FBPase/IMPase (right) in apo (1LBV.pdb, light gray) and holo (1LBX.pdb, dark gray) structures. An interactive view is available in the electronic version of the article. PRO394 Figure 1
One of the outstanding obstacles to understanding the Ca2+-dependent roles of CaBPs and to the rational design of novel CaBPs is our limited ability to predict Ca2+-binding pockets in apoprotein structures. A Ca2+-binding pocket is depicted by the group of ligand atoms or residues, (e.g., negatively charged Asp and Glu side chains in addition to main chain carbonyl and other noncharged carboxyl groups), that chelate the calcium ion.10,11 Binding pockets are more readily recognized in the bound state where conformational changes have already occurred. We have previously shown that a defined site should consist of at least four oxygen atoms with at least one possessing a formal negative charge.12–14 The ligand residues are typically oriented toward the central calcium ion. The distances between each two oxygen atoms involved in binding have an upper limit of 6.0 Å. Within the sphere formed by the central calcium ion and the oxygen atoms bound to it, no other atoms intervene.14 These criteria, however, do not necessarily pertain to the apoprotein, since, in the absence of calcium, this spherical form may be distorted. For example, repulsion between oxygen atoms, unshielded by the calcium charge, may result in conformational change of the binding pocket due to side chain rotation, backbone movement, or a combination of the two. Such movements may place oxygen atoms more distant than 14 Å (e.g., as seen with Scytalone dehydrates-inhibitor complex, 4STD.pdb), and distort their orientation toward a central point. Thus, the readily recognized oxygen geometry in holo CaBPs is often obscured in the apo state, rendering the recognition of Ca2+-binding pockets problematic.
Of the many approaches to prediction,14–19 the majority have been tested only with holoproteins, and succeed with apo forms only if they do not undergo conformational change. Several approaches have been applied to apo structures. SitePredict20 classifies each residue as either a ligand or nonligand residue; FEATURE17,21–23 represents each Ca2+-binding site as a point; and LIGSITECSC24 and FINDSITE,25 in addition to generating a point representing a predicted pocket, may output the residues lying within a distance of 4 Å from that point. Unfortunately, further analyses for apoproteins are required to identify the set of ligand residues or the pocket. Such analyses are generally nontrivial due to potential conformational rearrangement. To our knowledge, the accurate prediction of Ca2+-binding pockets from apo structures has not yet been achieved.
We have previously reported a successful approach applying multiple geometries and graph theory (MUG) to identify known Ca2+-binding pockets in protein holo structures.19 In this article, we augment that approach to predict Ca2+-binding pockets that undergo localized backbone displacement or side chain torsional rotations on calcium binding. Given an apoprotein structure as input, the output from this algorithm consists of groups of residues, typically comprising two to five residues, considered to be potential binding pockets. This new approach, designated MUGSR, begins with the original MUG algorithm, and then relaxes the parameters to allow for minor backbone conformational changes, which might occur when the site is not occupied. To allow for side chain movement, MUGSR systematically explores side chain rotations using a rotamer library,26 which might bring side chains into plausible Ca2+-binding conformation. Hits from MUGSR were validated by referring back to the corresponding holoprotein structures, which share >98% sequence similarity with the apoprotein. In a test dataset comprising 49 binding sites in such apo/holoprotein pairs (documented by X-ray crystallography), MUGSR is able to predict 44/49 sites using the apo structures, when a correct hit is required to contain at least two true ligand residues. For a study of six NMR structures MUGSR was able to identify all 16 Ca2+-binding pockets. Finally, the performance of MUGSR was compared with FEATURE and LIGSITECSC on the same X-ray test dataset. The high sensitivity of MUGSR suggests that Ca2+-binding pockets are at least partially prepositioned to chelate the ion in the apo form of the protein.
Results
Datasets
A training dataset was constructed based on data evaluated by Babor et al.27 for the purpose of analyzing Ca2+-induced conformational changes. The Babor dataset contained 59 binding pockets from 45 different structures deposited in the protein data bank (PDB). Our revised dataset was modified to eliminate binding sites with low-coordination numbers (<4); such sites may indicate nonspecific binding, implying reduced stability and lower binding affinity at best. Second, the original Babor dataset implicitly limited consideration to a single protein chain, excluding interchain sites. Although unusual, interchain binding is occasionally observed. For example, in hepatitis C virus RNA helicase domain (1HEI.pdb)28 the calcium ion is chelated with three atoms from chain B and one from chain A. Our final training dataset, summarized in Supporting Information Table S1, included 26 binding pockets.
The test dataset (Supporting Information Table S2) included 49 binding sites from 26 X-ray protein structures duplicated for both the apo and holo forms of each protein. The 26 holo/apo pairs were selected based on the following constraints: Resolutions better than 2.5 Å; protein sequence of at least 50 amino acids; sequence similarity between the apo and holo structures in one pair greater than 98%; sequence similarity between different pairs <30%; and each Ca2+-binding pocket containing at least four ligand oxygen atoms from protein.
Analysis of training dataset
An analysis of the training dataset was conducted to establish structural parameters applicable to apo structures. These parameters were the oxygen–oxygen (O–O) cutoff distance and χ angles of side chain rotation.
The distribution of O–O distances for ligand oxygen atoms in Ca2+-binding pockets from the training set (Fig. 2) illustrated, not unexpectedly, that oxygen atoms are more closely packed in the Ca2+-binding pockets from the holo when compared with the apo structures. It was determined that 24/26 binding pockets had at least four oxygen atoms in close proximity to each other (distance ≤7.5 Å). The remaining two pockets included three oxygen atoms within this range.
Figure 2.
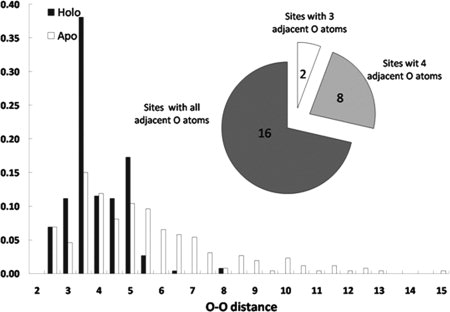
Distribution of O–O distances (in angstroms) for oxygen atoms in calcium-binding pockets in holo (black bar) and apo (white bar) proteins of the training dataset.
In solution, proteins, especially their flexible side chains, are in constant motion. The most frequently observed energy-favorable side chain conformations have been analyzed and documented in rotamer libraries, where a rotamer is defined as a single side chain conformation represented as a set of values, one for each dihedral-angle degree of freedom.29 Previously published data27,30 suggest that only a small portion (∼5%) of binding pockets exhibit significant rotation in more than one side chain in cases where the backbone is not rearranged on calcium binding. It is also expected that the side chain dihedral angles of ligand residues in holo structures are close to the rotamer dihedral angles described in a rotamer library. Analyses of side chain dihedral angles of ligand residues Asp and Glu in the training dataset are presented in Figure 3(A,B). The distributions of χ1 of Asp and χ1 and χ2 of Glu are concentrated at angles that correlate precisely with rotamer library conformations. With regard to χ2 of Asp (and χ3 of Glu), two values were initially calculated, one for OD1 (OE1) and one for OD2 (OE2), as the two atoms are viewed identically in MUGSR. The one that is closest to the rotamer library is retained. As shown in Figure 3(A,B), values for both χ2 of Asp and χ3 of Glu correlate well with those in the rotamer library. The analysis of Asn, Gln, Ser, Tyr, and Thr does not suggest a statistically significant discrepancy between observed χ angles and those recorded in the rotamer library.
Figure 3.
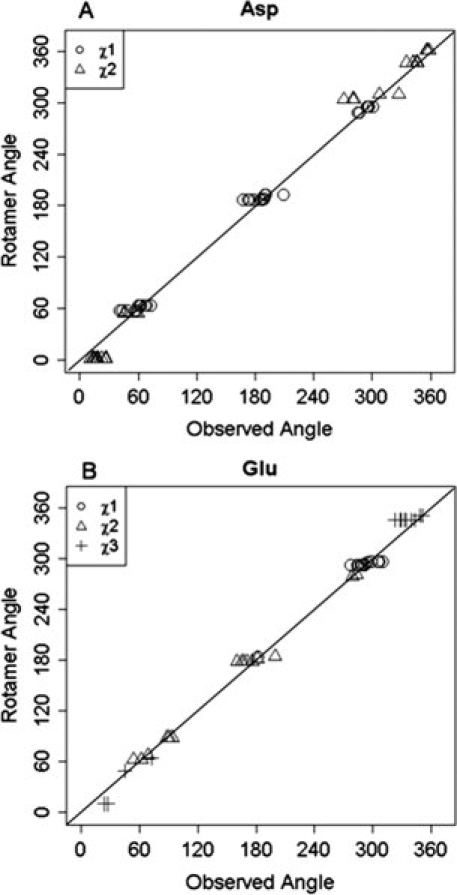
A: Distributions of side chain χ1 and χ2 of Asp in holoproteins. B: Distribution of side chain χ1, χ2, and χ3 of Glu in holoproteins.
Test results on X-ray dataset
A hit from MUGSR constitutes a group of oxygen atoms and their corresponding residues. The “correctness” of these hits can be scored by how many residues in the “hit” identify residues that truly participate in calcium binding, based on comparison of the apo structure with the corresponding bound holo structure. Results of the analysis of the X-ray test dataset, summarized in Figure 4, are broken down according to multiple criteria based on whether one, two or three residues of a predicted group are true Ca2+-binding ligands.
Figure 4.
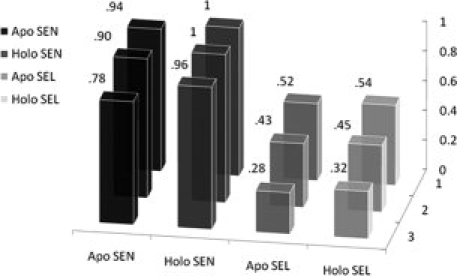
Sensitivity and selectivity on apo and holoproteins in X-ray datasets. The x-(horizontal) axis indicates a correct hit containing one (two, three) true ligand residues (z-axis).
When MUGSR was applied to the 26 apo structures in the X-ray test set, using the criterion that at least three residues in the predicted group must be in the true ligand group, we observed that, among the 49 sites documented as actual Ca2+-binding sites formed by four oxygen atoms from proteins, 38 included three or more residues, which had been predicted as a ligand group. Thus, sensitivity [Eq. (1)] was calculated to be 78% and selectivity [Eq. (2)] was 28%. Relaxing the criterion to two residues, MUGSR “correctly” predicted 44 of 49 Ca2+-binding pockets, giving a sensitivity of 90%, and a selectivity of 43%. If we score a prediction of just a single residue within a group as “correct” for the group, then MUGSR correctly predicted 46 of 49 documented sites, giving a sensitivity of 94% and a selectivity of 52%. The observation that 44/49 full or partial pockets (i.e., the number of Ca2+-binding pockets that are predicted according to the criterion of two true ligand residues contained in some “hit”) were successfully identified from the apoprotein structures suggests that the Ca2+-binding pockets are at least partially organized in the apo state. This observation suggests that Ca2+-induced side chain rotations are restricted predominantly to residues actually involved in calcium ligation.
Applying MUGSR only to the 26 holo structures, and defining a “correct hit” according to the aforementioned criteria of three, two or one residues, the results improved as expected (Fig. 4). For a group containing three (two, one) documented ligand residue(s), sensitivity is 96% (100%, 100%) and the selectivity is 32% (45%, 54%). The improvements observed for sensitivity and selectivity suggest that Ca2+-binding geometry is more recognizable in the Ca2+-loaded form. It is interesting to note that the number of hits that invoke side chain rotations is similar when comparing the holo (378) and apo structures (370), although the number of total hits is significantly different in holo (911) and apo (795) structures. This may be attributed to minimal changes in side chain packing in regions of the protein outside the binding site.
Prediction results from our analysis are consistent with studies showing that Asp and Glu, typically observed within loops and to lesser extent within helices, are more likely to change side chain positions between apo and holo structures than other amino acid side chains.31 In Table I, correct predictions (applying the two-residue criterion, i.e., that predictions contain at least two true residues) that require side chain rotations were analyzed. The results clearly indicate that Asp and Glu are the two types of residues rotated most frequently to coordinate calcium ions.
Tabel I.
Frequency of Rotated Side Chains by Three Categories
| By residue | By 2° structure | By position | |||
|---|---|---|---|---|---|
| Asp | 50 | Loop | 62 | Loop | 62 |
| Glu | 24 | α-Helix | 18 | Near loopa | 13 |
| Otherb | 18 | β-Strand | 12 | Middle of helix or strand | 17 |
| Total | 92 | 92 | 92 | ||
One or two residues preceding the beginning of a loop, or one or two residues succeeding the ending of a loop.
Six from Gln, three from Asn, four from Ser, and five from Thr.
Finally, many calcium binding sites, such as the pseudo EF-hand sites in S100's, utilize several carbonyl oxygen ligands, with only one or two side chain ligands. To evaluate how MUGSR would perform on those sites, we identified four apo S100 protein structures from the PDB for analysis: 1K8U (S100A6), 1K9P (S100A6), 1KSO (S100A3), and 2RGI (S100A2). Using chain A of the above structures for prediction, MUGSR identified all of the four pseudo EF-hand binding pockets when a two-residue criterion was applied (Supporting Information Table S5), with 38 correct hits out of 70 total hits.
Prediction based on NMR structures
One obstacle to the prediction of Ca2+-binding pockets in NMR solution structures is the imprecision of coordinates associated with oxygen atoms due to the intrinsic zero nuclear spin of isotopically-abundant 16O atoms which cannot be directly observed via NMR. To explore the effect of this imprecision on predictability, MUGSR was tested on a dataset reported in the literature32 of six Ca2+-loaded proteins whose structures have been determined by NMR. It should be noted that these were all EF-hand proteins, whose binding sites can also be identified by sequence analysis. Although the NMR solution contained calcium, two of the six structures were calculated without using constraint distances related to the calcium ion. As these proteins were deposited in the PDB with multiple conformations (i.e., models), predictions were made first by using each model separately, and then by combining the outcome from the model of least energy (Model 1)33 and the model containing the most predictions.
Results are presented in Table II. All 16 binding pockets were predicted if we consider a hit to be correct when it contains at least two, true ligand residues. The number of total hits is 239 of which 208 are correct. Thus, both the sensitivity (100%) and selectivity (87%) are high. Further inspections reveal that, if we take the predictions only from the first model (the energy-minimal model), the first and third sites of troponin C (1TNW.pdb) and the first site of calbindin D9K (2BCB.pdb) were not predicted. These two protein structures, interestingly, are the two calculated without using Ca2+-related constraints.
Tabel II.
Prediction on NMR holo Structures
| Protein | ID | Ma | Lb | True ligands | Predicted ligands |
|---|---|---|---|---|---|
| Epidermal growth factor receptor pathway substrate 15 | 1C07 | 20 | 95 | D28, D30, D32, F34, E39 | D28, D32, F34, E39 |
| Calcium binding protein NCS-1 | 1FPW | 20 | 190 | D73, D75, N77, F79, E84 | D73, N77, F79, E84 |
| D109, N111, D113, Y115, E120 | D109, N111, D113, Y115, E120 | ||||
| D157, N159, D161, Y163, E168 | D157, N159, D161, Y163, E168 | ||||
| Calmodulin | 2BBM | 1 | 148 | D20, D22, D24, T26, E31 | D20, D24, T26, E31 |
| D56, D58, N60, T62, E67 | D56, D58, N60, T62, E67 | ||||
| D93, D95, N97, Y99, E104 | D93, D95, N97, Y99, E104 | ||||
| N129, D131, D133, D135, E140 | N129, D131, D133, E140 | ||||
| Parvalbumin | 2PAS | 9 | 109 | D51, D53, S55, F57, E62 | D51, D53, F57, E62 |
| D90, D92, D94, K96, E101 | D90, D92, D94, K96 | ||||
| Calbindin D9K | 2BCB | 32 | 75 | A14, E17, D19, Q22, E27 | A14, E17, D19, Q22, E27 |
| D54, N56, D58, E60, E65 | D54, N58, E60, E65 | ||||
| Troponin C | 1TNW | 23 | 162 | D30, D32, G34, D36, E41 | D30, G33, D36, E41 |
| D66, D68, S70, T72, E77 | D66, T72, D74, E77 | ||||
| D106, N108, D110, F112, E117 | N108, A109, D110 | ||||
| D142, N144, D146, R148, E153 | D142, D146, R148, E153 |
All structures are calcium-loaded. 2BCB and 1TNW (italic) are calculated without using calcium constraints.
The number of models in a PDB file.
The length (number of residues) of a protein.
The observation that some NMR models contain well-organized Ca2+-binding pockets whereas others do not underscores the dynamic properties of protein Ca2+-binding sites. Presumably, the Ca2+-binding pockets of CaBPs in solution, in the presence of calcium, are in an equilibrium state between bound and unbound forms, correlated with the different models in PDB files.
MUGSR retains its high accuracy even with NMR holo structures solved without calcium constraints, owing to the complementary information provided by the multiple models. For example in troponin C (1TNW.pdb), the root mean square deviation (RMSD) values of heavy atoms for the whole protein and its Ca2+-binding loop (from residue 106–117) between Models 1 and 10 (the model resulting in the most hits) are 7.69 and 1.11 Å, respectively. By aligning just the loop of the second Ca2+-binding site, the C-terminal domain is well-aligned whereas the other domain is flipped [Fig. 1(B)]. Model 10 encodes the Ca2+-binding pocket with the side chain of N108 oriented toward the center of the binding loop whereas Model 1 does not.
The multiple models obtained from NMR structure calculations, representing multiple possible protein conformations in solution, do provide useful, complementary structural information that the model of least energy could not fully cover. This observation is consistent with a comparative study34 of X-ray versus NMR structures.
Discussion
Calcium-binding and rotamers
We observed that Ca2+-binding pockets in apo structures are sometimes only partially organized, usually with some of the ligand residues prepositioned, whereas one or two other side chain ligand atoms are displaced at a distance. By rotating these more distant side chains, the Ca2+-binding pocket can be brought into appropriate geometry, and thus rendered identifiable. The apo structure of lyase (1X1H.pdb) has a partially organized Ca2+-binding pocket consisting of three oxygen atoms from side chains of D516, D517, and E677 [Fig. 1(C)]. In contrast, in the holo state (1J0M.pdb) D515 is re-oriented toward the center of the Ca2+-binding pocket. It seems likely that in the apo state, the rotation of D515-oxygen away from the pocket is necessary to alleviate negative charge repulsion caused by the proximity of oxygen atoms. MUGSR rotated the χ1 and χ2 angles of D515 in the apo state. Since in the holo state, χ1 (52.9°) and χ2 (−32.6°) are close to the values in the rotamer library (62.4° and −55.8°), the Ca2+-binding pocket, as reconstructed by side chain rotation, was more closely congruent with the pocket in the holo structure, and was identified by MUGSR.
There are cases where a particular side chain of the binding pocket in the holo state does not conform to the predefined rotamers of MUGSR. This prevents the rotation procedure from accurately reconstructing the holo geometry. Nevertheless, the partially organized pocket can still be identified. For example in Figure 1(C), E367 of FBPase/IMPase undergoes both backbone and side chain movement between the apo (1LBV.pdb) and holo (1LBX.pdb) structures. Although the holo conformation of E367 was not reproduced from its apo conformation, MUGSR successfully identified the remaining ligand residues of the binding pocket—D382, D385, and D500.
Toward predicting the set of ligand residues
Existing prediction approaches may be classified into two general categories based on the types of input data they take: sequence or structural information.
Pure sequence-based approaches, although only requiring the more abundant sequence information, are more frequently reported to be able to predict conserved Ca2+-binding sites, while the prediction of noncontinuous sites remains challenging.35–38 Prediction approaches based on structural information typically either identify the location of the calcium ion or classify a residue as ligand or nonligand. The accurate in silico prediction of a Ca2+-binding pocket, that is, the location of the ion and the associated binding ligands, has yet to be achieved.
Using holo structures, some approaches are able to re-identify the calcium location near to the reported position within a solved structure,15,16,18 whereas others directly identify the Ca2+-binding pocket with reasonable accuracy. From a structural perspective, the fully formed binding site is easier to identify in holo structures where the ligand atoms form a recognizable cluster. Yamashita et al.15 were able to identify the position of a metal ion in the structure by embedding the whole protein into a three-dimensional grid and then measuring quantitatively the hydrophobicity contrast at each grid point, where grids with calculated high values were near the reported ion position. Nayal and Di Cera16 applied a similar grid approach but utilized a valence function for scoring where the points of the highest valences were usually near to a documented calcium ion. Schymkowitz et al.18 reported the capability of predicting the precise location of the calcium ion with high-coordination numbers based on a combined approach using geometrical search and Fold-X empirical force field. Our previous study14 exploited the strong correlation of Ca2+-binding sites with oxygen clusters containing exactly four atoms and lying within a sphere of specified radius. In this approach, clusters of four oxygen atoms that are geometrically qualified were identified as the ligand atoms. In a more recent study, we further exploited the properties of oxygen clusters involved in calcium binding and were able to successfully identify the set of ligand residues in 75% of the test cases.19
To date, prediction efforts based on apo structures have not been able to accurately identify the set of ligand residues comprising a binding pocket, due mainly to the complex reconfigurations which occur as a consequence of metal binding. The blind docking algorithms typically perform better with the binding of medium to large molecules.39 Metal-binding sites in metalloproteins pose a more serious challenge for the would-be predictor.40–42 The threading-based approach FINDSITE25,43 outputs a point representing the predicted pocket, and identifies a putative ligand residue if any of its heavy atoms lie within a distance of 4 Å from the predicted binding site center. Wei and Altman's FEATURE program combined a grid system with a probabilistic scoring function.17 This program utilized the frequency distributions of selected Ca2+-binding features (charge, hydrophobicity, secondary structure, etc.) within the framework of a Bayesian scoring function to compute the propensity of calcium binding for each grid point within an embedded grid system. Another machine learning method, SitePredict,20 utilizes random forest technique to generate a confidence value for identification of ligand residues. A related program, CHED,30 approached the prediction of transition metal-binding sites by identifying qualified triads consisting of three residues from only four residue types: C (cysteine), H (histidine) E (glutamic acid), or D (aspartic acid). A qualified triad containing at least one true ligand residue is defined as a “correct” prediction. This algorithm, however, does not directly fit the prediction of Ca2+-binding sites with diversified ligand types and coordination properties.
Comparison with FEATURE and LIGSITECSC
Compared with our previous MUG19 program that does not allow side chain rotation, MUGSR identifies 11 more true binding sites using the X-ray test dataset when the two-residue criterion is applied. We have further assessed the performance of MUGSR, by comparison with the FEATURE and LIGSITECSC algorithms using the same apo structures as in our X-ray test set.
FEATURE is one of the most successful machine learning programs for function recognition, including the “function” of calcium binding. It is not straightforward to directly compare prediction results between FEATURE and MUGSR, as a prediction (hit) from FEATURE is a three-dimensional coordinate set representing the predicted calcium site, rather than a group of residues as returned by MUGSR. To compare results, we translate the predicted location for a FEATURE “hit” into a group of residues by identifying residues within a 4 Å radius from the predicted calcium site (see Refs. 25 and 44 for selection of this cutoff value). A hit from FEATURE is correct if, after translation, it contains a specified number of true ligand residues. Sensitivity and selectivity are thus calculated in the same way described in Eqs. (1) and (2).
Table III presents the comparative results between MUGSR and FEATURE. As the performance of FEATURE depends on a score threshold, three kinds of choices of threshold values are made: values that reach the same selectivity as that of MUGSR, values that reach the same sensitivity as that of MUGSR, and the default value 50.0 used in FEATURE's web server. By choosing the default threshold value 50.0, FEATURE achieves higher selectivity but much lower sensitivity than MUGSR. Indeed, for all three criteria presented in Table III, MUGSR is shown to have higher sensitivity when selectivity is fixed and higher selectivity when sensitivity is fixed. Arguably, these results should be interpreted cautiously, as other methods may be applied to translate calcium location into ligand residues. For example, when selectivity reaches 43% for both MUGSR and FEATURE, sensitivity is 90% for MUGSR and 71% for FEATURE (Table III, criterion 2, i.e., a correct prediction contains at least two true ligand residues). In addition, to achieve high sensitivity, FEATURE produced thousands of predictions compared with hundreds for MUGSR.
Tabel III.
Comparison of MUGSR, FEATURE, and LIGSITECSC
| FEATURE |
||||||
|---|---|---|---|---|---|---|
| Criteriaa | MUGSR | SEL leveragedb to MUGSR | SEN leveraged to MUGSR | Score cutoff 50.0 | LIGSITECSC | |
| One | Hits | 795 | 2270 | 5881 | 142 | 78 |
| Correct hits | 417 | 1188 | 2174 | 123 | 9 | |
| Predicted pockets | 45 | 43 | 45 | 21 | 9 | |
| Sensitivity | 94% | 88% | 94% | 43% | 19% | |
| Selectivity | 52% | 52% | 40% | 87% | 11% | |
| Two | Hits | 795 | 1386 | 4706 | 142 | 78 |
| Correct hits | 341 | 599 | 1161 | 108 | 3 | |
| Predicted pockets | 44 | 33 | 44 | 21 | 3 | |
| Sensitivity | 90% | 67% | 90% | 43% | 6% | |
| Selectivity | 43% | 43% | 25% | 76% | 4% | |
| Three | Hits | 795 | 1010 | 3282 | 142 | 78 |
| Correct hits | 221 | 286 | 469 | 77 | 1 | |
| Predicted pockets | 38 | 29 | 38 | 20 | 1 | |
| Sensitivity | 78% | 59% | 78% | 41% | 2% | |
| Selectivity | 28% | 28% | 13% | 54% | 1% | |
A hit is correct if it contains one (two, three) true ligand residues.
SEL of FEATURE is adjusted, by tuning the cutoff score, to be the same as that of MUGSR.
Comparison was also made with LIGSITECSC which applies a geometry-based approach to identify a single point to represent the predicted pocket and then identifies ligand residues based on a 5 Å proximity to the predicted site.24,25 Unlike MUGSR but similar to FEATURE, a hit from LIGSITECSC is a point representing a binding pocket (not specifically targeting calcium binding, but a “general” binding pocket). LIGSITECSC differs from FEATURE in that it further probes a given radius surrounding the predicted “point” to obtain potential ligand residues. Consequently, sensitivity and selectivity are defined in Eqs. (1) and (2). From Table III, we note that, both the sensitivity and selectivity of LIGSITECSC are significantly lower than those of MUGSR and FEATURE. This suggests that, algorithms designed specifically for predicting Ca2+-binding sites have greater acuity in discovering such sites than do general pocket detection algorithms.
In summary, efforts to predict Ca2+-binding sites from apoprotein structures have, to date, met with very limited success due to global complex restructuring associated with Ca2+-binding and the difficulty associated with identifying binding ligands that may be distant either sequentially or structurally within the protein. The MUGSR algorithm discussed in this study combines geometric characteristics and graph theoretical properties of Ca2+-binding pockets, coupled with strategic filtering based on established rotamer libraries to account for possible side chain movements, to achieve improved results for identifying both the partially preformed binding sites in apo structures and the associated binding ligands. The identification of both the Ca2+ coordinates and a set of associated ligand residues will immediately enhance our understanding of calcium-protein interactions and our ability to design CaBPs. It also represents an important step toward true in silico prediction based on apo structure only, which will greatly benefit research associated with the Ca2+-mediated functions of proteins such as CaSR, which have known Ca2+-dependent functions but unidentified binding sites where potential mutations may interfere with Ca2+-binding resulting in disease states.
Methods
Algorithm description
For prediction from an apoprotein structure, MUGSR executes three major subroutines (Fig. 5). In S1 (subroutine 1), oxygen clusters are first identified. These are groups of oxygen atoms proximal to each other in the three-dimensional structure so as to be treated as a potential ligand group.
Figure 5.
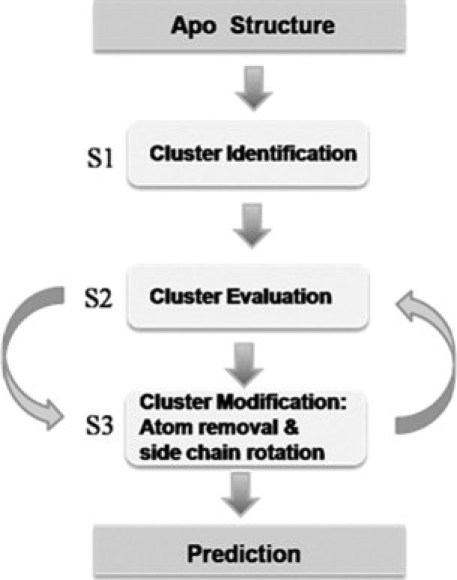
Schematic diagram of general MUGSR functions. S1, S2, and S3 are subroutine 1, subroutine 2, and subroutine 3, respectively.
In S2 (subroutine 2), for each oxygen cluster, a point CC (calcium center) is identified as the tentative calcium position by a grid algorithm. Filters consisting of various restrictions are sequentially applied to the structure of a (cluster, CC) pair. If a cluster passes all filters, the cluster is a considered a “predicted ligand group” and CC is the “predicted calcium position” within the group; otherwise, MUGSR modifies the cluster by calling subroutine S3.
S3 removes from the cluster the oxygen atom most distant from CC and recursively calls S2 until either a “pass” (i.e., the structure is qualified for calcium binding) is obtained, or the number of oxygen atoms remaining in the cluster is less than four. If (cluster, CC) passes all the filters, the subroutine outputs the results and exits; otherwise, it torsionally rotates the side chains of all residues in the cluster in turn (maximally two residues at a time), generating different local conformations of the oxygen cluster. Each generated potential conformation is then passed back to S2.
Currently, MUGSR was trained mainly for Ca2+ prediction and would require new chemical and structural data to modify the filters to identify other binding sites for other transition metal ions such as Zn2+, which utilizes sulfur and nitrogen in addition to oxygen atoms. However, in nominal calcium binding sites that also bind Mg2+ and Zn2+ ions with moderately high affinity, MUGSR has not been devised to distinguish different metal ions.
Finding oxygen clusters and calcium center
MUGSR identifies Ca2+-binding pockets using a graph theory approach. Previous work in our laboratory has demonstrated that identification of oxygen clusters, modeled as maximal cliques in graph theory, is sufficient to identify Ca2+-binding pockets in holo structures.19 To obtain the aforementioned maximal clique, a graph G(V, E) is constructed, where V is the set of all vertices and E is the set of all edges of G. Each vertex represents an oxygen atom. An edge is assigned between two vertices if the distance between these two vertices is within a preset O–O cutoff (7.5 Å). A clique Q is a subset of V such that every two vertices in Q are adjacent. A maximal clique M is a clique that is not a proper subset of any other clique.45 The size of a maximal clique is the number of vertices it contains.
MUGSR identifies the CC within each oxygen cluster by finding the point that accrues the least penalty according to a penalty function detailed in our previous work,19 so that the CC is located to optimize the structure of the (cluster, CC) pair to those observed in holo structures.
Filters
Filters are used to inspect each tentative (cluster, CC) pair. Two sets of filters, chemical-filters, and geometrical-filters,19 are currently applied in MUGSR. Chemical-filters examine the formal charge of each cluster. Geometrical-filters examine: the distances between the CC and oxygen atoms; the distances between the CC and the carbon atoms connected to the ligand oxygen atoms; the ratio of the above two distances; the angle among the CC, oxygen atom and carbon atom connected to the oxygen atom; and the dihedral angles between the plane formed by the side chain carboxyl group (—COO) and the plane formed by the two carboxyl oxygen atoms (bidentate pair) and CC.
Side chain rotation
If a tentative cluster does not pass the filters, MUGSR rotates the side chain of each residue contributing atoms to that cluster for all conformations in a back bone independent rotamer library,26 in which each side chain torsion angle has typically three dominant values. If a single chain rotation does not satisfy the geometrical filters, the process is repeated with two side chains at a time. The exact number of rotations tried is dependent on the residue type. Although rotation of more than two side chains is possible, the performance improvement by doing this is not significant according to the training dataset, and the corresponding computational time increases. The rotated structure should be free of interatomic clashing in that the distance between atom A and atom B should not be less than rA + rB where rA and rB are the van der Waals radii of atom A and B, respectively.
Measurements: Sensitivity and selectivity
Given a protein apo structure, a hit from MUGSR is a group of oxygen atoms (and their corresponding residues) that are expected to be able to bind calcium. We assess validity of a hit by referring back to the corresponding holo structure. A correct hit contains at least two, true ligand residues (alternatively, we also discuss the use of criteria requiring that one or three true residues be contained). A Ca2+-binding pocket is predicted if there is at least one correct hit for it. Sensitivity (SEN) is the percentage of predicted pockets in total pockets. Selectivity (SEL) is the percentage of correct hits in total hits.
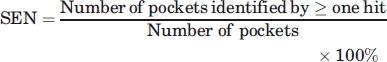 |
(1) |
| (2) |
Implementation and rendering tools
The MUGSR program was developed in C and C++ programming language and was run in parallel on URSA—an IBM system p5 575 with Power5+ processors. PyMOL software46 was used for molecular visualization.
Acknowledgments
The authors thank Shen Tang and Drs. Robert Wohlhueter, Min Luo, Jiawei Liu, and Donald Hamelberg for their helpful suggestions during preparation of this manuscript. They also thank Dr. Robert Kretsinger and another anonymous reviewer for their insightful comments and suggestions.
References
- 1.Herzberg O, Moult J, James MN. A model for the Ca2+-induced conformational transition of troponin C: a trigger for muscle contraction. J Biol Chem. 1986;261:2638–2644. [PubMed] [Google Scholar]
- 2.Holmes KC, Popp D, Gebhard W, Kabsch W. Atomic model of the actin filament. Nature. 1990;347:44–49. doi: 10.1038/347044a0. [DOI] [PubMed] [Google Scholar]
- 3.Mann KG, Nesheim ME, Church WR, Haley P, Krishnaswamy S. Surface-dependent reactions of the vitamin K-dependent enzyme complexes. Blood. 1990;76:1–16. [PubMed] [Google Scholar]
- 4.Berridge MJ, Bootman MD, Lipp P. Calcium—a life and death signal. Nature. 1998;395:645–648. doi: 10.1038/27094. [DOI] [PubMed] [Google Scholar]
- 5.Kretsinger RH. Calcium coordination and the calmodulin fold: divergent versus convergent evolution. Cold Spring Harb Symp Quant Biol. 1987;52:499–510. doi: 10.1101/sqb.1987.052.01.057. [DOI] [PubMed] [Google Scholar]
- 6.Brown EM, MacLeod RJ. Extracellular calcium sensing and extracellular calcium signaling. Physiol Rev. 2001;81:239–297. doi: 10.1152/physrev.2001.81.1.239. [DOI] [PubMed] [Google Scholar]
- 7.Yang W, Yang JJ. American peptide symposia. Springer: Netherlands; 1997. Investigation of conformational properties of Ca(II)-binding peptides in cell adhesion molecules. [Google Scholar]
- 8.Holder AN, Ellis AL, Zou J, Chen N, Yang JJ. Facilitating chromophore formation of engineered Ca2+ binding green fluorescent proteins. Arch Biochem Biophys. 2009;486:27–34. doi: 10.1016/j.abb.2009.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zou J, Hofer AM, Lurtz MM, Gadda G, Ellis AL, Chen N, Huang Y, Holder A, Ye Y, Louis CF, Welshhans K, Rehder V, Yang JJ. Developing sensors for real-time measurement of high Ca2+ concentrations. Biochemistry. 2007;46:12275–12288. doi: 10.1021/bi7007307. [DOI] [PubMed] [Google Scholar]
- 10.Marsden BJ, Shaw GS, Sykes BD. Calcium binding proteins. Elucidating the contributions to calcium affinity from an analysis of species variants and peptide fragments. Biochem Cell Biol. 1990;68:587–601. doi: 10.1139/o90-084. [DOI] [PubMed] [Google Scholar]
- 11.Falke JJ, Drake SK, Hazard AL, Peersen OB. Molecular tuning of ion binding to calcium signaling proteins. Q Rev Biophys. 1994;27:219–290. doi: 10.1017/s0033583500003012. [DOI] [PubMed] [Google Scholar]
- 12.Kirberger M, Wang X, Deng H, Yang W, Chen G, Yang JJ. Statistical analysis of structural characteristics of protein Ca2+-binding sites. J Biol Inorg Chem. 2008;13:1169–1181. doi: 10.1007/s00775-008-0402-7. [DOI] [PubMed] [Google Scholar]
- 13.Yang W, Lee HW, Hellinga H, Yang JJ. Structural analysis, identification and design of calcium-binding sites in proteins. Proteins. 2002;47:344–356. doi: 10.1002/prot.10093. [DOI] [PubMed] [Google Scholar]
- 14.Deng H, Chen G, Yang W, Yang JJ. Predicting calcium-binding sites in proteins—a graph theory and geometry approach. Proteins. 2006;64:34–42. doi: 10.1002/prot.20973. [DOI] [PubMed] [Google Scholar]
- 15.Yamashita MM, Wesson L, Eisenman G, Eisenberg D. Where metal ions bind in proteins. Proc Natl Acad Sci USA. 1990;87:5648–5652. doi: 10.1073/pnas.87.15.5648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nayal M, Di Cera E. Predicting Ca2+-binding sites in proteins. Proc Natl Acad Sci USA. 1994;91:817–821. doi: 10.1073/pnas.91.2.817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wei L, Altman RB. Recognizing protein binding sites using statistical descriptions of their 3D environments. In Pacific Symposium on Biocomputing. 1998. pp. 497–508. World Scientific. [PubMed]
- 18.Schymkowitz JW, Rousseau F, Martins IC, Ferkinghoff-Borg J, Stricher F, Serrano L. Prediction of water and metal binding sites and their affinities by using the Fold-X force field. Proc Natl Acad Sci USA. 2005;102:10147–10152. doi: 10.1073/pnas.0501980102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang X, Kirberger M, Qiu F, Chen G, Yang JJ. Towards predicting Ca2+-binding sites with different coordination numbers in proteins with atomic resolution. Proteins. 2009;75:787–798. doi: 10.1002/prot.22285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bordner AJ. Predicting small ligand binding sites in proteins using backbone structure. Bioinformatics. 2008;24:2865–2871. doi: 10.1093/bioinformatics/btn543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bagley SC, Altman RB. Characterizing the microenvironment surrounding protein sites. Protein Sci. 1995;4:622–635. doi: 10.1002/pro.5560040404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liang MP, Banatao DR, Klein TE, Brutlag DL, Altman RB. WebFEATURE: an interactive web tool for identifying and visualizing functional sites on macromolecular structures. Nucleic Acids Res. 2003;31:3324–3327. doi: 10.1093/nar/gkg553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Glazer DS, Radmer RJ, Altman RB. Combining molecular dynamics and machine learning to improve protein function recognition. Pac Symp Biocomput. 2008;13:332–343. [PMC free article] [PubMed] [Google Scholar]
- 24.Huang B, Schroeder M. LIGSITEcsc: predicting ligand binding sites using the Connolly surface and degree of conservation. BMC Struct Biol. 2006;6:19. doi: 10.1186/1472-6807-6-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Brylinski M, Skolnick J. A threading-based method (FINDSITE) for ligand-binding site prediction and functional annotation. Proc Natl Acad Sci USA. 2008;105:129–134. doi: 10.1073/pnas.0707684105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dunbrack RL, Jr, Cohen FE. Bayesian statistical analysis of protein side-chain rotamer preferences. Protein Sci. 1997;6:1661–1681. doi: 10.1002/pro.5560060807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Babor M, Greenblatt HM, Edelman M, Sobolev V. Flexibility of metal binding sites in proteins on a database scale. Proteins. 2005;59:221–230. doi: 10.1002/prot.20431. [DOI] [PubMed] [Google Scholar]
- 28.Yao N, Hesson T, Cable M, Hong Z, Kwong AD, Le HV, Weber PC. Structure of the hepatitis C virus RNA helicase domain. Nat Struct Biol. 1997;4:463–467. doi: 10.1038/nsb0697-463. [DOI] [PubMed] [Google Scholar]
- 29.Dunbrack RL., Jr Rotamer libraries in the 21st century. Curr Opin Struct Biol. 2002;12:431–440. doi: 10.1016/s0959-440x(02)00344-5. [DOI] [PubMed] [Google Scholar]
- 30.Babor M, Gerzon S, Raveh B, Sobolev V, Edelman M. Prediction of transition metal-binding sites from apo protein structures. Proteins. 2008;70:208–217. doi: 10.1002/prot.21587. [DOI] [PubMed] [Google Scholar]
- 31.Pidcock E, Moore GR. Structural characteristics of protein binding sites for calcium and lanthanide ions. J Biol Inorg Chem. 2001;6:479–489. doi: 10.1007/s007750100214. [DOI] [PubMed] [Google Scholar]
- 32.Bertini I, Lee YM, Luchinat C, Piccioli M, Poggi L. Locating the metal ion in calcium-binding proteins by using cerium(III) as a probe. Chembiochem. 2001;2:550–558. doi: 10.1002/1439-7633(20010803)2:7/8<550::AID-CBIC550>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 33.Ames JB, Hendricks KB, Strahl T, Huttner IG, Hamasaki N, Thorner J. Structure and calcium-binding properties of Frq1, a novel calcium sensor in the yeast Saccharomyces cerevisiae. Biochemistry. 2000;39:12149–12161. doi: 10.1021/bi0012890. [DOI] [PubMed] [Google Scholar]
- 34.Schneider M, Fu X, Keating AE. X-ray vs. NMR structures as templates for computational protein design. Proteins. 2009;77:97–110. doi: 10.1002/prot.22421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhou Y, Yang W, Kirberger M, Lee HW, Ayalasomayajula G, Yang JJ. Prediction of EF-hand calcium-binding proteins and analysis of bacterial EF-hand proteins. Proteins. 2006;65:643–655. doi: 10.1002/prot.21139. [DOI] [PubMed] [Google Scholar]
- 36.Lin H, Han L, Zhang H, Zheng C, Xie B, Cao Z, Chen Y. Prediction of the functional class of metal-binding proteins from sequence derived physicochemical properties by support vector machine approach. BMC Bioinformatics. 2006;7(Suppl 5):S13. doi: 10.1186/1471-2105-7-S5-S13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lin C-T, Lin K-L, Yang C-H, Chung I-F, Huang C-D, Yang Y-S. Protein metal binding residue prediction based on neural networks. Intl J Neural Systems. 2005;15:71–84. doi: 10.1142/S0129065705000116. [DOI] [PubMed] [Google Scholar]
- 38.Sodhi JS, Bryson K, McGuffin LJ, Ward JJ, Wernisch L, Jones DT. Predicting metal-binding site residues in low-resolution structural models. J Mol Biol. 2004;342:307–320. doi: 10.1016/j.jmb.2004.07.019. [DOI] [PubMed] [Google Scholar]
- 39.Halperin I, Ma B, Wolfson H, Nussinov R. Principles of docking: an overview of search algorithms and a guide to scoring functions. Proteins. 2002;47:409–443. doi: 10.1002/prot.10115. [DOI] [PubMed] [Google Scholar]
- 40.Perola E, Walters WP, Charifson PS. A detailed comparison of current docking and scoring methods on systems of pharmaceutical relevance. Proteins. 2004;56:235–249. doi: 10.1002/prot.20088. [DOI] [PubMed] [Google Scholar]
- 41.Seebeck B, Reulecke I, Kamper A, Rarey M. Modeling of metal interaction geometries for protein-ligand docking. Proteins. 2008;71:1237–1254. doi: 10.1002/prot.21818. [DOI] [PubMed] [Google Scholar]
- 42.Ferrara P, Gohlke H, Price DJ, Klebe G, Brooks CL., III Assessing scoring functions for protein-ligand interactions. J Med Chem. 2004;47:3032–3047. doi: 10.1021/jm030489h. [DOI] [PubMed] [Google Scholar]
- 43.Zhang Y, Arakaki AK, Skolnick J. TASSER: an automated method for the prediction of protein tertiary structures in CASP6. Proteins. 2005;61(Suppl 7):91–98. doi: 10.1002/prot.20724. [DOI] [PubMed] [Google Scholar]
- 44.Gunasekaran K, Nussinov R. How different are structurally flexible and rigid binding sites? Sequence and structural features discriminating proteins that do and do not undergo conformational change upon ligand binding. J Mol Biol. 2007;365:257–273. doi: 10.1016/j.jmb.2006.09.062. [DOI] [PubMed] [Google Scholar]
- 45.Bron C, Kerbosch J. Algorithm 457: finding all cliques of an undirected graph. Commun ACM. 1973;16:575–579. [Google Scholar]
- 46.DeLano WL. The PyMOL molecular graphics system. Palo Alto, CA: DeLano Scientific; 2002. [Google Scholar]


